Reduced Chemical Kinetic Reaction Mechanism for Dimethyl Ether-Air Combustion
Abstract
:1. Introduction
2. Mechanism Development
2.1. Mechanism Development Methodology
2.2. Base Mechanism
2.3. Fuel Breakdown Reactions
2.4. Intermediate Hydrocarbon Oxidation
3. Modelling Details
4. Mechanism Validation
4.1. Laminar Burning Velocity
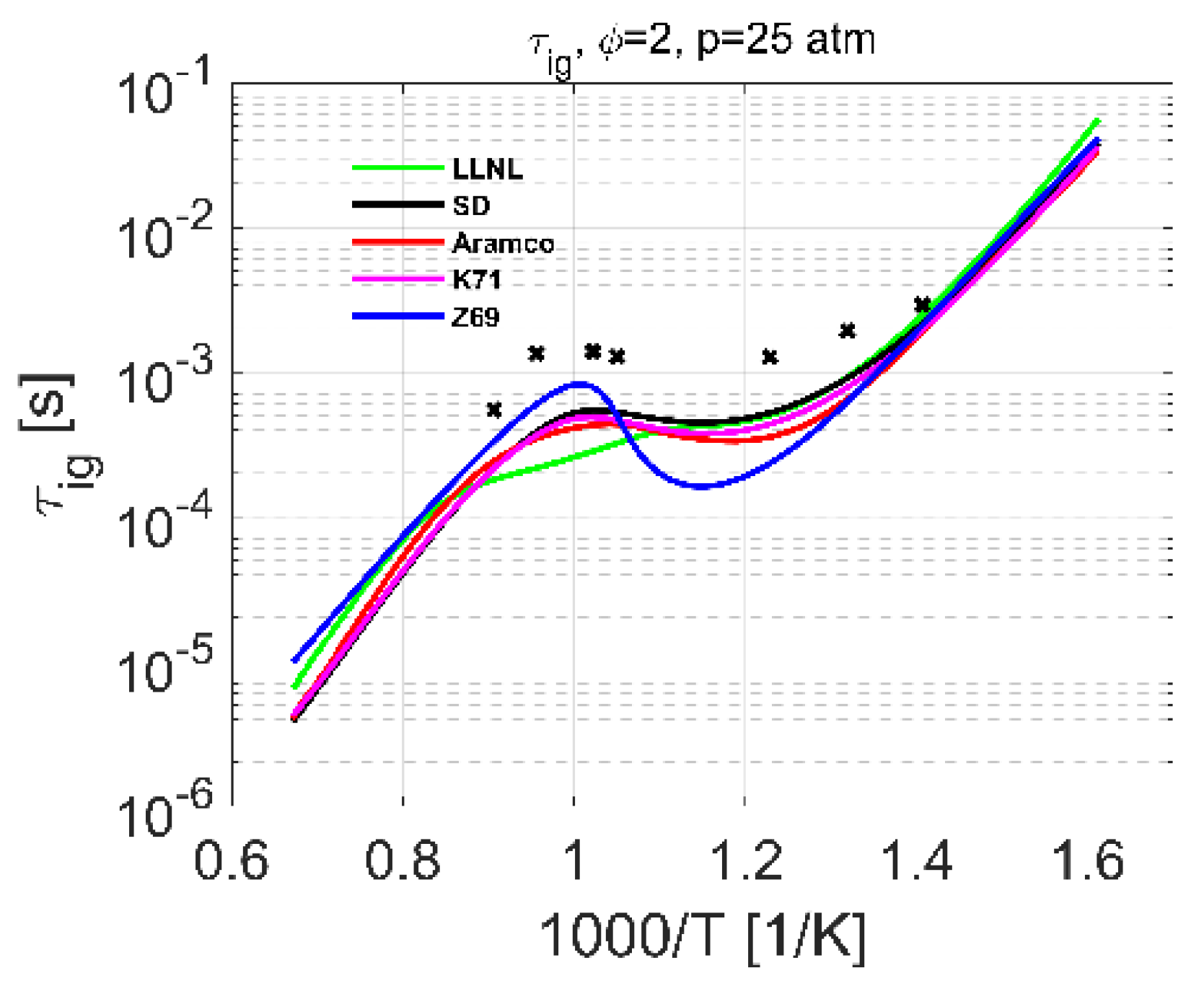
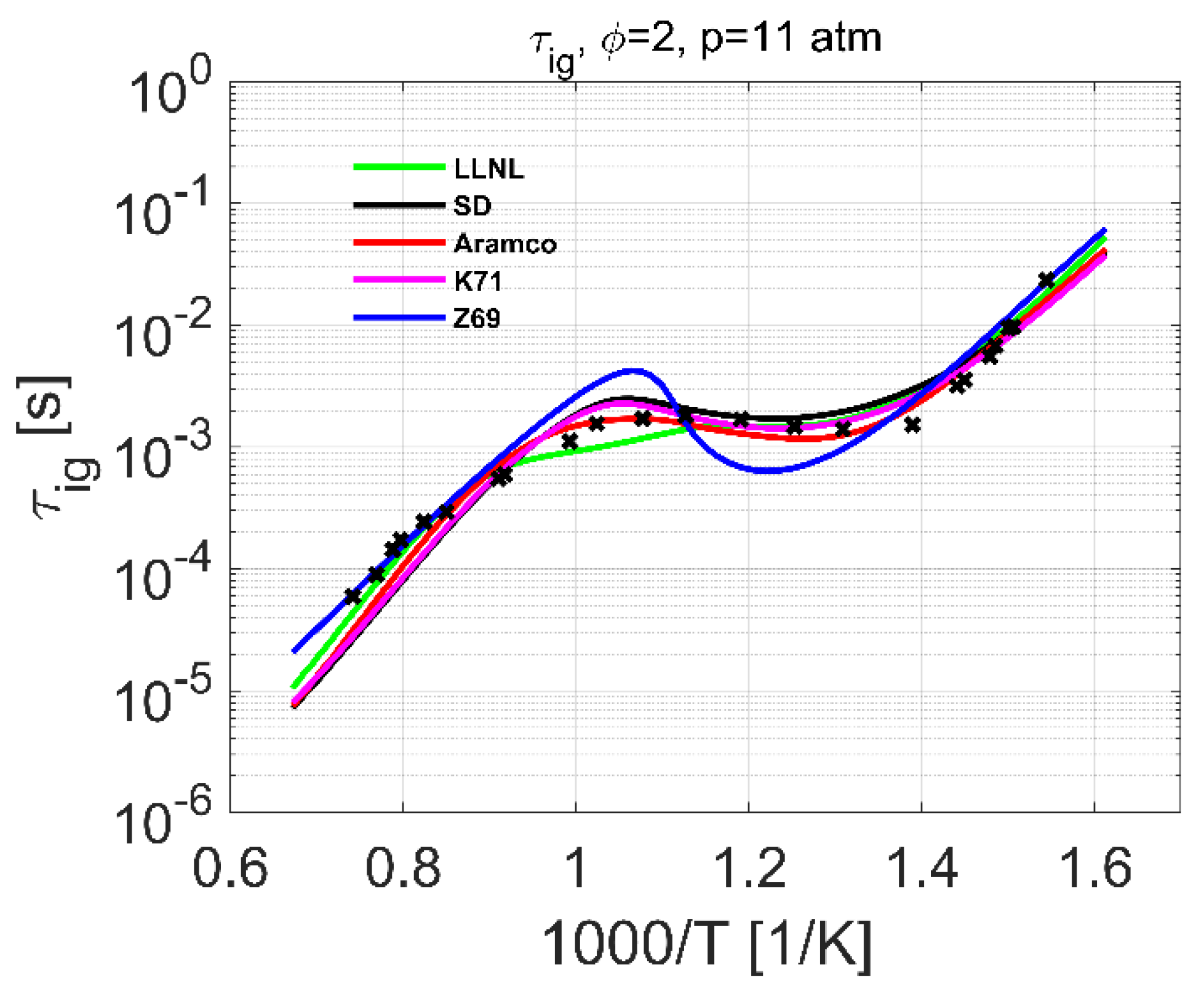
4.2. Ignition Delay Time
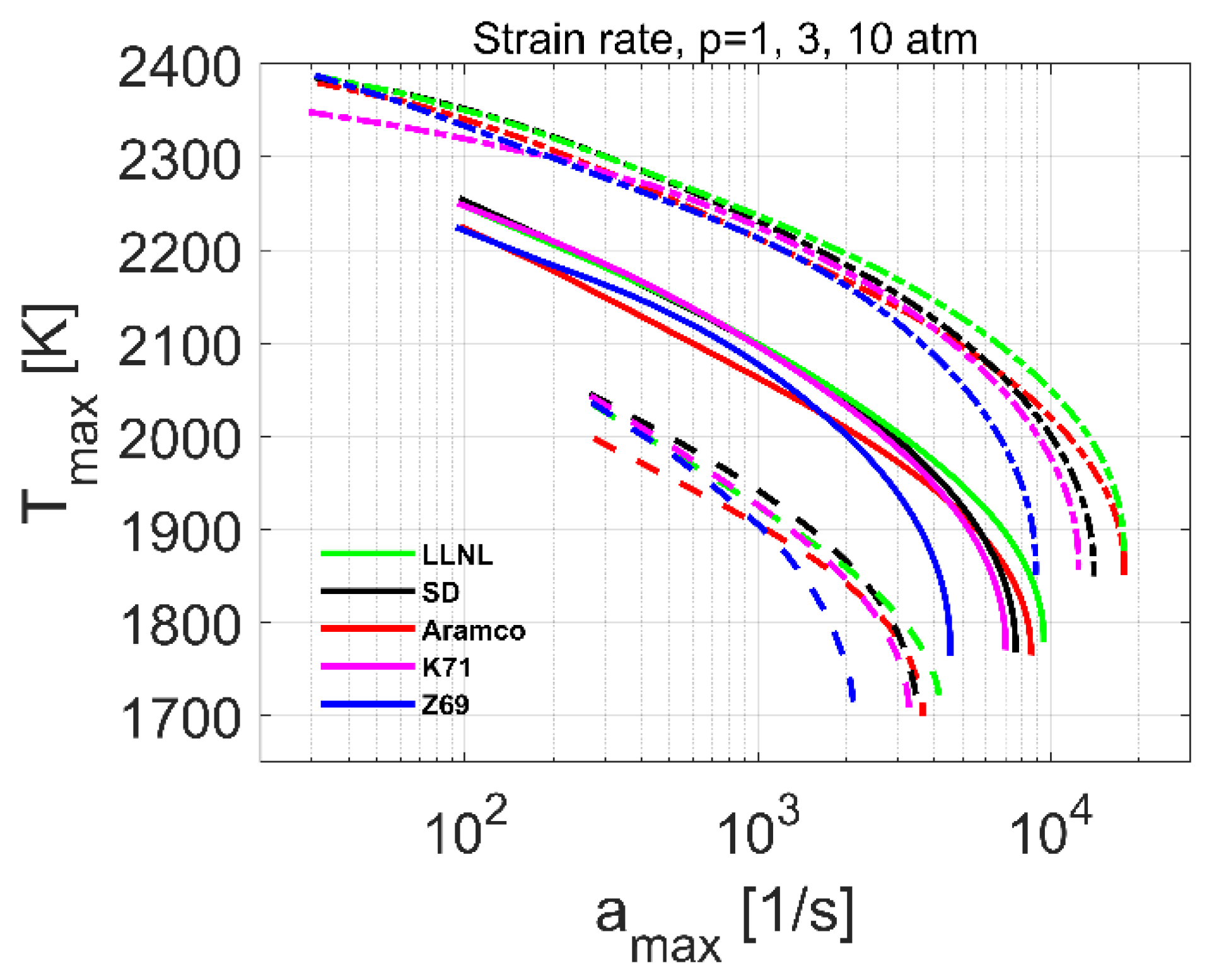
4.3. Extinction Strain Rate
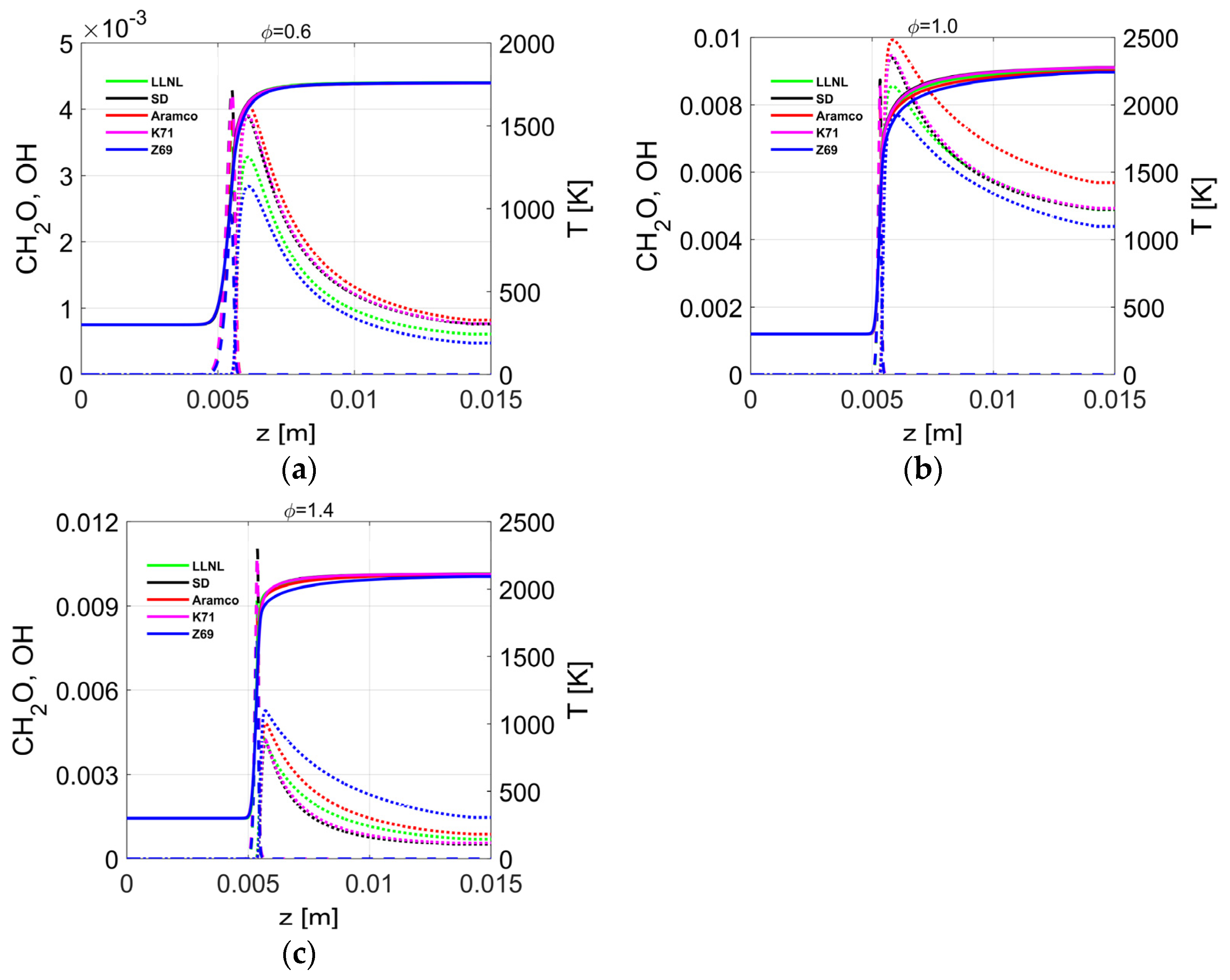
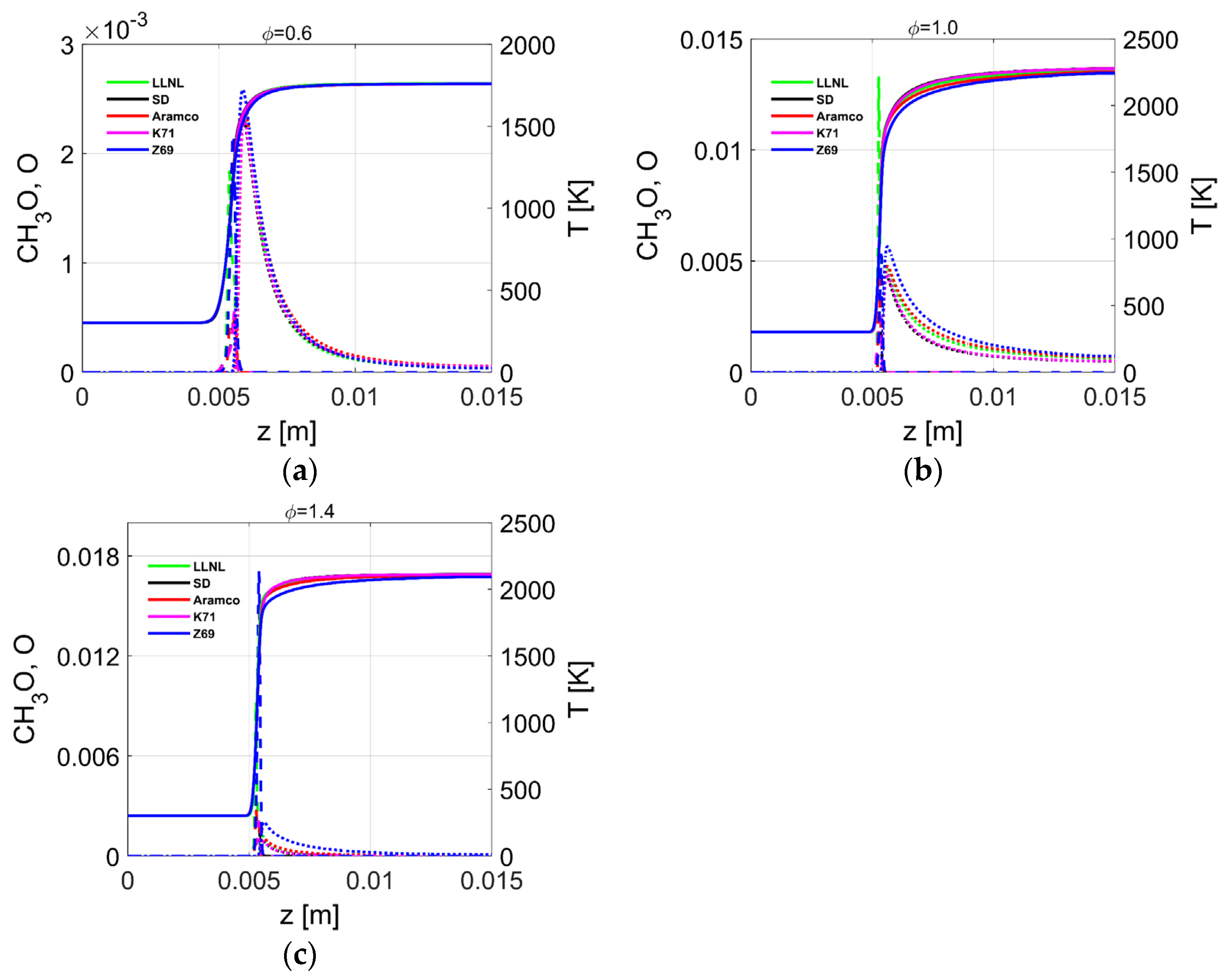
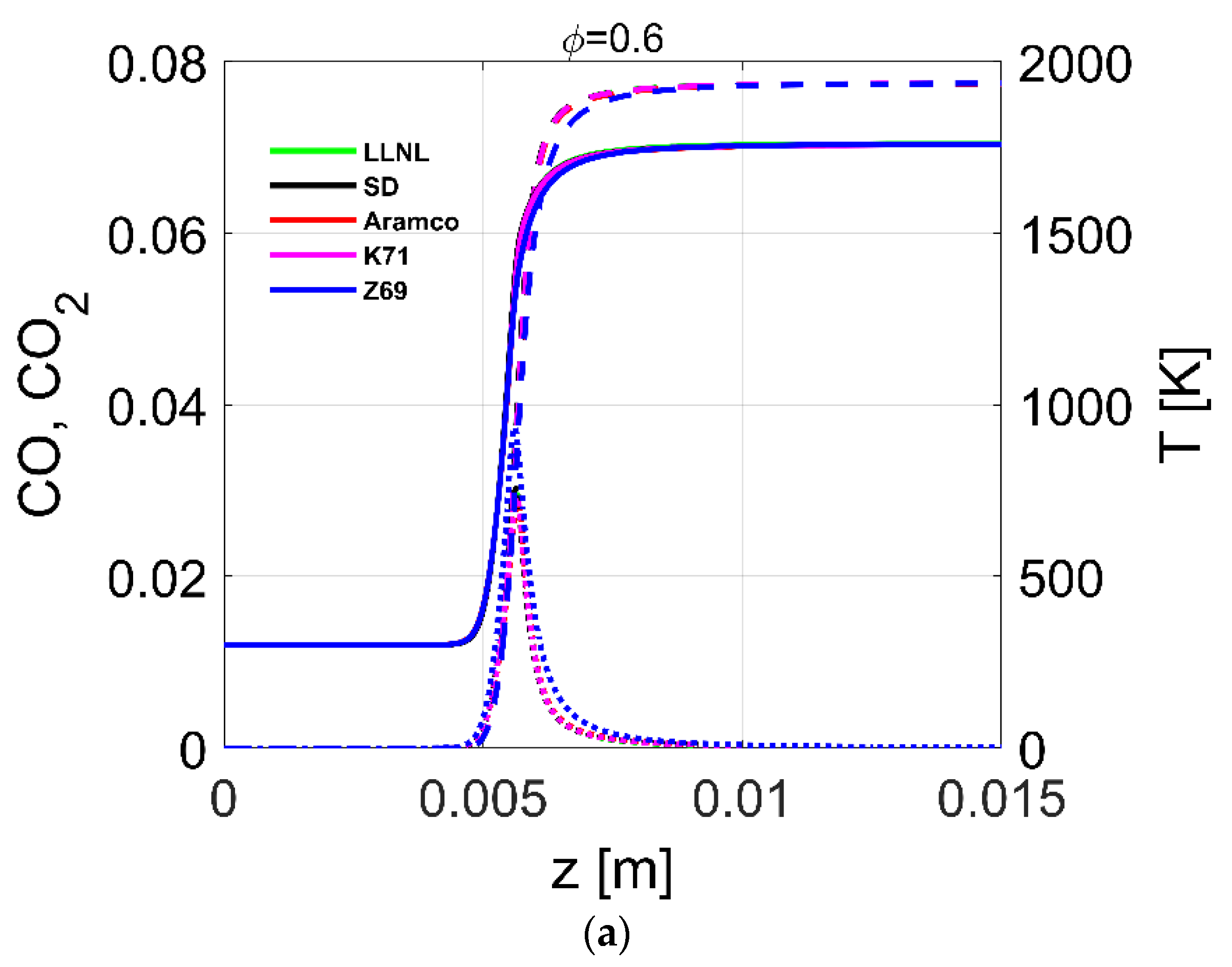
4.4. Flame Profiles
5. Summary and Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Semelsberger, T.A.; Borup, R.L.; Greene, H.L. Dimethyl Ether (DME) as an Alternative Fuel. J. Power Sources 2006, 156, 497–511. [Google Scholar] [CrossRef]
- Ying, W.; Longbao, Z. Performance and Emissions of a Compression-Ignition Engine Fueled with Dimethyl Ether and Rapeseed Oil Blends. Energy Fuels 2007, 21, 1454–1458. [Google Scholar] [CrossRef]
- Ying, W.; Genbao, L.; Wei, Z.; Longbao, Z. Study on the Application of DME/Diesel Blends in a Diesel Engine. Fuel Process. Technol. 2008, 89, 1272–1280. [Google Scholar] [CrossRef]
- Ying, W.; Longbao, Z.; Hewu, W. Diesel Emission Improvements by the Use of Oxygenated DME/Diesel Blend Fuels. Atmos. Environ. 2006, 40, 2313–2320. [Google Scholar] [CrossRef]
- Longbao, Z.; Hewu, W.; Deming, J.; Zuohua, H. Study of Performance and Combustion Characteristics of a DME-Fueled Light-Duty Direct-Injection Diesel Engine; SAE Technical Paper: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Kapus, P.; Ofner, H. Development of Fuel Injection Equipment and Combustion System for DI Diesels Operated on Dimethyl Ether; SAE Technical Paper: Warrendale, PA, USA, 1995. [Google Scholar] [CrossRef]
- Lee, M.C.; Seo, S.B.; Chung, J.H.; Joo, Y.J.; Ahn, D.H. Industrial Gas Turbine Combustion Performance Test of DME to Use as an Alternative Fuel for Power Generation. Fuel 2009, 88, 657–662. [Google Scholar] [CrossRef]
- Kobayashi, N.; Inoue, H.; Koizumi, H. Robust Design of the Coaxial Jet Cluster Nozzle Burner for DME Fuel. In Proceedings of the ASME Turbo EXPO, Atlanta, GA, USA, 16–19 June 2003; p. 38410. [Google Scholar]
- Gökalp, I.; Lebas, E. Alternative Fuels for Industrial Gas Turbines (AFTUR). Appl. Therm. Eng. 2004, 24, 1655–1663. [Google Scholar] [CrossRef]
- Oh, C.; Jang, J.; Bae, C. The Effect of LPG Composition on Combustion and Performance in a DME-LPG Dual-Fuel HCCI Engine; SAE Technical Paper: Warrendale, PA, USA, 2010. [Google Scholar] [CrossRef]
- Yeom, K.; Bae, C. Knock Characteristics in Liquefied Petroleum Gas (LPG)_dimethyl Ether (DME) and Gasoline-DME Homogeneous Charge Compression Ignition Engines. Energy Fuels 2009, 23, 1956–1964. [Google Scholar] [CrossRef]
- Song, R.; Li, K.; Feng, Y.; Liu, S. Performance and Emission Characteristics of DME Engine with High Ratio of EGR. Energy Fuels 2009, 23, 5460–5466. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Cao, C.; Elliott, D.C.; Stevens, D.J.; White, J.F. Conversion of Biomass Syngas to DME Using a Microchannel Reactor. Ind. Eng. Chem. Res. 2005, 44, 1722–1727. [Google Scholar] [CrossRef]
- Adachi, Y.; Komoto, M.; Watanabe, I.; Ohno, Y.; Fujimoto, K. Effective Utilization of Remote Coal through Dimethyl Ether Synthesis. Fuel 2000, 79, 229–234. [Google Scholar] [CrossRef]
- Jiang, X.; Tian, Z.; Zhang, Y.; Huang, Z. Shock Tube Measurement and Simulation of DME/n-Butane/Air Mixtures: Effect of Blending in the NTC Region. Fuel 2017, 203, 316–329. [Google Scholar] [CrossRef]
- Warnatz, J.; Maas, U.; Dibble, R.W. Combustion, 5th ed.; Springer: Berlin, Germany, 1999; Volume 26. [Google Scholar]
- Burke, U.; Somers, K.P.; O′Toole, P.; Zinner, C.M.; Marquet, N.; Bourque, G.; Petersen, E.L.; Metcalfe, W.K.; Serinyel, Z.; Curran, H.J. An Ignition Delay and Kinetic Modeling Study of Methane, Dimethyl Ether, and Their Mixtures at High Pressures. Combust. Flame 2015, 162, 315–330. [Google Scholar] [CrossRef] [Green Version]
- Pope, S.B. Small Scales, Many Species and the Manifold Challenges of Turbulent Combustion. Proc. Combust. Inst. 2013, 34, 1–31. [Google Scholar] [CrossRef]
- Bourque, G.; Healy, D.; Curran, H.; Zinner, C.; Kalitan, D.; De Vries, J.; Aul, C.; Petersen, E. Ignition and Flame Speed Kinetics of Two Natural Gas Blends with High Levels of Heavier Hydrocarbons. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Lieuwen, T.C.; Yang, V. Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms, and Modeling; AIAA: Danvers, MA, USA, 2005. [Google Scholar]
- Daly, C.A.; Simmie, J.M.; Würmel, J.; Djeballi, N.; Paillard, C. Burning Velocities of Dimethyl Ether and Air. Combust. Flame 2001, 125, 1329–1340. [Google Scholar] [CrossRef]
- Zhao, Z.; Kazakov, A.; Dryer, F.L. Measurements of Dimethyl Ether/Air Mixture Burning Velocities by Using Particle Image Velocimetry. Combust. Flame 2004, 139, 52–60. [Google Scholar] [CrossRef]
- Qin, X.; Ju, Y. Measurements of Burning Velocities of Dimethyl Ether and Air Premixed Flames at Elevated Pressures. Proc. Combust. Inst. 2005, 30, 233–240. [Google Scholar] [CrossRef]
- Jomaas, G. An Experimental Study on the Laminar Burning Velocities and Stability Boundaries of Outwardly Propagating Spherical Flames. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2005. [Google Scholar]
- Wang, Y.L.; Holley, A.T.; Ji, C.; Egolfopoulos, F.N.; Tsotsis, T.T.; Curran, H.J. Propagation and Extinction of Premixed Dimethyl-Ether/Air Flames. Proc. Combust. Inst. 2009, 32, 1035–1042. [Google Scholar] [CrossRef]
- De Vries, J.; Lowry, W.B.; Serinyel, Z.; Curran, H.J.; Petersen, E.L. Laminar Flame Speed Measurements of Dimethyl Ether in Air at Pressures up to 10 Atm. Fuel 2011, 90, 331–338. [Google Scholar] [CrossRef]
- Zhao, Z.; Chaos, M.; Kazakov, A.; Dryer, F.L. Thermal Decomposition Reaction and a Comprehensive Kinetic Model of Dimethyl Ether. Int. J. Chem. Kinet. 2008, 40, 1–18. [Google Scholar] [CrossRef]
- Fischer, S.L.; Dryer, F.L.; Curran, H.J. The Reaction Kinetics of Dimethyl Ether. I: High-temperature Pyrolysis and Oxidation in Flow Reactors. Int. J. Chem. Kinet. 2000, 32, 713–740. [Google Scholar] [CrossRef]
- Curran, H.J.; Fischer, S.L.; Dryer, F.L. The Reaction Kinetics of Dimethyl Ether. II: Low-temperature Oxidation in Flow Reactors. Int. J. Chem. Kinet. 2000, 32, 741–759. [Google Scholar] [CrossRef]
- “Chemical-Kinetic Mechanisms for Combustion Applications”, San Diego Mechanism Web Page; Mechanical and Aerospace Engineering (Combustion Research), University of California at San Diego: La Jolla, CA, USA, 2011; Available online: http://combustion.ucsd.edu (accessed on 29 August 2018).
- Bolshova, T.; Shvartsberg, V.; Dmitriev, A.; Knyazkov, D. Flame Structure and a Compact Reaction Mechanism for Combustion of Dimethyl Ether at Atmospheric Pressure. Fuel 2019, 255, 115752. [Google Scholar] [CrossRef]
- Khare, R.S.; Parimalanathan, S.K.; Raghavan, V.; Narayanaswamy, K. A Comprehensively Validated Compact Mechanism for Dimethyl Ether Oxidation: An Experimental and Computational Study. Combust. Flame 2018, 196, 116–128. [Google Scholar] [CrossRef]
- Pan, L.; Kokjohn, S.; Huang, Z. Development and Validation of a Reduced Chemical Kinetic Model for Dimethyl Ether Combustion. Fuel 2015, 160, 165–177. [Google Scholar] [CrossRef]
- Gicquel, L.Y.; Staffelbach, G.; Poinsot, T. Large Eddy Simulations of Gaseous Flames in Gas Turbine Combustion Chambers. Prog. Energy Combust. Sci. 2012, 38, 782–817. [Google Scholar] [CrossRef] [Green Version]
- Larsson, A.; Zettervall, N.; Hurtig, T.; Nilsson EJ, K.; Ehn, A.; Petersson, P.M.; Alden Larfeldt, J.; Fureby, C. Skeletal Methane—Air Reaction Mechanism for Large Eddy Simulation of Turbulent Microwave-Assisted Combustion. Energy Fuels 2017, 31, 1904–1926. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C. A Computational Study of Ramjet, Scramjet and Dual-Mode Ramjet Combustion in Combustor with a Cavity Flameholder. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1146. [Google Scholar]
- Zettervall, N. Methodology for Developing Reduced Reaction Mechanisms, and Their Use in Combustion Simulations. Ph.D. Thesis, Lund University, Lund, Sweden, 2021. [Google Scholar]
- Battin-Leclerc, F.; Simmie, J.M.; Blurock EBattin-Leclerc, F.; Simmie, J.M.; Blurock, E. Cleaner Combustion. Developing Detailed Chemical Kinetic Models. In Green Energy and Technology; Springer: Berlin, Germany, 2013. [Google Scholar]
- Wang, H.; Xu, R.; Wang, K.; Bowman, C.T.; Davidson, D.F.; Hanson, R.K.; Bre-zinsky, K.; Egolfopoulos, F.N. A Physics-Based Approach to Modeling Real-Fuel Combustion Chemistry-I. Evidence from Experiments, and Thermodynamic, Chemical Kinetic and Statistical Considerations. Combust. Flame 2018, 193, 502–519. [Google Scholar] [CrossRef]
- Bulat, G.; Fedina, E.; Fureby, C.; Meier, W.; Stopper, U. Reacting Flow in an Industrial Gas Turbine Combustor: LES and Experimental Analysis. Proc. Combust. Inst. 2015, 35, 3175–3183. [Google Scholar] [CrossRef]
- Zettervall, N.; Fedina, E.; Nordin-Bates, K.; Heimdal Nilsson, E.; Fureby, C. Combustion LES of a Multi-Burner Annular Aeroengine Combustor Using a Skeletal Reaction Mechanism for Jet-A Air Mixtures. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015; p. 4020. [Google Scholar]
- Zettervall, N.; Worth, N.A.; Mazur, M.; Dawson, J.R.; Fureby, C. Large Eddy Simulation of CH4-Air and C2H4-Air Combustion in a Model Annular Gas Turbine Combustor. Proc. Proc. Combust. Institute. 2019, 37, 5223–5231. [Google Scholar] [CrossRef]
- Zettervall, N.; Nordin-Bates, K.; Nilsson EJ, K.; Fureby, C. Large Eddy Simulation of a Premixed Bluff Body Stabilized Flame Using Global and Skeletal Reaction Mechanisms. Combust. Flame 2017, 179, 1–22. [Google Scholar] [CrossRef]
- Liu, B.; He, G.Q.; Qin, F.; An, J.; Wang, S.; Shi, L. Investigation of Influence of Detailed Chemical Kinetics Mechanisms for Hydrogen on Supersonic Combustion Using Large Eddy Simulation. Int. J. Hydrog. Energy 2019, 44, 5007–5019. [Google Scholar] [CrossRef]
- Fureby, C. A Comparative Study of Subgrid Models, Reaction Mechanisms and Combustion Models in LES of Supersonic Combustion. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; Volume AIAA-4273, p. 4273. [Google Scholar]
- Vincent-Randonnier, A.; Sabelnikov, V.; Ristori, A.; Zettervall, N.; Fureby, C. An Experimental and Computational Study of Hydrogen–Air Combustion in the LAPCAT II Supersonic Combustor. Proc. Combust. Inst. 2019, 37, 3703–3711. [Google Scholar] [CrossRef]
- Vincent-Randonnier, A.; Sabelnikov, V.; Ristori, A.; Zettervall, N.; Fureby, C. A Combined Experimental and Computational Study of the LAPCAT II Supersonic Combustor. In Proceedings of the 22nd AIAA International Space Planes and Hypersonics Systems and Technologies Conference, Orlando, FL, USA, 17–19 September 2018; p. 5208. [Google Scholar]
- Danel, K.; Zettervall, N.; Fureby, C. A Combined Experimental and Computational Study of Jet Engine Combustion–Baseline Engine Operation. In AIAA Propulsion and Energy; AIAA: Indianapolis, Indiana, 2019; p. 4328. [Google Scholar]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. Small Skeletal Kinetic Reaction Mechanism for Ethylene—Air Combustion. Energy Fuels 2017, 31, 14138–14149. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. Small Skeletal Kinetic Mechanism for Kerosene Combustion. Energy Fuels 2016, 30, 9801–9813. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. A Reduced Chemical Kinetic Reaction Mechanism for Kerosene-Air Combustion. Fuel 2020, 269, 117446. [Google Scholar] [CrossRef]
- Smoke, M.D.; Giovangigli, V. Formulation of the premixed and nonpremixed test problems. In Reduced Kinetic Mechanisms and Asymptotic Approximations for Methane-Air Flames; Elsevier: Berlin/Heidelberg, Germany, 1991; pp. 1–28. [Google Scholar]
- Ehn, A.; Zhu, J.J.; Petersson, P.; Li, Z.S.; Aldén, M.; Fureby, C.; Larfeldt, J. Plasma Assisted Combustion: Effects of O3 on Large Scale Turbulent Combustion Studied with Laser Diagnostics and Large Eddy Simulations. Proc. Combust. Inst. 2015, 35, 3487–3495. [Google Scholar] [CrossRef]
- Fureby, C.; Zettervall, N.; Kim, S.; Menon, S. Large Eddy Simulation of a Simplified Lean Premixed Gas Turbine Combustor. In Proceedings of the Ninth International Symposium on Turbulence and Shear Flow Phenomena, Melbourne, Australia, 3–30 June 2015. [Google Scholar]
- Glassman, I.; Yetter, R.A. Combustion, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.5.1. 2021. Available online: https://www.cantera.org (accessed on 4 August 2021).
- Goos, E.; Burcat, A.; Ruscic, B. Extended Third Millenium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables; Elke Goos: Remchingen, Germany, 2015. [Google Scholar]
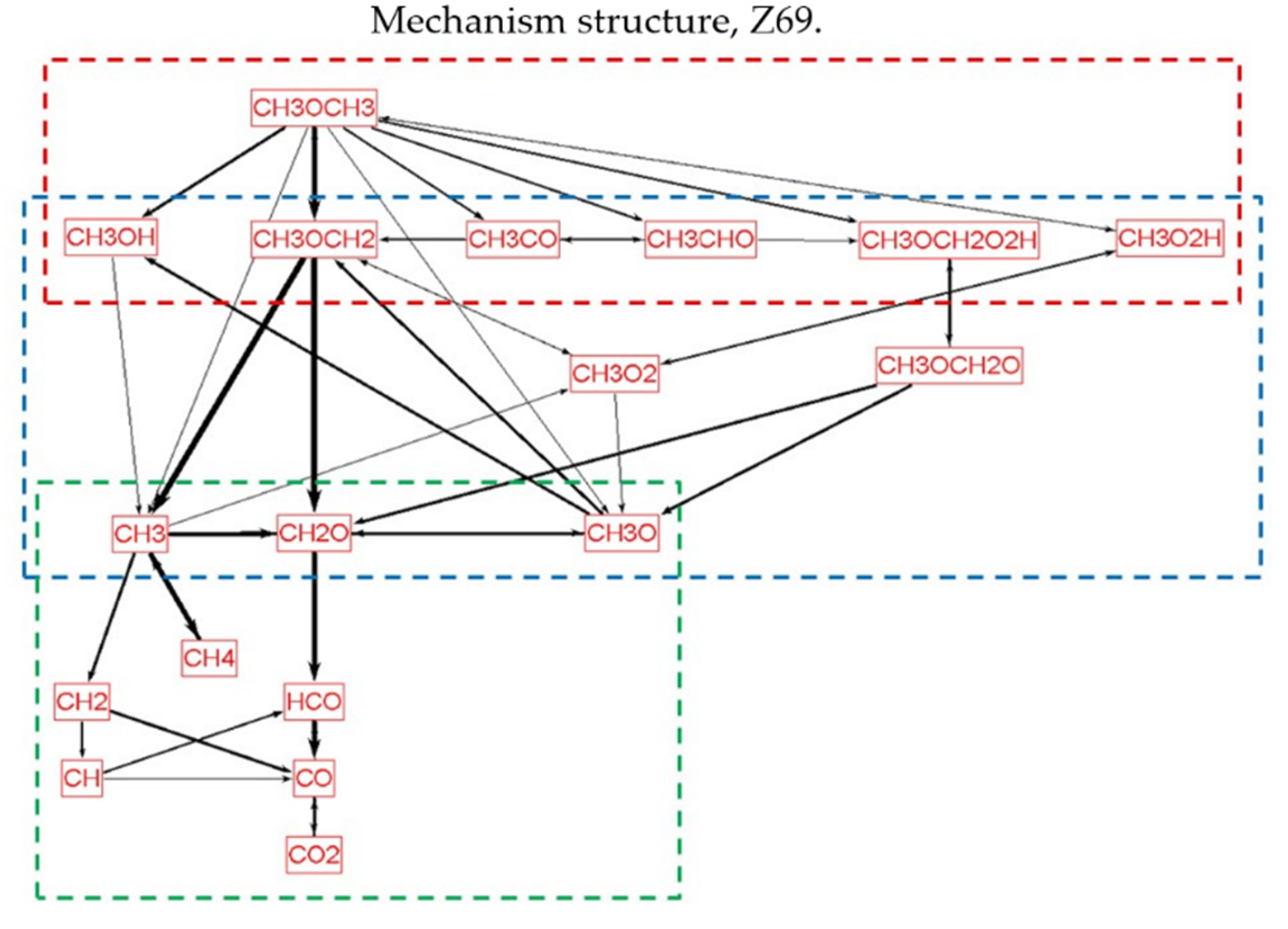
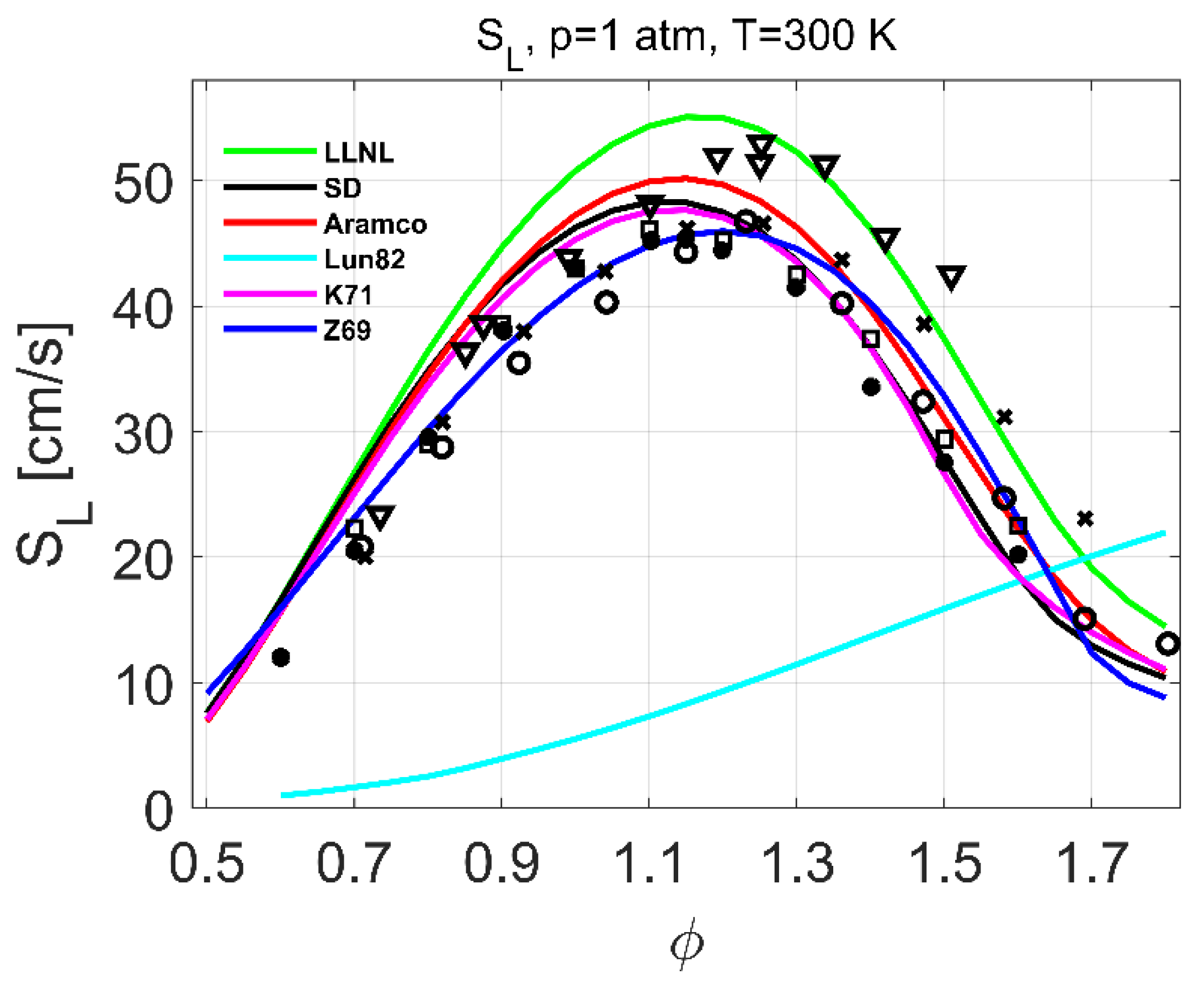
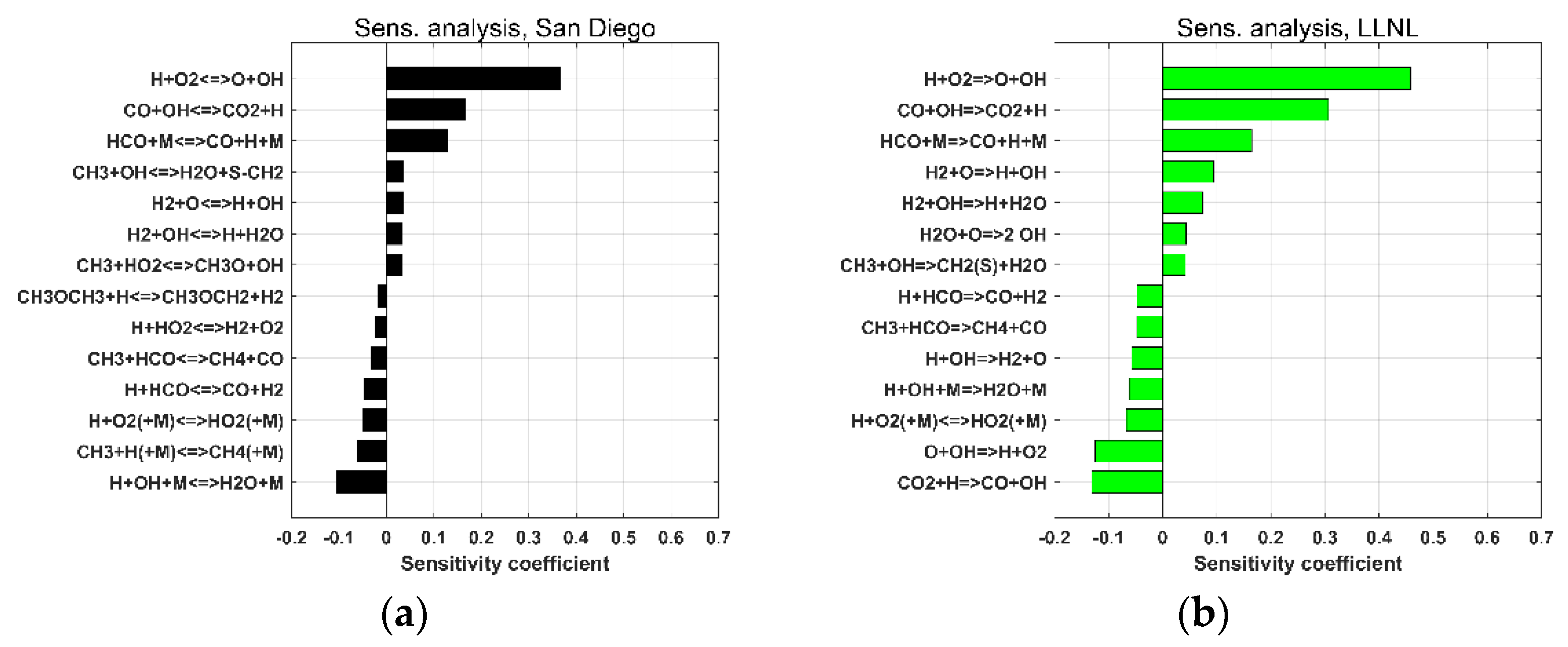
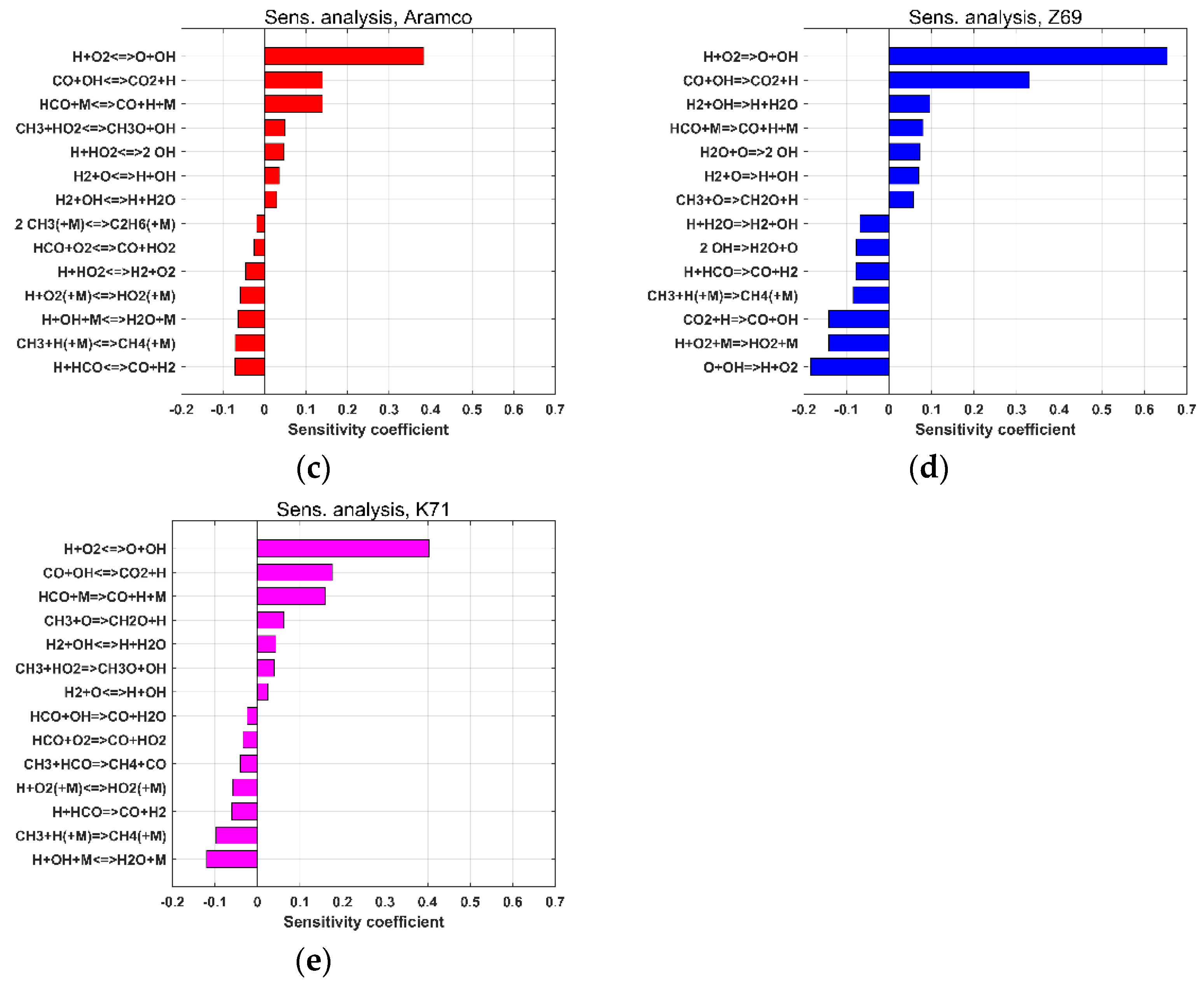
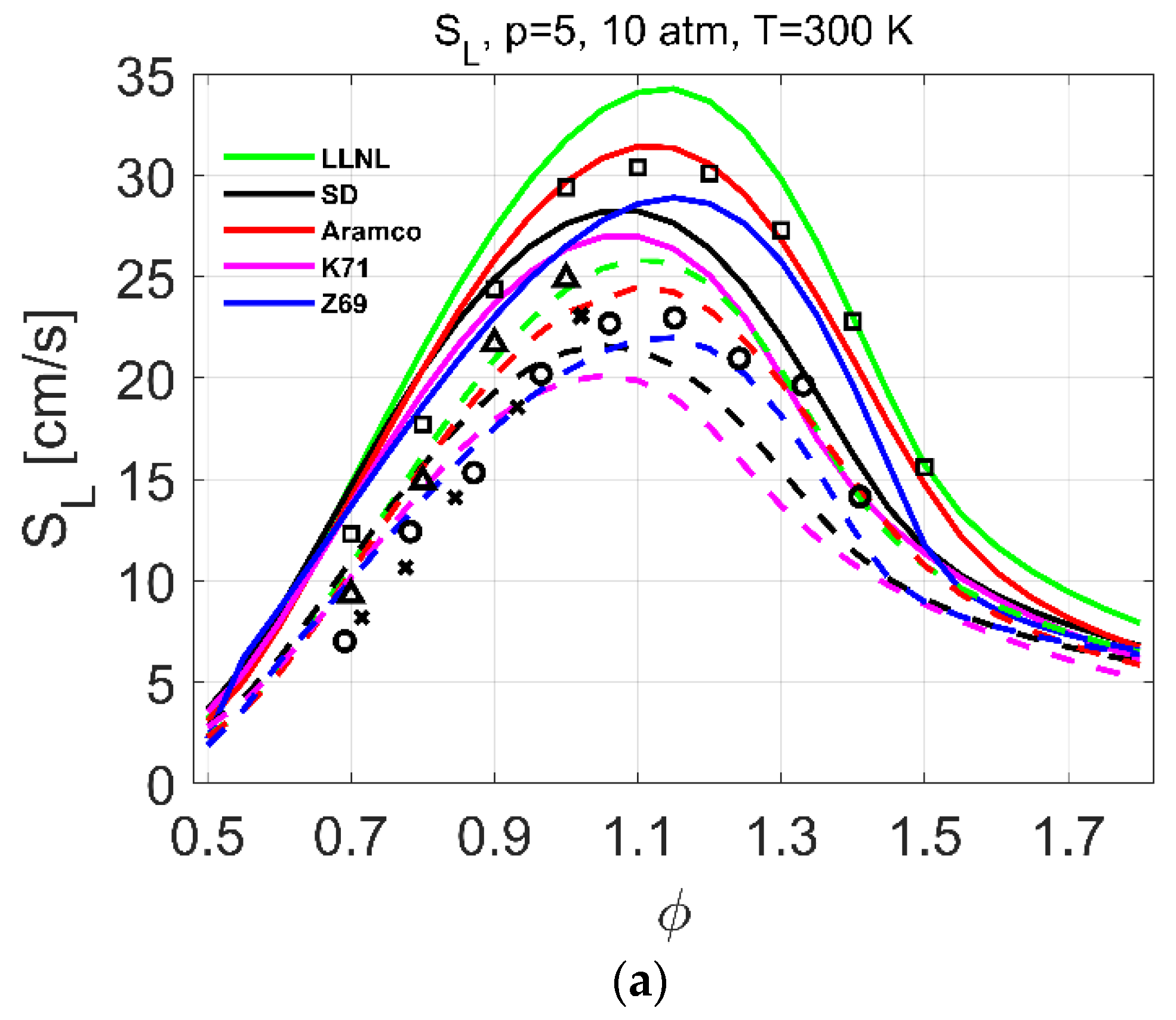
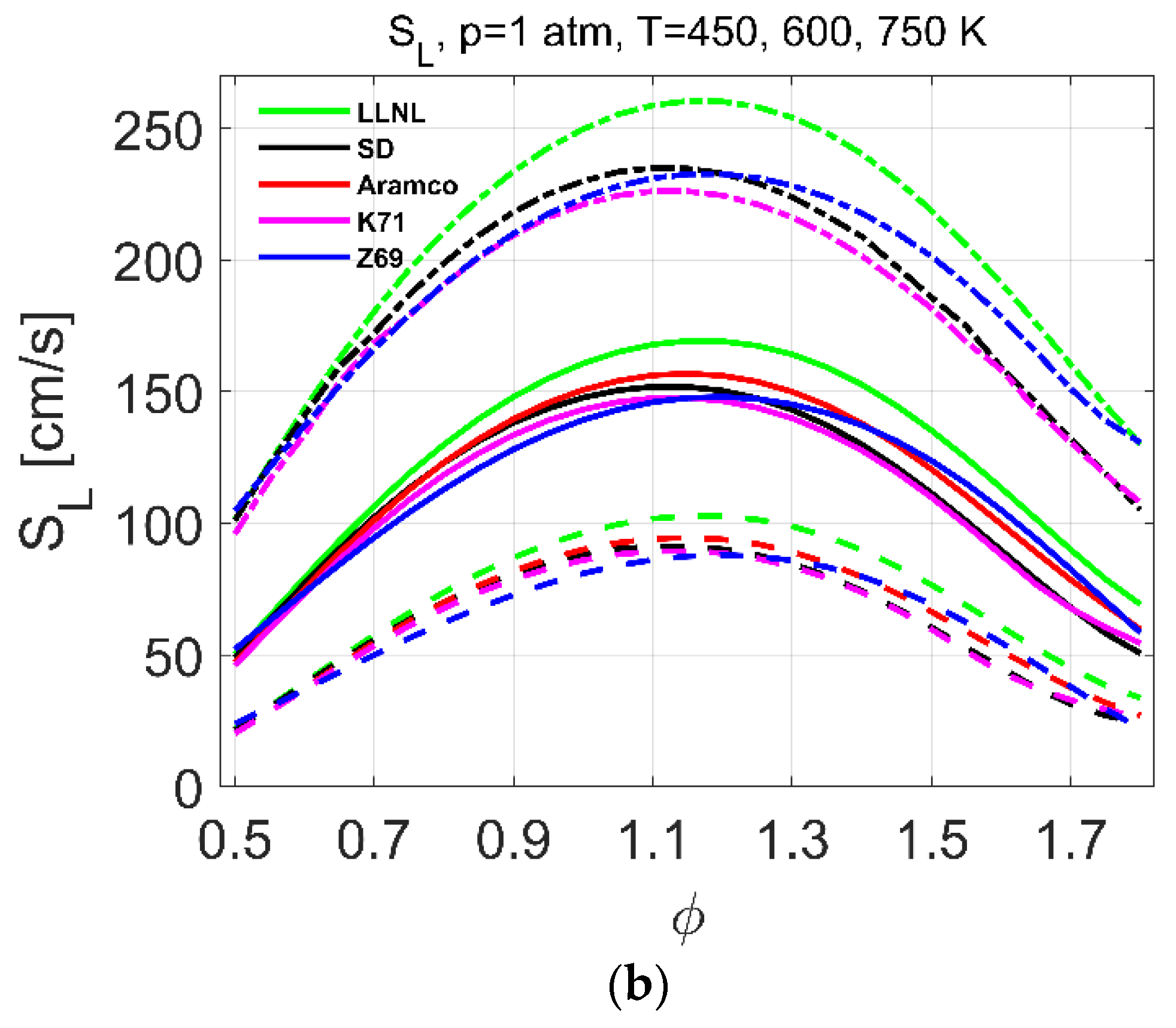
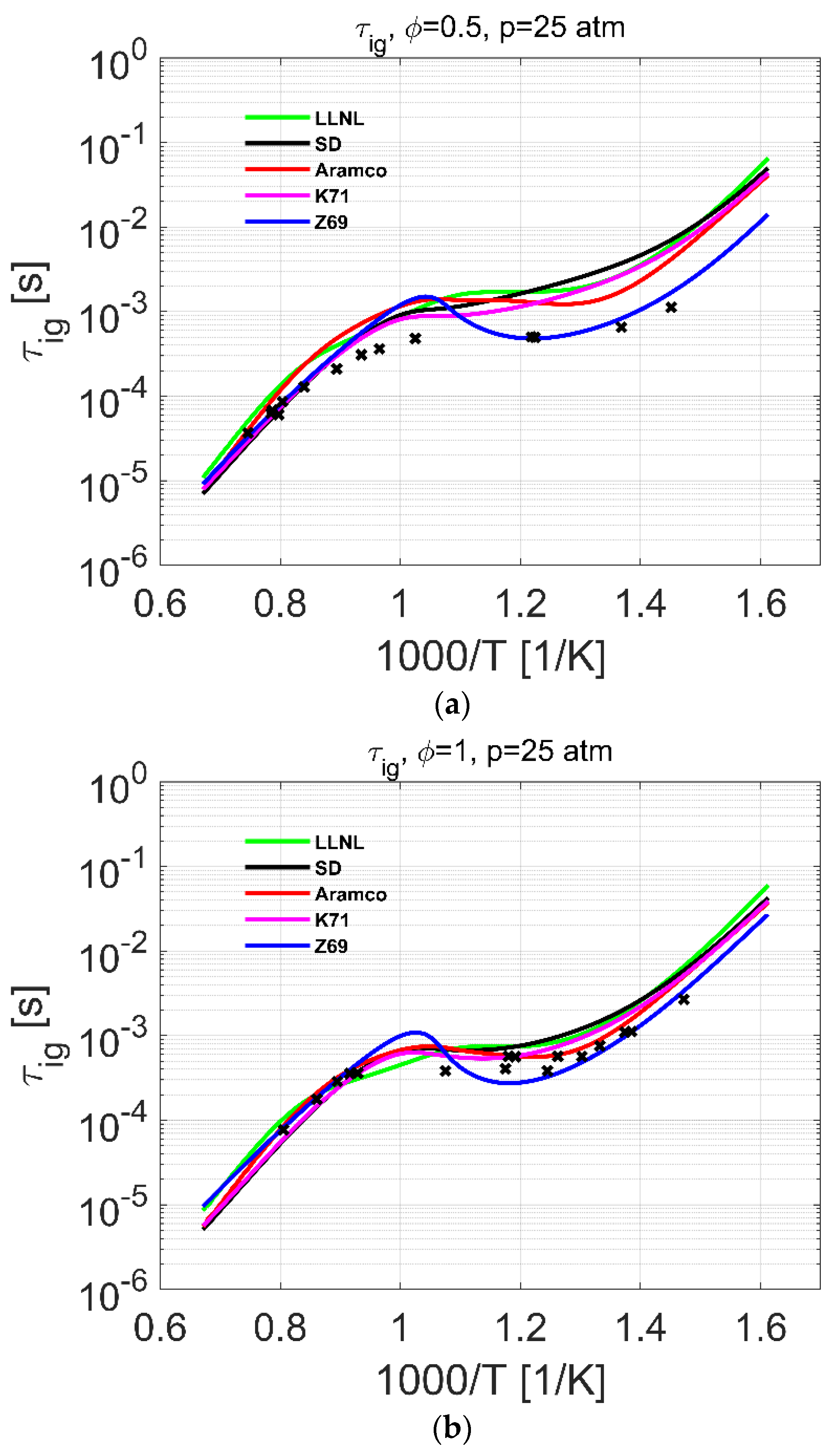

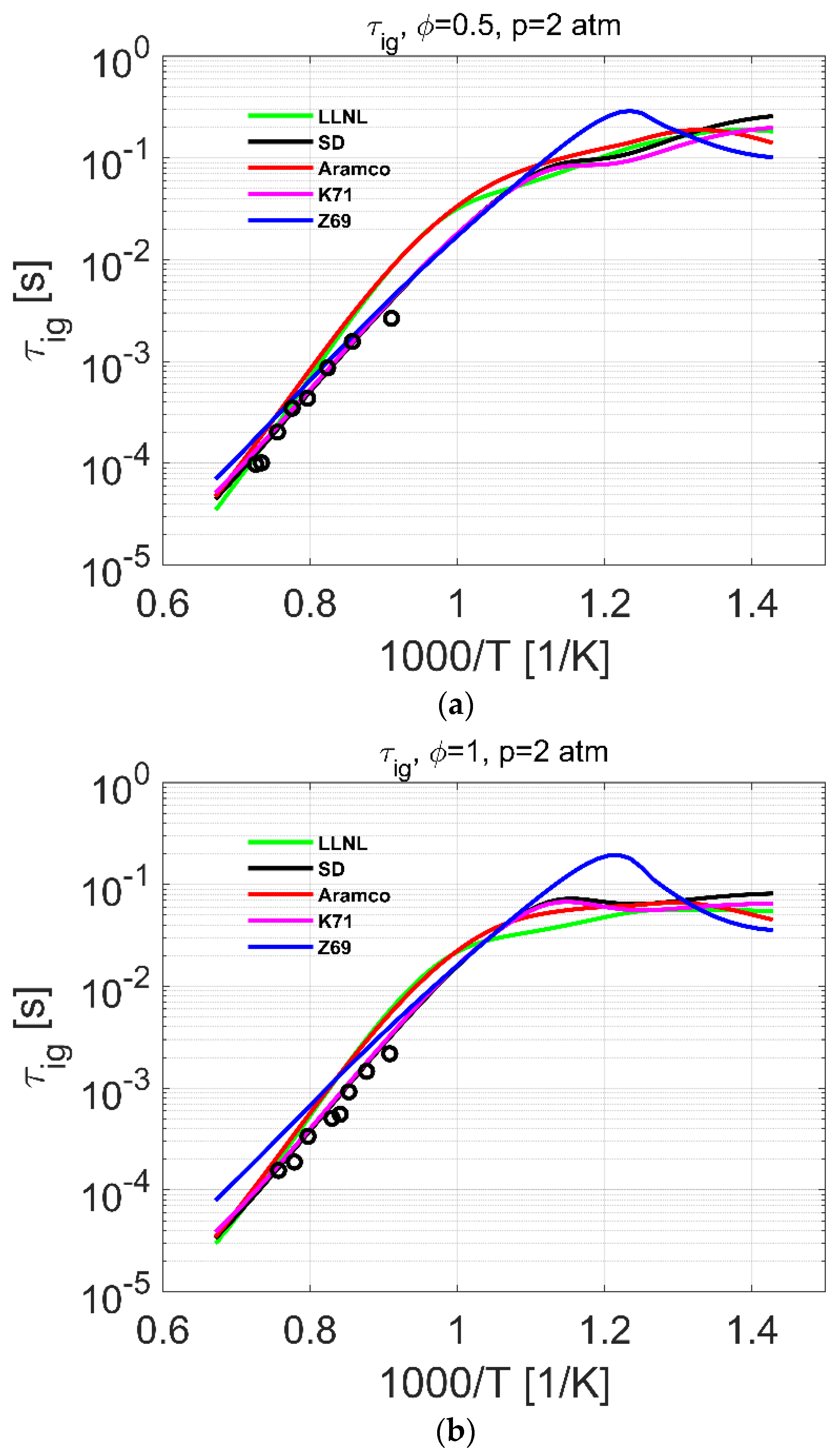

| Reference | Species | Reactions | Validation Targets | |
|---|---|---|---|---|
| Aramco | [17] | 433 | 1004 | FR, JSR, ST-ig, LF-SL, LF-s |
| LLNL | [28] | 79 | 697 | JSR, ST, LF |
| San Diego | [30] | 48 | 284 | JSR, ST, LF |
| P82 | [33] | 27 | 82 | ST-ig, engine emission data |
| K71 | [32] | 26 | 71 | ST-ig, LF-ext |
| Experiments | Reference Simulations | ||||||
|---|---|---|---|---|---|---|---|
| Type | P (atm) | T (K) | ϕ | Ref. | P (atm) | T (K) | ϕ |
| Laminar flames | 1–10 | 298 | 0.7–1.7 | [23] | 1–10 | 300–750 | 0.5–1.8 |
| 1–10 | 298 | 0.7–1.6 | [26] | ||||
| 1 | 293 | 0.6–1.6 | [25] | ||||
| 1 | 298 | 0.7–1.8 | [21] | ||||
| 1 | 298 | 0.7–1.4 | [24] | ||||
| 1 | 298 | 0.7–1.4 | [22] | ||||
| Ignition delay | 2–10 | 700–1400 | 0.5–1.0 | [15] | 2–25 | 600–1500 | 0.5–2.0 |
| 10–25 | 630–1450 | 0.5–2.0 | [17] | ||||
| Extinction strain rate | 1–10 | 300 | 1.0 | ||||
| Reaction | A | N | Ea | Ref. | |
|---|---|---|---|---|---|
| 1 | CH3OCH3 + M → CH3 + CH3O + M f | [17] | |||
| kf | 4.38 × 1021 | −1.57 | 83,890 | ||
| kf0 | 7.52 × 1015 | 0 | 42,790 | ||
| 2 | CH3OCH3 + OH → CH3OCH2 + H2O | 6.32 × 106 | 2.00 | −652 | [17] |
| 3 | CH3OCH3 + H → CH3OCH2 + H2 | 7.72 × 106 | 2.09 | 3384 | [17] |
| 4 | CH3OCH3 + O → CH3OCH2 + OH | 7.75 × 108 | 1.36 | 2250 | [17] |
| 5 | CH3OCH3 + CH3O2 → CH3OCH2 + CH3O2H | 1.68 × 1013 | 0 | 13,690 | [28] |
| 6 | CH3OCH3 + CH3CO → CH3OCH2 + CH3CHO | 7.75 × 1011 | 0.28 | 16,980 | [28] |
| 7 | CH3OCH3 + CH3O → CH3OCH2 + CH3OH | 6.02 × 1011 | 0 | 4074 | [28] |
| 8 | CH3OCH3 + O2 → CH3OCH2 + HO2 | 4.10 × 1013 | 0 | 44,910 | [17] |
| 9 | CH3OCH2 + CH3O2H → CH3OCH3 + CH3O2 | 2.29 × 1014 | −0.8 | 7270 | [28] |
| 10 | CH3OCH2 → CH2O + CH3 | 1.60 × 1013 | 0 | 25,500 | [17] |
| 11 | CH3OCH2 + O2 → CH3OCH2O2 | 2.00 × 1012 | 0 | 0 | [17] |
| 12 | CH3OCH2O2 + CH3OCH2O2 → O2 + CH3OCH2O + CH3OCH2O | 1.55 × 1023 | −4.5 | 0 | [17] |
| 13 | CH3OCH2O2 → CH3OCH2 + O2 | 4.44 × 1019 | −1.59 | 36,240 | [28] |
| 14 | CH3OCH2O2 + CH3CHO → CH3OCH2O2H + CH3CO | 2.80 × 1012 | 0 | 13,600 | [17] |
| 15 | CH3OCH2O2 + CH3OCH3 → CH3OCH2O2H + CH3CO + H2 | 2.80 × 1012 | 0 | 10,600 | a |
| 16 | CH3OCH2O2 → CH2OCH2O2H | 2.20 × 109 | 0 | 10,846 | [32] |
| 17 | CH2OCH2O2H → CH3OCH2O2 | 2.20 × 109 | 0 | 500 | a |
| 18 | CH2OCH2O2H → 2 CH2O + OH | 1.50 × 1013 | 0 | 30,500 | [32], c |
| 19 | CH2OCH2O2H + O2 → HO2CH2OCHO + OH | 2.86 × 1016 | −1.48 | 1873 | [32] |
| 20 | HO2CH2OCHO → CH2O + CO2 + OH + H | 2.50 × 1016 | 0 | 43,000 | [32] |
| 21 | HO2CH2OCHO → CH2O + CO + 2 OH | 2.50 × 1016 | 0 | 38,000 | [32], c |
| 22 | CH3OCH2O + OH → CH3OCH2O2H | 2.00 × 1013 | 0 | 0 | [28] |
| 23 | CH3OCH2O → CH3O + CH2O | 5.18 × 1012 | −0.13 | 19,370 | [28] |
| 24 | CH3OCH2O2H → CH3OCH2O + OH | 4.38 × 1021 | −1.94 | 41,700 | [28], c |
| 25 | CH3O2 + CH3O2 → O2 + CH3O + CH3O | 1.40 × 1016 | −1.61 | 1860 | [28] |
| 26 | CH3OH + M → CH3 + OH + M g | [28] | |||
| kf | 1.90 × 1016 | 0 | 91,730 | ||
| kf0 | 2.95 × 1044 | −7.35 | 95,460 | ||
| 27 | CH3 + O2 + M → CH3O2 + M | 2.40 × 1013 | 0 | 28,812 | a |
| 28 | CH4 (+ M) → CH3 + H (+ M) d | [35] | |||
| kf | 6.30 × 1014 | 0 | 104,000 | ||
| kf0 | 1.00 × 1017 | 0 | 86,000 | ||
| 29 | CH3 + H (+ M) → CH4 (+ M) d | [35] | |||
| kf | 5.20 × 1012 | 0 | −1310 | ||
| kf0 | 8.25 × 1014 | 0 | −19,310 | ||
| 30 | CH4 + H → CH3 + H2 | 2.20 × 104 | 3 | 8750 | [35] |
| 31 | CH3 + H2 → CH4 + H | 9.57 × 102 | 3 | 8750 | [35] |
| 32 | CH4 + OH → CH3 + H2O | 1.60 × 106 | 2.1 | 2460 | [35] |
| 33 | CH3 + H2O → CH4 + OH | 3.02 × 105 | 2.1 | 17,422 | [35] |
| 34 | CH3 + O → CH2O + H | 6.80 × 1013 | 0 | 0 | [35] |
| 35 | CH3 + O2 → CH3O + O | 3.00 × 1013 | 0 | 25,652 | [35], b |
| 36 | CH3 + OH → CH2 + H2O | 7.60 × 106 | 2 | 5000 | [35] |
| 37 | CH3O + H → CH2O + H2 | 2.00 × 1013 | 0 | 0 | [35] |
| 38 | CH3O + M → CH2O + H + M | 2.40 × 1013 | 0 | 28,812 | [35] |
| 39 | CH2 + O → CO + H2 | 3.00 × 1013 | 0 | 0 | [35] |
| 40 | CH2 + OH → CH + H2O | 1.13 × 107 | 2 | 3000 | [35], b |
| 41 | CH2O + H → HCO + H2 | 5.00 × 1013 | 0 | 3991 | [35], b |
| 42 | CH2O + OH → HCO + H2O | 1.40 × 1014 | 0 | 1100 | [35], b, c |
| 43 | CH + O → CO + H | 5.70 × 1013 | 0 | 0 | [35] |
| 44 | CH + OH → HCO + H | 3.00 × 1013 | 0 | 0 | [35] |
| 45 | CH + O2 → HCO + O | 3.30 × 1013 | 0 | 0 | [35] |
| 46 | CH + CO2 → HCO + CO | 8.40 × 1013 | 0 | 200 | [35] |
| 47 | HCO + H → CO + H2 | 4.00 × 1013 | 0 | 0 | [35] |
| 48 | HCO + M → CO + H + M | 1.60 × 1014 | 0 | 14,700 | [35] |
| 49 | CO + OH → CO2 + H | 1.51 × 107 | 1.3 | −758 | [35] |
| 50 | CO2 + H → CO + OH | 1.57 × 109 | 1.3 | 20,400 | [35], c |
| 51 | H + O2 → OH + O | 1.50 × 1014 | 0 | 16,800 | [35], b |
| 52 | OH + O → H + O2 | 1.20 × 1013 | 0 | 690 | [35] |
| 53 | O + H2 → OH + H | 1.80 × 1010 | 1 | 8826 | [35] |
| 54 | OH + H → O + H2 | 8.00 × 109 | 1 | 6760 | [35] |
| 55 | H2 + OH → H2O + H | 1.17 × 109 | 1.3 | 3626 | [35] |
| 56 | H2O + H → H2 + OH | 6.00 × 109 | 1.3 | 18,588 | [35], b |
| 57 | OH + OH → O + H2O | 6.00 × 108 | 1.3 | 0 | [35] |
| 58 | O + H2O → OH + OH | 4.00 × 109 | 1.3 | 17,029 | [35], b |
| 59 | H + O2 + M → HO2 + M e | 2.20 × 1018 | −0.8 | 0 | [35], b |
| 60 | H + HO2 → OH + OH | 1.50 × 1014 | 0 | 1004 | [35] |
| 61 | H + HO2 → H2 + O2 | 2.50 × 1013 | 0 | 700 | [35] |
| 62 | OH + HO2 → H2O + O2 | 2.00 × 1013 | 0 | 1000 | [35] |
| 63 | HO2 + HO2 → H2O2 + O2 | 2.00 × 1014 | 0 | 0 | [35], b |
| 64 | H2O2 + M → OH + OH + M | 1.30 × 1017 | 0 | 45,500 | [35] |
| 65 | OH + OH + M → H2O2 + M | 9.86 × 1014 | 0 | −5070 | [35] |
| 66 | H2O2 + OH → H2O + HO2 | 1.00 × 1013 | 0 | 1800 | [35] |
| 67 | H2O + HO2 → H2O2 + OH | 2.86 × 1013 | 0 | 32,790 | [35] |
| 68 | OH + H + M → H2O + M | 2.20 × 1022 | −2.0 | 0 | [35] |
| 69 | H + H + M → H2 + M | 1.80 × 1018 | −1.0 | 0 | [35] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zettervall, N.; Fureby, C.; Nilsson, E.J.K. Reduced Chemical Kinetic Reaction Mechanism for Dimethyl Ether-Air Combustion. Fuels 2021, 2, 323-344. https://doi.org/10.3390/fuels2030019
Zettervall N, Fureby C, Nilsson EJK. Reduced Chemical Kinetic Reaction Mechanism for Dimethyl Ether-Air Combustion. Fuels. 2021; 2(3):323-344. https://doi.org/10.3390/fuels2030019
Chicago/Turabian StyleZettervall, Niklas, Christer Fureby, and Elna J. K. Nilsson. 2021. "Reduced Chemical Kinetic Reaction Mechanism for Dimethyl Ether-Air Combustion" Fuels 2, no. 3: 323-344. https://doi.org/10.3390/fuels2030019
APA StyleZettervall, N., Fureby, C., & Nilsson, E. J. K. (2021). Reduced Chemical Kinetic Reaction Mechanism for Dimethyl Ether-Air Combustion. Fuels, 2(3), 323-344. https://doi.org/10.3390/fuels2030019








