High-Dimensional Contact Network Epidemiology
Abstract
1. Introduction
2. Methods
2.1. SEIR Model
2.2. Network Models
Graph Theory
2.3. Percolation
2.4. Computation of Edge-Weights
2.5. Dynamic Contact Network
3. Results
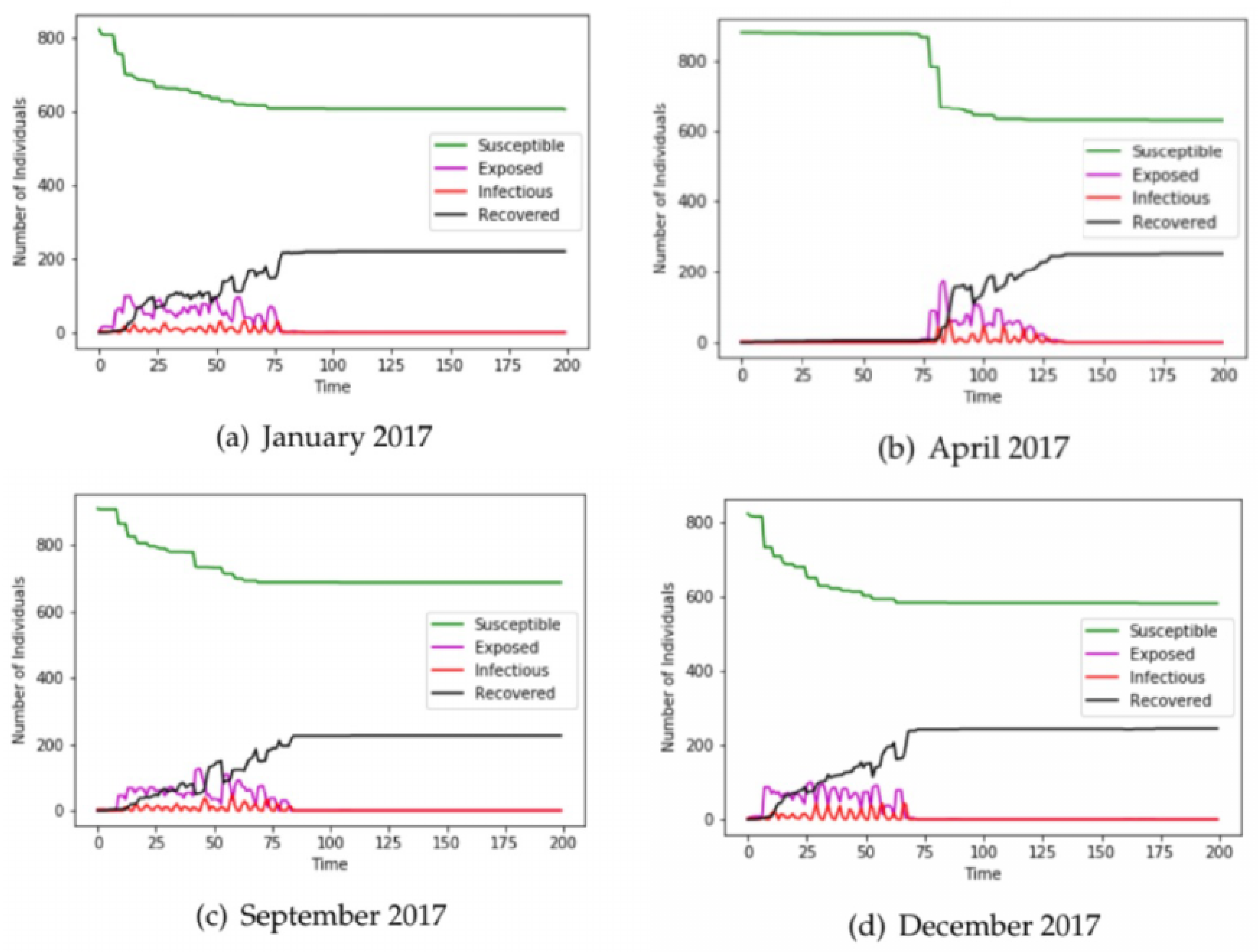
3.1. Airline Data
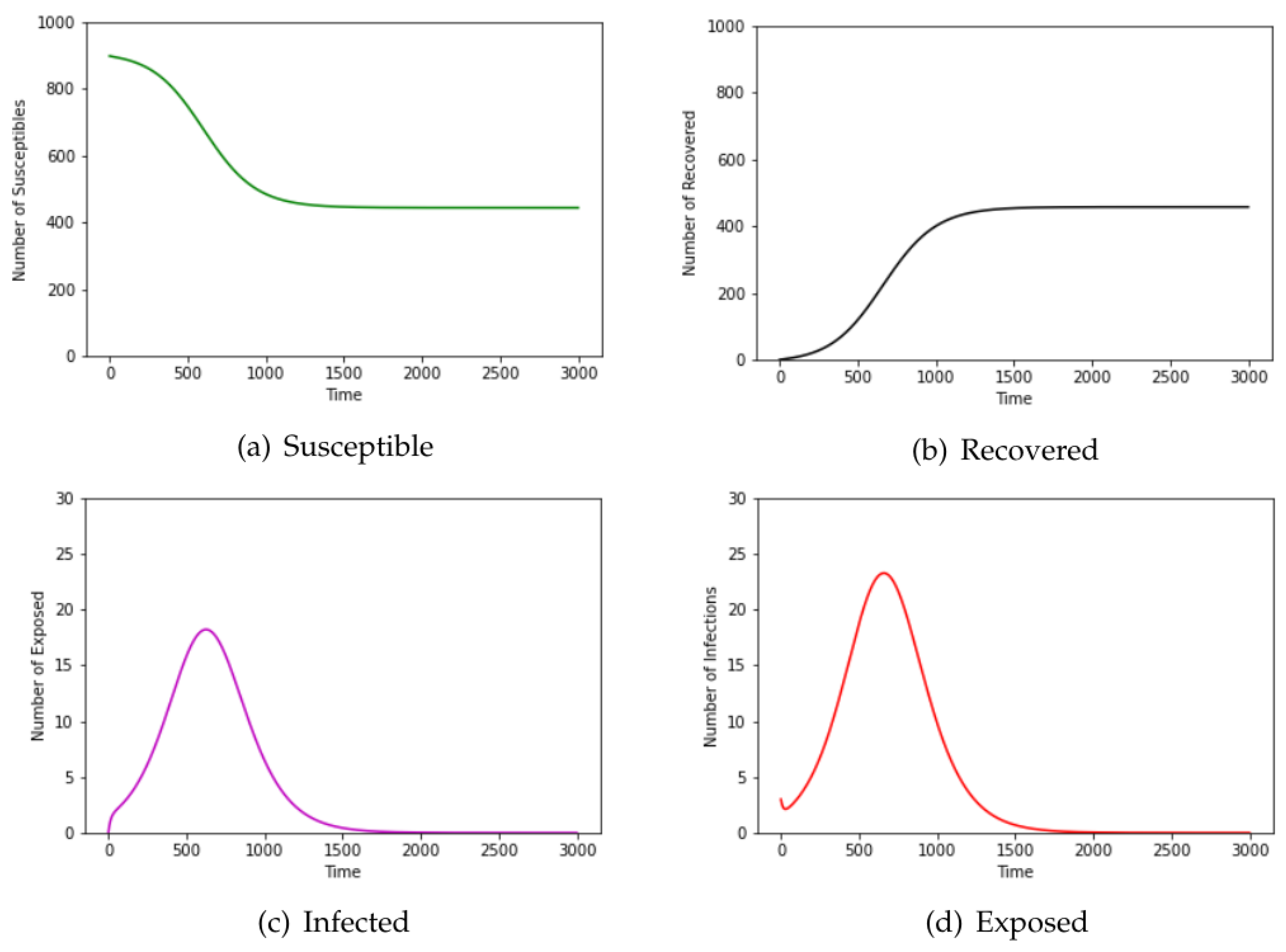
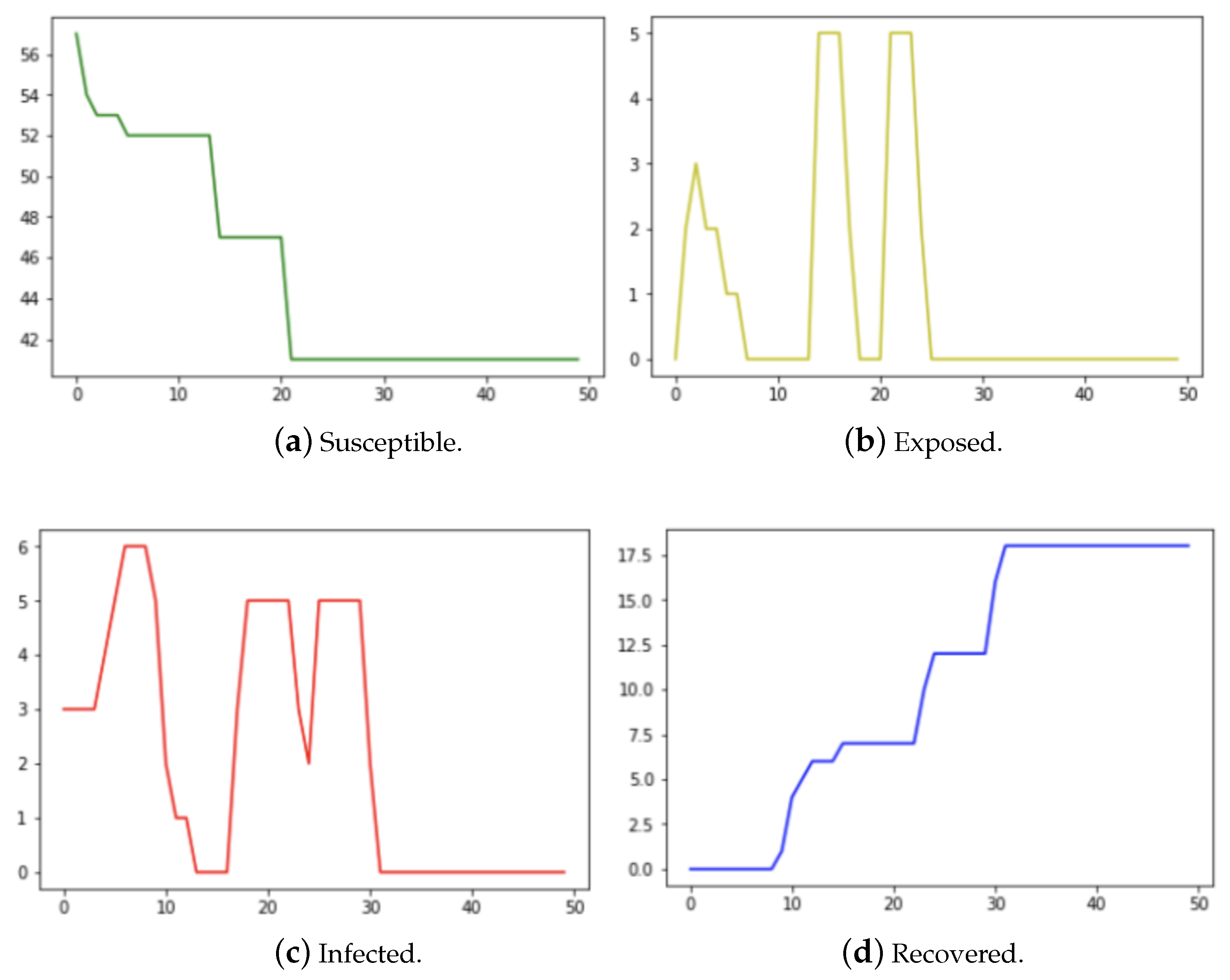
3.2. Kenyan Household Data
4. Discussions
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marathe, M.; Vullikanti, A. Computational epidemiology. Commun. ACM 2013, 56, 88–96. [Google Scholar] [CrossRef]
- Meyers, L. Contact Network Epidemiology: Bond Percolation Applied to Infectious Disease Prediction and Control. Bull. Am. Math. Soc. 2007, 44, 63–86. [Google Scholar] [CrossRef]
- Taubenberger, J.; Morens, D. 1918 Influenza: The Mother of All Pandemics. Emerg. Infect. Dis. 2006, 12, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Schult, A.H.D.; Swart, P. Exploring network structure, dynamics, and function using networkx. In Proceedings of the SciPy, Pasadena, CA, USA, 19–24 August 2008; Vaught, G.V.T., Millman, J., Eds.; Los Alamos National Laboratory: Los Alamos, NM, USA, 2008; pp. 11–16. [Google Scholar]
- Trawicki, M. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics 2017, 5, 7. [Google Scholar] [CrossRef]
- Stehle, J.; Voirin, N.; Barrat, A.; Cattuto, C.; Colizza, V.; Isella, L.; Régis, C.; Pinton, J.; Khanafer, N.; den Broeck, W.V.; et al. Simulation of an SEIR infectious disease model on the dynamic contact network of conference attendees. BMC Med. 2011, 9, 87. [Google Scholar] [CrossRef] [PubMed]
- Edoh, K.; MacCarthy, E. Network and equation-based models in epidemiology. Int. J. Biomath. 2018, 11, 1850046. [Google Scholar] [CrossRef]
- Bansal, S.; Read, J.; Pourbohloul, B.; Meyers, L.A. The dynamic nature of contact networks in infectious disease epidemiology. J. Biol. Dyn. 2010, 4, 479–489. [Google Scholar] [CrossRef] [PubMed]
- Kattis, A.; Holiday, A.; Stoica, A.; Kevrekidis, I. Modeling Epidemics on adaptively evolving networks: A data-mining perspective. Virulence 2016, 7, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. The Mathematics of Networks; Palgrave Macmillan: London, UK, 2008. [Google Scholar]
- Freeman, L. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Easley, D.; Kleinberg, J. Networks, Crowds, and Markets: Reasoning about a Highly Connected World; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Newman, M. Spread of epidemics disease on networks. Phys. Rev. E 2002, 66, 016128. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Nigmatulina, K.; Eckhoff, P. The scaling of contact rates with population density for the infectious disease model. Math. Biosci. 2013, 244, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, T.; Zheng, Y.; Wong, K.; Lu, S.; Lu, H. Poor responses to oseltamivir treatment in a patient with influenza A (H7N9) virus infection. Emerg. Microbes Infect. 2013, 2, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Masuda, N.; Holme, P. Temporal Network Epidemiology; Springer Nature: Singapore, 2017. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ackerman, A.; Martin, B.; Tanisha, M.; Edoh, K.; Ward, J.P. High-Dimensional Contact Network Epidemiology. Epidemiologia 2023, 4, 286-297. https://doi.org/10.3390/epidemiologia4030029
Ackerman A, Martin B, Tanisha M, Edoh K, Ward JP. High-Dimensional Contact Network Epidemiology. Epidemiologia. 2023; 4(3):286-297. https://doi.org/10.3390/epidemiologia4030029
Chicago/Turabian StyleAckerman, Andrew, Briquelle Martin, Martin Tanisha, Kossi Edoh, and John Paul Ward. 2023. "High-Dimensional Contact Network Epidemiology" Epidemiologia 4, no. 3: 286-297. https://doi.org/10.3390/epidemiologia4030029
APA StyleAckerman, A., Martin, B., Tanisha, M., Edoh, K., & Ward, J. P. (2023). High-Dimensional Contact Network Epidemiology. Epidemiologia, 4(3), 286-297. https://doi.org/10.3390/epidemiologia4030029





