A Trendline and Predictive Analysis of the First-Wave COVID-19 Infections in Malta
Abstract
1. Introduction
2. Methodologies
2.1. Trendline Analysis
2.1.1. Data Collection
2.1.2. Trendline Functions
2.2. Predictive Analysis
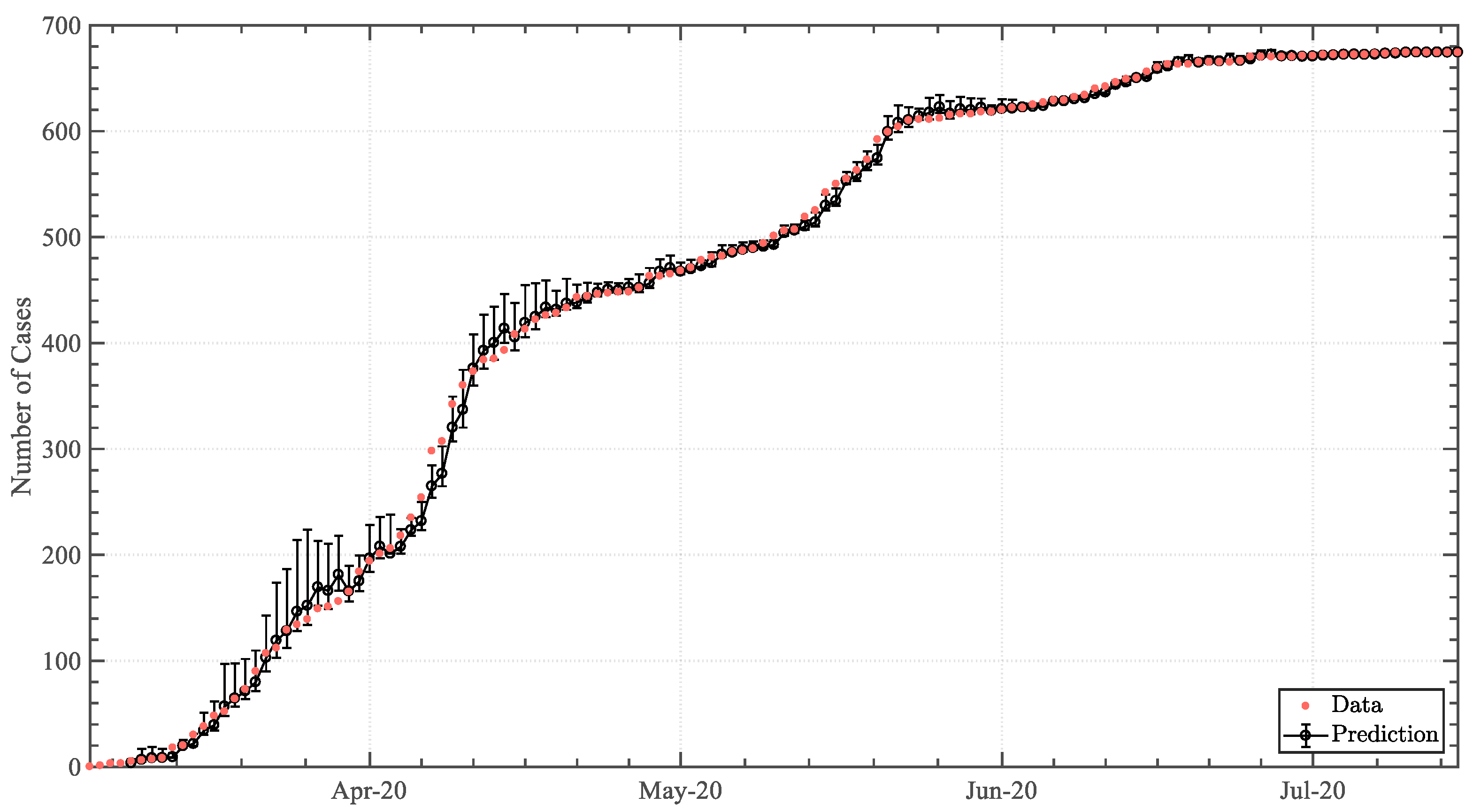
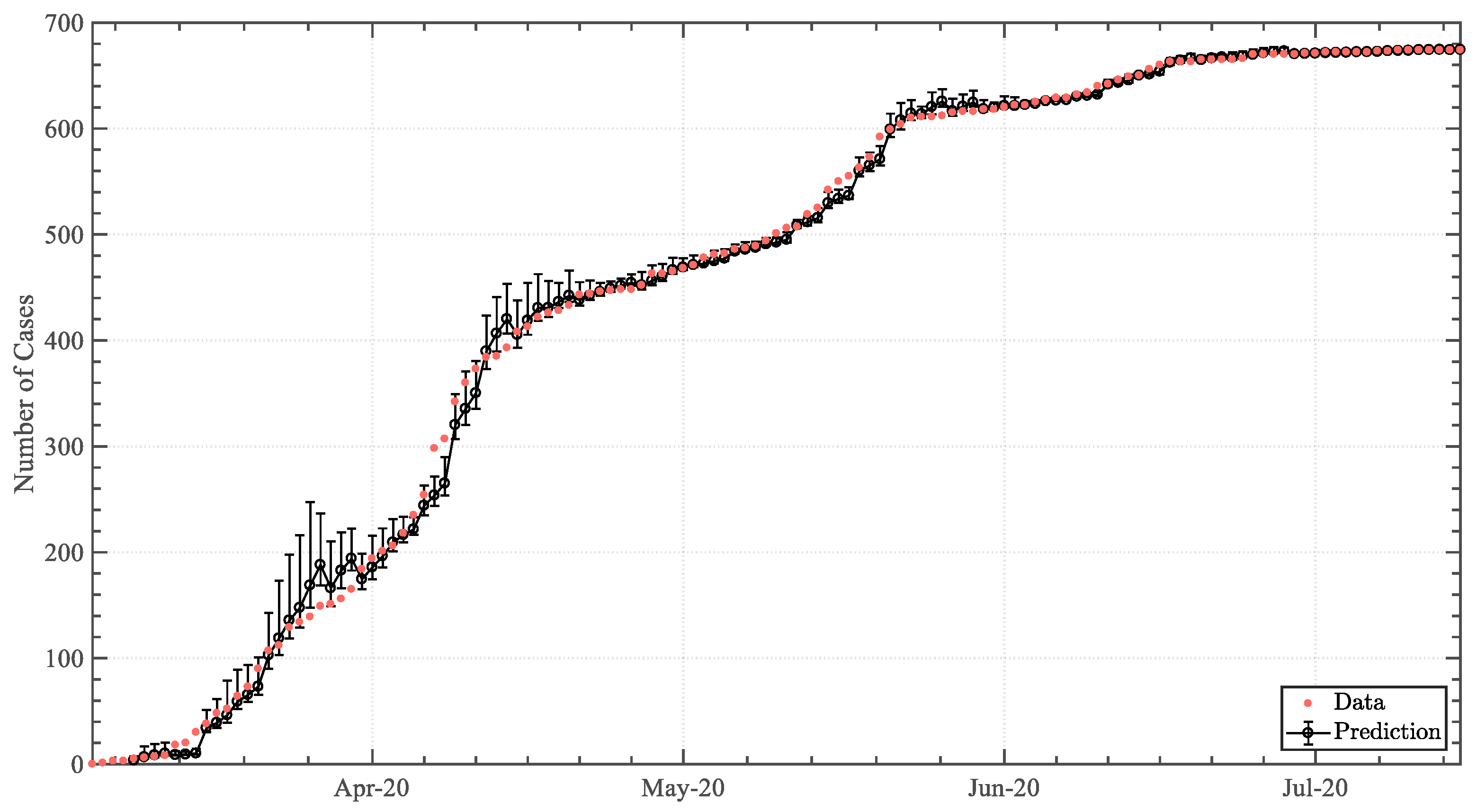
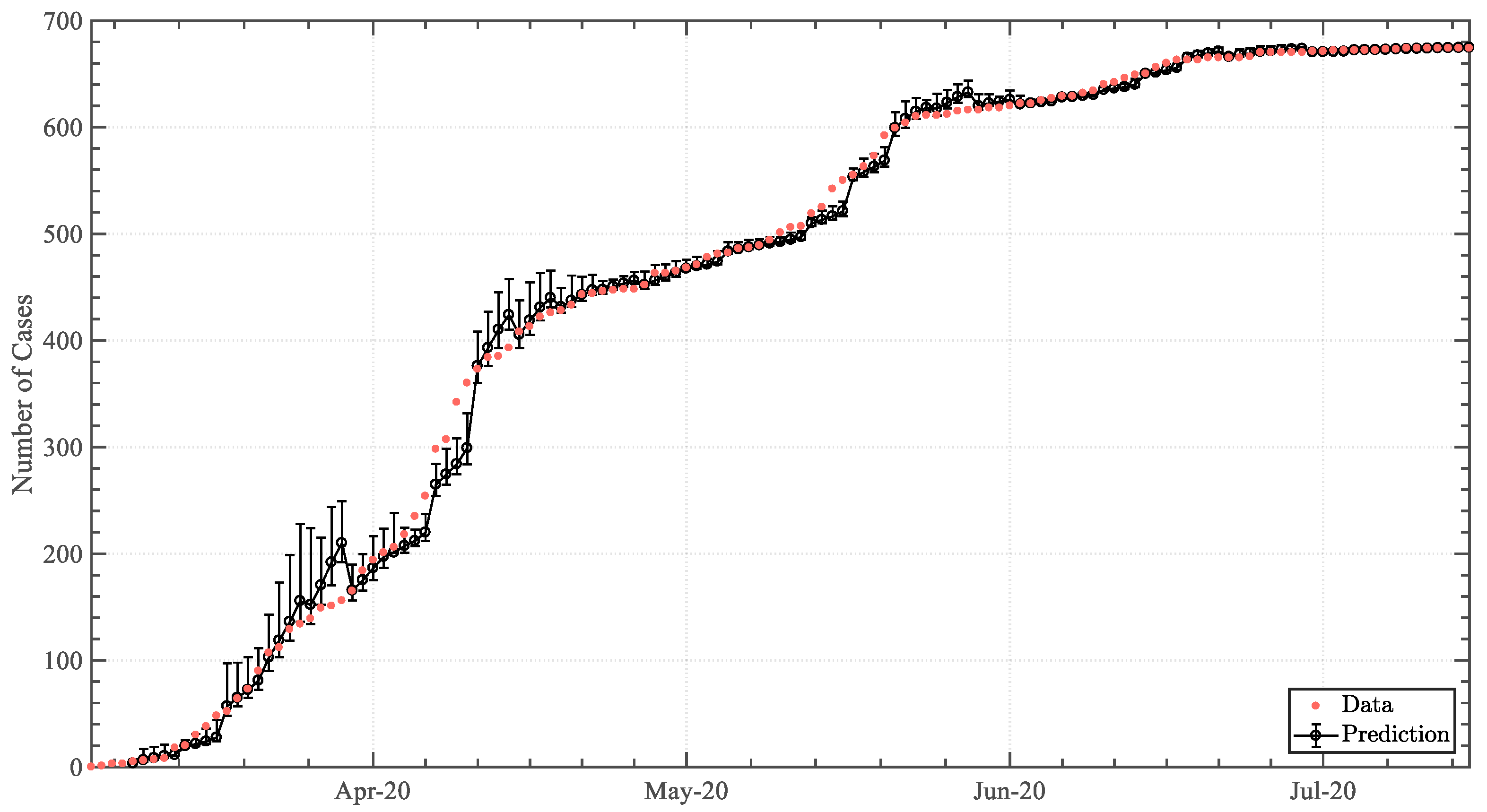
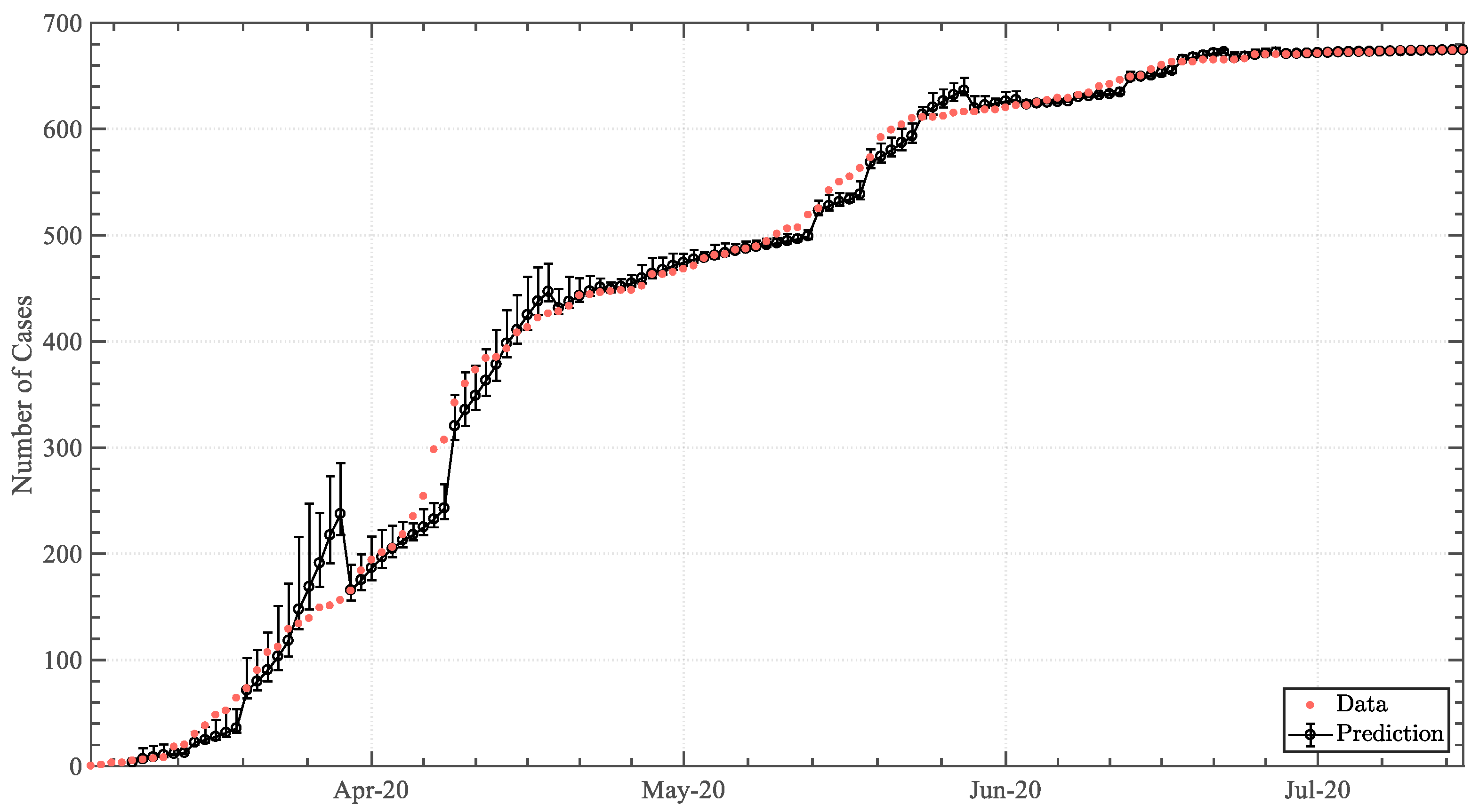
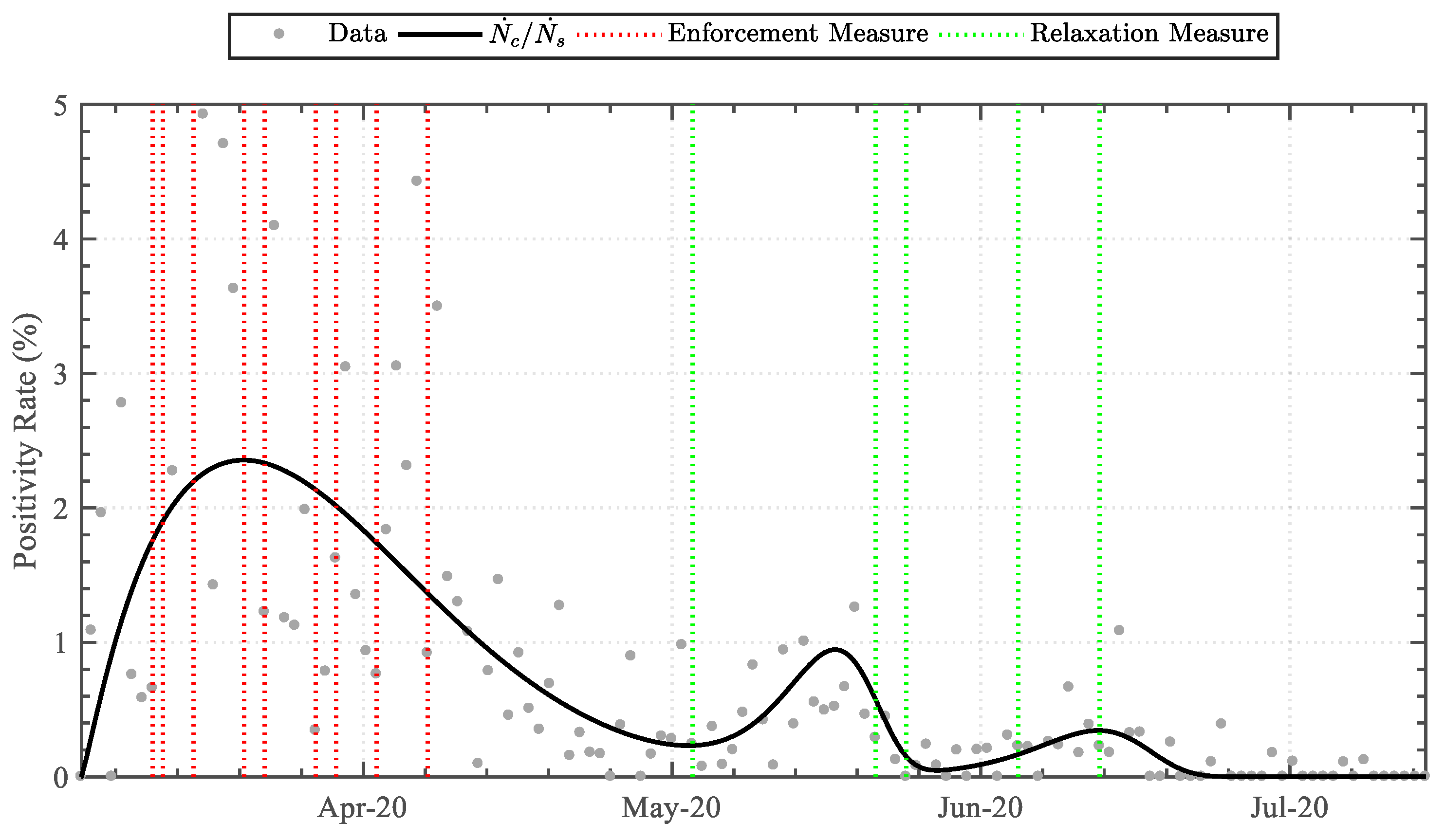
3. Results
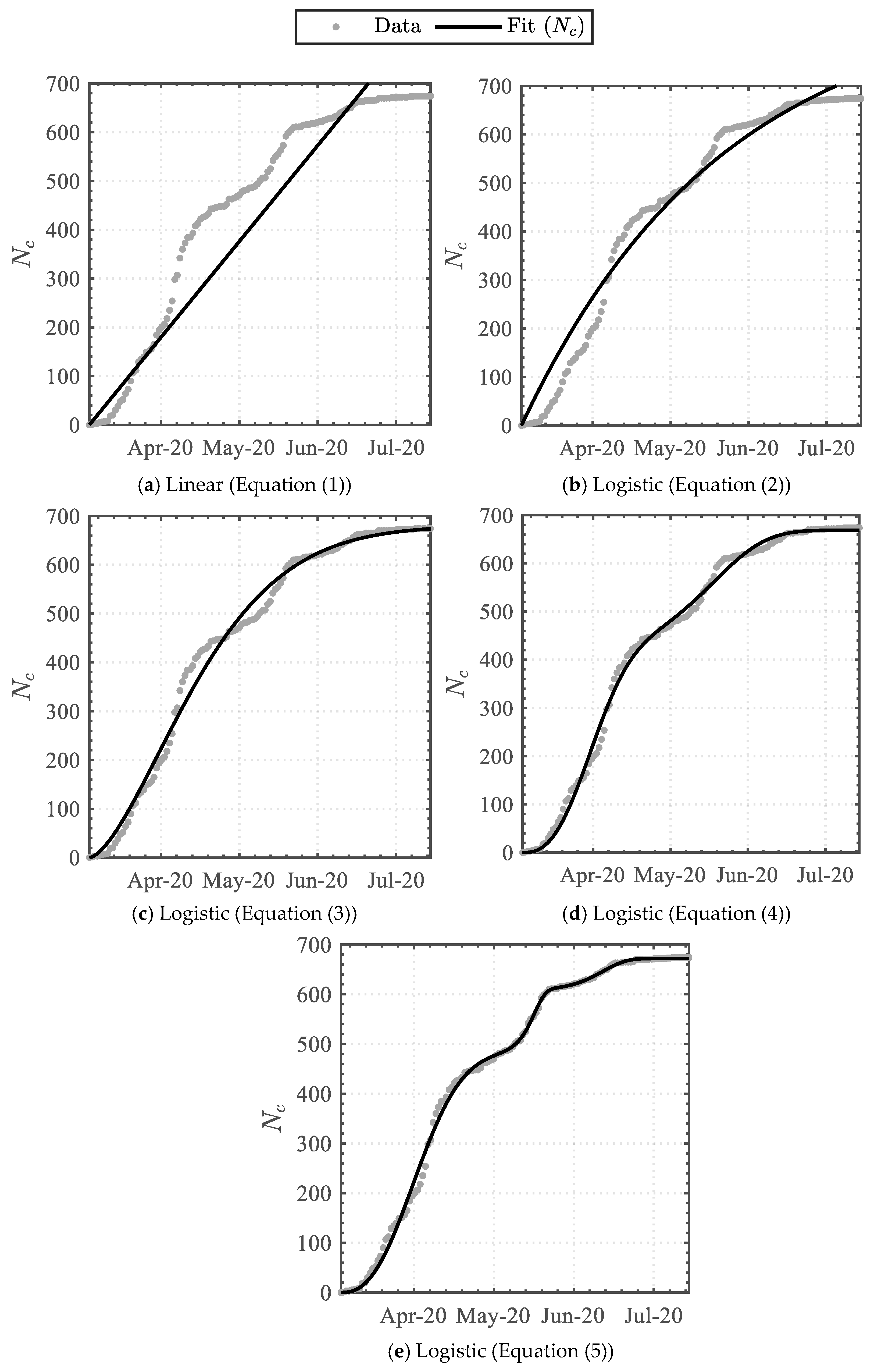
3.1. Trendline Analysis
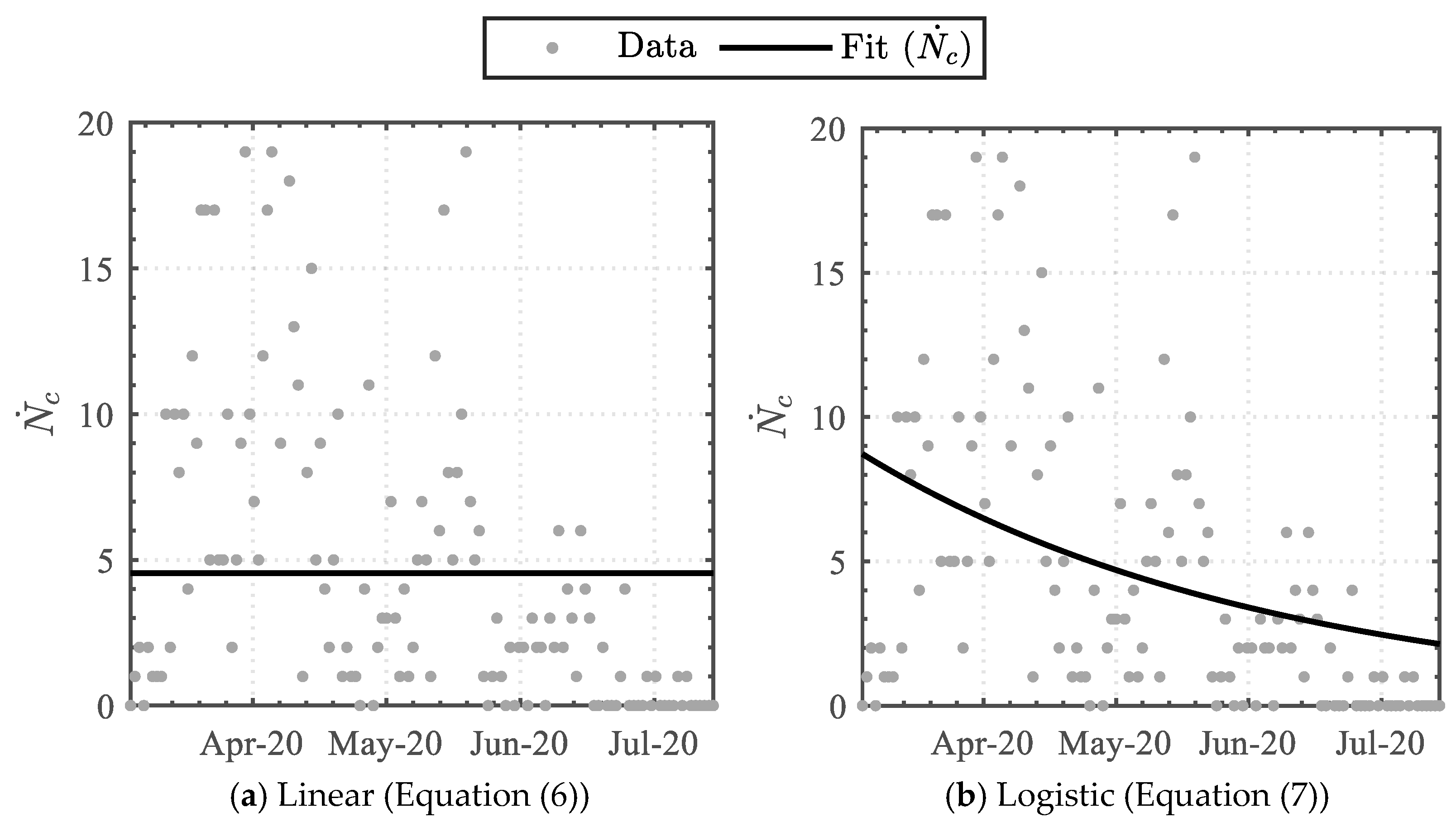
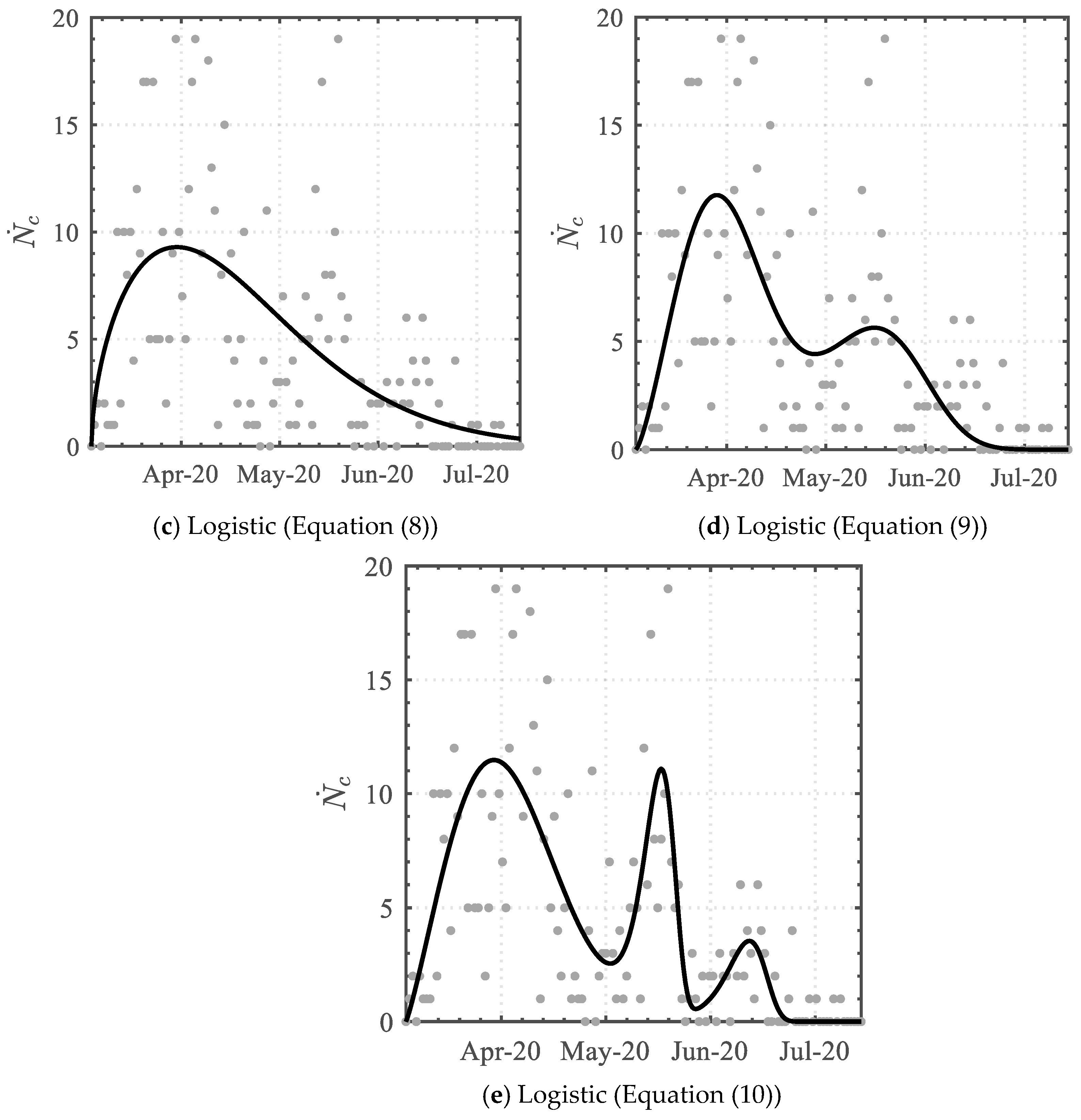
3.1.1. Positive Infected-Case Function
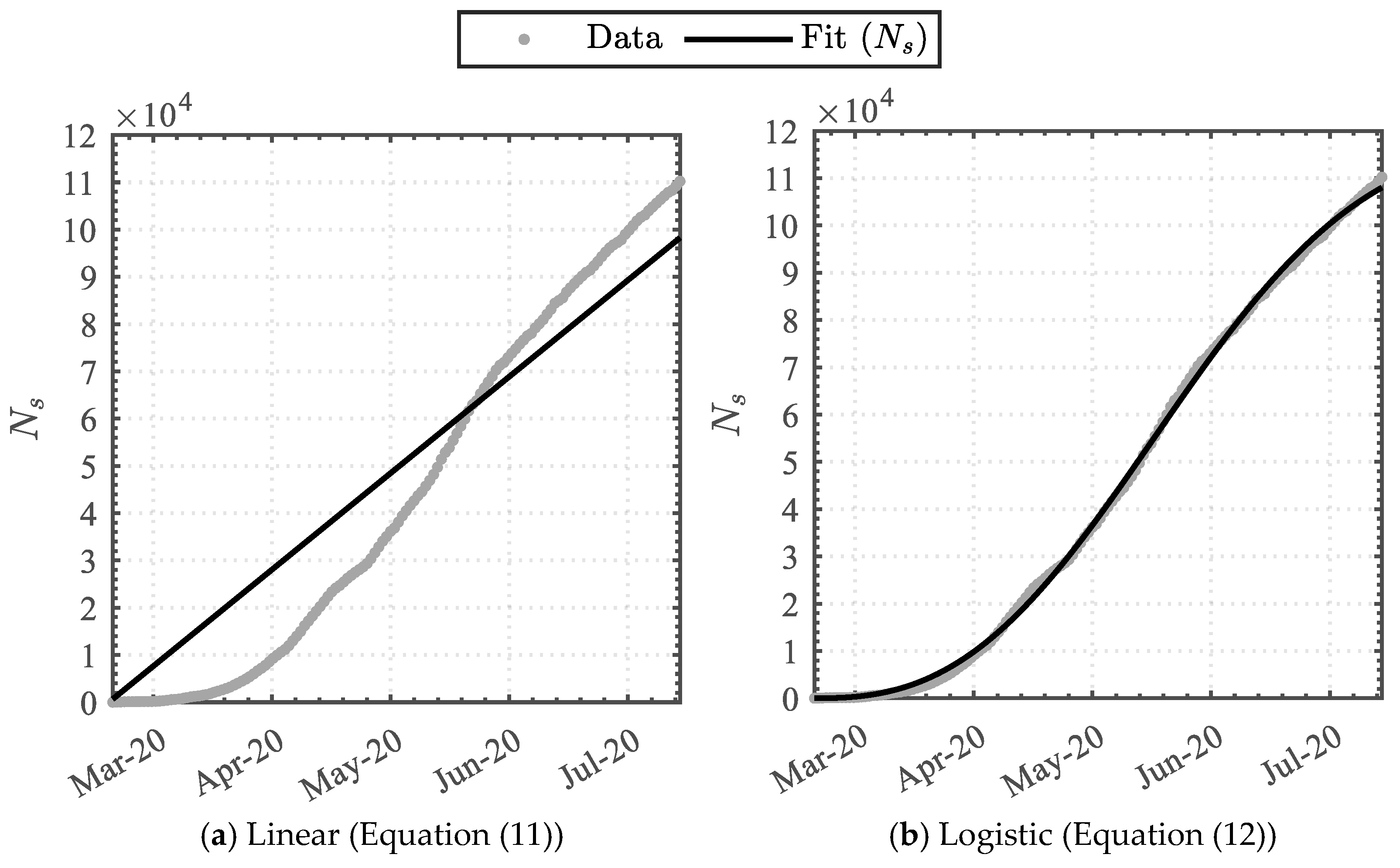
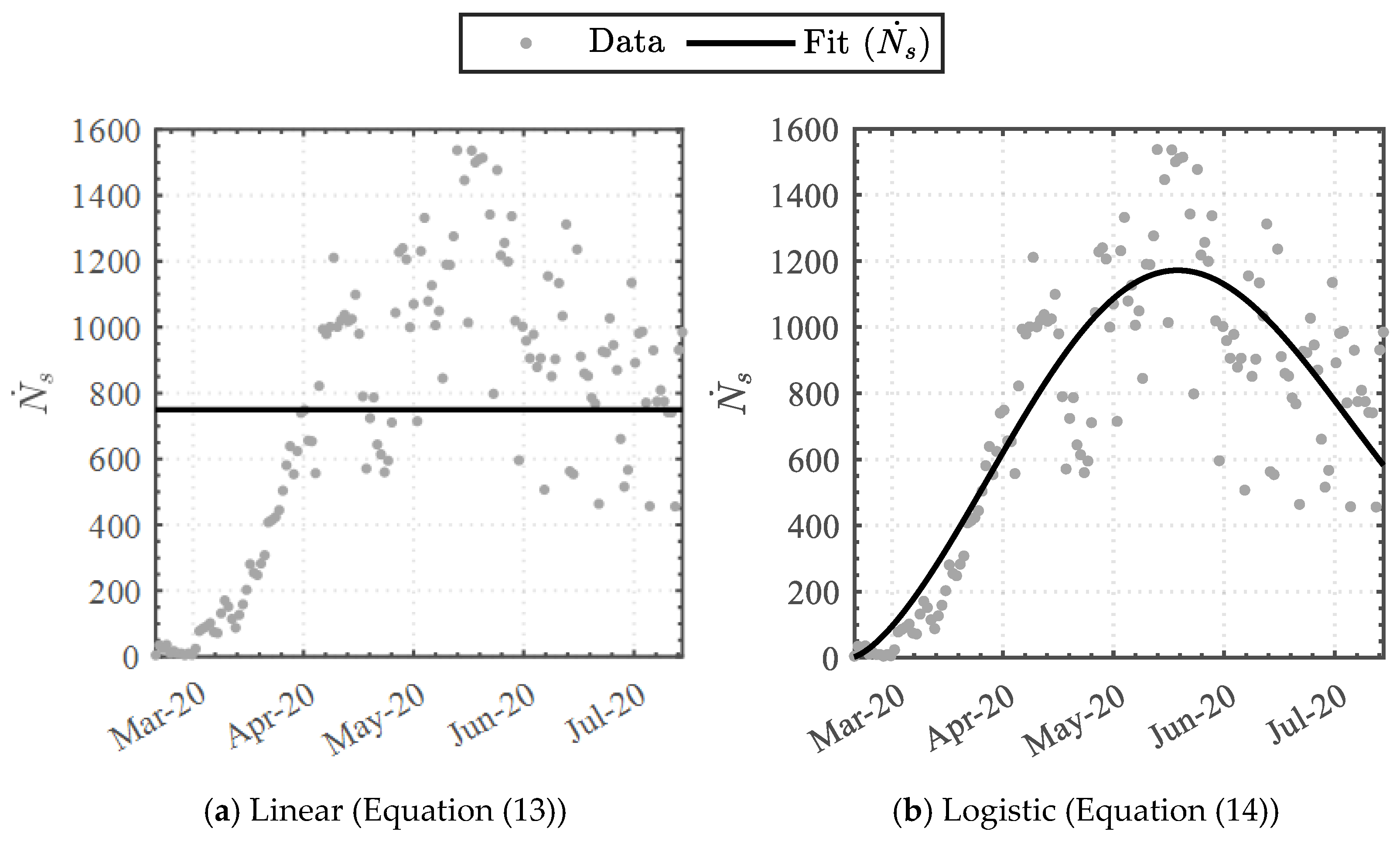
3.1.2. Swab-Test Function
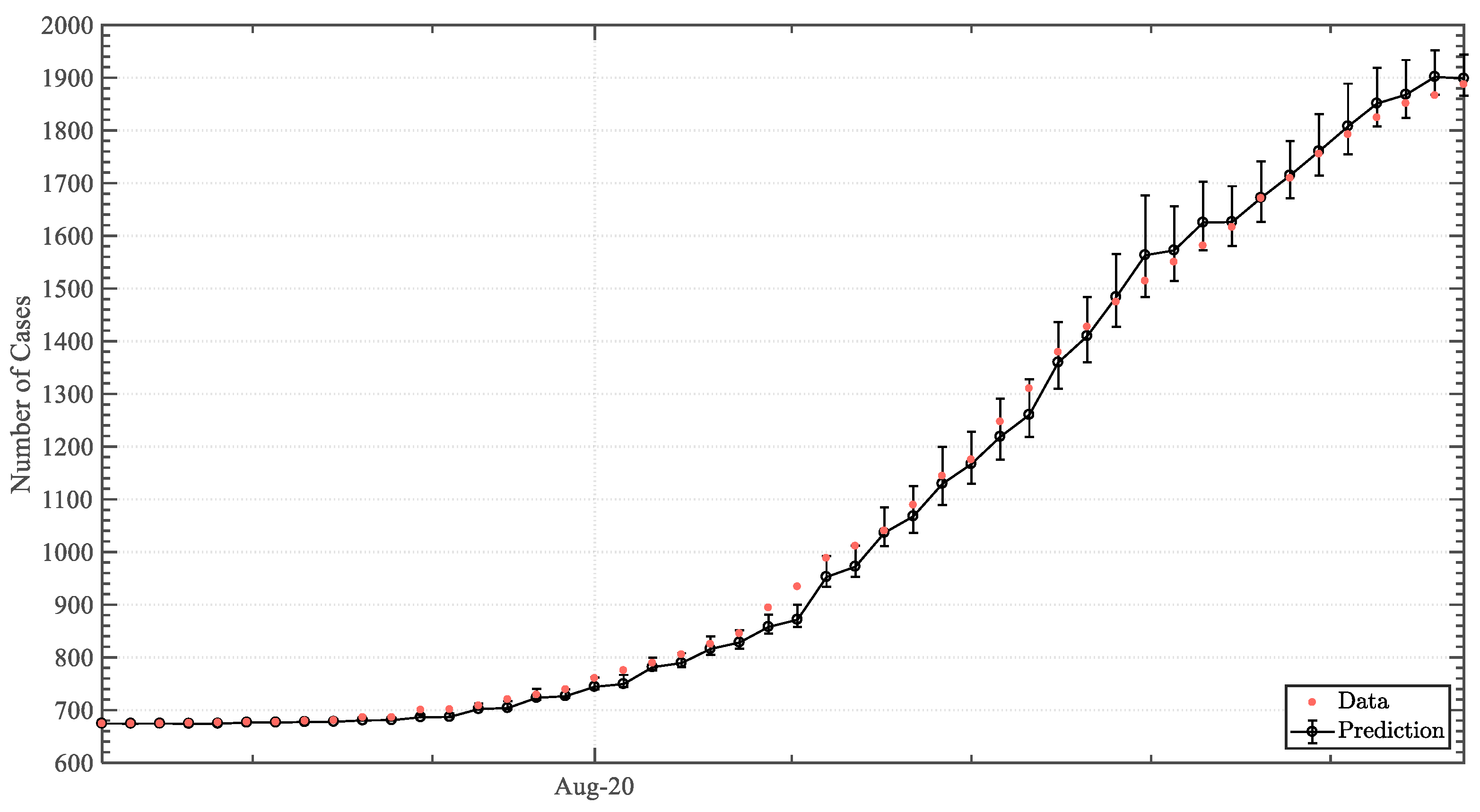
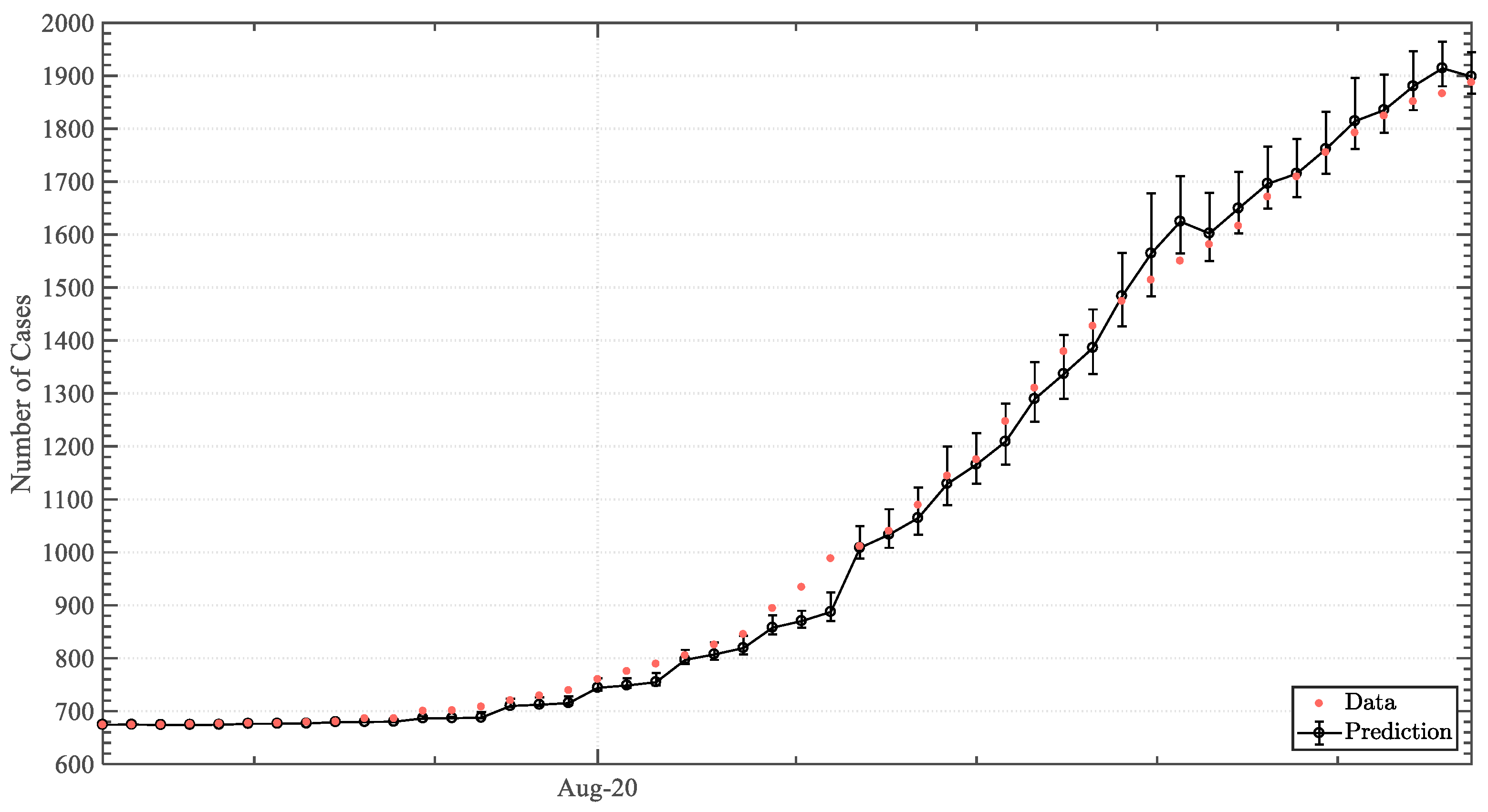
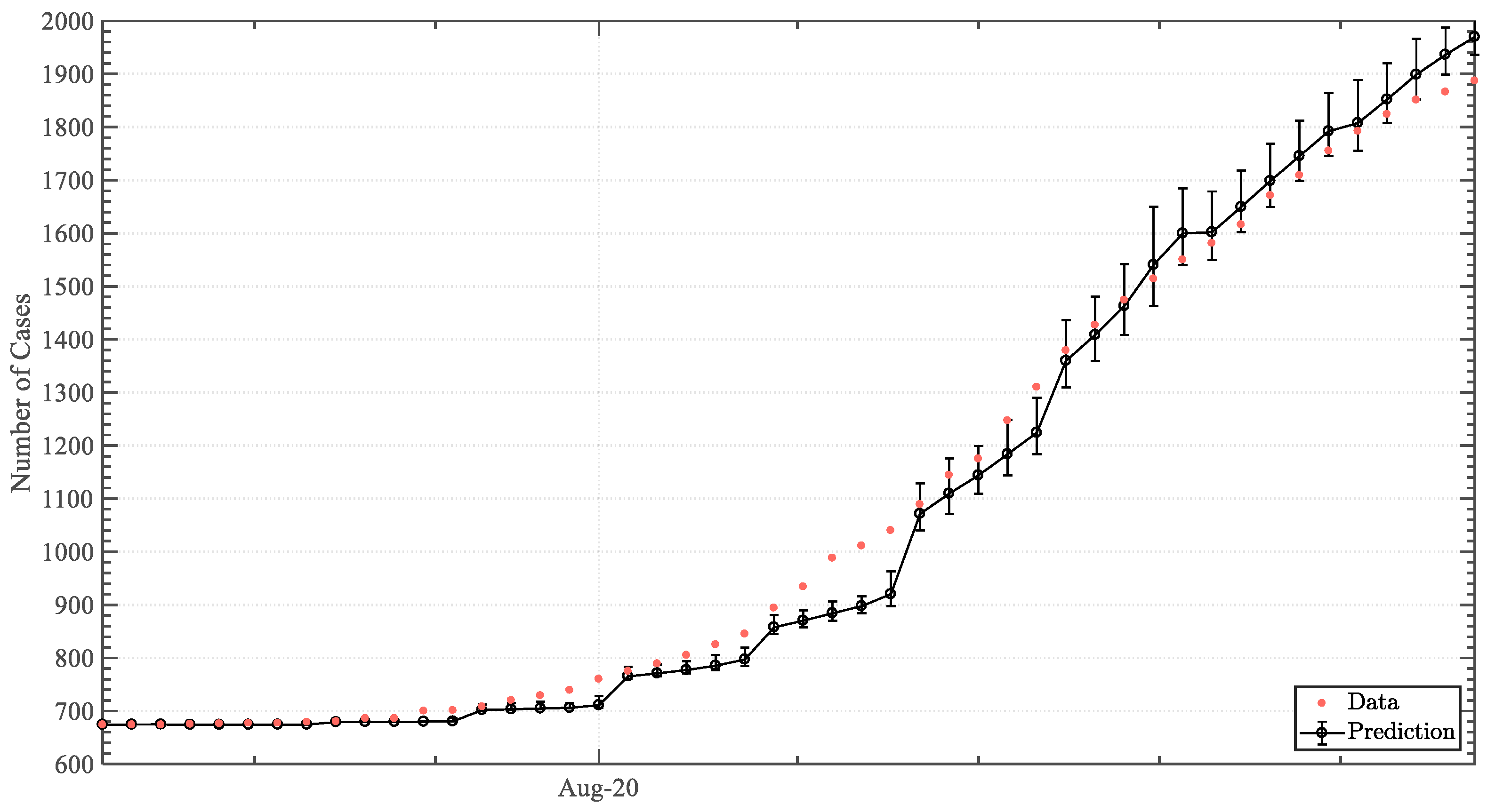
3.2. Predictive Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Zhou, P.; Yang, X.L.; Wang, X.G.; Hu, B.; Zhang, L.; Zhang, W. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020, 579, 270–273. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.; Chang, X.; Tan, K.J.K. The determinants of COVID-19 morbidity and mortality across countries. Sci. Rep. 2022, 12, 5888. [Google Scholar] [CrossRef]
- Khan, S.; Siddique, R.; Ali, A.; Bai, Q.; Li, Z.; Li, H. The spread of novel coronavirus has created an alarming situation worldwide. J. Infect. Public Health 2020, 13, 469–471. [Google Scholar] [CrossRef] [PubMed]
- Onder, G.; Rezza, G.; Brusaferro, S. Case-Fatality Rate and Characteristics of Patients Dying in Relation to COVID-19 in Italy. JAMA 2020, 323, 1775–1776. [Google Scholar] [CrossRef] [PubMed]
- Mareiniss, D.P. The impending storm: COVID-19, pandemics and our overwhelmed emergency departments. Am. J. Emerg. Med. 2020, 38, 1293–1294. [Google Scholar] [CrossRef] [PubMed]
- Laupacis, A. Working together to contain and manage COVID-19. CMAJ 2020, 192, 340–341. [Google Scholar] [CrossRef]
- Lau, H.; Khosrawipour, V.; Kocbach, P.; Mikolajczyk, A.; Schubert, J.; Bania, J. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. J. Travel Med. 2020, 27, 1–7. [Google Scholar] [CrossRef]
- Nicola, M.; Alsafi, Z.; Sohrabi, C. The socio-economic implications of the coronavirus pandemic (COVID-19): A review. Int. J. Surg. 2020, 78, 185–193. [Google Scholar] [CrossRef]
- Brauner, M.; Mindermann, S.; Sharma, M.; Johnston, D.; Salvatier, J.; Gavenčiak, T.; Stephenson, A.B.; Leech, G.; Altman, G.; Mikulik, V.; et al. Inferring the effectiveness of government interventions against COVID-19. Science 2020, 371, eabd9338. [Google Scholar] [CrossRef]
- Li, Y.; Campbell, H.; Kulkarni, D.; Harpur, A.; Nundy, M.; Wang, X.; Nair, H. The temporal association of introducing and lifting non-pharmaceutical interventions with the time-varying reproduction number (R) of SARS-CoV-2: A modelling study across 131 countries. Lancet Infect. Dis. 2021, 21, 193–202. [Google Scholar] [CrossRef]
- Davies, N.G.; Barnard, R.C.; Jarvis, C.I.; Russell, T.W.; Semple, M.G.; Jit, M.; Edmunds, W.J. Association of tiered restrictions and a second lockdown with COVID-19 deaths and hospital admissions in England: A modelling study. Lancet Infect. Dis. 2020, 21, 482–492. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Whittington, J.; Yuan, H.-Y.; Miao, H.; Tian, H.; Stenseth, N.C. Evaluating the effectiveness of control measures in multiple regions during the early phase of the COVID-19 pandemic in 2020. Biosaf. Health. 2021, 5, 264–275. [Google Scholar] [CrossRef] [PubMed]
- Hsiang, S.; Allen, D.; Annan-Phan, S.; Bell, K.; Bollinger, I.; Chong, T.; Drunkenmiller, H.; Huang, L.Y.; Hultgren, A.; Krasovich, E.; et al. The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 2020, 371, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Holmdahl, I.; Buckee, C. Wrong but Useful—What Covid-19 Epidemiologic Models Can and Cannot Tell Us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef] [PubMed]
- Dahal, S.; Luo, R.; Subedi, R.K.; Dhimal, M.; Chowell, G. Transmission Dynamics and Short-Term Forecasts of COVID-19: Nepal 2020/2021. Epidemiologia 2021, 2, 639–659. [Google Scholar] [CrossRef]
- Pajuelo-Reyes, C.; Valencia, H.J.; Montenegro, C.C.; Quezada, E.; Gonzales, L.; Cruz, N.; Canelo, C.; Ordinola, C.; Maicelo Quintana, J.L.; Tejedo, J.R.; et al. Epidemiological Analysis of COVID-19 Cases in Native Amazonian Communities from Peru. Epidemiologia 2021, 2, 490–501. [Google Scholar] [CrossRef]
- Olumoyin, K.D.; Khaliq, A.Q.M.; Furati, K.M. Data-Driven Deep-Learning Algorithm for Asymptomatic COVID-19 Model with Varying Mitigation Measures and Transmission Rate. Epidemiologia 2021, 2, 471–489. [Google Scholar] [CrossRef]
- Fonseca, L.M.; Sousa, D.S.D.; Cardoso, J.C.; Severino, P.; Cano, A.; Souto, E.B.; Lima, S.O.; Oliveira, C.C.C.D.; Reis, F.P. Epidemiology of COVID-19 in the State of Sergipe/Brazil and Its Relationship with Social Indicators. Epidemiologia 2021, 2, 262–270. [Google Scholar] [CrossRef]
- Marinho, P.R.D.; Cordeiro, G.M.; Coelho, H.F.C.; Cabral, P.C. The COVID-19 Pandemic in Brazil: Some Aspects and Tools. Epidemiologia 2021, 2, 243–255. [Google Scholar] [CrossRef]
- Ogwara, C.A.; Mallhi, A.K.; Hua, X.; Muniz-Rodriguez, K.; Schwind, J.S.; Zhou, X.; Jones, J.A.; Chopak-Foss, J.; Chowell, G.; Fung, I.C.-H. Spatially Refined Time-Varying Reproduction Numbers of COVID-19 by Health District in Georgia, USA, March–December 2020. Epidemiologia 2021, 2, 179–197. [Google Scholar] [CrossRef]
- Fain, B.; Dobrovolny, H.M. Initial Inoculum and the Severity of COVID-19: A Mathematical Modeling Study of the Dose-Response of SARS-CoV-2 Infections. Epidemiologia 2020, 1, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Hwang, S.S.; Song, I.H.M. COVID-19 in South Korea: Epidemiological and spatiotemporal patterns of the spread and the role of aggressive diagnostic tests in the early phase. Int. J. Epidemiol. 2020, 49, 1106–1116. [Google Scholar] [CrossRef]
- Lewnard, J.A.; Lo, N.C. Scientific and ethical basis for social-distancing interventions against COVID-19. Lancet Infect. Dis. 2020, 20, 631–633. [Google Scholar] [CrossRef] [PubMed]
- Matrajt, L.; Leung, T. Evaluating the Effectiveness of Social Distancing Interventions to Delay or Flatten the Epidemic Curve of Coronavirus Disease. Emerg. Infect. Dis. 2020, 26, 1740–1748. [Google Scholar] [CrossRef]
- Chou, R.; Dana, T.; Jungbauer, R.; Weeks, C.; McDonagh, M.S. Masks for Prevention of Respiratory Virus Infections, Including SARS-CoV-2, in Health Care and Community Settings. Ann. Intern. Med. 2020, 173, 542–555. [Google Scholar] [CrossRef] [PubMed]
- Kretzschmar, M.E.; Rozhnova, G.; Bootsma, M.C.J.; van Boven, M.; van de Wijgert, J.H.H.M.; Bonten, M.J.M. Impact of delays on effectiveness of contact tracing strategies for COVID-19: A modelling study. Lancet Public Health 2020, 5, e452–e459. [Google Scholar] [CrossRef]
- Abernethy, R.B. The New Weibull Handbook: Reliability and Statistical Analysis for Predicting Life, Safety, Supportability, Risk, Cost and Warranty Claims, 5th ed.; Dr. Robert B. Abernethy: North Miami, FL, USA, 2004. [Google Scholar]
- Ioannidis, J.P.A.; Cripps, S.; Tanner, M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2022, 38, 423–438. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Mariani, V.C.; Coelho, L.S. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. Chaos Solitons Fractals 2020, 135, 109853. [Google Scholar] [CrossRef]
- Yadav, S.K.; Akhter, Y. Statistical Modeling for the Prediction of Infectious Disease Dissemination with Special Reference to COVID-19 Spread. Front. Public Health. 2021, 9, 645405. [Google Scholar] [CrossRef]
- Clifford Cohen, A. Maximum Likelihood Estimation in the Weibull Distribution Based on Complete and on Censored Samples. Technometrics 1965, 7, 579–588. [Google Scholar] [CrossRef]
- Engelhardt, M.; Bain, L.J.; Blumenthal, S. Statistical Analysis of a Weibull Process with Left-Censored Data. In Survival Analysis: State of the Art, 1st ed.; Klein, J.P., Goel, P.K., Eds.; Nato Science (Series E: Applied Sciences); Springer: Dordrecht, The Netherlands, 1992; Volume 211. [Google Scholar]
- Cole, R. Data Errors and Forecasting Accuracy. In Economic Forecasts and Expectations: Analysis of Forecasting Behavior and Performance, 1st ed.; National Bureau of Economic Research (NBER): Cambridge, MA, USA, 1969; pp. 42–87. [Google Scholar]
- Collett, D. Parametric proportional hazards models. In Modelling Survival Data in Medical Research, 1st ed.; Chapman & Hall/CRC: London, UK, 2015; pp. 171–220. [Google Scholar]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.-M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.K.C.; Ng, R.W.Y.; Wong, M.C.S. Epidemiological characteristics of the first 100 cases of coronavirus disease 2019 (COVID-19) in Hong Kong Special Administrative Region, China, a city with a stringent containment policy. Int. J. Epidemiol. 2020, 49, 1096–1105. [Google Scholar] [CrossRef] [PubMed]


| Enforcement Date | Relaxation Date |
| International travel ban | 21 March 2020 | 1 July 2020 |
| Lockdown of vulnerable persons | 28 March 2020 | 5 June 2020 |
| National travel ban (essential travel only between the Maltese islands) | 3 April 2020 | 4 May 2020 |
| Enforcement Date | Relaxation Date |
| Public transport measures (daily decontamination; passenger screening; standing passengers disallowed; windows open; air-conditioning system off; no monetary change) | 12 March 2020 | 4 May 2020 |
| Closure of workplaces and distancing of workers | 13 March 2020 | 5 June 2020 |
| Closure of sports facilities | 13 March 2020 | 5 June 2020 |
| Closure of law courts and local tribunals | 13 March 2020 | 5 June 2020 |
| Closure of religious places | 13 March 2020 | 13 June 2020 |
| Closure of service outlets and public places | 16 March 2020 | 22 May 2020 |
| Closure of education establishments | 21 March 2020 | 5 June 2020 |
| Closure of non-essential retail outlets | 23 March 2020 | 4 May 2020 |
| Closure of non-essential service outlets | 23 March 2020 | 22 May 2020 |
| Measures to protect elderly and high-risk groups | 28 March 2020 | 5 June 2020 |
| Prohibition of public gatherings (limits of 3 persons, 4 persons, and 6 persons) | 30 March 2020 | 4 May 2020, 22 May 2020, 5 June 2020 |
| Suspension of visits to homes for the elderly and the national hospital | 8 April 2020 | 25 May 2020 |
| Equation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Equation (1) | 6.486 | - | - | - | - | - | - | - | - | 0.806 |
| 95% CI | 6.677 | - | - | - | - | - | - | - | - | |
| 6.296 | ||||||||||
| Equation (2) | 885.6 | 78.32 | - | - | - | - | - | - | - | 0.970 |
| 95% CI | 940.3 | 87.12 | - | - | - | - | - | - | - | |
| 830.9 | 69.53 | |||||||||
| Equation (3) | 680.0 | 49.61 | 1.581 | - | - | - | - | - | - | 0.991 |
| 95% CI | 691.2 | 51.01 | 1.655 | - | - | - | - | - | - | |
| 668.9 | 48.21 | 1.508 | ||||||||
| Equation (4) | 434.8 | 31.38 | 2.628 | 234.3 | 79.05 | 4.687 | - | - | - | 0.996 |
| 95% CI | 472.0 | 33.12 | 2.836 | 273.8 | 82.32 | 5.888 | - | - | - | |
| 397.6 | 29.64 | 2.419 | 194.7 | 75.78 | 3.486 | |||||
| Equation (5) | 484.6 | 33.64 | 2.486 | 64.03 | 100.2 | 12.25 | 123.4 | 73.59 | 17.98 | 0.998 |
| 95% CI | 495.6 | 34.41 | 2.606 | 82.83 | 103.7 | 20.26 | 145.1 | 74.73 | 23.93 | |
| 473.6 | 32.86 | 2.367 | 45.23 | 96.69 | 4.327 | 101.7 | 72.45 | 12.03 |
| Equation (6) | 4.542 | - | - | - | - | - | - | - | - | 0.0 |
| 95% CI | 5.427 | - | - | - | - | - | - | - | - | |
| 3.657 | ||||||||||
| Equation (7) | 818.4 | 93.88 | - | - | - | - | - | - | - | 0.183 |
| 95% CI | 1077 | 137.1 | - | - | - | - | - | - | - | |
| 560.0 | 50.71 | |||||||||
| Equation (8) | 618.8 | 50.32 | 1.568 | - | - | - | - | - | - | 0.376 |
| 95% CI | 716.3 | 57.79 | 1.809 | - | - | - | - | - | - | |
| 521.3 | 42.84 | 1.327 | ||||||||
| Equation (9) | 371.1 | 30.77 | 2.357 | 222.4 | 76.42 | 5.118 | - | - | - | 0.459 |
| 95% CI | 476.9 | 36.07 | 2.836 | 273.8 | 82.32 | 5.888 | - | - | - | |
| 265.3 | 29.64 | 2.419 | 194.7 | 75.78 | 3.486 | |||||
| Equation (10) | 429.6 | 33.94 | 2.168 | 51.61 | 99.86 | 18.60 | 124.8 | 74.35 | 17.37 | 0.556 |
| 95% CI | 495.6 | 34.41 | 2.606 | 82.83 | 103.7 | 20.26 | 145.1 | 74.73 | 23.93 | |
| 473.6 | 32.86 | 2.367 | 45.23 | 96.69 | 4.327 | 101.7 | 72.45 | 12.03 |
| Equation (11) | 673.0 | - | - | 0.901 |
| 95% CI | 650.1 | - | - | |
| 695.9 | ||||
| Equation (12) | 118,770.3 | 104.9 | 2.652 | 0.999 |
| 95% CI | 117,054.6 | 103.7 | 2.612 | |
| 120,486.0 | 106.1 | 2.692 |
| Equation (13) | 749.8 | - | - | 0.0 |
| 95% CI | 678.8 | - | - | |
| 820.9 | ||||
| Equation (14) | 127,657.8 | 110.0 | 2.499 | 0.762 |
| 95% CI | 118,635.2 | 105.2 | 2.317 | |
| 136,680.4 | 114.8 | 2.681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borg, M.G.; Borg, M.A. A Trendline and Predictive Analysis of the First-Wave COVID-19 Infections in Malta. Epidemiologia 2023, 4, 33-50. https://doi.org/10.3390/epidemiologia4010003
Borg MG, Borg MA. A Trendline and Predictive Analysis of the First-Wave COVID-19 Infections in Malta. Epidemiologia. 2023; 4(1):33-50. https://doi.org/10.3390/epidemiologia4010003
Chicago/Turabian StyleBorg, Mitchell G., and Michael A. Borg. 2023. "A Trendline and Predictive Analysis of the First-Wave COVID-19 Infections in Malta" Epidemiologia 4, no. 1: 33-50. https://doi.org/10.3390/epidemiologia4010003
APA StyleBorg, M. G., & Borg, M. A. (2023). A Trendline and Predictive Analysis of the First-Wave COVID-19 Infections in Malta. Epidemiologia, 4(1), 33-50. https://doi.org/10.3390/epidemiologia4010003






