Deep-Data-Driven Neural Networks for COVID-19 Vaccine Efficacy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
- S(t):
- The individuals that are susceptible per time
- I(t):
- The individuals that are infected per time
- R(t):
- The individuals that are recovered per time
- N(t):
- The total population per timewith , , transmission rate, recovery rate, efficacy rate and vaccination rate v. The population per time is assumed to be constant throughout the vaccination regime.
2.1.1. Non-Negativity of the Model
2.1.2. Boundedness of the Model
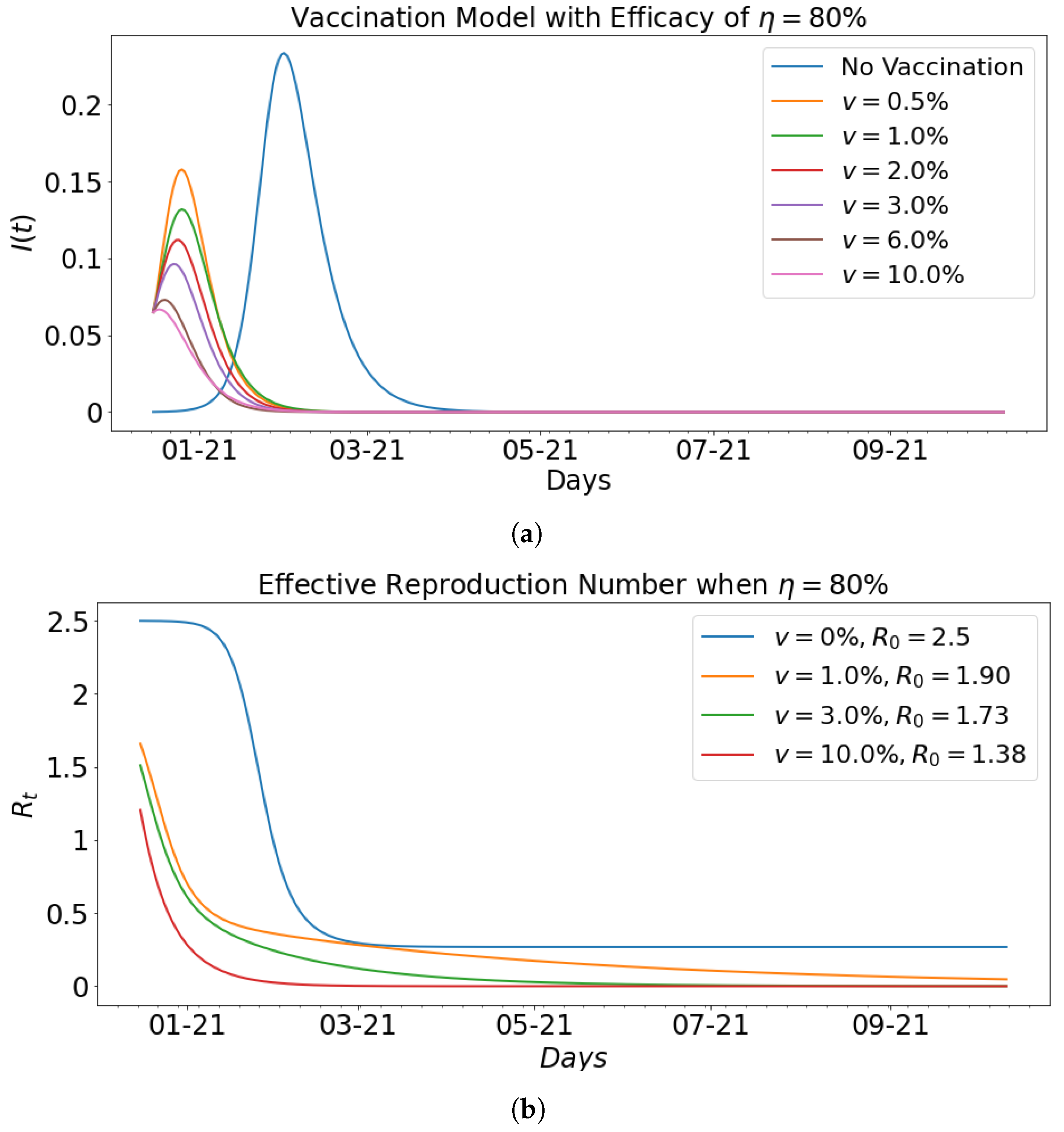
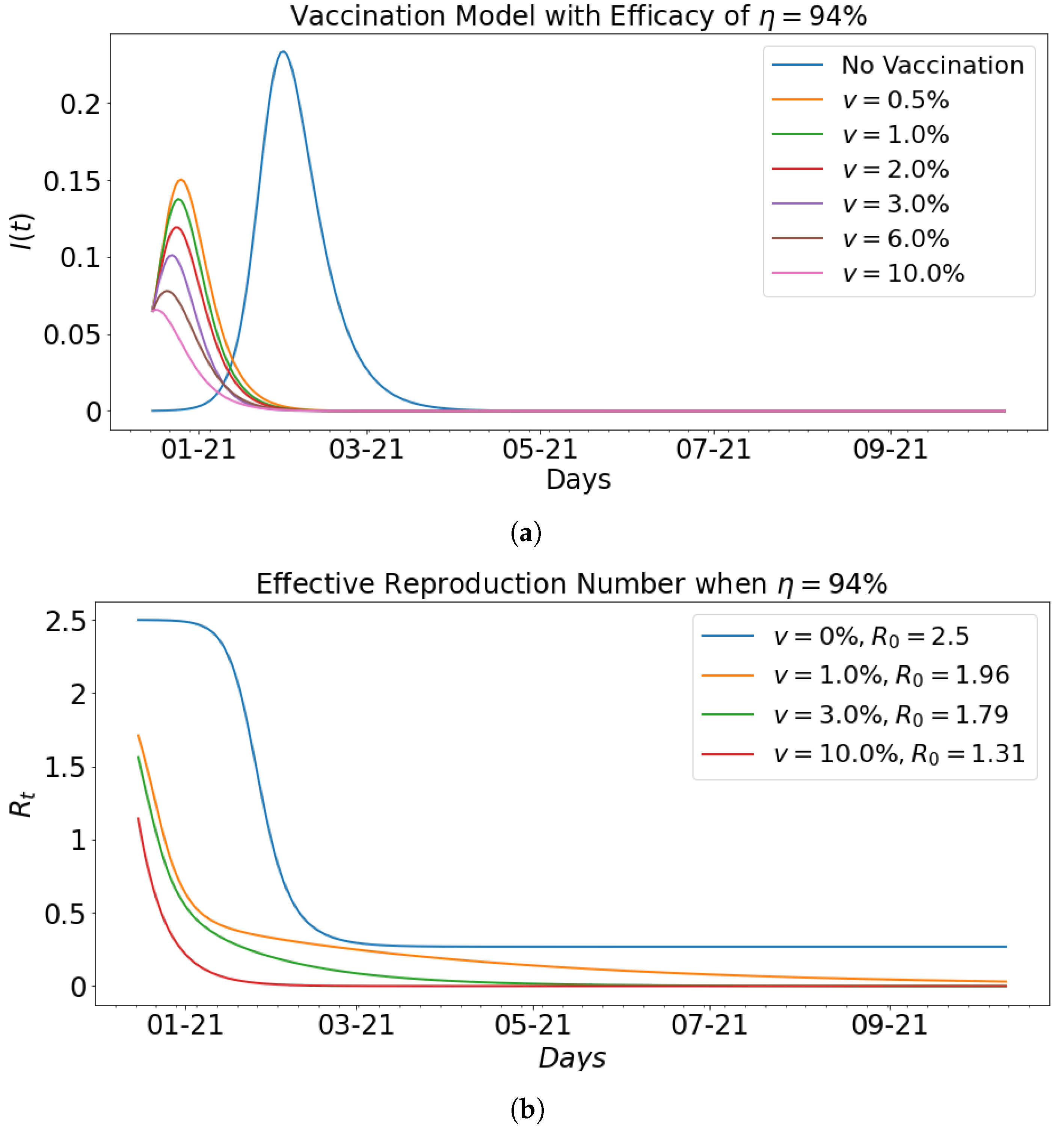
2.1.3. The Basic Reproduction Number
2.2. Deep Learning Algorithms
2.2.1. Feedforward Neural Network (FNN)
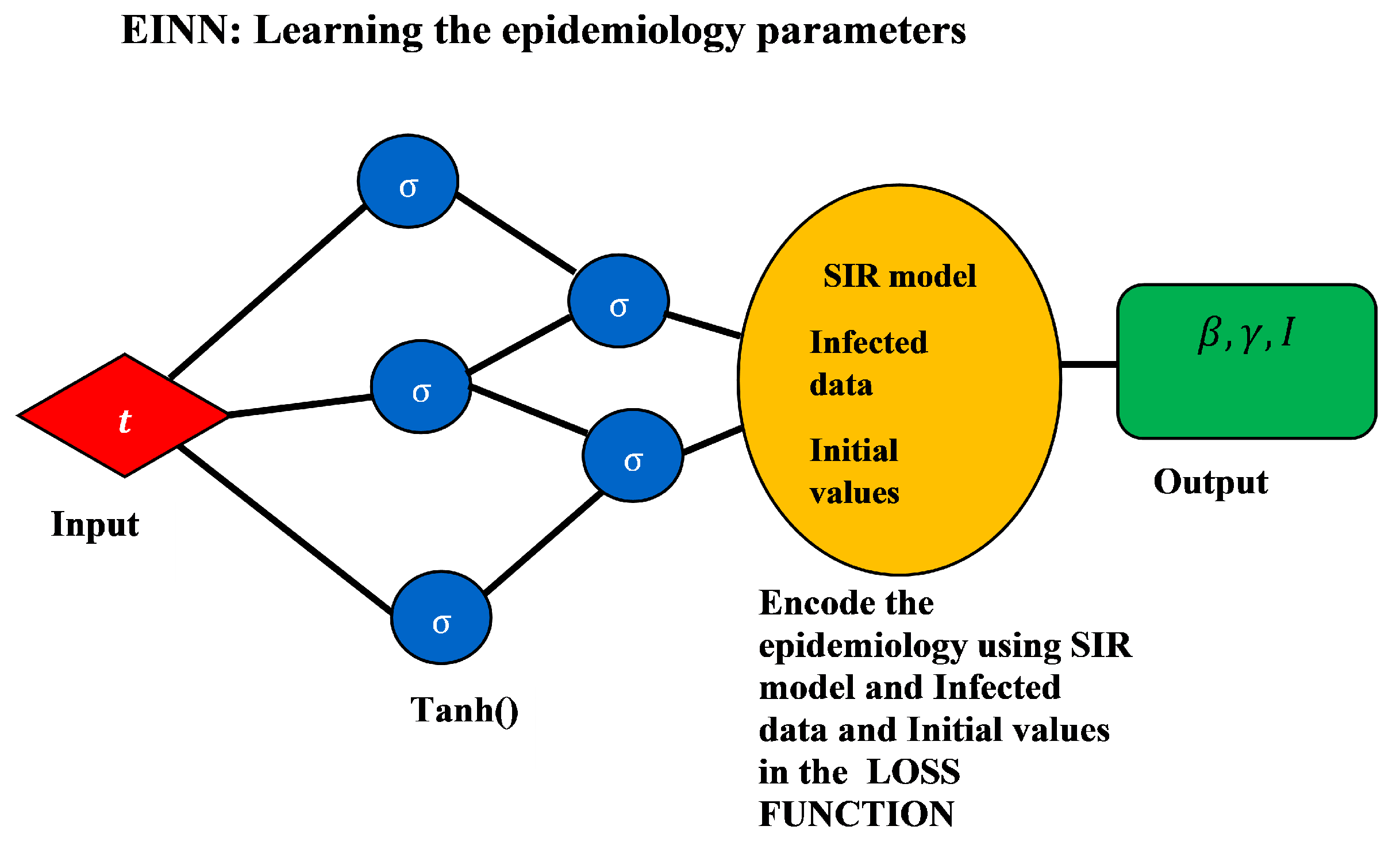
- Epidemiology Informed Neural Network (EINN)The epidemiology informed neural network (EINN) is inspired by a physics informed neural network (PINN) [13] which incorporates the epidemiological parameters of the model and initial values into the loss function. . The output from EINN satisfies the differential equations in model (1). This is achieved by encoding the the residuals of the model (1) into the loss function. The method of automatic differentiation [24] is used to compute the derivatives of the output with respect to time for each residual equation. In this study, the mean squared error (MSE) is encoded as the loss function which consists ofwherewhere the residualThe Adam optimizer which is a first order gradient-based optimization is employed to update the networks’ parameters by minimizing the loss function.Figure 1 shows the schematic diagram of the epidemiology informed neural network (EINN). The data is preprocessed by using a mini-max scaler factor to allow for smooth training in the neural network. 80 neurons are used for each of the five hidden layers. The Adam optimizer is used in all the data-driven simulations. In order to impose the epidemiological constraints, the Latin hypercube sampling [25] is employed to sample 3000 data points and the spline cubic interpolation is also used to sample 5000 data points. The tangent hyperbolic activation function is applied to all the hidden layers while the softplus activation is applied to the output layer. Implementation of EINN is done in Tensorflow which is run on Python.
| Algorithm 1 Epidemiology Informed Neural Network (EINN) |
|

2.2.2. Recurrent Neural Network (RNN)
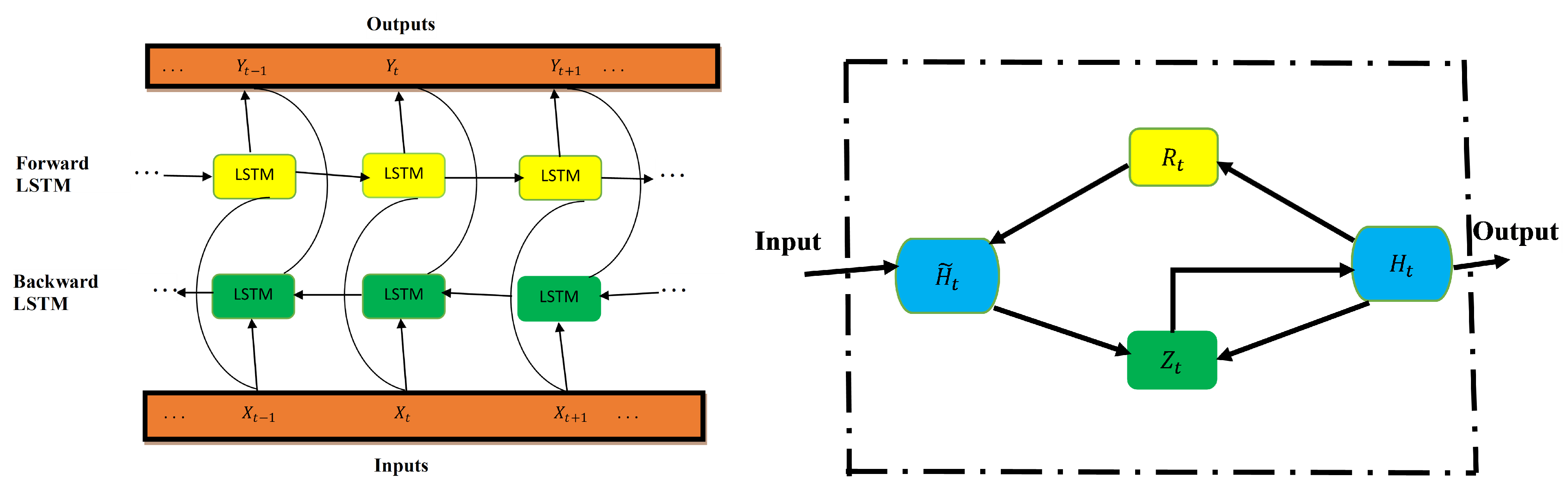
- Long Short-Term Memory (LSTM)The long short-term memory (LSTM) is a variant of recurrent neural network (RNN) used to handle sequential data like time series data. It was developed to solve the vanishing gradient problem [26]. The LSTM has three gates that control the flow of information: input, forget, and output gates. These gates have logistic functions that control the weighted sums obtained during training by backpropagation [4]. The cell state manages the input and forget gates. The output comes from either the output gate or hidden state. The unique feature of this network is that it is able to learn long dependencies within the data and able to effectively handle time series data. Given the input data , and the number of hidden units h, the gates of the LSTM can be defined as follows.
- Input Gate:
- Output Gate:
- Forget Gate:
- Intermediate cell state:
- Cell State (next memory input):
- New State: ,
where- are the weight parameters and are the bias parameters of each respective gate.
- denote the weight parameters, and is the bias parameter and ∘ is the element-wise multiplication. The value of is ascertained from the output of memory cells and the current time step .
- ∘ is the element-wise multiplication.
Figure 2 shows LSTM architecture. The input, forget, and output gates are represented by , respectively. The memory cells and memory cell content are denoted, respectively, as C and . - Bidirectional LSTMThe improved version of the LSTM is bidirectional LSTM (BiLSTM). The network is structured in a way that allows for both backward and forward propagation through the sequential layers [4]. In contrast to LSTM (which only allows for forward pass through the current state), the BiLSTM’s unique advantage is that there is an improvement in accuracy in state reconstruction. This structure combines two hidden states, which allows for information flow from the forward layer to the backward layer. The forward, backward, and output sequences are defined as follows:
- Forward hidden:
- Backward hidden:
- Output: .
where is the sigmoid function application which is the LSTM unit in the structure of BiLSTM. - Gated Recurrent Unit (GRU)GRU is built to improve the performance of LSTM and reduce the number of its parameters. The input and forget gates from the LSTM model are merged into one gate called the update gate [4]. It is made up of only two gates, update and reset gates, instead of three gates in LSTM. The update gate couples the input and forget gates of the LSTM and the output gate as a reset gate. This gives the GRU an enhanced improvement in LSTM. The relationships among the gates are defined as follows.
- Update gate:
- Reset gate:
- Cell State:
- New state: ,
where- are the weight parameters and are the bias parameters.
- are the weight parameters and is a bias parameter. The current update gate is a combination of the previous hidden state and current candidate hidden state .
Figure 3 presents BiLSTM architecture (left) and GRU architecture (right). In BiLSTM, the forward and backward layers are indicated by yellow and green colors, respectively. In GRU, the reset and update gates are represented by and , respectively.
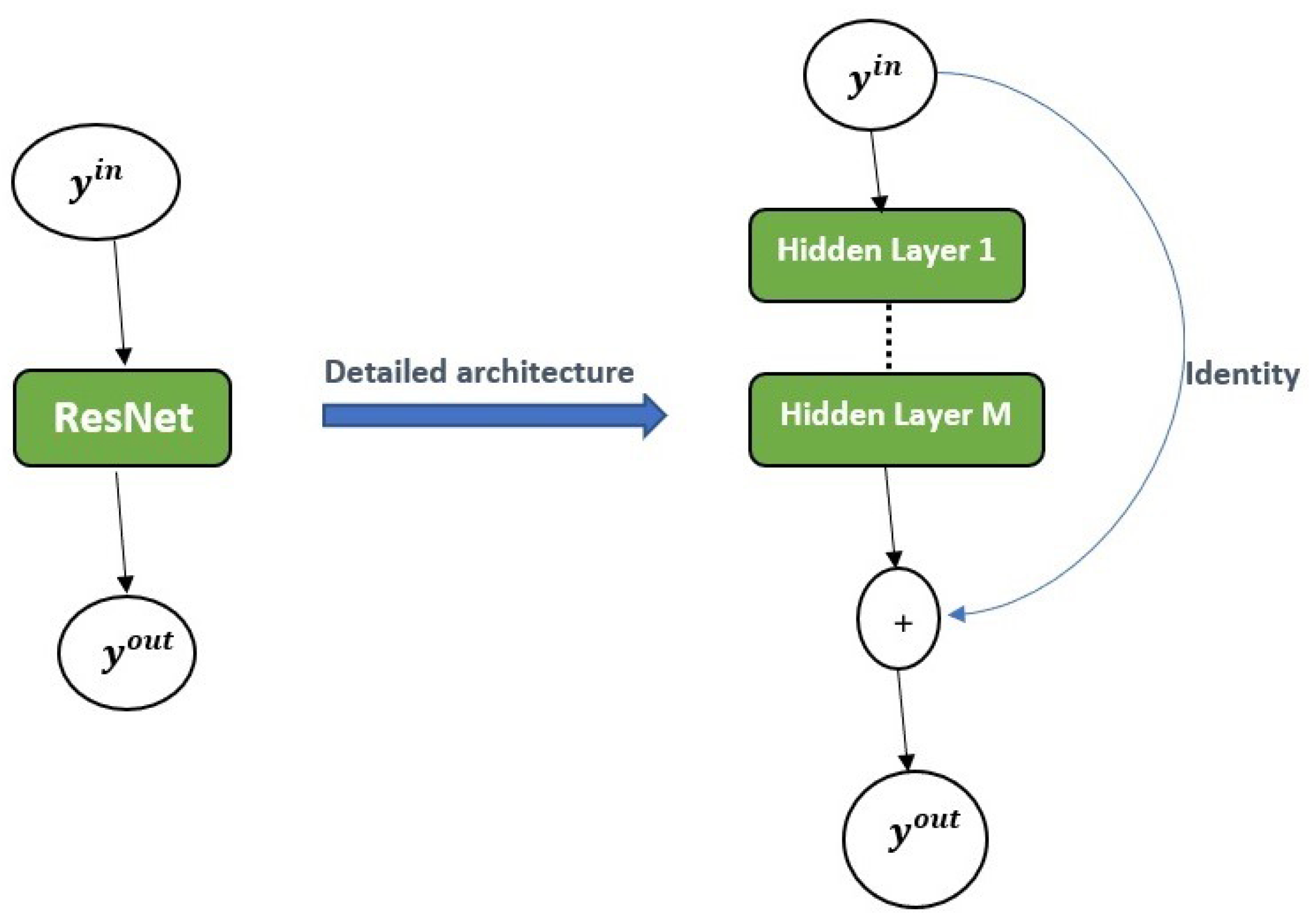
2.2.3. Residual Neural Network (ResNet)
2.3. Data Preprocessing
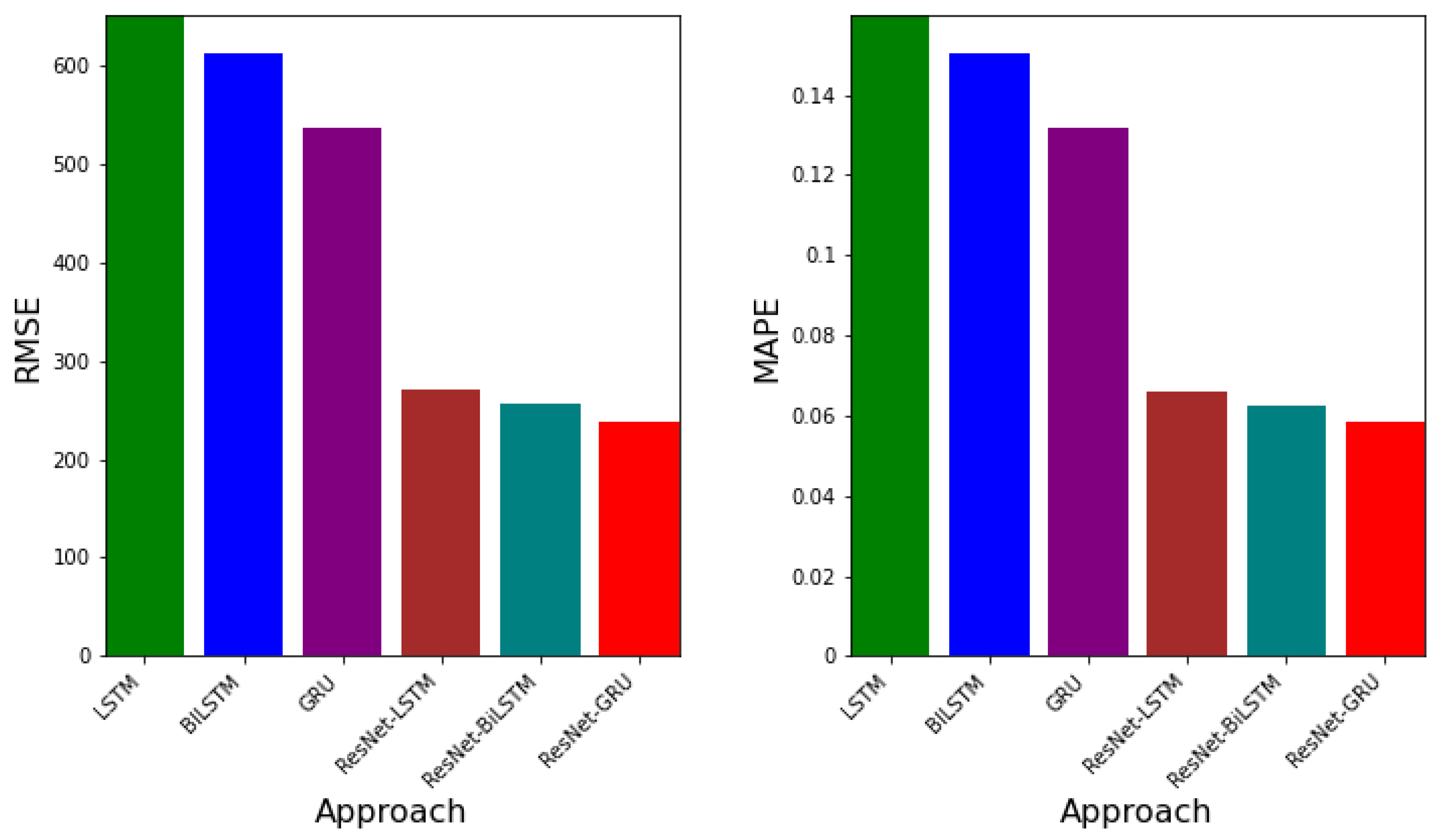
2.4. Error Metrics
- RMSE: By the taking the square root of the mean squared error (MSE), the Root Mean Squared Error (RMSE) is obtained and defined as follows:This error metric scales the mean squared error (MSE) which serves as a normalizer of large errors. The RMSE serves as a general-purpose error metric and is excellent for numerical predictions [28]. In terms of measuring model accuracy, the RMSE, as a scale-dependent variable, is used to compare errors of prediction from different models or model configurations for a particular variable.
- MAPE: The Mean Absolute Percent Error (MAPE) is the relative error in the mean absolute error.The main advantage of using MAPE is that since it is weighted mean absolute error, it is useful for quantile regression. Drawbacks include that it cannot have small values close to zero or zero in the denominator; since percentages cannot exceed , any values high or low cannot be captured; and high negative errors are penalized [29].
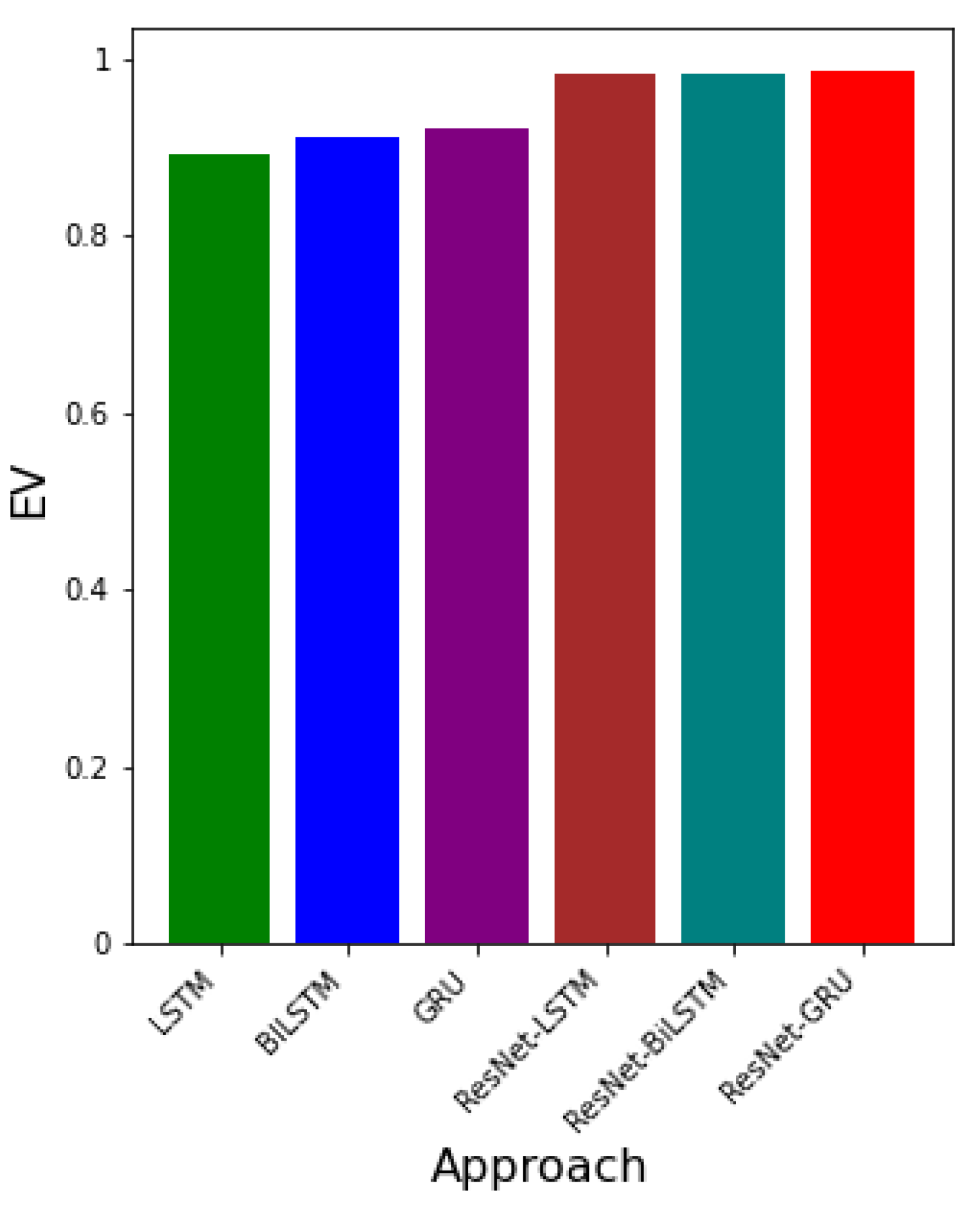
- EV-The Explained Variance is the measure of variation in the predicted y as explained by the neural network algorithm [4].where is the variance between the predicted and the real data. The Explained Variance (EV) is analogous to the co-efficient of determination used for linear regression. The EV is ideal for nonlinear regression. When gets closer to 1, it means the algorithm predicted the targets correctly.
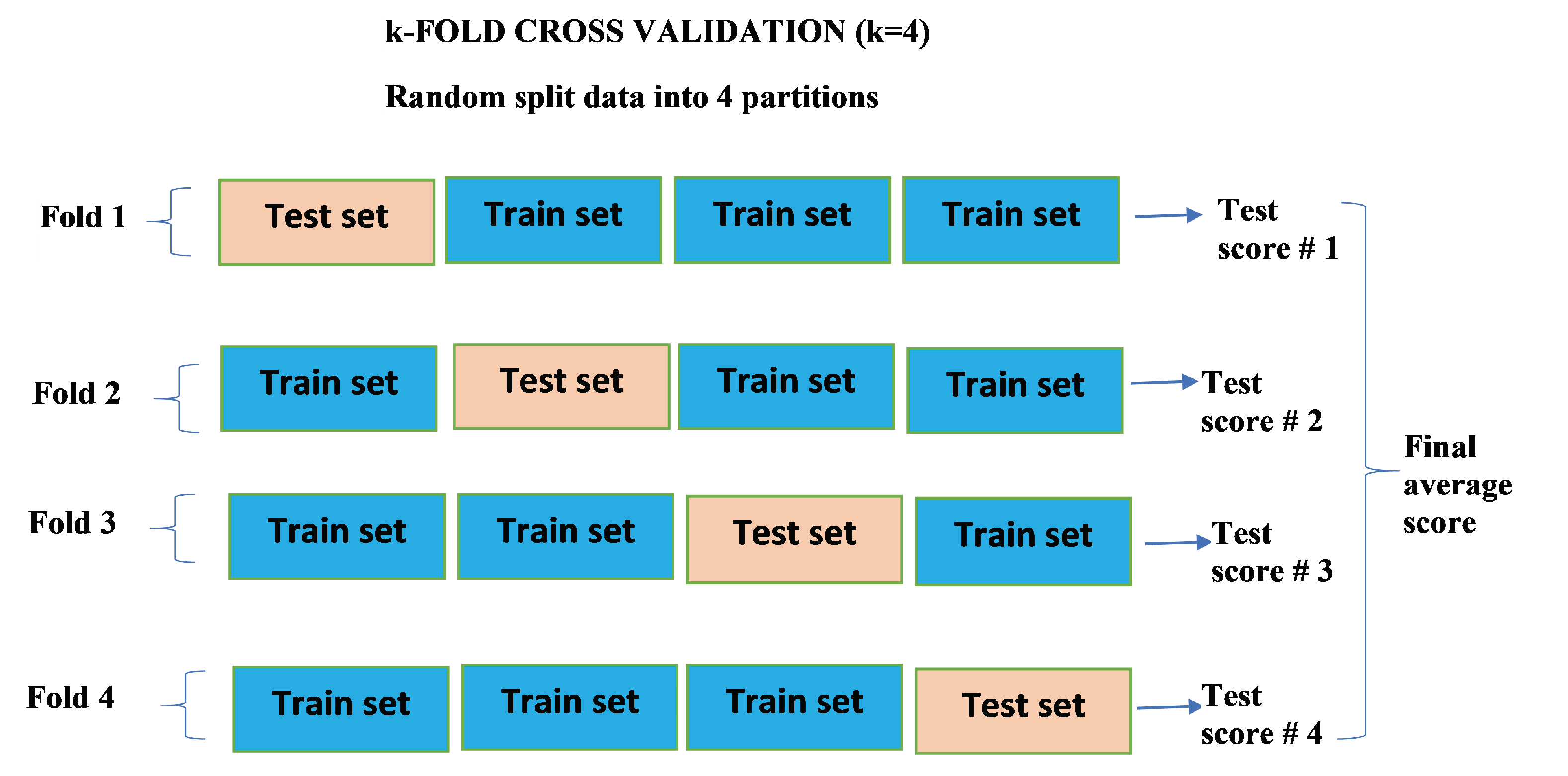
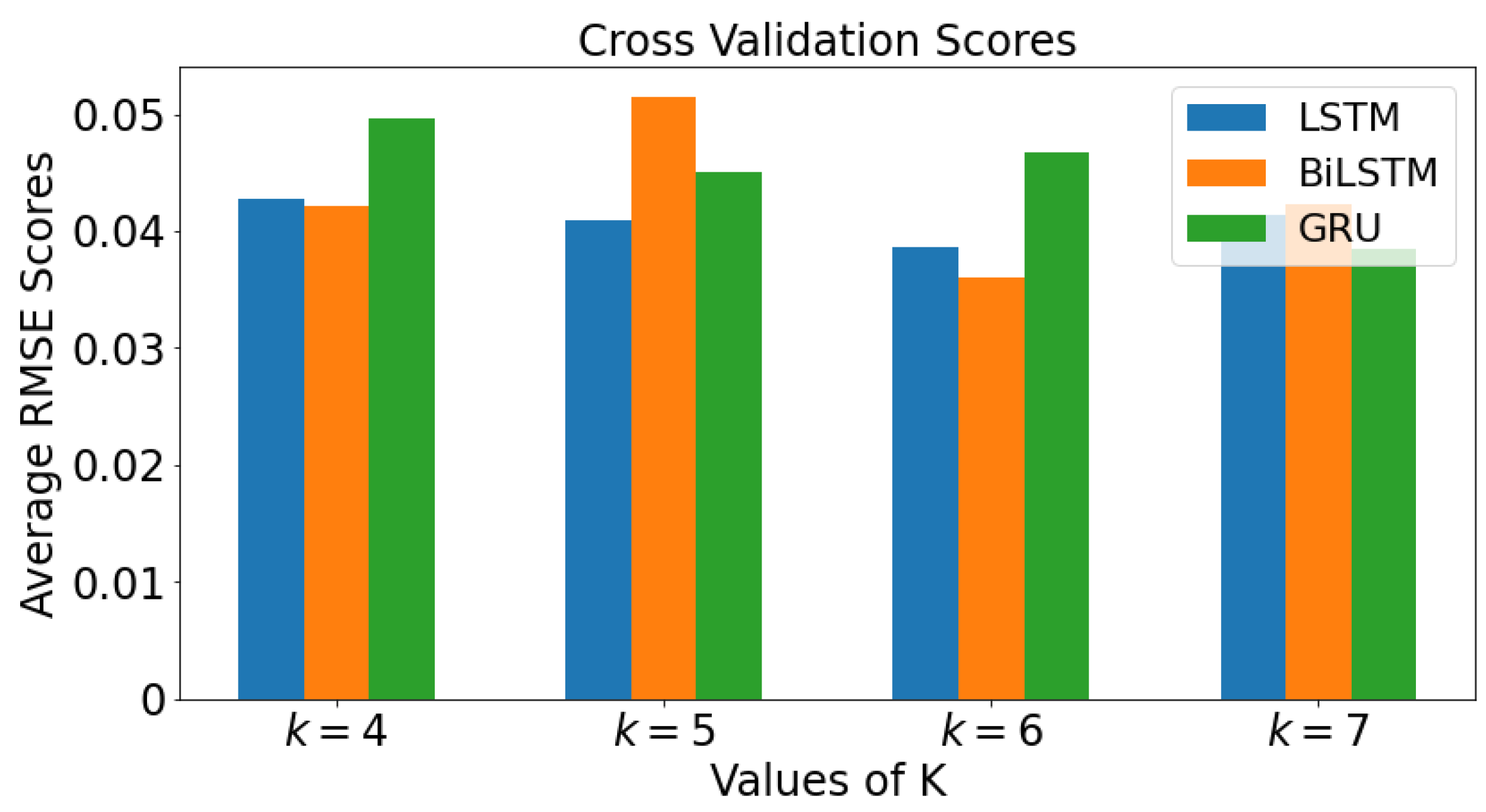
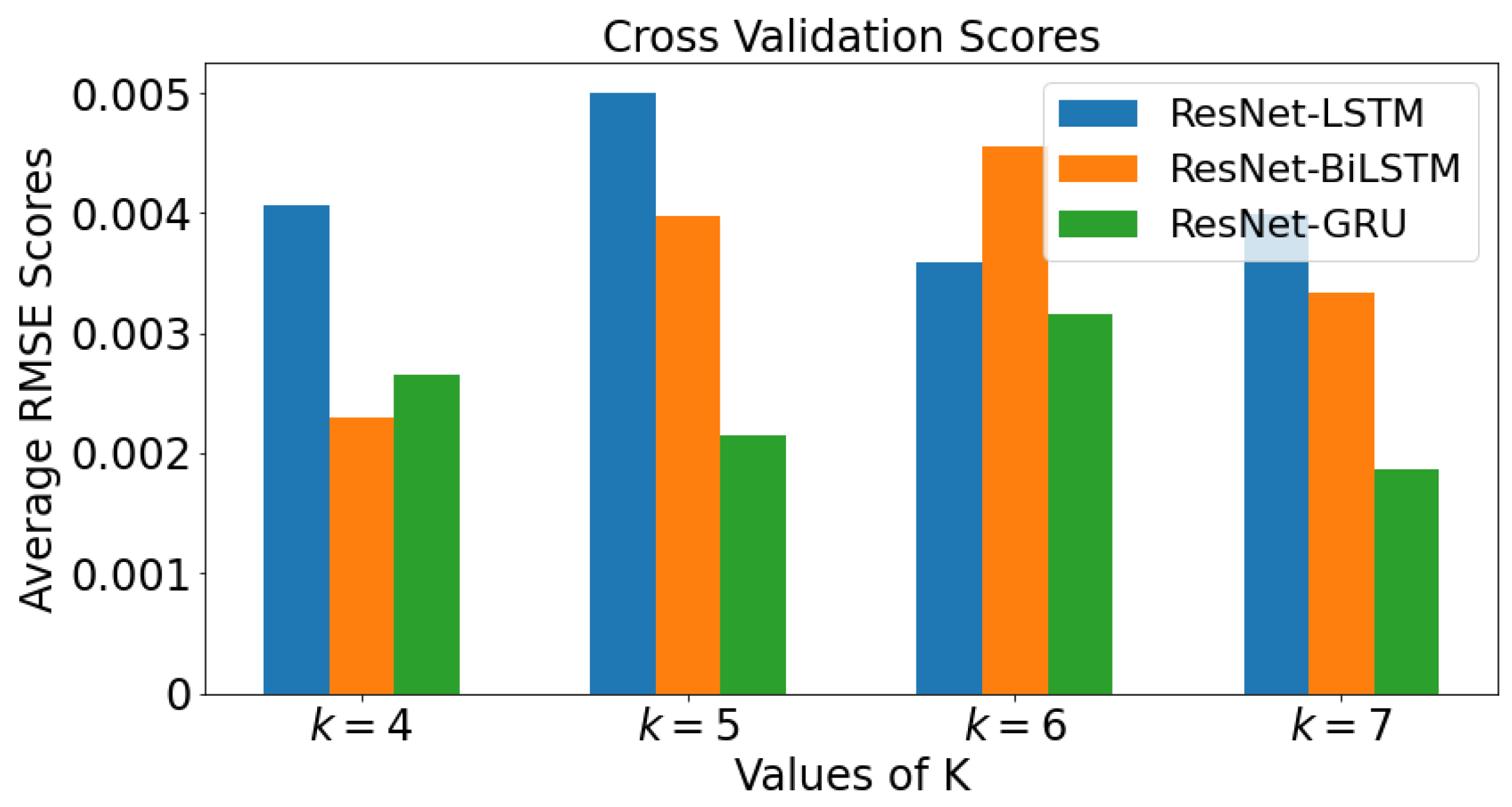
2.5. k-Fold Cross Validation
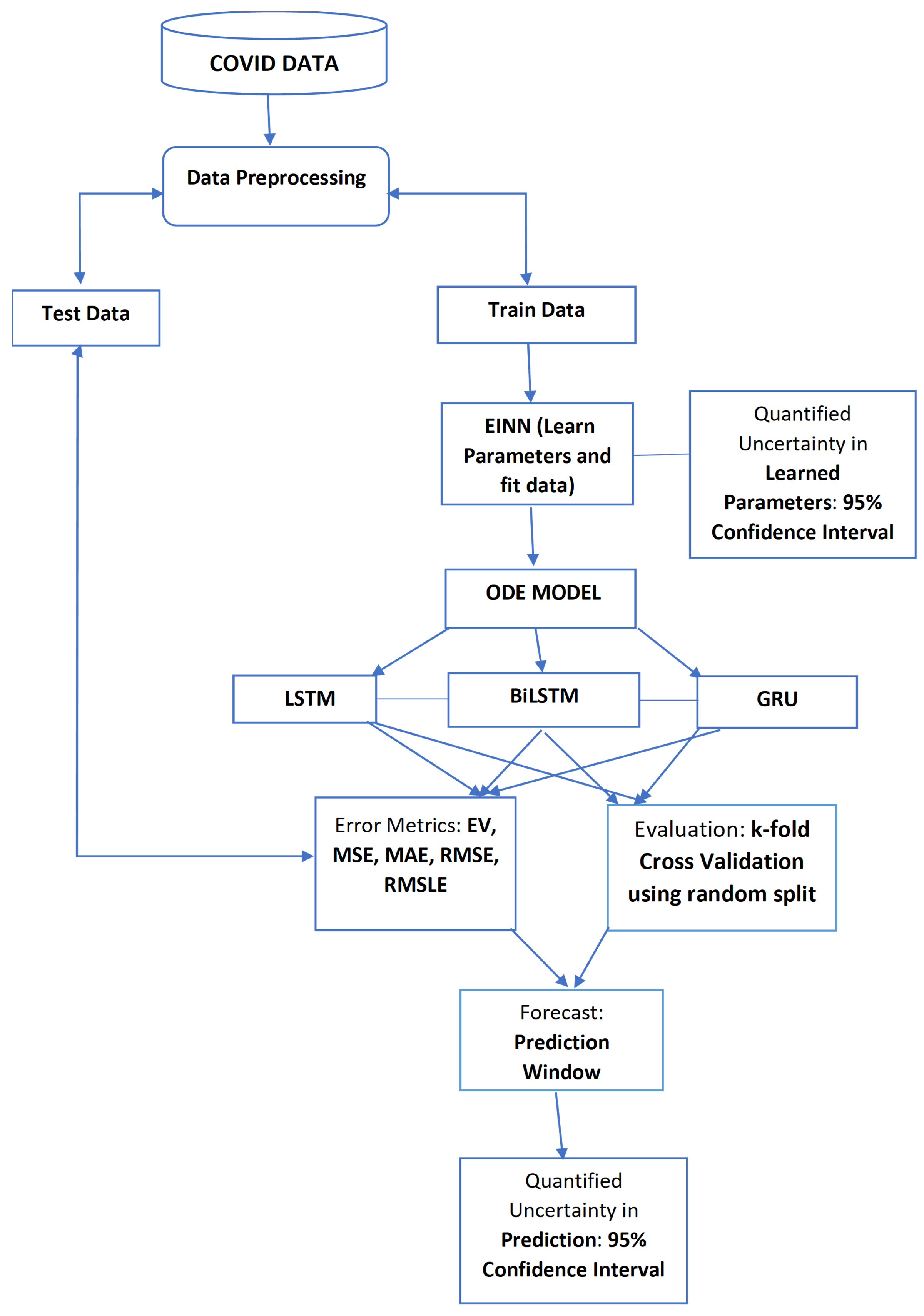
2.6. Proposed System
3. Results and Discussion
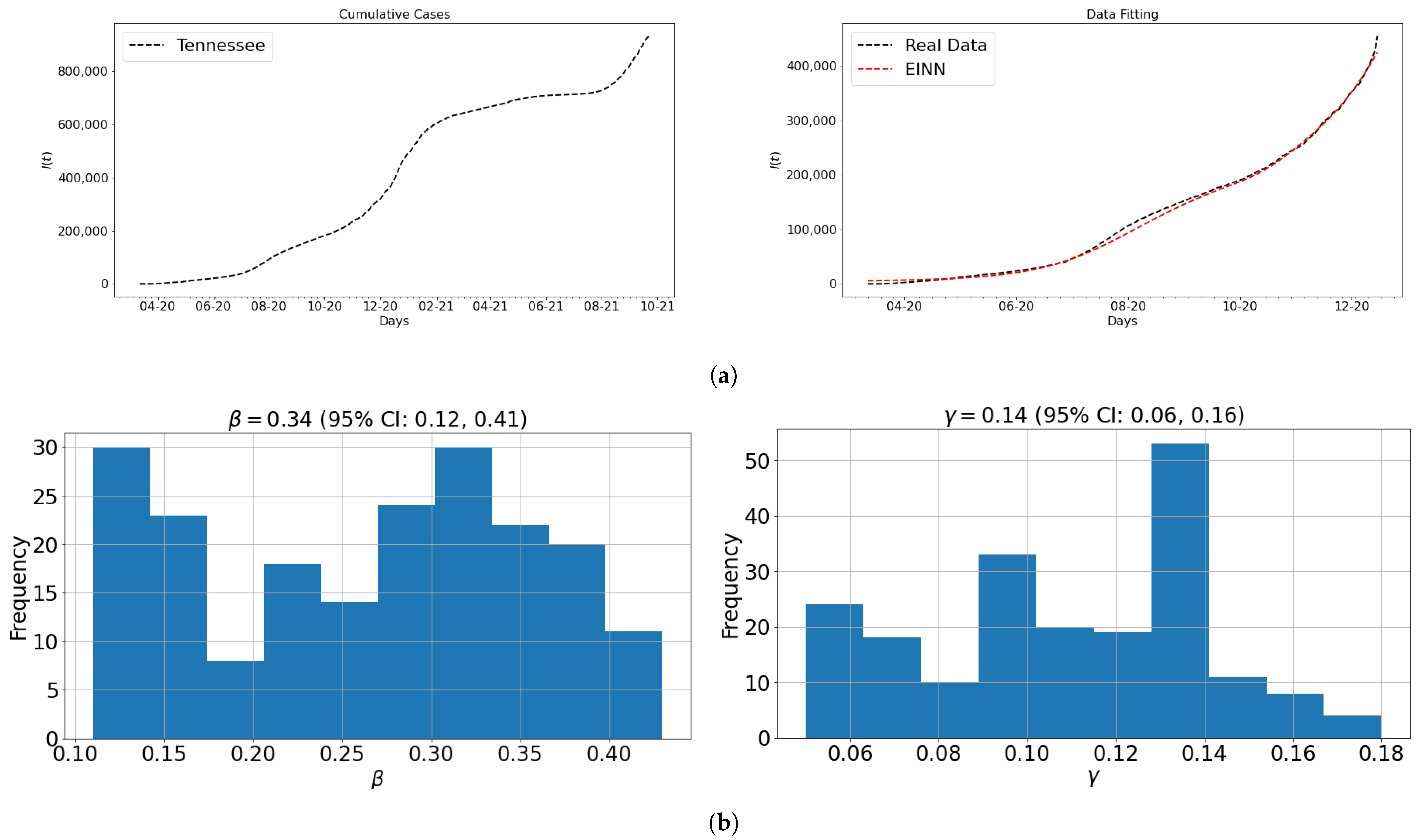
3.1. Data and Parameter Identification
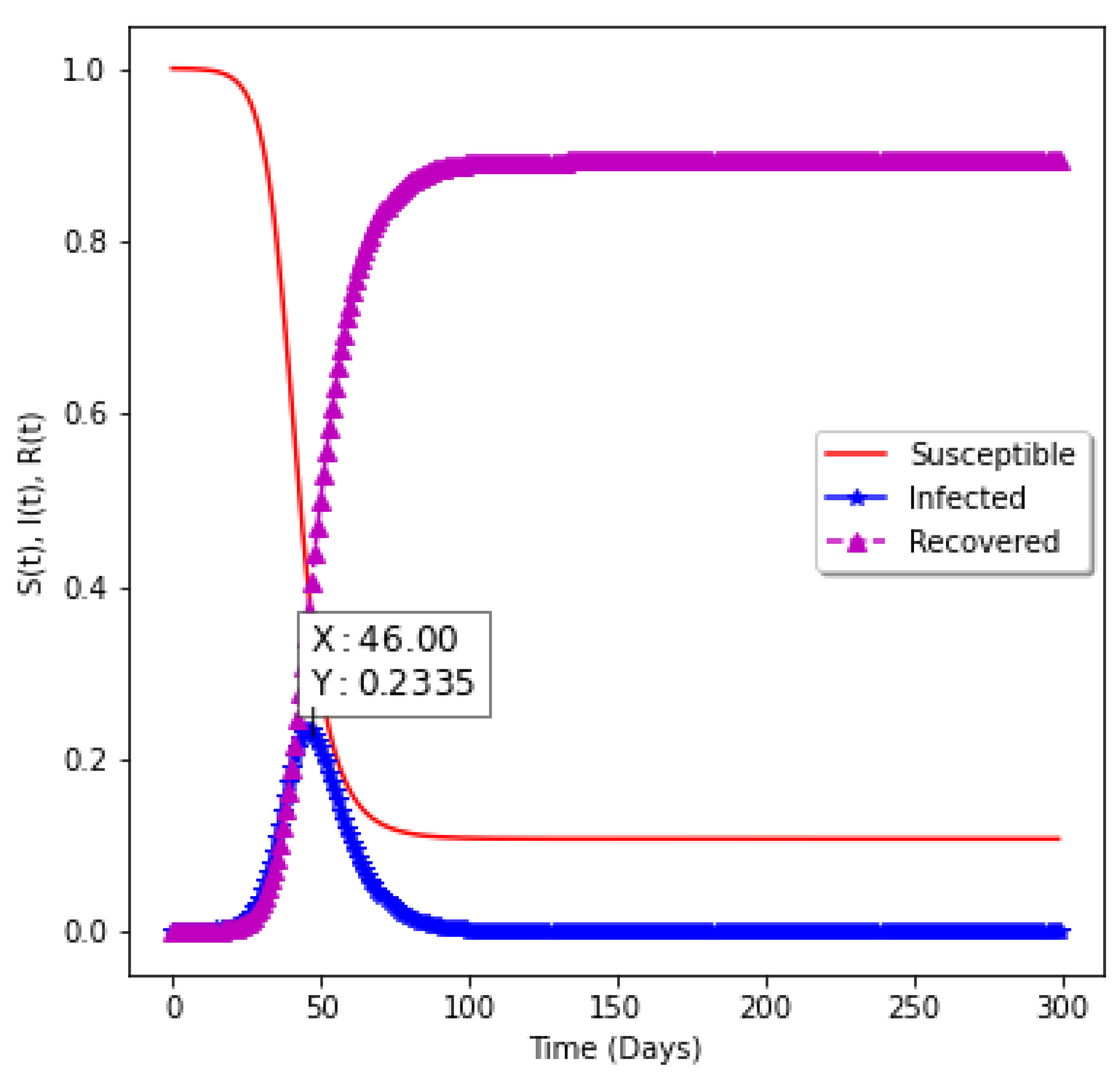
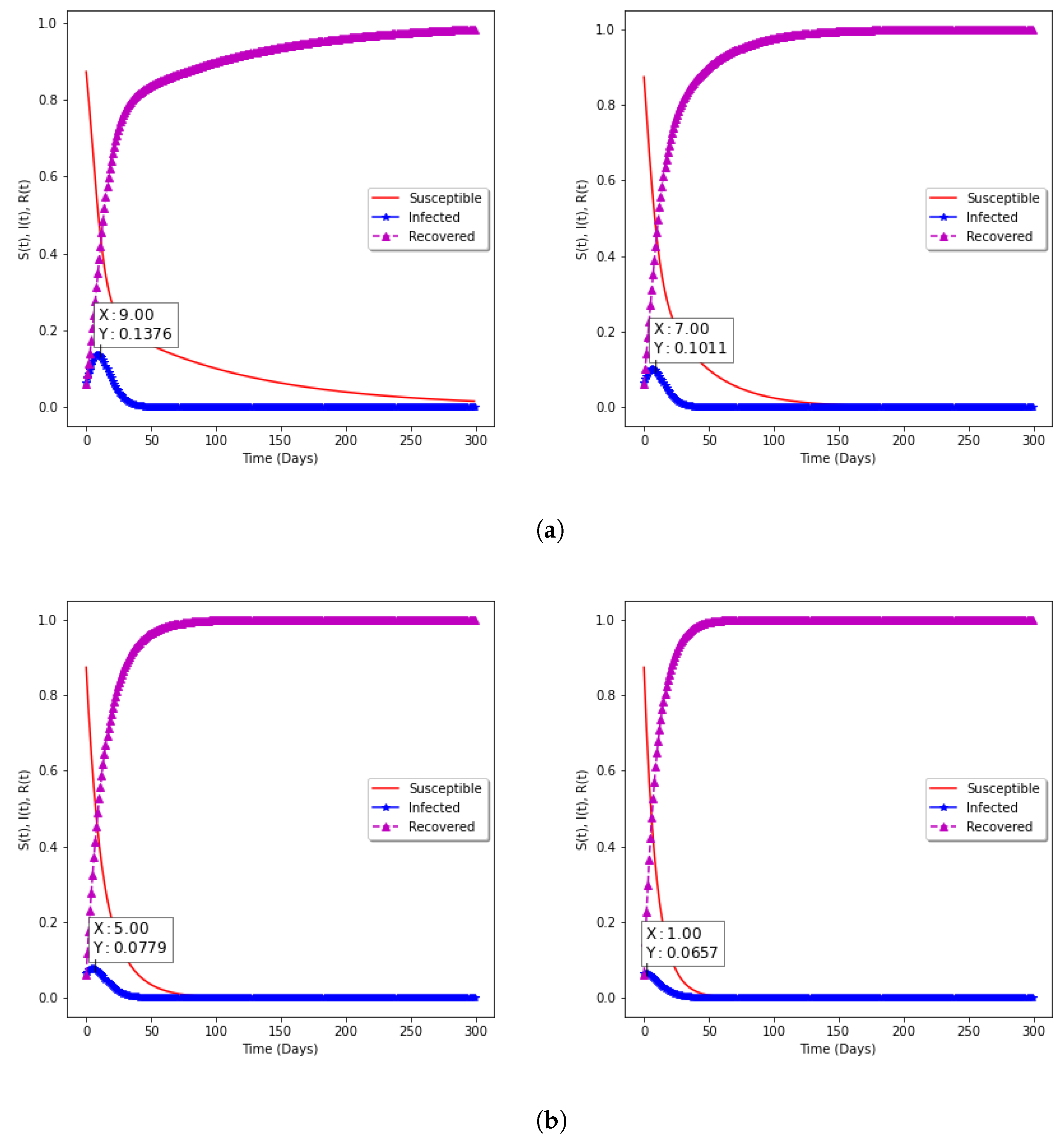
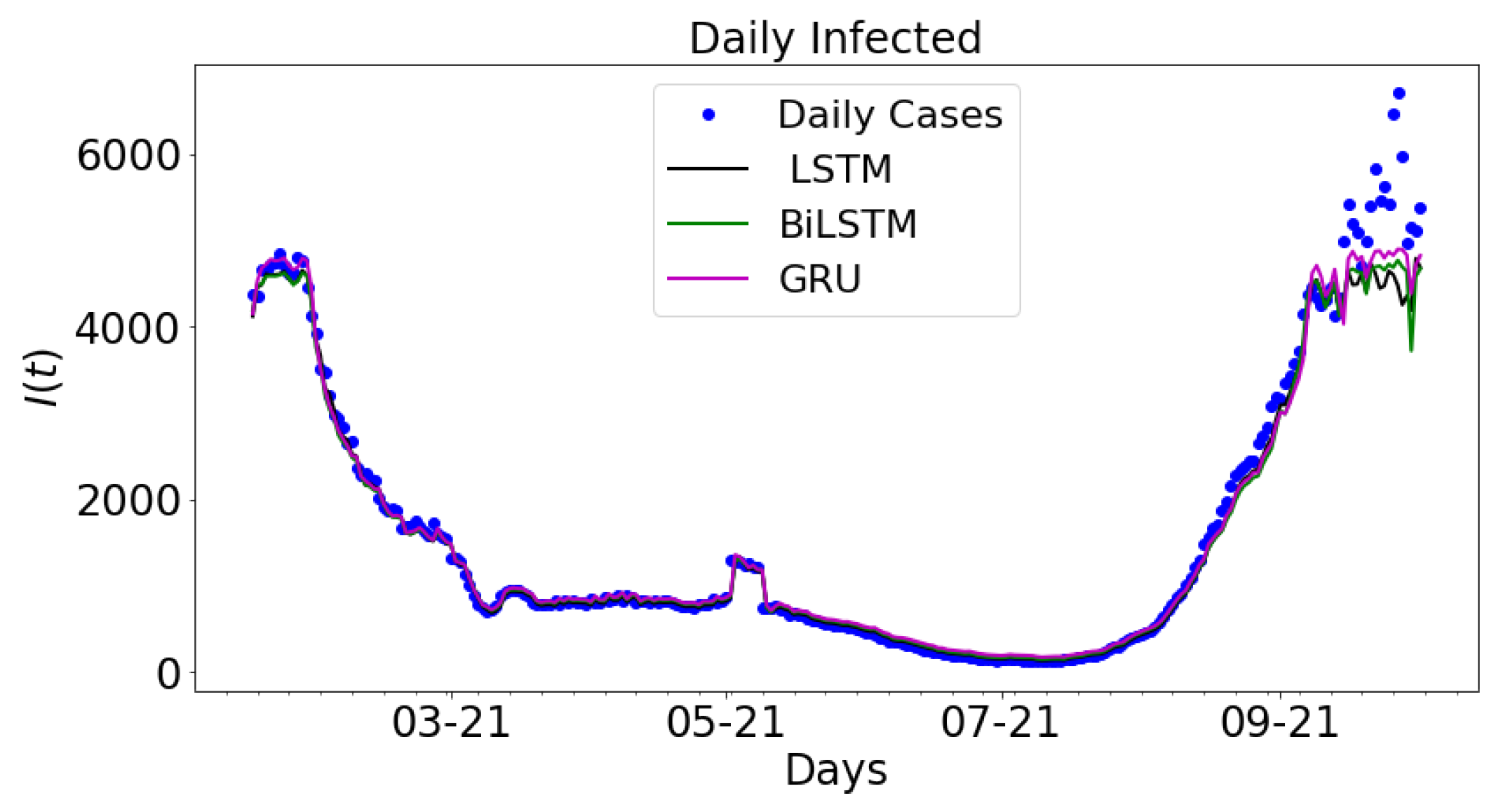
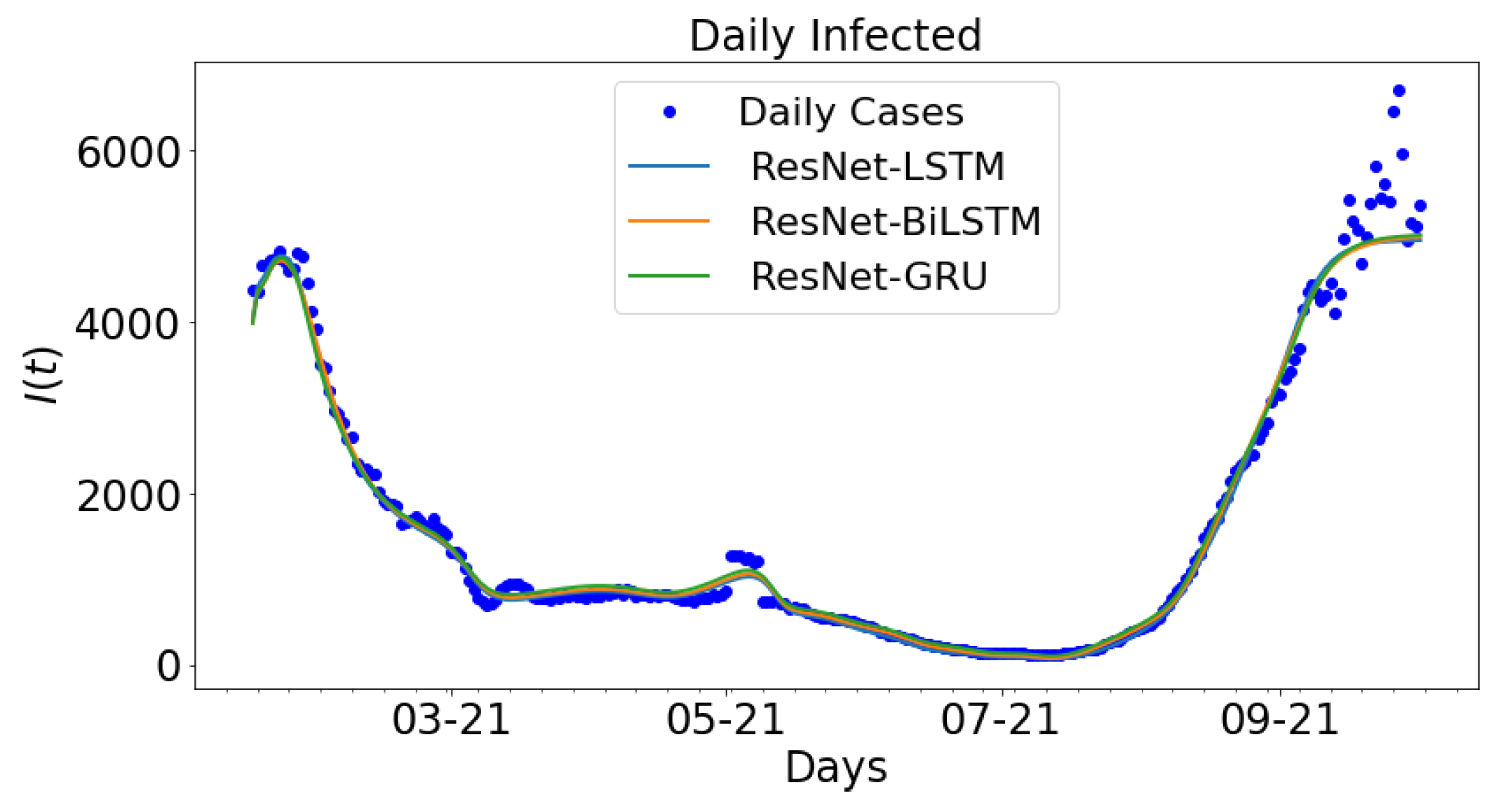
3.2. Data-Driven Simulations
3.3. Error Metrics for Data-Driven Simulations
3.4. k-Fold Cross Validation
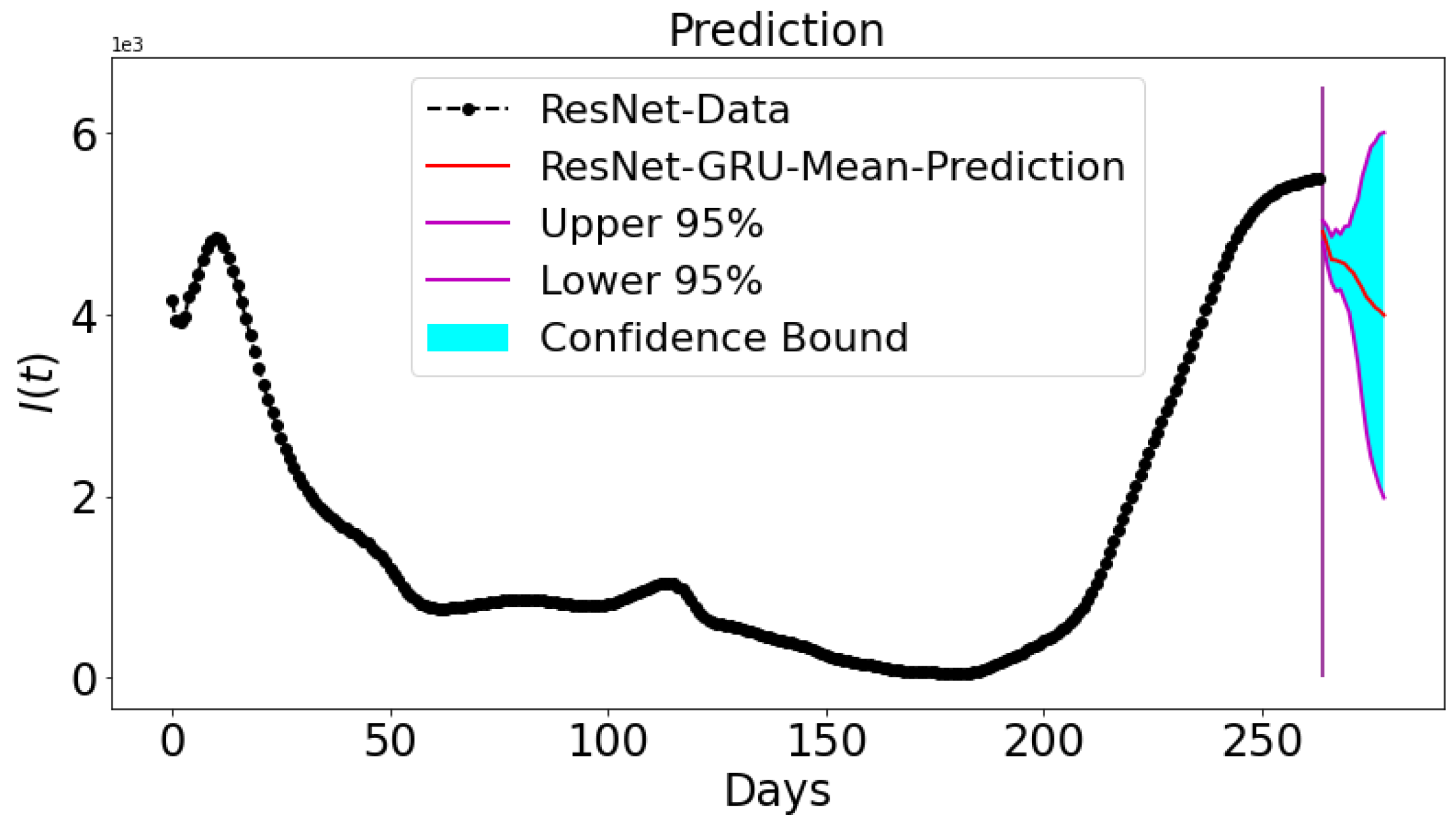
3.5. Prediction and Confidence Interval
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghamizi, S.; Rwemalika, R.; Cordy, M.; Veiber, L.; Bissyandé, T.F.; Papadakis, M.; Klein, J.; Le Traon, Y. Data-driven simulation and optimization for COVID-19 exit strategies. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 3434–3442. [Google Scholar]
- Long, J.; Khaliq, A.; Furati, K. Identification and prediction of time-varying parameters of COVID-19 model: A data-driven deep learning approach. Int. J. Comput. Math. 2021, 98, 1617–1632. [Google Scholar] [CrossRef]
- Martínez-Rodríguez, D.; Gonzalez-Parra, G.; Villanueva, R.J. Analysis of key factors of a SARS-CoV-2 vaccination program: A mathematical modeling approach. Epidemiologia 2021, 2, 140–161. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110–121. [Google Scholar] [CrossRef]
- Webb, G. A COVID-19 epidemic model predicting the effectiveness of vaccination. Math. Appl. Sci. Eng. 2021, 2, 134–148. [Google Scholar] [CrossRef]
- Verger, P.; Dubé, È. Restoring confidence in vaccines in the COVID-19 era. Expert Rev. Vaccines 2020, 19, 991–993. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Kuznetsov, Y.A.; Piccardi, C. Bifurcation analysis of periodic SEIR and SIR epidemic models. J. Math. Biol. 1994, 32, 109–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biswas, M.H.A.; Paiva, L.T.; De Pinho, M. A SEIR model for control of infectious diseases with constraints. Math. Biosci. Eng. 2014, 11, 761. [Google Scholar] [CrossRef]
- Hao, Y.; Xu, T.; Hu, H.; Wang, P.; Bai, Y. Prediction and analysis of corona virus disease 2019. PLoS ONE 2020, 15, e0239960. [Google Scholar] [CrossRef] [PubMed]
- Chowell, G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infect. Dis. Model. 2017, 2, 379–398. [Google Scholar] [CrossRef]
- Kharazmi, E.; Cai, M.; Zheng, X.; Lin, G.; Karniadakis, G.E. Identifiability and predictability of integer-and fractional-order epidemiological models using physics-informed neural networks. Nat. Comput. Sci. 2021, 1, 744–753. [Google Scholar] [CrossRef]
- Raissi, M.; Ramezani, N.; Seshaiyer, P. On parameter estimation approaches for predicting disease transmission through optimization, deep learning and statistical inference methods. Lett. Biomath. 2019, 6, 1–26. [Google Scholar] [CrossRef]
- Grimm, V.; Heinlein, A.; Klawonn, A.; Lanser, M.; Weber, J. Estimating the Time-Dependent Contact Rate of SIR and SEIR Models in Mathematical Epidemiology Using Physics-Informed Neural Networks; Technical Report; Universität zu Köln: Cologne, Germany, 2020. [Google Scholar]
- Dehesh, T.; Mardani-Fard, H.; Dehesh, P. Forecasting of COVID-19 confirmed cases in different countries with arima models. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Rustam, F.; Reshi, A.A.; Mehmood, A.; Ullah, S.; On, B.W.; Aslam, W.; Choi, G.S. COVID-19 future forecasting using supervised machine learning models. IEEE Access 2020, 8, 101489–101499. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Lu, L.; Guo, L.; Karniadakis, G.E. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. J. Comput. Phys. 2019, 397, 108850. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Wu, K.; Xiu, D. Data driven governing equations approximation using deep neural networks. J. Comput. Phys. 2019, 395, 620–635. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Xiu, D. On generalized residual network for deep learning of unknown dynamical systems. J. Comput. Phys. 2021, 438, 110–362. [Google Scholar] [CrossRef]
- Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. An extended SEIR model with vaccination for forecasting the COVID-19 pandemic in Saudi Arabia using an ensemble kalman filter. Mathematics 2021, 9, 636. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 24 June 2021).
- Gray, D.L.; Michel, A.N. A training algorithm for binary feedforward neural networks. IEEE Trans. Neural Netw. 1992, 3, 176–194. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Tennessee Health Department. Available online: https://www.tn.gov/health/cedep/ncov/data (accessed on 28 June 2021).
- Root Mean Squared Error. Available online: https://www.sciencedirect.com/topics/engineering/root-mean-squared-error (accessed on 24 June 2021).
- Mean Absolute Percentage Error. Available online: https://en.wikipedia.org/wiki/Mean_absolute_percentage_error (accessed on 12 July 2021).
- How to Configure k-Fold Cross-Validation. Available online: https://machinelearningmastery.com/how-to-configure-k-fold-cross-validation/ (accessed on 29 June 2021).


| State | Min | Max | STD | Skewness | Kurtosis | |||
|---|---|---|---|---|---|---|---|---|
| Tennessee | 1 | 717,916 | 279,540.7136 | 63,503.5 | 275,565 | 656,462 | 0.10058 | −1.6981 |
| Vaccination Rate | Infected | Days of Peak | |||
|---|---|---|---|---|---|
| 0.00 | 0.35 | 0.14 | 2.5 | 23.35 | 46 |
| 0.5 | 0.45 | 0.22 | 2.05 | 15.78 | 10 |
| 1 | 0.4 | 0.21 | 1.90 | 13.19 | 10 |
| 2 | 0.4 | 0.22 | 1.82 | 11.19 | 9 |
| 3 | 0.38 | 0.22 | 1.73 | 9.63 | 7 |
| 6 | 0.3 | 0.2 | 1.5 | 7.30 | 4 |
| 10 | 0.18 | 0.13 | 1.38 | 6.67 | 2 |
| Vaccination Rate | Infected | Days of Peak | |||
|---|---|---|---|---|---|
| 0.00 | 0.35 | 0.14 | 2.5 | 23.35 | 46 |
| 0.5 | 0.44 | 0.22 | 2.0 | 15.04 | 10 |
| 1 | 0.45 | 0.23 | 1.96 | 13.76 | 9 |
| 2 | 0.42 | 0.22 | 1.91 | 11.92 | 8 |
| 3 | 0.43 | 0.24 | 1.79 | 10.11 | 7 |
| 6 | 0.27 | 0.16 | 1.89 | 7.79 | 5 |
| 10 | 0.17 | 0.13 | 1.31 | 6.57 | 1 |
| Approach | Parameter | Value |
|---|---|---|
| LSTM/BiLSTM/GRU | Learning rate | 0.01 |
| Training Epochs | 500 | |
| Batch Size | 100 | |
| Layers | 02 | |
| Features | 01 | |
| Hidden units | 24 | |
| ResNet | Learning rate | 0.001 |
| Training Epochs | 200 | |
| Batch Size | 45 | |
| Layers | 03 | |
| Features | 01 | |
| Hidden units | 50 | |
| Cross Validation | Learning rate | 0.01 |
| Training Epochs | 1000 | |
| Batch Size | 100 | |
| Layers | 01 | |
| Features | 01 | |
| Hidden units | 12 |
| Approach | RMSE | MAPE | EV |
|---|---|---|---|
| LSTM | |||
| BiLSTM | |||
| GRU | |||
| ResNet-LSTM | |||
| ResNet-BiLSTM | |||
| ResNet-GRU |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torku, T.K.; Khaliq, A.Q.M.; Furati, K.M. Deep-Data-Driven Neural Networks for COVID-19 Vaccine Efficacy. Epidemiologia 2021, 2, 564-586. https://doi.org/10.3390/epidemiologia2040039
Torku TK, Khaliq AQM, Furati KM. Deep-Data-Driven Neural Networks for COVID-19 Vaccine Efficacy. Epidemiologia. 2021; 2(4):564-586. https://doi.org/10.3390/epidemiologia2040039
Chicago/Turabian StyleTorku, Thomas K., Abdul Q. M. Khaliq, and Khaled M. Furati. 2021. "Deep-Data-Driven Neural Networks for COVID-19 Vaccine Efficacy" Epidemiologia 2, no. 4: 564-586. https://doi.org/10.3390/epidemiologia2040039
APA StyleTorku, T. K., Khaliq, A. Q. M., & Furati, K. M. (2021). Deep-Data-Driven Neural Networks for COVID-19 Vaccine Efficacy. Epidemiologia, 2(4), 564-586. https://doi.org/10.3390/epidemiologia2040039






