Previous Article in Journal
Titanium Alloys at the Interface of Electronics and Biomedicine: A Review of Functional Properties and Applications
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronic Materials
Volume 7
Issue 1
10.3390/electronicmat7010002
electronicmat-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modeling SnC-Anode Material for Hybrid Li, Na, Be, Mg Ion-Batteries: Structural and Electronic Analysis by Mastering the Density of States

by
Fatemeh Mollaamin
1,* and
Majid Monajjemi
2
1
Department of Biomedical Engineering, Faculty of Engineering and Architecture, Kastamonu University, Kastamonu 37150, Turkey
2
Department of Biology, Faculty of Science, Kastamonu University, Kastamonu 37100, Turkey
*
Author to whom correspondence should be addressed.
Electron. Mater. 2026, 7(1), 2; https://doi.org/10.3390/electronicmat7010002 (registering DOI)
Submission received: 21 November 2025 / Revised: 19 December 2025 / Accepted: 29 December 2025 / Published: 1 January 2026
Browse Figures
Versions Notes

Abstract

The increasing demand for next-generation rechargeable batteries that offer high energy density, a long lifespan, high safety, and low cost has led to a need for better electrode materials for lithium-ion batteries. This also involves developing alternative storage systems using common resources such as sodium-ion batteries, beryllium-ion batteries, or magnesium-ion batteries. Tin carbide (SnC) is highly promising as an anode material for lithium, sodium, beryllium, and magnesium ion batteries due to its ability to form nanoclusters like Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C. A detailed study was done using computational methods, including analysis of charge density differences, total density of states, and electron localization function for these hybrid clusters. This research suggests that SnC could be useful in multivalent-ion batteries using Be2+ ions because its properties can match or even exceed those of monovalent ions. The study also shows that the maximum capacity, stability energy, and ion movement in these materials can be understood by looking at atomic-level properties like the coordination between host atoms and ions. Recent findings on using tin carbide in these types of batteries and methods to improve their performance have been discussed.

1. Introduction

Compared to the increasing demand for electronic energy storage, lithium-ion batteries (LIBs) still struggle to provide sufficient energy density [1,2]. The standard anode in LIBs is graphite, which operates by inserting and removing lithium ions, but it has a limited capacity (378 mAhg−1) and is not suitable for sodium-ion batteries (SIBs) because sodium ions are larger than lithium ions. Therefore, not everything that works in LIBs will necessarily work in SIBs. Typically, materials like graphene and non-graphitic carbon, such as hard carbon and carbon black, are utilized in SIBs [3].
Other materials, such as TiO2, Na2Ti3O7, tin (Sn), tin oxide (SnO2), tin disulfide (SnS2), antimony (Sb), and phosphorus (P), are also under investigation as potential anodes for sodium-ion batteries [4]. Tin-based anodes, which involve alloying and dealloying reactions, have been extensively studied because they perform well in both LIBs and SIBs and can store a significant amount of energy [5]. Tin and its compounds are attractive due to their environmentally friendly nature, cost-effectiveness, and lower operating voltages compared to graphite. However, they do come with inherent challenges [6].
Magnesium-ion batteries (MIBs) are also attracting attention due to their high energy density resulting from the larger magnesium ion (Mg2+) and the abundance of magnesium resources. Recent research indicates that tin can even be combined with potassium and magnesium [7].
Researchers have recently utilized first-principles calculations to investigate two-dimensional beryllium carbide (2D-Be2C) as a potential anode material for metal-ion batteries, specifically sodium and potassium batteries. The findings demonstrate that alkali metals can adsorb stably on a single layer of Be2C, and the diffusion barrier and the most efficient energy path were analyzed using the climbing image nudged elastic band method [8].
Tin and its compounds are seen as promising candidates for next-generation lithium and sodium-ion batteries due to their high theoretical capacity, low cost, and suitable working voltages. However, a major challenge is the significant volume changes that occur during the insertion and removal of lithium (or sodium) ions, which can result in capacity loss and a shortened lifespan. To address these challenges, it is crucial to focus on structural design and the synergistic effects of combining compatible materials or metals to enhance electrochemical performance [9,10].
The authors investigated how applying tensile strain can alter the electronic structure of tin carbide and enhance lithium adhesion to it. When tin carbide was stretched by 6%, it exhibited metallic properties. The stretched structure of SnC has the ability to accommodate a significant amount of lithium [11,12].
The electronic structure of tin carbide indicates that it behaves like an indirect-gap semiconductor, with a band gap of 1.72 eV using the “HSE06” method and 0.92 eV using the “GGA-PBE” method. Increasing the amount of sodium causes tin carbide to transition from being a semiconductor to a semi-metal. These results suggest that monolayer tin carbide could be a promising material for sodium-ion batteries [13].
This research study investigates the potential of using Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters for energy storage. The study focuses on analyzing the physical and chemical characteristics of these mixed-metal nanoclusters. A [SnC] nanocluster was synthesized and examined, with Li, Na, Be, and Mg being considered as potential cathode materials for comparison. Following a thorough analysis, the samples were tested to assess their performance, and the results were correlated with changes in their chemical composition to determine their suitability for use in batteries powered by Li, Na, Be, or Mg.

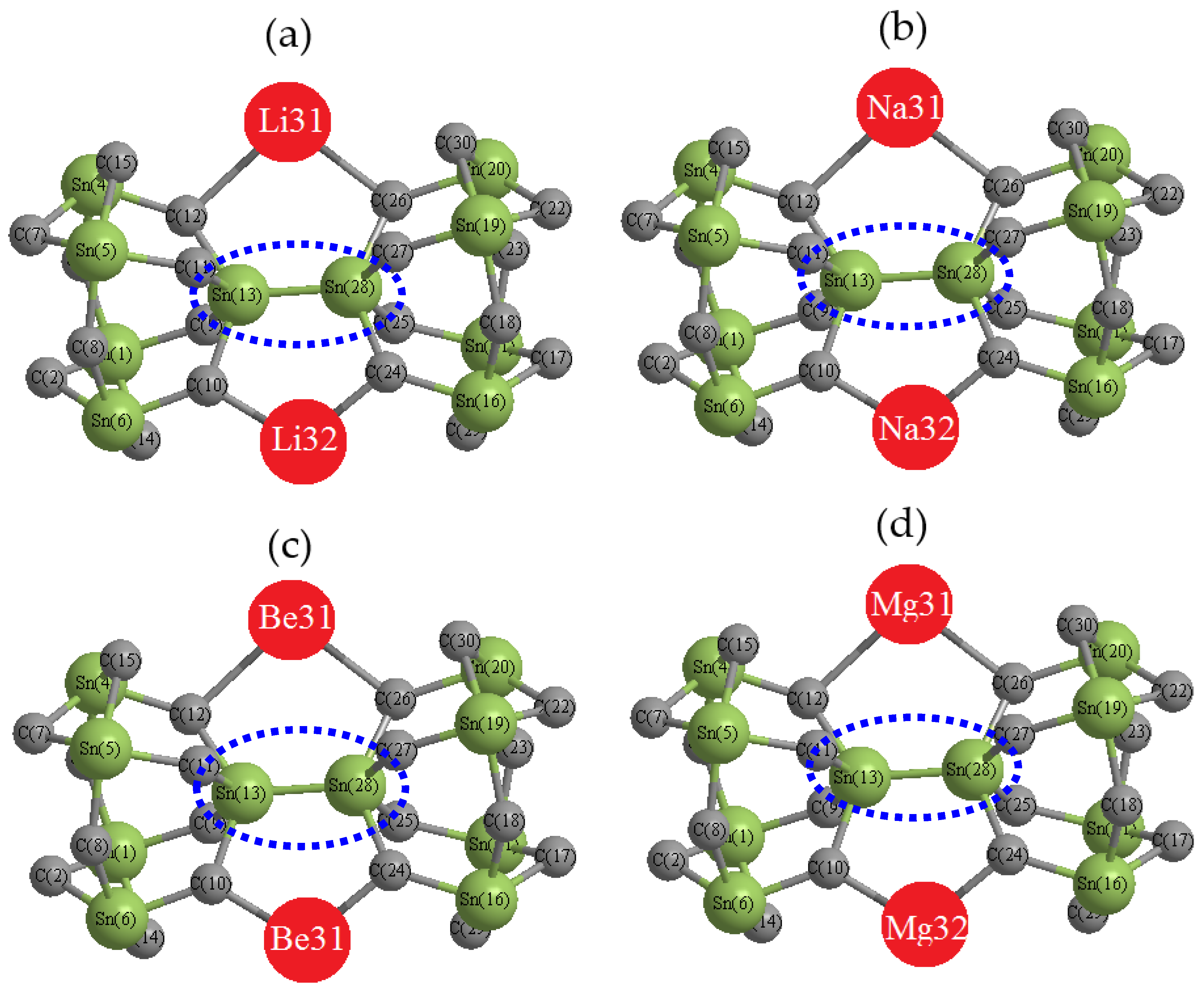
2. Materials and Methods

The development of the applied Density Functional Theory (DFT) approach did not gain much attention until W. Kohn and L. J. Sham introduced their well-regarded set of equations, called the Kohn-Sham (KS) equations [14].
H ^ s = − ∑ i M 1 2   V ¯ i 2 + ∑ i M v s ( r → i ) =   ∑ i M h ^ s
h ^ s = − 1 2   V ¯ i 2 + v s r → i      
By using ψ i to represent the single-particle orbitals, all physically valid electronic densities for the system of non-interacting electrons are expressed in Equation (3).
ρ   r → = ∑ i M ψ i   ( r → ) 2  
So, the total energy could be evaluated using the KS approach, as shown in Equation (4):
E ρ =   ∑ i M n i ψ i − 1 2   V ¯ 2 +   v e x t   r → +   1 2   ∫ ρ ( r → ′ ) r → − r → ′   d r → ′ ψ i + E x c   ρ + 1 2     ∑ β N ∑ α ≠ β N Z α Z β R → α −   R → β                                                    
Therefore, the exact exchange energy functional is described using Kohn-Sham orbitals rather than the electron density, in an approach known as the indirect density functional approach. This study utilized the hybrid functional B3LYP, developed by Becke, Lee, Yang, and Parr, along with a three-parameter basis set within the framework of density functional theory for theoretical calculations. The basis sets chosen were LANL2DZ for metal atoms and 6-311+G (d,p) for all other atoms [15].
Figure 1a–d shows nanoclusters based on alkali metals and alkaline earth metals, including Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C. These nanoclusters have the potential to improve energy saving in battery cells, transistors, and other semiconductor instruments.
Electronicmat 07 00002 g001
Figure 1. Adding Li, Na, Be and Mg to SnC nanoclusters leads to the formation of four different complexes: (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C. These complexes show promise for energy storage in innovative batteries. The atoms of Sn(13) and Sn(28) in the blue frame are the most efficient electron donors in Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, or Sn(Mg2)C complexes (Table 1).
Figure 1. Adding Li, Na, Be and Mg to SnC nanoclusters leads to the formation of four different complexes: (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C. These complexes show promise for energy storage in innovative batteries. The atoms of Sn(13) and Sn(28) in the blue frame are the most efficient electron donors in Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, or Sn(Mg2)C complexes (Table 1).
Electronicmat 07 00002 g001
Table 1. The atomic charge (Q/coulomb) for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C and Sn(Mg2)C nanoclusters.
Table 1. The atomic charge (Q/coulomb) for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C and Sn(Mg2)C nanoclusters.
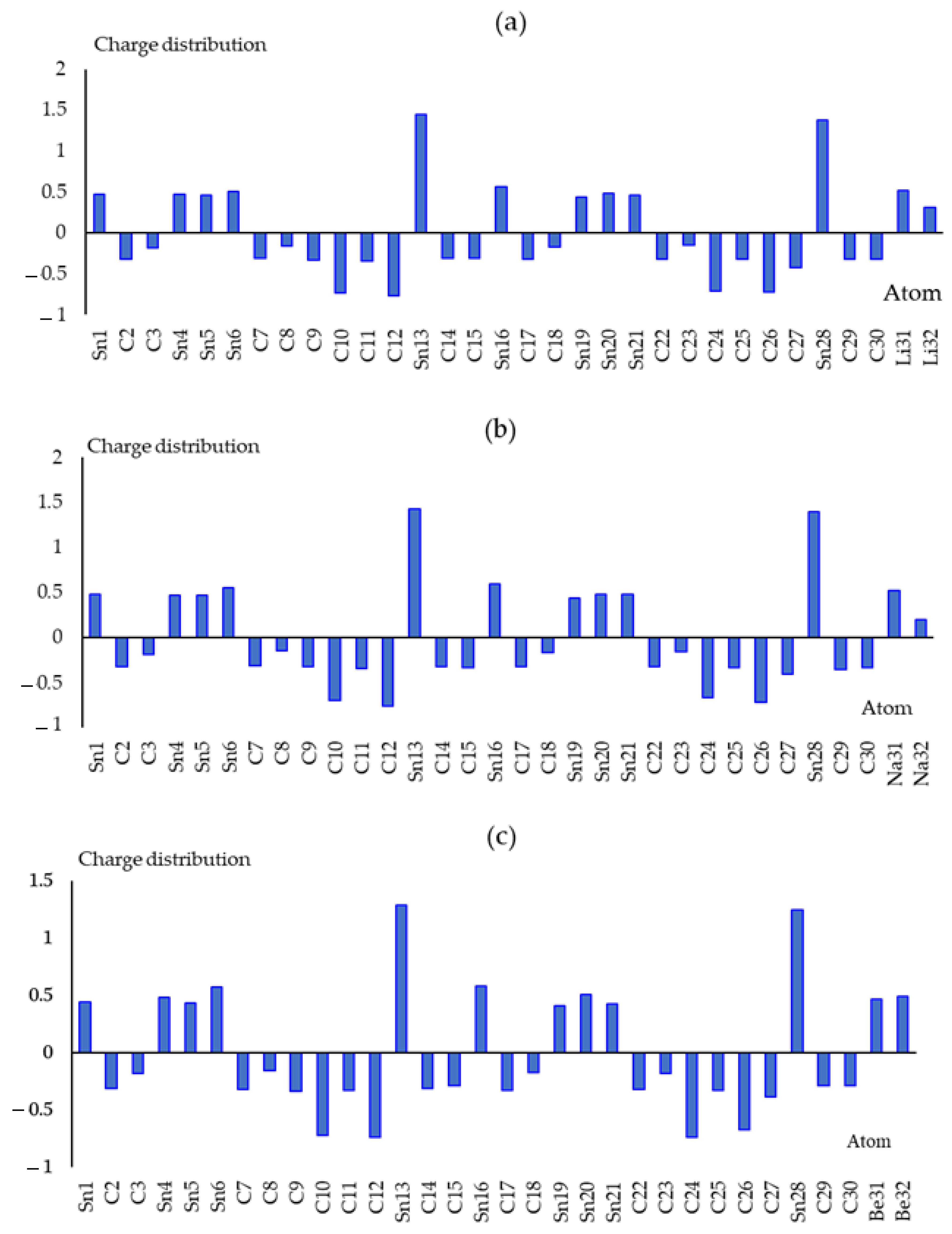
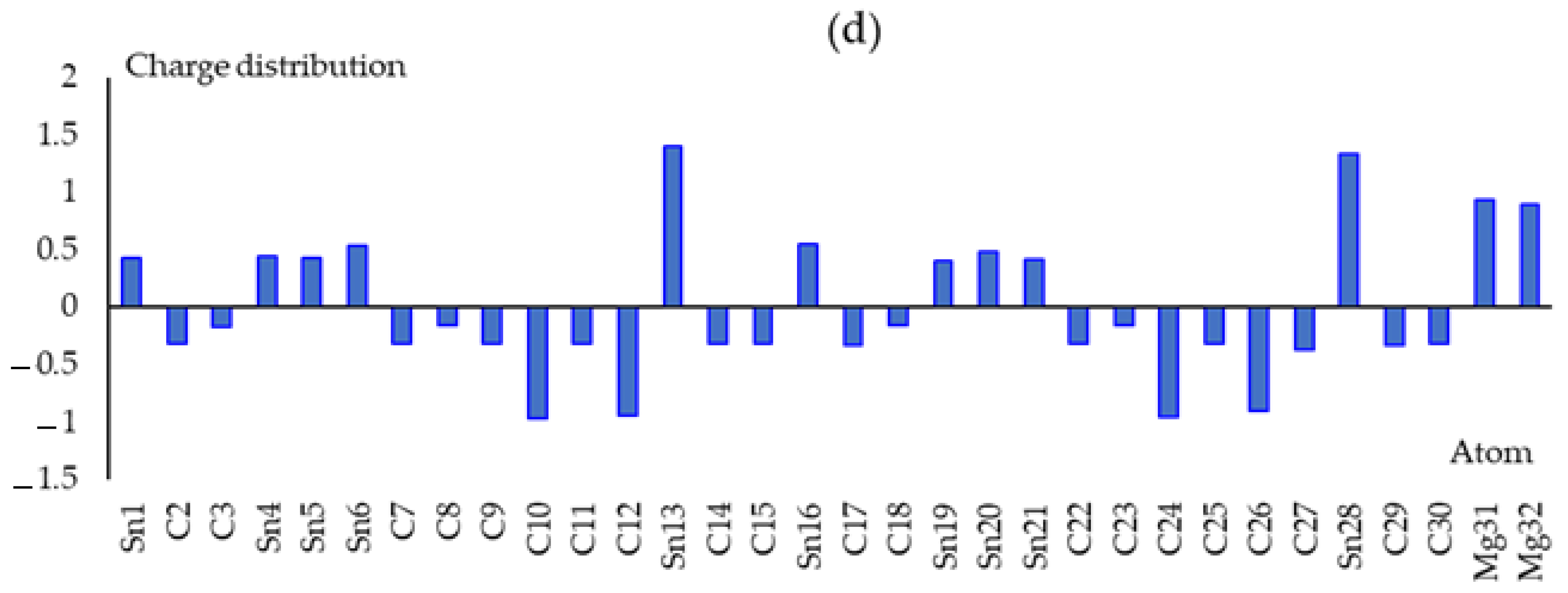
Sn(Li2)CSn(Na2)CSn(Be2)CSn(Mg2)C
AtomQAtomQAtomQAtomQ
Sn(1)0.476Sn(1)0.483Sn(1)0.443Sn(1)0.434
C(2)−0.318C(2)−0.322C(2)−0.313C(2)−0.314
C(3)−0.179C(3)−0.182C(3)−0.182C(3)−0.166
Sn(4)0.470Sn(4)0.470Sn(4)0.483Sn(4)0.442
Sn(5)0.464Sn(5)0.471Sn(5)0.440Sn(5)0.431
Sn(6)0.511Sn(6)0.553Sn(6)0.572Sn(6)0.538
C(7)−0.310C(7)−0.310C(7)−0.318C(7)−0.310
C(8)−0.156C(8)−0.150C(8)−0.157C(8)−0.151
C(9)−0.335C(9)−0.327C(9)−0.333C(9)−0.315
C(10)−0.735C(10)−0.699C(10)−0.720C(10)−0.971
C(11)−0.344C(11)−0.342C(11)−0.325C(11)−0.309
C(12)−0.763C(12)−0.765C(12)−0.733C(12)−0.933
Sn(13)1.442Sn(13)1.430Sn(13)1.285Sn(13)1.397
C(14)−0.303C(14)−0.319C(14)−0.306C(14)−0.319
C(15)−0.311C(15)−0.330C(15)−0.287C(15)−0.317
Sn(16)0.558Sn(16)0.597Sn(16)0.583Sn(16)0.553
C(17)−0.321C(17)−0.322C(17)−0.326C(17)−0.325
C(18)−0.169C(18)−0.168C(18)−0.168C(18)−0.156
Sn(19)0.435Sn(19)0.441Sn(19)0.409Sn(19)0.398
Sn(20)0.484Sn(20)0.484Sn(20)0.508Sn(20)0.480
Sn(21)0.466Sn(21)0.477Sn(21)0.428Sn(21)0.418
C(22)−0.320C(22)−0.319C(22)−0.320C(22)−0.320
C(23)−0.149C(23)−0.152C(23)−0.179C(23)−0.161
C(24)−0.705C(24)−0.664C(24)−0.736C(24)−0.949
C(25)−0.323C(25)−0.328C(25)−0.327C(25)−0.314
C(26)−0.721C(26)−0.724C(26)−0.668C(26)−0.898
C(27)−0.418C(27)−0.407C(27)−0.384C(27)−0.373
Sn(28)1.379Sn(28)1.397Sn(28)1.245Sn(28)1.336
C(29)−0.323C(29)−0.349C(29)−0.289C(29)−0.329
C(30)−0.315C(30)−0.333C(30)−0.289C(30)−0.320
Li(31)0.522Na(31)0.519Be(31)0.471Mg(31)0.929
Li(32)0.311Na(32)0.194Be(32)0.494Mg(32)0.896
The Bader charge parameter analysis [16] was utilized to investigate energy storage in hybrid clusters composed of Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C complexes (Figure 1a–d), each carrying a charge of +1. The calculations achieved convergence with an RMS density matrix value of 1.00D–08 and a MAX density matrix value of 1.00D–06 using the Gaussian 16 revision C.01 computational software [17] in conjunction with the GaussView 6.1 graphical interface [18]. The theoretical studies on energy storage for these complexes were conducted based on the LANL2DZ and 6-311+G (d,p) basis sets.
Using SnC nanoclusters as the anode in batteries that run on lithium, sodium, beryllium, or magnesium provides a major benefit. These nanoclusters allow multiple ways for lithium, sodium, beryllium, or magnesium ions to be stored within a stable SnC material. This leads to better electrical conductivity because of the combination of tin and carbon, as well as a larger surface area due to the nanocluster shape. In this research, tin and carbon are spread out and locked into the SnC structure, which prevents them from clumping together during the charging and discharging process of the battery. The insertion of Li/Na/Be/Mg may also lead to the cleavage of some C–Li, C–Na, C–Be, or C–Mg bonds in the SnC anode material, causing expansion and creating favorable sites for subsequent ion insertion in the network (see Figure 1a–d). Additionally, Li, Na, Be, or Mg atoms could react quickly with tin or carbide in the SnC nanocluster to form Sn(Li2)C (Figure 1a), Sn(Na2)C (Figure 1b), Sn(Be2)C (Figure 1c), and Sn(Mg2)C (Figure 1d) heteroclusters. By studying how amorphous tin materials interact with various multivalent ions through first-principles research, scientists can gain a deeper understanding of their electrochemical behavior. This knowledge can then assist experimental researchers in developing more effective methods for constructing multivalent-ion batteries.

3. Results and Discussion

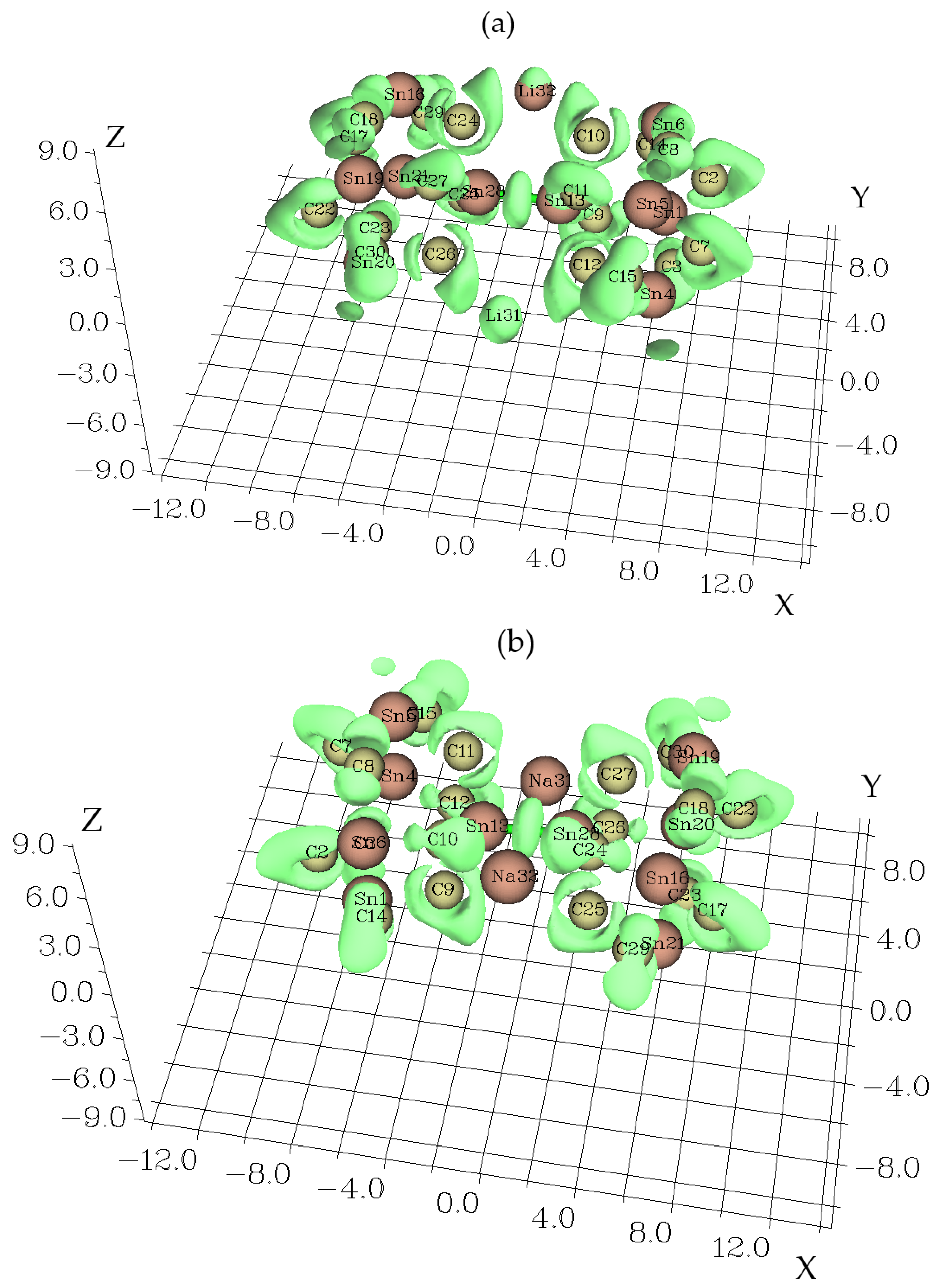
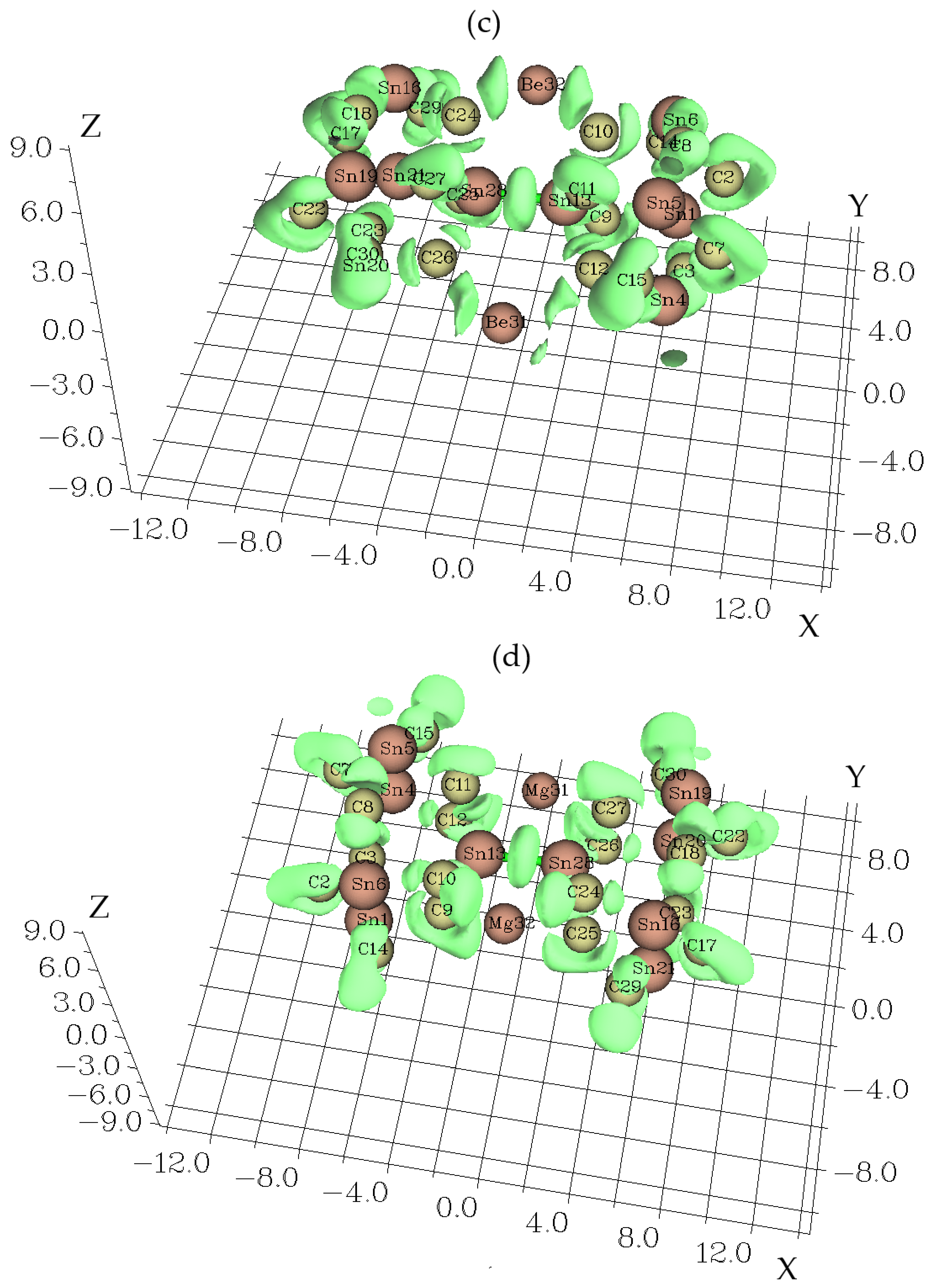
3.1. Charge Density Differences Analysis

In Figure 2a–d, charge density differences (CDDs) [19] are displayed for the nanoclusters Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C. These differences are caused by vibrations ranging from −12 to +9 Bohr, resulting from interactions between alkali metal pairs such as Li(31)-Li(32), Na(31)-Na(32), and alkaline earth metal pairs like Be(31)-Be(32) and Mg(31)-Mg(32). Additionally, specific carbon atoms in these nanoclusters, including C(2), C(3), C(7)–C(12), C(14), C(15), C(17), C(18), C(22)–C(27), C(29), and C(30), also exhibit vibrations within the same range of −12 to +9 Bohr, as shown in Figure 2a–d.
Carbon materials are very attractive as supports for electrocatalysis due to their relatively high chemical and thermal stability, conductivity, tunable structure, texture, and morphology, low cost, and easy availability. They are good electronic conductors and appropriate platforms for advancing electrodes for electrocatalytic processes. Therefore, electronic interactions between carbon and lithium, sodium, beryllium, or magnesium in the SnC nanocage play a key role in tuning the electrocatalytic behavior of the metal active phase. The basis of these interactions is the presence of structural defects or topological specifications, as well as heteroatom functional groups that disrupt the perfect symmetry of a graphitic layer of SnC, providing growth zones for lithium, sodium, beryllium, or magnesium.
The charge distribution has been illustrated for alkali and alkaline earth metals captured by SnC nanostructure, leading to the formation of Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters, as shown in Table 1.
By adding Li, Na, Be, and Mg atoms, the negative charge on certain carbon atoms in the nanoclusters increases, making them more efficient at accepting electrons. These carbon atoms include C(2), C(3), C(7) through C(12), C(14), C(15), C(17), C(18), C(22) through C(27), C(29), and C(30) in the structures Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C (Figure 3a–d).

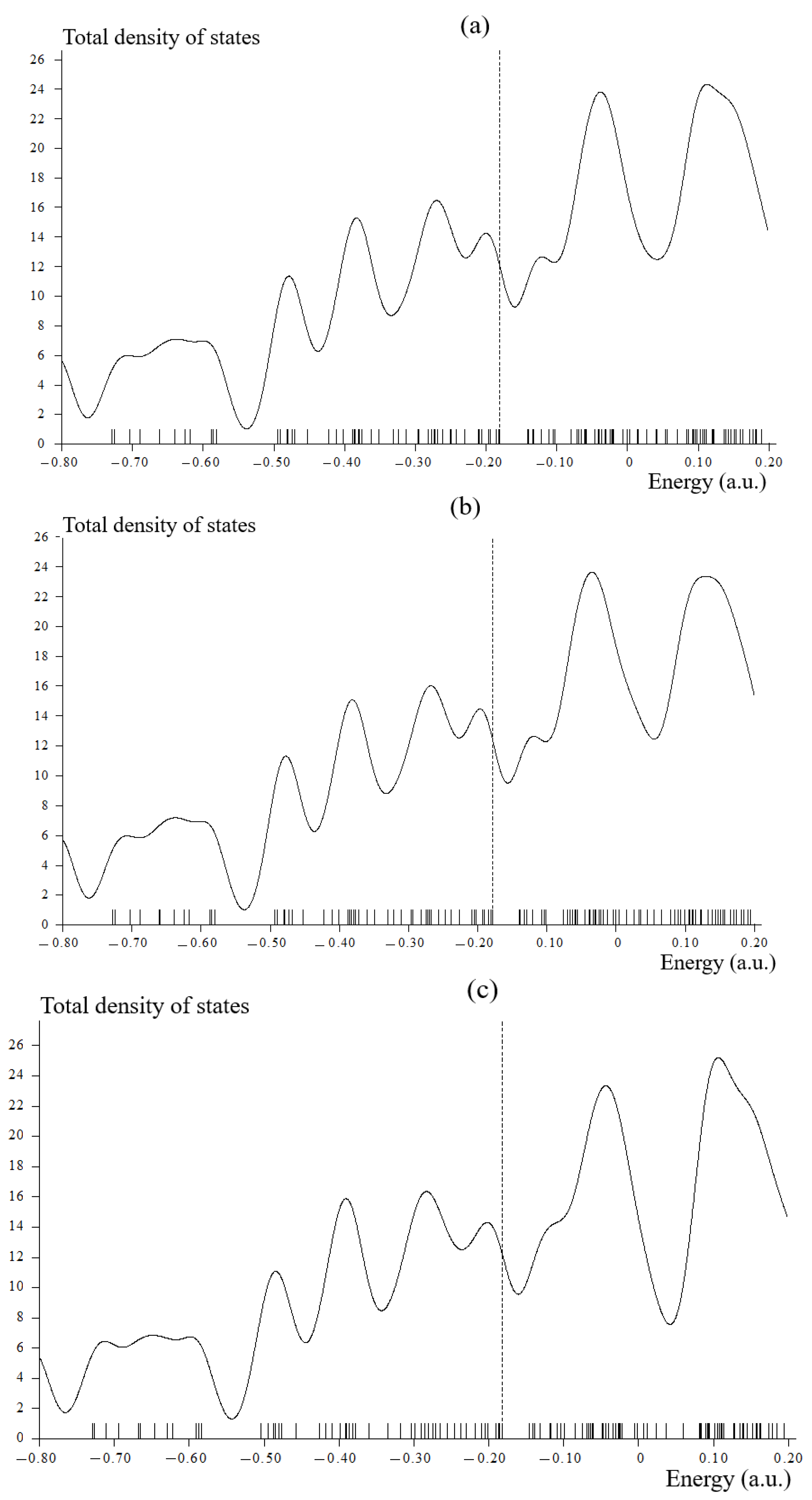
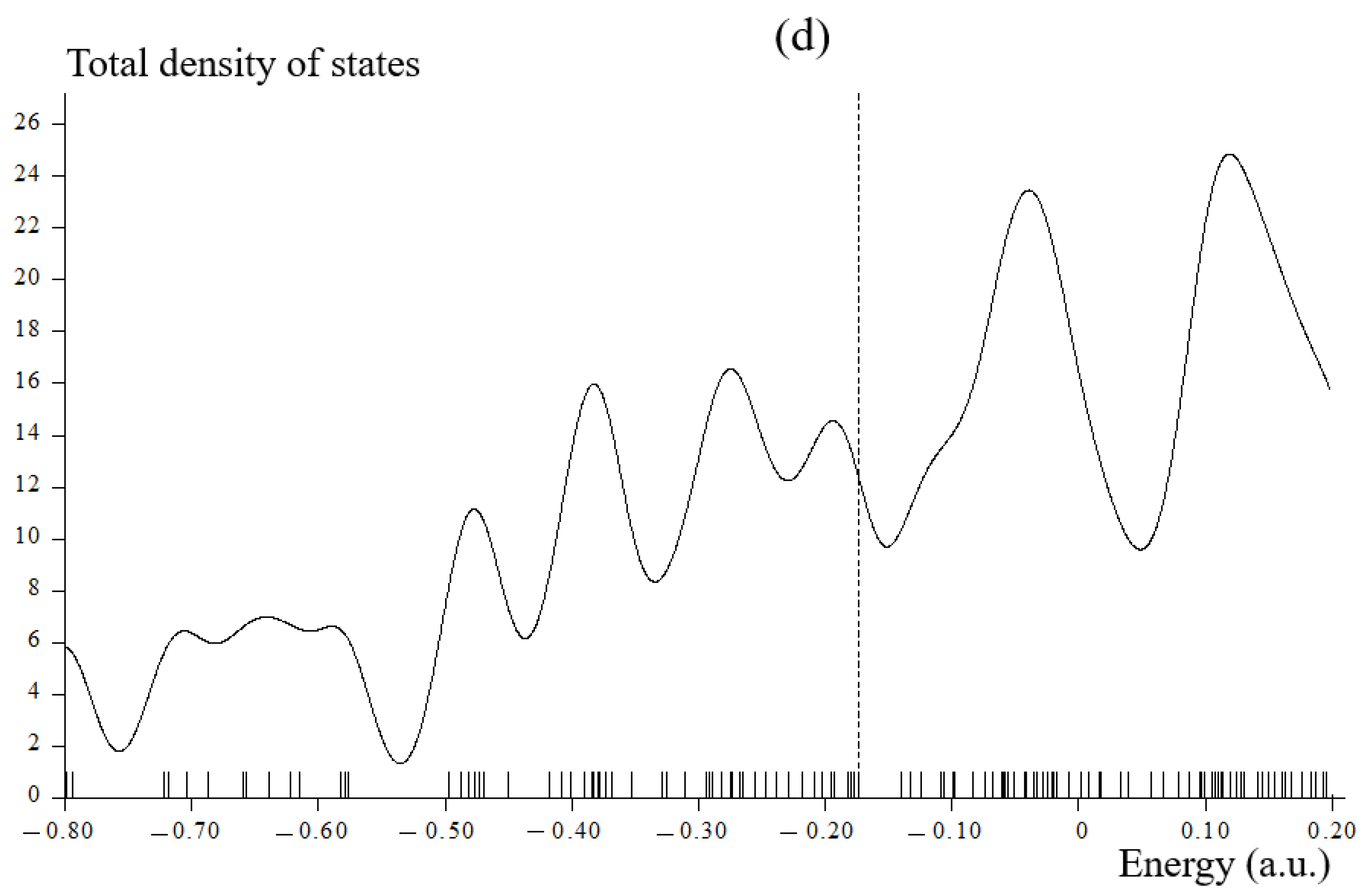
3.2. Total Density of States

In an isolated system, such as a molecule, the energy levels are discrete. In this situation, the concept of “density of states (DOS)” is considered to be completely irrelevant. Therefore, the “original total DOS (TDOS)” of an isolated system can be expressed as [20]:
T D O S   E =   ∑ i δ   ( E − ϵ i   )
The normalized Gaussian function is defined as:
                                                  G x = 1 c 2 π e − x 2 2 c 2 where   c = F W H M 2 2 l n x
“FWHM (full width at half maximum)” is an adjustable parameter in “Multiwfn” [21,22]. Additionally, the curve maps of “broadened partial DOS (PDOS)” and “overlap DOS (OPDOS)” are helpful for visualizing the orbital composition analysis. The “PDOS function of fragment “A” is defined as: #
                                    P D O S A   E = ∑ i Ξ i , A   F   ( E − ϵ i   )
where “ Ξ i , A “ represents the composition of fragment A in orbital i. The “OPDOS” between fragment “A” and “B” is defined as:”
O P D O S A , B   E = ∑ i X A , B i   F   ( E − ϵ i   )
“ X A , B i ” represents the total cross term between fragments “A” and “B” in orbital “i”.
In the “TDOS map,” each separate vertical line represents a “molecular orbital (MO),” with the dashed line indicating the location of the “HOMO.” The curve illustrates the “TDOS” calculated based on the distribution of energy levels of the “MOs”.
The analysis of the total density of states (TDOS) in Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters has been conducted. This analysis helps to reveal the presence of strong chemical interactions, typically observed on the “convex side” as shown in Figure 4a–d.
Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters (Figure 4a–d) exhibit the highest peaks in total density of states (TDOS) around –0.30, –0.40, –0.50, and –0.60 atomic units (a.u.), respectively. This is due to the covalent bonds between the Li, Na, Be, Mg atoms and the SnC nanostructure, with a maximum density of states of approximately 12.
Fragment 1 has been defined for C(9) to C(12), Sn(13), C(24) to C(27), Sn(28), and X(31)/X(32) (X = Li, Na, Be, Mg) in Figure 4a–d. Fragment 2 has indicated the fluctuation of Sn1, Sn4 to Sn6, alongside the similar atoms involved in Fragment 1 in Figure 4a–d. Finally, the fluctuation of Sn(16), Sn(19) to Sn(21), C(17), C(18), C(22), C(23), C(29), and C(30) was considered in Figure 4a–d.

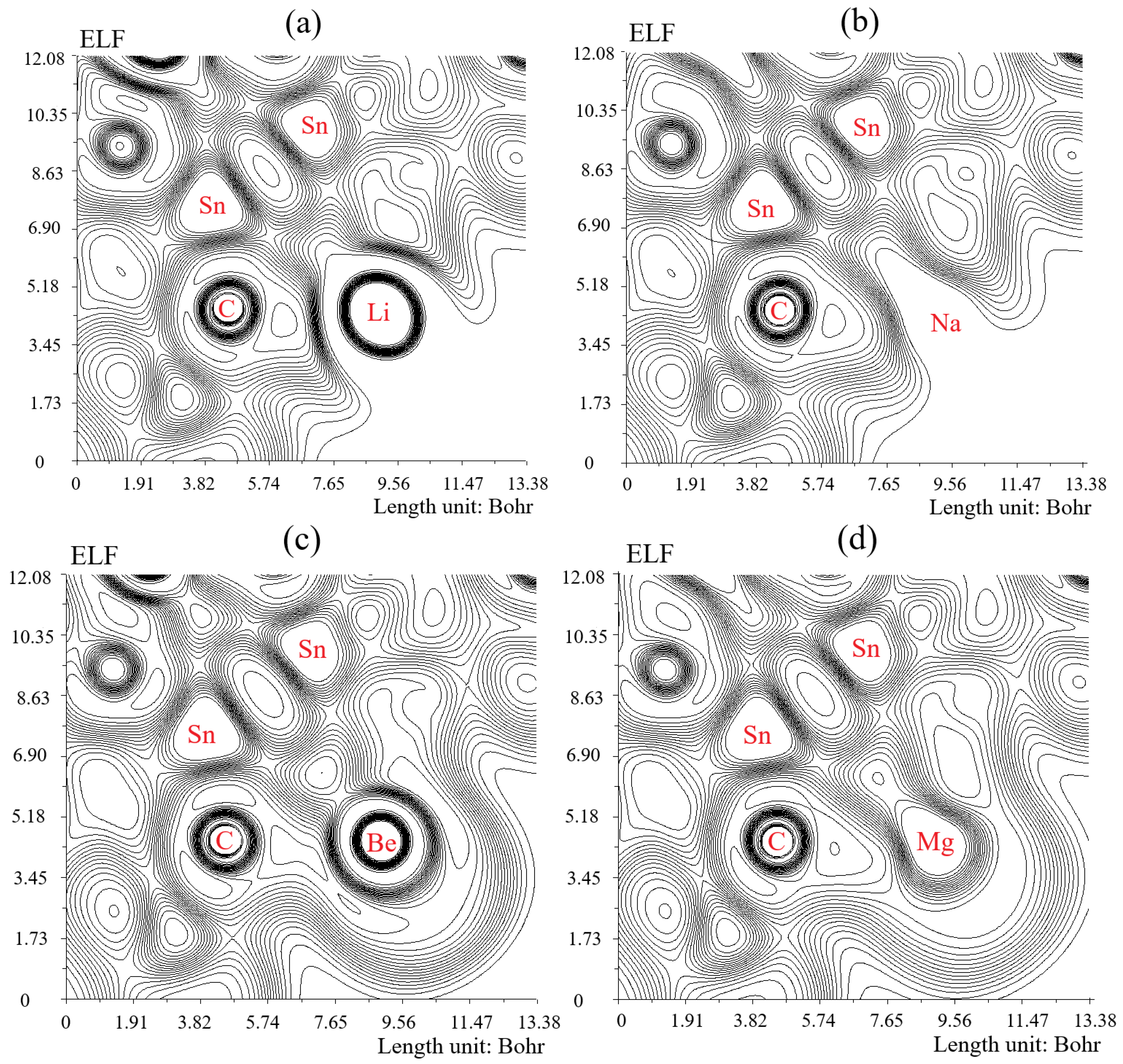
3.3. Electron Localization Function Analysis

A type of scalar field called ELF may demonstrate a wide range of bonding patterns. However, the distinction between deduced/raised electron delocalization/localization into cyclic π-conjugated sets remains important for ELF [23]. The more localized electrons are in an area, the more restricted their movement is within it. Therefore, they can be distinguished from those further away if electrons are completely localized. As Bader found, areas with high electron localization have significant levels of Fermi hole integration [24]. However, with a six-dimensional function for the Fermi hole, direct study seems challenging. Becke and Edgecombe noted that the spherically averaged spin conditional pair probability has a direct correlation with the Fermi hole and introduced the parameter of ELF in the Multiwfn program [21,22], which became popular for spin-polarized calculations [25]. In terms of kinetic energy, ELF was found to be more accurate for both Kohn-Sham DFT and post-HF wavefunctions [26].
Trapping Li, Na, Be, and Mg atoms by SnC nanostructures (Figure 5a–d) to form Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters can be analyzed using ELF graphs with Multiwfn [21,22]. This approach helps achieve delocalization/localization characterizations of electrons and chemical bonds (Figure 5a–d) for these systems.
Sn(Li2)C (Figure 5a), Sn(Na2)C (Figure 5b), Sn(Be2)C (Figure 5c), and Sn(Mg2)C (Figure 5d) have demonstrated electron delocalization through an isosurface map labeling atoms C(10), C(12), Sn(13), C(24), C(26), Sn(28), X(31)/X(32) (X = Li, Na, Be, Mg). The counter map of ELF confirms that Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters may enhance energy storage efficiency (Figure 5a–d).
Furthermore, the intermolecular orbital overlap integral is crucial in illustrating intermolecular charge transfer, allowing for the calculation of HOMO–HOMO and LUMO–LUMO overlap integrals between Li, Na, Be, Mg atoms, and SnC nanostructures. The layered tin carbide, enhanced by alkali and alkaline earth metals such as lithium, sodium, beryllium, and magnesium, demonstrates structural stability in Li, Na, Be, and Mg-ion batteries, as shown by the reported stability energies in Table 2. Additionally, the intermolecular orbital overlap integral is vital in discussions of intermolecular charge transfer, enabling the calculation of HOMO-HOMO and LUMO-LUMO overlap integrals between alkali/alkaline earth metals and tin carbide. We used the CAM–B3LYP–D3/6–311+G(d,p) wavefunction levels corresponding to HOMO and LUMO, as shown in Table 2. Consequently, ELUMO (a.u.), ELUMO (a.u.), local bandgap energies (∆E/a.u.), and immobile charges induced by polarization discontinuity are all simultaneously controlled throughout the structures, resulting in optimized band profiles for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters. A small amount of Li, Na, Be, or Mg entering the Sn–C layer to replace alkaline earth metals sites could enhance the structural stability of the electrode material at high multiplicity, consequently improving the capacity retention rates to 100.2018, 94.529, 198.863, and 188.186 mAhg−1 for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C complexes, respectively (Table 2).
In addition, the “Mayer bond order” [27] usually correlates well with actual bond orders, with a single bond typically around 1.0. The “Mulliken bond order” [28] also aligns somewhat with actual bond orders, but it is not the most accurate measure of bonding strength. In this case, the Mayer bond order is a more reliable indicator. Higher bond orders indicate stronger and shorter bonds, leading to increased heterocluster stability. This concept is fundamental in both valence bond theory and molecular orbital theory, providing insights into chemical structures. The effectiveness of this method has been demonstrated through the examination of bonding in various systems, including detailed studies on the SnC nanocage. The highest Mayer bond orders have been observed for the [C–B] bonding in Sn(Be2)C heteroclusters, with values of 0.9185 for C(10)–Be(32), 0.881 for C(24)–Be(32), 0.704 for C(26)–Be(31), and 0.619 for C(12)–Be(31) (Table 3). Additionally, the Wiberg bond order for [C–B] bonding in Sn(Be2)C heteroclusters has been estimated to be 0.8378 for C(10)–Be(32), 0.808 for C(24)–Be(32), 0.659 for C(26)–Be(31), and 0.548 for C(12)–Be(31) (Table 3). The concept of bond order, as suggested by Wiberg [29], is a measured bond property using orthonormalized atomic orbitals as a basis set for semi-empirical molecular orbitals.
However, the “Mulliken bond order” is a good qualitative indicator of the amount of bonding and antibonding present in a molecule. The positive amount indicates bonding, while the negative amount indicates antibonding, which is localized and evacuated, respectively. The Mulliken bond order for [C–B] bonding in the Sn(Be2)C heterocluster has been estimated to be the highest, with values of 0.939, 0.900, 0.592, and 0.524 for C(10)–Be(32), C(24)–Be(32), C(26)–Be(31), and C(12)–Be(31), respectively (Table 3).
As shown in Table 3, the “Laplacian bond order” [30] is closely connected to bond polarity, bond dissociation energy, and bond vibrational frequency. A low value of Laplacian bond order may suggest that the calculation of electron density levels has little effect. The “Fuzzy bond order” is similar to the Mayer bond order, especially for bonds with low polarity, but it is more reliable when the basis set changes. To calculate the “Fuzzy bond order,” Becke’s DFT numerical integration method is used, which gives a higher value than the Mayer bond order and leads to more accurate results [31]. For the [Sn(13)–Sn(28)] system, the Fuzzy bond order is highest in the Sn(Be2)C, Sn(Li2)C, Sn(Mg2)C, and Sn(Na2)C heteroclusters, with values of 0.886, 0.846, 0.846, and 0.815, respectively (Table 3). Based on the discussion of Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters, we can say that host–host and host–ion values are important for assessing the electrochemical performance of alloy-based anode materials, such as formation energy, specific capacity, and ion diffusivity.

4. Conclusions

Alkali and alkaline earth metals captured by tin carbide during the formation of Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C nanoclusters were examined using a computational approach. The shift in charge density indicated a significant transfer of charge in all of these compounds. Tin carbide, naturally a semiconductor, is often combined with carbon to enhance its ionic and electronic conductivity. It is widely known that adding lithium, sodium, beryllium, or magnesium to battery cells can improve energy efficiency. The findings of this study suggest that the structure of Sn(X2)C (where X = Li, Na, Be, Mg) can enhance the capacity of battery cells. By introducing a small amount of Li, Na, Be, or Mg into the Sn-C layer to replace sites where alkali and alkaline earth metals typically reside, the structural stability of the electrode material at high levels can be improved, resulting in capacity retention rates of 100.202, 94.529, 198.863, and 188.186 mAhg−1 for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C, and Sn(Mg2)C complexes, respectively. This research is valuable for developing Li, Na, Be, or Mg hybrid batteries with high power and energy density, excellent cycle stability, and potential for industrial use. The average coordination numbers between host–host and host–ion were identified as key factors in understanding specific capacity, volume expansion, and ion movement in alloy-based negative electrode materials. The study also suggests that the Be2+ ion shows the greatest potential among multivalent ions as a carrier in Sn anodes, and the performance of Be-Sn alloys is comparable to that of monovalent ions. For lithium-ion batteries (LIBs), sodium-ion batteries (SIBs), beryllium-ion batteries (BIBs), and magnesium-ion batteries (MIBs), further improvements in the electrolyte system should focus on understanding the interactions between the electrode and electrolyte, as well as gaining deeper insights into the reaction mechanisms involving magnesium ions and tin-based materials.

Author Contributions

Conceptualization, F.M.; Methodology, F.M. and M.M.; Software, F.M. and M.M.; Validation, F.M. and M.M.; Formal Analysis, F.M. and M.M.; Investigation, M.M.; Resources, M.M.; Data Curation, F.M. and M.M.; Writing—Original Draft, F.M.; Writing—Review and Editing, M.M.; Visualization, F.M. and M.M.; Supervision, F.M.; Project Administration, F.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Xiao, W.; Wang, Z.; Zhang, Y.; Fang, R.; Yuan, Z.; Miao, C.; Yan, X.; Jiang, Y. Enhanced performance of P(VDF-HFP)-based composite polymer electrolytes doped with organic-inorganic hybrid particles PMMA-ZrO2 for lithium ion batteries. J. Power Sources 2018, 382, 128–134. [Google Scholar] [CrossRef]
  2. Mollaamin, F. Anchoring of 2D layered materials of Ge5Si5O20 for (Li/Na/K)-(Rb/Cs) batteries towards Eco-friendly energy storage. BMC Chem. 2025, 19, 233. [Google Scholar] [CrossRef] [PubMed]
  3. Qian, J.; Xiong, Y.; Cao, Y.; Ai, X.; Yang, H. Synergistic Na-storage reactions in Sn4P3 as a high-capacity, cycle-stable anode of Na-ion batteries. Nano Lett. 2014, 14, 1865–1869. [Google Scholar] [CrossRef]
  4. Guan, P.; Zhou, L.; Yu, Z.; Sun, Y.; Liu, Y.; Wu, F.; Jiang, Y.; Chu, D. Recent progress of surface coating on cathode materials for high-performance lithium-ion batteries. J. Energy Chem. 2020, 43, 220–235. [Google Scholar] [CrossRef]
  5. Zhu, H.; Jia, Z.; Chen, Y.; Weadock, N.; Wan, J.; Vaaland, O.; Han, X.; Li, T.; Hu, L. Tin anode for sodium-ion batteries using natural wood fiber as a mechanical buffer and electrolyte reservoir. Nano Lett. 2013, 13, 3093–3100. [Google Scholar] [CrossRef]
  6. Fu, S.; Ni, J.; Xu, Y.; Zhang, Q.; Li, L. Hydrogenation driven conductive Na2Ti3O7 nanoarrays as robust binder-free anodes for sodium-ion batteries. Nano Lett. 2016, 16, 4544–4551. [Google Scholar] [CrossRef]
  7. Singh, N.; Arthur, T.S.; Ling, C.; Matsui, M.; Mizuno, F. A high energy-density tin anode for rechargeable magnesium-ion batteries. Chem. Commun. 2013, 49, 149–151. [Google Scholar] [CrossRef]
  8. Jadav, H.; Matth, S.; Pandey, H. Density Functional Investigations on 2D-Be2C as an Anode for Alkali Metal-Ion Batteries. Energy Storage 2024, 6, e70048. [Google Scholar] [CrossRef]
  9. Mou, H.; Xiao, W.; Miao, C.; Li, R.; Yu, L. Tin and Tin Compound Materials as Anodes in Lithium-Ion and Sodium-Ion Batteries: A Review. Front Chem. 2020, 8, 141. [Google Scholar] [CrossRef]
  10. Mollaamin, F.; Monajjemi, M. Nanomaterials for Sustainable Energy in Hydrogen-Fuel Cell: Functionalization and Characterization of Carbon Nano-Semiconductors with Silicon, Germanium, Tin or Lead through Density Functional Theory Study. Russ. J. Phys. Chem. B 2024, 18, 607–623. [Google Scholar] [CrossRef]
  11. Rehman, J.; Fan, X.; Zheng, W.T. 2D SnC sheet with a small strain is a promising Li host material for Li-ion batteries. Mater. Today Commun. 2021, 26, 101768. [Google Scholar] [CrossRef]
  12. Mollaamin, F. Alkali Metals Doped on Tin-Silicon and Germanium-Silicon Oxides for Energy Storage in Hybrid Biofuel Cells: A First-Principles Study. Russ. J. Phys. Chem. B 2025, 19, 722–736. [Google Scholar] [CrossRef]
  13. Butt, M.K.; Zeeshan, H.M.; Dinh, V.A.; Zhao, Y.; Wang, S.; Jin, K. Monolayer SnC as anode material for Na ion batteries. Comput. Mater. Sci. 2021, 197, 110617. [Google Scholar] [CrossRef]
  14. Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  15. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
  16. Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
  17. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016.
  18. Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6.06.16; Semichem Inc.: Shawnee Mission, KS, USA, 2016.
  19. Xu, Z.; Qin, C.; Yu, Y.; Jiang, G.; Zhao, L. First-principles study of adsorption, dissociation, and diffusion of hydrogen on α-U (110) surface. AIP Adv. 2024, 14, 055114. [Google Scholar] [CrossRef]
  20. Rukelj, Z.; Kupčić, I.; Radić, D. Density of States in the 3D System with Semimetallic Nodal-Loop and Insulating Gapped Phase. Symmetry 2024, 16, 38. [Google Scholar] [CrossRef]
  21. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  22. Lu, T. A comprehensive electron wavefunction analysis toolbox for chemists, Multiwfn. J. Chem. Phys. 2024, 161, 082503. [Google Scholar] [CrossRef]
  23. Matta, C.F.; Ayers, P.W.; Cook, R. The Physics of Electron Localization and Delocalization. In Electron Localization-Delocalization Matrices; Lecture Notes in Chemistry; Springer: Cham, Switzerland, 2024; Volume 112, pp. 7–20. [Google Scholar] [CrossRef]
  24. Bader, R. The zero-flux surface and the topological and quantum definitions of an atom in a molecule. Theor. Chem. Acc. 2001, 105, 276–283. [Google Scholar] [CrossRef]
  25. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  26. Savin, A.; Jepsen, O.; Flad, J.; Andersen, O.K.; Preuss, H.; von Schnering, H.G. Electron Localization in Solid-State Structures of the Elements: The Diamond Structure. Angew. Chem. Int. 1992, 31, 187–188. [Google Scholar] [CrossRef]
  27. Mayer, I. Improved definition of bond orders for correlated wave functions. Chem. Phys. Lett. 2012, 544, 83–86. [Google Scholar] [CrossRef]
  28. Mollaamin, F. Competitive Intracellular Hydrogen-Nanocarrier Among Aluminum, Carbon, or Silicon Implantation: A Novel Technology of Eco-Friendly Energy Storage using Research Density Functional Theory. Russ. J. Phys. Chem. B 2024, 18, 805–820. [Google Scholar] [CrossRef]
  29. Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
  30. Lu, T.; Chen, F. Bond Order Analysis Based on the Laplacian of Electron Density in Fuzzy Overlap Space. J. Phys. Chem. A 2013, 117, 3100–3108. [Google Scholar] [CrossRef]
  31. Wang, X.; Zhang, X.; Pedrycz, W.; Yang, S.-H.; Boutat, D. Consensus of T-S Fuzzy Fractional-Order, Singular Perturbation, Multi-Agent Systems. Fractal Fract. 2024, 8, 523. [Google Scholar] [CrossRef]
Electronicmat 07 00002 g002aElectronicmat 07 00002 g002b
Figure 2. CDD graphs for (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Figure 2. CDD graphs for (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Electronicmat 07 00002 g002aElectronicmat 07 00002 g002b
Electronicmat 07 00002 g003aElectronicmat 07 00002 g003b
Figure 3. The charge distribution changes for (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Figure 3. The charge distribution changes for (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Electronicmat 07 00002 g003aElectronicmat 07 00002 g003b
Electronicmat 07 00002 g004aElectronicmat 07 00002 g004b
Figure 4. TDOS graphs of (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Figure 4. TDOS graphs of (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Electronicmat 07 00002 g004aElectronicmat 07 00002 g004b
Electronicmat 07 00002 g005
Figure 5. Maps of ELF graphs for (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Figure 5. Maps of ELF graphs for (a) Sn(Li2)C, (b) Sn(Na2)C, (c) Sn(Be2)C and (d) Sn(Mg2)C nanoclusters.
Electronicmat 07 00002 g005
Table 2. Stability energy (kcal/mol), dipole moment (debye), LUMO (eV), HOMO (eV), energy gap (∆E) (eV) and cell capacity (C, mAh g−1 ) for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C and Sn(Mg2)C nanoclusters.
Table 2. Stability energy (kcal/mol), dipole moment (debye), LUMO (eV), HOMO (eV), energy gap (∆E) (eV) and cell capacity (C, mAh g−1 ) for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C and Sn(Mg2)C nanoclusters.
HeteroclustersEs × 10−3
(kcal/mol)		Dipole Moment (Debye)EHOMO (eV)ELUMO (eV)∆E = ELUMO–EHOMO (eV)C
(C, mAh g−1)
Sn(Li2)C−503.7081.203−4.931−3.8371.094370.695
Sn(Na2)C−494.4561.232−4.855−3.8121.043303.354
Sn(Be2)C−512.7171.248−4.969−3.9720.997720.734
Sn(Mg2)C−495.2960.626−4.713−3.8120.900597.810
Table 3. The bond order of Mayer, Wiberg, Mulliken, Laplacian and Fuzzy from mixed alpha and beta density matrix for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C and Sn(Mg2)C nanoclusters.
Table 3. The bond order of Mayer, Wiberg, Mulliken, Laplacian and Fuzzy from mixed alpha and beta density matrix for Sn(Li2)C, Sn(Na2)C, Sn(Be2)C and Sn(Mg2)C nanoclusters.
CompoundBond TypeBond Order
MayerWibergMullikenLaplacianFuzzy
Sn(Li2)CSn(13)–Sn(28)0.1890.5160.5040.3630.846
C(10)–Li(32)0.5210.4490.6240.2620.313
C(12)–Li(31)0.2890.2910.3060.3450.156
C(24)–Li(32)0.4820.4300.5560.5990.297
C(26)–Li(31)0.3230.3450.3550.3910.200
Sn(Na2)CSn(13)–Sn(28)0.1660.5150.5770.3700.815
C(10)–Na(32)0.5680.2910.8540.2310.470
C(12)–Na(31)0.2830.2110.3790.3050.280
C(24)–Na(32)0.5540.2860.7360.2050.461
C(26)–Na(31)0.3290.2430.4560.2770.334
Sn(Be2)CSn(13)–Sn(28)0.3590.5660.6870.5450.886
C(10)–Be(32)0.9180.8380.9390.1750.595
C(12)–Be(31)0.6190.5480.5240.3700.361
C(24)–Be(32)0.8810.8080.9000.1630.572
C(26)–Be(31)0.7040.6590.5920.2130.454
Sn(Mg2)CSn(13)–Sn(28)0.1890.5160.5040.3630.846
C(10)–Mg(32)0.5210.4490.6240.2620.697
C(12–Mg(31)0.2890.2910.3060.3450.450
C(24)–Mg(32)0.4820.4300.5560.1990.673
C(26)–Mg(31)0.3230.3450.3550.1910.556
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Mollaamin, F.; Monajjemi, M. Modeling SnC-Anode Material for Hybrid Li, Na, Be, Mg Ion-Batteries: Structural and Electronic Analysis by Mastering the Density of States. Electron. Mater. 2026, 7, 2. https://doi.org/10.3390/electronicmat7010002

AMA Style

Mollaamin F, Monajjemi M. Modeling SnC-Anode Material for Hybrid Li, Na, Be, Mg Ion-Batteries: Structural and Electronic Analysis by Mastering the Density of States. Electronic Materials. 2026; 7(1):2. https://doi.org/10.3390/electronicmat7010002

Chicago/Turabian Style

Mollaamin, Fatemeh, and Majid Monajjemi. 2026. "Modeling SnC-Anode Material for Hybrid Li, Na, Be, Mg Ion-Batteries: Structural and Electronic Analysis by Mastering the Density of States" Electronic Materials 7, no. 1: 2. https://doi.org/10.3390/electronicmat7010002

APA Style

Mollaamin, F., & Monajjemi, M. (2026). Modeling SnC-Anode Material for Hybrid Li, Na, Be, Mg Ion-Batteries: Structural and Electronic Analysis by Mastering the Density of States. Electronic Materials, 7(1), 2. https://doi.org/10.3390/electronicmat7010002

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop