Performance Comparison of Hybrid and Standalone Piezoelectric Energy Harvesters Under Vortex-Induced Vibrations

Abstract

This study investigates the effect of incorporating an electromagnetic harvester inside the bluff body of a 2-DoF hybrid harvester in comparison to a standalone piezoelectric harvester for various external loads. The harvester is excited through a vortex-induced vibration owing to the resultant wake vortices created behind the bluff body. The coupled dynamics of the two harvester components are modeled, and numerical simulations are conducted to evaluate the system’s performance under varying electrical loads. Numerical results show that at high, optimum electrical load, the standalone piezoelectric harvester outperforms the hybrid harvester. Nevertheless, for small electrical loads, the results show that the hybrid harvester outperforms the standalone PZT harvester by up to 18% in peak power output, while reducing the bandwidth by approximately 10% compared to the standalone piezoelectric harvester. Optimal spring stiffness values were identified, with the hybrid harvester achieving its maximum output power at a spring stiffness of 83.56 N/m. These findings underscore the need for careful design considerations, as the hybrid harvester may not achieve enhanced power output and bandwidth under higher electrical loads.

1. Introduction

Energy harvesting devices are sustainable and environmentally friendly solutions for powering electronics. They can be categorized by observing their assumed transduction mechanisms, including piezoelectric [1], electromagnetic [2], electrostatic [3], thermoelectric [4], triboelectric [5], or a hybrid combination of these mechanisms [6]. The energy conversion mechanism of these harvesters is to harness energy from various ambient sources and convert it into electrical energy that can be stored and used [7]. For instance, vibration-based energy harvesters convert the ambient mechanical vibrations into electrical energy. Among the various ambient sources, wind energy is an abundant and renewable source of energy that induces various modes of harvester oscillations, such as galloping [8], fluttering [9], and Vortex-Induced Vibrations (VIV) [10].

VIV-based wind energy harvesters offer a higher wind speed bandwidth (i.e., the lock-in region or the usable wind speed range) and require a lower onset wind velocity to harness energy compared to other oscillation modes [11]. A typical VIV harvester features a piezoelectric ceramic (PZT) sheet mounted near the fixed end of a cantilever substrate with a cylindrical bluff body attached at the free end. Recently, several approaches have been proposed to enhance the performance of the VIV-based harvesters. This includes introducing nonlinear magnetic restoring forces, increasing the harvester’s degree of freedom, integration of multiple transduction mechanisms (i.e., a hybrid harvester), and combining VIV and galloping oscillations into a single harvester. Both theoretical and experimental research investigations have significantly contributed to different designs of VIV-based wind energy harvesters, enhancing their output power, bandwidth, and efficiency. Dynamic modeling of harvesters provides deeper insights into the design parameters that govern and enhance their performance. Clementi et al. [12] developed an equivalent circuit model for bimorph cantilevers, incorporating two mechanical and one electrical degree of freedom. The model, validated through experiments, achieved less than 2% prediction uncertainty, thereby offering a sustainable and accurate framework for the modeling of advanced piezoelectric harvesters.

Hou et al. [13] examined a magnet-induced, monostable, nonlinear, VIV piezoelectric energy harvester. The study reported that the bandwidth and output power for such a design increase with an increase in the bluff body diameter and length of the PZT layer, and a decrease in the bluff body mass. Nasser et al. [14] performed a performance analysis of piezo-magnetoelastic energy harvesting from VIVs by using monostable characteristics. The analysis showed a left shift in the synchronization region of the harvester, which in turn is very beneficial for a higher efficiency for the energy harvesting at low wind speed conditions. Furthermore, the harvester design exhibited a monostable hardening behavior mainly resulting from the assumed nonlinear magnetic force, offering the prospect to use such a design arrangement as an ultra-wide bandwidth VIV-based energy harvester with an enhanced output energy performance when the ambient wind condition is variable. Su and Wang [15] investigated numerically and experimentally a bi-directional VIV-based Piezoelectric Energy Harvester (PEH) to capture wind energy simultaneously from the vertical and horizontal directions. A set of magnets was assumed to enhance the harvesting performance. The resultant generated magnetic force improved the harvester lock-in region and an enhancement of the peak voltage of the horizontal mode, but had a slight effect on the vertical direction.

Combining the VIV and other vibration-based oscillation modes can enhance the performance of the VIV-based harvesters. Yang et al. [16] investigated the aerodynamic parametric influence on the performance of a piezoelectric wind energy harvester subjected to a coupled VIV and galloping oscillations. They have suggested an effective structural optimization of the bluff body geometry, through a genetic algorithm, for an energy harvesting enhancement. By introducing a coupled VIV-galloping parameter, an interesting hump phenomenon was observed. Although the VIV-galloping coupling parameter degrades harvester performance in low wind speeds, it improves the output voltage at wind speeds above 1.6 m/s. Hou et al. [17] developed experimentally and analyzed theoretically a hybrid Electromagnetic-Piezoelectric Energy harvester (PEEH) to scavenge a VIV superimposed on a base excitation oscillation. The hybrid harvesting design increases the harvested peak power and bandwidth as compared to that under base excitation or VIV only. As such, combining oscillations is suggested, when possible, to harness more power at a higher bandwidth.

In vibration-based energy harvesters, the peak energy output occurs near the fundamental resonance of the system. By increasing the harvester’s Degrees of Freedom (DOF), additional resonances are introduced, effectively broadening the operational bandwidth. Aligned with this objective, Lu et al. [18] investigated the energy harvesting performance of a two Degree-of-Freedom small-scale VIV wind energy harvester using numerical simulations. Their study showed the existence of two “lock-in” regions beneficial for broadening the useful wind energy bounds.

Sun and Seok [19] recommended an innovative self-tuning VIV wind energy harvesting system, assuming a moving bluff body. Such a self-tuning design showed proficiencies to broaden the frequency lock-in range and enhance accordingly the harvester’s overall energy efficiency performances. Lai et al. [20] proposed a hybrid piezoelectric-dielectric energy harvester to convert energy from VIVs into electricity using both PZT sheets and the vibro-impact dielectric elastomer generator. Their numerical simulations showed that such a design is capable of harvesting wind energy effectively within a narrow low wind speed range, as compared to the prevailing galloping-based wind energy harvesters.

Recent studies have proposed hybrid energy harvesting systems that combine multiple transduction mechanisms, such as piezoelectric and electromagnetic components, to overcome the limitations of standalone systems. Hybrid PEEH are generally utilized to increase the output power and the operational bandwidth. Zhang et al. [21] suggested a hybrid VIV PEEH attached to a direction adaptive mechanism (a rotating shaft), permitting harvesting wind energy from different directions. It was also observed experimentally that the performance of the energy harvester improved through increasing the bandwidth and decreasing the onset wind speed by adding an extra mass to the lower end of the rotating shaft. To further improve the VIV harvester efficiency, Al-Riyami et al. [6] explored using a hybrid VIV PEEH that comprises a PZT cantilever beam and an embedded electromagnetic harvester inside the bluff body. The design is to increase the DoFs and combine two transduction mechanisms in a single harvester. Numerical analysis showed that the harvester power and wind speed bandwidth extended near the two resonances of the harvester. However, despite these advancements, there is a lack of detailed dynamic analysis and optimization studies for hybrid VIV harvesters, especially under varying operating conditions such as low-speed flow and different electrical loads. A recent study by Truong et al. [22] shows that a linear hybrid PEEH generates less power than a standalone piezoelectric or electromagnetic harvester when the electrical losses of one of them or both components exceed a certain figure of merit threshold. As such, this suggests the need for careful design considerations when optimizing hybrid PEEH under a given external load. Nonetheless, the PEEH remains a recommended approach for broadening the operational bandwidth. Their findings highlighted the need for careful design optimization to ensure that the combined system performs better than the individual components. Similarly, Rosso et al. [23] introduced a mono-axial hybrid piezoelectric harvester that integrates magnetic plucking with indirect impacts to overcome the frequency limitations of resonant devices. Their experiments demonstrated that the combined mechanism significantly broadened the bandwidth and yielded a seven-fold increase in stored energy compared to impacts alone, proving effective for low-frequency and non-periodic excitations such as human motion. This underscores the value of nonlinear hybrid mechanisms for enhancing both harvested power and operational versatility.

This work examines the dynamics of a hybrid VIV PEEH. The harvester under study was previously investigated at various boundary conditions in [24,25]. Experimental results indicated a modest 23% improvement in the output voltage of the hybrid PEEH compared to the conventional standalone piezoelectric harvester, suggesting the need for a more detailed dynamic analysis of the harvester to optimize both the output power and bandwidth. The main contribution of this paper lies in developing a dynamic model of the harvester and conducting a detailed parametric study to analyze the influence of key design parameters, such as spring stiffness and load variations, on the performance of the hybrid harvester. Additionally, a comparative performance analysis of the hybrid harvester against a standalone piezoelectric harvester at different external loads is performed. Section 2 describes the harvester’s design and components. The piezo-electromagnetic dynamic model driven by vortex-induced vibrations is developed in Section 3. Section 4 outlines the findings of the numerical analysis and the parametric study. Conclusions are summarized in Section 5.

2. Harvester Design and Components

This section presents the design geometry and structure of the proposed hybrid energy harvester, which integrates both piezoelectric and electromagnetic transduction mechanisms to harness energy from VIV. The design combines the advantages of the two transduction mechanisms to increase the degrees of freedom of the system, thereby expanding the operational bandwidth.

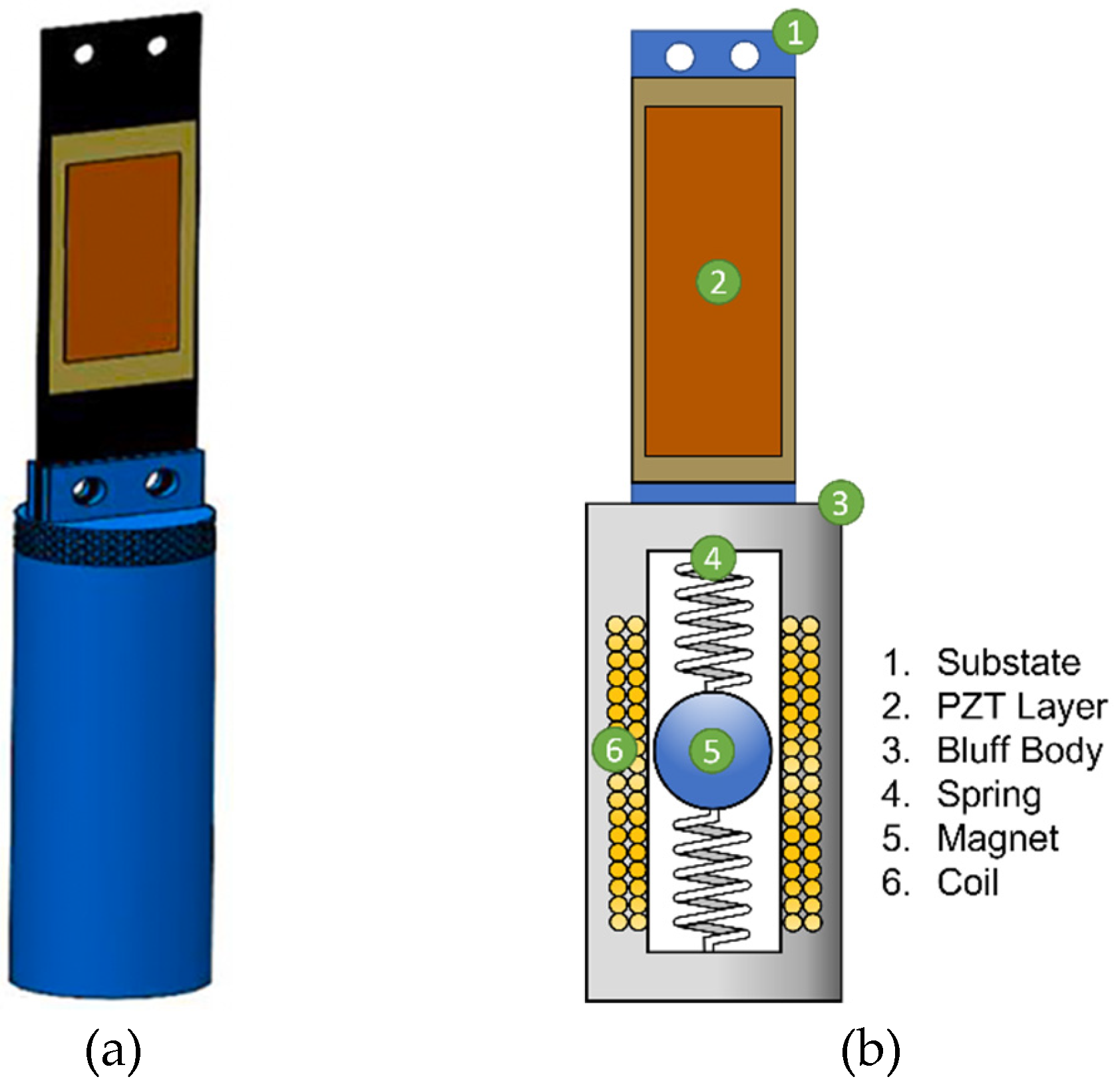
The schematic representation of the hybrid harvester is depicted in Figure 1. The harvester features a bluff body mounted on the free end of an aluminum-PZT composite cantilever beam. As the bluff body oscillates due to vortex shedding, strain is induced in the piezoelectric layer, generating an electrical output. Additionally, an Electromagnetic Energy Harvester (EEH) that consists of a coil and a spherical permanent magnet is embedded within the bluff body. When the bluff body oscillates, the magnet moves relative to the coil, inducing a current in the coil, so additional electrical energy is generated. It is worth mentioning that the spherical permanent magnet is strained to move along the longitudinal axis of the bluff body, guided by compressive springs.

The overall performance of the harvester, in terms of the output power and bandwidth, is influenced by several key design parameters such as the substrate material properties and geometry, bluff body mass and dimensions, and spring stiffness. For instance, research studies have shown that an excessive bluff body mass degrades the total output power of the harvester [25]. Furthermore, the spring stiffness can be used as a controlled parameter to maximize the output power within a narrow flow speed, as it will be demonstrated in Section 4. The parameters and material properties of the hybrid energy harvester are listed in

Table 1. Harvester parameters and material properties.

Symbol	Description	Value	Unit
D	Bluff-body diameter	21	mm
$L_b$	Bluff body height	65	mm
$m_b$	Bluff body mass	0.0157	kg
L	Substrate beam length	70	mm
w	Substrate beam width	10	mm
h	Substrate beam thickness	0.5	mm
${\rho }_s$	Substrate beam density	7800	kg/m3
Es	Substrate beam Young’s modulus of elasticity	71	GPa
${\rho }_p$	Piezoelectric layer density	7800	kg/m3
Ep	Piezoelectric layer Young’s modulus of elasticity	61	GPa
$m_c$	Magnetic coil mass	0.0076	kg
$L_e$	Coil inductance	2.7767 × 10−4	H
$R_c$	Coil resistance	0.8996	Ω
$m_s$	Sliding magnet mass	0.0455	kg
$\alpha$	Electromechanical coupling coefficient	−9.9760 × 10−4	N/V
$\beta$	Electromagnetic coupling factor	0.3280	N/A
$C_p$	Piezoelectric capacitance	1.2845 × 10−8	F

. The detailed description of the actual manufactured harvester is presented in [24]. The coupled dynamic model of the harvester that incorporates all design parameters is outlined in the next section.

3. Piezo-Electromagnetic Dynamic Model

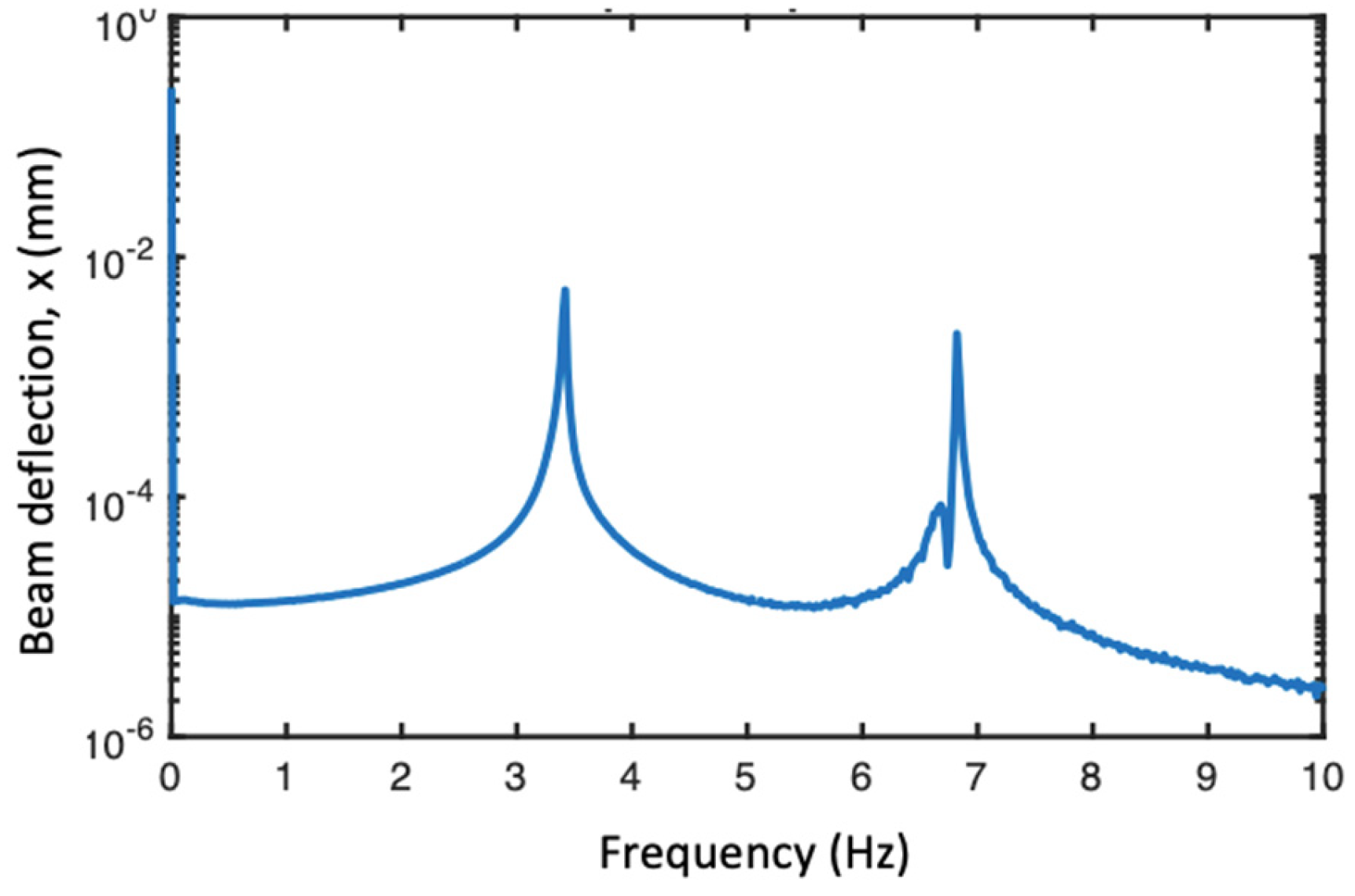
In this section, the nonlinear dynamic model of the hybrid piezo-electromagnetic harvester under VIV is developed using the Lagrange formulation. The lumped-mass equivalent dynamic model of the harvester is illustrated in Figure 2. The electromagnetic energy harvester inside the bluff body is modeled as a linear oscillator attached to a lumped mass representing the piezoelectric energy harvester (PEH). As the PEH oscillates due to the VIV force, the magnet inside the bluff body moves linearly relative to the electromagnetic coil. This coupled motion results in an interaction between the harvesters. The electrical energy generated by both harvesters is represented by resistive loads ($R_p$ and $R_e$), as shown in Figure 2.

The Equations of motion for the hybrid PEEH are derived using the following Lagrange formulation [26],

$${\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial \mathcal{L}}{\partial {\dot{q}}_i}}-{\displaystyle \frac{\partial \mathcal{L}}{\partial q_i}}+{\displaystyle \frac{\partial R}{\partial {\dot{q}}_i}}=Q_i+\lambda {\displaystyle \frac{\partial C}{\partial q_i}},$$

(1)

where $\mathcal{L}=T-U$ represents the Lagrangian, defined as the difference between the kinetic ($T$) and potential ($U$) energies of the harvester. For $i=\mathrm{1,2},\cdots n$, $q_i$ denotes the generalized coordinates of the harvester, which include the beam deflection ($q_1=x$), the bluff body rotation angle ($q_2=\theta$), the magnet sliding motion ($q_3=s$) relative to the bluff body and its attached coil, the piezoelectric charge ($q_4=q_p$), and the electromagnetic charge ($q_5=q_e$). $Q_i$ are the generalized forces acting on the harvester and $R$ represents the Rayleigh dissipation function of the harvester. It is worth mentioning that the rotational motion of the bluff body is constrained by the beam deflection, as the bluff body is fixed to the free end of the beam rather than being pivoted for free rotation. Thus, Lagrange multiplier ($\lambda$) is introduced to enforce restriction on the rotational motion of the bluff body. The constraint Equation that correlates the rotational angle of the bluff body and the beam deflection is expressed as

$$C\left(x,\theta ,t\right)=\theta \left(t\right)-rx\left(t\right)=0,$$

(2)

in which the parameter $r$ is calculated by [27]

$$r=-{\displaystyle \frac{{\beta }_1\left[\mathit{sin}{\beta }_1+\mathit{sinh}{\beta }_1-{\gamma }_1\left(\mathit{cos}{\beta }_1+\mathit{cosh}{\beta }_1\right)\right]}{L\left[\mathit{cos}{\beta }_1-\mathit{cosh}{\beta }_1+{\gamma }_1\left(\mathit{sin}{\beta }_1-\mathit{sinh}{\beta }_1\right)\right]}},$$

(3)

where ${\beta }_1$ and ${\gamma }_1$ are the first eigenvalue and modal parameter of a cantilever beam carrying a tip mass, respectively. $L$ is the substrate beam length.

The kinetic energy of the coupled harvester is given by

$$T={\displaystyle \frac{1}{2}}{m}_x{\dot{x}}^2+{\displaystyle \frac{1}{2}}{m}_s\left[{\left(\dot{x}+\dot{s}\sin \theta +s\dot{\theta }\cos \theta \right)}^2+{\left(s\dot{\theta }\sin \theta -\dot{s}\cos \theta \right)}^2\right]+{\displaystyle \frac{1}{2}}{m}_c\left[{\left(\dot{x}+l_c\dot{\theta }\cos \theta \right)}^2+{\left(l_c\dot{\theta }\sin \theta \right)}^2\right]+{\displaystyle \frac{1}{2}}{L}_e{\dot{q}}_e^2+\beta {\dot{q}}_{e}s,$$

(4)

where $m_x$ represents the total mass of the beam equivalent mass and bluff body mass. $k_x$ and $c_x$ are the equivalent spring stiffness and the total damping of the composite PZT beam, respectively. The coil mass is denoted as $m_c$ while $k_s$ is the linear spring stiffness attached to the sliding mass of the magnet ($m_s$). $q_e$ and $L_e$ are the electromagnetic charge and coil inductance, respectively. $\beta$ is the electromagnetic coupling factor. $l_c$ represents the distance from the end of the composite beam to the center of mass of the coil.

The harvester’s potential energy arises from (i) the elastic deformation of the composite PZT beam, (ii) the restoring force from the spring attached to the sliding magnet, the gravitational potential energy, and (iii) the piezoelectric energy. As such, the total potential energy of the harvester is given by

$$U={\displaystyle \frac{1}{2}}{k}_x{x}^2+{\displaystyle \frac{1}{2}}{k}_s{\left(s-l_0\right)}^2-m_{s}gs\cos \theta -m_{c}g{l}_c\cos \theta +{\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{C_p}}{q}_p^2-{\displaystyle \frac{\alpha }{C_p}}x{q}_p,$$

(5)

Here, $q_p$ and $C_p$ are the charge and the capacitance of the piezoelectric layer, respectively. The initial length of the spring attached to the sliding magnet is represented by $l_0$. $\alpha$ is the electromechanical coupling coefficient of the PEH.

The harvester is assumed to be fully submerged in water. Therefore, the dissipation energy in the harvester is due to the drag force exerted by the surrounding water, the resistive loads, and the coil’s electrical resistance ($R_c$). The dissipation function is expressed by the following term

$$\mathrm{R}={\displaystyle \frac{1}{2}}{c}_x{\dot{x}}^2+{\displaystyle \frac{1}{2}}\left(R_c+R_e\right){\dot{q}}_e^2+{\displaystyle \frac{1}{2}}{R}_p{\dot{q}}_p^2.$$

(6)

In addition, the harvester is excited only by the lift VIV force ($F$) due to vortex shedding beyond the bluff body. To capture oscillatory phenomena of the vortex shedding, the VIV are modeled using a Van der Pol oscillator [28]. Thus, the generalized force $Q_1$ which is the VIV force ($F)$ is then given by

$$F={\displaystyle \frac{1}{2}}{\rho }_w{U}^{2}D{L}_b{C}_L,$$

(7)

where ${\rho }_w$ is the density of water. $D$ and $L_b$ are the diameter and length of the bluff body, respectively. $U$ denotes the water stream speed across the bluff body. $C_L$ is the lift coefficient, expressed by [28]

$$C_L={\displaystyle \frac{1}{2}} {C_L}_{0}p,$$

(8)

in which, ${C_L}_0$ is the static lift coefficient of a fixed cylinder that is approximately 0.3 for Reynold’s numbers (Re) between 10³ and 10⁵ [28]. $p$ is the wake variable of the Van der Pol oscillator that captures the alternating motion and the lock-in phenomena of the vortex shedding. The Van der Pol oscillator Equation is given as

$$\ddot{p}+\epsilon {\omega }_s\left(p^2-1\right)\dot{p}+{\omega }_s^{2}p={\displaystyle \frac{S}{D}}\left(\ddot{x}+l_c\ddot{\theta }\right),$$

(9)

where ${\mathit{\omega }}_{\mathit{s}}$ is the vortex shedding frequency, ${\omega }_s=2\pi S_{t}U/D$ in which $S_t$ denotes the Strouhal number (approximately 0.2 for 300 < Re < 10⁶). The parameters S and ε are oscillator tuning parameters to fit the experimental data. The approximate values of these tuning parameters used in this study are 12 and 0.3, respectively.

Substituting Equations (2)–(7) in Lagrange formulation given in (1), the equations of motion for the hybrid piezoelectric–electromagnetic energy harvester are obtained. The resulting set of equations that represents the coupled dynamics of the harvester are

$$\left(m_T+m_s+m_x\right)\ddot{x}+c_x\dot{x}+k_{x}x+m_s\sin \theta \ddot{s}-m_s\sin \theta s{\dot{\theta }}^2+m_s\cos \theta s\ddot{\theta }+2m_s\cos \theta \dot{\theta }\dot{s}-l_c{m}_T\sin \theta {\dot{\theta }}^2+l_c{m}_T\cos \theta \ddot{\theta }-{\displaystyle \frac{\alpha }{C_p}}{q}_p+r\lambda ={\displaystyle \frac{1}{4}}\rho U^{2}D{L}_b{C}_{L0}p,$$

(10)

$$m_s{s}^2\ddot{\theta }+l_c^2{m}_T\ddot{\theta }+m_s\cos \theta s\ddot{x}+2m_{s}s\dot{\theta }\dot{s}+g{m}_s\sin \theta s+l_c{m}_T\cos \theta \ddot{x}+g{l}_c{m}_T\sin \theta -\lambda =0,$$

(11)

$$m_s\ddot{s}+c_s\dot{s}+k_s\left(s-l_s\right)+m_s\sin \theta \ddot{x}-g{m}_s\cos \theta -m_{s}s{\dot{\theta }}^2-\beta {\dot{q}}_e=0,$$

(12)

$$R_p{\dot{q}}_p+{\displaystyle \frac{q_p}{C_p}}-{\displaystyle \frac{\alpha }{C_p}}x=0,$$

(13)

$$L_c{\ddot{q}}_e+\left(R_c+R_e\right){\dot{q}}_e+\beta \dot{s}=0,$$

(14)

$$\ddot{p}+\epsilon {\omega }_s\left(p^2-1\right)\dot{p}+{\omega }_s^{2}p={\displaystyle \frac{S}{D}}\left(\ddot{x}+l_c\ddot{\theta }\right),$$

(15)

$$\ddot{\theta }-r\ddot{x}=0.$$

(16)

Equation (16) represents the constrain equation between the beam deflection and the rotational angle of the bluff body. Here, $m_T$ represents the total mass, including the coil mass and the fluid added mass ($\pi {\rho }_w{D}^2{L}_b/4$). The equations of motion are solved numerically using MATLAB (R2023a) ode45 solver with the system parameters listed in Table 1. The total output electrical power ($P_T$) of the harvester is subsequently calculated as

$$P_T={{{\displaystyle \frac{1}{2}}R}_p\dot{q}}_p^2+{{{\displaystyle \frac{1}{2}}R}_e\dot{q}}_e^2.$$

(17)

It is evident that the equations of motion are highly coupled. For example, the piezoelectric charge ($q_p$) affects that beam deflection ($x$) and vice versa, as shown in Equations (11) and (13). Additionally, in Equation (14), the sliding motion of the magnet ($s$) influences the electromagnetic output charge ($q_e$). This coupling extends further to the interaction between the beam deflection (or bluff body rotation) and the sliding motion of the magnet. This interaction results in nonlinear centrifugal and Coriolis ($2m_{s}s\dot{\theta }\dot{s}$) forces. In such coupled systems, dynamic nonlinearities can potentially affect the output power and bandwidth of the harvester. Therefore, careful consideration is essential during designing a hybrid harvester, as will be shown by the analytical results presented in the following section.

4. Results and Discussion

The hybrid piezoelectric–electromagnetic energy harvester under study was manufactured and experimentally investigated in our previous work [24,25], with the harvester parameters and material properties listed in Table 1. The harvester is assumed to be fully submerged in an open water channel, with the flow occurring perpendicular to the bluff body, causing it to oscillate due to vortex shedding. In this section, the results of the numerical simulations are presented. The primary objective of this study is to examine the contribution of the electromagnetic energy harvester (EEH) to the overall performance of the hybrid piezoelectric–electromagnetic energy harvester. The EEH is modeled dynamically as a spring-mass oscillator attached to the free end of the piezoelectric composite harvester.

4.1. Power Contribuation of EEH

The analysis compares the Root Mean Square (RMS) output power of the standalone piezoelectric harvester with that of the hybrid harvester. To ensure a valid comparison, both harvesters should have the same total mass and geometry. For this reason, the hybrid PEEH is treated as a standalone piezoelectric harvester when the spring attached to the sliding magnet inside the bluff body is sufficiently stiff. As such, the spring stiffness is set to 10⁶ N/m, representing the standalone piezoelectric harvester.

The hybrid piezoelectric–electromagnetic energy harvester represents a 2-DoF system, namely the beam deflection ($x$) and the sliding motion of the magnet ($s$). The fundamental frequency of the hybrid PEEH, as simulated in this study, is 3.42 Hz, which closely matches the experimentally measured value of 3.20 Hz from our previous work [24,25]. The second natural frequency of the harvester is numerically estimated to be 6.82 Hz, as shown in the amplitude spectrum of the harvester in Figure 3. The ratio of these two frequencies is approximately 1 : 2, indicating an internal resonance phenomenon that can be excited by VIV forces, which could potentially lead to enhanced energy transfer between the components, depending on the system’s operating conditions.

Figure 4 shows the sensitivity analysis of the hybrid piezoelectric–electromagnetic energy harvester performance with respect to variations in the external electrical load of the piezoelectric energy harvester. The figure clearly illustrates the optimal loads for the piezoelectric subsystem of the hybrid harvester, with peak performance occurring at electrical loads of 0.4 MΩ. Figure 5 shows the output power of the hybrid harvester at a water flow speed of 0.3 m/s at its optimum electrical load and an electromagnetic circuit load of $R_e$ = 1.25 Ω. The RMS power of the piezoelectric subsystem of the hybrid harvester contributes 0.1977 mW in the total power, whereas the electromagnetic subsystem of the hybrid harvester generates only 0.0092 mW, which is 20 times lower than the piezoelectric harvester. In comparison, the simulation results of a standalone piezoelectric show a comparable output power of 0.2051 mW. This indicates that adding an electromagnetic harvester does not significantly enhance the output performance of a hybrid harvester. However, further numerical investigations are required to explore this further, as outlined in the next analysis.

Figure 6 shows the RMS output power of both the hybrid piezoelectric–electromagnetic energy harvester and standalone piezoelectric energy harvesters at an optimum external load of 0.4 MΩ. The results indicate that the standalone PZT harvester outperforms the hybrid harvester at higher water flow speeds, while the performance of both harvesters is comparable at lower speeds. Additionally, the bandwidth, or the span of the lock-in region, is broader for the standalone piezoelectric energy harvester than that of the hybrid harvester. This suggests that the standalone piezoelectric energy harvester has the potential for greater performance at optimal electrical loads. The simulation is repeated at a lower electrical load of 0.04 MΩ, as shown in Figure 7. Although the standalone piezoelectric energy harvester has a broader lock-in region, the hybrid harvester generates more RMS output power. In both cases, the hybrid harvester has a lower onset flow speed at which power is generated. This indicates that the hybrid PEEH under study is preferable for low-speed flow and low electrical loads applications, suggesting that the EEH enhances the overall performance when the load is not optimum.

Table 2. Comparison of Hybrid PEEH and Standalone PEH.

Operating Load (M$\mathit{\Omega }$)	Harvester Type	Max. Power (mW)	Onset Speed (m/s)	Bandwidth (m/s)	Power Difference (%)	Bandwidth Difference (%)
0.40	Standalone PEH	0.613	0.269	0.157	-	-
	Hybrid PEEH	0.496	0.260	0.142	$-$19.09%	$-$9.55%
0.04	Standalone PEH	0.199	0.266	0.165	-	-
	Hybrid PEEH	0.235	0.260	0.148	$+$18.09%	$-$10.20%

summarizes the performance of each harvester in terms of maximum RMS power, onset flow speed, and bandwidth under both external electrical load conditions. The percentage differences are calculated relative to the metrics of the standalone harvester.

4.2. The Effect of Spring Stiffness of EEH on the PEEH Performance

The spring stiffness attached to the magnet is a key design parameter that can be tuned to optimize the PEEH output power across different flow speeds and external electrical loads. To examine the effect of spring stiffness and, thus, the EEH on the overall performance of the hybrid system, the analysis considers the harvester at two representative flow speeds: 0.30 m/s, shown in Figure 6 and Figure 7, which corresponds to the low-speed regime where the hybrid harvester consistently produces higher power regardless of the electrical load; and 0.38 m/s, which represents a higher-speed regime where the electrical load becomes more influential and the standalone harvester outperforms the hybrid design under optimal loading conditions. Two external loads ($R_p$) are investigated: 0.4 MΩ, representing the optimum load condition for the standalone PEH, and 0.04 MΩ, representing a non-optimum load condition, in order to capture the contrasting scenarios of load sensitivity in hybrid and standalone harvesters.

Figure 8 illustrates both the total output power and the individual contributions of each harvester (PEH and EEH) as the spring stiffness varies, at a flow speed of 0.3 m/s and an electrical load of 0.40 MΩ. At this flow speed and load, the output power peaks when the spring stiffness is set to 25.8 N/m. Notably, at this optimal spring stiffness, the total power of the hybrid PEEH is mainly generated by the piezoelectric energy harvester, with minimal contribution from the EEH. The EEH generates maximum output power when the spring stiffness is approximately 83.56 N/m. But, at this spring stiffness, the power from the PEH decreases considerably, causing the overall power to decrease. In this case, the EEH is treated as an absorber that suppresses the PZT beam vibrations and, hence, reduces the overall output power of the harvester.

Figure 9 shows the output power of the hybrid harvester as the spring stiffness varies, with a higher flow speed of 0.38 m/s and an external load of 0.40 MΩ. As the spring stiffness increases, the power also increases. This clearly indicates that the standalone PZT harvester is preferable under these operating conditions. The EEH produces maximum electrical power at a spring stiffness of 87.44 N/m. However, the power generated by the EEH is extracted from the PEH, which reduces the overall power of the hybrid system. The piezoelectric energy harvester remains the primary source of power across various spring stiffness values, and no dynamic benefits from using the EEH are observed under these conditions.

It is important to note that the EEH still plays a dynamic role in enhancing the overall performance of the hybrid PEEH. The oscillatory motion of the magnet in the EEH contributes to the dynamics of the hybrid PEEH that increases the output power. As mentioned earlier, the hybrid harvester functions similarly to a standalone PZT harvester when the spring stiffness is sufficiently high. Figure 9 clearly shows that as spring stiffness increases towards 150 N/m, the output power decreases. In these operating conditions, this confirms that the hybrid harvester outperforms the standalone PZT harvester due to its coupled dynamics, even though the EEH does not directly contribute to the total output power.

The effect of spring stiffness on the overall output power of the hybrid PEEH at a low flow speed of 0.3 m/s and a high external load of 0.04 MΩ is illustrated in Figure 10. As the spring stiffness increases, the total output power rises to a peak around 83.56 N/m. At this point, the EEH generates its maximum power, while the contribution of the PEH decreases. In this configuration, it is evident that the EEH contributes more to the overall power of the hybrid harvester near its optimum spring stiffness. However, this is attributed to the significant reduction in the PEH output power under a low external electrical load that is much lower than its optimum value of 0.4 MΩ. Overall, this demonstrates that the hybrid harvester outperforms the standalone PZT harvester at low external loads. The final operating condition considers the hybrid harvester at a flow speed of 0.38 m/s at an electrical load of 0.04 MΩ. The output power of the hybrid PEEH at various spring stiffnesses is presented in Figure 11. In general, the performance of the harvester is similar to the case presented in the previous section. The EEH contributes more to the overall power near an optimum spring stiffness at low external loads.

The coupled dynamics between both harvesters at this optimum spring stiffness result in an increase in output power. From the equations of motion, the sliding magnet in the EEH is driven at the second harmonic of the PEH. Therefore, the EEH power is maximized when the second harmonic of the PEH matches the EEH resonance. In this scenario, the hybrid harvester is operating under a 1 : 2 internal resonance. However, meeting this condition does not necessarily guarantee that the hybrid PEEH generates more power than the standalone PZT harvester. This is demonstrated in Figure 9, where at high flow speed and high electrical load, the standalone PZT harvester produces more power than the hybrid PEEH, even when it is at its 1:2 internal resonance status.

5. Conclusions

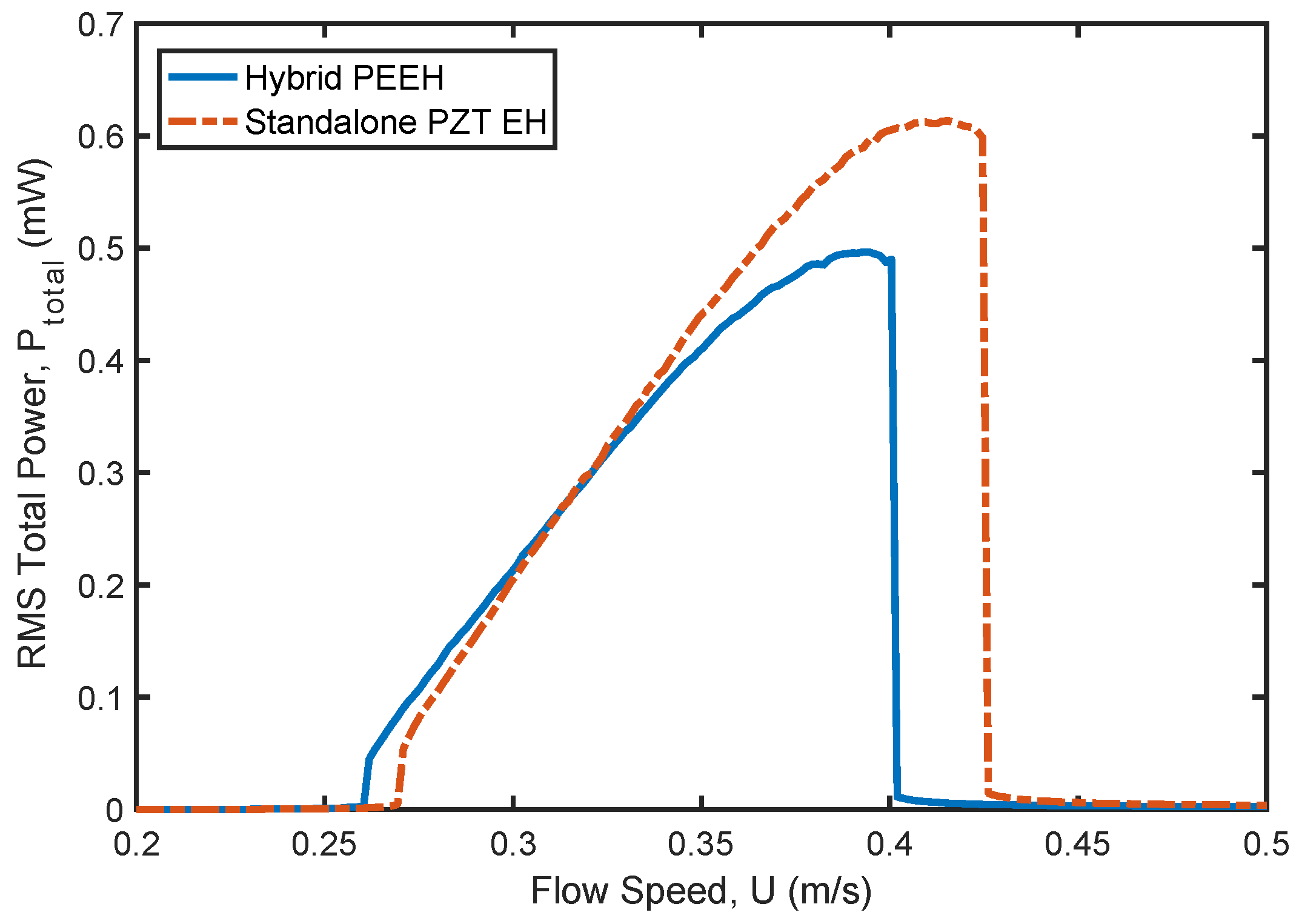
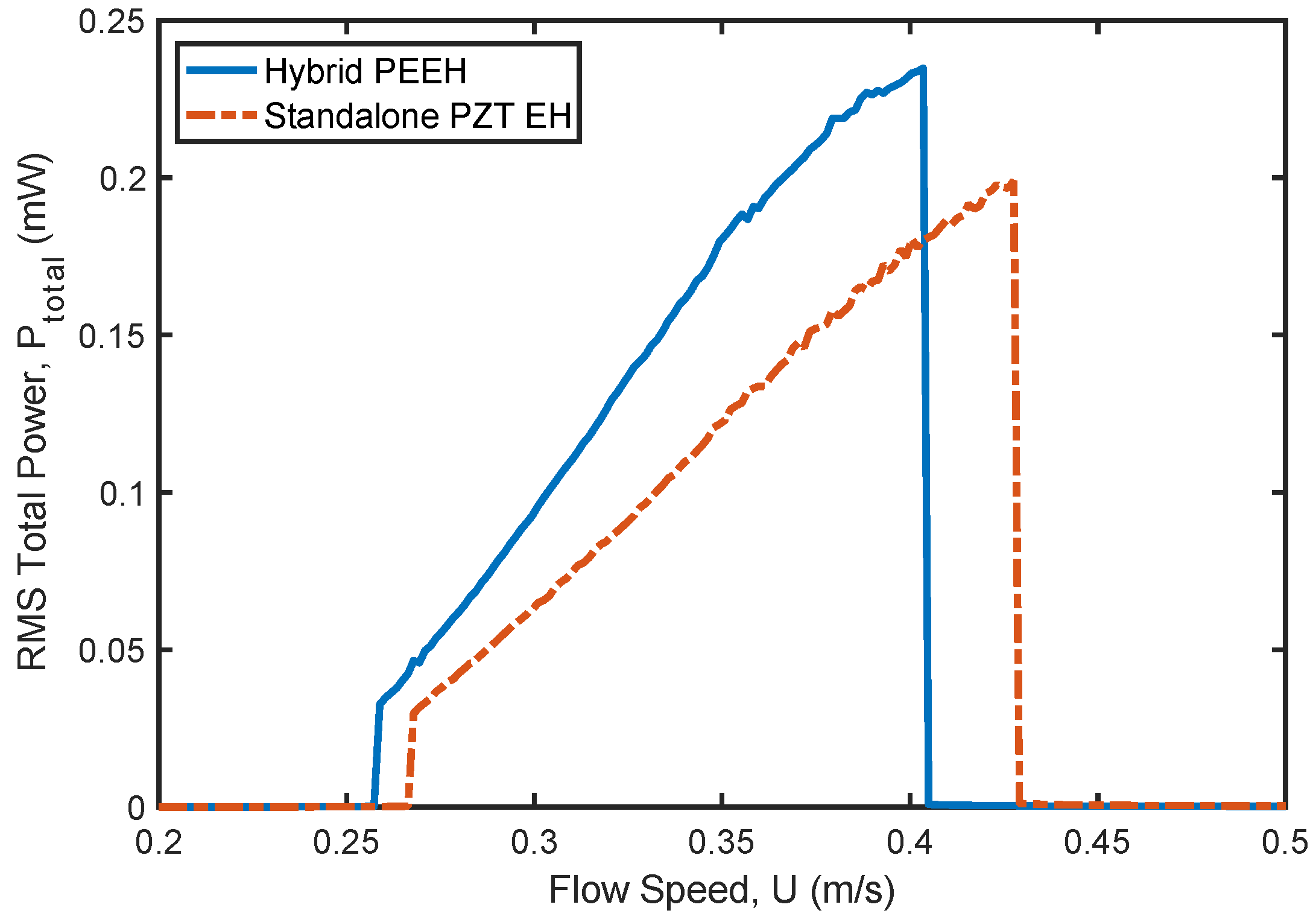
In this study, the dynamics of a hybrid piezoelectric-electromagnetic energy harvester driven by vortex-induced vibration are investigated. The equations of motion reveal a strong coupling between the various electrical and mechanical domains of the harvester. The primary objective of the numerical analysis is to evaluate the contribution of the electromagnetic harvester to the overall performance of the hybrid system in comparison to a standalone PZT harvester. The numerical results indicate that the hybrid harvester outperforms the standalone piezoelectric harvester only at low electrical loads and low-speed water flow. In particular, the electromagnetic harvester enhances the output power of the hybrid harvester in two ways: (i) by directly contributing to the output power, and (ii) by dynamically interacting with the PEH to increase its output power.

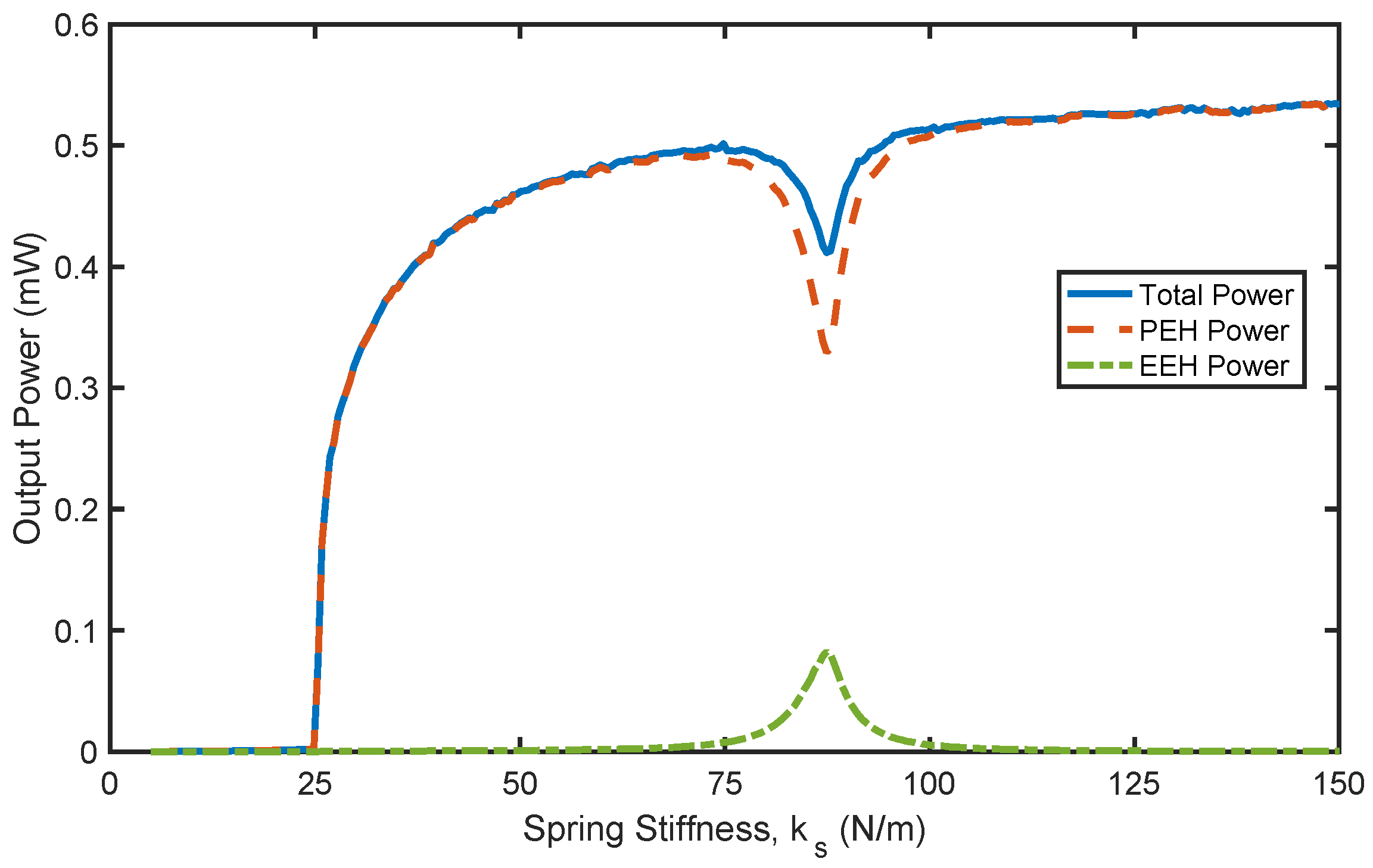
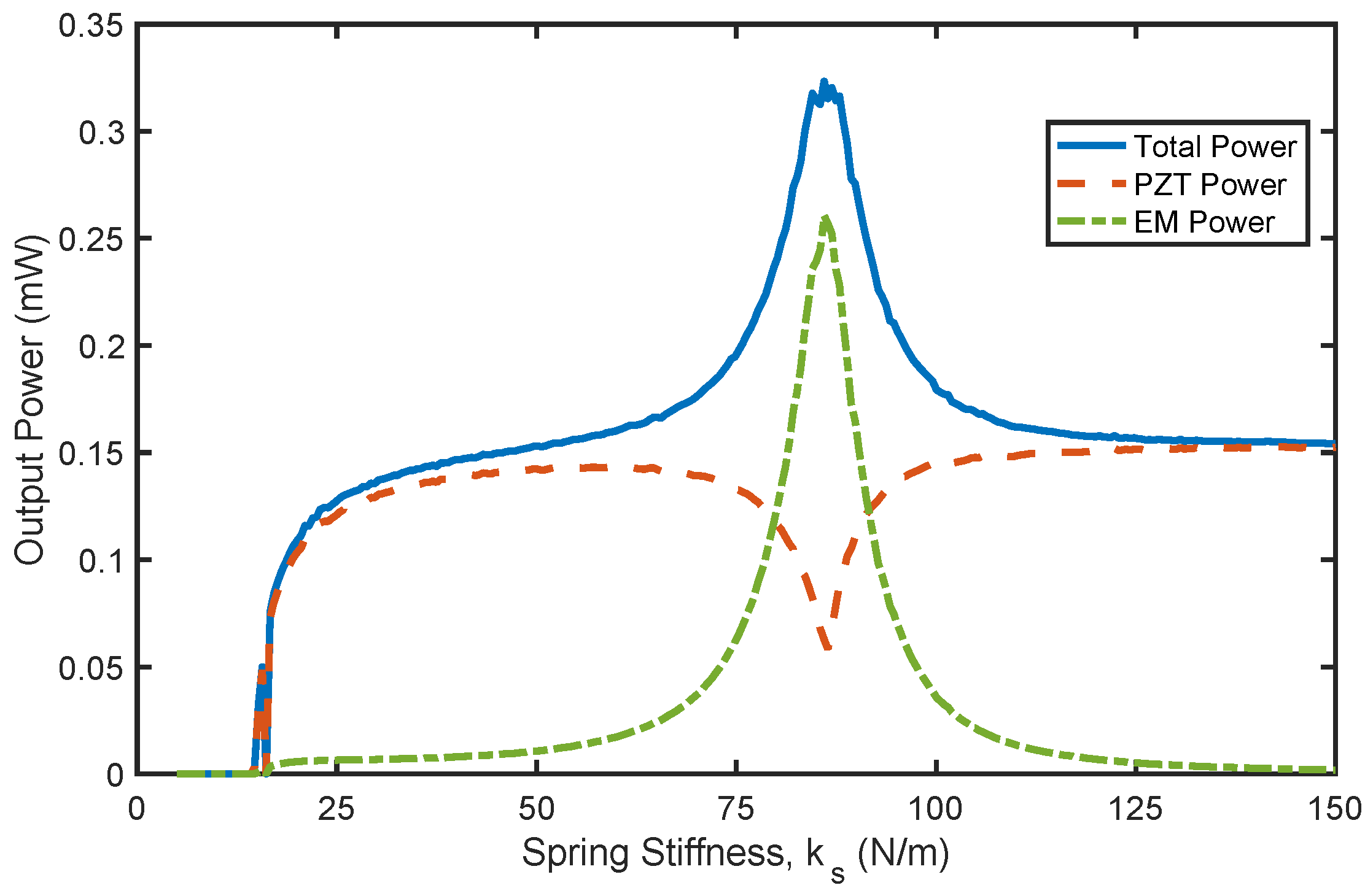
Optimal spring stiffness values that maximize the output power of the hybrid harvester are identified under various operating conditions. At low electrical loads, the optimal spring stiffness corresponds to the point where the EEH power is at its maximum, contributing most to the overall output power. This is attributed to the internal resonance phenomenon that enhances energy exchange between the harvester components. However, beyond this optimal value, the contribution of the EEH becomes minimal. At higher flow speed and electrical loads, the standalone PZT harvester generates higher output power. This is because the electromagnetic part is acting as an auxiliary oscillator that suppresses the dynamics of the hybrid harvester, resulting in a reduction in the output power.

This conclusion agrees with the findings in the recent study by Truong et al. [22]. Their study revealed that a linear hybrid harvester generates less power than a standalone piezoelectric when the electrical loads exceed a certain figure of merit threshold. As such, further numerical investigations are necessary to refine the design of the hybrid harvester and enhance its performance at varying load conditions and flow speeds. A dimensionless or normalized analysis of the hybrid piezoelectric–electromagnetic energy harvester could provide in-depth insights into the general design criteria for an optimized hybrid harvester with output power greater than a standalone PZT harvester under various operating conditions.