Numerical Investigation of Fracture Behavior and Current-Carrying Capability Degradation in Bi2212/Ag Composite Superconducting Wires Subjected to Mechanical Loads Using Phase Field Method
Abstract
1. Introduction
2. Phase Field Model for Crack Propagation in Bi2212 Round Wires Under Tensile Load
2.1. Basic Equations of Phase Field Model
2.2. Numerical Examples
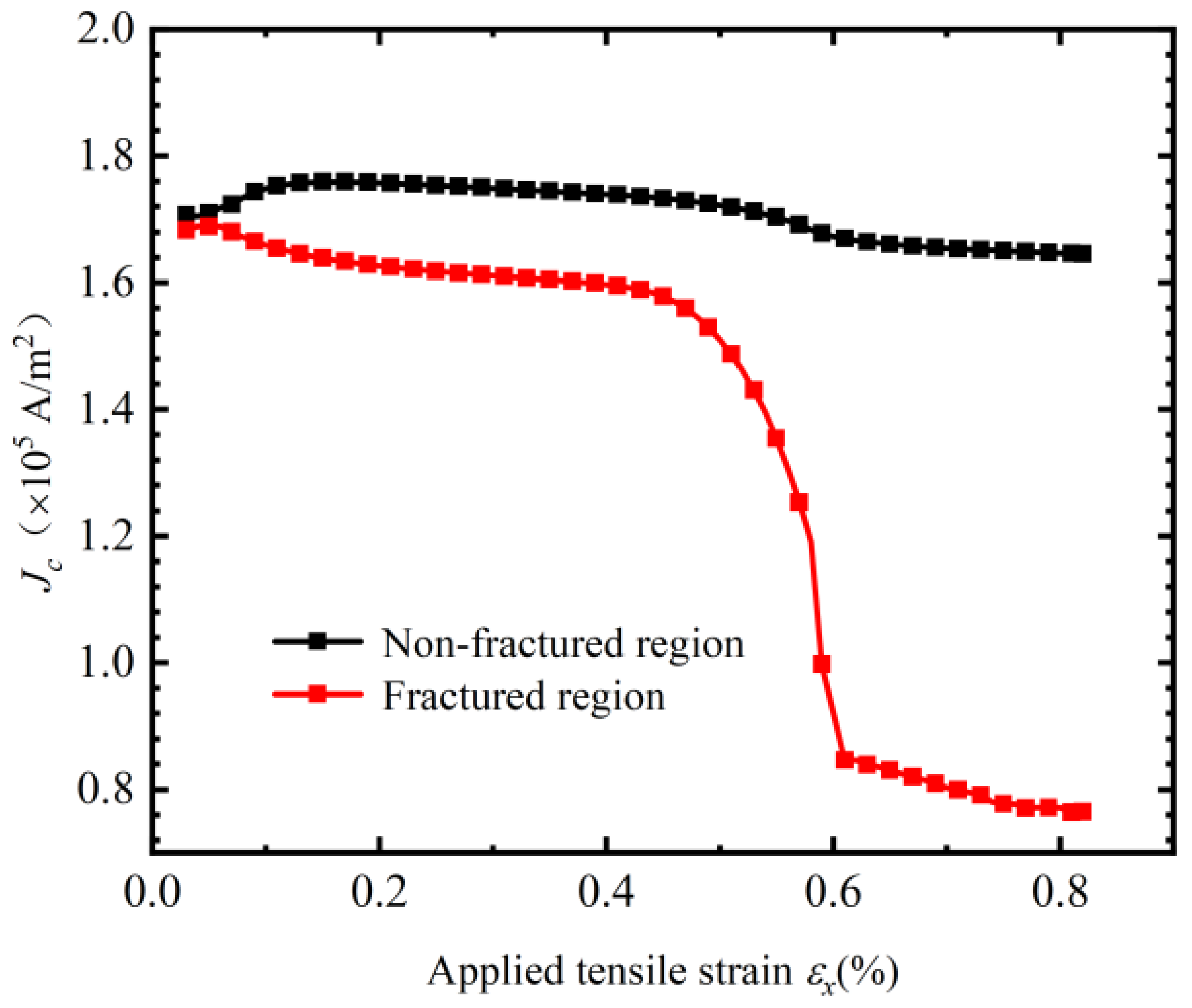
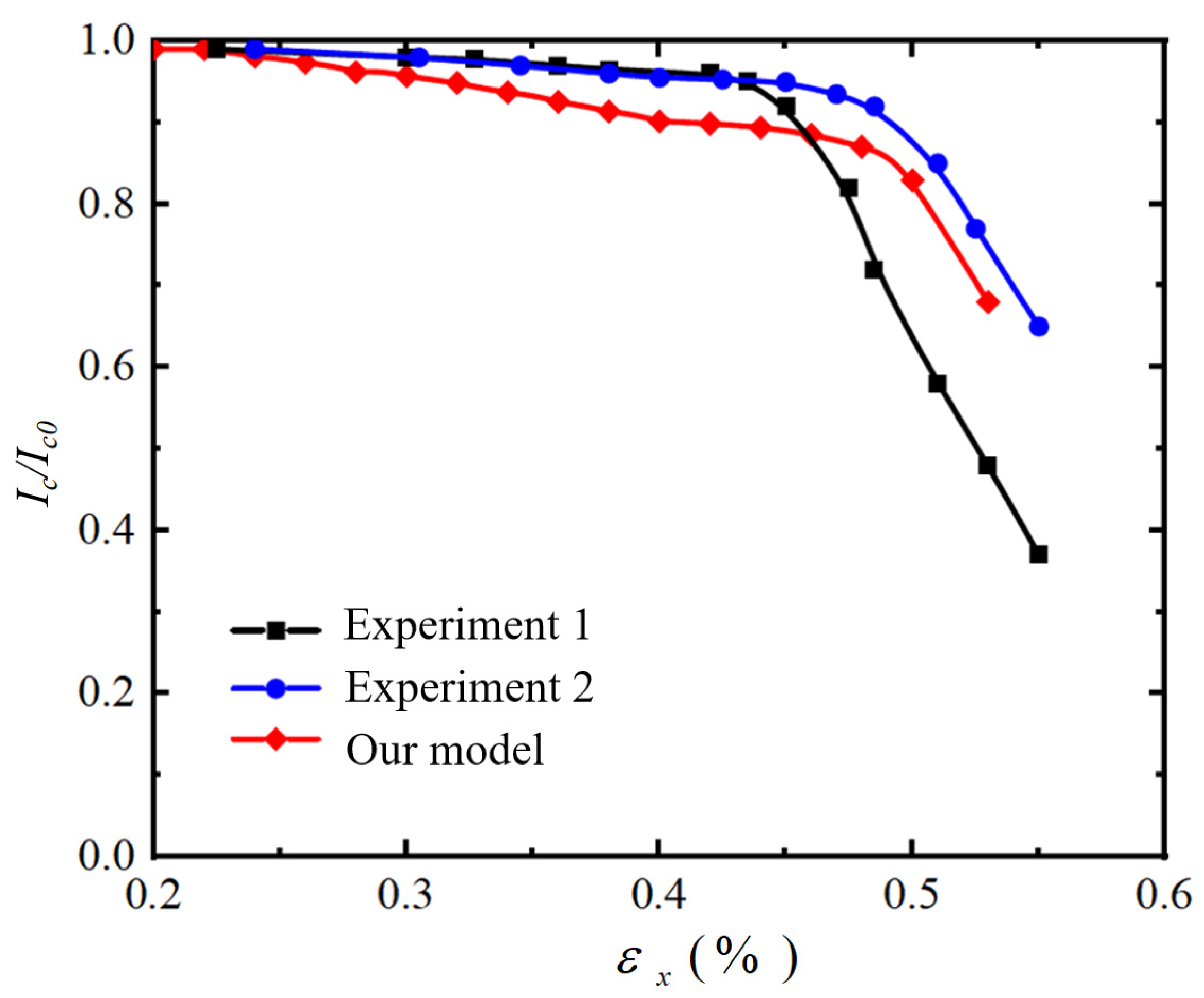
3. The Effect of Crack Propagation on Critical Current
Finite Element Calculation Example
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shin, J.; Ochiai, S.; Okuda, H.; Mukai, Y.; Matsubayashi, H.; Oh, S.; Ha, D.; Kim, S.; Sato, M. Estimation of Young’s modulus, residual strain and intrinsic fracture strain of Bi2212 filaments in Bi2212/Ag/Ag alloy composite wire. Phys. C Supercond. 2008, 468, 1792–1795. [Google Scholar] [CrossRef]
- Katagiri, K.; Shin, H.; Shoji, Y.; Ebisawa, N.; Watanabe, K.; Noto, K.; Okada, T.; Hiraoka, M.; Yuya, S. Tensile strain/transverse compressive stress dependence of critical current in Ag-sheathed Bi (2212) 7-core superconducting wires. Cryogenics 1996, 36, 491–494. [Google Scholar] [CrossRef]
- Mao, Z.-H.; Jin, H.; Qin, J.-G.; Liu, F.; Dai, C.; Hao, Q.-B.; Li, C.-S. Axial tensile stress–strain characterization of Bi-2212 round wire with different heat treatments. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Godeke, A.; Hartman, M.H.C.; Mentink, M.G.T.; Jiang, J.; Matras, M.; Hellstrom, E.E.; Larbalestier, D.C. Critical current of dense Bi-2212 round wires as a function of axial strain. Supercond. Sci. Technol. 2015, 28, 032001. [Google Scholar] [CrossRef]
- Bjoerstad, R.; Scheuerlein, C.; Rikel, M.O.; Ballarino, A.; Bottura, L.; Jiang, J.; Matras, M.; Sugano, M.; Hudspeth, J.; Di Michiel, M. Strain induced irreversible critical current degradation in highly dense Bi-2212 round wire. Supercond. Sci. Technol. 2015, 28, 062002. [Google Scholar] [CrossRef]
- Cheggour, N.; Lu, X.F.; Holesinger, T.G.; Stauffer, T.C.; Jiang, J.; Goodrich, L.F. Reversible effect of strain on transport critical current in Bi2Sr2CaCu2O8+x superconducting wires: A modified descriptive strain model. Supercond. Sci. Technol. 2011, 25, 015001. [Google Scholar] [CrossRef]
- Li, P.; Naderi, G.; Schwartz, J.; Shen, T. On the role of precursor powder composition in controlling microstructure, flux pinning, and the critical current density of Ag/Bi2Sr2CaCu2Ox conductors. Supercond. Sci. Technol. 2017, 30, 035004. [Google Scholar] [CrossRef]
- Shen, T.; Ghosh, A.; Cooley, L.; Jiang, J. Role of internal gases and creep of Ag in controlling the critical current density of Ag-sheathed Bi2Sr2CaCu2Ox wires. J. Appl. Phys. 2013, 113, 213901. [Google Scholar] [CrossRef]
- Han, Z.; Skov-Hansen, P.; Freltoft, T. The mechanical deformation of superconducting BiSrCaCuO/Ag composites. Supercond. Sci. Technol. 1997, 10, 371–387. [Google Scholar] [CrossRef]
- Wang, Z.; Yong, H.; Zhou, Y. Degradation of critical current in Bi2212 composite wire under compression load. Appl. Math. Mech. 2017, 38, 1773–1784. [Google Scholar] [CrossRef]
- Liu, D.; Yong, H.; Zhou, Y. Analysis of critical current density in Bi2Sr2CaCu2O8+x round wire with filament fracture. J. Supercond. Nov. Magn. 2016, 29, 2299–2309. [Google Scholar] [CrossRef]
- Yang, Y.; Yong, H.; Zhou, Y. Mechanical behavior in superconducting composite wires. Eur. J. Mech.-A/Solids 2018, 70, 191–202. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Z.; Yong, H.; Zhou, Y. Modeling effects of gas bubbles on the mechanical behaviors of Ag/Bi-2212 round wires using a double cantilever beam bridge model. Cryogenics 2016, 77, 65–73. [Google Scholar] [CrossRef]
- Peng, X.; Yong, H.; Zhou, Y. Damage analysis of superconducting composite wire with bridging model. Acta Mech. Solida Sin. 2018, 31, 19–31. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Jiang, Z.-F.; Zhang, Z.-X.; Gou, X.-F. Interpretation of compressive strain causing critical current degradation of Bi2212 round wires. IEEE Trans. Appl. Supercond. 2022, 32, 1–8. [Google Scholar] [CrossRef]
- Jiang, Z.-F.; Gou, X.-F.; Shen, T.-M. Impact of the complex interface between Bi2Sr2CaCu2Ox filaments and Ag matrix on the quench behavior of composite round wires. IEEE Trans. Appl. Supercond. 2018, 29, 1–9. [Google Scholar] [CrossRef]
- Fries, T.-P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Strouboulis, T.; Copps, K.; Babuška, I. The generalized finite element method. Comput. Methods Appl. Mech. Eng. 2001, 190, 4081–4193. [Google Scholar] [CrossRef]
- Chau-Dinh, T.; Zi, G.; Lee, P.-S.; Rabczuk, T.; Song, J.-H. Phantom-node method for shell models with arbitrary cracks. Comput. Struct. 2012, 92–93, 242–256. [Google Scholar] [CrossRef]
- Rabczuk, T.; Zi, G.; Gerstenberger, A.; Wall, W.A. A new crack tip element for the phantom—Node method with arbitrary cohesive cracks. Int. J. Numer. Methods Eng. 2008, 75, 577–599. [Google Scholar] [CrossRef]
- Khoei, A.R. Extended Finite Element Method: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zhao, W.; Du, C.; Jiang, S. An adaptive multiscale approach for identifying multiple flaws based on XFEM and a discrete artificial fish swarm algorithm. Comput. Methods Appl. Mech. Eng. 2018, 339, 341–357. [Google Scholar] [CrossRef]
- Alessi, R.; Marigo, J.-J.; Vidoli, S. Gradient damage models coupled with plasticity: Variational formulation and main properties. Mech. Mater. 2015, 80, 351–367. [Google Scholar] [CrossRef]
- Askes, H.; Pamin, J.; De Borst, R. Dispersion analysis and element-free Galerkin solutions of second-and fourth-order gradient-enhanced damage models. Int. J. Numer. Methods Eng. 2000, 49, 811–832. [Google Scholar] [CrossRef]
- Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; de Borst, R. An isogeometric analysis approach to gradient damage models. Int. J. Numer. Methods Eng. 2011, 86, 115–134. [Google Scholar] [CrossRef]
- Bui, T.Q.; Hu, X. A review of phase-field models, fundamentals and their applications to composite laminates. Eng. Fract. Mech. 2021, 248, 107705. [Google Scholar] [CrossRef]
- Diehl, P.; Lipton, R.; Wick, T.; Tyagi, M. A comparative review of peridynamics and phase-field models for engineering fracture mechanics. Comput. Mech. 2022, 69, 1259–1293. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Diehl, P.; Prudhomme, S.; Lévesque, M. A review of benchmark experiments for the validation of peridynamics models. J. Peridynamics Nonlocal Model. 2019, 1, 14–35. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Hai, L.; Li, J. A rate-dependent phase-field framework for the dynamic failure of quasi-brittle materials. Eng. Fract. Mech. 2021, 252, 107847. [Google Scholar] [CrossRef]
- Han, J.; Matsubara, S.; Moriguchi, S.; Terada, K. Variational crack phase-field model for ductile fracture with elastic and plastic damage variables. Comput. Methods Appl. Mech. Eng. 2022, 400, 115577. [Google Scholar] [CrossRef]
- Teichtmeister, S.; Kienle, D.; Aldakheel, F.; Keip, M.-A. Phase field modeling of fracture in anisotropic brittle solids. Int. J. Non-linear Mech. 2017, 97, 1–21. [Google Scholar] [CrossRef]
- Wu, J.-Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Wu, J.-Y. A geometrically regularized gradient-damage model with energetic equivalence. Comput. Methods Appl. Mech. Eng. 2018, 328, 612–637. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Nguyen, V.P. A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 2018, 119, 20–42. [Google Scholar] [CrossRef]
- Chen, W.-X.; Wu, J.-Y. Phase-field cohesive zone modeling of multi-physical fracture in solids and the open-source implementation in Comsol Multiphysics. Theor. Appl. Fract. Mech. 2022, 117, 103153. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Ulmer, H.; Hofacker, M.; Miehe, C. Phase field modeling of brittle and ductile fracture. PAMM 2013, 13, 533–536. [Google Scholar] [CrossRef]
- Li, B.; Peco, C.; Millán, D.; Arias, I.; Arroyo, M. Phase-field modeling and simulation of fracture in brittle materials with strongly anisotropic surface energy. Int. J. Numer. Methods Eng. 2015, 102, 711–727. [Google Scholar] [CrossRef]
- Kuhn, C.; Müller, R. Phase field simulation of thermomechanical fracture. Proc. Appl. Math. Mech. 2009, 9, 191–192. [Google Scholar] [CrossRef]
- Francfort, G.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Ahoranta, M.; Lehtonen, J.; Tarhasaari, T. Finite element models for thermal stress, axial tension, bending, and transversalcompression of filamentary Bi-2223 tapes. Supercond. Sci. Technol. 2008, 22, 015012. [Google Scholar] [CrossRef]
- Sugano, M.; Osamura, K.; Nyilas, A. Estimation of the coefficient of thermal expansion of Bi2223 at low temperature. Supercond. Sci. Technol. 2003, 16, 1064–1070. [Google Scholar] [CrossRef]
- Yusheng, H.; Jiong, X.; Sheng, J.; Aisheng, H.; Jincang, Z. Ultrasonic investigations of the layered perovskite ceramic superconducting systems. Phys. B Condens. Matter 1990, 165–166, 1283–1284. [Google Scholar] [CrossRef]
- Shin, J.K.; Ochiai, S.; Okuda, H.; Sugano, M.; Oh, S.S. Change of the V–I curve and critical current with applied tensile strain due to cracking of filaments in Bi2223composite tape. Supercond. Sci. Technol. 2008, 21, 115007. [Google Scholar] [CrossRef]
- Gelhausen, J.; Eschrig, M. Theory of a weak-link superconductor-ferromagnet Josephson structure. Phys. Rev. B 2016, 94, 104502. [Google Scholar] [CrossRef]
- Maeda, A.; Espinoza, L.B.G. Josephson Junction and Josephson Device. U.S. Patent 8200304 B2, 12 June 2012. [Google Scholar]
- Pomorski, K.; Prokopow, P. Possible existence of field-induced Josephson junctions. Phys. Status Solidi B 2012, 249, 1805–1813. [Google Scholar] [CrossRef]



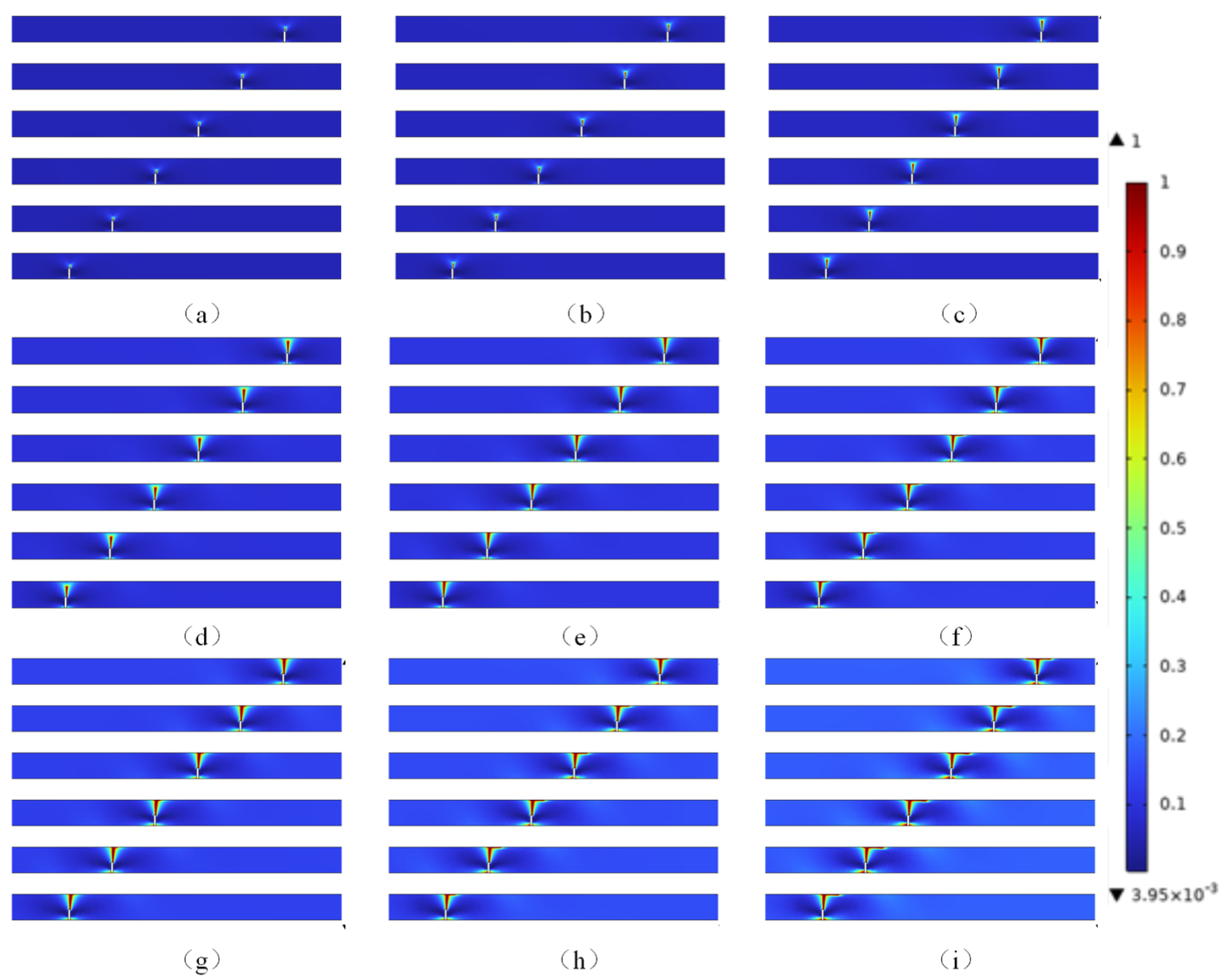



| Thickness of the model for the Bi2212 round wire | |
| Thickness of superconducting core wire | μm |
| Thickness of Ag monolayer | |
| Thickness of AgMg protective layer |
| E (GPa) | ||
|---|---|---|
| Bi2212 | 38.8 | 0.2 |
| Ag | 92 | 0.37 |
| AgMg | 104.23 | 0.37 |
| Critical energy release rate | |
| Length scale parameter | |
| Mesh size |
| (S/m) | E (GPa) | |||
|---|---|---|---|---|
| Bi2212 | 25 | 38.8 | 0.2 | |
| Ag | 1 | 92 | 0.37 | |
| AgMg | 1 | 104.23 | 0.37 |
| 0~1% | |
| 20 |
| Right end of the model | |
| Left end of the model | |
| Upper and lower boundaries | |
| Bi2212/Ag interface |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, F.; Zhou, K. Numerical Investigation of Fracture Behavior and Current-Carrying Capability Degradation in Bi2212/Ag Composite Superconducting Wires Subjected to Mechanical Loads Using Phase Field Method. Modelling 2025, 6, 119. https://doi.org/10.3390/modelling6040119
Xue F, Zhou K. Numerical Investigation of Fracture Behavior and Current-Carrying Capability Degradation in Bi2212/Ag Composite Superconducting Wires Subjected to Mechanical Loads Using Phase Field Method. Modelling. 2025; 6(4):119. https://doi.org/10.3390/modelling6040119
Chicago/Turabian StyleXue, Feng, and Kexin Zhou. 2025. "Numerical Investigation of Fracture Behavior and Current-Carrying Capability Degradation in Bi2212/Ag Composite Superconducting Wires Subjected to Mechanical Loads Using Phase Field Method" Modelling 6, no. 4: 119. https://doi.org/10.3390/modelling6040119
APA StyleXue, F., & Zhou, K. (2025). Numerical Investigation of Fracture Behavior and Current-Carrying Capability Degradation in Bi2212/Ag Composite Superconducting Wires Subjected to Mechanical Loads Using Phase Field Method. Modelling, 6(4), 119. https://doi.org/10.3390/modelling6040119






