Aerodynamic Lift Modeling and Analysis of a Bat-like Flexible Flapping-Wing Robot
Abstract
1. Introduction
2. The Structure and Movement of Wings
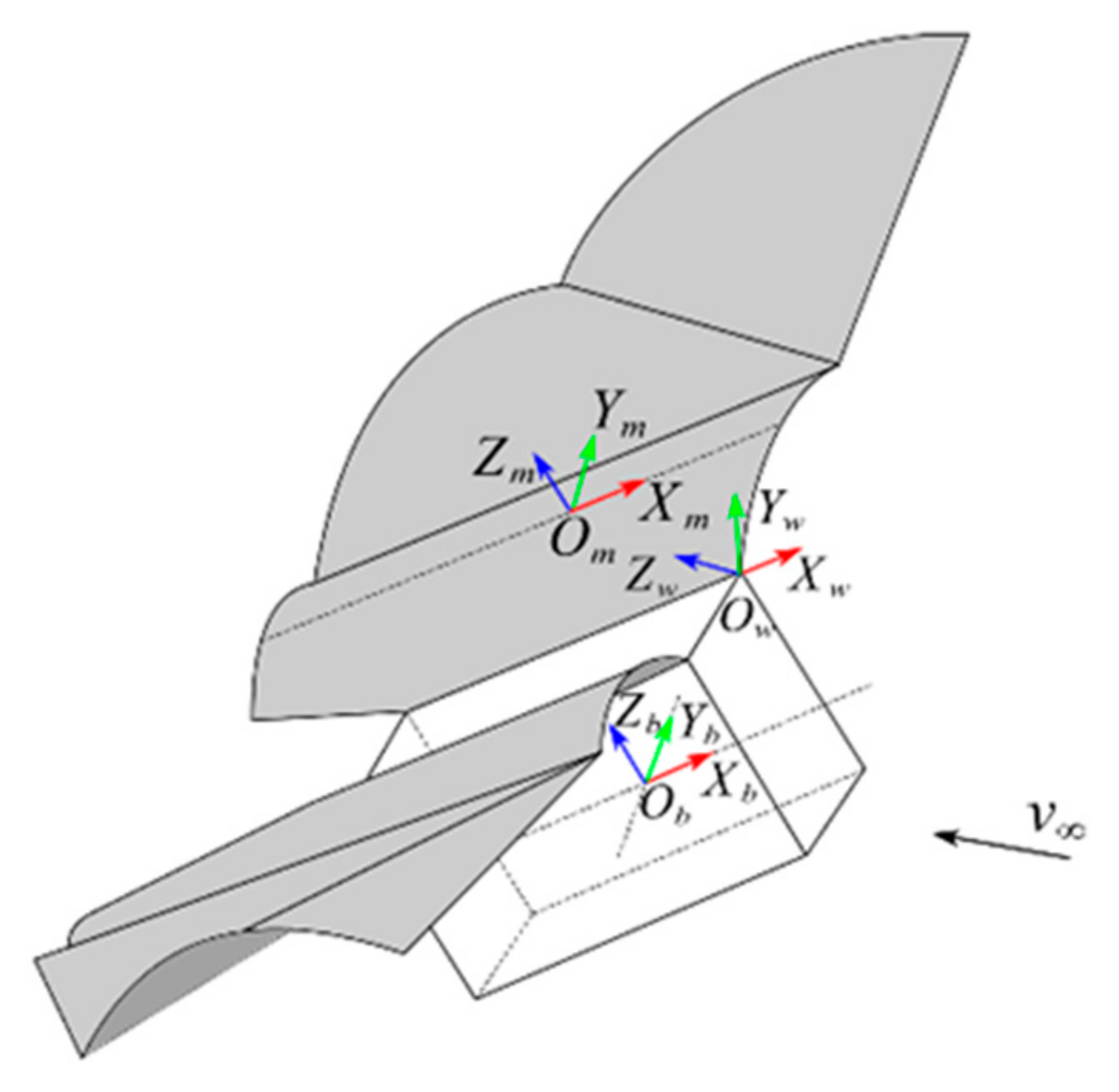
2.1. Definition of Coordinate System
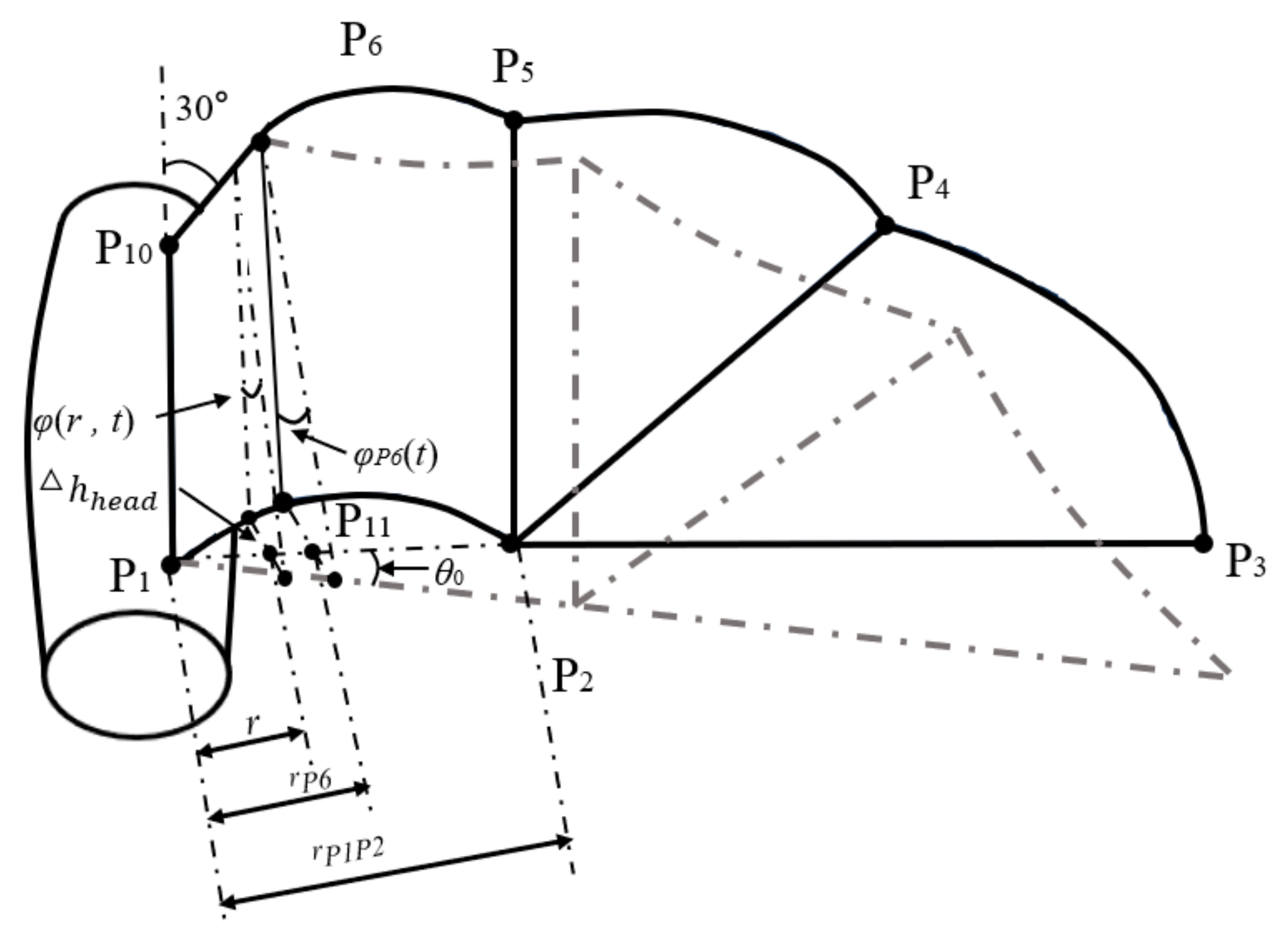
2.2. Calculation of Chord Length and Passive Torsion Angle of the Flexible Wing Membrane Based on the Blade Element Method
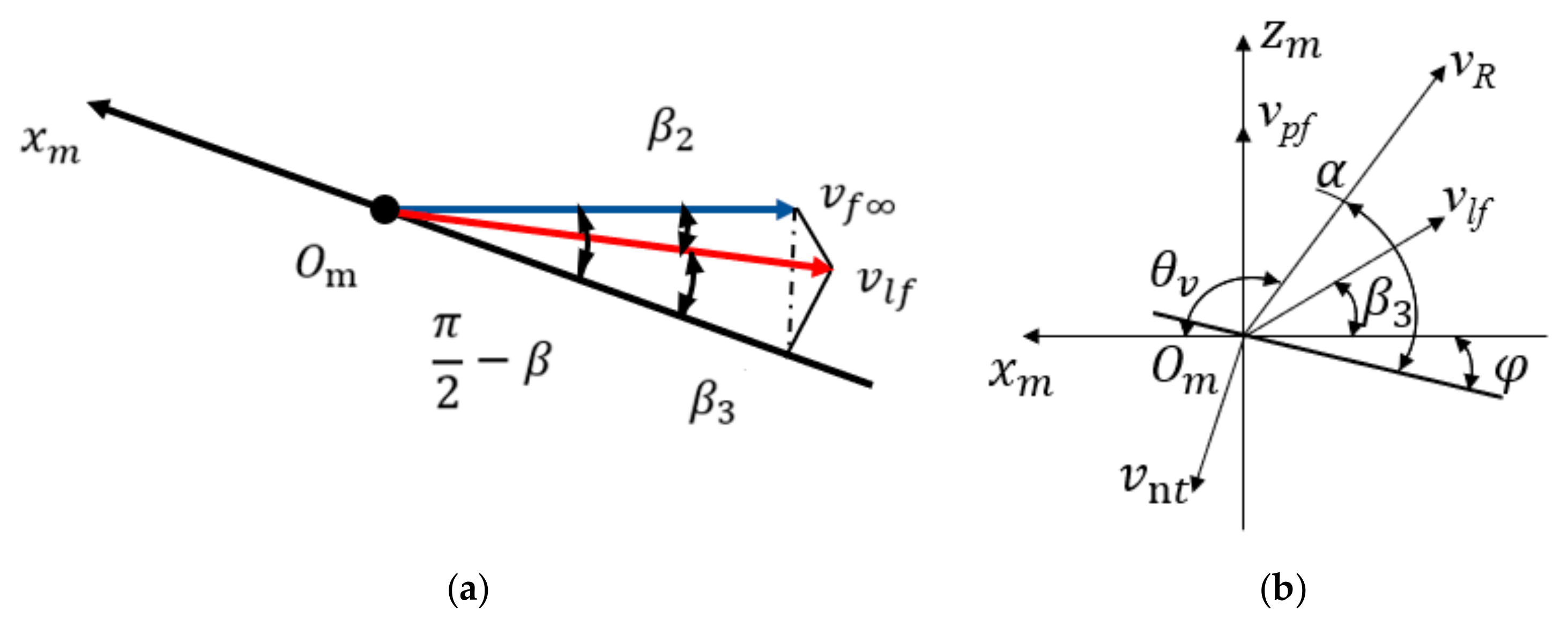
2.3. Calculation of Relative Velocity and Relative Angle of Attack of Flexible Wing Membranes Based on the Blade Element Method
3. Building on the Extended Quasi-Steady-State Lift Model
3.1. Lift Model of Libration Circulation from Freestream
3.2. Lift Model Derived from the Translational Circulation of the Beat Around the Beat Axis
3.3. Lift Model of Rotational Circulation Derived from Flexible Deformation
3.4. Added-Mass Force Model
3.5. Inertia Force Model
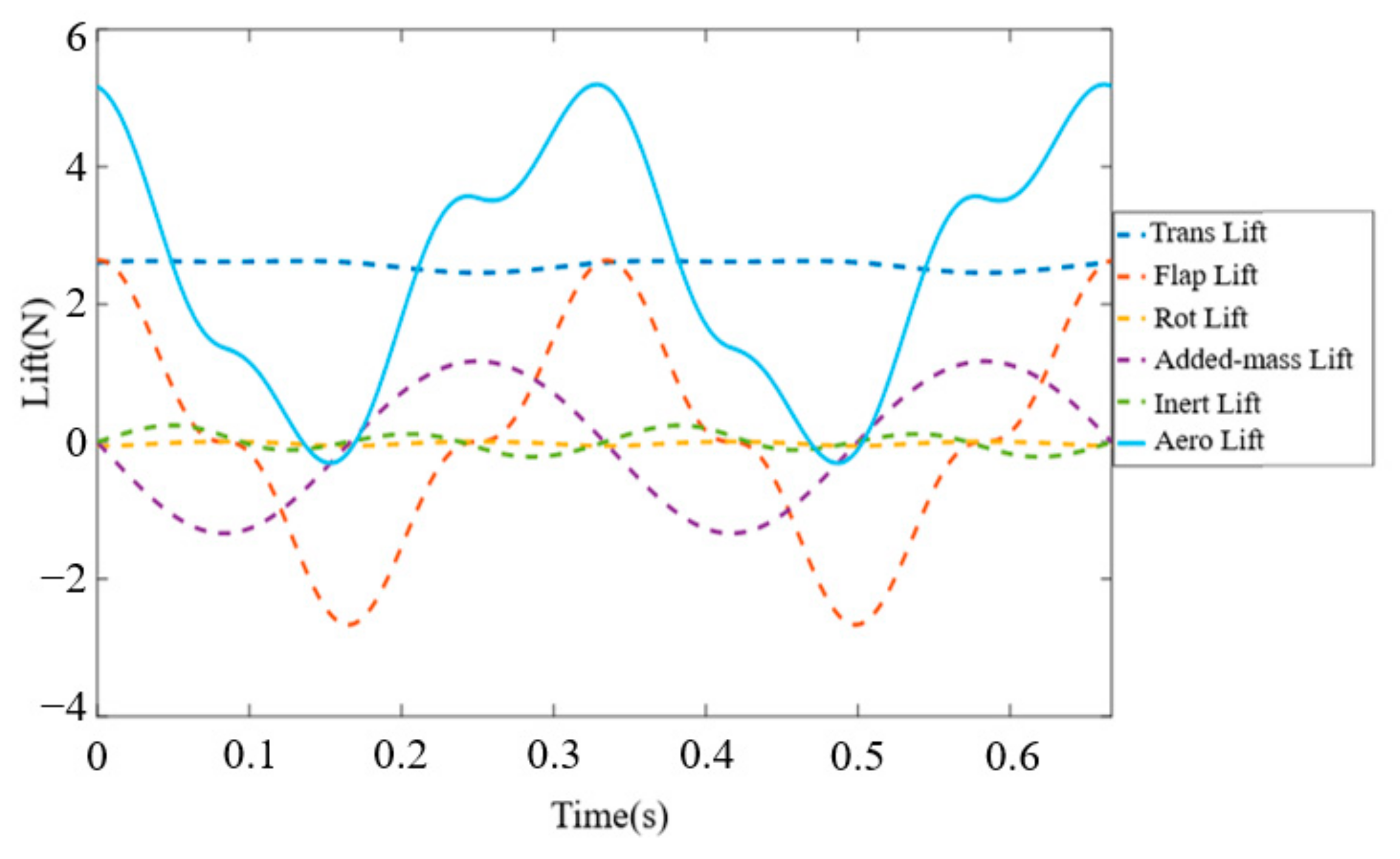
3.6. Combined Lift Model
4. Instructions
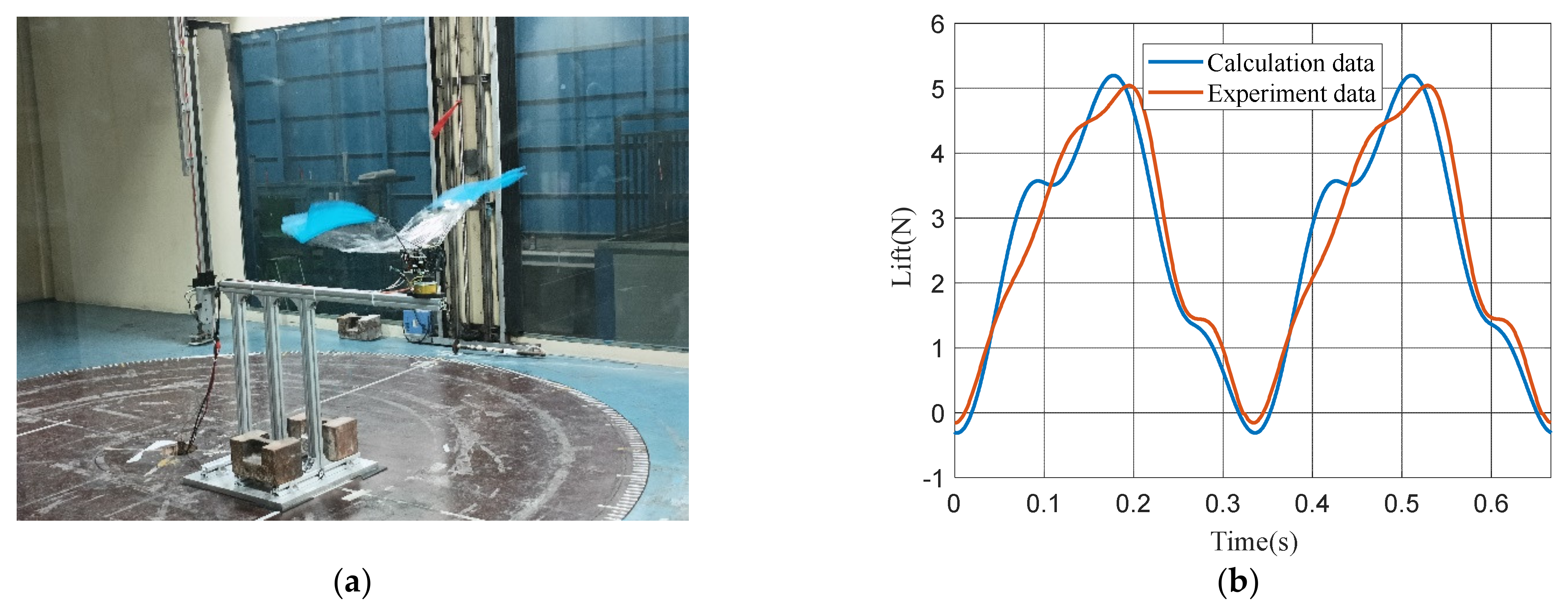
5. Comparative Analysis of Wind Tunnel Test Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gerdes, J.W.; Gupta, S.K.; Wilkerson, S.A. A review of bird-inspired flapping wing miniature air vehicle designs. J. Mech. Robot.-Trans. ASME 2012, 4, 5484–5494. [Google Scholar] [CrossRef]
- Couceiro, M.; Luz, J.M.A.; Figueiredo, C.M.; Ferreira, N.F. Modeling and control of biologically inspired flying robots. Robotica 2011, 30, 107–121. [Google Scholar] [CrossRef]
- Pan, Y.; Guo, S.; Huang, X. Research progress on bio-inspired flapping-wing rotor micro aerial vehicle development. J. Bionic Eng. 2024, 21, 1621–1643. [Google Scholar] [CrossRef]
- Kan, Z.; Yao, Z.; Li, D.; Bie, D.; Wang, Z.; Li, H.; Xiang, J.W. Design and flight test of the fixed-flapping hybrid morphing wing aerial vehicle. Aerosp. Sci. Technol. 2023, 143, 108705. [Google Scholar] [CrossRef]
- Zhang, M.; Song, B.; Yang, X.; Lang, X.; Xuan, J.; Wang, L. Analysis of the integrated pattern of hoverable flapping wing micro-air vehicle. J. Eng. Res. 2024, 13, 1901–1915. [Google Scholar] [CrossRef]
- Han, J.K.; Hui, Z.; Tian, F.B.; Chen, G. Review on bio-inspired flight systems and bionic aerodynamics. Chin. J. Aeronaut. 2021, 34, 170–186. [Google Scholar] [CrossRef]
- Wang, J.X.; Xuan, J.L.; Yang, X.J.; Zheng, R. Research progress of flapping wing aircraft with multimodal motion ability. Acta Aeronaut. Astronaut. Sin. 2024, 45, 029842. [Google Scholar]
- Dadashi, S.; Gregory, J.; Lei, Y.; Kurdila, A.; Bayandor, J.; Mueller, R. Adaptive control of a flapping wing robot inspired by bat flight. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Fei, F.; Zhan, T.; Yang, Y.L.; Zhang, J.; Deng, X.Y. Flappy Hummingbird: An Open Source Dynamic Simulation of Flapping Wing Robots and Animals wing robots and animals. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA; pp. 9223–9229.
- Jafferis, N.T.; Helbling, E.F.; Karpelson, M.; Wood, R.J. Untethered flight of an insect-sized flapping-wing microscale aerial vehicle. Nature 2019, 570, 491–495. [Google Scholar] [CrossRef]
- Sihite, E.; Alireza, R. A morphology-centered view towards describing bats dynamically versatile wing conformations. Int. J. Robot. Res. 2025, 44, 431–464. [Google Scholar] [CrossRef]
- Norberg, U.M.; Rayner, J.M. Ecological morphology and flight in bats (Mammalia; Chiroptera): Wing adaptations, flight performance, foraging strategy and echolocation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1985, 316, 335–427. [Google Scholar]
- Ramezani, A.; Chung, S.J.; Hutchinson, S. A biomimetic robotic platform to study flight specializations of bats. Sci. Robot. 2017, 2, eaal2505. [Google Scholar] [CrossRef]
- Hoff, J.; Ramezani, A.; Chung, S.J.; Hutchinson, S. Synergistic Design of a Bio-Inspired Micro Aerial Vehicle with Articulated Wings. In Proceedings of the Robotics: Science and Systems, Online, 12–16 July 2016; Volume 22. [Google Scholar]
- Zhang, K.; Chen, S.; Yang, Q.; Guo, S.; Chen, Q.; Liu, Z.; Mo, W. The Oligodendrocyte Transcription Factor 2 OLIG2 regulates transcriptional repression during myelinogenesis in rodents. Nat. Commun. 2022, 13, 1423. [Google Scholar] [CrossRef] [PubMed]
- Bender, M.; Guo, J.; Powell, N.; Kurdila, A.; Müller, R. Learning bioinspired joint geometry from motion capture data of bat flight. Bioinspiration Biomim. 2019, 14, 036013. [Google Scholar] [CrossRef]
- Hoeijmakers, H.W. Aerodynamics Flapping-Flight Robotic Bird using Unsteady Lifting-Line Method. In Proceedings of the AIAA Aviation, San Diego, CA, USA, 12–16 June 2023; p. 4527. [Google Scholar]
- Timmermans, S.; Vanierschot, M.; Vandepitte, D. Aerodynamic model updating using wind-tunnel setup for hummingbirdlike flapping wing nanorobot. AIAA J. 2022, 60, 902–912. [Google Scholar] [CrossRef]
- Iriarte-Díaz, J.; Riskin, D.K.; Willis, D.J.; Breuer, K.S.; Swartz, S.M. Whole-body kinematics of a fruit bat reveal the influence of wing inertia on body accelerations. J. Exp. Biol. 2011, 214, 1546. [Google Scholar] [CrossRef]
- Colorado, J.; Barrientos, A.; Rossi, C.; Breuer, K.S. Biomechanics of smart wings in a bat robot: Morphing wings using SMA actuators. Bioinspir. Biomim. 2012, 7, 036006. [Google Scholar] [CrossRef]
- Li, X.P.; Wang, W.; Tang, Y.; Wang, L.; Bai, T.; Zhao, F.; Bai, Y. Research on gliding aerodynamic effect of deformable membrane wing for a robotic flying squirrel. J. Bionic Eng. 2018, 15, 379–396. [Google Scholar] [CrossRef]
- Ismail, N.I.; Zulkifli, A.H.; Abdullah, M.Z.; Basri, M.H.; Abdullah, N.S. Computational aerodynamic analysis on perimeter reinforced (PR)-compliant wing. Chin. J. Aeronaut. 2013, 26, 1093–1105. [Google Scholar] [CrossRef]
- Hedenström, A.; Johansson, L.C. Bat flight: Aerodynamics, kinematics and flight morphology. J. Exp. Biol. 2015, 218, 653–663. [Google Scholar] [CrossRef]
- Duan, B.; Guo, C.; Liu, H. Aerodynamic analysis for a bat-like robot with a deformable flexible wing. Robotica 2023, 41, 306–325. [Google Scholar] [CrossRef]
- Ramezani, A.; Shi, X.; Chung, S.J.; Hutchinson, S. Modeling and nonlinear flight controller synthesis of a bat-inspired micro aerial vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, AIAA Paper, San Diego, CA, USA, 4–8 January 2016; p. 1376. [Google Scholar]
- Joshi, V.; Jaiman, R.K.; Li, G.; Breuer, K.; Swartz, S. Full-scale aeroelastic simulations of hovering bat flight. In Proceedings of the AIAA Scitech, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing Rotation and the Aerodynamic Basis of Insect Flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 2002, 205, 1087–1096. [Google Scholar] [CrossRef]
- Whitney, J.P.; Wood, R.J. Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 2010, 660, 197–220. [Google Scholar] [CrossRef]
- Ke, X.; Zhang, W.; Shi, J.; Chen, W. The modeling and numerical solution for flapping wing hovering wingbeat dynamics. Aerosp. Sci. Technol. 2021, 110, 106474. [Google Scholar] [CrossRef]






| Structural Parameter | Numerical Value |
|---|---|
| Arm1 (mm) | 100 |
| Arm2 (mm) | 100 |
| Arm3 (mm) | 132 |
| Arm4 (mm) | 132 |
| Finger1 (mm) | 300 |
| Finger2 (mm) | 275 |
| Finger3 (mm) | 247 |
| Angle of attack (°) | 10 |
| Beat amplitude (°) | 30 |
| Beat frequency (Hz) | 3 |
| Wind velocity (m/s) | 5 |
| Experimental Parameters | Numerical Value |
|---|---|
| Angle of attack | 10° |
| Wind velocity | 5 m/s |
| Beat frequency | 3 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, B.; Chen, Z.; Wang, S.; Liu, J.; Ju, B.; Sun, A. Aerodynamic Lift Modeling and Analysis of a Bat-like Flexible Flapping-Wing Robot. Modelling 2025, 6, 117. https://doi.org/10.3390/modelling6040117
Duan B, Chen Z, Wang S, Liu J, Ju B, Sun A. Aerodynamic Lift Modeling and Analysis of a Bat-like Flexible Flapping-Wing Robot. Modelling. 2025; 6(4):117. https://doi.org/10.3390/modelling6040117
Chicago/Turabian StyleDuan, Bosong, Zhaoyang Chen, Shuai Wang, Junlei Liu, Bingfeng Ju, and Anyu Sun. 2025. "Aerodynamic Lift Modeling and Analysis of a Bat-like Flexible Flapping-Wing Robot" Modelling 6, no. 4: 117. https://doi.org/10.3390/modelling6040117
APA StyleDuan, B., Chen, Z., Wang, S., Liu, J., Ju, B., & Sun, A. (2025). Aerodynamic Lift Modeling and Analysis of a Bat-like Flexible Flapping-Wing Robot. Modelling, 6(4), 117. https://doi.org/10.3390/modelling6040117






