Directed Douglas–Rachford Splitting Method with Application to Feature Selection

Abstract

In this article, we study a directed version of Douglas–Rachford splitting method in real Hilbert spaces. By using new, self-contained, and simplified techniques, we prove its weak convergence. The major innovation is that we exploit the firm non-expansiveness of the Douglas–Rachford operator for the first time to derive the best possible upper bounds on direction factors, assuming that the involved factors remain constant. We give a new rare feature selection model equipped with the TripAdvisor hotel-review dataset. Numerical results confirm the user-friendliness and efficiency of directed Douglas–Rachford splitting in solving this model.

1. Introduction

Let $\mathcal{H}$ be an infinite-dimensional real Hilbert space equipped with the standard inner product $\langle x,y\rangle$ and the induced norm $\parallel x\parallel =\sqrt{\langle x,x\rangle }$ for $x,y\in \mathcal{H}$. We are mainly concerned with the following monotone inclusion:

$$\begin{array}{c}\hfill 0\in A\left(x\right)+B\left(x\right),\end{array}$$

(1)

where both $A:\mathcal{H}\rightrightarrows \mathcal{H}$ and $B:\mathcal{H}\rightrightarrows \mathcal{H}$ are maximal monotone operators, and the notation “double arrows” means that the mapping may be multi-valued. Throughout this article, we always assume that (1) has at least zero point. This problem model covers monotone variational inequalities, convex minimizations, optimal control and feature selection in deep learning and so on [1,2].

A popular iterative scheme is the following Douglas–Rachford (DR for short) splitting method (cf. Equation (10) of [3]). Choose $\mu >0$. Choose $z^0\in \mathcal{H}$. At k-th iteration, compute the following:

$$z^{k+1}=\left[{(I+\mu B)}^{-1}(2{(I+\mu A)}^{-1}-I)+I-{(I+\mu A)}^{-1}\right]\left(z^k\right).$$

(2)

Denote the DR operator by the following:

$$N:={(I+\mu B)}^{-1}(2{(I+\mu A)}^{-1}-I)+I-{(I+\mu A)}^{-1}.$$

(3)

Then (2) becomes the following:

$$z^{k+1}=N\left(z^k\right).$$

(4)

To improve numerical efficiency of the DR splitting method, we may resort to its directed version, written as follows: [4]

$$z^{k+1}=(1-{\alpha }_k)z^k+{\alpha }_{k}N\left(z^k\right)+(1-{\alpha }_k){\delta }_k(z^k-z^{k-1}),$$

(5)

where ${\alpha }_k\in (0,1]$ and ${\delta }_k\ge 0$ further satisfy some assumptions (to be specified later), and $(1-{\alpha }_k){\delta }_k$ is called directed factors. Obviously, in the case of ${\alpha }_k\equiv 1$, it reduces to the DR splitting method above.

For the directed DR splitting method (5), an important task is to find the largest possible upper bound of directed factors. As we know, the traditional technique of estimating this bound is as follows. First, view (5) as the Krasnosel’skiĭ–Mann iteration for non-expansive DR operator. Then, borrow the corresponding estimate concerning this iteration as the upper bound of directed factors [2,4].

In this article, we aim at deriving the best possible estimates of the directed factors. To this end, we skillfully exploit firm non-expansiveness (Lemma 1 of [3]) of the DR operator for the first time. Thus, as long as the directed factors are concerned, our new estimates of their upper bounds are much larger than those [2,4].

Clearly, the new technique corresponds to firm non-expansiveness of the DR operator, whereas the traditional one corresponds to its non-expansiveness.

For an application to deep learning, we model rare feature selection [5,6] (see (33) below) into an appropriate monotone inclusion (36) below, which has been a special case of (1). As shown in Section 6, both DR splitting method and its directed version can be used to solve this inclusion, without worrying about the issue of choosing multiple proximal parameters involved in those splitting methods [7]. Numerical results indicate that they can solve (36) to similar accuracy to those [7] in about 7 or 8 seconds for given stopping criteria, but they avoid the time-consuming (tens of minutes or more) trial and error process of determining the parameters. In this sense, the directed the DR splitting method is user-friendly and efficient in solving this feature selection model.

The rest of this article is organized as follows. In Section 2, we review the definitions of firmly non-expansive operator and maximal monotone operator, and give some related properties. In Section 3, we formally state the aforementioned directed DR splitting method, with new and much weaker conditions on the directed factors; see (7) and (8) below. In Section 4, we prove its weak convergence of the directed DR splitting method. In Section 5, we compare new conditions on the directed factors with existing ones, and we numerically demonstrate upper bounds derived by the former are much larger. In Section 6, we model rare feature selection in deep learning in a new way, and we conduct numerical experiments to confirm the efficiency of our directed DR splitting method in solving the corresponding test problems. Finally, in Section 7, we conclude this article.

2. Preliminaries

In this section, we first give some basic definitions and then provide some auxiliary results for later use.

Definition 1 

([3,8]). Let $\mathcal{C}\subseteq \mathcal{H}$ be a nonempty subset. An operator $N:\mathcal{C}\to \mathcal{C}$ is called non-expansive if and only if the following is met:

$$\Vert N\left(x\right)-N\left(y\right)\Vert \le \Vert x-y\Vert ,\forall x,y\in \mathcal{C};$$

firmly non-expansive if and only if the following is met:

$${\parallel N\left(x\right)-N\left(y\right)\parallel }^2\le \langle x-y,N\left(x\right)-N\left(y\right)\rangle ,\forall x,y\in \mathcal{C}.$$

Definition 2 

([3,8]). Let $A:\mathcal{H}\rightrightarrows \mathcal{H}$ be an operator. It is called monotone iff, written as follows:

$$\langle x-x^{\prime },a-a^{\prime }\rangle \ge 0,\forall (x,a)\in A,\forall (x^{\prime },a^{\prime })\in A;$$

maximal monotone iff it is monotone and for given $\widehat{x}\in \mathcal{H}$ and $\widehat{a}\in \mathcal{H}$ the following implication relation holds:

$$\langle x-\widehat{x},a-\widehat{a}\rangle \ge 0,\forall (x,a)\in A\Rightarrow (\widehat{x},\widehat{a})\in A.$$

For any given operator $A:\mathcal{H}\rightrightarrows \mathcal{H}$, its effective domain is defined by the following: $domA=\{x\in \mathcal{H}:A(x)\ne \varnothing \}$.

Assume that $A:\mathcal{H}\rightrightarrows \mathcal{H}$ is maximal monotone. A fundamental property is that, as proved by Minty [9], for any given positive number $\mu >0$ and $\widehat{x}\in \mathcal{H}$, there exists a unique $x\in \mathcal{H}$ such that $(\mu I+A)\left(x\right)\ni \widehat{x}$ or $(I+\mu A)\left(x\right)\ni \widehat{x}$, where I is the identity operator, i.e., $I:x\to x$ for all $x\in \mathcal{H}$. Thus, $J_{\mu A}={(I+\mu A)}^{-1}$ is well-defined and is called the resolvent of A.

Definition 3. 

Let $f:\mathcal{H}\to [-\infty ,+\infty ]$ be a convex function. Then for any given $x\in \mathcal{H}$ the sub-differential of f at x is defined by the following:

$$\partial f\left(x\right):=\{s\in \mathcal{H}:f(y)-f(x)\ge \langle s,y-x\rangle ,\forall y\in \mathcal{H}\}.$$

Each s is called a sub-gradient of f at x. Moreover, if f is further continuously differentiable, then $\partial f\left(x\right)=\{\nabla f(x\left)\right\}$, where $\nabla f\left(x\right)$ is the gradient of f at x.

As is well known, the sub-differential of any closed proper convex function in an infinite-dimensional Hilbert space is maximal monotone as well. An important example is the sub-differential of the indicator function defined by

$${\delta }_{\mathcal{C}}\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}x\in \mathcal{C},\hfill \\ +\infty ,\hfill & \mathrm{if}x\notin \mathcal{C},\hfill \end{array}\right.$$

where $\mathcal{C}$ is some nonempty closed convex set in ${\mathcal{R}}^n$. Moreover, for any given positive number $\mu >0$, we have $P_{\mathcal{C}}={(I+\mu \partial {\delta }_{\mathcal{C}})}^{-1},$ where $P_{\mathcal{C}}$ is usual projection onto $\mathcal{C}$.

Lemma 1 

(Theorem 2 of [8]). Let μ be any positive number. An operator A on H is monotone if and only if its resolvent $J_{\mu A}={(I+\mu A)}^{-1}$ is firmly non-expansive.

Below, we give a lemma, which characterizes the relation between the problem’s zero point and the fixed-point of N.

Lemma 2 

([3]). If $x\in \mathcal{H}$ solves (1), then there exists $z\in \mathcal{H}$ such that the following is written:

$$x=J_{\mu A}\left(z\right),N\left(z\right)=z.$$

Lemma 3. 

Assume that both $A:\mathcal{H}\rightrightarrows \mathcal{H}$ and $B:\mathcal{H}\rightrightarrows \mathcal{H}$ are maximal monotone operators. Then the resulting eigenoperator is calculated as follows:

$$\begin{array}{c}\hfill T(x,u):=\left(\begin{array}{cc}A& \\ & B^{-1}\end{array}\right)\left(\begin{array}{c}x\\ u\end{array}\right)+\left(\begin{array}{cc}0& I\\ -I& 0\end{array}\right)\left(\begin{array}{c}x\\ u\end{array}\right)\end{array}$$

which must be maximal monotone.

Proof. 

Note that A and B are maximal monotone. Thus, the first operator on the right-hand side is maximal monotone. Meanwhile, the linearity of the identity operator means that the second is also maximal monotone [9]. Maximality of T follows from [10].    □

Lemma 4 

([11,12]). Consider any maximal monotone operator $T:\mathcal{H}\rightrightarrows \mathcal{H}$. Assume that the sequence $\left\{w^k\right\}$ in $\mathcal{H}$ converges weakly to w, and the sequence $\left\{s^k\right\}$ on domT converges strongly to s. If $T\left(w^k\right)\ni s^k$ for any k, then the relation $T\left(w\right)\ni s$ must hold.

3. Direcdted DR Splitting

In this section, we describe in details the directed DR splitting method, i.e., Algorithm 1 just below and make assumptions on ${\alpha }_k$ and the directed factors.

Algorithm 1 Directed DR splitting method

1: Choose $z^{-1}=z^0\in \mathcal{H}$. Choose $\mu >0$, ${\delta }_0=0$ and ${\alpha }_0=0.9$. Set $k:=0$. 2: Choose ${\alpha }_k>0$ and ${\delta }_k\ge 0$ satisfying (7) and (8). Compute $$\begin{array}{c}\hfill z^{k+1}=(1-{\alpha }_k)z^k+{\alpha }_{k}N\left(z^k\right)+(1-{\alpha }_k){\delta }_k(z^k-z^{k-1}).\end{array}$$ (6)  Set $k:=k+1.$

In this article, to guarantee its weak convergence, we make the following assumptions.

Assumption 1. 

Assume that ${\alpha }_k$ and ${\delta }_k$ in directed DR splitting method satisfy the following:

$$\begin{array}{c}\hfill {\alpha }_k\in [\epsilon ,1-\epsilon ],(1-{\alpha }_{k-1}){\delta }_{k-1}\le (1-{\alpha }_k){\delta }_k,\end{array}$$

(7)

where ε is a prescribed sufficiently small positive number.

$$\begin{array}{cc}\hfill & {\delta }_k^{+}:=0.5{\displaystyle \frac{{\alpha }_k-1+\sqrt{{(1-{\alpha }_k)}^2+4\frac{2{(1-{\alpha }_k)}^2}{{\alpha }_k}(\frac{2}{\sigma (2-{\alpha }_k)}-1)((1-\sigma )\frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}-\epsilon )}}{\frac{2{(1-{\alpha }_k)}^2}{{\alpha }_k}\left(\frac{2}{\sigma (2-{\alpha }_k)}-1\right)}},\hfill \\ \hfill & {\delta }_k\le min\left\{{\delta }_k^{+},{\displaystyle \frac{1}{1-{\alpha }_k}}\left(1-\epsilon -{\displaystyle \frac{1}{1+(1-\sigma )(2-{\alpha }_{k-1}){\alpha }_{k-1}^{-1}}}\right)\right\},\hfill \end{array}$$

(8)

where σ is chosen in $(0,1)$ in advance.

In particular, in the case of ${\alpha }_k\equiv 0.95$ and ${\delta }_k\equiv \delta >0$, (7) and (8) can be replaced by the following:

$${\alpha }_k\equiv 0.95,{\delta }_k\equiv \delta \le 4.68.$$

(9)

In contrast, other existing upper bounds in Section 5 are around $0.34$.

As to $N\left(z^k\right)$ in (6), we may evaluate it in the following way. First solve the following:

$$(I+\mu A)\left(x\right)\ni z^k$$

(10)

to obtain $x^k$, then solve the following:

$$(I+\mu B)\left(y\right)\ni (2{(I+\mu A)}^{-1}-I)\left(z^k\right)=2x^k-z^k$$

(11)

to obtain $y^k$. Thus, we write the following:

$$N\left(z^k\right)=z^k-(x^k-y^k).$$

(12)

The directed DR splitting method above reminds us of the Krasnosel’skiĭ–Mann iteration, which is used for finding a fixed point of a non-expansive operator N (whose non-expansiveness is implied by firm expansiveness); see [2,4,13] for recent discussions and the references cited therein.

4. Weak Convergence

In this section, we prove weak convergence of Algorithm 1 in the Hilbert space.

For brevity, we may write $N\left(z\right)$ as $Nz$ throughout this section.

Lemma 5. 

Assume that $\alpha >0$. If $4\alpha \beta \ge {\gamma }^2$, then the following:

$${\alpha \Vert a\Vert }^2+\beta {\Vert b\Vert }^2+\gamma \langle a,b\rangle \ge 0,\forall a,b\in \mathcal{H}.$$

Notice that this lemma was given in the first author’s manuscript, further mentioned in Remark 1. Its proof is elementary and based on the following:

$${\alpha \Vert a\Vert }^2+{\beta \Vert b\Vert }^2\ge 2\sqrt{\alpha \beta }\Vert a\Vert \Vert b\Vert \ge \gamma \Vert a\Vert \Vert b\Vert .$$

To simplify proof of weak convergence of Algorithm 1, we first give the following result.

Theorem 1. 

If Assumption 1 holds, then the following is calculated:

$$\begin{array}{cc}& \Vert z^{k+1}{-z\Vert }^2\hfill \\ \hfill \le & \left(1+(1-{\alpha }_k){\delta }_k\right)\Vert z^k{-z\Vert }^2-(1-{\alpha }_k){\delta }_k{\Vert z^{k-1}-z\Vert }^2\hfill \\ & +(1-{\alpha }_k){\delta }_k\left(1-2(1-{\alpha }_k){\delta }_k{\alpha }_k^{-1}\right)\Vert z^k-z^{k-1}{\Vert }^2-(2{\alpha }_k^{-1}-1){\Vert z^{k+1}-z^k\Vert }^2\hfill \\ & +4(1-{\alpha }_k){\delta }_k{\alpha }_k^{-1}\langle z^{k+1}-z^k,z^k-z^{k-1}\rangle .\hfill \end{array}$$

Proof. 

It follows from (6) that the following is valid:

$${\widehat{z}}^k=z^k+{\delta }_k(z^k-z^{k-1}),z^{k+1}=(1-{\alpha }_k){\widehat{z}}^k+{\alpha }_{k}N{z}^k.$$

On the other side, Lemma 2 implies that there must exist $z\in \mathcal{H}$ such that the following is written:

$$Nz=z.$$

Thus, we have the following:

$$z^{k+1}-z=(1-{\alpha }_k)({\widehat{z}}^k-z)+{\alpha }_k(N{z}^k-Nz).$$

So, we can obtain the following:

$$\begin{array}{cc}\hfill & \Vert z^{k+1}{-z\Vert }^2\hfill \\ \hfill & ={(1-{\alpha }_k)}^2\Vert {\widehat{z}}^k{-z\Vert }^2+2(1-{\alpha }_k){\alpha }_k\langle {\widehat{z}}^k-z,N{z}^k-Nz\rangle +{\alpha }_k^2{\Vert N{z}^k-Nz\Vert }^2\hfill \\ \hfill & \le {(1-{\alpha }_k)}^2{\Vert {\widehat{z}}^k-z\Vert }^2+2(1-{\alpha }_k){\alpha }_k\langle {\widehat{z}}^k-z,N{z}^k-Nz\rangle +{\alpha }_k^2\langle z^k-z,N{z}^k-Nz\rangle ,\hfill \end{array}$$

(13)

where the inequality follows from the firm non-expansiveness (Lemma 1 of [3]) of the DR operator. As to the $\Vert {\widehat{z}}^k{-z\Vert }^2$ term, it is direct to obtain the following:

$$\begin{array}{cc}& \Vert {\widehat{z}}^k{-z\Vert }^2\hfill \\ \hfill =& \Vert z^k-z+{\delta }_k(z^k-z^{k-1}){\Vert }^2\hfill \\ \hfill =& \Vert z^k{-z\Vert }^2+2{\delta }_k\langle z^k-z,z^k-z^{k-1}\rangle +{\delta }_k^2{\Vert z^k-z^{k-1}\Vert }^2\hfill \\ \hfill =& \Vert z^k{-z\Vert }^2+{\delta }_k\left(\Vert z^k{-z\Vert }^2+\Vert z^k-z^{k-1}{\Vert }^2-{\Vert z^{k-1}-z\Vert }^2\right)+{\delta }_k^2{\Vert z^k-z^{k-1}\Vert }^2\hfill \\ \hfill =& (1+{\delta }_k)\Vert z^k{-z\Vert }^2+({\delta }_k+{\delta }_k^2)\Vert z^k-z^{k-1}{\Vert }^2-{\delta }_k{\Vert z^{k-1}-z\Vert }^2.\hfill \end{array}$$

Combining this with (13) and the following:

$$\langle {\widehat{z}}^k-z,N{z}^k-Nz\rangle =\langle z^k-z,N{z}^k-Nz\rangle +{\delta }_k\langle z^k-z^{k-1},N{z}^k-Nz\rangle$$

yields the following:

$$\begin{array}{cc}\hfill & \Vert z^{k+1}{-z\Vert }^2\hfill \\ \hfill \le & {(1-{\alpha }_k)}^2\left((1+{\delta }_k)\Vert z^k{-z\Vert }^2+({\delta }_k+{\delta }_k^2)\Vert z^k-z^{k-1}{\Vert }^2-{\delta }_k{\Vert z^{k-1}-z\Vert }^2\right)\hfill \\ \hfill & +2(1-{\alpha }_k){\alpha }_k\left(\langle z^k-z,N{z}^k-Nz\rangle +{\delta }_k\langle z^k-z^{k-1},N{z}^k-Nz\rangle \right)+{\alpha }_k^2\langle z^k-z,N{z}^k-Nz\rangle \hfill \\ \hfill =& {(1-{\alpha }_k)}^2(1+{\delta }_k)\Vert z^k{-z\Vert }^2+{(1-{\alpha }_k)}^2({\delta }_k+{\delta }_k^2)\Vert z^k-z^{k-1}{\Vert }^2-{(1-{\alpha }_k)}^2{\delta }_k{\Vert z^{k-1}-z\Vert }^2\hfill \\ \hfill & +(2{\alpha }_k-{\alpha }_k^2)\langle z^k-z,N{z}^k-Nz\rangle +2(1-{\alpha }_k){\delta }_k{\alpha }_k\langle z^k-z^{k-1},N{z}^k-Nz\rangle .\hfill \end{array}$$

(14)

Below, we bound the inner product $\langle z^k-z,N{z}^k-Nz\rangle$ in (14). In view of (10)–(12), we have $N{z}^k=z^k-(x^k-y^k).$ Thus, we obtain the following:

$$\begin{array}{cc}\hfill \langle z^k-z,N{z}^k-Nz\rangle & =\langle z^k-z,z^k-z-(x^k-y^k)\rangle \hfill \\ \hfill & = \Vert z^k{-z\Vert }^2-\langle z^k-z,x^k-y^k\rangle \hfill \\ \hfill & \le \Vert z^k{-z\Vert }^2-{\Vert x^k-y^k\Vert }^2\hfill \\ \hfill & = \Vert z^k{-z\Vert }^2-{\Vert z^k-N{z}^k\Vert }^2,\hfill \end{array}$$

(15)

where the inequality follows from (Lemma 4 of [14]). Combining this with the following:

$${\alpha }_k(z^k-N{z}^k)\stackrel{\left(6\right)}{=}(1-{\alpha }_k){\delta }_k(z^k-z^{k-1})-(z^{k+1}-z^k)$$

(16)

yields the following:

$$\begin{array}{cc}\hfill & \langle z^k-z,N{z}^k-Nz\rangle \hfill \\ \hfill \le & \Vert z^k{-z\Vert }^2-{\alpha }_k^{-2}{(1-{\alpha }_k)}^2{\delta }_k^2\Vert z^k-z^{k-1}{\Vert }^2-{\alpha }_k^{-2}{\Vert z^{k+1}-z^k\Vert }^2\hfill \\ \hfill & +2{\alpha }_k^{-2}(1-{\alpha }_k){\delta }_k\langle z^k-z^{k-1},z^{k+1}-z^k\rangle .\hfill \end{array}$$

(17)

Next, we bound the inner product $\langle z^k-z^{k-1},N{z}^k-Nz\rangle$ in (14). Since the following is calculated:

$$\begin{array}{cc}& \langle z^k-z^{k-1},N{z}^k-Nz\rangle \hfill \\ \hfill =& \langle z^k-z^{k-1},N{z}^k-z^k+z^k-z\rangle \hfill \\ \hfill =& \langle z^k-z^{k-1},z^k-z\rangle +\langle N{z}^k-z^k,z^k-z^{k-1}\rangle \hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left(\Vert z^k-z^{k-1}{\Vert }^2+\Vert z^k{-z\Vert }^2-{\Vert z^{k-1}-z\Vert }^2\right)+\langle z^k-N{z}^k,z^{k-1}-z^k\rangle \hfill \end{array}$$

and

$$\begin{array}{cc}& \langle z^k-N{z}^k,z^{k-1}-z^k\rangle \hfill \\ \hfill \stackrel{\left(16\right)}{=}& {\alpha }_k^{-1}\langle (1-{\alpha }_k){\delta }_k(z^k-z^{k-1})-(z^{k+1}-z^k),z^{k-1}-z^k\rangle \hfill \\ \hfill =& -(1-{\alpha }_k){\delta }_k{\alpha }_k^{-1}{\Vert z^k-z^{k-1}\Vert }^2+{\alpha }_k^{-1}\langle z^{k+1}-z^k,z^k-z^{k-1}\rangle ,\hfill \end{array}$$

we have the following:

$$\begin{array}{cc}& \langle z^k-z^{k-1},N{z}^k-Nz\rangle \hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left(\Vert z^k-z^{k-1}{\Vert }^2+\Vert z^k{-z\Vert }^2-{\Vert z^{k-1}-z\Vert }^2\right)-(1-{\alpha }_k){\delta }_k{\alpha }_k^{-1}{\Vert z^k-z^{k-1}\Vert }^2\hfill \\ & +{\alpha }_k^{-1}\langle z^{k+1}-z^k,z^k-z^{k-1}\rangle .\hfill \end{array}$$

In a word, using the last equality and (17) to bound (14) yields the desired result. □

Now we state and prove weak convergence of the sequence generated by Algorithm 1.

Theorem 2. 

Let $\left\{z^k\right\}$ be the sequence generated by Algorithm 1. If (7) and (8) hold, then the sequence $\left\{z^k\right\}$ weakly converges to a fixed point of N.

Proof. 

In view of Theorem 1 and (7), we can obtain the following:

$$\begin{array}{cc}& \Vert z^{k+1}{-z\Vert }^2-(1-{\alpha }_{k+1}){\delta }_{k+1}\Vert z^k{-z\Vert }^2+(1-\sigma ){\displaystyle \frac{2-{\alpha }_k}{{\alpha }_k}}{\Vert z^{k+1}-z^k\Vert }^2\hfill \\ \hfill \le & \Vert z^k{-z\Vert }^2-(1-{\alpha }_k){\delta }_k\Vert z^{k-1}{-z\Vert }^2+(1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}{\Vert z^k-z^{k-1}\Vert }^2-{\Delta }_k,\hfill \end{array}$$

where $\sigma \in (0,1)$ and the following is calculated:

$$\begin{array}{cc}\hfill {\Delta }_k& :=\sigma {\displaystyle \frac{2-{\alpha }_k}{{\alpha }_k}}{\Vert z^{k+1}-z^k\Vert }^2-{\displaystyle \frac{4(1-{\alpha }_k){\delta }_k}{{\alpha }_k}}\langle z^{k+1}-z^k,z^k-z^{k-1}\rangle \hfill \\ & +\left((1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}-(1-{\alpha }_k){\delta }_k(1-{\displaystyle \frac{2(1-{\alpha }_k){\delta }_k}{{\alpha }_k}})\right){\Vert z^k-z^{k-1}\Vert }^2.\hfill \end{array}$$

We set the following:

$${\phi }_k:=\Vert z^k{-z\Vert }^2-(1-{\alpha }_k){\delta }_k\Vert z^{k-1}{-z\Vert }^2+(1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}{\Vert z^k-z^{k-1}\Vert }^2.$$

(18)

Then we obtain the following:

$${\phi }_{k+1}\le {\phi }_k-{\Delta }_k.$$

(19)

Notice the following:

$$\begin{array}{cc}\hfill {\phi }_k& =\Vert z^k{-z\Vert }^2-(1-{\alpha }_k){\delta }_k\Vert z^{k-1}{-z\Vert }^2+(1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}{\Vert z^k-z^{k-1}\Vert }^2\hfill \\ & =\Vert z^{k-1}{-z\Vert }^2+2\langle z^{k-1}-z,z^k-z^{k-1}\rangle +{\Vert z^k-z^{k-1}\Vert }^2\hfill \\ & -(1-{\alpha }_k){\delta }_k\Vert z^{k-1}{-z\Vert }^2+(1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}{\Vert z^k-z^{k-1}\Vert }^2\hfill \\ & =(1-(1-{\alpha }_k){\delta }_k)\Vert z^{k-1}{-z\Vert }^2+2\langle z^{k-1}-z,z^k-z^{k-1}\rangle +\left(1+(1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}\right){\Vert z^k-z^{k-1}\Vert }^2.\hfill \end{array}$$

Combining this with Lemma 5 and (8) results in the following:

$$\begin{array}{cc}& {\delta }_k\le {\displaystyle \frac{1}{1-{\alpha }_k}}\left(1-\epsilon -{\displaystyle \frac{1}{1+(1-\sigma )(2-{\alpha }_{k-1}){\alpha }_{k-1}^{-1}}}\right)\hfill \\ \hfill \iff & 4(1-(1-{\alpha }_k){\delta }_k-\epsilon )(1+(1-\sigma )(2-{\alpha }_{k-1}){\alpha }_{k-1}^{-1})\ge 2^2\hfill \end{array}$$

yields the following:

$${\phi }_k\ge \epsilon {\Vert z^{k-1}-z\Vert }^2.$$

(20)

Meanwhile, by Lemma 2 and (8) we obtain the following:

$$\begin{array}{cc}& {\delta }_k\le 0.5{\displaystyle \frac{{\alpha }_k-1+\sqrt{{(1-{\alpha }_k)}^2+4\frac{2{(1-{\alpha }_k)}^2}{{\alpha }_k}\left(\frac{2}{\sigma (2-{\alpha }_k)}-1\right)\left((1-\sigma )\frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}-\epsilon \right)}}{\frac{2{(1-{\alpha }_k)}^2}{{\alpha }_k}\left(\frac{2}{\sigma (2-{\alpha }_k)}-1\right)}}\hfill \\ \hfill \iff & {\displaystyle \frac{2{(1-{\alpha }_k)}^2}{{\alpha }_k}}\left({\displaystyle \frac{2}{\sigma (2-{\alpha }_k)}}-1\right){\delta }_k^2+(1-{\alpha }_k){\delta }_k-(1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}+\epsilon \le 0\hfill \\ \hfill \iff & 4\sigma {\displaystyle \frac{2-{\alpha }_k}{{\alpha }_k}}\left((1-\sigma ){\displaystyle \frac{2-{\alpha }_{k-1}}{{\alpha }_{k-1}}}-(1-{\alpha }_k){\delta }_k(1-{\displaystyle \frac{2(1-{\alpha }_k){\delta }_k}{{\alpha }_k})}-\epsilon \right)\ge {\displaystyle \frac{4^2{(1-{\alpha }_k)}^2}{{\alpha }_k^2}}{\delta }_k^2,\hfill \end{array}$$

we can obtain the following:

$${\Delta }_k\ge \epsilon {\Vert z^k-z^{k-1}\Vert }^2.$$

(21)

Obviously, based on (19)–(21), we can conclude the following:

$$\begin{array}{cc}\hfill & \lim {\phi }_k\mathrm{exists}\Rightarrow \left\{z^k\right\}\mathrm{is}\mathrm{bounded}\mathrm{in}\mathrm{norm};\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & \lim {\Delta }_k=0\Rightarrow z^k-z^{k-1}\to 0,k\to +\infty .\hfill \end{array}$$

(23)

It follows from (7), (6) and (23) the following:

$${\alpha }_k(z^k-N{z}^k)=(1-{\alpha }_k){\delta }_k(z^k-z^{k-1})-(z^{k+1}-z^k)\to 0\Rightarrow (I-N)\left(z^k\right)\to 0.$$

(24)

On the other hand, as proved in (22), $\left\{z^k\right\}$ is bounded in norm, thus there exists at least one weak cluster point $z^{\infty }$, i.e., written as follows:

$$z^{k_j}\rightharpoonup z^{\infty }.$$

(25)

Finally, since $I-N$ is continuous and monotone, it must be maximal monotone. In view of Lemma 4, $(I-N)\left(z^{\infty }\right)=0$.

Denoted as the following:

$${\varphi }_k\left(z\right):=\Vert z^k{-z\Vert }^2-(1-{\alpha }_k){\delta }_k{\Vert z^{k-1}-z\Vert }^2.$$

Then, it follows from (18), (22) and (23) that $lim{\varphi }_k\left(z\right)$ exists as well.

Below, we show that $\left\{z^k\right\}$ weakly converges to $z^{\infty }$. Let $z_1^{\infty }$ and $z_2^{\infty }$ be two weak cluster points of $\left\{z^k\right\}$. Then, repeating the arguments above yields that $z_1^{\infty }$ and $z_2^{\infty }$ are solutions. Correspondingly, we set the following:

$$l_i:=lim{\varphi }_k\left(z_i^{\infty }\right),i=1,2.$$

Consider the following:

$$\begin{array}{cc}\hfill & \Vert z^k-z_1^{\infty }{\Vert }^2-(1-{\alpha }_k){\delta }_k{\Vert z^{k-1}-z_1^{\infty }\Vert }^2\hfill \\ \hfill =& \Vert z^k-z_2^{\infty }{\Vert }^2-2\langle z^k-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle +{\Vert z_1^{\infty }-z_2^{\infty }\Vert }^2\hfill \\ \hfill & -(1-{\alpha }_k){\delta }_k\left(\Vert z^{k-1}-z_2^{\infty }{\Vert }^2-2\langle z^{k-1}-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle +{\Vert z_1^{\infty }-z_2^{\infty }\Vert }^2\right)\hfill \\ \hfill =& \Vert z^k-z_2^{\infty }{\Vert }^2-(1-{\alpha }_k){\delta }_k{\Vert z^{k-1}-z_2^{\infty }\Vert }^2-2\langle z^k-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle \hfill \\ \hfill & +2(1-{\alpha }_k){\delta }_k\langle z^{k-1}-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle +(1-(1-{\alpha }_k){\delta }_k){\Vert z_1^{\infty }-z_2^{\infty }\Vert }^2\hfill \\ \hfill \ge & \Vert z^k-z_2^{\infty }{\Vert }^2-(1-{\alpha }_k){\delta }_k{\Vert z^{k-1}-z_2^{\infty }\Vert }^2-2\langle z^k-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle \hfill \\ \hfill & +2(1-{\alpha }_k){\delta }_k\langle z^{k-1}-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle +\epsilon {\Vert z_1^{\infty }-z_2^{\infty }\Vert }^2,\hfill \end{array}$$

where the inequality follows from (8), which indicates the following:

$$(1-{\alpha }_k){\delta }_k\le 1-\epsilon .$$

Meanwhile, we obtain the following:

$$\langle z^{k-1}-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle =\langle z^k-z_2^{\infty },z_1^{\infty }-z_2^{\infty }\rangle -\langle z^k-z^{k-1},z_1^{\infty }-z_2^{\infty }\rangle .$$

Combing this with (23) and taking the limit along $k\in {\mathcal{N}}_1$, where ${\mathcal{N}}_1$ such that $\left\{z^k\right\}$ along $k\in {\mathcal{N}}_1$ weakly converges to $z_2^{\infty }$, we obtain the following:

$$l_1\ge l_2+\epsilon {\Vert z_1^{\infty }-z_2^{\infty }\Vert }^2.$$

Similarly, we also obtain the following:

$$l_2\ge l_1+\epsilon {\Vert z_2^{\infty }-z_1^{\infty }\Vert }^2.$$

Adding these two inequalities yields the following:

$$\Vert z_2^{\infty }-z_1^{\infty }{\Vert }^2=0\Rightarrow z_1^{\infty }=z_2^{\infty }$$

(26)

and $\left\{z^k\right\}$ converges weakly. □

Finally, with the help of the theorem above, we further state and prove weak convergence of the main sequence $\left\{J_{\mu A}\left(z^k\right)\right\}$.

Theorem 3. 

Let $\left\{z^k\right\}$ be the sequence generated by Algorithm 1. If (7) and (8) hold, then the main sequence $\left\{J_{\mu A}\left(z^k\right)\right\}$ weakly converges to a solution of (1).

Proof. 

In view of (10)–(12), we have the following:

$$\begin{array}{cc}\hfill & (I+\mu A)\left(x^k\right)\ni z^k\iff A\left(x^k\right)\ni {\mu }^{-1}(z^k-x^k)\iff x^k=J_{\mu A}\left(z^k\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & (I+\mu B)\left(y^k\right)\ni 2x^k-z^k\iff B^{-1}\left({\mu }^{-1}(2x^k-z^k-y^k)\right)\ni y^k,\hfill \\ \hfill & N\left(z^k\right)=z^k-(x^k-y^k).\hfill \end{array}$$

(28)

Thus, we obtain the following:

$$x^k-y^k=(I-N)\left(z^k\right)\stackrel{\left(24\right)}{\to }0.$$

(29)

Note that (22) and the following:

$$\Vert x^k-x^0\Vert =\Vert J_{\mu A}\left(z^k\right)-J_{\mu A}\left(z^0\right)\Vert \le \Vert z^k-z^0\Vert$$

imply that $\left\{x^k\right\}$ is bounded in norm as well.

On the other hand side, by the definition of T, we have the following:

$$T(x^k,{\mu }^{-1}(2x^k-z^k-y^k))=\left(\begin{array}{c}A\left(x^k\right)+{\mu }^{-1}(2x^k-z^k-y^k)\\ B^{-1}\left({\mu }^{-1}(2x^k-z^k-y^k)\right)-x^k\end{array}\right)\ni \left(\begin{array}{c}{\mu }^{-1}(x^k-y^k)\\ -x^k+y^k\end{array}\right),$$

where the relation ∋ follows from (27) and (28).

Since $\left\{(z^k,x^k)\right\}$ is bounded in norm, so does $\left\{(z^{k_j},x^{k_j})\right\}$, where $k_j$ corresponds to the one in (25). Thus, there exists at least one weak cluster point, written as follows:

$$(z^{k_{j_l}},x^{k_{j_l}})\rightharpoonup (z^{\infty },x^{\infty }),k\to +\infty .$$

Combining this with (29), Lemma 3 and Lemma 4 yields the following:

$$T(x^{\infty },{\mu }^{-1}(x^{\infty }-z^{\infty }))=\left(\begin{array}{c}A\left(x^{\infty }\right)+{\mu }^{-1}(x^{\infty }-z^{\infty })\\ B^{-1}\left({\mu }^{-1}(x^{\infty }-z^{\infty })\right)-x^{\infty }\end{array}\right)\ni \left(\begin{array}{c}0\\ 0\end{array}\right).$$

Namely, the following:

$$\begin{array}{cc}& A\left(x^{\infty }\right)+{\mu }^{-1}(x^{\infty }-z^{\infty })\ni 0,\hfill \\ & B^{-1}\left({\mu }^{-1}(x^{\infty }-z^{\infty })\right)-x^{\infty }\ni 0\iff {\mu }^{-1}(x^{\infty }-z^{\infty })\in B\left(x^{\infty }\right).\hfill \end{array}$$

This shows the following:

$$0\in A\left(x^{\infty }\right)+{\mu }^{-1}(x^{\infty }-z^{\infty })\in A\left(x^{\infty }\right)+B\left(x^{\infty }\right).$$

Finally, we prove uniqueness of the weak cluster point $x^{\infty }$. Let $x_1^{\infty }$ and $x_2^{\infty }$ be two weak cluster points of $\left\{x^k\right\}$. In view of (27), we have the following:

$$(I+\mu A)\left(x^k\right)\ni z^k\Rightarrow z^k=x^k+\mu a^k,a^k\in A\left(x^k\right).$$

Since A is monotone, we further have the following:

$$\Vert z_1^{\infty }-z_2^{\infty }{\Vert }^2=\Vert x_1^{\infty }+\mu a_1^{\infty }-(x_2^{\infty }+\mu a_2^{\infty }){\Vert }^2\ge {\Vert x_1^{\infty }-x_2^{\infty }\Vert }^2,$$

as proved in [14]. Combining this with (26) yields $x_1^{\infty }=x_2^{\infty }$. □

Remark 1. 

In the proof of Theorem 1, there are two crucial parts. One is that, by fully exploiting firm non-expansiveness of the DR operator, we obtain the inequality (13). The other is an appropriate application of (Lemma 4 of [14]) in deriving the inequality (15). In the proof of Theorem 2 except for uniqueness, we point-by-point follow the analytical techniques recently developed in the first author’s manuscript entitled “On an accelerated Krasnosel’skiĭ-Mann iteration”. This manuscript and a revised version entitled “Directed Krasnosel’skiĭ-Mann iteration” can be found in a single pdf file via https://ydong2024.github.io/downloads/directedKM.pdf, (accessed on 22 August 2025).

Almost all the main results in the three theorems above are taken from the second author’s thesis, completed in April of 2024, and here are some of them with slight revisions. The exceptions are two proofs of uniqueness of weak cluster point in Theorem 2 and Theorem 3, which are absent in this thesis. Later on, in the revised version just mentioned, the first author completed a detailed proof. Furthermore, proof of the uniqueness of weak cluster points in Theorem 3 is due to the first author.

5. Comparisons

In this section, we numerically demonstrate the assumption (8) to some extent. Meanwhile, we compare (8) with other recently proposed ones.

For brevity, we simply set ${\alpha }_k\equiv \alpha ,{\delta }_k\equiv \delta$. Then (8) reduces to the following:

$$\begin{array}{cc}\hfill & {\delta }^{+}:=0.5{\displaystyle \frac{-1+\sqrt{1+\frac{8}{\alpha }\left(\frac{2}{\sigma (2-\alpha )}-1\right)(1-\sigma )\left(\frac{2-\alpha }{\alpha }\right)}}{\frac{2(1-\alpha )}{\alpha }\left(\frac{2}{\sigma (2-\alpha )}-1\right)}},\hfill \\ \hfill & {\delta }_{new}^{+}\le min\left\{{\delta }^{+},{\displaystyle \frac{1}{1-\alpha }}\left(1-{\displaystyle \frac{1}{1+(1-\sigma )(2-\alpha ){\alpha }^{-1}}}\right)\right\}:=f\left(\sigma \right).\hfill \end{array}$$

(30)

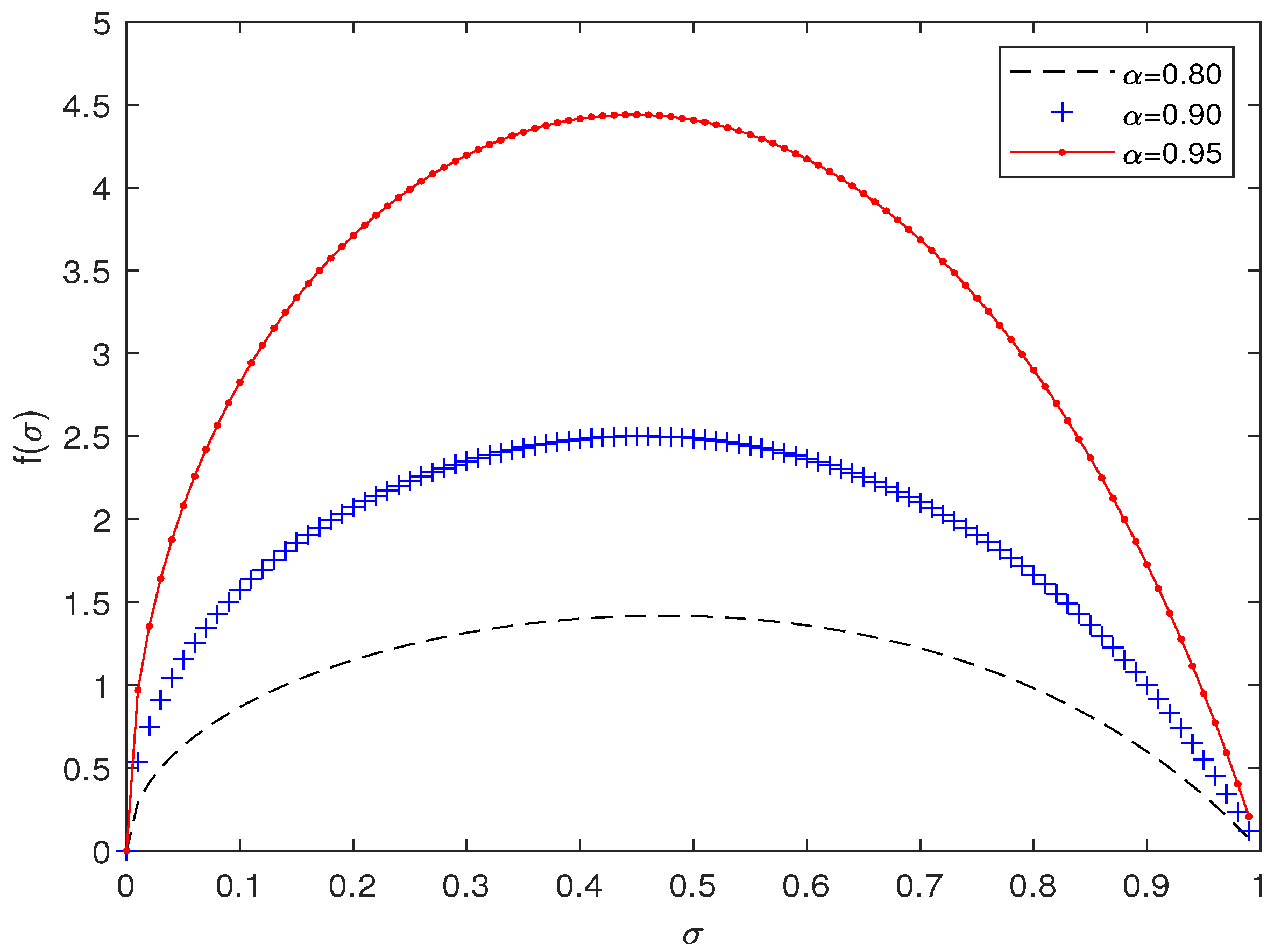
Be aware that, in contrast to (8), we no longer introduce the extra $\epsilon$ above. First, we present the function of $\sigma$ and $f\left(\sigma \right)$ under different values of $\alpha$, as shown in Figure 1:

Numerical demonstration of (30) is given in

Table 1. Numerical demonstration of (30) with respect to $\sigma$.

$\mathit{\alpha }$	0.5	0.55	0.6	0.65	0.7	0.75
${\delta }_{new}^{+}$	0.8138	0.8516	0.9025	0.9716	1.0674	1.2056
$\sigma$	0.54	0.53	0.52	0.50	0.49	0.48
$(1-\alpha ){\delta }_{new}^{+}$	0.4069	0.3832	0.3610	0.3400	0.3202	0.3014
$\mathbf{\alpha }$	0.8	0.85	0.9	0.95	0.99
${\delta }_{new}^{+}$	1.4174	1.7758	2.4999	4.6859	22.2192
$\sigma$	0.47	0.46	0.45	0.45	0.44
$(1-\alpha ){\delta }_{new}^{+}$	0.2835	0.2664	0.2500	0.2343	0.2222

, where ${\delta }_{new}^{+}$ stands for a slightly lower approximation of the maximum of f in (30) with respect to $\sigma$, $(1-\alpha ){\delta }_{new}^{+}$ stands for the directed factor.

Next, we consider those assumptions made in the first author’s manuscript mentioned in Remark 1. We set ${\alpha }_k\equiv \alpha ,{\delta }_k\equiv \delta$. Thus, they become the following:

$$\begin{array}{cc}\hfill & {\delta }^{-}:=0.5{\displaystyle \frac{-1+\sqrt{1+4((\frac{1}{\sigma }-1)\frac{1}{\alpha }+1)(1-\sigma )\frac{1}{\alpha }}}{(\frac{1}{\sigma }-1)\frac{1}{\alpha }+1}},\hfill \\ \hfill & {\delta }_{new}^{-}\le min\left\{{\delta }^{-},{\displaystyle \frac{1}{1-\alpha }}\left(1-{\displaystyle \frac{1}{1+(1-\sigma )(1-\alpha )/\alpha }}\right)\right\}:=h\left(\sigma \right).\hfill \end{array}$$

(31)

Numerical demonstration of (31) is given in

Table 2. Numerical demonstration of (31) with respect to $\sigma$.

$\mathit{\alpha }$	0.5	0.55	0.6	0.65	0.7	0.75
${\delta }_{new}^{-}$	0.4769	0.4575	0.4397	0.4230	0.4075	0.3930
$(1-\alpha ){\delta }_{new}^{-}$	0.2385	0.2059	0.1759	0.1480	0.1223	0.0983
$\mathbf{\alpha }$	0.8	0.85	0.9	0.95	0.99
${\delta }_{new}^{-}$	0.3795	0.3668	0.3549	0.3437	0.3353
$(1-\alpha ){\delta }_{new}^{-}$	0.0759	0.0550	0.0355	0.0172	0.0034

.

Finally, we consider the assumptions made in [2] very recently. We set the following:

$${\beta }_k={ϵ}_k={\rho }_k={\theta }_k\equiv 0,T_k\equiv N,$$

in our notation, the algorithm therein can also be written in the form (6), and the corresponding assumptions become the following:

$$\begin{array}{cc}& 0\le \delta <1,(1-\alpha )\delta <1,\hfill \\ & (1-\alpha )\delta (1+\delta )+({\displaystyle \frac{1}{\alpha }}-1)\delta (1-\delta )-({\displaystyle \frac{1}{\alpha }}-1)(1-\delta )<0.\hfill \end{array}$$

Namely, the following:

$$0\le \delta <{\displaystyle \frac{\alpha +2-\sqrt{{\alpha }^2+8\alpha }}{2(1-\alpha )}}.$$

(32)

Numerical demonstration of (32) is given in

Table 3. Numerical demonstration of (32) with respect to $\alpha$.

$\mathit{\alpha }$	0.5	0.55	0.6	0.65	0.7	0.75
${\delta }_{new}$	0.4384	0.4239	0.4105	0.3983	0.3870	0.3765
$(1-\alpha ){\delta }_{new}$	0.2192	0.1907	0.1642	0.1394	0.1161	0.0941
$\mathbf{\alpha }$	0.8	0.85	0.9	0.95	0.99
${\delta }_{new}$	0.3668	0.3576	0.3490	0.3410	0.3348
$(1-\alpha ){\delta }_{new}$	0.0734	0.0536	0.0349	0.0170	0.0033

.

From Table 1, Table 2 and Table 3, we can observe that our computed values of $(1-\alpha ){\delta }_{new}^{+}$ are consistently larger than the other two for each sampling point. In particular, in the case of ${\alpha }_k\equiv 0.95$, our new upper bound of $\delta$ is $4.6859$, in a sharp contrast to $0.3437$ in Table 2 and $0.3410$ in Table 3, respectively.

6. Modeling and Numerical Experiments

In this section, we modeled rare feature selection in deep learning in a new way and confirmed efficiency of Algorithm 1 in solving the corresponding test problems. In our writing style, rather than striving for maximal test problems, we tried to make the basic ideas and techniques as clear as possible.

We performed all numerical experiments via Python 3.9.2.

We compared Algorithm 1 with the classical DR splitting method, selected for their similarities in features, applicability, and implementation effort.

Our test problem is motivated by “rare feature selection” formulated in Johnstone and Eckstein (Section 6.3 of [6]) (TripAdvisor data are available at https://github.com/yanxht/TripAdvisorData, accessed on 1 May 2024), which can be stated as follows:

$$\underset{{\beta }_0,\gamma }{min}\Vert {\beta }_0{e+XH\gamma -y\Vert }_2^2/\left(2n\right)+\lambda \left(\right|{\gamma }_1|+\dots +|{\gamma }_{r-1}\left|\right)+{\lambda \Vert H\gamma \Vert }_1,$$

(33)

where X is the n-by-d data matrix, H is the d-by-r coefficient matrix, $y\in {\mathcal{R}}^n$ is the target vector, $e\in {\mathcal{R}}^n$ is the all-one vector, and ${\beta }_0\in \mathcal{R}$ is an offset and $\gamma \in {\mathcal{R}}^r$. In [5,6], the authors gave a detailed description of the relationship of $H,\gamma$ (see (Section 6.3 of [6]) and (Section 3 of [5]) for more details). The ${\ell }_1$ norm on $\gamma$ enforces sparsity of $\gamma$, which in turn fuses together coefficients associated with similar features. The ${\ell }_1$ norm on $H\gamma$ additionally enforces sparsity on these coefficients, which is also desirable.

As described in [5,6], we applied this model on the TripAdvisor hotel-review dataset. The response variable y was the overall rating of the hotel, in the set $\left\{1,2,3,4,5\right\}$. The features were the counts of certain adjectives in the review. Many adjectives were very rare, with 95% of the adjectives appearing in less than 5% of the reviews. There were 7573 adjectives from 169,987 reviews, and the auxiliary similarity tree $\mathcal{T}$ had 15,145 nodes. The 169,987 × 7573 design matrix X and the 7573 × 15,145 matrix H arising from the similarity tree $\mathcal{T}$ were both sparse, having 0.32% and 0.15% nonzero entries, respectively.

By replacing the least squares term with the ${\ell }_1$ norm term, we obtained:

$$\underset{x\in {\mathcal{R}}^{r+1}}{\min }\varphi \left(x\right):={\Vert \mathbb{X}\mathbb{H}x-y\Vert }_1/\left(n\right)+\lambda (\left|x_2\right|+\dots +\left|x_r\right|)+\lambda {\Vert \mathbb{M}x\Vert }_1,$$

(34)

(note that $\lambda$ here corresponds to $0.5\lambda$ in (Equation (7.4) of [7]) when mu there was taken to be $0.5$) and the corresponding optimality condition is written as follows:

$$0\in \lambda \mathbb{J}x+{\left(\mathbb{X}\mathbb{H}\right)}^T{\partial \Vert ·\Vert }_1\left(\mathbb{X}\mathbb{H}x-y\right)/n+\lambda {\mathbb{M}}^T\partial {\Vert ·\Vert }_1\left(\mathbb{M}x\right),$$

(35)

where $\mathbb{J}=\mathrm{diag}(0,\partial \left|·\right|,\dots ,\partial \left|·\right|,0).$

In this article, we rewrote (34) as follows:

$$\underset{x\in {\mathcal{R}}^{r+1}}{\min }|x_2|+\dots +|x_r|+{‖\left(\begin{array}{c}{\displaystyle \frac{1}{n\lambda }}\mathbb{X}\mathbb{H}\\ \mathbb{M}\end{array}\right)x-\left(\begin{array}{c}{\displaystyle \frac{1}{n\lambda }}y\\ 0\end{array}\right)‖}_1.$$

(36)

Denoted as follows:

$$f\left(x\right)=|x_2|+\dots +|x_r|,g(Qx-q)={‖\left(\begin{array}{c}{\displaystyle \frac{1}{n\lambda }}\mathbb{X}\mathbb{H}\\ \mathbb{M}\end{array}\right)x-\left(\begin{array}{c}{\displaystyle \frac{1}{n\lambda }}y\\ 0\end{array}\right)‖}_1,$$

(37)

and the corresponding optimality condition is as follows:

$$0\in \partial f\left(x\right)+Q^T\partial g(Qx-q).$$

(38)

Thus, we obtain the following:

$$\left\{\begin{array}{cc}\hfill 0& \in \partial f\left(x\right)+Q^{T}u\hfill \\ \hfill 0& \in -Qx+q+\partial g^{-1}\left(u\right)\hfill \end{array}\right.$$

or

$$0\in F\left(w\right)+B\left(w\right),$$

(39)

where

$$w:=\left(\begin{array}{c}x\\ u\end{array}\right),F\left(w\right)=\left(\begin{array}{cc}0& Q^T\\ -Q& 0\end{array}\right)\left(\begin{array}{c}x\\ u\end{array}\right)+\left(\begin{array}{c}0\\ q\end{array}\right),B=\left(\begin{array}{cc}\partial f& 0\\ 0& \partial g^{-1}\end{array}\right).$$

Note that the classical DR splitting method reads as follows:

$$\left\{\begin{array}{cc}& {\overline{w}}^k={(I+\mu B)}^{-1}(w^k-\mu F\left(w^k\right))\hfill \\ & w^{k+1}+\mu F\left(w^{k+1}\right)=w^k+\mu F\left(w^k\right)-(w^k-{\overline{w}}^k).\hfill \end{array}\right.$$

So, we obtained the intermediate iterates, written as follows:

$$\left\{\begin{array}{cc}& {\overline{x}}^k={(I+\mu \partial f)}^{-1}(x^k-\mu Q^T{u}^k)\hfill \\ & {\overline{u}}^k={(I+\mu \partial g)}^{-1}(u^k+\mu (Q{x}^k-q)).\hfill \end{array}\right.$$

Moreover, the resolvent of the ${\ell }_1$ norm term can be computed by the following:

$${\overline{x}}^k=\left\{\begin{array}{cccc}& {(I+\mu \partial |·\left|\right)}^{-1}\left(x_i^k\right)=sgn\left(x_i^k\right)max\left\{\right|x_i^k|-\mu ,0\},\hfill & & i=2,\dots ,n-1,\hfill \\ & x_i^k,\hfill & & i=1,n.\hfill \end{array}\right.$$

As for Algorithm 1, we first used the same way of generating intermediate iterates, then we considered the following:

$$\begin{array}{r}\left(\begin{array}{cc}I& \mu Q^T\\ -\mu Q& I\end{array}\right)\left(\begin{array}{c}\Delta x\\ \Delta u\end{array}\right)=-\alpha \left(\begin{array}{c}{x}^k-{\overline{x}}^k\\ u^k-{\overline{u}}^k\end{array}\right)+(1-\alpha )\delta \left(\begin{array}{cc}I& \mu Q^T\\ -\mu Q& I\end{array}\right)\left(\begin{array}{c}{x}^k-x^{k-1}\\ u^k-u^{k-1}\end{array}\right).\end{array}$$

Equivalently, we obtain the following:

$$\begin{array}{c}\hfill \Delta x+\mu Q^T\Delta u=-\alpha (x^k-{\overline{x}}^k)+(1-\alpha )\delta [x^k-x^{k-1}+\mu Q^T(u^k-u^{k-1})],\end{array}$$

$$\begin{array}{c}\hfill -\mu Q\Delta x+\Delta u=-\alpha (u^k-{\overline{u}}^k)+(1-\alpha )\delta [-\mu Q(x^k-x^{k-1})+u^k-u^{k-1}].\end{array}$$

Thus, we first solve the following:

$$(I+{\mu }^{2}Q{Q}^T)\Delta u=-\alpha \mu Q(x^k-{\overline{x}}^k)-\alpha (u^k-{\overline{u}}^k)+(1-\alpha )\delta (I+{\mu }^{2}Q{Q}^T)(u^k-u^{k-1})$$

(40)

to obtain $\Delta u^k$, then the following:

$$\Delta x^k=-\alpha (x^k-{\overline{x}}^k)+(1-\alpha )\delta [(x^k-x^{k-1})+\mu Q^T(u^k-u^{k-1})]-\mu Q^T\Delta u.$$

Finally, we compute the following:

$$x^{k+1}=x^k+\Delta x^k,u^{k+1}=u^k+\Delta u^k.$$

Note that we implemented the celebrated conjugate gradient method with one iteration (not too much!) to solve subproblem (40).

DR: The classical DR splitting method.

dDR $\alpha =0.95$, $\delta =0.34$: Algorithm 1 with an upper bound given in [2].

dDR $\alpha =0.95$, $\delta =4.68$: Algorithm 1 with an upper bound given in this article.

For the starting points, we chose

$$x^0=0,z^0=0.$$

For the parameter $\lambda$, we considered the following two cases.

• Case 1

In this case, we set $\lambda =0.5\times {10}^{-4}$ (corresponds to $\lambda ={10}^{-4}$ in [7]), and we took $\mu =1/\Vert Q\Vert$, where $\Vert Q\Vert \approx 4925$. We used the stopping criterion, written as follows:

$$\varphi \left(x^k\right)/\varphi \left(x^0\right)\le 0.589.$$

• Case 2

In this case, we set $\lambda =0.5\times {10}^{-5}$ (corresponds to $\lambda ={10}^{-5}$ in [7]), and we took $\mu =1/\Vert Q\Vert$, where $\Vert Q\Vert \approx$ 49,233. We used the following stopping criterion:

$$\varphi \left(x^k\right)/\varphi \left(x^0\right)\le 0.575.$$

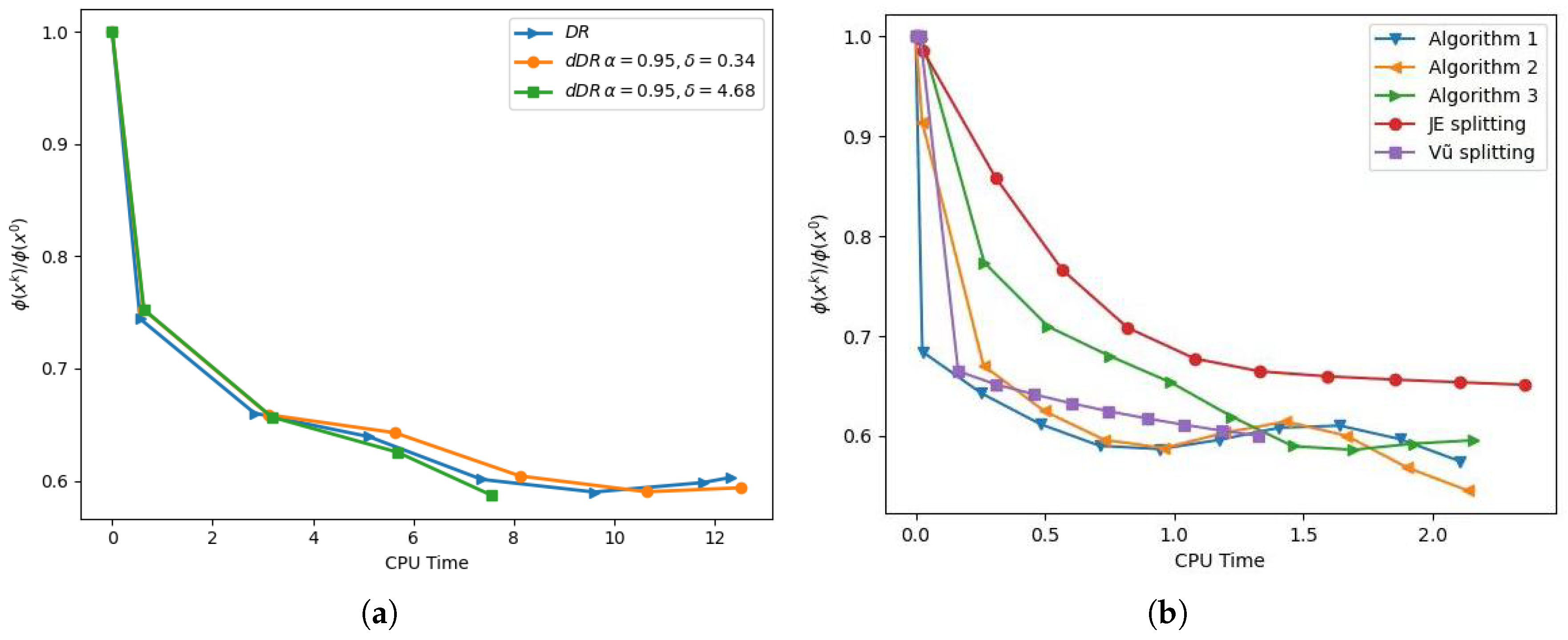
The corresponding numerical results were plotted in the figures (left) in Figure 2 and Figure 3, where “CPU Time” stands for the elapsed time using tic and toc in seconds. Notice that the figures (right) were taken from [7], in which “Algorithm 1”, “Algorithm 2” and “Algorithm 3” are those algorithms recently proposed in [7], “JE splitting” is a splitting method of (Algorithm 1 of [6]), and “Vũ splitting” is a splitting method proposed in [15].

From Figure 2 and Figure 3, it can be seen that dDR with $\alpha =0.95$, $\delta =4.68$ was faster than the other two.

Be aware that the ratio $\varphi \left(x^k\right)/\varphi \left(x^0\right)$ is actually identical to the counterpart given in [7] provided that $x^k$, $x^0$ are the same. So, comparisons within those numerical results in [7] (i.e., the figures (right) in Figure 2 and Figure 3) are meaningful. At first sight, those algorithms [7] outperformed dDR with $\alpha =0.95$, $\delta =4.68$. However, we would like to stress that the latter solved (36) to similar accuracy to those [7] in about 7 or 8 s, compared to the time-consuming (tens of minutes or more) trial and error process of determining those proximal parameters, rooted in those algorithms [7]. In this sense, the directed DR splitting method is user-friendly and efficient in solving this feature selection model.

7. Conclusions

In this article, we have studied the directed version of the DR splitting method in real Hilbert spaces. By using new, self-contained, and simplified techniques, we have proved its weak convergence. The major innovation is that we exploit the firm non-expansiveness of the DR operator. To the best of our knowledge, this is for the first time. Thus, our upper bounds on direction factors surpass existing ones, assuming that the involved factors remain constant. To apply the method to feature selection in deep learning, we have given a new rare feature selection model equipped with the TripAdvisor hotel-review dataset. Numerical results have confirmed the user-friendliness and efficiency of directed DR splitting in solving this model.

For the directed DR splitting, this deserves developing self-adaptive ways of choosing the directed factors, at least for the first few iterations, and this would also be interesting to apply to hyperspectral unmixing [16]. While these topics are beyond the scope of this article, we hope to tackle them in the future.