Identification of Sparse Interdependent Edges in Heterogeneous Network Models via Greedy Module Matching
Abstract
1. Introduction
- Leveraging mid-level modular structural features as the foundation for interdependent edge identification, particularly in similar-order heterogeneous networks with significant edge density differences.
- Determining the range of interdependent edges based on structural differences between heterogeneous subnetworks and employing a greedy matching algorithm to iteratively identify sparse interdependent edges.
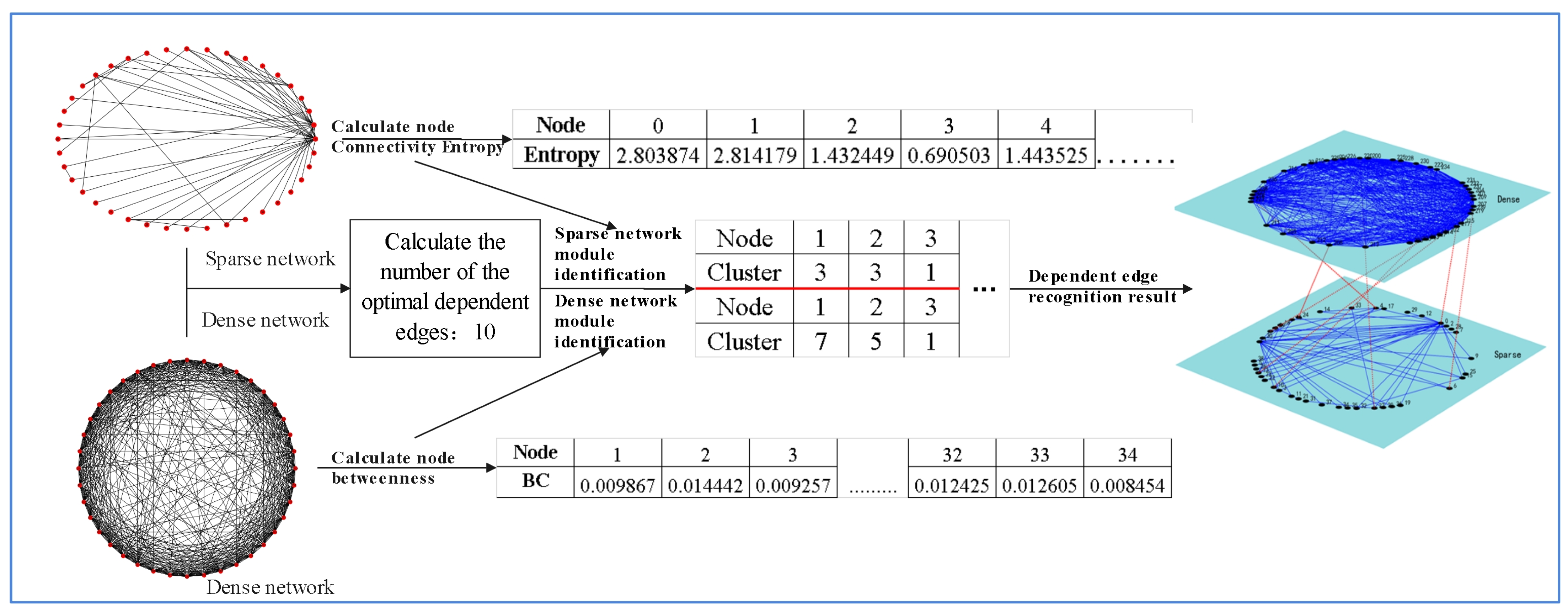
2. Materials and Methods
2.1. Calculation of Node Characteristic Values Based on Network Topology
2.2. Network Module Identification Based on Clustering
2.3. Identification of Interdependent Patterns Based on the Greedy Algorithm
2.4. Network Robustness Evaluation
2.5. Interdependent Edge Configuration Efficiency Index
- NP represents the number of nodes in the sparse network.
- NC represents the number of nodes in the dense network.
- NPC denotes the total number of nodes in the interdependent network.
- dij is the shortest path length between nodes i and j in the interdependent network.
- V represents the set of nodes in the interdependent network.
- A is a weight parameter.
- EPC denotes the set of interdependent edges in the interdependent network.
- u and v represent nodes in the sparse and dense networks, respectively.
- (u, v) represents an interdependent edge.
- σuv is the total number of shortest paths between nodes u and v in the interdependent network.
- σuv(e) represents the number of shortest paths passing through edge (u, v).
3. Results and Discussion
3.1. Validation on Synthetic Interdependent Networks
3.1.1. Identification of Interdependent Edges in Synthetic Networks
3.1.2. Robustness Analysis of Synthetic Interdependent Networks
- Degree-Electric Degree (DED) coupling method;
- Nearest-Neighbor Prioritized Coupling (NPC) method;
- Random Linking (RL) method;
- The proposed Greedy Strategy method (CBG).
- Figure 5 illustrates the changes in robustness under different attack scenarios;
- Figure 5a: Variation in natural connectivity under random node attacks;
- Figure 5b: Variation in natural connectivity under random edge attacks;
- Figure 5c: Variation in network efficiency under high-betweenness node attacks;
- Figure 5d: Variation in network efficiency under high-betweenness edge attacks.
3.1.3. Evaluation of Connection Efficiency in Synthetic Interdependent Networks
3.2. Real-World Power-Communication Network
3.2.1. Identification of Interdependent Edges in Power-Communication Networks
3.2.2. Robustness Analysis of the Power-Communication Interdependent Network
3.2.3. Analysis of Network Connection Efficiency in the Power-Communication Interdependent Network
3.3. Identification of Interdependent Edges in the Question–Answer Network
Prediction of Interdependent Edges
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DED | Degree-Electric Degree coupling method |
| NPC | Nearest-Neighbor Prioritized Coupling method |
| RL | Random Linking method |
| CBG | The proposed Greedy Strategy method |
Appendix A


References
- Liu, Q.; Chen, B.; Yan, Y.; Wang, C. Robustness Improvement Strategy for Smart Grid Infrastructure Scenarios. In Proceedings of the 2023 3rd Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 25–27 February 2023; pp. 45–49. [Google Scholar]
- Xie, X.; Ma, D.; Na, Z.; Lu, Y.; Luo, X. Improvement strategy for robustness of power grid complex network by distributed photovoltaic power system. E3S Web Conf. 2020, 143, 02019. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, N.; Cheng, Z.; Gu, W. Reliability Evaluation of Cyber–Physical Power Systems Considering Supply- and Demand-Side Uncertainties. Energies 2022, 15, 118. [Google Scholar] [CrossRef]
- Yang, L.; Gu, Z.; Dang, Y.; He, P. Analysis of Vulnerability on Weighted Power Networks under Line Breakdowns. Entropy 2022, 24, 1449. [Google Scholar] [CrossRef]
- Fang, Y.; Tang, X.; Tang, L.; Chen, Y.; Wang, W. Local Evolution Model of the Communication Network for Reducing Outage Risk of Power Cyber-Physical System. Energies 2022, 15, 7876. [Google Scholar] [CrossRef]
- Wu, G.; Li, M.; Li, Z.S. A Gene Importance based Evolutionary Algorithm (GIEA) for identifying critical nodes in Cyber–Physical Power Systems. Reliab. Eng. Syst. Saf. 2021, 214, 107760. [Google Scholar] [CrossRef]
- Pan, H.; Li, X.; Na, C.; Cao, R. Modeling and Analysis of Cascading Failures in Cyber-Physical Power Systems Under Different Coupling Strategies. IEEE Access 2022, 10, 108684–108696. [Google Scholar] [CrossRef]
- Kong, P.-Y. Optimal Configuration of Interdependence Between Communication Network and Power Grid. IEEE Trans. Ind. Inform. 2019, 15, 4054–4065. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Liu, C.; Zang, W.; Zhang, S.; Li, R.; Ouyang, Q. A multi-population quantum genetic algorithm for improving the robustness of interdependent networks. In Proceedings of the 2023 9th International Conference on Communication and Information Processing, Lingshui, China, 27–29 December 2024; pp. 326–332. [Google Scholar]
- Yang, Y.; Tu, L.; Li, K.; Guo, T. Optimized inter-structure for enhancing the synchronizability of interdependent networks. Phys. A Stat. Mech. Its Appl. 2019, 521, 310–318. [Google Scholar] [CrossRef]
- Liu, X.; Sun, S.; Wang, J.; Xia, C. Onion structure optimizes attack robustness of interdependent networks. Phys. A Stat. Mech. Its Appl. 2019, 535, 122374. [Google Scholar] [CrossRef]
- Parshani, R.; Buldyrev, S.V.; Havlin, S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett. 2010, 105, 048701. [Google Scholar] [CrossRef]
- Sun, S.; Wu, Y.; Ma, Y.; Wang, L.; Gao, Z.; Xia, C. Impact of Degree Heterogeneity on Attack Vulnerability of Interdependent Networks. Sci. Rep. 2016, 6, 32983. [Google Scholar] [CrossRef]
- Dong, Z.; Fang, Y.; Tian, M. Influences of various coupled patterns and coupling strength on power-communication coupled networks. High Volt. Eng. 2015, 41, 3464–3469. [Google Scholar]
- Su, Q.; Sun, J.; Li, J. Vulnerability analysis of cyber-physical power systems based on failure propagation probability. Int. J. Electr. Power Energy Syst. 2024, 157, 109877. [Google Scholar] [CrossRef]
- Chen, L.; Yue, D.; Dou, C.; Cheng, Z.; Chen, J. Robustness of cyber-physical power systems in cascading failure: Survival of interdependent clusters. Int. J. Elec. Power 2020, 114, 105374. [Google Scholar] [CrossRef]
- Dong, G.; Wang, F.; Shekhtman, L.M.; Danziger, M.M.; Fan, J.; Du, R.; Liu, J.; Tian, L.; Stanley, H.E.; Havlin, S. Optimal resilience of modular interacting networks. Proc. Natl. Acad. Sci. USA 2021, 118, e1922831118. [Google Scholar] [CrossRef] [PubMed]
- Morteza, A.; Chou, R.A. Distributed Matrix Multiplication: Download Rate, Randomness and Privacy Trade-Offs. In Proceedings of the 2024 60th Annual Allerton Conference on Communication, Control, and Computing, Urbana, IL, USA, 24–27 September 2024; pp. 1–7. [Google Scholar]
- Zou, Q.; Ding, L. Research on Key Fragile Dependency Links Removal Strategies in Interdependent Power and Communication Networks under Cascading Failures. In Proceedings of the 2023 3rd International Conference on Neural Networks, Information and Communication Engineering (NNICE), Guangzhou, China, 24–26 February 2023; pp. 565–570. [Google Scholar]
- Wang, X.; Zhou, W.; Li, R.; Cao, J.; Lin, X. Improving robustness of interdependent networks by a new coupling strategy. Phys. A Stat. Mech. Its Appl. 2018, 492, 1075–1080. [Google Scholar] [CrossRef]
- Dong, Z.; Tian, M.; Liang, J.; Fang, Y.; Lu, Y. Research on the connection radius of dependency links in interdependent spatial networks against cascading failures. Phys. A Stat. Mech. Its Appl. 2019, 513, 555–564. [Google Scholar] [CrossRef]
- Liu, D.; Tse, C.K.; Zhang, X. Tradeoff Between Robustness and Functionality in Cyber-Coupled Power Systems. IEEE Syst. J. 2022, 16, 499–509. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Dai, H.; Eun, D.Y.; Hosseinalipour, S. Designing Optimal Interlink Patterns to Maximize Robustness of Interdependent Networks Against Cascading Failures. IEEE Trans. Commun. 2017, 65, 3847–3862. [Google Scholar] [CrossRef]
- Marashi, K.; Sarvestani, S.S.; Hurson, A.R. Identification of interdependencies and prediction of fault propagation for cyber–physical systems. Reliab. Eng. Syst. Saf. 2021, 215, 107787. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Katsikas, S. Identifying and Analyzing Dependencies in and among Complex Cyber Physical Systems. Sensors 2021, 21, 1685. [Google Scholar] [CrossRef]
- Turalska, M.; Swami, A. Greedy control of cascading failures in interdependent networks. Sci. Rep. 2021, 11, 3276. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, C.; Liu, S.; Wang, K.; Zang, W. Percolation Transitions in Edge-Coupled Interdependent Networks with Reinforced Inter-Layer Links. Entropy 2024, 26, 693. [Google Scholar] [CrossRef]
- He, Z.; Wang, Y.; Xia, W.; Shen, Y.; Hao, Y.; Ren, Q. A method for reliability assessment of complex electromechanical system based on improved network connectivity entropy. Phys. A—Stat. Mech. Its Appl. 2023, 632, 129331. [Google Scholar] [CrossRef]
- López-Rourich, M.A.; Rodríguez-Pérez, F.J. Efficient Data Transfer by Evaluating Closeness Centrality for Dynamic Social Complex Network-Inspired Routing. Appl. Sci. 2023, 13, 10766. [Google Scholar] [CrossRef]
- Park, J.; Newman, M.E.J. Origin of degree correlations in the Internet and other networks. Phys. Rev. E 2003, 68, 7. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhou, T.; Zhu, S.; Jia, C. Optimal control of grid-connected overvoltage of distributed photovoltaic power generation based on cluster division. Arch. Electr. Eng. 2024, 73, 1047–1067. [Google Scholar] [CrossRef]
- Schuetz, P.; Caflisch, A. Efficient modularity optimization by multistep greedy algorithm and vertex mover refinement. Phys. Rev. E 2008, 77, 046112. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Madani, O.; Averineni, S.A.; Gandham, S. A Dataset of Networks of Computing Hosts. In Proceedings of the 2022 ACM on International Workshop on Security and Privacy Analytics, New York, NY, USA, 25–27 April 2022; pp. 100–104. [Google Scholar]
- Choi, E.; He, H.; Iyyer, M.; Yatskar, M.; Yih, W.-t.; Choi, Y.; Liang, P.; Zettlemoyer, L. QuAC: Question answering in context. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 2174–2184. [Google Scholar]
- Zou, Q.; Yan, L.; Gong, Y.; Hou, J. Predicting Dependent Edges in Nonequilibrium Complex Systems Based on Overlapping Module Characteristics. Systems 2024, 12, 433. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]












| No. | Authors | Network Model | Method Features | Problem Addressed |
|---|---|---|---|---|
| 1 | Wang et al. (2018) [21] | Random and scale-free interdependent networks | Neighbor-prioritized connection strategy | Enhancing robustness under cascading failure |
| 2 | Dong et al. (2019) [22] | Spatially embedded scale-free networks | Five coupling modes and hybrid coupling | Optimizing dependency link radius to improve attack resilience |
| 3 | Liu et al. (2022) [23] | Power-communication coupled networks | Multi-objective optimization and correlation coefficients | Balancing trade-offs between robustness and functionality |
| 4 | Chattopadhyay et al. (2017) [24] | Scale-free networks | Optimal interconnection design based on degree sequences | Maximizing robustness against random and targeted attacks |
| 5 | Marashi et al. (2021) [25] | IEEE power grid | Correlation analysis and neural network prediction | Fault propagation prediction and interdependence identification |
| 6 | Akbarzadeh & Katsikas (2021) [26] | MDSM graph model | Multi-order dependency indicators | Analyzing interdependent structures in complex CPS |
| 7 | Turalska & Swami (2021) [27] | BTW sandpile model | Greedy control strategy | Controlling cascading failures and exploring optimal coupling relations |
| 8 | Zhang et al. (2024) [28] | Edge-coupled random and scale-free networks | Reinforced inter-layer edges and percolation theory | Preventing abrupt collapses and enhancing system robustness |
| Sorting | DC | BC | CC |
|---|---|---|---|
| 1 | 234 | 234 | 234 |
| 2 | 201 | 211 | 211 |
| 3 | 211 | 230 | 201 |
| 4 | 209 | 209 | 230 |
| 5 | 210 | 233 | 209 |
| 6 | 214 | 236 | 233 |
| 7 | 215 | 214 | 236 |
| 8 | 227 | 215 | 214 |
| 9 | 230 | 232 | 215 |
| 10 | 231 | 231 | 231 |
| Number of Nodes | Number of Edges | Density | Average Clustering Coefficient | Average Closeness | |
|---|---|---|---|---|---|
| Question Network Model | 378 | 663 | 0.0093 | 0.2558 | 0.2389 |
| Answer Network Model | 379 | 1773 | 0.0248 | 0.6282 | 0.2399 |
| Question Network Model | Answer Network Model | ||||
|---|---|---|---|---|---|
| Node | Entropy | Module | Node | Entropy | Module |
| happened | 3.8937 | 63 | KARVELAS | 0.154788357 | 7 |
| album | 3.449835 | 114 | GRAHAM | 0.149007681 | 13 |
| article | 3.221585 | 32 | CLAIMED | 0.148506505 | 2 |
| interesting | 3.142876 | 33 | ALBUM | 0.11580243 | 10 |
| work | 2.872722 | 99 | FAMILY | 0.104835427 | 1 |
| aspects | 2.770941 | 31 | TV | 0.103442594 | 23 |
| world | 2.667937 | 177 | LATER | 0.096974915 | 5 |
| win | 2.610799 | 90 | ROCK | 0.091662983 | 8 |
| second | 2.58643 | 126 | COURT | 0.086465684 | 18 |
| successful | 2.533686 | 125 | VISSI | 0.083930992 | 18 |
| No. | Question Network Node | Answer Network Node | No. | Question Network Node | Answer Network Node |
|---|---|---|---|---|---|
| 1 | happened | KARVELAS | 13 | important | ORGANIZATION |
| 2 | album | GRAHAM | 14 | influence | HIRED |
| 3 | article | CLAIMED | 15 | war | PLAYED |
| 4 | interesting | ALBUM | 16 | say | MCMAHON |
| 5 | work | MANHUNT | 17 | play | AGE |
| 6 | aspects | NEW | 18 | make | POLICE |
| 7 | world | LATER | 19 | happen | VOW |
| 8 | win | ROCK | 20 | john | NIKOS |
| 9 | second | COURT | 21 | receive | PEPYS |
| 10 | successful | PLAGUE | 22 | awards | CERTAINLY |
| 11 | role | CONVICTED | 23 | life | UNUSUAL |
| 12 | songs | THOMPSON |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Q.; Gong, Y. Identification of Sparse Interdependent Edges in Heterogeneous Network Models via Greedy Module Matching. Modelling 2025, 6, 92. https://doi.org/10.3390/modelling6030092
Zou Q, Gong Y. Identification of Sparse Interdependent Edges in Heterogeneous Network Models via Greedy Module Matching. Modelling. 2025; 6(3):92. https://doi.org/10.3390/modelling6030092
Chicago/Turabian StyleZou, Qingyu, and Yue Gong. 2025. "Identification of Sparse Interdependent Edges in Heterogeneous Network Models via Greedy Module Matching" Modelling 6, no. 3: 92. https://doi.org/10.3390/modelling6030092
APA StyleZou, Q., & Gong, Y. (2025). Identification of Sparse Interdependent Edges in Heterogeneous Network Models via Greedy Module Matching. Modelling, 6(3), 92. https://doi.org/10.3390/modelling6030092






