Switched Modeling and Sampled Switching Control for DC-DC Boost Converters with Uncertainty
Abstract
1. Introduction
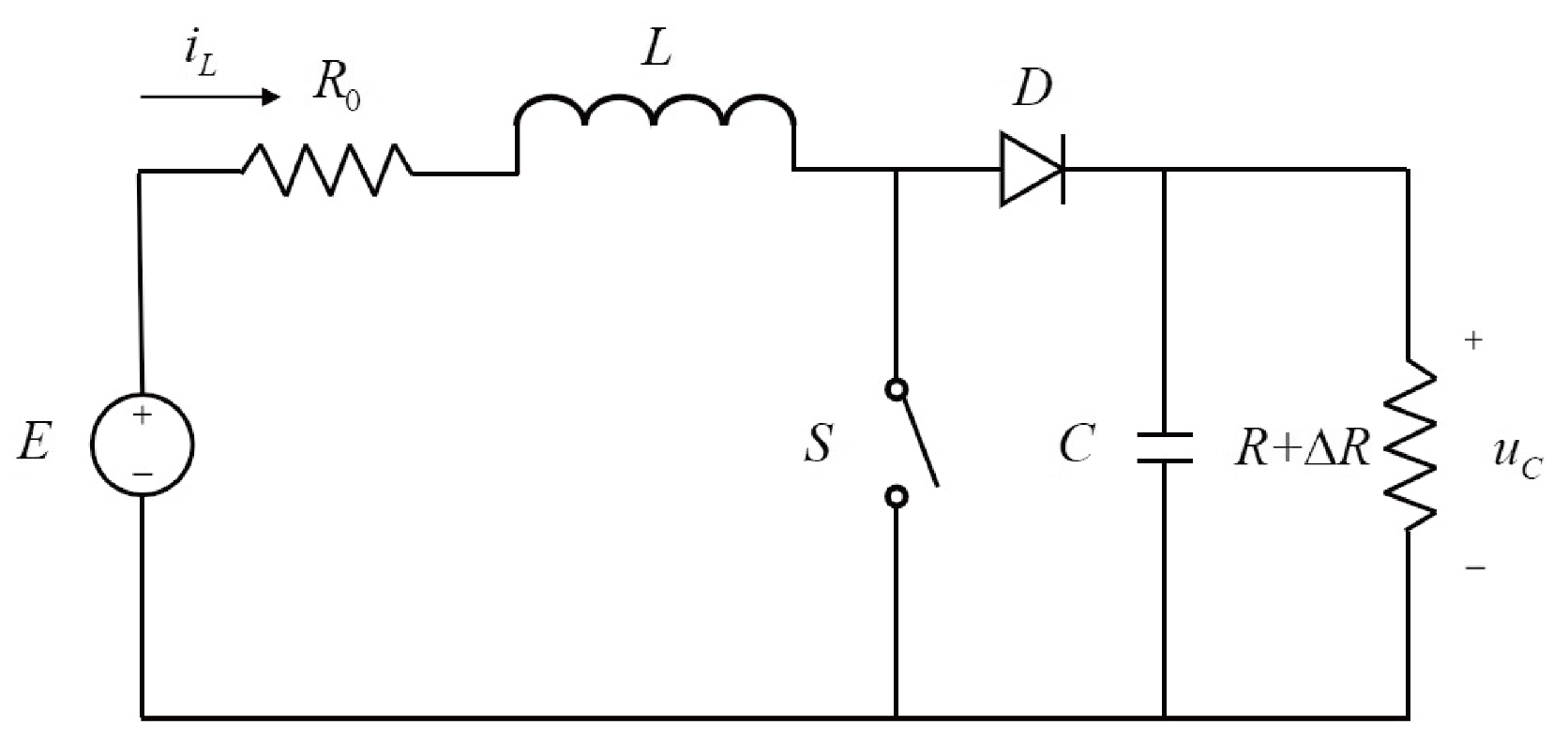
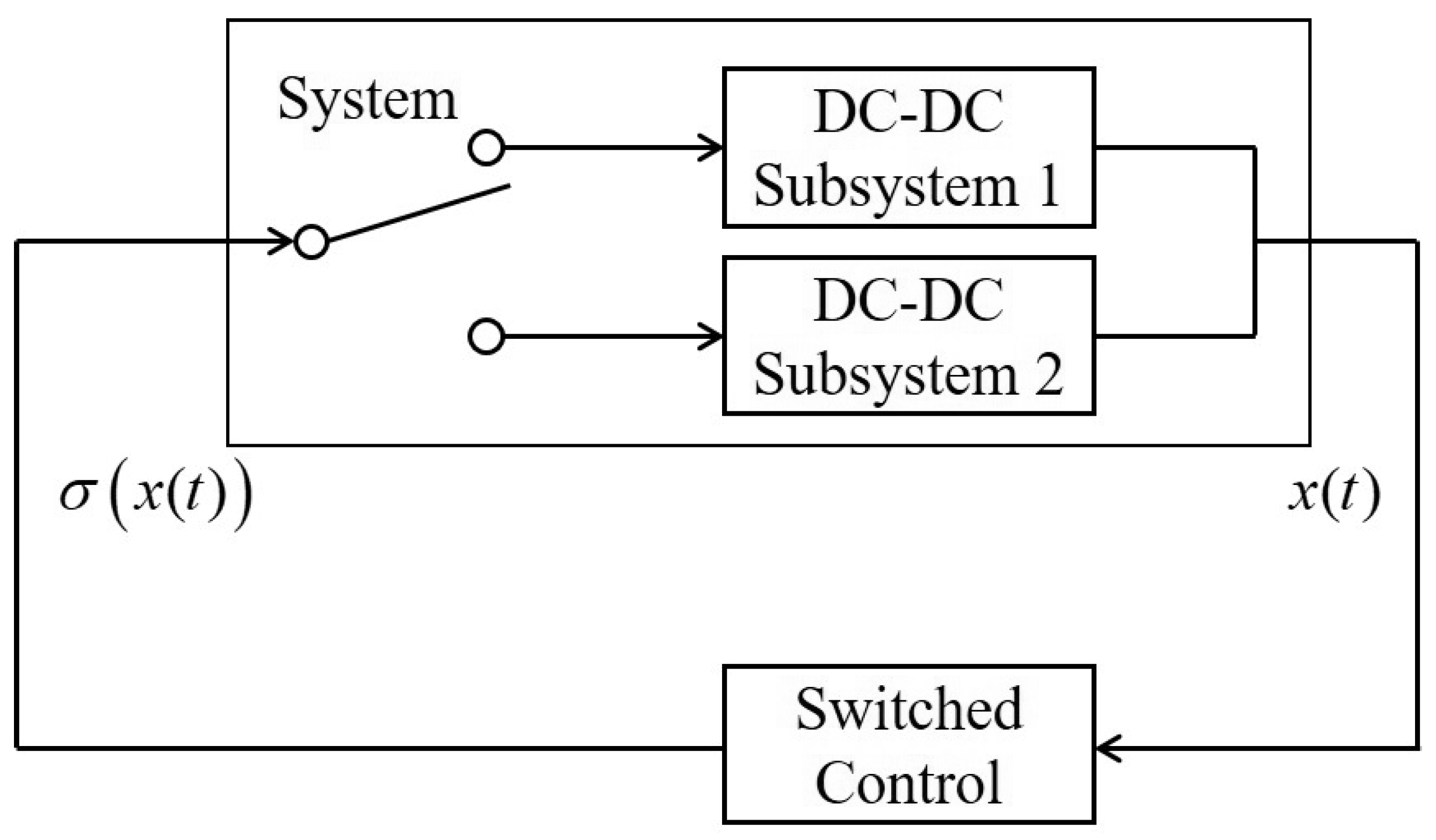
2. Problem Statement
3. Main Results
3.1. Continuous Switching Strategy Design
- Step 1.
- Offline Design:
- Step 2.
- Online Execution (at each time t):
- (a)
- Measure state and compute error .
- (b)
- Determine active Lyapunov matrix
- (c)
- Compute switching signal
- (d)
- Step 3.
- Repeat Step 2 continuously.
3.2. Sampled Switching Strategy Design
- Step 1.
- Offline Design:
- Step 2.
- Online Execution (at each sampling instant :):
- Step 3.
- Repeat Step 2 at next sampling instant .
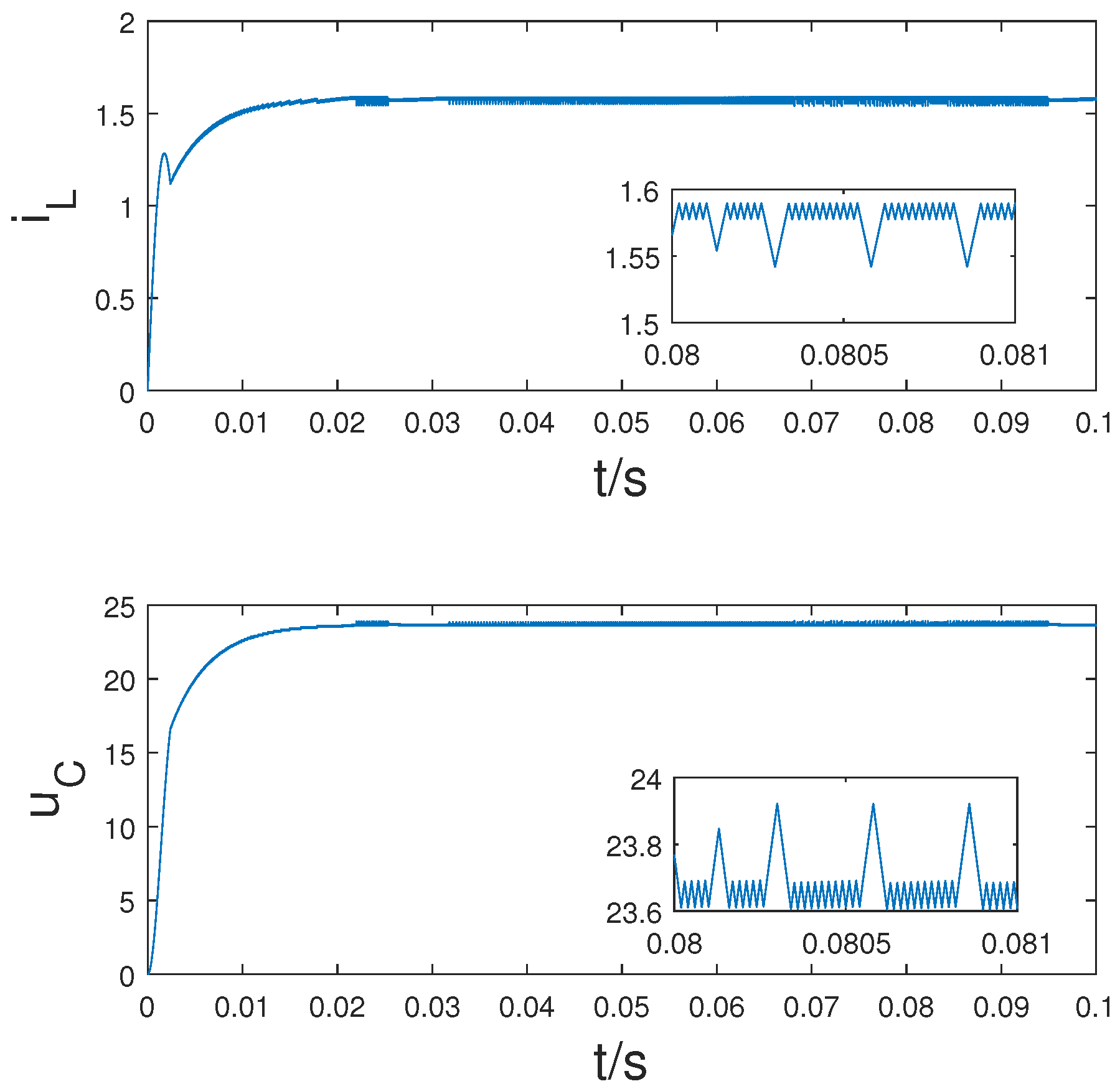
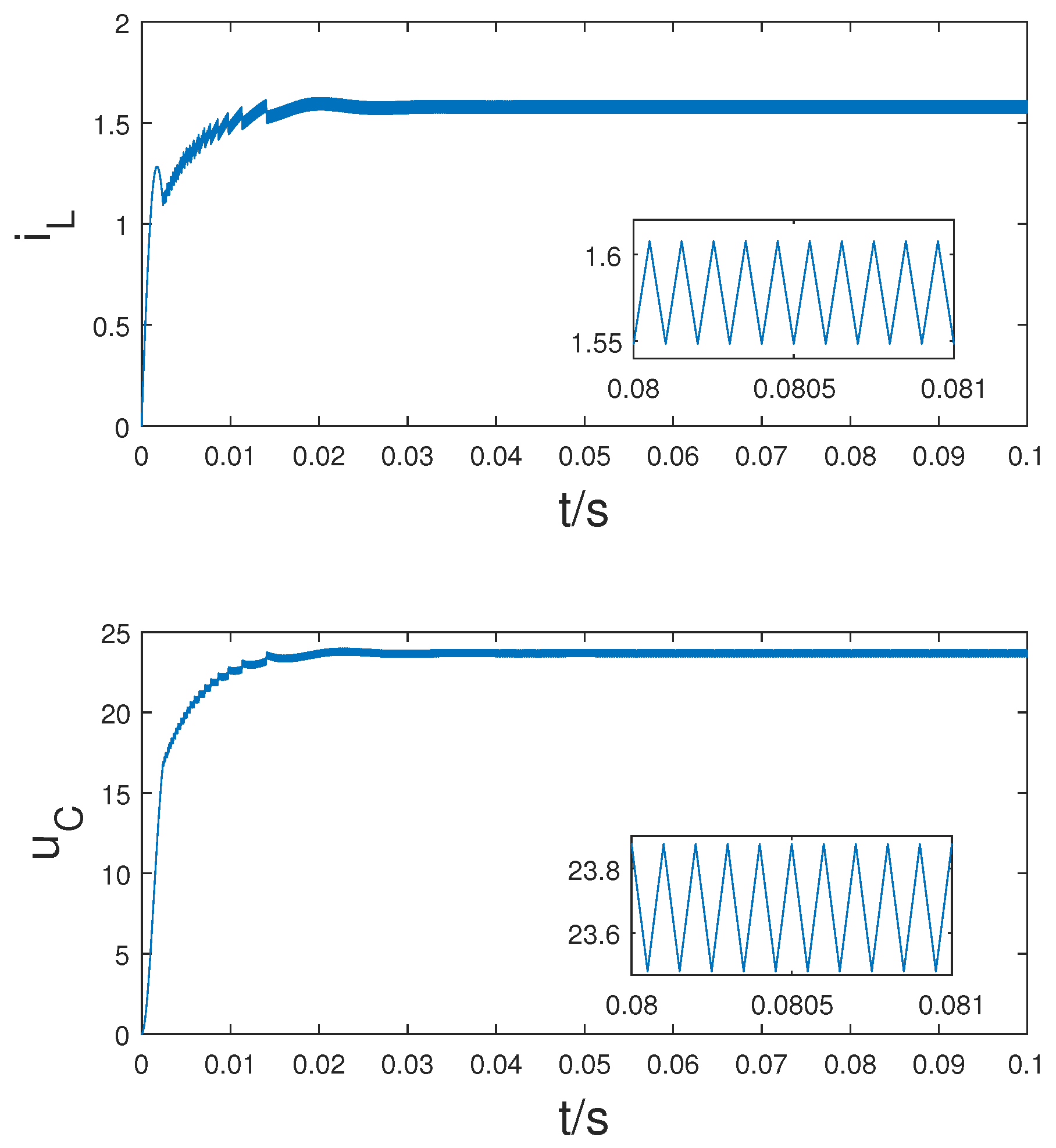
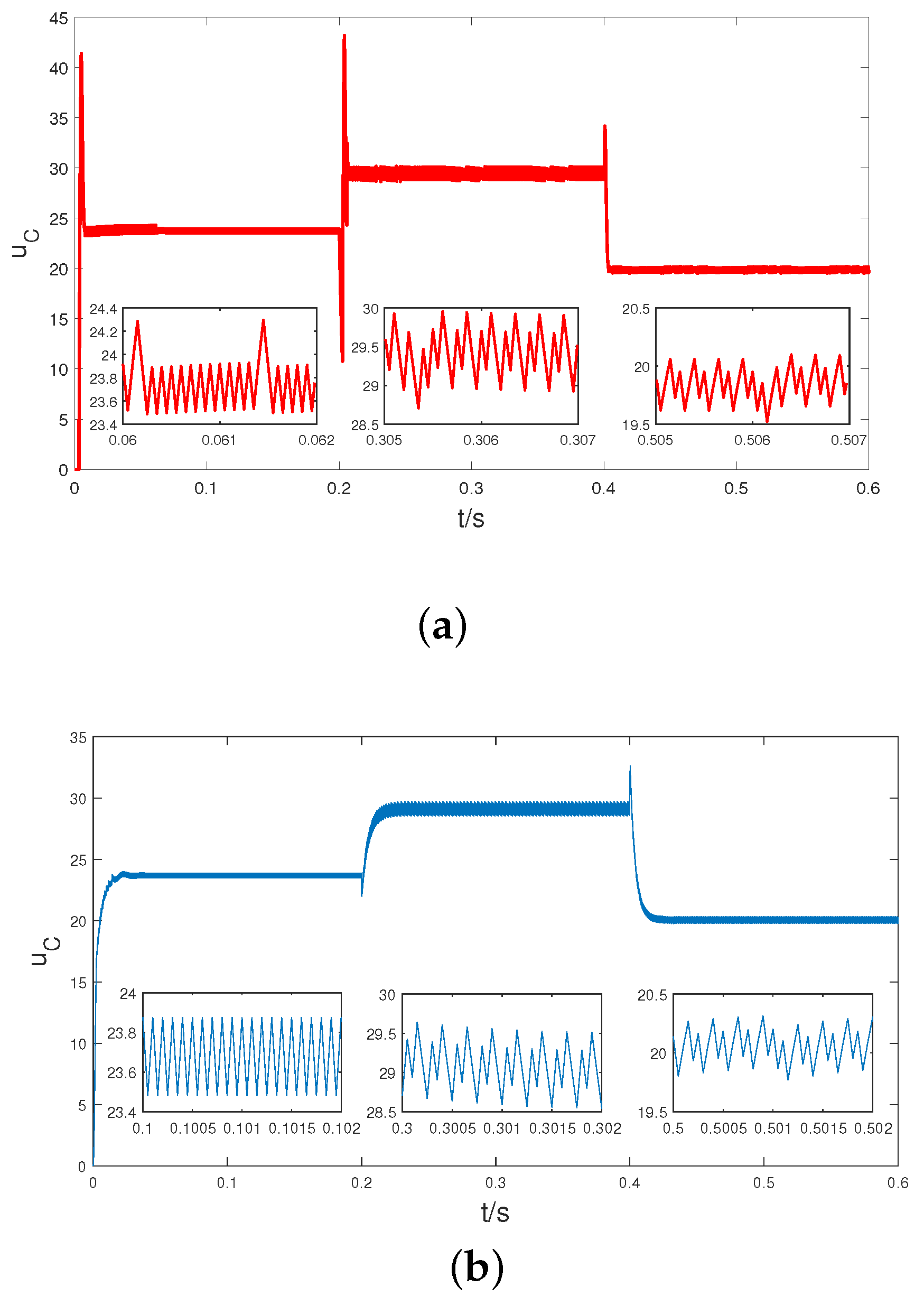
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Middlebrook, R.D.; Cuk, S. A general unified approach to modelling switching-converter power stages. Power Electron. Spec. Conf. 1976, 1, 18–34. [Google Scholar]
- Renaudineau, H.; Martin, J.P.; Nahid-Mobarakeh, B.; Pierfederici, S. DC-DC converters dynamic modeling with state observer-based parameter estimation. IEEE Trans. Power Electron. 2014, 30, 3356–3363. [Google Scholar] [CrossRef]
- Kok, C.L.; Tang, H.; Teo, T.H.; Koh, Y.Y. A DC-DC Converter with Switched-Capacitor Delay Deadtime Controller and Enhanced Unbalanced-Input Pair Zero-Current Detector to Boost Power Efficiency. Electronics 2024, 13, 1237. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Ahn, C.K.; Xiang, Z. Sampled-data output voltage regulation for a DC-DC buck converter nonlinear system with actuator and sensor failures. Nonlinear Dyn. 2020, 99, 1243–1252. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Li, S.; Wu, B.; Qian, C. Robust control for PWM-based DC-DC buck power converters with uncertainty via sampled-data output feedback. IEEE Trans. Power Electron. 2014, 30, 504–515. [Google Scholar] [CrossRef]
- Du, H.; Cheng, Y.; He, Y.; Jia, R. Finite-time output feedback control for a class of second-order nonlinear systems with application to DC-DC buck converters. Nonlinear Dyn. 2014, 78, 2021–2030. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Yang, J.; Wu, B.; Li, Q. Extended state observer-based sliding mode control for PWM-based DC-DC buck power converter systems with mismatched disturbances. IET Control Theory Appl. 2015, 9, 579–586. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Ahn, C.K.; Xiang, Z. Stabilization for a class of stochastic nonlinear systems with arbitrary switching via the common Lyapunov function method. Int. J. Control Autom. Syst. 2013, 11, 926–937. [Google Scholar]
- He, Z.; Zhang, S.; Wu, J. Sliding mode control of switched linear systems based on common Lyapunov function. Int. Symp. Syst. Control Aeronaut. Astronaut. 2010, 300–304. [Google Scholar]
- Kosov, A.A.; Kozlov, M.V. On the existence and construction of common Lyapunov functions for switched discrete systems. J. Appl. Ind. Math. 2018, 12, 668–677. [Google Scholar] [CrossRef]
- Li, L.L.; Zhao, J.; Dimirovski, G.M. Multiple Lyapunov functions approach to observer-based H∞ control for switched systems. Int. J. Syst. Sci. 2013, 44, 812–819. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, P.; Yin, Y.; Nguang, S.K. New results on stability of slowly switched systems: A multiple discontinuous Lyapunov function approach. IEEE Trans. Autom. Control 2017, 62, 3502–3509. [Google Scholar] [CrossRef]
- Wang, R.; Hou, L.; Zong, G.; Fei, S.; Yang, D. Stability and stabilization of continuous-time switched systems: A multiple discontinuous convex Lyapunov function approach. Int. J. Robust Nonlinear Control 2019, 29, 1499–1514. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, W.X. Multiple Lyapunov functions analysis approach for discrete-time switched piecewise-affine systems under dwell-time constraints. IEEE Trans. Autom. Control 2020, 65, 2177–2184. [Google Scholar] [CrossRef]
- Geromel, J.C.; Colaneri, P.; Bolzern, P. Dynamic output feedback control of switched linear systems. IEEE Trans. Autom. Control 2008, 53, 720–733. [Google Scholar] [CrossRef]
- Geromel, J.C.; Deaecto, G.S. Switched state feedback control for continuous-time uncertain systems. Automatica 2009, 45, 593–597. [Google Scholar] [CrossRef]
- Cui, J.; Chen, X.; Wang, R. New stability results for discrete-time switched systems: A new multiple piecewise convex Lyapunov function approach. Proc. Chin. Control Conf. 2019, 1746–1751. [Google Scholar]
- Wang, R.; Jiao, T.; Zhang, T.; Fei, S. Improved stability results for discrete-time switched systems: A multiple piecewise convex Lyapunov function approach. Appl. Math. Comput. 2019, 353, 54–65. [Google Scholar] [CrossRef]
- Deaecto, G.S.; Geromel, J.C.; Garcia, F.S.; Pomilio, J.A. Switched affine systems control design with application to DC-DC converters. IET Control Theory Appl. 2010, 4, 1201–1210. [Google Scholar] [CrossRef]
- Yan, X.; Shu, Z.; Sharkh, S.M. Prediction-based sampled-data control for DC-DC buck converters. In Proceedings of the 2015 First Workshop on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 22–23 March 2015; pp. 1–6. [Google Scholar]
- Yan, X.; Shu, Z.; Sharkh, S.M.; Wu, Z.G.; Chen, M.Z. Sampled-data control with adjustable switching frequency for DC-DC converters. IEEE Trans. Ind. Electron. 2019, 66, 8060–8071. [Google Scholar] [CrossRef]
- Ren, L.; Wang, D.; Yan, X.; Zhang, Y.; Wang, J. A Novel Chaotic Particle Swarm Optimized Backpropagation Neural Network PID Controller for Four-Switch Buck–Boost Converters. Actuators 2024, 13, 464. [Google Scholar] [CrossRef]
- Yang, Y.; Karimi, H.R.; Xiang, Z. Robust H∞ switching rule design for boost converters with uncertain parameters and disturbances. Abstr. Appl. Anal. 2013, 2013, 120543. [Google Scholar] [CrossRef]
- Ahmad, S.; De Souza, R.P.C.; Kergus, P.; Kader, Z.; Caux, S. Estimation-Based Robust Switching Control of a DC-DC Boost Converter. IEEE Trans. Ind. Appl. 2025, 61, 1292–1304. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, Y.; Wu, F.; Ahn, C.K. Sampled-Data Control for Buck-Boost Converter Using a Switched Affine Systems Approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 3380–3389. [Google Scholar] [CrossRef]
- Petersen, I.R. A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- De Souza, C.E.; Li, X. Delay-dependent robust H∞ control of uncertain linear state-delayed systems. Automatica 1999, 35, 1313–1321. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Lou, X. Switched Modeling and Sampled Switching Control for DC-DC Boost Converters with Uncertainty. Modelling 2025, 6, 86. https://doi.org/10.3390/modelling6030086
Lin H, Lou X. Switched Modeling and Sampled Switching Control for DC-DC Boost Converters with Uncertainty. Modelling. 2025; 6(3):86. https://doi.org/10.3390/modelling6030086
Chicago/Turabian StyleLin, Haojie, and Xuyang Lou. 2025. "Switched Modeling and Sampled Switching Control for DC-DC Boost Converters with Uncertainty" Modelling 6, no. 3: 86. https://doi.org/10.3390/modelling6030086
APA StyleLin, H., & Lou, X. (2025). Switched Modeling and Sampled Switching Control for DC-DC Boost Converters with Uncertainty. Modelling, 6(3), 86. https://doi.org/10.3390/modelling6030086






