Equivalent Porous Medium (EPM) Modeling of Karst Features for Slope Stability Analysis in Karst-Prone Weak Rock Masses
Abstract
1. Introduction
1.1. Equivalent Porous Medium (EPM): Conceptualization and Modeling Framework
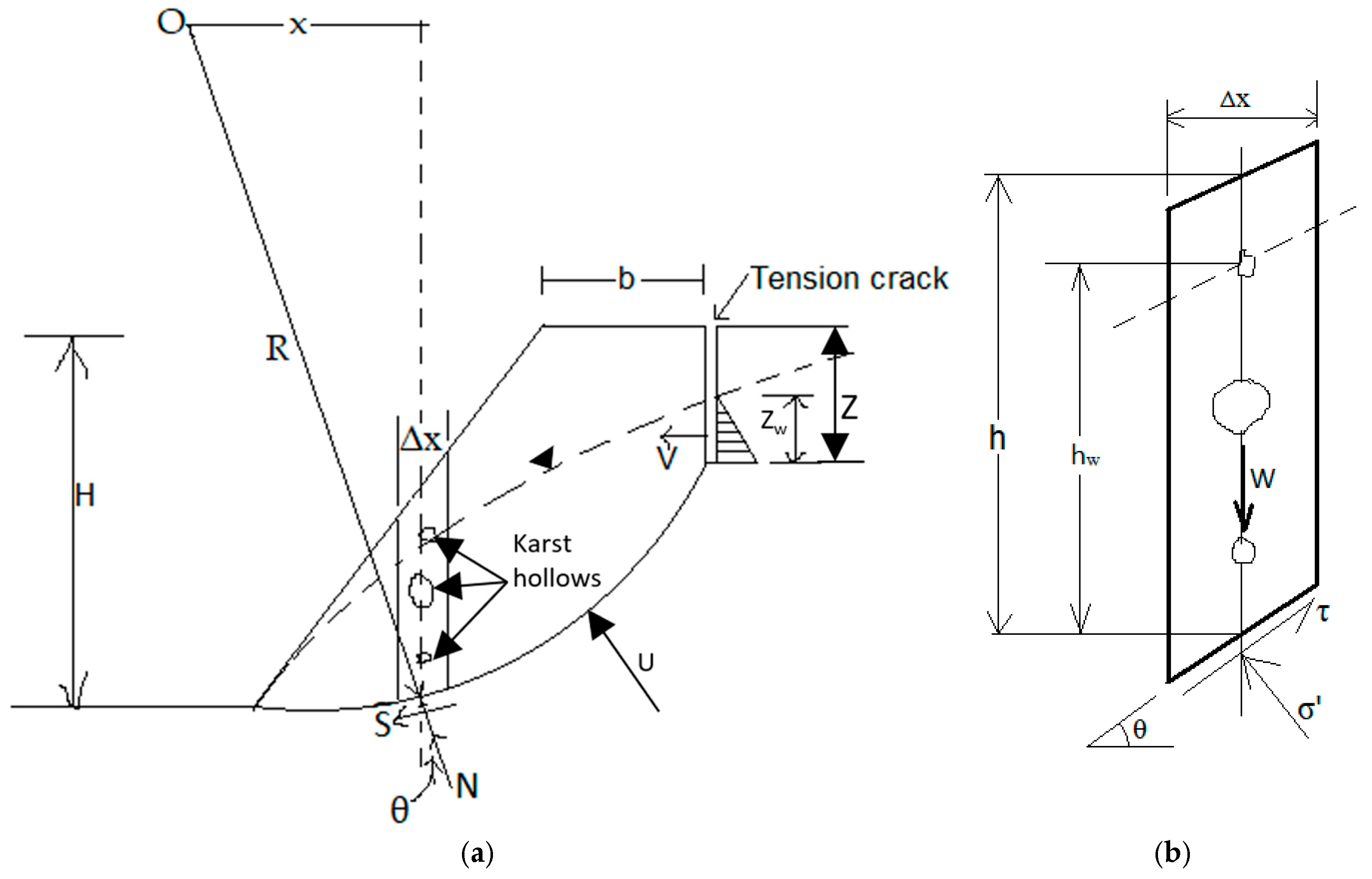
1.2. Mathematical Representation of the EPM Using the Method of Slices
- O: center of rotation
- x: distance of the slice from the center of rotation
- Δx: slice width
- R: radius of the critical circle
- Z: depth of tension crack
- Zw: height of water in the tension crack
- H: height of slope face
- h: height of the slice
- θ: inclination of failure plane
- W: weight of sliding mass = γr*Ab
- N: total normal force acting on the base of the slice
- S: shear force acting on the base of the slice
- γr: density of rock; γw: density of water
- σ: total normal stress acting at the bottom of the slice
- τ: shear stress at the bottom of the slice
- σ′: effective normal stress at the base of each slice
- P: weight of water in the karst hollows
- V: driving force due to water pressure in the tension crack
- U: uplift force due to water pressure on the sliding surface
- c: cohesive strength of failure surface
- : friction angle of the failure surface
- A: area of sliding plane= slice length*unit slice width = l*Δx/cosθ
- N: total normal force acting on the base of the slice = Wcosθ
- S: shear force acting on the base of the slice
- P = γw ∙ d ∙ Ab
- V = 1/2 ∙ γw ∙ (Zw)2
- U = ½ ∙ γw ∙ Zw ∙ A
- τ-shear stress at the bottom of the slice
- A′ = (1 − d)A: effective area of the sliding plane
- D = void density = (Total hollow area)/(Slice area)
- sub>∙ Ab′ = (1 − d)Ab: effective area of the sliding block
- Ab = l ∙ h = h ∙ Δx/cosθ
- U′ = 1/2 γwZwA′
- V′ = 1/2 γw (Zw)2d
- P′ = γwdAb′
- W′ = γrAb (1 − d)
- : instantaneous cohesion
- : instantaneous friction angle
- :
- GSI: Geological Strength Index
- D: disturbance factor
2. Materials and Methods
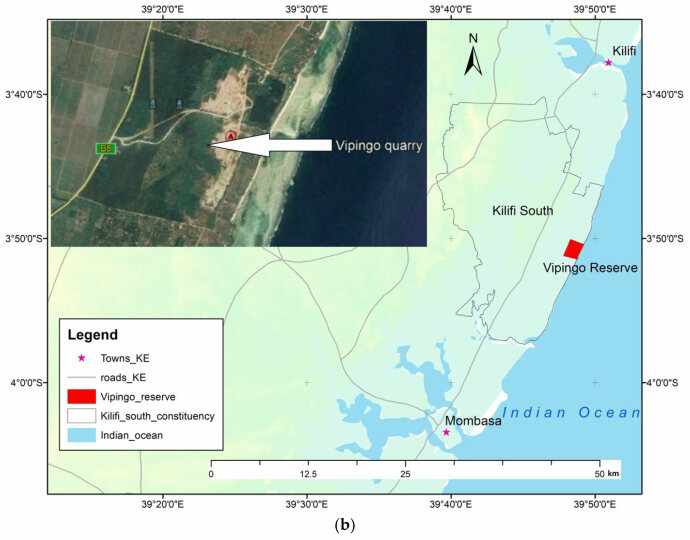
2.1. Study Area and Geological Context
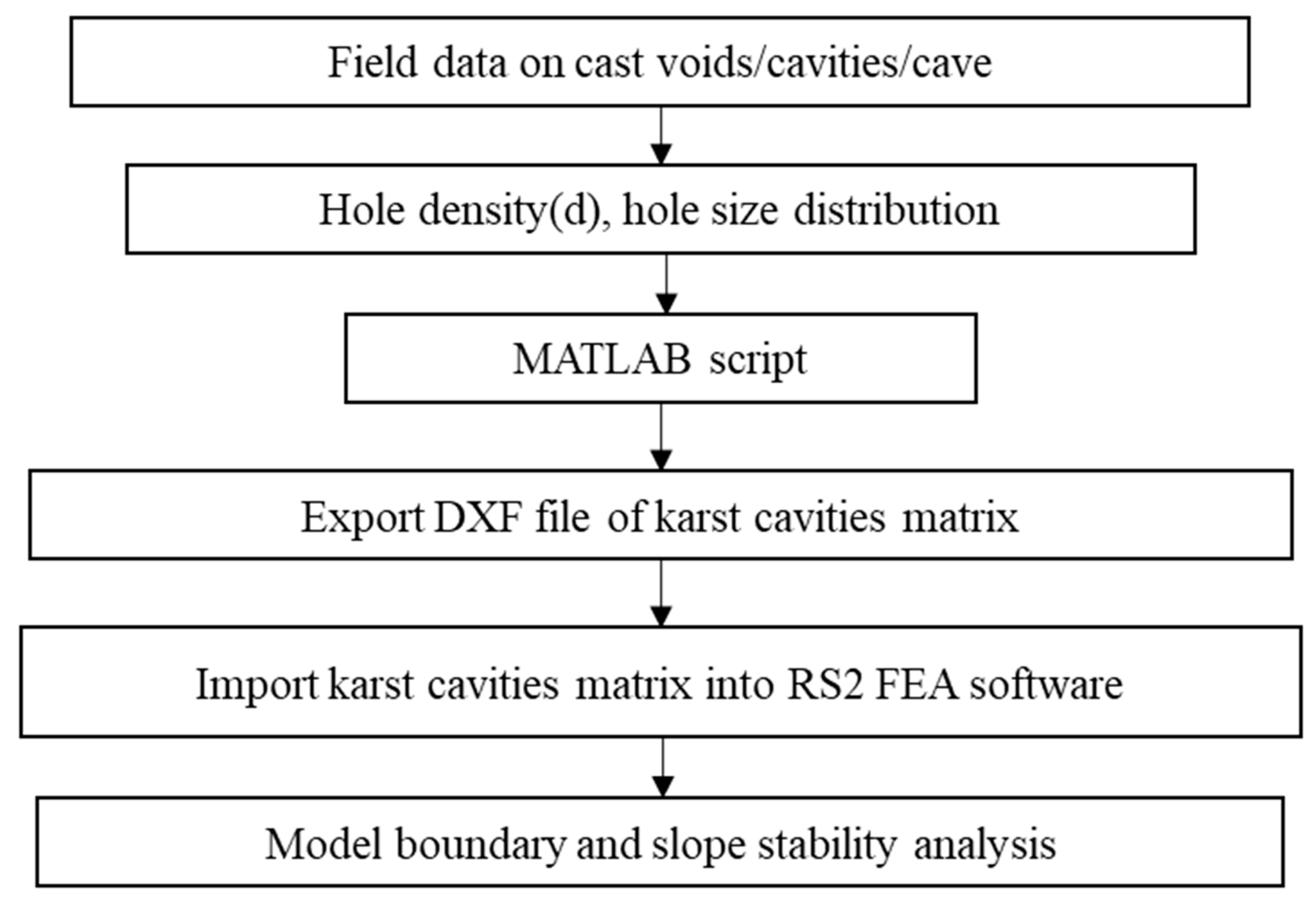
2.2. Generating the Equivalent Porous Medium
2.2.1. Karst Data Collection
2.2.2. Generating the EPM Matrix in MATLAB
- (i)
- Major caves or large karst features have already been identified through prior mapping and are modeled explicitly if necessary;
- (ii)
- All voids are assumed to be unfilled (air-filled, with no internal support);
- (iii)
- The analysis focuses on the void area, not the precise shape, assuming that mechanical effects are area-dominant at the scale of interest.
2.3. Model Setup in RS2
2.4. Material Properties and Parameters
2.5. Seepage Modeling
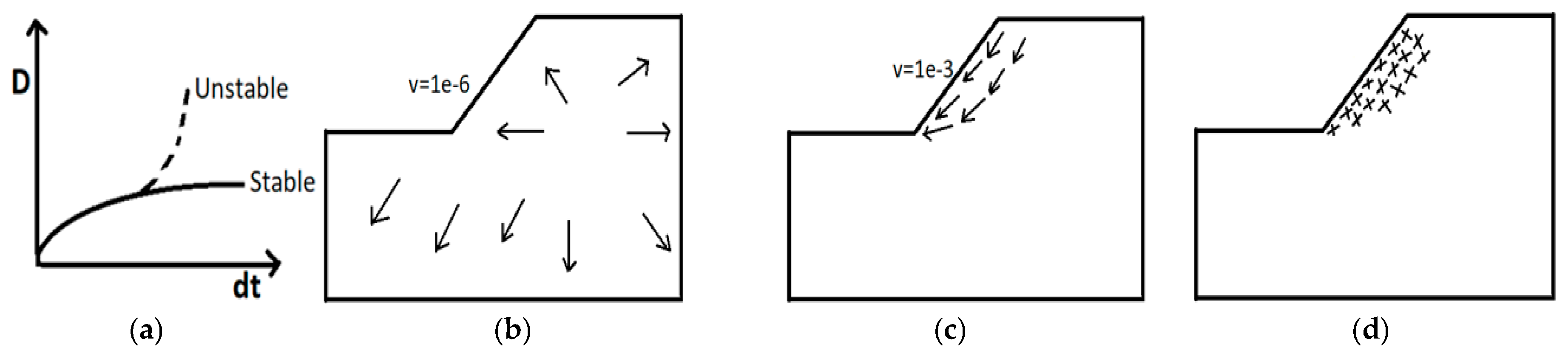
2.6. Simulation and Failure Evaluation
2.7. Interpretation of RS2 Analysis Results
3. Results
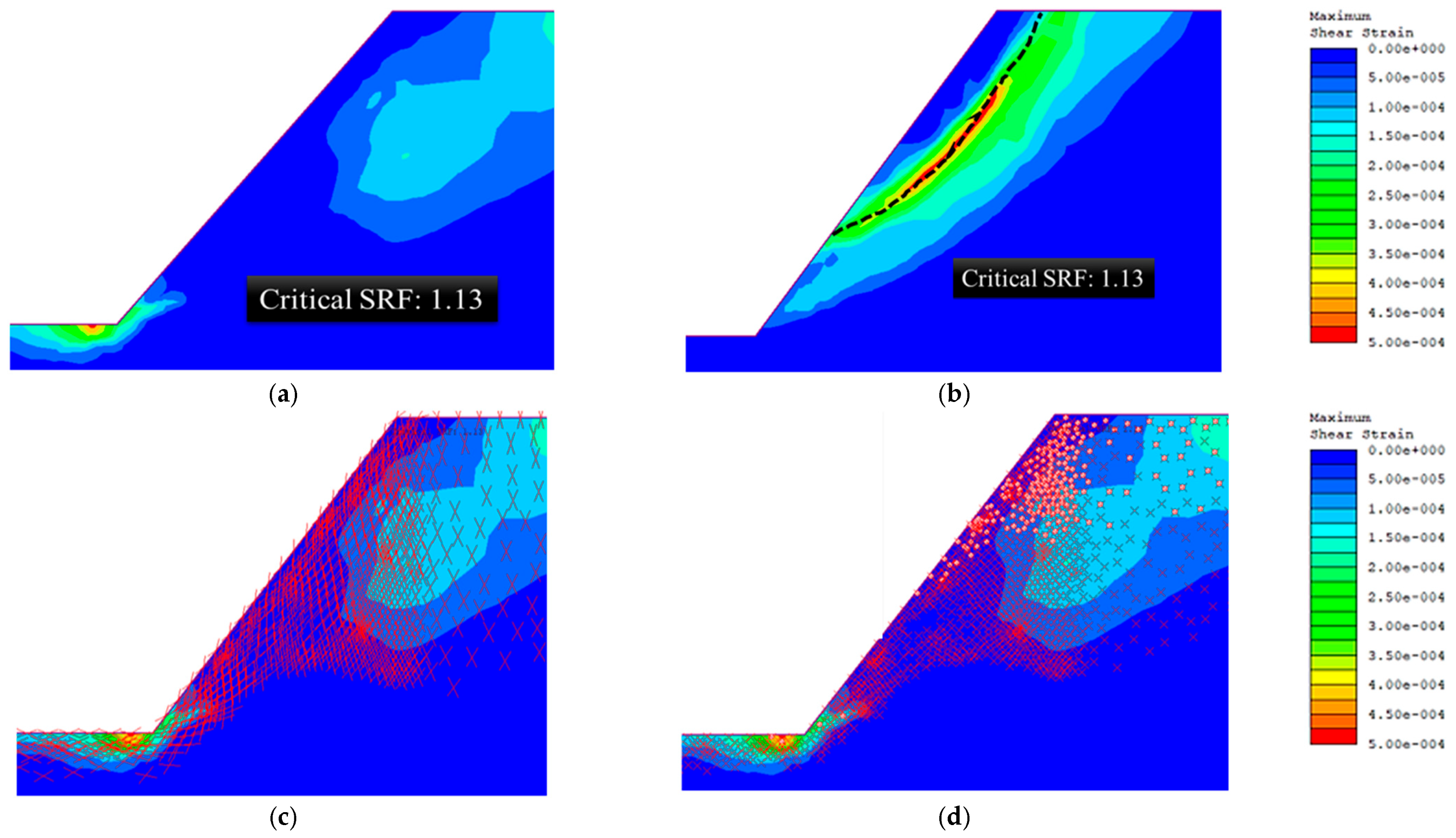
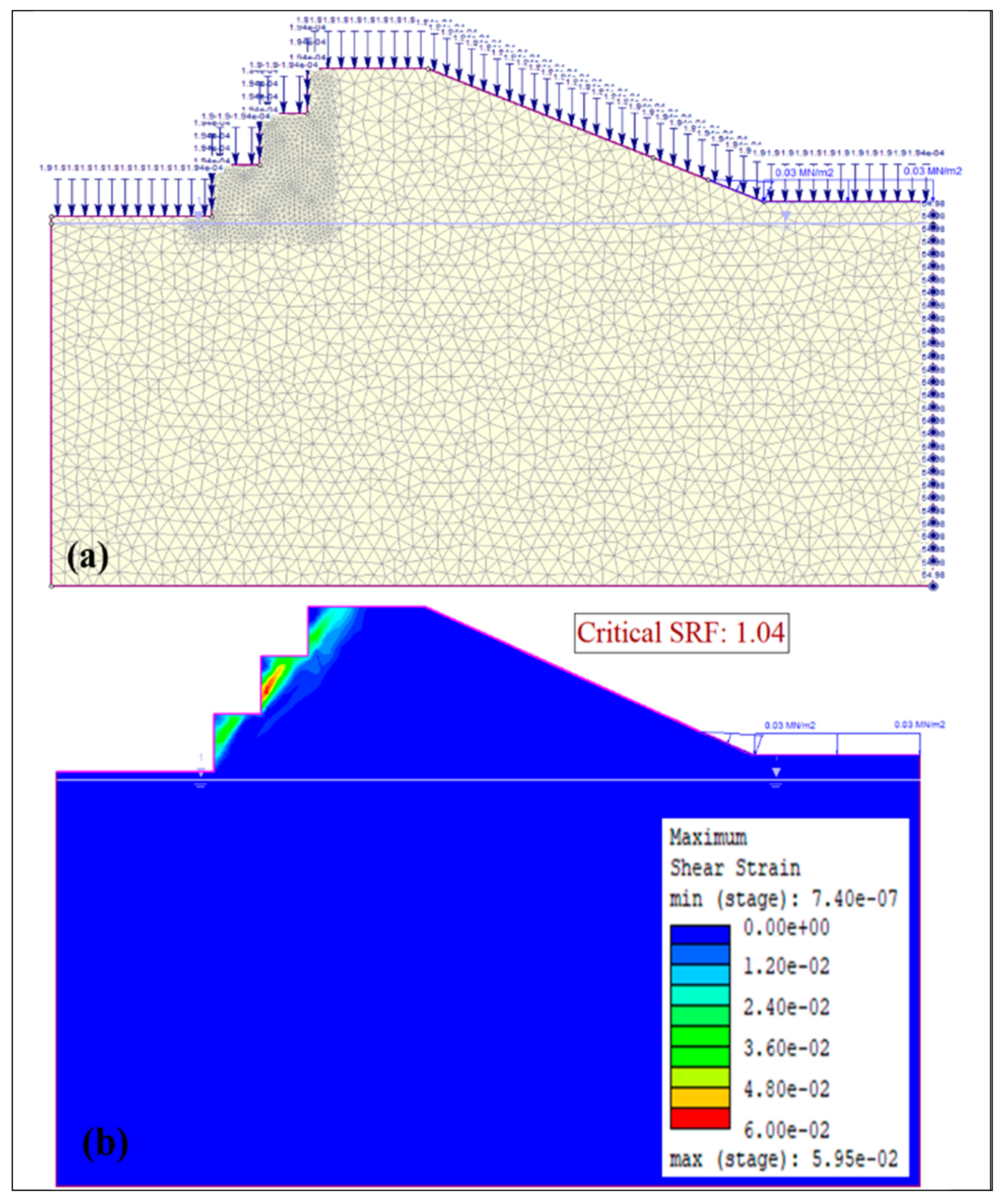
3.1. Stability Condition of Dry Slope in the Absence of Karst
3.2. Slope Stability Condition Under Seepage Boundary Conditions
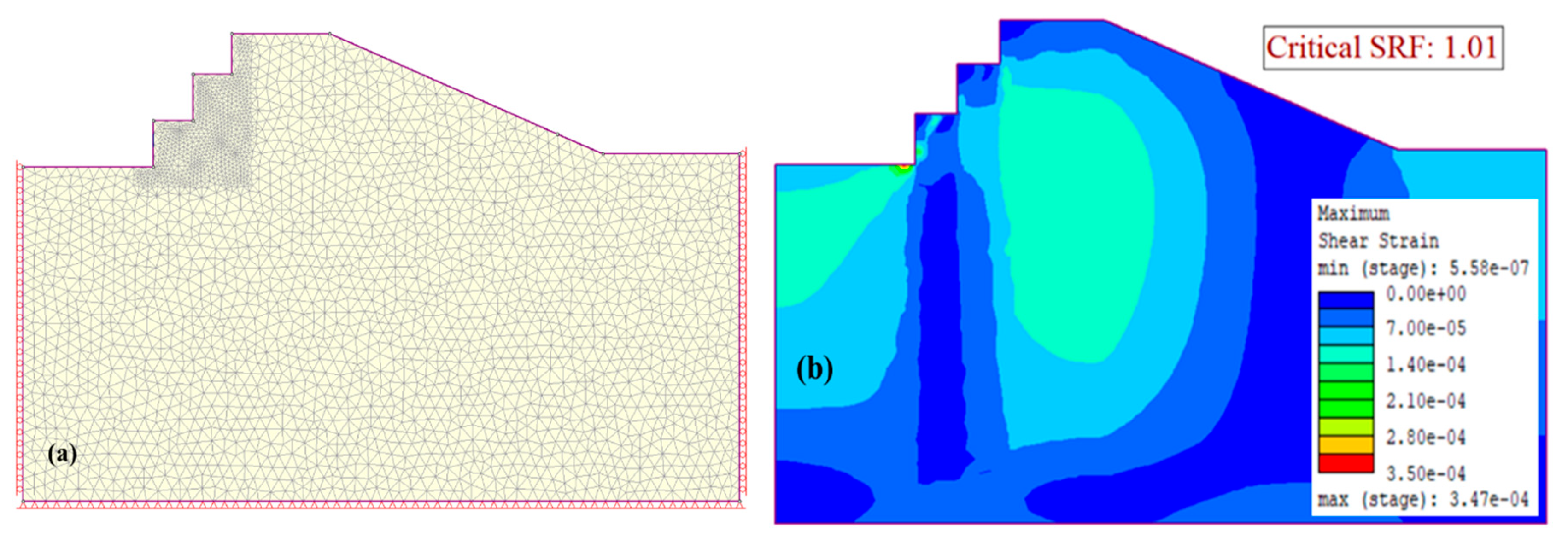
3.3. Slope Stability Condition with Karst Hollows
3.4. Slope Stability Condition with Karst Hollows and Seepage Boundary Conditions
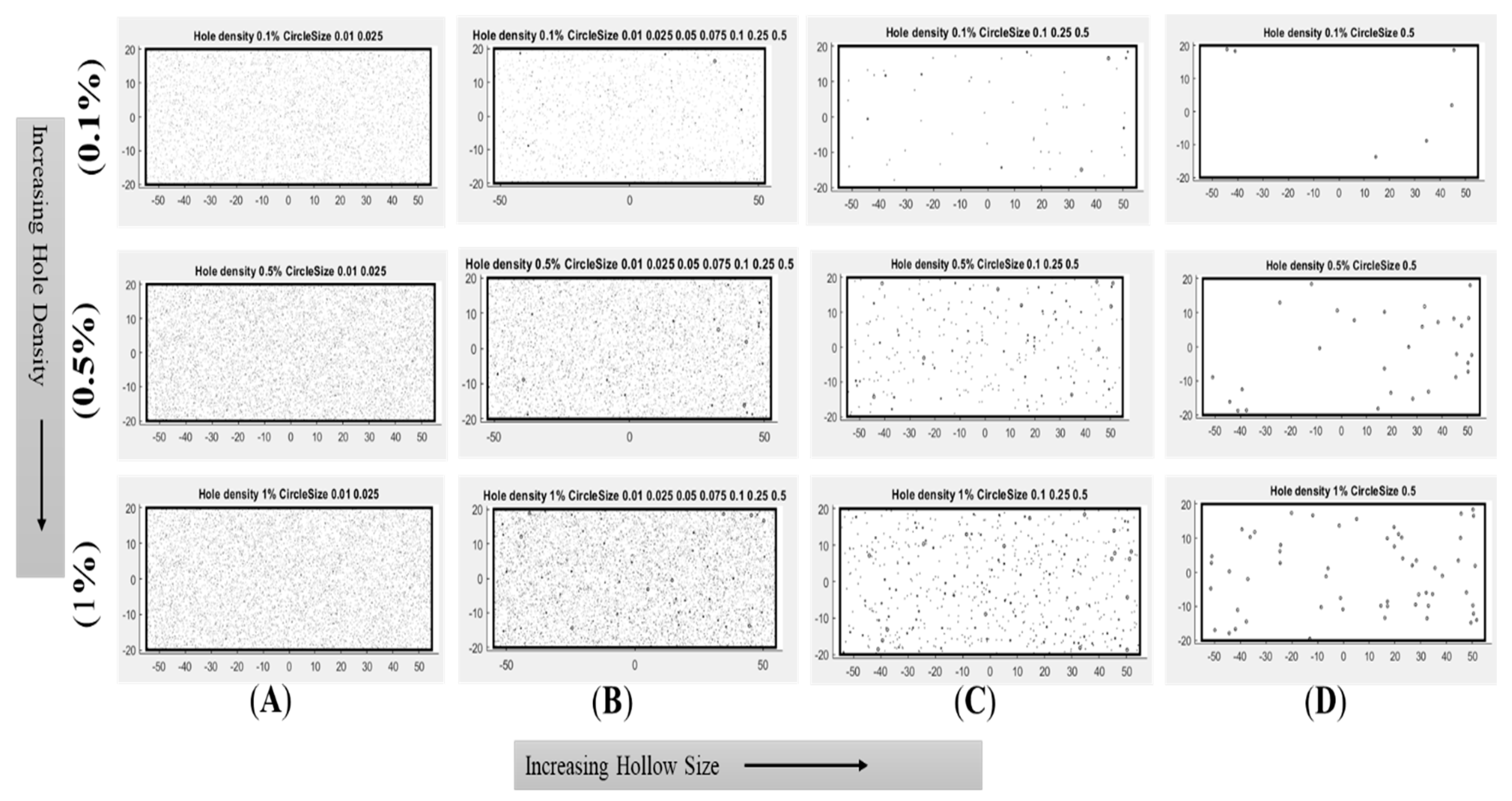
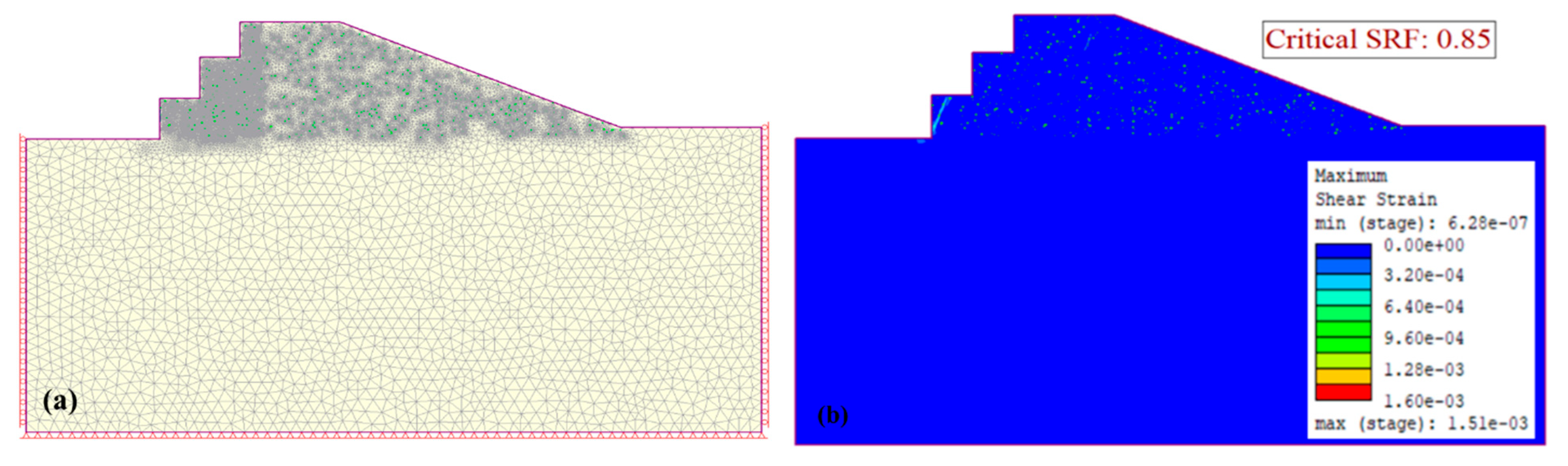
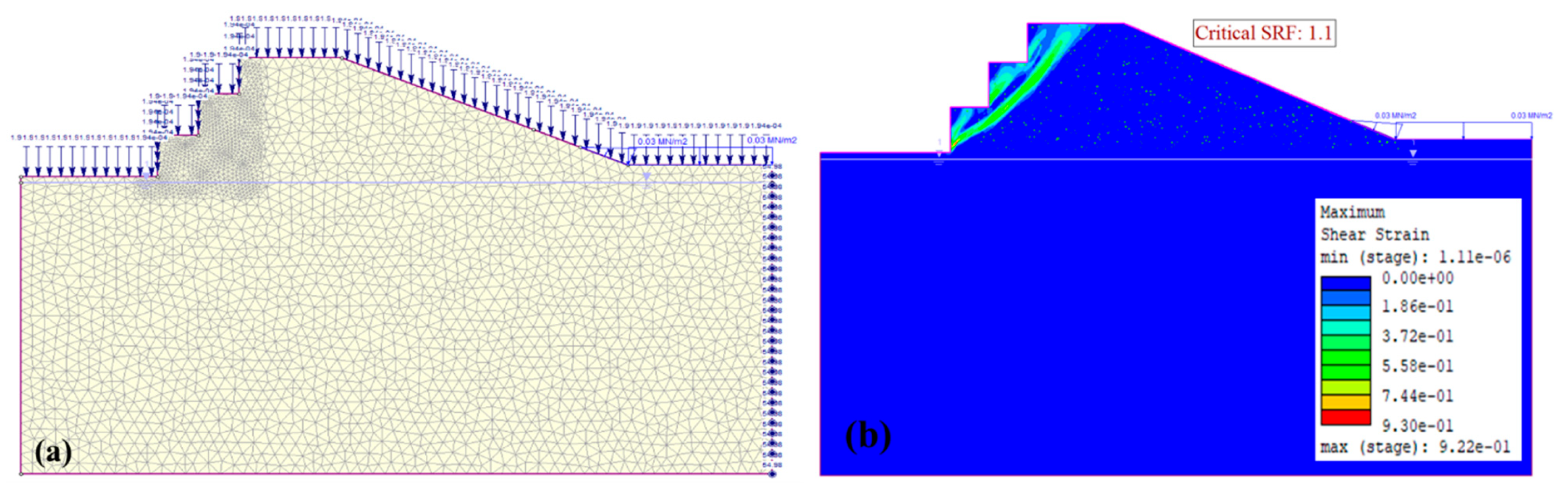
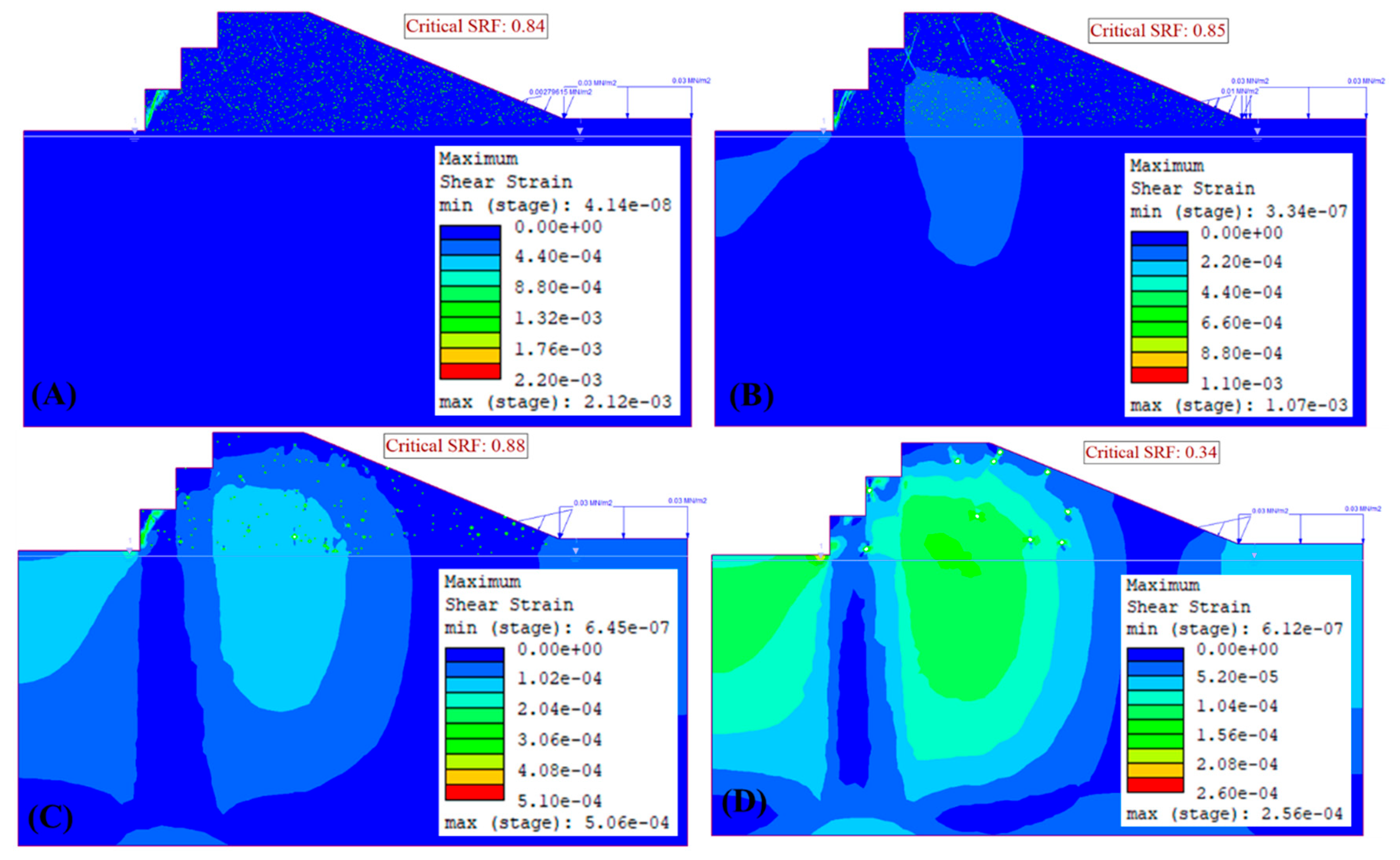
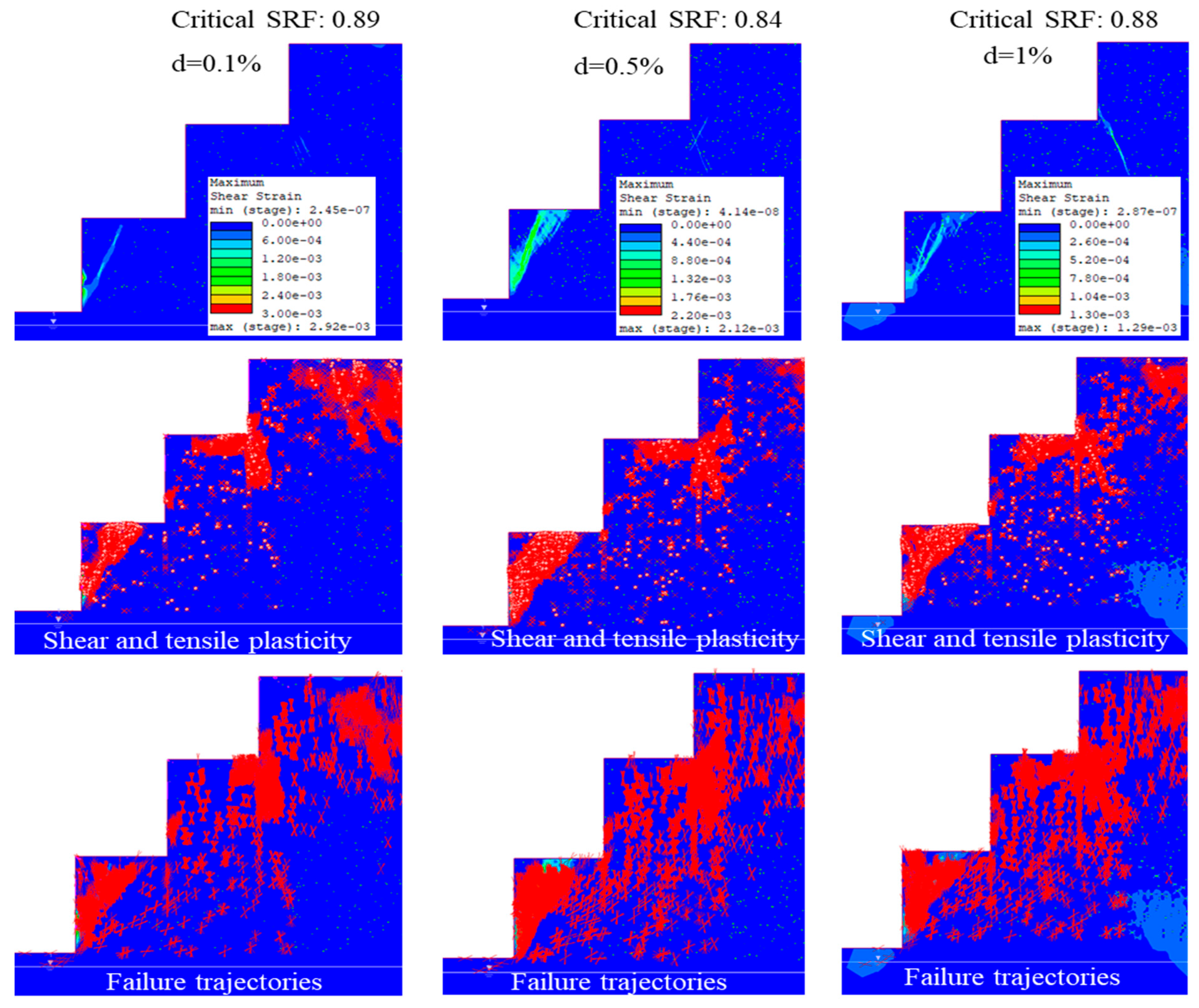
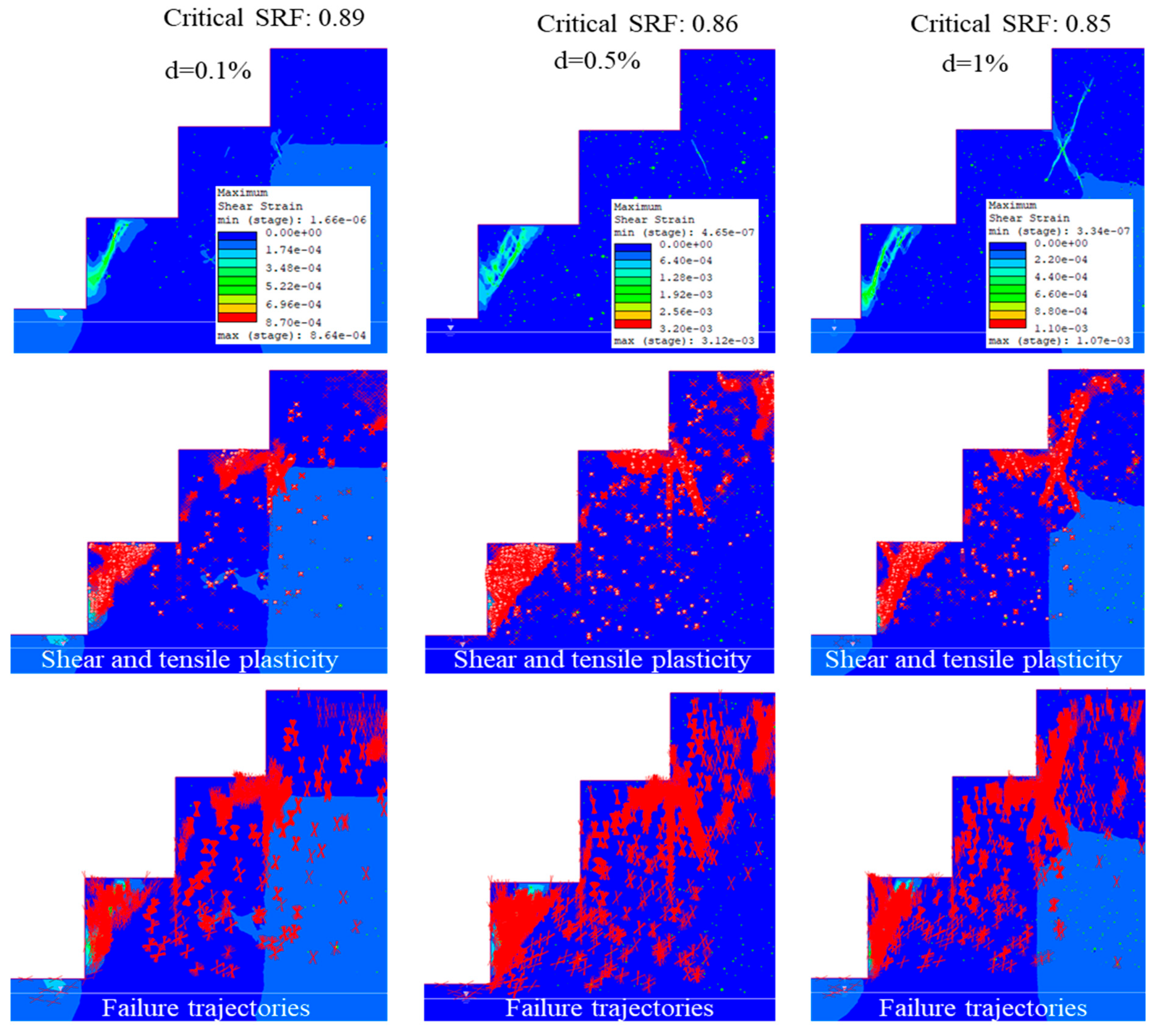
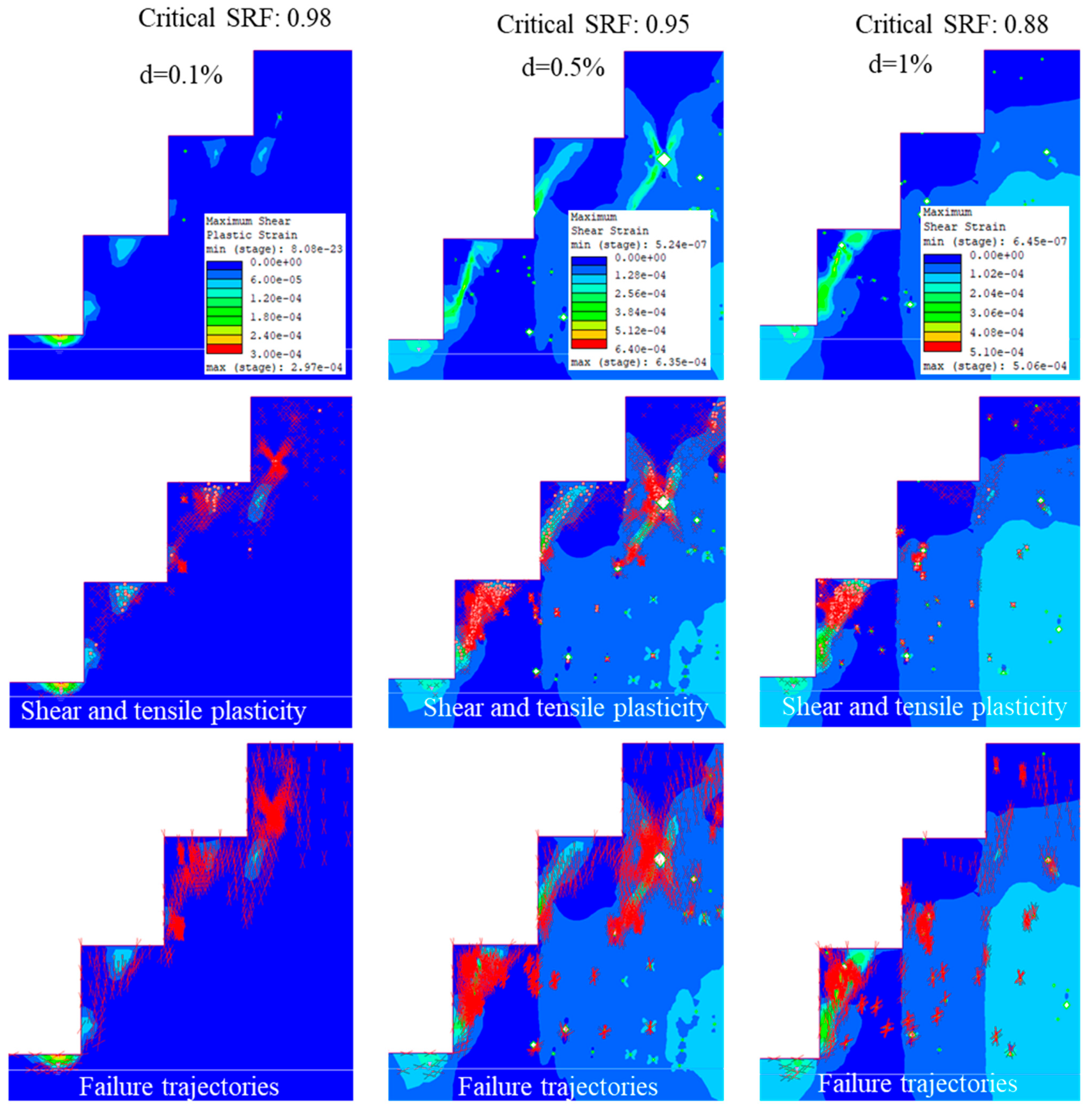
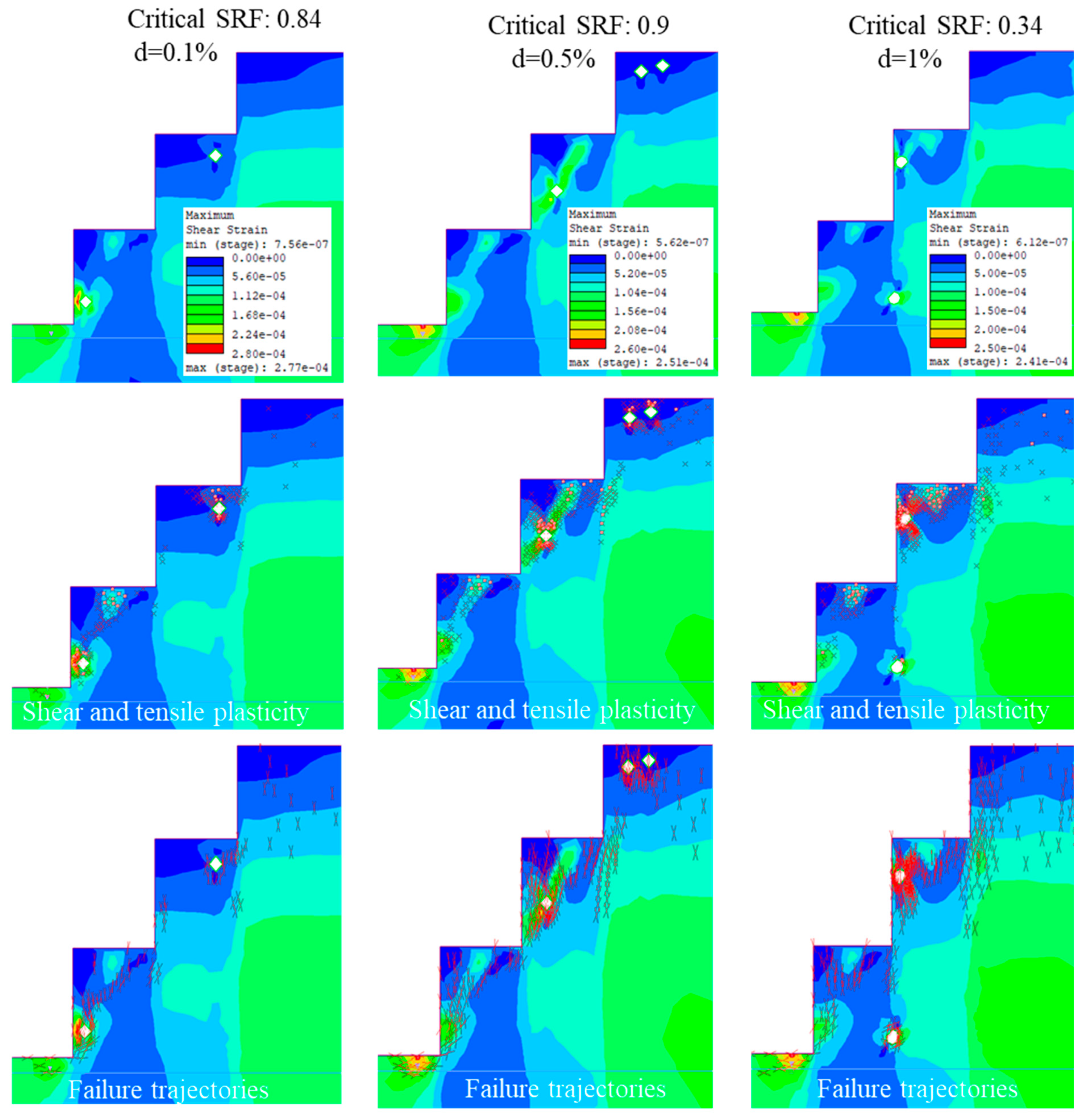
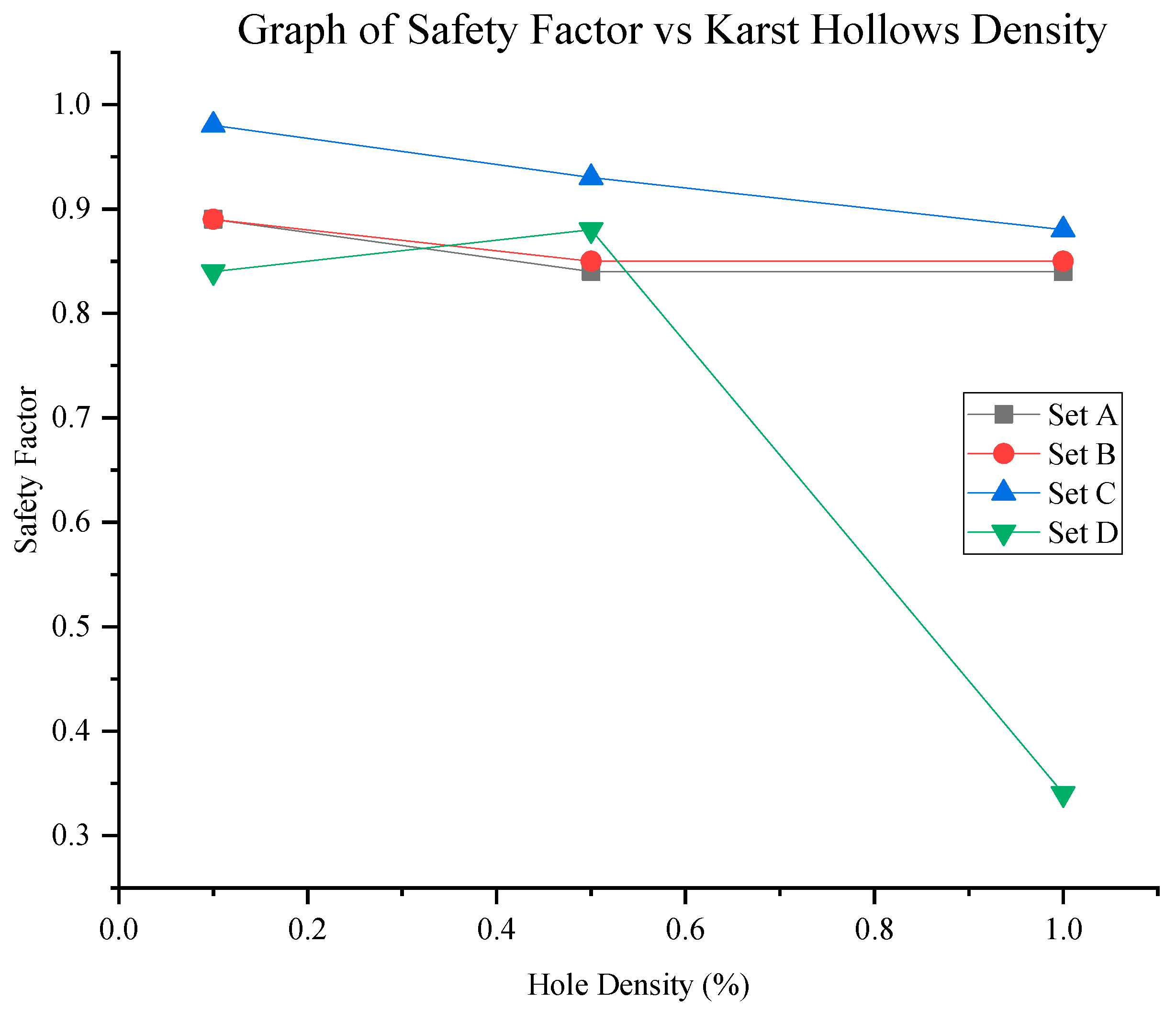
3.5. Influence of Karst Void Density on Slope Stability
3.5.1. Karst Hollows Density of 0.1%
3.5.2. Karst Hollows Density of 0.5%
3.5.3. Karst Hollows Density of 1%
3.6. Variation of Safety Factor with GSI
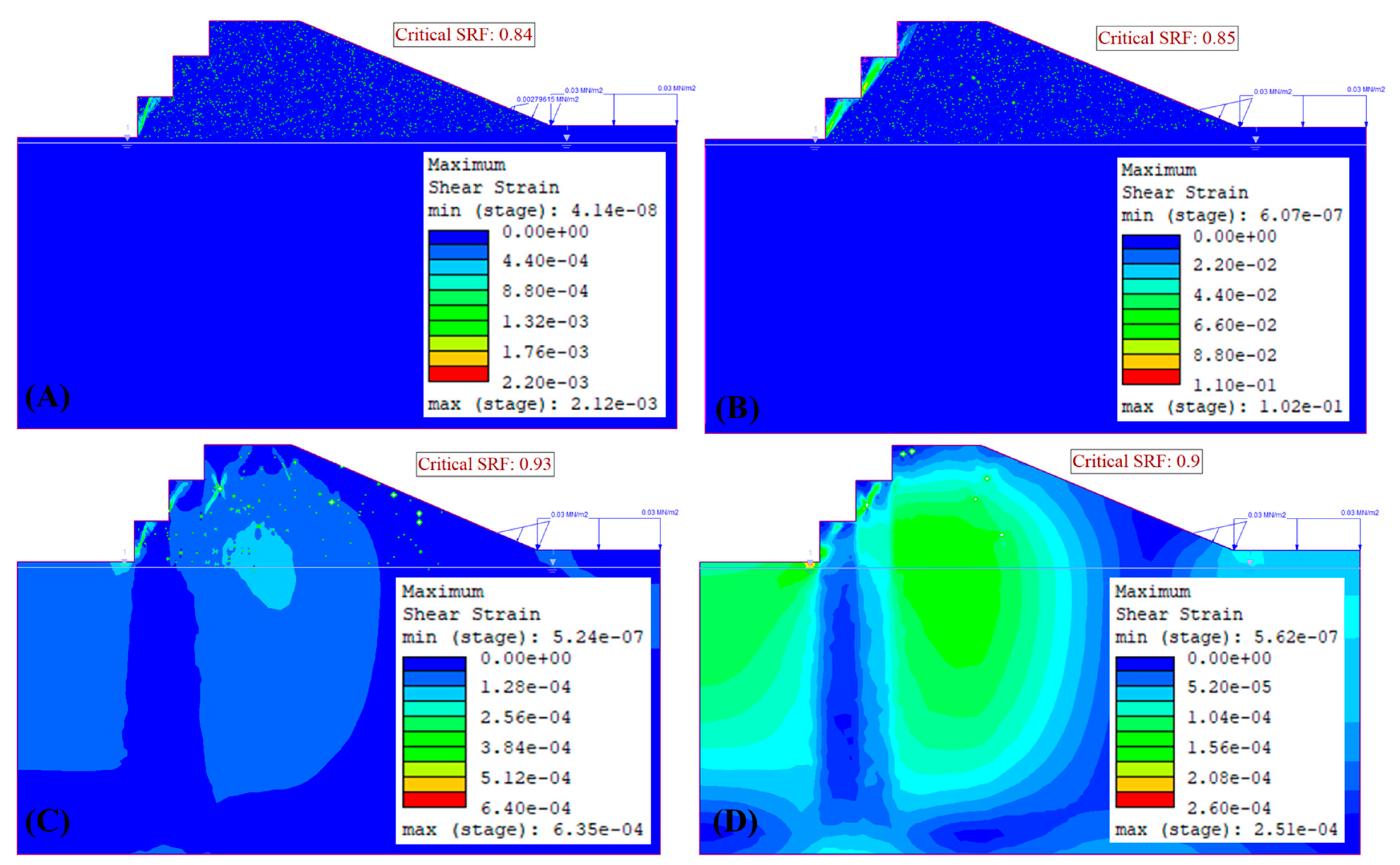
3.7. Failure Modes/Failure Trajectories Observed
3.7.1. Failure in Set A
3.7.2. Failure in Set B
3.7.3. Failure in Set C
3.7.4. Failure in Set D
3.8. Correlation of Numerical Results with Field Observations
4. Discussion
4.1. General Impact of Karst Hollows on Slope Stability
4.2. Combined Impact of Karst Hollows and Water Seepage
4.3. Variation of Karst Hollows Sizes and Densities
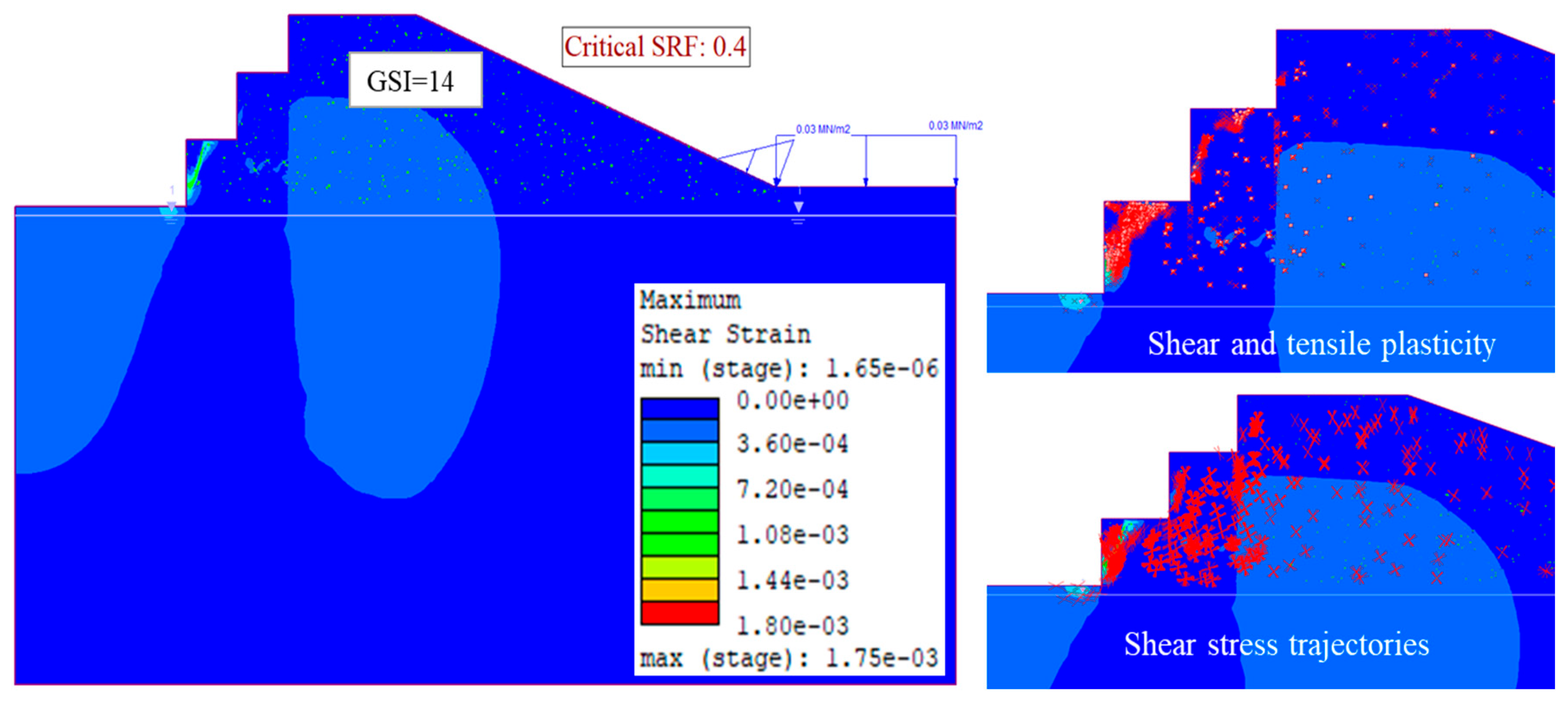
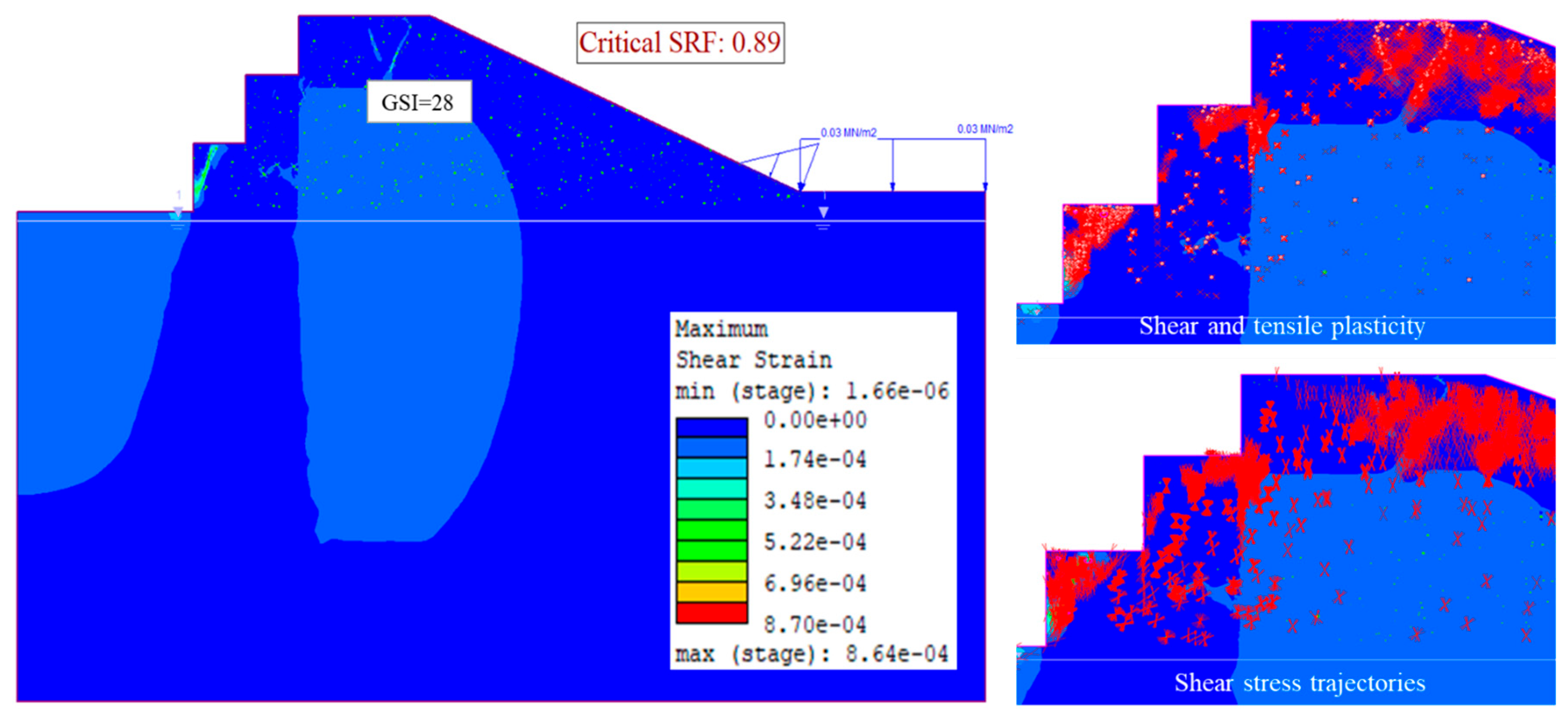
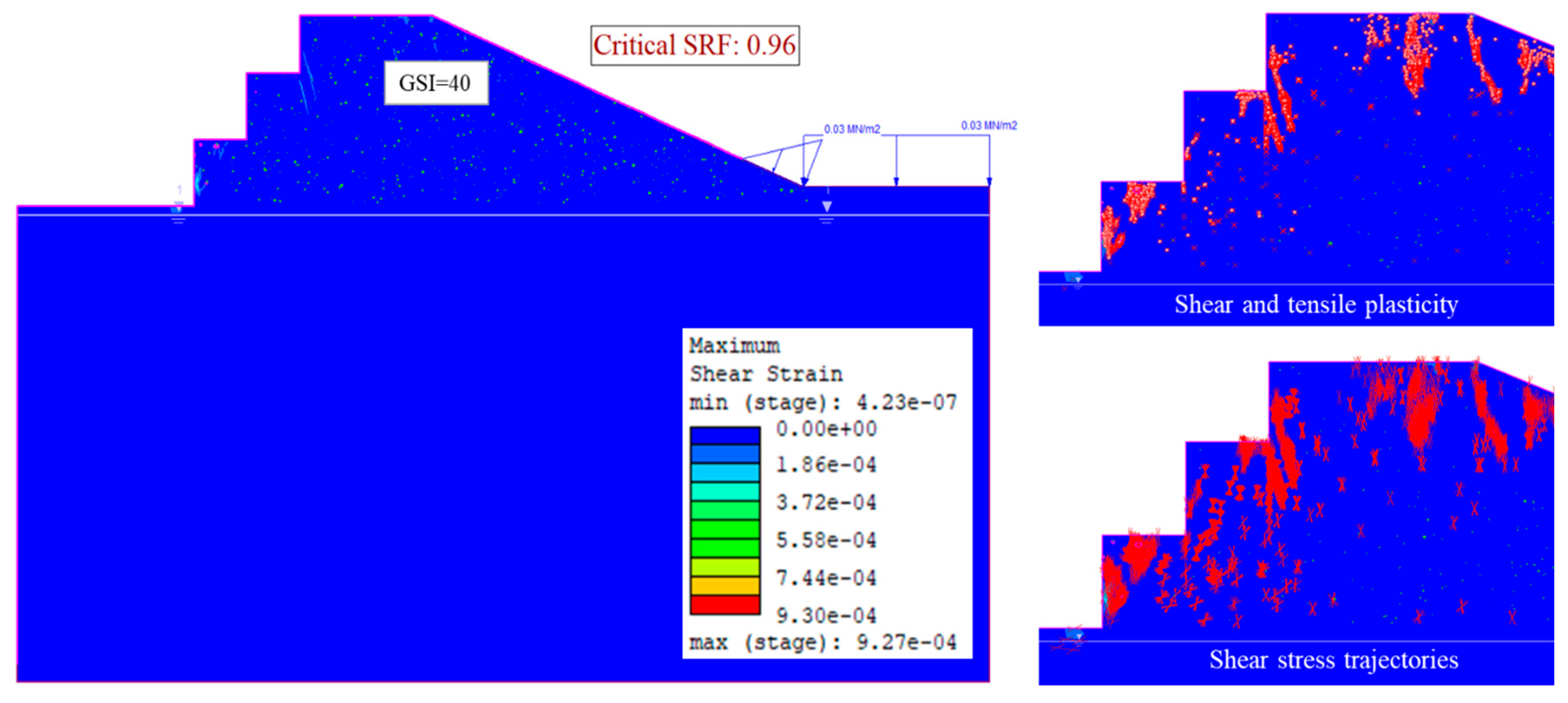
4.4. Relationship Between Karst Hollows and GSI
4.5. Failure Mode Evolution
4.6. Influence of Fractures on Rock Mass Response
4.7. Measures for Improving Slope Stability
4.8. Limitations and Future Work
4.8.1. Challenges Encountered
- ⮚
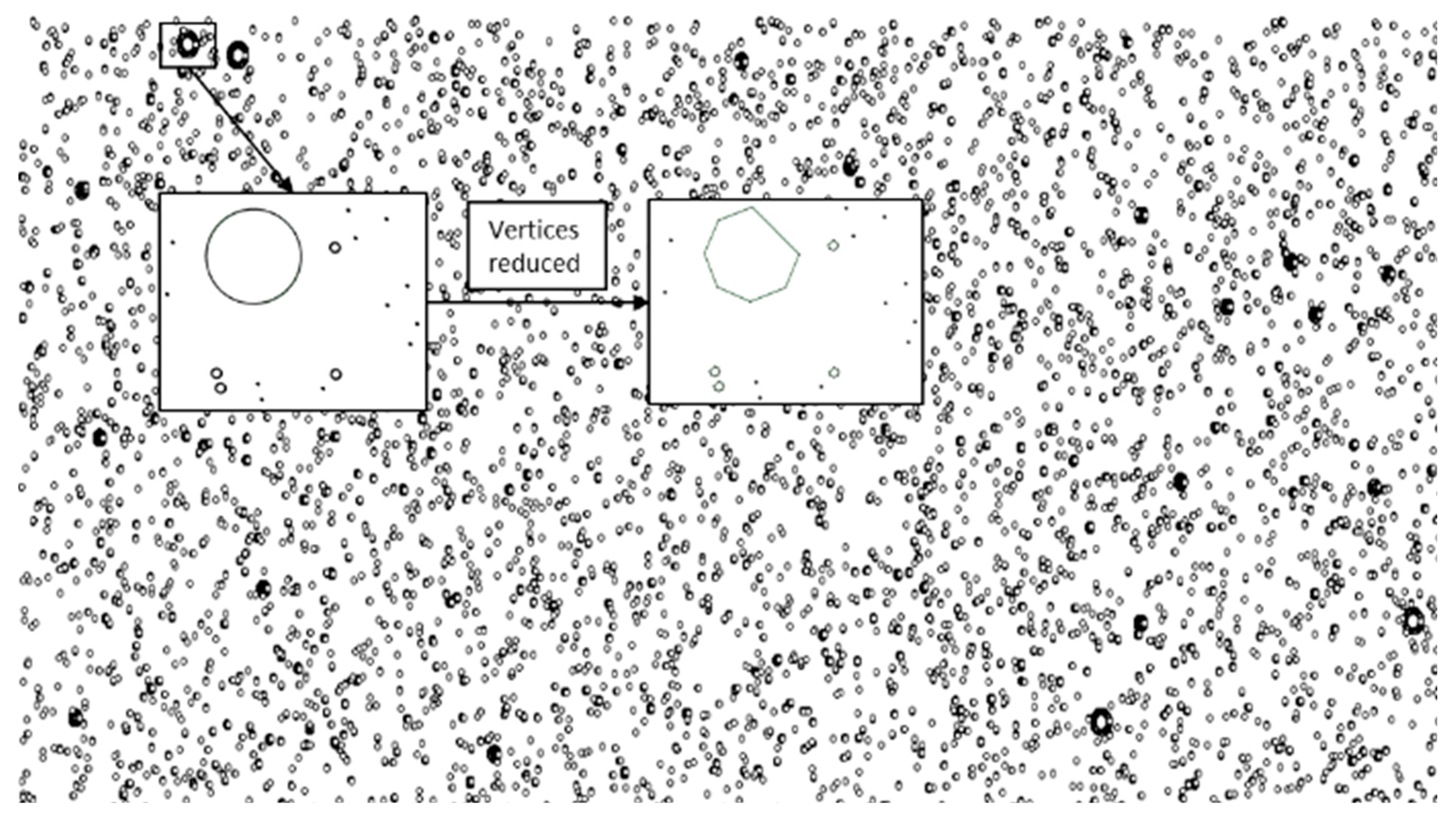
- The primary challenge was balancing modeling complexity with computational feasibility. RS2’s import of detailed karst geometries from DXF files resulted in numerous vertices, making the model bulky and slowing the simulation. Some models crashed at the onset of simulation. To address this, the number of vertices was reduced, preserving total area but simplifying shape, which may have slightly affected local stress redistribution.
- ⮚
- At higher void densities (>1%), simulations struggled to converge due to geometric complexity from closely packed voids, causing mesh distortion and localized strain accumulation. This limited the range of densities that could be practically simulated.
4.8.2. Recommendations for Future Work
- ⮚
- Future studies should further investigate the effect of void shape. While this study focused on void area, comparing circular, elliptical, or irregular shapes could clarify how geometry influences local stress redistribution and failure propagation.
- ⮚
- Coupling the EPM approach with discrete fracture models would be valuable, especially where joints and cavities interact, to simulate failure more realistically in anisotropic or fractured rock masses.
- ⮚
- Machine learning algorithms could be trained on existing karst data to identify spatial patterns and inform stochastic generation of void fields in numerical models, reducing manual parameterization and increasing representativeness.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chalikakis, K.; Plagnes, V.; Guerin, R.; Valois, R.; Bosch, F.P. Contribution of geophysical methods to karst-system exploration: An overview. Hydrogeol. J. 2011, 19, 1169–1180. [Google Scholar] [CrossRef]
- El Aal, A.A. Identification and characterization of near surface cavities in Tuwaiq Mountain Limestone, Riyadh, KSA, “detection and treatment”. Egypt. J. Pet. 2017, 26, 215–223. [Google Scholar] [CrossRef]
- Yilmaz, I.; Marschalko, M.; Bednarik, M. Gypsum collapse hazards and importance of hazard mapping. Carbonates Evaporites 2011, 26, 193–209. [Google Scholar] [CrossRef]
- Parise, M.; Ravbar, N.; Živanović, V.; Mikszewski, A.; Kresic, N.; Mádl-Szőnyi, J.; Kukurić, N. Hazards in Karst and Managing Water Resources Quality. In Karst Aquifers—Characterization and Engineering; Stevanović, Z., Ed.; Professional Practice in Earth Sciences; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kuhn, A.K. Geotechnical considerations in surface mine reclamation. In Mining and Reclamation in the Next Millennium, Proceedings of the 16th Annual National Meeting of the American Society for Surface Mining Reclamation, Scottsdale, AZ, USA, 1 July 1999; American Society for Surface Mining and Reclamation: Blacksburg, VA, USA, 1999. [Google Scholar]
- Youssef, A.M.; El-Shater, A.-H.; El-Khashab, M.H.; El-Haddad, B.A. Karst Induced Geo-hazards in Egypt: Case Study Slope Stability Problems Along Some Selected Desert Highways. In Engineering Geology and Geological Engineering for Sustainable Use of the Earth’s Resources, Urbanization and Infrastructure Protection from Geohazards; International Congress and Exhibition Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Jiang, J.; Zhang, Z.; Wang, D.; Wang, L.; Han, X. Web pillar stability in open-pit highwall mining. Int. J. Coal Sci. Technol. 2022, 9, 12. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z.; Zhang, Y.; Wang, D. The weakening mechanisms of the rock mechanics of marlite bank slopes under water–rock interaction conditions. Carbonates Evaporites 2020, 35, 60. [Google Scholar] [CrossRef]
- Sasaoka, T.; Karian, T.; Hamanaka, A.; Shimada, H.; Matsui, K.; Ichinose, M. Effect of Mine Water on the Stability of Underground Coal Mine Roadways. Geotech. Geol. Eng. 2016, 34, 671–678. [Google Scholar] [CrossRef]
- Supandi. The Influence of Water Balance for Slope Stability on the High Mine Waste Dump. Geotech. Geol. Eng. 2021, 39, 5253–5266. [Google Scholar] [CrossRef]
- Jele, R.; Dunn, M. Economic Significance of Geotechnical Uncertainties In MGR 2019, Proceedings of the First International Conference on Mining Geomechanical Risk; Australian Centre for Geomechanics: Perth, Australia, 2019. [Google Scholar]
- Kannan, R.C. Designing Foundations Around Sinkholes. Eng. Geol. 1999, 52, 75–82. [Google Scholar] [CrossRef]
- Al-Halbouni, D.; Holohan, E.P.; Taheri, A.; Schöpfer, M.P.J.; Emam, S.; Dahm, T. Geomechanical modelling of sinkhole development using distinct elements. Solid Earth 2018, 9, 1341–1373. [Google Scholar] [CrossRef]
- Ford, D.C.; Ewers, R.O. The development of limestone cave systems in the dimensions of length and depth. Can. J. Earth Sci. 1978, 15, 1783–1798. [Google Scholar] [CrossRef]
- El Aal, A.K.A.; Nabawy, B.S.; Aqeel, A.; Abidi, A. Geohazards assessment of the karstified limestone cliffs for safe urban constructions, Sohag, West Nile Valley, Egypt. J. Afr. Earth Sci. 2020, 161, 103671. [Google Scholar] [CrossRef]
- Onyango, J.A.; Moses, D.N. Karst-Induced Geoharzards in Kenya’s Coastal Region: A Case Study of Vipingo Coral Limestone Quarry. Eur. J. Environ. Earth Sci. 2021, 2, 5–17. [Google Scholar] [CrossRef]
- Andriani, G.F.; Parise, M. On the applicability of geomechanical models for carbonate rock masses interested by karst processes. Environ. Earth Sci. 2015, 74, 7813–7821. [Google Scholar] [CrossRef]
- Fleurisson, J.-A. Slope Design and Implementation in Open Pit Mines: Geological and Geomechanical Approach. Procedia Eng. 2012, 46, 27–38. [Google Scholar] [CrossRef]
- Fleurisson, J.-A.; Cojean, R. Error Reduction in Slope Stability Assessment. In Surface Mining Methods, Technology and Systems; Wide: Fontainebleau, France, 2014; Volume 1, p. 41. [Google Scholar]
- Shapka-Fels, T.; Elmo, D. Numerical Modelling Challenges in Rock Engineering with Special Consideration of Open Pit to Underground Mine Interaction. Geosciences 2022, 12, 199. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, Z.; Jiang, Y.; Chen, M.; Liu, J.; Yin, Q. Effect of Hole Density and Confining Pressure on Mechanical Behavior of Porous Specimens: An Insight from Discrete Element Modeling. Comput. Model. Eng. Sci. 2020, 125, 259–280. [Google Scholar] [CrossRef]
- Han, Y.; Hu, D.; Matzar, L. Numerical computation of elastic properties for porous rocks based on CT-scanned images using direct mapping method. J. Pet. Sci. Eng. 2014, 122, 346–353. [Google Scholar] [CrossRef]
- Hertel, S.A.; Rydzy, M.; Anger, B.; Berg, S.; Appel, M.; Jong, H.D. Upscaling of Digital Rock Porosities by Correlation with Whole-Core CT-Scan Histograms. Petrophysics SPWLA J. Form. Eval. Reserv. Descr. 2018, 59, 694–702. [Google Scholar] [CrossRef]
- Liu, S.; Wang, H.; Xu, W.; Cheng, Z.; Xiang, Z.; Xie, W.-C. Numerical Investigation of the Influence of Rock Characteristics on the Soil-Rock Mixture (SRM) Slopes Stability. KSCE J. Civ. Eng. 2020, 24, 3247–3256. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, P.; Ma, G.; Fan, W.; Meng, J.; Li, K. A New Methodology for Open Pit Slope Design in Karst-Prone Ground Conditions Based on Integrated Stochastic-Limit Equilibrium Analysis. Rock Mech. Rock Eng. 2016, 49, 2737–2752. [Google Scholar] [CrossRef]
- Li, B.; Lin, Z.; Chen, Y.; Xu, C.; Li, P.; Ding, H. Numerical analysis for supporting and deformation of complex foundation pit groups in unstable areas of karst strata. Front. Earth Sci. 2023, 11, 1283184. [Google Scholar] [CrossRef]
- Zou, Y.; Tang, Q.; Peng, L. Stability Analysis and Instability Time Prediction of Tunnel Roofs in a Karst Region Based on Catastrophe Theory. Appl. Sci. 2025, 15, 978. [Google Scholar] [CrossRef]
- Sheng, M.; Lu, F.; Jiang, N.; Guo, P.; Li, X.; An, R.; Wang, Y. Bearing behavior of pile foundation in karst region: Physical model test and finite element analysis. Appl. Rheol. 2024, 34, 20230115. [Google Scholar] [CrossRef]
- Wang, F.; Zhai, W.; Man, J.; Huang, H. A hybrid cohesive phase-field numerical method for the stability analysis of rock slopes with discontinuities. Can. Geotech. J. 2025, 62, 1–16. [Google Scholar] [CrossRef]
- Aminpour, M.; Alaie, R.; Khosravi, S.; Kardani, N.; Moridpour, S.; Nazem, M. Slope stability machine learning predictions on spatially variable random fields with and without factor of safety calculations. Comput. Geotech. 2023, 153, 105094. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, J. Analysis of Slope Stability Based on Four Machine Learning Models: An Example of 188 Slopes. Period. Polytech. Civ. Eng. 2025, 69, 505–518. [Google Scholar] [CrossRef]
- Onyango, J.A. Rock Mass Classification of Limestone Considering Karst Formation and Its Application to Evaluation of Slope Stability in Open Pit Limestone Quarry. Ph.D. Thesis, Kyushu University Institutional Repository, Fukuoka, Japan, 2024. [Google Scholar]
- Bishop, A.W. The use of the Slip Circle in the Stability Analysis of Slopes. Geotech. 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Aladejare, A.E.; Akeju, V.O. Design and Sensitivity Analysis of Rock Slope Using Monte Carlo Simulation. Geotech. Geol. Eng. 2019, 38, 573–585. [Google Scholar] [CrossRef]
- Sasowsky, I.; Bishop, M. Empirical Study of Conduit Radial Cross-Section Determination and Representation Methods On Cavernous Limestone Porosity Characterization. J. Cave Karst Stud. 2006, 68, 130–136. [Google Scholar]
- Jouves, J.; Viseur, S.; Arfib, B.; Baudement, C.; Camus, H.; Collon, P.; Guglielmi, Y. Speleogenesis, geometry, and topology of caves: A quantitative study of 3D karst conduits. Geomorphology 2017, 298, 86–106. [Google Scholar] [CrossRef]
- Martin, D.; Stacey, P. Guidelines for Open Pit Slope Design in Weak Rocks; CRC Press; Taylor & Francis Group: New York, NY, USA, 2018. [Google Scholar]
- Rocscience. Stress Trajectories. 2023. Available online: https://www.rocscience.com/help/rs2/documentation/rs2-interpret/viewing-and-display-options/stress-trajectories (accessed on 9 September 2023).
- Onyango, J.A.; Sasaoka, T.; Shimada, H.; Hamanaka, A.; Moses, D. Stability Assessment of the Slopes of an Oceanside Coral Limestone Quarry under Drawdown Condition of Semidiurnal Ocean Tides. Mining 2022, 2, 589–615. [Google Scholar] [CrossRef]
- Wu, D.; Shen, F. Stability assessment of coastal clay slopes considering strength nonlinearity and sea level drawdown. Mar. Georesour. Geotechnol. 2023, 41, 476–492. [Google Scholar] [CrossRef]
- Vacher, H.L.; Bengtsson, T.O. Effect of Hydraulic Conductivity on the Residence Time of Meteoric Ground Water in Bermudian and Bahamian-type Islands. In Proceedings of the Fourth Symposium on the Geology of the Bahamas, San Salvador, Bahamas, 17–22 June 1988. [Google Scholar]
- Zengin, E.; Erguler, Z.A. Experimental investigation of pore-fracture relationship on failure behaviour of porous rock materials. Bull. Eng. Geol. Environ. 2022, 81, 351. [Google Scholar] [CrossRef]
- Lee, H.J.; Locat, J.; Desgagnés, P.; Parsons, J.D.; McAdoo, B.G.; Orange, D.L.; Pere, P.; Wong, F.L.; Dartnell, P.; Boulanger, E. Submarine mass movements on continental margins. In Continental Margin Sedimentation: From Sediment Transport to Sequence Stratigraphy; Blackwell Publishing: Malden, MA, USA, 2007; pp. 213–274. [Google Scholar]
- Yang, Y.-C.; Xing, H.-G.; Yang, X.-G.; Chen, M.-L.; Zhou, J.-W. Experimental study on the dynamic response and stability of bedding rock slopes with weak interlayers under heavy rainfall. Environ. Earth Sci. 2018, 77, 433. [Google Scholar] [CrossRef]
- Caldwell, J.; Robertson, A. Geotechnical stability considerations in the design and reclamation of tailings impoundments. In Geotechnical Stability in Surface Mining; CRC Press: New York, NY, USA, 2022; pp. 255–258. [Google Scholar]
- Hansen, L.; LaFronz, N.; Yasin, M. Stabilization of the Pinto Valley tailings impoundment slide. In Tailings and Mine Waste 2000; CRC Press: New York, NY, USA, 2022; pp. 477–487. [Google Scholar]
- Wang, T.; Kang, Q.; Zhang, X.; Xu, X.; Li, W.; Zhang, H. Effects of hole structure on the mechanical properties and failure characteristics of random porous sandstone under uniaxial compression test. PLoS ONE 2022, 17, e0263387. [Google Scholar]
- Xu, J.; Wang, Y.; Yuan, B. Stability Analysis and Support Design Methods for Rock Foundation Pit with Combination of Structural Plane and Karst Cave. Adv. Civ. Eng. 2022, 1, 5662079. [Google Scholar] [CrossRef]
- Martino, S.; Prestininzi, A.; Scarascia Mugnozza, G. Geological-evolutionary model of a gravity-induced slope deformation in the carbonate Central Apennines (Italy). Q. J. Eng. Geol. Hydrogeol. 2004, 37, 31–47. [Google Scholar] [CrossRef]
- Qiu, J.; Huang, R.; Wang, H.; Wang, F.; Zhou, C. Rate-dependent tensile behaviors of jointed rock masses considering geological conditions using a combined BPM-DFN model: Strength, fragmentation, and failure modes. Soil Dyn. Earthq. Eng. 2025, 195, 109393. [Google Scholar] [CrossRef]
- Hamanakaa, A.; Inouea, N.; Shimadaa, H.; Sasaokaa, T.; Matsui, K.; Miyajima, I. Design of self-sustainable land surface against soil erosion at rehabilitation areas in open-cut mines in tropical regions. Int. J. Min. Reclam. Environ. 2015, 29, 305–315. [Google Scholar] [CrossRef]
- Huang, B.; Hanping, X.; Gang, D. Study on Application of Vetiver Eco-engineering Technique for Stabilization and Revegetation of Karst Stony Slopes. In Proceedings of the Third International Conference on Vetiver and Exhibition, Guangzhou, China, 6–9 October 2003. [Google Scholar]
- Moses, D.; Shimada, H.; Onyango, J.A.; Sasaoka, T.; Hamanaka, A. Slope design in brecciated carbonatite complexes under high-stress regimes. Bull. Eng. Geol. Environ. 2022, 81, 494. [Google Scholar] [CrossRef]
- Mgiba, C.; Rupprecht, S.M. Slope Stability Analysis and Design for Small-Scale Mines. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023. [Google Scholar]
- Barnett, W.P. Geological control on slope failure mechanisms in the open pit at the Venetia Mine. S. Afr. J. Geol. 2003, 106, 149–164. [Google Scholar] [CrossRef]


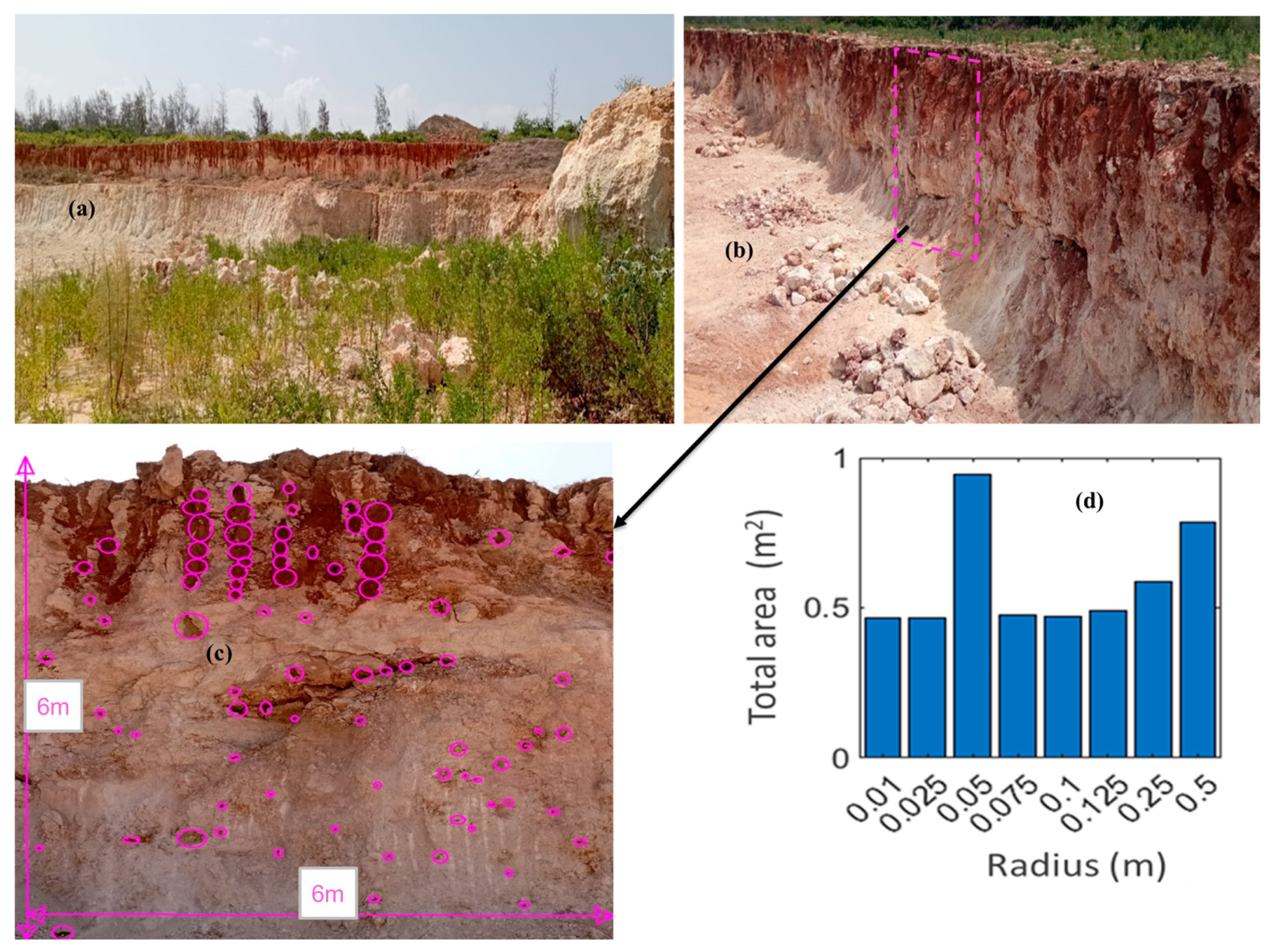
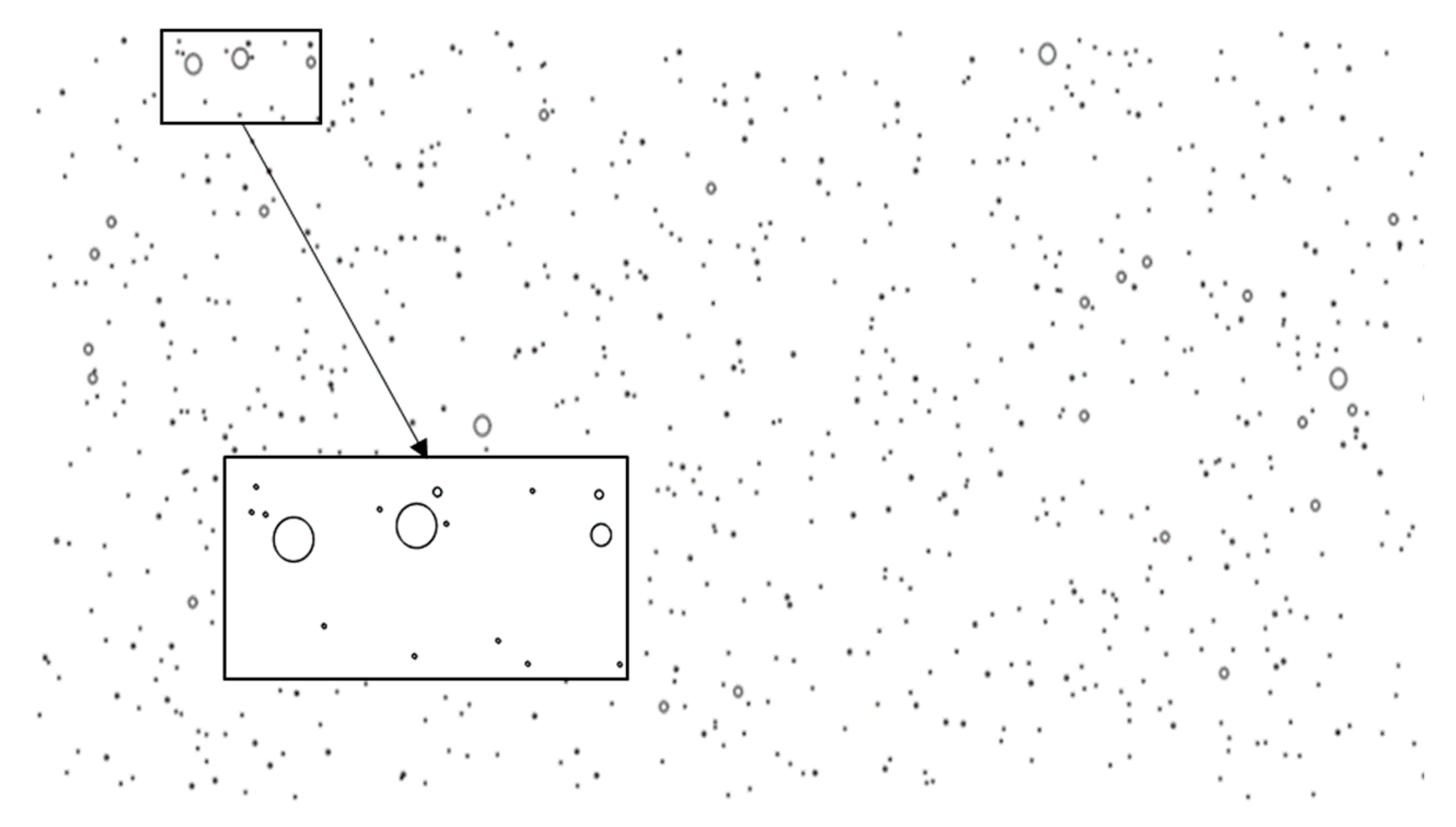
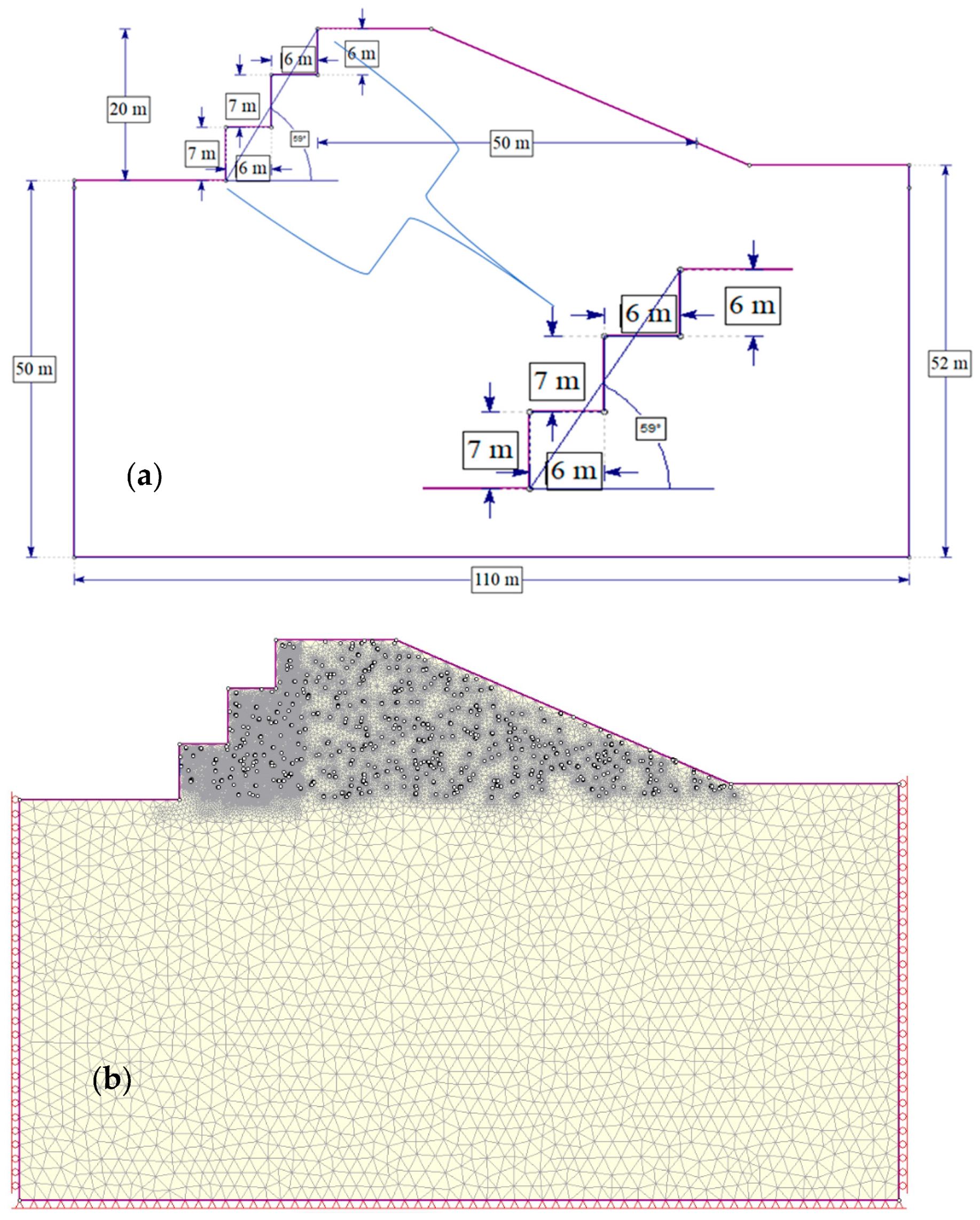




| Sampled Section | Sampling Area (m × m) | Total Void Area (m2) | Calculated Hollows Density, d (%) |
|---|---|---|---|
| Slope A | 6 × 6 | 0.0256 | 0.071 |
| Slope B | 6 × 6 | 0.0328 | 0.091 |
| Slope C | 6 × 6 | 0.0645 | 0.179 |
| Slope D | 6 × 6 | 0.1215 | 0.337 |
| Slope E | 6 × 6 | 0.3011 | 0.836 |
| Slope F | 6 × 6 | 0.8329 | 2.313 |
| Slope G | 6 × 6 | 1.3315 | 3.698 |
| Material Property | Value |
|---|---|
| Uniaxial Compressive Strength (UCS) MPa | 23.49 |
| Geological Strength Index (GSI) | 28 |
| Intact rock constant (mi) | 9 |
| Disturbance factor | 0.7 |
| Unit weight (MN/m3) | 0.0228 |
| Young’s modulus (GPa) | 35.91 |
| Poisson’s ratio | 0.39 |
| Hydraulic conductivity (m/s) | 1.62 × 10−4 |
| Hollows Sizes | Factor of Safety | ||
|---|---|---|---|
| Holes Density of 0.1% | Holes Density of 0.5% | Holes Density of 1% | |
| Set A (Smallest two) | 0.89 | 0.84 | 0.9 |
| Set B (Varied) | 0.85 | 0.86 | 0.88 |
| Set C (Largest three) | 0.97 | 0.93 | 0.86 |
| Set D (1 m dia) | 0.85 | 0.9 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onyango, J.A.; Sasaoka, T.; Shimada, H.; Hamanaka, A.; Moses, D. Equivalent Porous Medium (EPM) Modeling of Karst Features for Slope Stability Analysis in Karst-Prone Weak Rock Masses. Modelling 2025, 6, 81. https://doi.org/10.3390/modelling6030081
Onyango JA, Sasaoka T, Shimada H, Hamanaka A, Moses D. Equivalent Porous Medium (EPM) Modeling of Karst Features for Slope Stability Analysis in Karst-Prone Weak Rock Masses. Modelling. 2025; 6(3):81. https://doi.org/10.3390/modelling6030081
Chicago/Turabian StyleOnyango, Joan Atieno, Takashi Sasaoka, Hideki Shimada, Akihiro Hamanaka, and Dyson Moses. 2025. "Equivalent Porous Medium (EPM) Modeling of Karst Features for Slope Stability Analysis in Karst-Prone Weak Rock Masses" Modelling 6, no. 3: 81. https://doi.org/10.3390/modelling6030081
APA StyleOnyango, J. A., Sasaoka, T., Shimada, H., Hamanaka, A., & Moses, D. (2025). Equivalent Porous Medium (EPM) Modeling of Karst Features for Slope Stability Analysis in Karst-Prone Weak Rock Masses. Modelling, 6(3), 81. https://doi.org/10.3390/modelling6030081







