Three-Dimensional Modelling for Interfacial Behavior of a Thin Penny-Shaped Piezo-Thermo-Diffusive Actuator

Abstract

This paper presents a theoretical model of a thin, penny-shaped piezoelectric actuator bonded to an isotropic thermo-elastic substrate under coupled electrical-thermal-diffusive loading. The problem is assumed to be axisymmetric, and the peeling stress of the film is neglected in accordance with membrane theory, yielding a simplified equilibrium equation for the piezoelectric film. By employing potential theory and the Hankel transform technique, the surface strain of the substrate is analytically derived. Under the assumption of perfect bonding, a governing integral equation is established in terms of interfacial shear stress. The solution to this integral equation is obtained numerically using orthotropic Chebyshev polynomials. The derived results include the interfacial shear stress, stress intensity factors, as well as the radial and hoop stresses within the system. Finite element analysis is conducted to validate the theoretical predictions. Furthermore, parametric studies elucidate the influence of material mismatch and actuator geometry on the mechanical response. The findings demonstrate that, the performance of the piezoelectric actuator can be optimized through judicious control of the applied electrical-thermal-diffusive loads and careful selection of material and geometric parameters. This work provides valuable insights for the design and optimization of piezoelectric actuator structures in practical engineering applications.

1. Introduction

Owing to their exceptional electromechanical coupling properties [1,2,3], piezoelectric materials are extensively employed as actuators and sensors in civil engineering and biotechnology [4,5,6,7]. When bonded to a substrate, piezoelectric sensors can transduce mechanical deformation into measurable electrical signals, enabling remote monitoring. Conversely, when an external electric field is applied to piezoelectric actuators, they generate interfacial stresses that alter the mechanical response of the substrate [8]. However, under prolonged service conditions, these induced stresses may lead to interfacial delamination, compromising the structural integrity and reliability of the system. Consequently, accurate evaluation of interfacial mechanical behavior and determination of critical failure conditions are essential for the functional design and safety assessment of piezoelectric actuator systems [9].

Extensive research has been conducted on interfacial analysis in piezoelectric actuator systems. Crawley and de Luis [10,11,12] pioneered the treatment of piezoelectric actuator structures as conventional film/substrate systems, introducing a modified Euler beam model for a thin piezoelectric actuator. Their work demonstrated that interfacial shear stress transfer occurs predominantly within an infinitesimal region near the actuator edges. Subsequent theoretical developments investigated the interfacial behavior of both perfectly and imperfectly bonded piezoelectric actuators under an applied electric voltage [13]. When electromechanical coupling effects are considered, studies reveal that while the electric field distribution remains uniform in the central region, significant field distortion occurs near the actuator extremities [14,15].

The inclusion of an adhesive layer has been shown to substantially enhance the performance of piezoelectric actuators [16], prompting numerous investigations into adhesive-bonded piezoelectric actuator systems [17,18,19]. These studies typically formulate governing integral equations for interfacial shear stress, which are subsequently solved numerically via Chebyshev polynomial expansion. Through this approach, researchers have systematically examined the effects of aspect ratio, adhesive layer properties, and material gradation parameters on interfacial behavior. Of particular concern is the phenomenon of interfacial debonding, which has been demonstrated to significantly compromise both the functional control capability and mechanical response of piezoelectric actuators [20,21]. To address this issue, layer-wise displacement models have been developed to characterize partial debonding behavior [22,23]. For advanced functional design applications, particularly those involving depth-wise functionally graded substrates, comprehensive analyses have been conducted to evaluate interfacial behavior with and without adhesive layers [24,25,26,27]. These investigations provide critical insights into the effects of substrate inhomogeneity on system performance. Recent research has increasingly focused on nonlinear response characteristics of piezoelectric actuators [28]. Advanced nonlinear models have been proposed to predict buckling behavior and axial deformation [29], enabling quantitative assessment of load transfer mechanisms between actuator and substrate. Meanwhile, the mechanical response such as bending moment, axial force, axial displacement and deflection are all determined, these developments provide valuable theoretical foundations for the design of advanced piezoelectric actuator systems.

In practical applications, piezoelectric actuators are subjected to multifield loading conditions extending beyond electrical excitation. The concurrent presence of thermal and diffusive fields significantly influences system performance, making their characterization essential for reliable design and safety evaluation. As established in the literature, elevated thermal loading induces substantial thermoelastic stresses and deformations that may precipitate interfacial delamination, necessitating rigorous thermal analysis [30]. The diffusion phenomenon, defined as the spontaneous movement of particles from a region of high concentration to low concentration, represents another critical consideration. Diffusion occurs fundamentally to the Second Law of Thermodynamics, which mandates continuous increase in system entropy over time [31,32]. The theoretical framework for these coupled phenomena was initially established through thermoelastic diffusion modeling [33], with subsequent development of a generalized theory incorporating finite wave propagation speeds with one relaxation time [34]. Further theoretical advancements extended thermo-diffusion analysis to pyroelectricity [35], and Green’s functions were derived for an orthotropic piezo-thermo-elastic diffusion (PTD) medium [36]. Recent work by Othman et al. [37,38] has focused on the gravity effect in PTD media through dual-phase-lag model and Lord-Shulman theory, providing comprehensive solutions for coupled stress, temperature and diffusion fields. Notably, despite these theoretical developments, the interfacial mechanics of PTD actuators under multifield loading remains unexplored in the literature-a critical knowledge gap given its practical significance in actuator design and reliability assessment.

Previous works are mainly focused on two-dimensional (2D) problems of piezoelectric actuators. Nevertheless, a three-dimensional (3D) model is irreplaceable in engineering applications. Therefore, it is vital to study the influence of thermal-diffusive loads in a 3D model, to the best of our knowledge, however, no related studies have been reported. Motivated by this, we aim to study the interfacial mechanical response and delamination behavior of an axisymmetric PTD actuator.

The paper is organized as follows. Section 2 describes the theoretical modal in detail, and presents the solution for a PTD actuator and an isotropic half-plane substrate. In Section 3, the integral equation is established on the basis of the perfectly bonding condition and is numerically solved by orthotropic Chebyshev polynomials. Section 4 derives the deformations, radial stresses and hoop stresses of both the PTD actuator and substrate, and the stress intensity factors (SIFs) are given as the delamination fracture criterion. Detailed results and discussion are given in Section 5. Some important conclusions are drawn in Section 6.

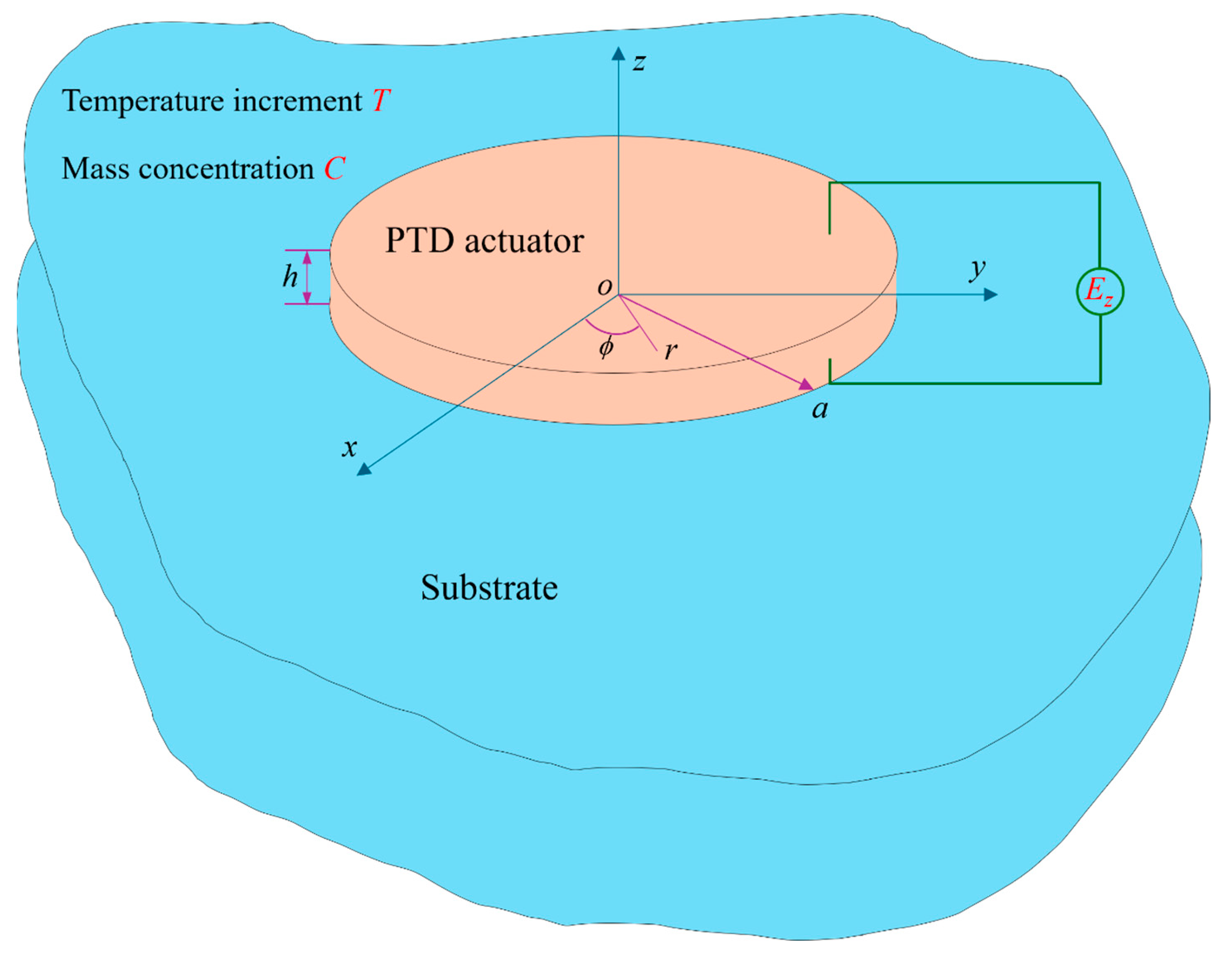
2. Problem Statement

Let us consider a thin PTD actuator with thickness h and radius $r=a$ perfectly bonded to a homogeneous isotropic elastic substrate. The cylindrical coordinate system $\left(r,\varphi ,z\right)$ is selected so that the $ro\varphi$-plane is coincident with the transverse plane and the z-axis is identical to the poling direction. An electric filed E_z is applied in the z-axis by applying a voltage (V) between the upper and lower electrodes of the PTD actuator, with $E_z=V/h=\left(V^{-}-V^{+}\right)/h$. In addition, a temperature load T and mass concentration C are applied along the actuator, as illustrated in Figure 1. It is important to emphasize that mass concentration, operationally defined as “the mass of a constituent per unit volume or unit mass of material”, serves as a fundamental parameter in PTD materials. This critical parameter can be modulated through several methods, including but not limited to chemical doping, photo-induced mass transport, and interfacial exchange reactions.

Compared to the thin PTD actuator with thickness h, the substrate dimensions are sufficiently large to be modeled as a semi-infinite medium. The analysis employs membrane theory, which neglects the bending stiffness of actuator. In this case, peel stresses do not build up in the direction normal to actuator, and only interfacial shear stress transfers across contact interface. The combined loads mainly result in a radial deformation. Membrane theory is a simplified theoretical framework for analyzing film-substrate structures. This theory is based on small-strain assumption, and the film is assumed to be primarily governed by in-plane stresses. Meanwhile, shear deformation along the thickness direction is ignored, with only in-plane strains and stresses considered. In most film-substrate systems, interfacial failure primarily occurs via shear failure, whereas peeling stress becomes significant only under large-curvature deformation or local debonding [17,24].

2.1. Analysis of an Axisymmetric PTD Actuator

The constitutive equations of a transversely isotropic piezo-thermo-diffusive actuator are given in the cylindrical coordinate system as [36]

$${\sigma }_{rr}=c_{11}{\displaystyle \frac{\partial u_r}{\partial r}}+c_{12}\left({\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u_{\varphi }}{\partial \varphi }}+{\displaystyle \frac{u_r}{r}}\right)+c_{13}{\displaystyle \frac{\partial u_z}{\partial z}}-e_{31}{E}_z-{\beta }_{1}T-b_{1}C,$$

(1a)

$${\sigma }_{\varphi \varphi }=c_{11}\left({\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u_{\varphi }}{\partial \varphi }}+{\displaystyle \frac{u_r}{r}}\right)+c_{12}{\displaystyle \frac{\partial u_r}{\partial r}}+c_{13}{\displaystyle \frac{\partial u_z}{\partial z}}-e_{31}{E}_z-{\beta }_{1}T-b_{1}C,$$

(1b)

$${\sigma }_{zz}=c_{13}\left({\displaystyle \frac{\partial u_r}{\partial r}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u_{\varphi }}{\partial \varphi }}+{\displaystyle \frac{u_r}{r}}\right)+c_{33}{\displaystyle \frac{\partial u_z}{\partial z}}-e_{33}{E}_z-{\beta }_{3}T-b_{3}C,$$

(1c)

$$D_r=e_{15}\left({\displaystyle \frac{\partial u_r}{\partial z}}+{\displaystyle \frac{\partial u_z}{\partial r}}\right)+e_{11}^{\prime }{E}_r,$$

(1d)

$$D_z=e_{31}{\displaystyle \frac{\partial u_r}{\partial r}}+e_{33}{\displaystyle \frac{\partial u_z}{\partial z}}+e_{33}^{\prime }{E}_z+p_{3}T,$$

(1e)

where u_i, σ_ij, and D_i are respectively the components of displacement, stress, and electric displacement; E_i, T, and C are electric field, temperature increment, and mass concentration, respectively; c_ij, e_ij, $e_{ij}^{\prime }$, p₃, β_i, and b_i are elastic, piezoelectric, dielectric, pyroelectric, thermal and diffusion constants, respectively.

In the absence of body forces, heat sources and concentration sources, equilibrium equations of the PTD actuator can be expressed as [36]

$${\displaystyle \frac{\partial {\sigma }_{rr}}{\partial r}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial {\sigma }_{r\varphi }}{\partial \varphi }}+{\displaystyle \frac{{\sigma }_{rr}-{\sigma }_{\varphi \varphi }}{r}}+{\displaystyle \frac{\partial {\sigma }_{zr}}{\partial z}}=0,$$

(2a)

$${\displaystyle \frac{\partial {\sigma }_{r\varphi }}{\partial \varphi }}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial {\sigma }_{\varphi \varphi }}{\partial \varphi }}+{\displaystyle \frac{2{\sigma }_{r\varphi }}{r}}+{\displaystyle \frac{\partial {\sigma }_{z\varphi }}{\partial \varphi }}=0,$$

(2b)

$${\displaystyle \frac{\partial {\sigma }_{zr}}{\partial r}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial {\sigma }_{z\varphi }}{\partial \varphi }}+{\displaystyle \frac{{\sigma }_{zr}}{r}}+{\displaystyle \frac{\partial {\sigma }_{zz}}{\partial z}}=0,$$

(2c)

$${\displaystyle \frac{\partial D_r}{\partial r}}+{\displaystyle \frac{D_r}{r}}+{\displaystyle \frac{\partial D_z}{\partial z}}=0,$$

(2d)

$$\left[{\lambda }_1\left({\displaystyle \frac{{\partial }^2}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{{\partial }^2}{\partial r\partial \varphi }}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^2}{\partial {\varphi }^2}}\right)+{\lambda }_3{\displaystyle \frac{{\partial }^2}{\partial z^2}}\right]T=0,$$

(2e)

$$\left[{\gamma }_1\left({\displaystyle \frac{{\partial }^2}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{{\partial }^2}{\partial r\partial \varphi }}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^2}{\partial {\varphi }^2}}\right)+{\gamma }_3{\displaystyle \frac{{\partial }^2}{\partial z^2}}\right]C=0,$$

(2f)

where λ_i and γ_i are the thermal conductivity and diffusion parameters, respectively.

In the following discussion, the superscript “a” and “s” denote to the PTD actuator and the substrate, respectively. The symmetry conditions of the geometry and the loading permits to seek an axisymmetric solution type, all the stress components should be independent on the variable ϕ, and we have [39]

$${\sigma }_{z\varphi }^a={\sigma }_{zz}^a=0, \mathrm{for} 0<r<a$$

(3)

In addition, the stress component ${\sigma }_{r\varphi }^a$ is nonexistent and the stress component ${\sigma }_{\varphi \varphi }^a$ remains the same value in the hoop direction due to the symmetry. In addition, only the interfacial shear stress τ, i.e., ${\sigma }_{rz}^a$, dominates the interfacial behavior of the axisymmetric film/substrate structure. Therefore, the equilibrium of forces along r-direction can be rewritten as

$${\displaystyle \frac{\partial {\sigma }_{rr}^a}{\partial r}}+{\displaystyle \frac{{\sigma }_{rr}^a-{\sigma }_{\varphi \varphi }^a}{r}}-{\displaystyle \frac{\tau }{h}}=0.$$

(4)

Inserting Equation (1c) into Equation (3) and recalling that the problem is non-axisymmetric, we have the following relation

$${\displaystyle \frac{\partial u_z}{\partial z}}=-{\displaystyle \frac{c_{13}}{c_{33}}}\left({\displaystyle \frac{\partial u_r}{\partial r}}+{\displaystyle \frac{u_r}{r}}\right)+{\displaystyle \frac{e_{33}{E}_z+{\beta }_{3}T+b_{3}C}{c_{33}}}.$$

(5)

Substituting Equation (5) into Equation (1a) yields

$${\sigma }_{rr}^a\left(r\right)={\Re }_1{\displaystyle \frac{\partial u_r}{\partial r}}+{\Re }_2{\displaystyle \frac{u_r}{r}}-{\Im }_1{E}_z-{\Im }_{2}T-{\Im }_{3}C,$$

(6a)

$${\sigma }_{\varphi \varphi }^a\left(r\right)={\Re }_2{\displaystyle \frac{\partial u_r}{\partial r}}+{\Re }_1{\displaystyle \frac{u_r}{r}}-{\Im }_1{E}_z-{\Im }_{2}T-{\Im }_{3}C,$$

(6b)

where ${\Re }_i$ and ${\Im }_i$ are respectively the effective Young’s modulus and electrical, thermal and diffusive constants for PTD actuator with their definitions given by

$${\Re }_1=c_{11}-c_{13}^2/c_{33}, {\Re }_2=c_{12}-c_{13}^2/c_{33},$$

(7a)

$${\Im }_1=e_{31}-{\displaystyle \frac{c_{13}}{c_{33}}}{e}_{33}, {\Im }_2={\beta }_1-{\displaystyle \frac{c_{13}}{c_{33}}}{\beta }_3, {\Im }_3=b_1-{\displaystyle \frac{c_{13}}{c_{33}}}{b}_3.$$

(7b)

Substituting Equation (6) into Equation (4) and integrating with respect to r leads to

$${\displaystyle \frac{\partial u_r^a}{\partial r}}+{\displaystyle \frac{u_r^a}{r}}={\displaystyle \frac{1}{{\Re }_{1}h}}{\displaystyle {\int }_0^r\tau \left(t\right)}dt+{\displaystyle \frac{{\Im }_1}{{\Re }_1}}{E}_z+{\displaystyle \frac{{\Im }_2}{{\Re }_1}}T+{\displaystyle \frac{{\Im }_3}{{\Re }_1}}C+d_0,$$

(8)

where the constant d₀ is determined by the boundary conditions.

2.2. Analysis of an Isotropic Elastic Substrate

The substrate is assumed to be thermally conducted while electrically and diffusively insulated. The axisymmetric constitutive equations of an isotropic thermo-elastic substrate can be expressed as

$${\sigma }_{rr}^s=\left(\lambda +2\mu \right){\displaystyle \frac{\partial u_r^s}{\partial r}}+\lambda {\displaystyle \frac{u_r^s}{r}}+\lambda {\displaystyle \frac{\partial u_z^s}{\partial z}}-\alpha T,$$

(9a)

$${\sigma }_{\varphi \varphi }^s=\lambda {\displaystyle \frac{\partial u_r^s}{\partial r}}+\left(\lambda +2\mu \right){\displaystyle \frac{u_r^s}{r}}+\lambda {\displaystyle \frac{\partial u_z^s}{\partial z}}-\alpha T,$$

(9b)

$${\sigma }_{zz}^s=\lambda {\displaystyle \frac{\partial u_r^s}{\partial r}}+\lambda {\displaystyle \frac{u_r^s}{r}}+\left(\lambda +2\mu \right){\displaystyle \frac{\partial u_z^s}{\partial z}}-\alpha T,$$

(9c)

$${\sigma }_{zr}^s=\mu \left({\displaystyle \frac{\partial u_r^s}{\partial z}}+{\displaystyle \frac{\partial u_z^s}{\partial r}}\right),$$

(9d)

where α is the thermal modulus, λ and μ are respectively the Lamé constant and shear modulus which are in the following forms

$$\lambda ={\displaystyle \frac{Ev}{\left(1+v\right)\left(1-2v\right)}}, \mu ={\displaystyle \frac{E}{2\left(1+v\right)}},$$

(10)

where E and v are the Young’s modulus and Poisson’s ratio of the substrate, respectively.

Besides, the governing equations for the axisymmetric problem can be written as

$${\displaystyle \frac{\partial {\sigma }_{rr}^s}{\partial r}}+{\displaystyle \frac{{\sigma }_{rr}^s-{\sigma }_{\varphi \varphi }^s}{r}}+{\displaystyle \frac{\partial {\sigma }_{zr}^s}{\partial z}}=0,$$

(11a)

$${\displaystyle \frac{\partial {\sigma }_{zr}^s}{\partial r}}+{\displaystyle \frac{{\sigma }_{zr}^s}{r}}+{\displaystyle \frac{\partial {\sigma }_{zz}^s}{\partial z}}=0,$$

(11b)

$$\left({\displaystyle \frac{{\partial }^2}{\partial r^2}}+{\displaystyle \frac{{\partial }^2}{\partial z^2}}\right)T=0.$$

(11c)

According to the general solution for an isotropic thermo-elastic material [40], one obtains the completed non-torsional axisymmetric general solution around the z-axis in terms of potential functions ${\psi }_i$ as

$$2\mu u_r^s={\displaystyle \frac{\partial {\psi }_1}{\partial r}}+z{\displaystyle \frac{\partial {\psi }_2}{\partial r}},$$

$$2\mu u_z^s={\displaystyle \frac{\partial {\psi }_1}{\partial z}}-\left(3-4v\right){\psi }_2+z{\displaystyle \frac{\partial {\psi }_2}{\partial z}}+4\left(1-v\right){\psi }_3,$$

$${\displaystyle \frac{2\mu }{\Gamma }}T={\displaystyle \frac{\partial {\psi }_3}{\partial z}},$$

$${\sigma }_{rr}^s={\displaystyle \frac{{\partial }^2{\psi }_1}{\partial r^2}}-2v{\displaystyle \frac{\partial {\psi }_2}{\partial z}}+z{\displaystyle \frac{{\partial }^2{\psi }_2}{\partial r^2}}-2\left(1-v\right){\displaystyle \frac{\partial {\psi }_3}{\partial z}},$$

$${\sigma }_{zz}^s={\displaystyle \frac{{\partial }^2{\psi }_1}{\partial z^2}}-2\left(1-v\right){\displaystyle \frac{\partial {\psi }_2}{\partial z}}+z{\displaystyle \frac{{\partial }^2{\psi }_2}{\partial z^2}}+2\left(1-v\right){\displaystyle \frac{\partial {\psi }_3}{\partial z}},$$

$${\sigma }_{zr}^s={\displaystyle \frac{{\partial }^2{\psi }_1}{\partial r\partial z}}-\left(1-2v\right){\displaystyle \frac{\partial {\psi }_2}{\partial r}}+z{\displaystyle \frac{{\partial }^2{\psi }_2}{\partial r\partial z}}+2\left(1-v\right){\displaystyle \frac{\partial {\psi }_3}{\partial r}},$$

(12)

where $\Gamma =2\left(\lambda +2\mu \right)/\alpha$ is the material-related constant, and ${\psi }_i$ satisfy harmonic relations. Using the Hankel transform to the potential functions as

$${\psi }_j\left(r,z\right)={\displaystyle {\int }_0^{\infty }{A}_j{e}^{\xi z}{J}_0\left(\xi r\right)}\mathrm{d}\xi , \mathrm{for} j=1,2,3,$$

(13)

where $\xi$ is the Hankel transform parameter, and A_j are the coefficients to be determined by surface boundary conditions. As the peeling stress between the film and the substrate is neglected, the surface traction condition is given as

$${\sigma }_{zz}^s\left(r,0\right)=0, {\sigma }_{zr}^s\left(r,0\right)=\tau \left(r\right).$$

(14)

Keep in mind that for Hankel transform $y\left(r\right)={\displaystyle {\int }_0^{\infty }\xi \overline{y}\left(\xi \right)J_0\left(\xi r\right)}\mathrm{d}\xi$, its reverse transform is $\overline{y}\left(\xi \right)={\displaystyle {\int }_0^{\infty }ry\left(r\right)J_0\left(\xi r\right)}\mathrm{d}r$. Inserting Equation (13) into Equations (12) and (14) yields

$$\left\{\begin{array}{l}{A}_1\xi -2\left(1-v\right)A_2+2\left(1-v\right)A_3=0,\\ A_1\xi -\left(1-2v\right)A_2+2\left(1-v\right)A_3=-{\displaystyle {\int }_0^{\infty }r\tau \left(r\right)J_1\left(\xi r\right)}\mathrm{d}r,\\ A_3{e}^{\xi z}={\displaystyle \frac{2\mu }{\Gamma }}T{\displaystyle {\int }_0^{\infty }r{J}_0\left(\xi r\right)}\mathrm{d}r.\end{array}\right.$$

(15)

After solving Equation (15), one obtains

$$A_1\xi =-2\left(1-v\right)\left[{\displaystyle {\int }_0^{\infty }t\tau \left(t\right)J_1\left(\xi t\right)}\mathrm{d}t+{\displaystyle \frac{2\mu }{\Gamma e^{\xi z}}}T{\displaystyle {\int }_0^{\infty }t{J}_0\left(\xi t\right)}\mathrm{d}t\right],$$

(16)

then the radial displacement on the surface of the substrate is obtained as

$$u_r^s\left(r,0\right)={\displaystyle \frac{1-v}{\mu }}{\displaystyle {\int }_0^{\infty }\left[{\displaystyle {\int }_0^{\infty }t\tau \left(t\right)J_1\left(\xi t\right)}\mathrm{d}t+\frac{2\mu }{\Gamma }T{\displaystyle {\int }_0^{\infty }t{J}_0\left(\xi t\right)}\mathrm{d}t\right]J_1\left(\xi r\right)}\mathrm{d}\xi ,$$

(17)

which can be rewritten as

$$\begin{array}{l}{u}_r^s\left(r,0\right)={\displaystyle \frac{1-v}{\mu }}{\displaystyle {\int }_0^a\left[{\displaystyle {\int }_0^{\infty }{J}_1\left(\xi t\right)J_1\left(\xi r\right)}d\xi \right]t\tau \left(t\right)}\mathrm{d}t\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{2\left(1-v\right)}{\Gamma }}T{\displaystyle {\int }_0^a\left[{\displaystyle {\int }_0^{\infty }{J}_0\left(\xi t\right)J_1\left(\xi r\right)}d\xi \right]t}\mathrm{d}t.\end{array}$$

(18)

Equation (18) can be further calculated as

$$u_r^s\left(r,0\right)={\displaystyle \frac{1-v}{\mu }}{\displaystyle {\int }_0^a{H}_{11}\left(t,r\right)t\tau \left(t\right)}\mathrm{d}t+{\displaystyle \frac{2\left(1-v\right)}{\Gamma }}T{\displaystyle {\int }_0^a{H}_{12}\left(t,r\right)t}\mathrm{d}t,$$

(19)

where the arisen functions $H_{1j}$ are defined as

$$\left\{\begin{array}{l}{H}_{11}\left(t,r\right)={\displaystyle {\int }_0^{\infty }{J}_1\left(\xi t\right)J_1\left(\xi r\right)}\mathrm{d}\xi ,\\ H_{12}\left(t,r\right)={\displaystyle {\int }_0^{\infty }{J}_0\left(\xi t\right)J_1\left(\xi r\right)}\mathrm{d}\xi .\end{array}\right.$$

(20)

According to the property of Bessel functions, Equation (20) can be expressed as

$$H_{11}\left(t,r\right)={\displaystyle \frac{2}{\pi }}\left\{\begin{array}{l}\left[K\left(t/r\right)-E\left(t/r\right)\right]/t,\hspace{1em}\mathrm{for}\hspace{1em}t\le r,\\ \left[K\left(r/t\right)-E\left(r/t\right)\right]/r,\hspace{1em}\mathrm{for}\hspace{1em}t\ge r,\end{array}\right.$$

(21a)

$$H_{12}\left(t,r\right)=\left\{\begin{array}{l}1/r,\hspace{1em}\hspace{1em}\mathrm{for}\hspace{1em}t<r,\\ 1/\left(2r\right),\hspace{1em}\mathrm{for}\hspace{1em}t=r,\\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{for}\hspace{1em}t>r,\end{array}\right.$$

(21b)

where the functions $K\left(x\right)$ and $E\left(x\right)$ are respectively the complete elliptic integrals of the first and second kind. Substituting Equation (21b) into Equation (19) yields

$$u_r^s\left(r,0\right)={\displaystyle \frac{1-v}{\mu }}{\displaystyle {\int }_0^a{H}_{11}\left(t,r\right)t\tau \left(t\right)}\mathrm{d}t+{\displaystyle \frac{1-v}{\Gamma }}Tr.$$

(22)

3. The Governing Integral Equation

The perfect bonding condition between the actuator and the substrate leads to

$$u_r^a\left(r,0\right)=u_r^s\left(r,0\right), \mathrm{for} 0\le r\le a.$$

(23)

Substituting Equations (8) and (22) into Equation (23) yields

$${\displaystyle {\int }_0^{a}F\left(t,r\right)t\tau \left(t\right)}\mathrm{d}t-{\displaystyle \frac{D_0}{h}}{\displaystyle {\int }_0^r\tau \left(t\right)}\mathrm{d}t=D_1{E}_z+D_{2}T+D_{3}C+D_4,$$

(24)

where

$$F\left(t,r\right)={\displaystyle \frac{\partial H_{11}\left(t,r\right)}{\partial r}}+{\displaystyle \frac{H_{11}\left(t,r\right)}{r}},$$

$$D_0={\displaystyle \frac{\mu }{\left(1-v\right){\Re }_1}}, D_1={\displaystyle \frac{\mu {\Im }_1}{\left(1-v\right){\Re }_1}}, D_2=\mu \left[{\displaystyle \frac{{\Im }_2}{\left(1-v\right){\Re }_1}}-{\displaystyle \frac{2}{\Gamma }}\right],$$

$$D_3={\displaystyle \frac{\mu {\Im }_3}{\left(1-v\right){\Re }_1}}, D_4={\displaystyle \frac{\mu }{1-v}}{d}_0.$$

(25)

After mathematical derivation, the function $F\left(t,r\right)$ can be further written as

$$F\left(t,r\right)={\displaystyle \frac{2}{\pi }}\left\{\begin{array}{lll}{\displaystyle \frac{1}{rt}}K\left({\displaystyle \frac{t}{r}}\right)+{\displaystyle \frac{r}{t\left(t^2-r^2\right)}}E\left({\displaystyle \frac{t}{r}}\right),& \mathrm{for}& t<r\\ {\displaystyle \frac{1}{t^2-r^2}}E\left({\displaystyle \frac{r}{t}}\right),& \mathrm{for}& t>r\end{array}\right.$$

(26)

For small a value of $\left|t-r\right|$, the singularity of the kernel function $F\left(t,r\right)$ can be extracted as [39]

$$tF\left(t,r\right)={\displaystyle \frac{1}{\pi }}\left[{\displaystyle \frac{1}{t-r}}+{\displaystyle \frac{1}{t+r}}+{\displaystyle \frac{M\left(t,r\right)-1}{t-r}}+{\displaystyle \frac{M\left(t,r\right)-1}{t+r}}\right],$$

(27)

where

$$M\left(t,r\right)=\left\{\begin{array}{lll}{\displaystyle \frac{t^2-r^2}{rt}}K\left({\displaystyle \frac{t}{r}}\right)+{\displaystyle \frac{r}{t}}E\left({\displaystyle \frac{t}{r}}\right),& \mathrm{for}& t<r\\ E\left({\displaystyle \frac{r}{t}}\right),& \mathrm{for}& t>r\end{array}\right.$$

(28)

It should be noted that [41]

$${\displaystyle \frac{M\left(t,r\right)-1}{t-r}}\approx -{\displaystyle \frac{1}{2r}}\ln \left|t-r\right|,$$

(29)

thus the integral Equation (24) can be rewritten as

$${\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^a\left[\frac{1}{t-r}+\frac{1}{t+r}-\frac{1}{2r}\ln \left|t-r\right|+N\left(t,r\right)\right]\tau \left(t\right)}\mathrm{d}t-{\displaystyle \frac{D_0}{h}}{\displaystyle {\int }_0^r\tau \left(t\right)}\mathrm{d}t=D_1{E}_z+D_{2}T+D_{3}C+D_4,$$

(30)

where

$$N\left(t,r\right)={\displaystyle \frac{M\left(t,r\right)-1}{t-r}}+{\displaystyle \frac{M\left(t,r\right)-1}{t+r}}+{\displaystyle \frac{1}{2r}}\ln \left|t-r\right|.$$

(31)

Equation (30) is a singular integral equation with a Cauchy kernel, thus the interfacial shear stress exhibits a square root singularity near the film edge [42]. As is noted, the constant D₄ has not yet been determined as d₀ is not given. The integral constant d₀ can be determined from the additional traction boundary condition at the actuator front by combining Equations (6a), (8) and (22) as

$${\sigma }_{rr}^a\left(a\right)={\displaystyle \frac{1}{h}}{\displaystyle {\int }_0^a\tau \left(t\right)}\mathrm{d}t+\left(c_{12}-c_{11}\right){\displaystyle \frac{1-v}{\mu a}}{\displaystyle {\int }_0^a{H}_{11}\left(t,a\right)t\tau \left(t\right)}\mathrm{d}t+{\Re }_1{d}_0+\left(c_{12}-c_{11}\right){\displaystyle \frac{1-v}{\Gamma }}T=0.$$

(32)

Then, the constant D₄ can be obtained as

$$D_4={\displaystyle \frac{\mu }{\left(1-v\right){\Re }_1}}\left[-{\displaystyle \frac{1}{h}}{\displaystyle {\int }_0^a\tau \left(t\right)}\mathrm{d}t+\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\mu a}}{\displaystyle {\int }_0^a{H}_{11}\left(t,a\right)t\tau \left(t\right)}\mathrm{d}t+\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\Gamma }}T\right].$$

(33)

Inserting Equation (33) into Equation (30) yields the final governing integral equation for interfacial shear stress τ as

$$\begin{array}{l}{\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^a\left[\frac{1}{t-r}+\frac{1}{t+r}-\frac{1}{2r}\ln \left|t-r\right|+N\left(t,r\right)\right]\tau \left(t\right)}\mathrm{d}t-{\displaystyle \frac{D_0}{h}}{\displaystyle {\int }_0^r\tau \left(t\right)}\mathrm{d}t-\\ {\displaystyle \frac{\mu }{\left(1-v\right){\Re }_{1}h}}{\displaystyle {\int }_0^a\tau \left(t\right)}\mathrm{d}t-{\displaystyle \frac{c_{11}-c_{12}}{{\Re }_{1}a}}{\displaystyle {\int }_0^a{H}_{11}\left(t,a\right)t\tau \left(t\right)}\mathrm{d}t\\ =D_1{E}_z+D_{2}T+D_{3}C+{\displaystyle \frac{c_{11}-c_{12}}{{\Re }_1\Gamma }}T.\end{array}$$

(34)

Introducing the normalized quantities

$$r=a\zeta ,\hspace{1em}\hspace{1em}t=a\eta ,\hspace{1em}\hspace{1em}\widehat{N}\left(\zeta ,\eta \right)=aN\left(r,t\right),\hspace{1em}\hspace{1em}\widehat{\tau }=\tau \left(r\right)/{\tau }_0,$$

$${\tau }_0=D_1{E}_z+\left(D_2+{\displaystyle \frac{c_{11}-c_{12}}{{\Re }_1\Gamma }}\right)T+D_{3}C,$$

(35)

Equation (34) can be rewritten as

$$\begin{array}{l}{\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^1\left[\frac{1}{\eta -\zeta }+\frac{1}{\eta +\zeta }-\frac{1}{2\zeta }\ln \left|\zeta -\eta \right|+\widehat{N}\left(\zeta ,\eta \right)\right]\widehat{\tau }\left(\eta \right)}\mathrm{d}\eta -{\displaystyle \frac{a{D}_0}{h}}{\displaystyle {\int }_0^{\zeta }\widehat{\tau }\left(\eta \right)}\mathrm{d}\eta -\\ {\displaystyle \frac{\mu a}{\left(1-v\right){\Re }_{1}h}}{\displaystyle {\int }_0^1\widehat{\tau }\left(\eta \right)}\mathrm{d}\eta -{\displaystyle \frac{2\left(c_{11}-c_{12}\right)}{\pi {\Re }_1}}{\displaystyle {\int }_0^1\left[K\left(\eta \right)-E\left(\eta \right)\right]\widehat{\tau }\left(\eta \right)}\mathrm{d}\eta =1.\end{array}$$

(36)

The integral equation in Equation (36) cannot be solved analytically. According to the singularity and characteristic of the integral, the interfacial shear stress τ can be expressed in terms of orthogonal Chebyshev polynomials as [43,44]

$$\tau \left(\eta \right)=\sqrt{{\displaystyle \frac{\eta }{1-\eta }}}{\displaystyle \sum _{j=0}^{\infty }{b}_j{L}_j\left(m\right)},$$

(37)

where b_j is the unknown coefficients to be determined, and

$$L_j\left(m\right)={\displaystyle \frac{T_j\left(m\right)+T_{j+1}\left(m\right)}{1+m}},$$

(38)

in which $m=2\eta -1$, and $T_j\left(m\right)$ is the Chebyshev polynomials of the first kind.

During the solution of Equation (36), the following properties of the Chebyshev polynomials can be used [41]

$$I_{1j}\left(\zeta \right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^1\sqrt{\frac{\eta }{1-\eta }}\frac{L_j\left(2\eta -1\right)}{\eta -\zeta }}\mathrm{d}\eta =\left\{\begin{array}{l}{U}_0\left(2\zeta -1\right),\hspace{1em}j=0\\ U_{j-1}\left(2\zeta -1\right)+U_j\left(2\zeta -1\right),\hspace{1em}j\ge 1\end{array}\right.,$$

$$I_{2j}\left(\zeta \right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^1\sqrt{\frac{\eta }{1-\eta }}\frac{L_j\left(2\eta -1\right)}{\eta +\zeta }}\mathrm{d}\eta ={\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_0^1\sqrt{\frac{\eta }{1-\eta }}\frac{T_j\left(2\eta -1\right)+T_{j+1}\left(2\eta -1\right)}{\eta \left(\eta +\zeta \right)}}\mathrm{d}\eta ,$$

$$\begin{array}{ll}{I}_{3j}\left(\zeta \right)& =-{\displaystyle \frac{1}{\pi }}{\displaystyle \frac{1}{2\zeta }}{\displaystyle {\int }_0^1\ln \left|\zeta -\eta \right|\sqrt{\frac{\eta }{1-\eta }}{L}_j\left(2\eta -1\right)}\mathrm{d}\eta \\ & ={\displaystyle \frac{1}{4\zeta }}\left\{\begin{array}{l}{T}_1\left(2\zeta -1\right)+2\ln 2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}j=0\\ {\displaystyle \frac{T_j\left(2\zeta -1\right)}{j}}+{\displaystyle \frac{T_{j+1}\left(2\zeta -1\right)}{j+1}},\hspace{1em}j\ge 1\end{array}\right.\end{array},$$

$$I_{4j}\left(\zeta \right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^1\sqrt{\frac{\eta }{1-\eta }}{L}_j\left(2\eta -1\right)\widehat{N}\left(\zeta ,\eta \right)}\mathrm{d}\eta ,$$

$$\begin{array}{ll}{I}_{5j}\left(\zeta \right)& ={\displaystyle {\int }_0^{\zeta }\sqrt{\frac{\eta }{1-\eta }}{L}_j\left(2\eta -1\right)}\mathrm{d}\eta \\ & =-{\displaystyle \frac{1}{2}}\left\{\begin{array}{l}{U}_0\left(2\zeta -1\right)\sqrt{1-{\left(2\zeta -1\right)}^2}-\pi +\arccos \left(2\zeta -1\right),\hspace{1em}\hspace{1em}j=0\\ \left[{\displaystyle \frac{U_{j-1}\left(2\zeta -1\right)}{j}}+{\displaystyle \frac{U_j\left(2\zeta -1\right)}{j+1}}\right]\sqrt{1-{\left(2\zeta -1\right)}^2},\hspace{1em}\hspace{1em}\hspace{1em}j\ge 1\end{array}\right.\end{array},$$

$$I_{6j}={\displaystyle {\int }_0^1\sqrt{\frac{\eta }{1-\eta }}{L}_j\left(2\eta -1\right)}d\eta =\left\{\begin{array}{ll}{\displaystyle \frac{\pi }{2}},& j=0\\ 0,& j\ge 1\end{array}\right.,$$

$$I_{7j}={\displaystyle {\int }_0^1\left[K\left(\eta \right)-E\left(\eta \right)\right]\sqrt{\frac{\eta }{1-\eta }}{L}_j\left(2\eta -1\right)}d\eta ,$$

(39)

where $U_j\left(m\right)$ is the Chebyshev polynomials of the second kind. Then the discretized form of the integral Equation (36) can be rewritten as

$${\displaystyle \sum _{j=0}^{\infty }{b}_j\left[I_{1j}+I_{2j}+I_{3j}+I_{4j}-\frac{a{D}_0}{h}{I}_{5j}-\frac{\mu a}{\left(1-v\right){\Re }_{1}h}{I}_{6j}-\frac{2\left(c_{11}-c_{12}\right)}{\pi {\Re }_1}{I}_{7j}\right]}=1.$$

(40)

Finally truncating the series in Equation (40) to have a finite number of $N+1$ terms, the collocation points along PTD actuator can be properly selected as

$${\zeta }_k={\displaystyle \frac{1}{2}}\left[1+\cos {\displaystyle \frac{\pi \left(2k-1\right)}{2\left(N+1\right)}}\right],\hspace{1em}\hspace{1em}k=1,2,\dots ,N+1$$

(41)

Then, Equation (40) can be rewritten as the $N+1$ linear algebraic equations, corresponding to $N+1$ unknown coefficients b_j as

$$\begin{array}{l}{\displaystyle \sum _{j=0}^N{b}_j\left[I_{1j}\left({\zeta }_k\right)+I_{2j}\left({\zeta }_k\right)+I_{3j}\left({\zeta }_k\right)+I_{4j}\left({\zeta }_k\right)-\frac{a{D}_0}{h}{I}_{5j}\left({\zeta }_k\right)\right.}\\ \left.\hspace{1em}-{\displaystyle \frac{\mu a}{\left(1-v\right){\Re }_{1}h}}{I}_{6j}-{\displaystyle \frac{2\left(c_{11}-c_{12}\right)}{\pi {\Re }_1}}{I}_{7j}\right]=1,\hspace{1em}\mathrm{for}k=1,\dots ,N+1\end{array}$$

(42)

After solving Equation (42), one can get all the coefficients b_j. Thus, the interfacial shear stress of the PTD actuator is obtained as

$$\tau \left(t\right)={\tau }_0\sqrt{{\displaystyle \frac{\eta }{1-\eta }}}{\displaystyle \sum _{j=0}^N{b}_j{L}_j\left(m\right)}.$$

(43)

4. Other Quantities of Interest

As the shear stress is determined, keep in mind that ${\displaystyle \frac{\partial \left(r{u}_r^a\right)}{\partial r}}=r\left({\displaystyle \frac{\partial u_r^a}{\partial r}}+{\displaystyle \frac{u_r^a}{r}}\right)$, one can get the radial displacement $u_r\left(r\right)$ by integrating Equation (8) as

$$\begin{array}{ll}{\displaystyle \frac{u_r\left(r\right)}{a}}=& {\displaystyle \frac{2}{\pi }}{\displaystyle \frac{1-v}{\mu }}{\tau }_0\left\{{\displaystyle {\int }_0^{\zeta }\left[K\left(\frac{\eta }{\zeta }\right)-E\left(\frac{\eta }{\zeta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right.\\ & \left.+{\displaystyle {\int }_{\zeta }^1\frac{\eta }{\zeta }\left[K\left(\frac{\zeta }{\eta }\right)-E\left(\frac{\zeta }{\eta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right\}+{\displaystyle \frac{1-v}{\Gamma }}T\zeta +d_r,\end{array}$$

(44)

where ${\tau }_0$ has been defined in Equation (35), and the constant d_r can be determined from the additional condition

$$\underset{r\to 0}{\lim }{u}_r\left(r\right)=0.$$

(45)

Meanwhile, the radial and hoop stresses of PTD actuator can be obtained as

$${\sigma }_{rr}^a\left(r\right)={\displaystyle \frac{1}{h}}{\displaystyle {\int }_0^r\tau \left(t\right)}dt+\left(c_{12}-c_{11}\right){\displaystyle \frac{u_r}{r}}+{\Re }_1{d}_0,$$

(46a)

$${\sigma }_{\varphi \varphi }^a\left(r\right)={\displaystyle \frac{1}{h}}{\displaystyle {\int }_0^r\tau \left(t\right)}dt+\left(c_{11}-c_{12}\right){\displaystyle \frac{u_r}{r}}+{\Re }_2{d}_0,$$

(46b)

which can be rewritten as

$$\begin{array}{ll}{\sigma }_{rr}^a\left(r\right)=& {\displaystyle \frac{1}{h}}\left[{\displaystyle {\int }_0^r\tau \left(t\right)}dt-{\displaystyle {\int }_0^a\tau \left(t\right)}dt\right]-\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\mu }}\\ & \left[{\displaystyle \frac{1}{r}}{\displaystyle {\int }_0^a{H}_{11}\left(t,r\right)t\tau \left(t\right)}dt-{\displaystyle \frac{1}{a}}{\displaystyle {\int }_0^a{H}_{11}\left(t,a\right)t\tau \left(t\right)}dt\right],\end{array}$$

(47a)

$$\begin{array}{ll}{\sigma }_{\varphi \varphi }^a\left(r\right)=& {\displaystyle \frac{{\Re }_2}{{\Re }_1}}{\displaystyle \frac{1}{h}}\left[{\displaystyle {\int }_0^r\tau \left(t\right)}dt-{\displaystyle {\int }_0^a\tau \left(t\right)}dt\right]+\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\mu }}T\left(1+{\displaystyle \frac{{\Re }_2}{{\Re }_1}}\right)\\ & +\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\mu }}\left[{\displaystyle \frac{1}{r}}{\displaystyle {\int }_0^a{H}_{11}\left(t,r\right)t\tau \left(t\right)}dt+{\displaystyle \frac{1}{a}}{\displaystyle \frac{{\Re }_2}{{\Re }_1}}{\displaystyle {\int }_0^a{H}_{11}\left(t,a\right)t\tau \left(t\right)}dt\right]\\ & -\left(1-{\displaystyle \frac{{\Re }_2}{{\Re }_1}}\right)\left({\Im }_1{E}_z+{\Im }_{2}T+{\Im }_{3}C\right),\end{array}$$

(47b)

and the normalized expressions are

$$\begin{array}{ll}{\displaystyle \frac{{\sigma }_{rr}^a\left(r\right)}{{\tau }_0}}=& {\displaystyle \frac{a}{h}}\left[{\displaystyle {\int }_0^{\zeta }\widehat{\tau }\left(\eta \right)}d\eta -{\displaystyle {\int }_0^1\widehat{\tau }\left(\eta \right)}d\eta \right]-\left(c_{11}-c_{12}\right){\displaystyle \frac{2}{\pi }}{\displaystyle \frac{1-v}{\mu }}\cdot \\ & \left\{{\displaystyle \frac{1}{\zeta }}{\displaystyle {\int }_0^{\zeta }\left[K\left(\frac{\eta }{\zeta }\right)-E\left(\frac{\eta }{\zeta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta +{\displaystyle {\int }_{\zeta }^1\frac{\eta }{{\zeta }^2}\left[K\left(\frac{\zeta }{\eta }\right)-E\left(\frac{\zeta }{\eta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right.\\ & \left.-{\displaystyle {\int }_0^1\left[K\left(\eta \right)-E\left(\eta \right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right\},\end{array}$$

(48a)

$$\begin{array}{ll}{\displaystyle \frac{{\sigma }_{\varphi \varphi }^a\left(r\right)}{{\tau }_0}}=& {\displaystyle \frac{{\Re }_2}{{\Re }_1}}{\displaystyle \frac{a}{h}}\left[{\displaystyle {\int }_0^{\zeta }\widehat{\tau }\left(\eta \right)}d\eta -{\displaystyle {\int }_0^1\widehat{\tau }\left(\eta \right)}d\eta \right]+\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\mu {\tau }_0}}T\left(1+{\displaystyle \frac{{\Re }_2}{{\Re }_1}}\right)\\ & +\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{\mu {\tau }_0}}\left\{{\displaystyle \frac{1}{\zeta }}{\displaystyle {\int }_0^{\zeta }\left[K\left(\frac{\eta }{\zeta }\right)-E\left(\frac{\eta }{\zeta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right.\\ & +{\displaystyle {\int }_{\zeta }^1\frac{\eta }{{\zeta }^2}\left[K\left(\frac{\zeta }{\eta }\right)-E\left(\frac{\zeta }{\eta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \left.-{\displaystyle \frac{{\Re }_2}{{\Re }_1}}{\displaystyle {\int }_0^1\left[K\left(\eta \right)-E\left(\eta \right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right\}\\ & -\left(1-{\displaystyle \frac{{\Re }_2}{{\Re }_1}}\right){\displaystyle \frac{{\Im }_1{E}_z+{\Im }_{2}T+{\Im }_{3}C}{{\tau }_0}}.\end{array}$$

(48b)

Moreover, considering the peel stress neglected, i.e., ${\sigma }_{zz}^s\left(r,0\right)=0$, one can obtain the vertical strain on the surface of the substrate from Equation (9c) as

$${\displaystyle \frac{\partial u_z^s}{\partial z}}=-{\displaystyle \frac{\lambda }{\lambda +2\mu }}\left({\displaystyle \frac{\partial u_r^s}{\partial r}}+{\displaystyle \frac{u_r^s}{r}}\right)+{\displaystyle \frac{\alpha T}{\lambda +2\mu }}.$$

(49)

Inserting Equation (49) into Equation (9a,b), one gets the radial and hoop stresses of the upper surface of substrate as

$${\sigma }_{rr}^s\left(r,0\right)={\displaystyle \frac{4\mu \left(\lambda +\mu \right)}{\lambda +2\mu }}\left({\displaystyle \frac{\partial u_r}{\partial r}}+{\displaystyle \frac{u_r}{r}}\right)-2\mu {\displaystyle \frac{u_r}{r}}-{\displaystyle \frac{2\mu }{\lambda +2\mu }}\alpha T,$$

(50a)

$${\sigma }_{\varphi \varphi }^s\left(r,0\right)={\displaystyle \frac{2\lambda \mu }{\lambda +2\mu }}\left({\displaystyle \frac{\partial u_r}{\partial r}}+{\displaystyle \frac{u_r}{r}}\right)+2\mu {\displaystyle \frac{u_r}{r}}-{\displaystyle \frac{2\mu }{\lambda +2\mu }}\alpha T.$$

(50b)

Substituting Equations (8), (22), (25) and (33) into Equation (50) yields the normalized expressions for the radial and hoop stresses of the upper surface of substrate as

$$\begin{array}{ll}{\displaystyle \frac{{\sigma }_{rr}^s\left(r\right)}{{\tau }_0}}=& {\displaystyle \frac{a}{{\Re }_{1}h}}{\displaystyle \frac{4\mu \left(\lambda +\mu \right)}{\lambda +2\mu }}\left[{\displaystyle {\int }_0^{\zeta }\widehat{\tau }\left(\eta \right)}d\eta -{\displaystyle {\int }_0^1\widehat{\tau }\left(\eta \right)}d\eta \right]\\ & +\left(c_{11}-c_{12}\right){\displaystyle \frac{8\left(\lambda +\mu \right)}{\lambda +2\mu }}{\displaystyle \frac{1-v}{\pi {\Re }_1}}{\displaystyle {\int }_0^1\left[K\left(\eta \right)-E\left(\eta \right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \\ & -{\displaystyle \frac{4}{\pi }}\left(1-v\right){\displaystyle \frac{1}{\zeta }}\left\{\left[{\displaystyle {\int }_0^{\zeta }\left[K\left(\frac{\eta }{\zeta }\right)-E\left(\frac{\eta }{\zeta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right.\right.\\ & \left.\left.+{\displaystyle {\int }_{\zeta }^1\frac{\eta }{\zeta }\left[K\left(\frac{\zeta }{\eta }\right)-E\left(\frac{\zeta }{\eta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right]\right\}-2\mu {\displaystyle \frac{1-v}{{\tau }_0\Gamma }}T\\ & +\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{{\tau }_0\Gamma {\Re }_1}}{\displaystyle \frac{4\mu \left(\lambda +\mu \right)}{\lambda +2\mu }}T-{\displaystyle \frac{2\mu }{\lambda +2\mu }}{\displaystyle \frac{\alpha T}{{\tau }_0}}\\ & -{\displaystyle \frac{4\mu \left(\lambda +\mu \right)}{\left(\lambda +2\mu \right){\Re }_1}}{\displaystyle \frac{{\Im }_1{E}_z+{\Im }_{2}T+{\Im }_{3}C}{{\tau }_0}},\end{array}$$

(51a)

$$\begin{array}{ll}{\displaystyle \frac{{\sigma }_{\varphi \varphi }^s\left(r\right)}{{\tau }_0}}=& {\displaystyle \frac{a}{{\Re }_{1}h}}{\displaystyle \frac{2\lambda \mu }{\lambda +2\mu }}\left[{\displaystyle {\int }_0^{\zeta }\widehat{\tau }\left(\eta \right)}d\eta -{\displaystyle {\int }_0^1\widehat{\tau }\left(\eta \right)}d\eta \right]\\ & +\left(c_{11}-c_{12}\right){\displaystyle \frac{4\lambda \mu }{\lambda +2\mu }}\cdot {\displaystyle \frac{1-v}{\pi \mu {\Re }_1}}{\displaystyle {\int }_0^1\left[K\left(\eta \right)-E\left(\eta \right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \\ & +{\displaystyle \frac{4}{\pi }}\left(1-v\right){\displaystyle \frac{1}{\zeta }}\left\{{\displaystyle {\int }_0^{\zeta }\left[K\left(\frac{\eta }{\zeta }\right)-E\left(\frac{\eta }{\zeta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right.\\ & \left.+{\displaystyle {\int }_{\zeta }^1\frac{\eta }{\zeta }\left[K\left(\frac{\zeta }{\eta }\right)-E\left(\frac{\zeta }{\eta }\right)\right]\stackrel{⏜}{\tau }\left(\eta \right)}d\eta \right\}+2\mu {\displaystyle \frac{1-v}{{\tau }_0\Gamma }}T\\ & +\left(c_{11}-c_{12}\right){\displaystyle \frac{1-v}{{\tau }_0\Gamma {\Re }_1}}\cdot {\displaystyle \frac{2\lambda \mu }{\lambda +2\mu }}T-{\displaystyle \frac{2\mu }{\lambda +2\mu }}{\displaystyle \frac{\alpha T}{{\tau }_0}}\\ & -{\displaystyle \frac{2\lambda \mu }{\left(\lambda +2\mu \right){\Re }_1}}{\displaystyle \frac{{\Im }_1{E}_z+{\Im }_{2}T+{\Im }_{3}C}{{\tau }_0}}.\end{array}$$

(51b)

According to Equations (35), (44), (48) and (51), the normalization ${\tau }_0$ depends on the material constants and is strongly determined by the applied electric voltage, temperature change, and mass concentration. Meanwhile, all the displacements and stresses show a linear relation with the normalization ${\tau }_0$. This solution allows regulation and control of the mechanical response by adjusting the applied voltage when the structure is placed in a certain temperature and mass concentration environment. As the asymptotic behavior of the shear stress near the edge of the actuator can be interpreted as a measure of edge debonding failure mechanism, the Mode II SIF can be defined as

$$K_{\mathrm{II}}\left(a\right)=\underset{r\to a}{\lim }\sqrt{2\pi \left(a-r\right)}\tau \left(r\right).$$

(52)

Inserting Equations (35) and (37) into Equation (52) and considering the property of Chebyshev polynomials, the SIF can be calculated as

$$K_{\mathrm{II}}\left(a\right)=\sqrt{2\pi a}{\tau }_0{\displaystyle \sum _{j=0}^N{b}_j}.$$

(53)

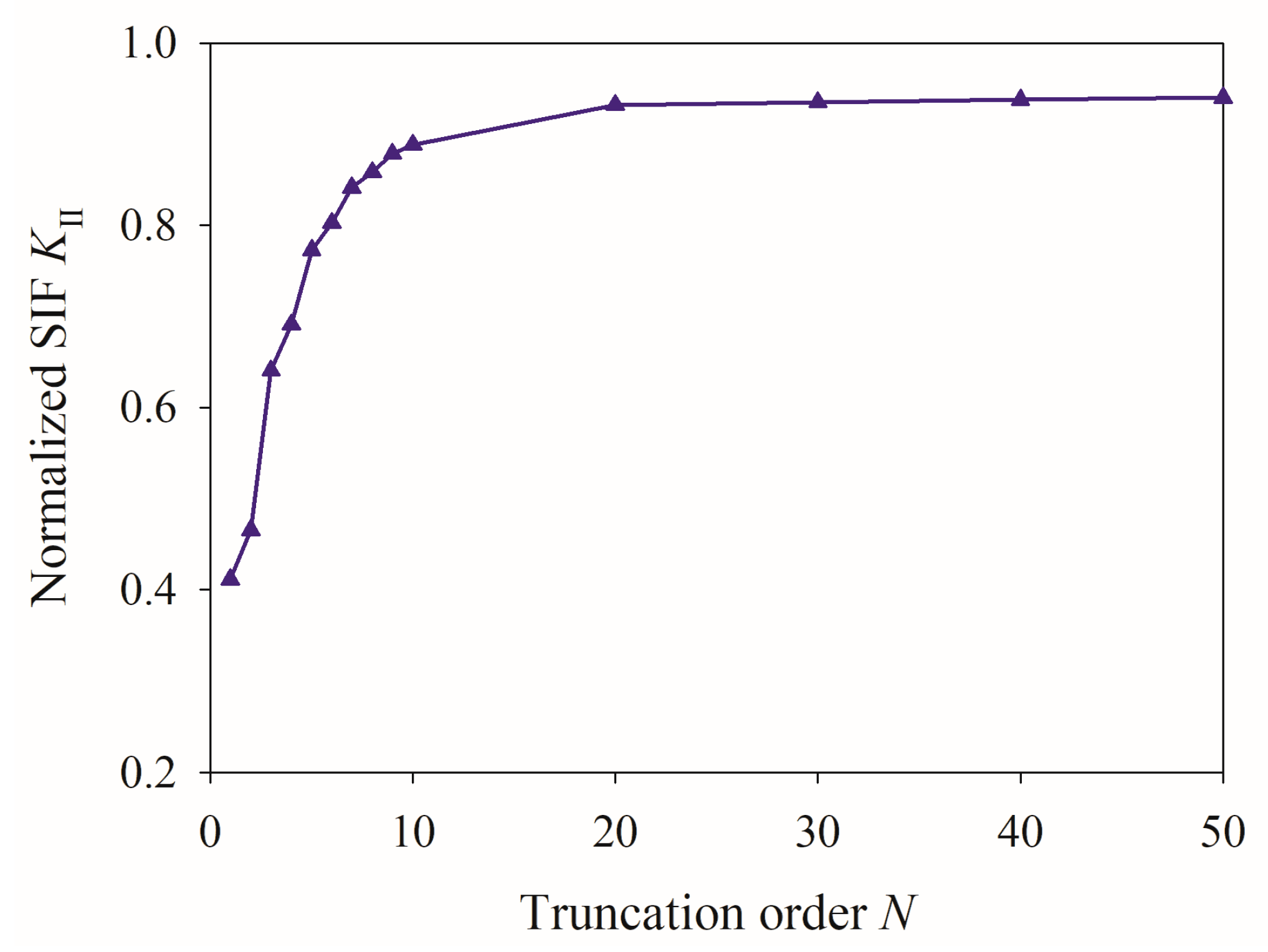
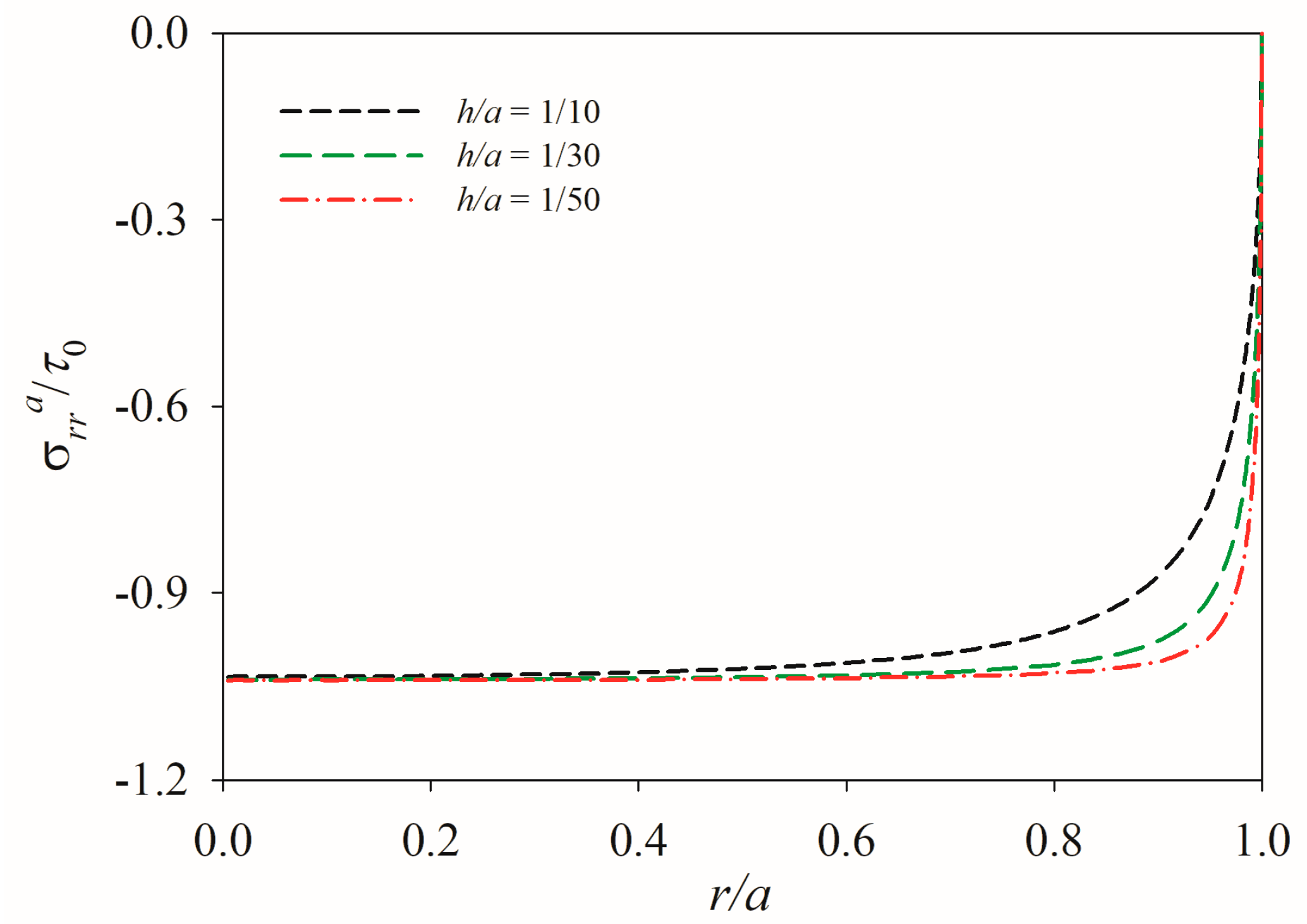
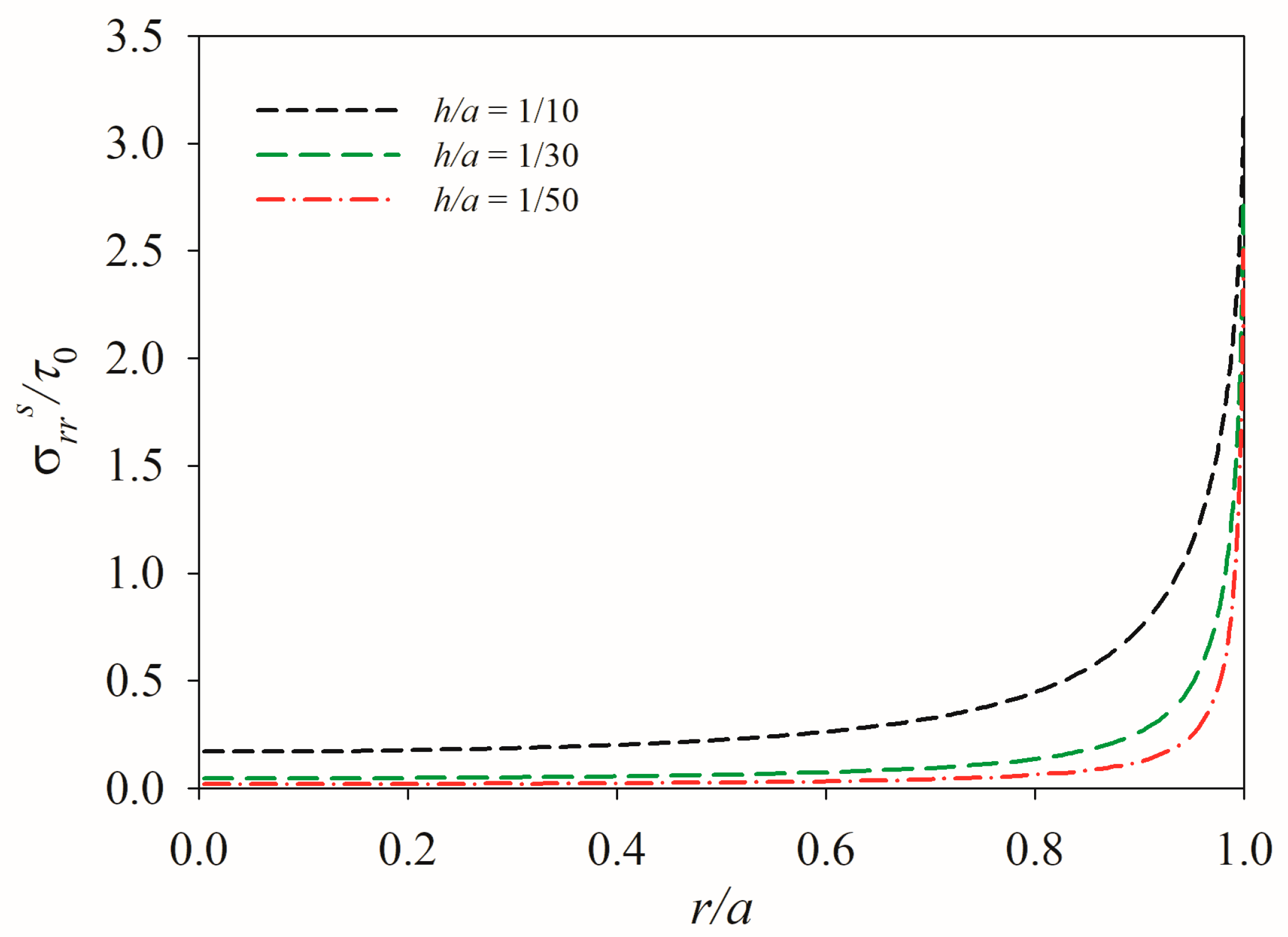
5. Results and Discussion

To systematically examine the factors governing the interfacial behavior of the PTD actuator, a series of numerical simulations were conducted. For conciseness while maintaining generality, all stresses, displacements and SIFs were normalized by ${\tau }_0$, a, and ${\tau }_0\sqrt{a}$, respectively. Cadmium selenide (CdSe), a representative II–VI compound semiconductor, exhibits exceptional piezoelectric performance and pronounced ionic diffusion capabilities. These distinctive properties endow CdSe with significant potential for diverse applications spanning sensor technologies, energy devices and environmental monitoring systems. Consequently, CdSe was selected as the PTD material in this study, with its complete material constants referenced from [36]. Three typical substrate materials, i.e., copper (Cu), zirconium dioxide (ZrO₂), and silicon (Si) were investigated, and their material properties are listed in

Table 1. The material properties of three kinds of substrate materials.

Material	E (GPa)	v	a (10−6/K)
Cu	129	0.35	17.0
ZrO2	244	0.29	10.6
Si	169	0.22	2.6

.

The selection of the truncation order N critically influences the reliability and computational accuracy of the calculation. As illustrated in Figure 2, the SIF converges to a stable value once N exceeds 20. To ensure high numerical precision, a truncation order of N = 40 was adopted in subsequent computations.

5.1. Influence of Aspect Ratio

At first, the influence of aspect ratio is discussed, and the substrate material is fixed as Cu. As depicted in Figure 3, the interfacial shear stress nearly vanishes in the center of the actuator while increases monotonically along the radial direction. An obvious singularity emerges near the actuator edge, which serves as the likely initiation site for interfacial delamination. Notably, thicker actuator induces higher shear stress magnitudes, suggesting an increased propensity for debonding compared to their thinner counterparts.

Figure 3 also demonstrates that, the analytical results coincide well with finite element (FE) simulations by COMSOL Multiphysics 3.5a, particularly at higher aspect ratio. The minor discrepancies observed arise from inherent model simplifications, i.e., the present theoretical framework employs membrane theory under axisymmetric assumptions, effectively reducing the problem to a quasi-1D formulation, whereas the FE analysis retain full 3D resolution. This comparison confirms that the membrane approximation remains valid for high aspect ratio configurations.

In the FE simulation was performed using a 3D axisymmetric model implemented in COMSOL’s PDE module. The computational domain comprised over 40,000 hexahedral elements, yielding approximately 1.2 million degrees of freedom. Perfect bonding conditions were enforced at interfaces, with hexahedral elements maintained throughout the domain boundaries (see Figure 4). Convergence studies verified mesh independence, and the truncated outer boundary was set at eight times the film radius (R = 8a). remarkably, while the analytical solution required only 40 collocation points to achieve sufficient accuracy, it demonstrated significantly lower computational expense compared to the full 3D FE simulation.

The radial displacement shows an obvious distribution in the actuator, and a thicker actuator possesses a larger radial displacement (see Figure 5). It is easy to find that the absolute value of the radial stress and hoop stress are almost constant in the center of the actuator, and then the radial stress starts to decrease and tends to zero at the film front, which agrees well with the free traction boundary condition at the film edge, while the hoop stress increases to a certain value at the actuator edge (see Figure 6 and Figure 7). At the same time, a thinner actuator possesses a larger radial stress and less hoop stress. It is readily observed from Figure 8 and Figure 9 that, the variation trend of stresses at the surface of the substrate is quite opposite to that in the actuator, and a thicker actuator induces larger values of radial stress and hoop stress. Therefore, designing a thinner axisymmetric PTD actuator can greatly alleviate the failure risk of the substrate near the edge of the actuator.

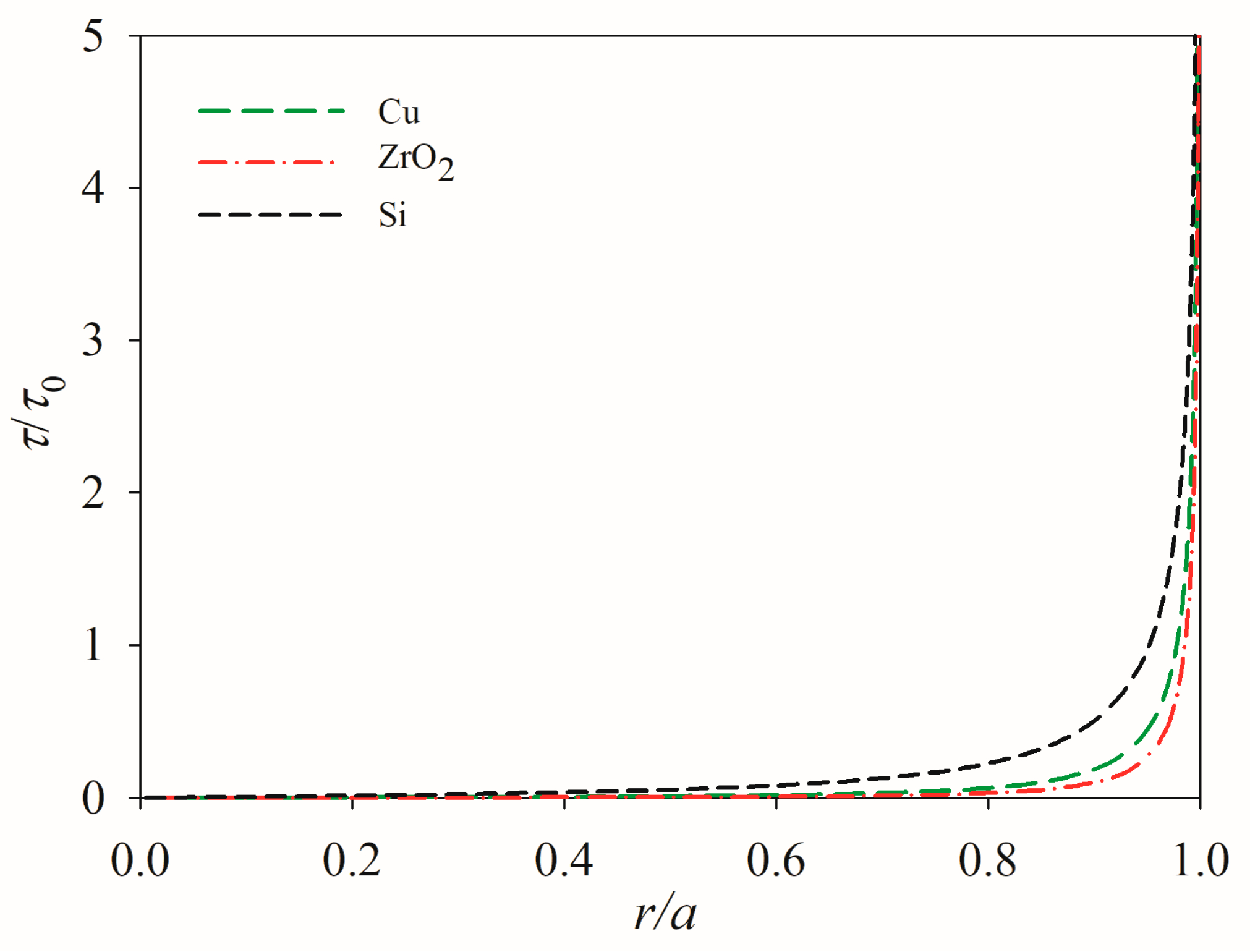
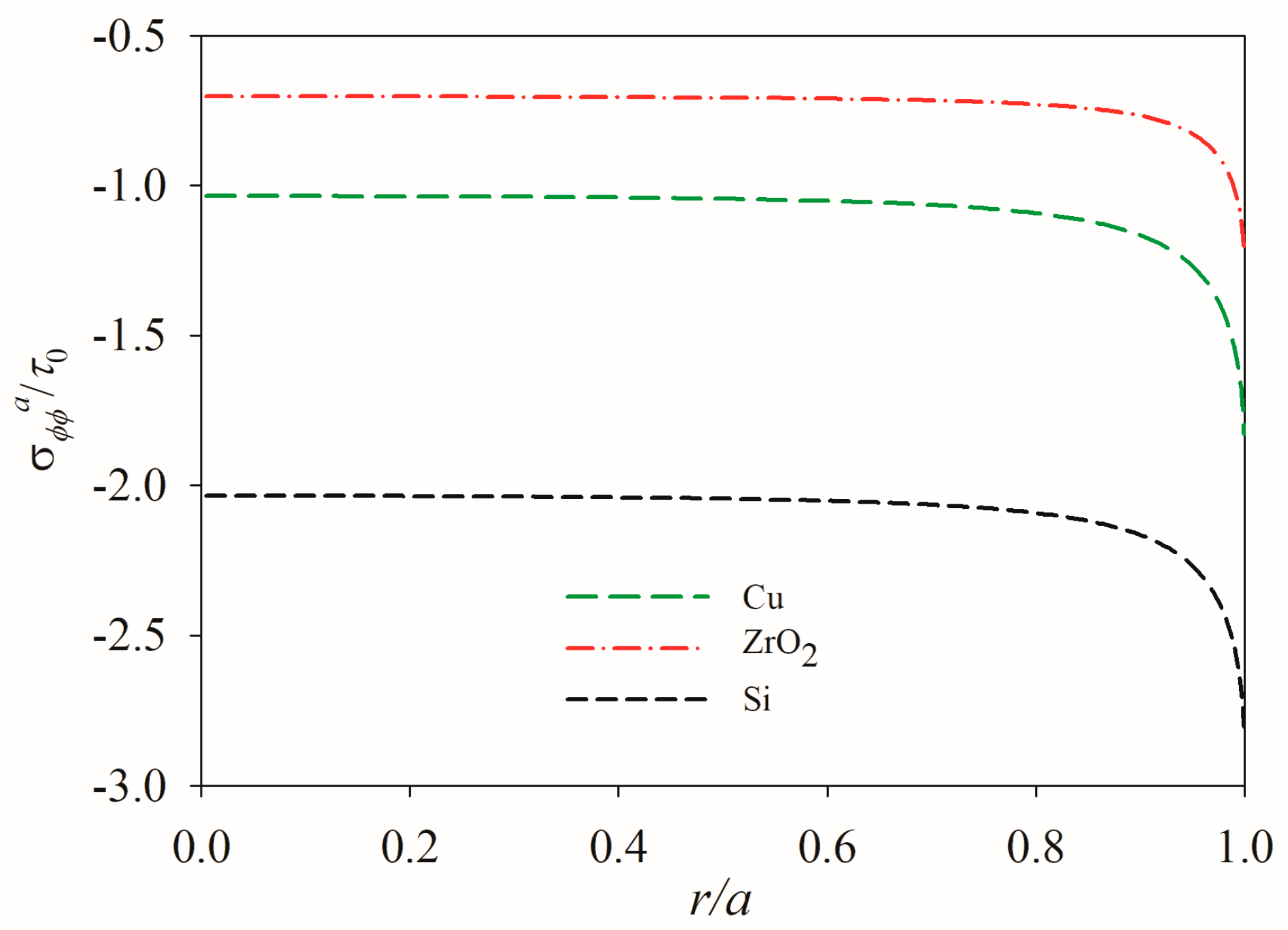
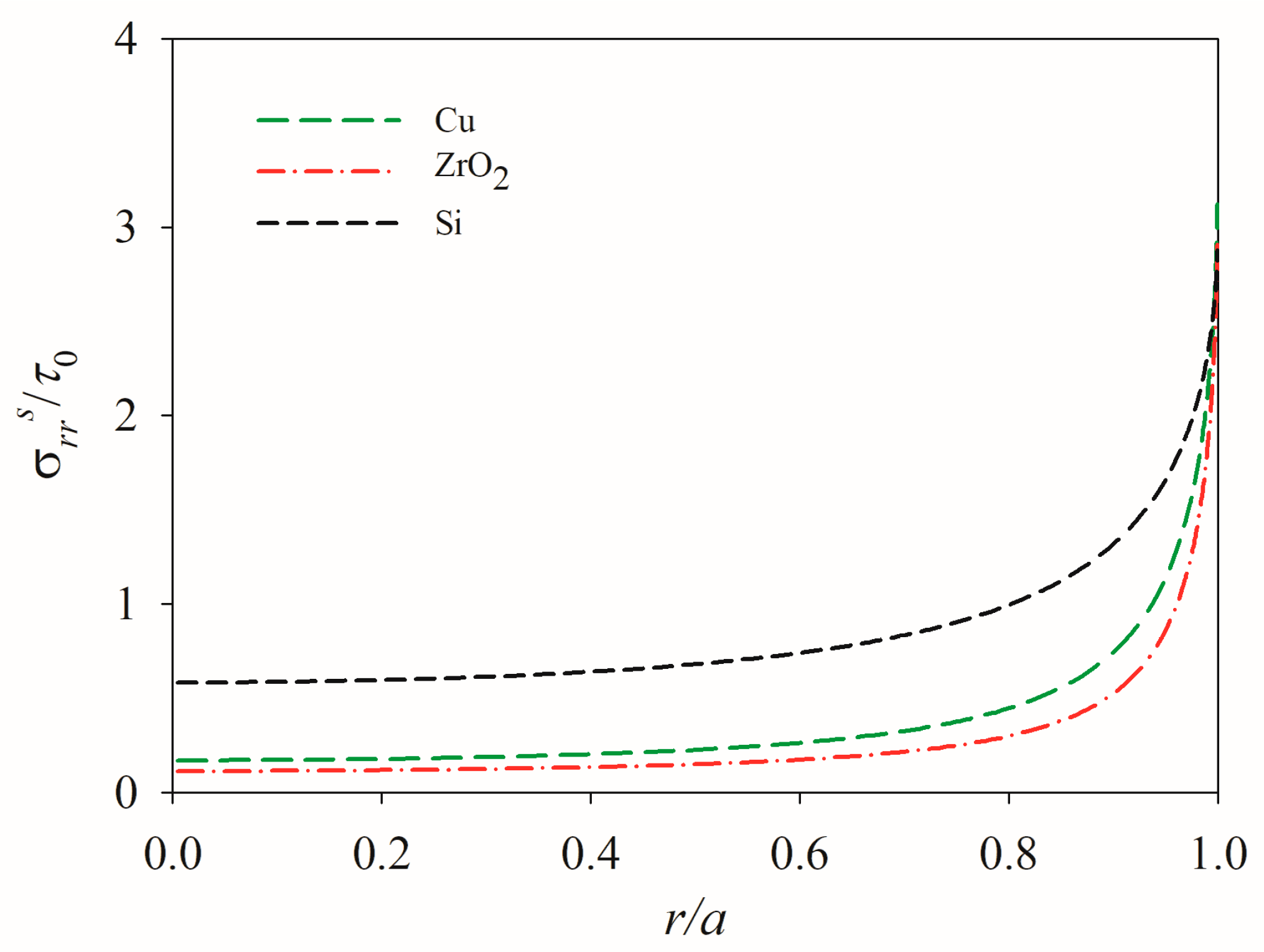
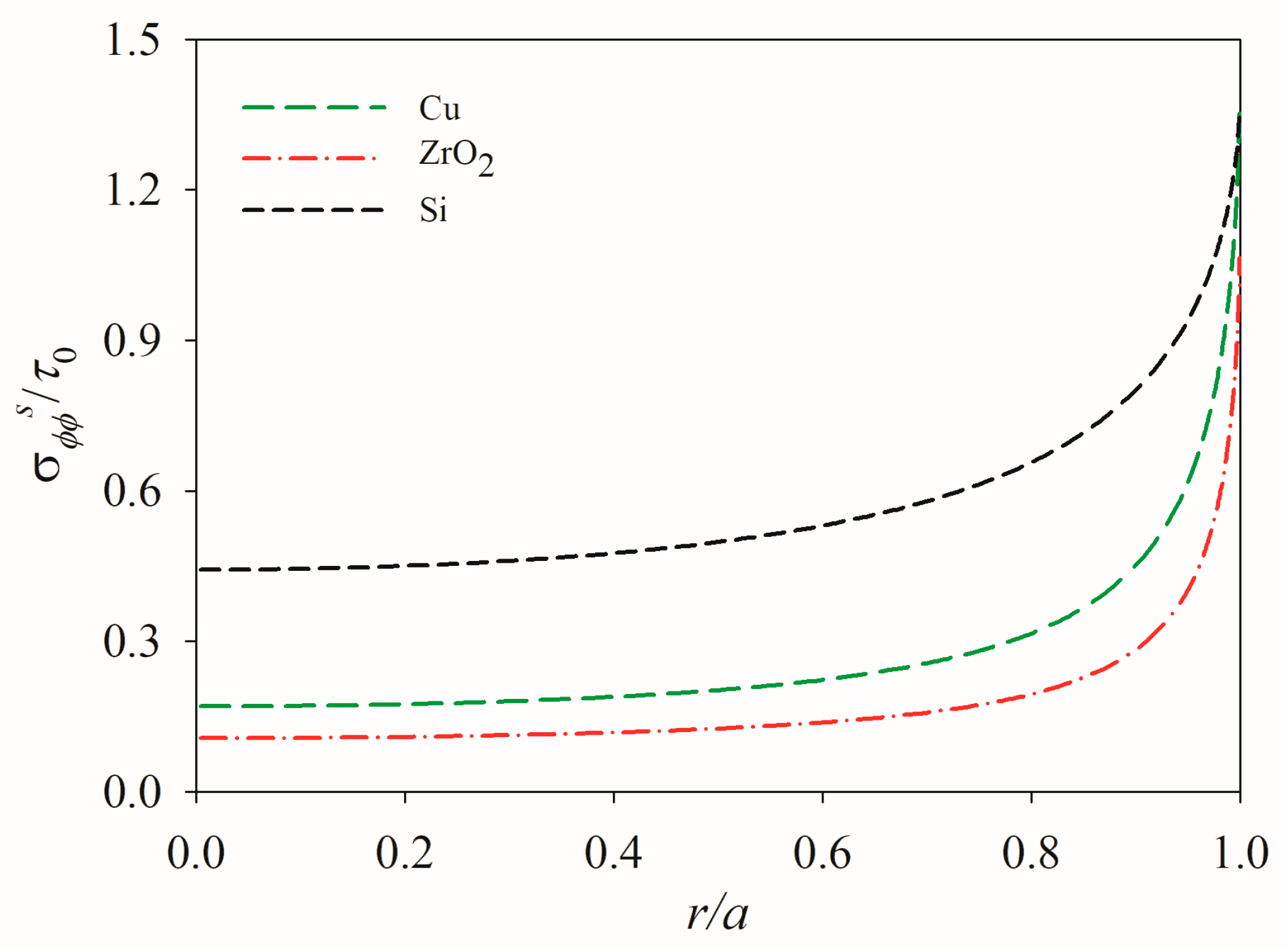
5.2. Influence of Material Mismatch

As illustrated in Figure 10, different substrate materials have great influence on the interfacial shear stress. Based on the governing integral equation in Equation (36), the influencing factors of material mismatch are dependent on material constants of PTD actuator and substrate. For a fixed PTD material, the influencing factor of substrate material is mainly related to a comprehensive parameter ${\beta }_s=\mu /\left(1-v\right)$. A lower value of ${\beta }_s$ leads to a higher level of interfacial shear stress. As the radial displacement, radial stress and hoop stress are all related to the shear stress, a substrate with lower value of ${\beta }_s$ possesses larger displacement and stresses (see Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15). Therefore, selecting a substrate with lower ${\beta }_s$ can reduce the level of stresses and enhance the bonding strength. Figure 16 shows that, increasing the film thickness and value of ${\beta }_s$ will enlarge the value of stress intensity factor and eventually lead to delamination.

6. Conclusions

A thin axisymmetric PTD actuator was analyzed under electrical–thermal–diffusive loads based perfect bonding condition. The integral equation was established in terms of interfacial shear stress. The integral equation was numerically solved by Chebyshev polynomials. Delamination behavior was studied using the fracture parameter of stress intensity factor. The membrane theory approximation adopted in this study renders the solution particularly suitable for high aspect ratio configuration (a/h >>1). For cases where bending moment and peeling stresses become non-negligible, higher-order theories (e.g., beam or plate theories) would be required for accurate modeling. The following important conclusions are drawn.

• The proposed analytical model effectively captures the mechanical response of an axisymmetric PTD actuator. Numerical results reveal that interfacial shear stress concentration near the actuator edge periphery governs delamination initiation.
• The total strain exhibits linear dependence on applied multi-physical loads while being modulated by material properties. This linearity enables precise control of mechanical response through load parameter manipulation.
• Both material properties and geometric factors significantly influence the mechanical performance. Specifically, thicker PTD actuators bonded to substrates with lower stiffness ratios are more susceptible to edge debonding.

The present work provides fundamental insights into the intrinsic relationships between mechanical performance, material properties, and geometric parameters in PTD systems. Compared with FE simulations, the proposed method offers substantial computational efficiency while maintaining satisfactory accuracy. These findings contribute valuable theoretical foundations for both functional design optimization and failure mode assessment in PTD actuator systems.