A Modified Nonlocal Macro–Micro-Scale Damage Model for the Simulation of Hydraulic Fracturing
Abstract
1. Introduction
2. Brief Summary of NMMD Model
2.1. Microstructural-Scale Damage
2.2. Geometric Damage Reflecting Macro-Scale Continuity Loss and Free Energy Damage Reflecting Stiffness Degradation
2.3. Nonlocal Damage Constitutive Model for Tensile or Tensile–Shear Fracture
3. Modified NMMD Model for Hydraulic Fracture in Porous Media
3.1. Fluid Flow in the Isotropic Medium
3.2. Governing Equations
4. Numerical Examples
4.1. Verification: KGD Hydraulic Fracturing Problem
4.1.1. Convergence of Mesh Sizes with Semi-Analytical Solution
4.1.2. Influence of the Interpenetrating Parameter
4.1.3. Comparison with Phase Field Models
4.2. Double-Fracture Hydraulic Fracturing with Different Spacing
4.3. Hydraulic Fracturing with Natural Pores
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, W.; Geng, Y.; Zhou, Z.; Li, L.; Ding, R.; Wu, Z.; Zhai, M. True triaxial hydraulic fracturing test and numerical simulation of limestone. J. Cent. South Univ. 2020, 27, 3025–3039. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Yuan, L.; Xiong, Z.-Y.; Hou, B.; Chen, M.; Wan, L.-M. Understanding hydraulic fracture propagation behavior in tight sandstone–coal interbedded formations: An experimental investigation. Pet. Sci. 2019, 16, 148–160. [Google Scholar] [CrossRef]
- Chen, D.; Li, N.; Sun, W. Rupture properties and safety assessment of raw coal specimen rupture process under true triaxial hydraulic fracturing based on the source parameters and magnitude. Process Saf. Environ. Prot. 2022, 158, 661–673. [Google Scholar] [CrossRef]
- Li, M.; Zhou, F.; Dong, E.; Zhang, G.; Zhuang, X.; Wang, B. Experimental study on the multiple fracture simultaneous propagation during extremely limited-entry fracturing. J. Petrol. Sci. Eng. 2022, 218, 110906. [Google Scholar] [CrossRef]
- Bao, J.Q.; Fathi, E.; Ameri, S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique. Eng. Fract. Mech. 2014, 131, 269–281. [Google Scholar] [CrossRef]
- Bao, J.Q.; Fathi, E.; Ameri, S. Uniform investigation of hydraulic fracturing propagation regimes in the plane strain model. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 507–523. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Gordeliy, E.; Peirce, A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM. Comput. Methods Appl. Mech. Eng. 2013, 253, 305–322. [Google Scholar] [CrossRef]
- Li, J.; Dong, S.; Hua, W.; Yang, Y.; Li, X. Numerical Simulation on Deflecting Hydraulic Fracture with Refracturing Using Extended Finite Element Method. Energies 2019, 12, 2044. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Z.; Xia, X. Interface stress element method and its application in analysis of anti-sliding stability of gravity dam. Sci. China Technol. Sci. 2012, 55, 3285–3291. [Google Scholar] [CrossRef]
- Yan, C.; Jiao, Y.-Y.; Zheng, H. A fully coupled three-dimensional hydro-mechanical finite discrete element approach with real porous seepage for simulating 3D hydraulic fracturing. Comput. Geotech. 2018, 96, 73–89. [Google Scholar] [CrossRef]
- Huang, L.; Liu, J.; Zhang, F.; Dontsov, E.; Damjanac, B. Exploring the influence of rock inherent heterogeneity and grain size on hydraulic fracturing using discrete element modeling. Int. J. Solids Struct. 2019, 176–177, 207–220. [Google Scholar] [CrossRef]
- Yang, W.; Li, S.; Geng, Y.; Zhou, Z.; Li, L.; Gao, C.; Wang, M. Discrete element numerical simulation of two-hole synchronous hydraulic fracturing. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 55. [Google Scholar] [CrossRef]
- Deng, S.; Li, H.; Ma, G.; Huang, H.; Li, X. Simulation of shale–proppant interaction in hydraulic fracturing by the discrete element method. Int. J. Rock Mech. Min. Sci. 2014, 70, 219–228. [Google Scholar] [CrossRef]
- Marina, S.; Imo-Imo, E.K.; Derek, I.; Mohamed, P.; Yong, S. Modelling of hydraulic fracturing process by coupled discrete element and fluid dynamic methods. Environ. Earth Sci. 2014, 72, 3383–3399. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic States Constitutive Modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Gu, X.; Li, X.; Xia, X.; Madenci, E.; Zhang, Q. A robust peridynamic computational framework for predicting mechanical properties of porous quasi-brittle materials. Compos. Struct. 2023, 303, 116245. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Madenci, E.; Xia, X. Possible causes of numerical oscillations in non-ordinary state-based peridynamics and a bond-associated higher-order stabilized model. Comput. Methods Appl. Mech. Eng. 2019, 357, 112592. [Google Scholar] [CrossRef]
- Cao, C.; Gu, C.; Wang, C.; Wang, C.; Xu, P.; Wang, H. A Peridynamics-Smoothed Particle Hydrodynamics Coupling Method for Fluid-Structure Interaction. J. Mar. Sci. Eng. 2024, 12, 1968. [Google Scholar] [CrossRef]
- Zeleke, M.A.; Ageze, M.B. A Review of Peridynamics (PD) Theory of Diffusion Based Problems. J. Eng. 2021, 2021, 7782326. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Wu, J.-Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Xia, X.; Qin, C.; Lu, G.; Gu, X.; Zhang, Q. Simulation of Corrosion-Induced Cracking of Reinforced Concrete Based on Fracture Phase Field Method. Comput. Model. Eng. Sci. 2024, 138, 2257–2276. [Google Scholar] [CrossRef]
- Deogekar, S.; Vemaganti, K. A computational study of the dynamic propagation of two offset cracks using the phase field method. Eng. Fract. Mech. 2017, 182, 303–321. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J. A phase-field method for two-phase fluid flow in arbitrary domains. Comput. Math. Appl. 2020, 79, 1857–1874. [Google Scholar] [CrossRef]
- Shen, R.; Waisman, H.; Guo, L. Fracture of viscoelastic solids modeled with a modified phase field method. Comput. Methods Appl. Mech. Eng. 2019, 346, 862–890. [Google Scholar] [CrossRef]
- Huang, D.; Lu, G.; Liu, Y. Nonlocal Peridynamic Modeling and Simulation on Crack Propagation in Concrete Structures. Math. Probl. Eng. 2015, 2015, 858723. [Google Scholar] [CrossRef]
- Lu, G.; Chen, J. A new nonlocal macro-meso-scale consistent damage model for crack modeling of quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2020, 362, 112802. [Google Scholar] [CrossRef]
- Lu, G.; Chen, J. Dynamic cracking simulation by the nonlocal macro-meso-scale damage model for isotropic materials. Int. J. Numer. Methods Eng. 2021, 122, 3070–3099. [Google Scholar] [CrossRef]
- Lv, W.; Lu, G.; Xia, X.; Gu, X.; Zhang, Q. Discrepancy-informed quadrature strategy for the nonlocal macro-meso-scale consistent damage model. Comput. Methods Appl. Mech. Eng. 2024, 432, 117315. [Google Scholar] [CrossRef]
- Lv, W.; Lu, G.; Xia, X.; Gu, X.; Zhang, Q. Energy degradation mode in nonlocal Macro-Meso-Scale damage consistent model for quasi-brittle materials. Theor. Appl. Fract. Mech. 2024, 130, 104288. [Google Scholar] [CrossRef]
- Xia, X.; Wang, X.; Lu, G.; Gu, X.; Lv, W.; Zhang, Q.; Ma, L. A new nonlocal macro-micro-scale consistent damage model for layered rock mass. Theor. Appl. Fract. Mech. 2024, 133, 104540. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D. Numerical investigation of hydraulic fracture height growth in layered rock based on peridynamics. Theor. Appl. Fract. Mech. 2023, 125, 103885. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Chen, W.; Yang, S. Hydraulic fracturing model of a layered rock mass based on peridynamics. Eng. Fract. Mech. 2021, 258, 108088. [Google Scholar] [CrossRef]
- Chukwudozie, C.; Bourdin, B.; Yoshioka, K. A variational phase-field model for hydraulic fracturing in porous media. Comput. Methods Appl. Mech. Eng. 2019, 347, 957–982. [Google Scholar] [CrossRef]
- Santillán, D.; Juanes, R.; Cueto-Felgueroso, L. Phase Field Model of Hydraulic Fracturing in Poroelastic Media: Fracture Propagation, Arrest, and Branching Under Fluid Injection and Extraction. JGR Solid Earth 2018, 123, 2127–2155. [Google Scholar] [CrossRef]
- Yoshioka, K.; Naumov, D.; Kolditz, O. On crack opening computation in variational phase-field models for fracture. Comput. Methods Appl. Mech. Eng. 2020, 369, 113210. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X. Phase field modeling of hydraulic fracture propagation in transversely isotropic poroelastic media. Acta Geotech. 2020, 15, 2599–2618. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S.; Sheng, M.; Li, G. On the hydraulic fracturing in naturally-layered porous media using the phase field method. Eng. Geol. 2020, 266, 105306. [Google Scholar] [CrossRef]
- Ren, Y.; Lu, G.; Chen, J. Physically consistent nonlocal macro–meso-scale damage model for quasi-brittle materials: A unified multiscale perspective. Int. J. Solids Struct. 2024, 293, 112738. [Google Scholar] [CrossRef]
- Lu, G.; Chen, J.; Ren, Y. New insights into fracture and cracking simulation of quasi-brittle materials based on the NMMD model. Comput. Methods Appl. Mech. Eng. 2024, 432, 117347. [Google Scholar] [CrossRef]
- Ren, Y.; Chen, J.; Lu, G. A structured deformation driven nonlocal macro-meso-scale consistent damage model for the compression/shear dominate failure simulation of quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2023, 410, 115945. [Google Scholar] [CrossRef]
- Ren, Y.; Chen, J.; Lu, G. Characterize the pairwise deformation gradient without least squares in 2D: Application in the NMMD model. Comput. Methods Appl. Mech. Eng. 2025, 436, 117715. [Google Scholar] [CrossRef]
- Lu, G. On the Choice of the Characteristic Length in the NMMD Model for the Simulation of Brittle Fractures. Buildings 2024, 14, 3932. [Google Scholar] [CrossRef]
- Detournay, E.; Garagash, D.I. The near-tip region of a fluid-driven fracture propagating in a permeable elastic solid. J. Fluid Mech. 2003, 494, 1–32. [Google Scholar] [CrossRef]
- Detournay, E. Propagation Regimes of Fluid-Driven Fractures in Impermeable Rocks. Int. J. Geomech. 2004, 4, 35–45. [Google Scholar] [CrossRef]












| Parameter | Value |
|---|---|
| Shear modulus G | 9.0 GPa |
| Poisson’s ratio | 0.2 |
| Biot coefficient | 1.0 |
| Fluid viscosity | 0.001 Pa·s |
| Injection rate | m2/s. |
| Permeability coefficient of undamaged area | |
| Permeability coefficient of completely damaged area | |
| Porosity n | 0.19 |
| Critical elongation rate | |
| Brittleness index | 2000 |
| p | 3.0 |
| q | 15.0 |
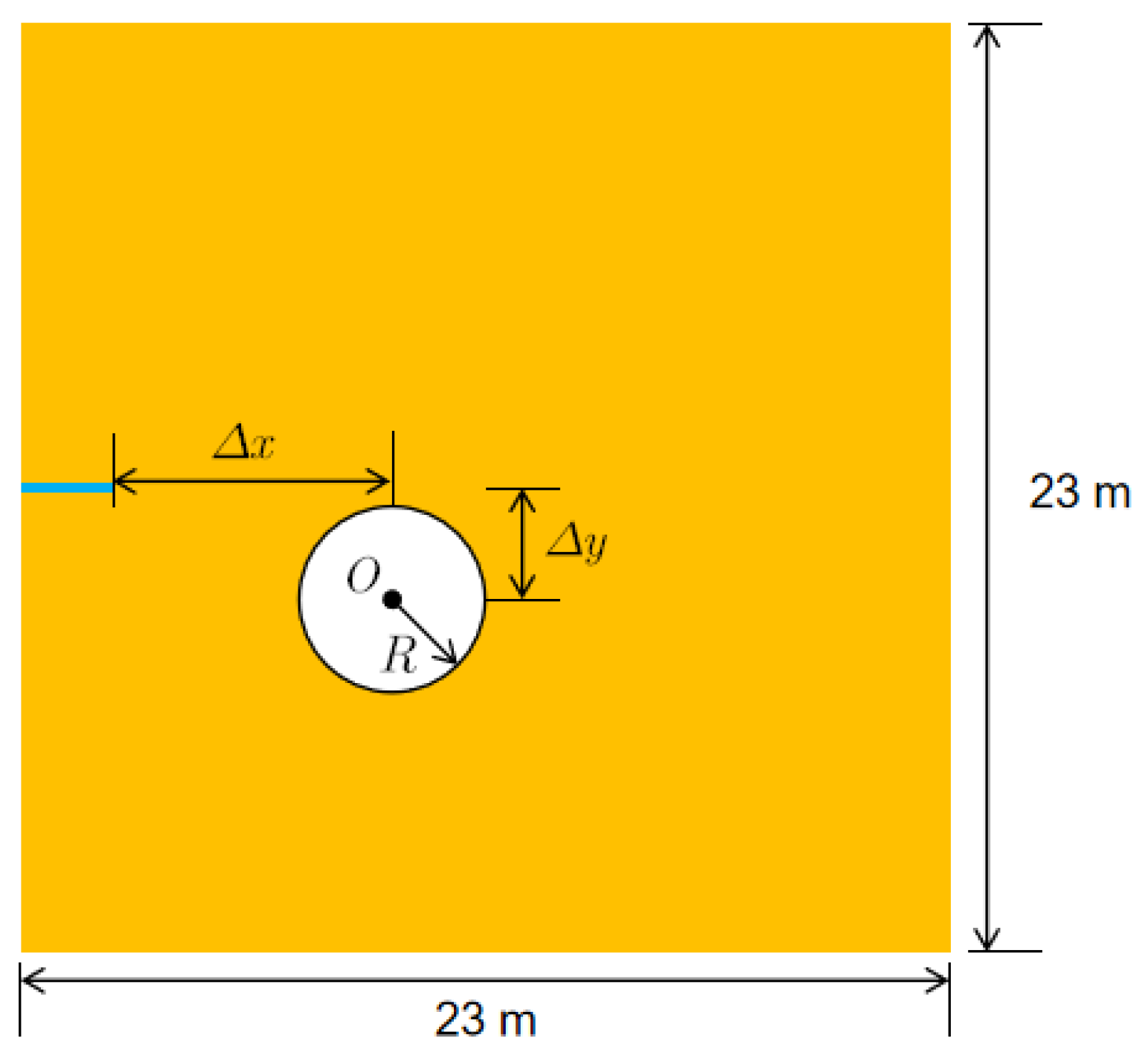
| Case | (m) | R (m) | |
|---|---|---|---|
| A | 5.7 | 0 | 2.3 |
| B | 8.7 | 0 | 2.3 |
| C | 5.7 | 4.5 | 2.3 |
| D | 8.7 | 4.5 | 2.3 |
| E | 5.7 | 0 | 1 |
| F | 5.7 | 0 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Xia, X. A Modified Nonlocal Macro–Micro-Scale Damage Model for the Simulation of Hydraulic Fracturing. Modelling 2025, 6, 58. https://doi.org/10.3390/modelling6030058
Liu C, Xia X. A Modified Nonlocal Macro–Micro-Scale Damage Model for the Simulation of Hydraulic Fracturing. Modelling. 2025; 6(3):58. https://doi.org/10.3390/modelling6030058
Chicago/Turabian StyleLiu, Changgen, and Xiaozhou Xia. 2025. "A Modified Nonlocal Macro–Micro-Scale Damage Model for the Simulation of Hydraulic Fracturing" Modelling 6, no. 3: 58. https://doi.org/10.3390/modelling6030058
APA StyleLiu, C., & Xia, X. (2025). A Modified Nonlocal Macro–Micro-Scale Damage Model for the Simulation of Hydraulic Fracturing. Modelling, 6(3), 58. https://doi.org/10.3390/modelling6030058






