Minimizing Waste and Costs in Multi-Level Manufacturing: A Novel Integrated Lot Sizing and Cutting Stock Model Using Multiple Machines
Abstract
1. Introduction
2. Literature Review
- Cutting stock problem: The CSP is almost divided evenly between one and two-dimensional CSP, and the most recent papers are studying the one-dimensional problem. The one-dimensional case appears widely in the paper industry, while the two-dimensional case appears in the furniture industry. Most of the recent papers consider the presence of multiple types of objects. The most used formulations for CSP are Gilmore and Gomory and Valerio de Carvalho, and some authors compared them.
- Lot sizing problem: Most papers considered inventory of items, and less than half of the papers considered inventory of objects and final products. Regarding including setup in LSP, setup cost was included in approximately 40% of the papers, and few of them incorporated setup time. The authors concentrated on handling the integrated problem across either a single or two levels, where two operations are sequentially executed. There is a scarcity in integrating both problems over three production levels. Few research works considered the capacity constraints in the different production levels, and the capacity of cutting machines was the focus of the researchers. Multiple cutting machines were not considerably included in the reviewed papers.
- Mathematical model: The primary objective in most of the models was to minimize material waste and storage costs. In addition to these primary objectives, some authors also considered production or setup costs. The integrated problem is mostly formulated as a mixed integer linear programming model.
- Application area: The integrated problem appeared widely in the paper and furniture industries.
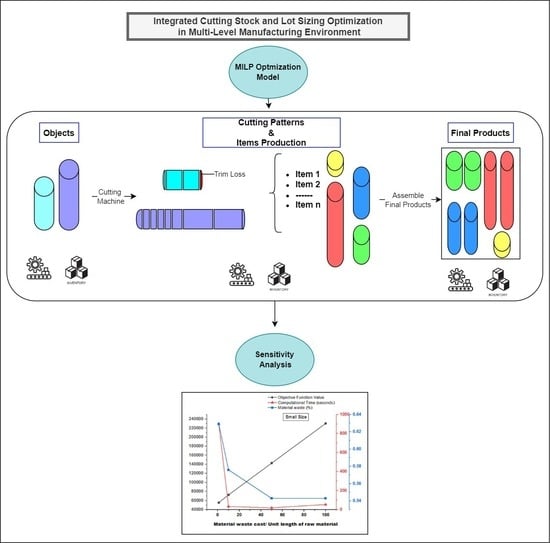
3. Proposed Model for the Integrated Problem
3.1. Model Description
3.2. Model Assumptions
- No initial inventory is considered over the three production levels;
- No limitations on stored quantities over the three production levels;
- Any item produced at a certain time period can be used in producing the final products within the same time period;
- Cutting machines have different capacities and costs;
- Safety stock levels are included in the final products’ demand.
3.3. Model Elements
3.3.1. Indexes
| t = 1, ….., T: number of time periods; |
| k = 1, ….., K: number of objects; |
| i = 1, ….., I: number of items; |
| f = 1, ….., F: number of final products; |
| m = 1, ….., M: number of cutting machines. |
3.3.2. Parameters
| Object length of type k; | |
| setup/ordering cost of object type k in time period t; | |
| setup time of object type k in period t; | |
| production/purchasing cost of object type k in time period t; | |
| production time of object type k in time period t; | |
| production time capacity to produce objects in time period t; | |
| holding cost of object type k in period t; | |
| item length of type i; | |
| cw | unit length cost of raw material waste; |
| setup cost of machine type m in time period t; | |
| setup time of machine type m in time period t; | |
| production cost of cutting object type k on machine m in time period t; | |
| production time of cutting object type k on machine m in time period t; | |
| cutting time capacity of machine m in time period t; | |
| holding cost of item type i in time period t; | |
| demand of final product type f in time period t; | |
| number of required items of type i for assembling final product f; | |
| setup cost of final product type f in time period t; | |
| setup time of final product type f in time period t; | |
| production cost of final product type f in time period t; | |
| production time of final product type f in time period t; | |
| production time capacity to produce final products in the time period t; | |
| holding cost of final product type f in time period t; | |
| M | big positive number. |
3.3.3. Decision Variables
| Quantity produced/purchased of object type k in the time period t; | |
| binary variable that indicates whether there is a production of object type k or not in the time period t; | |
| quantity stored of object type k at end of the time period t; | |
| flow through the network of object type k cut on machine type m in the time period t; | |
| quantity produced of item type i on machine type m in the time period t; | |
| binary variable that indicates whether machine type m is utilized or not in the time period t; | |
| quantity stored of item type i at the end of the time period t; | |
| number of items cut from an object on machine type m in the time period t, corresponding to an item of length (l-g) allocated at a distance g from the beginning of the object (considering all cutting patterns); | |
| quantity produced of final product type f in the time period t; | |
| binary variable that indicates whether there is a production of final product type f or not in the time period t; | |
| quantity stored of final product type f at the end of time period t. |
3.3.4. Objective Function
3.3.5. Constraints
4. Numerical Experiments, Sensitivity Analysis, Managerial Insights
4.1. Numerical Experiments
4.2. Data Generation
4.3. Instances’ Classes
4.4. Computational Results of Instances
4.5. Sensitivity Analysis
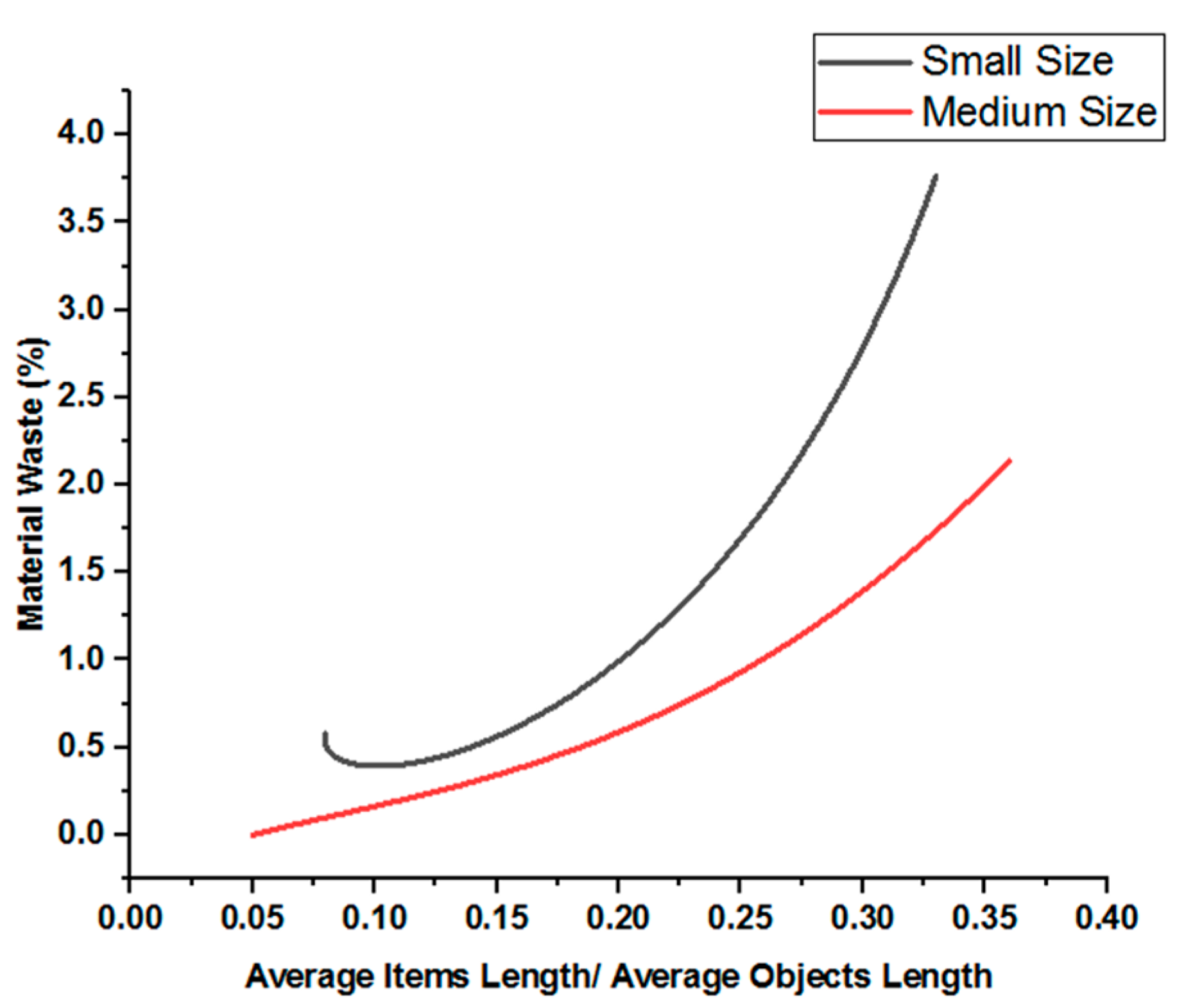
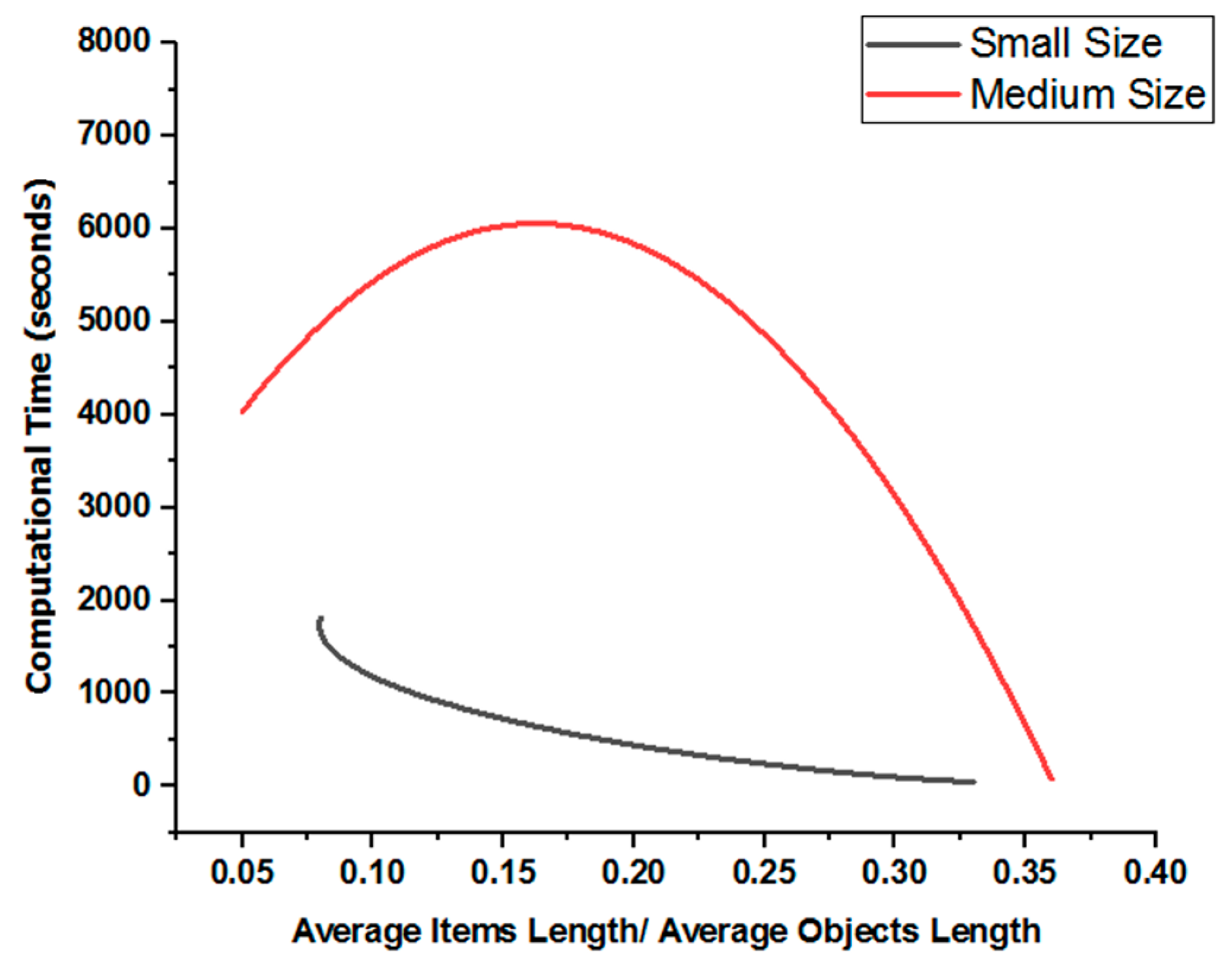
4.5.1. Studying Changing Items’ Length with Respect to Object Length
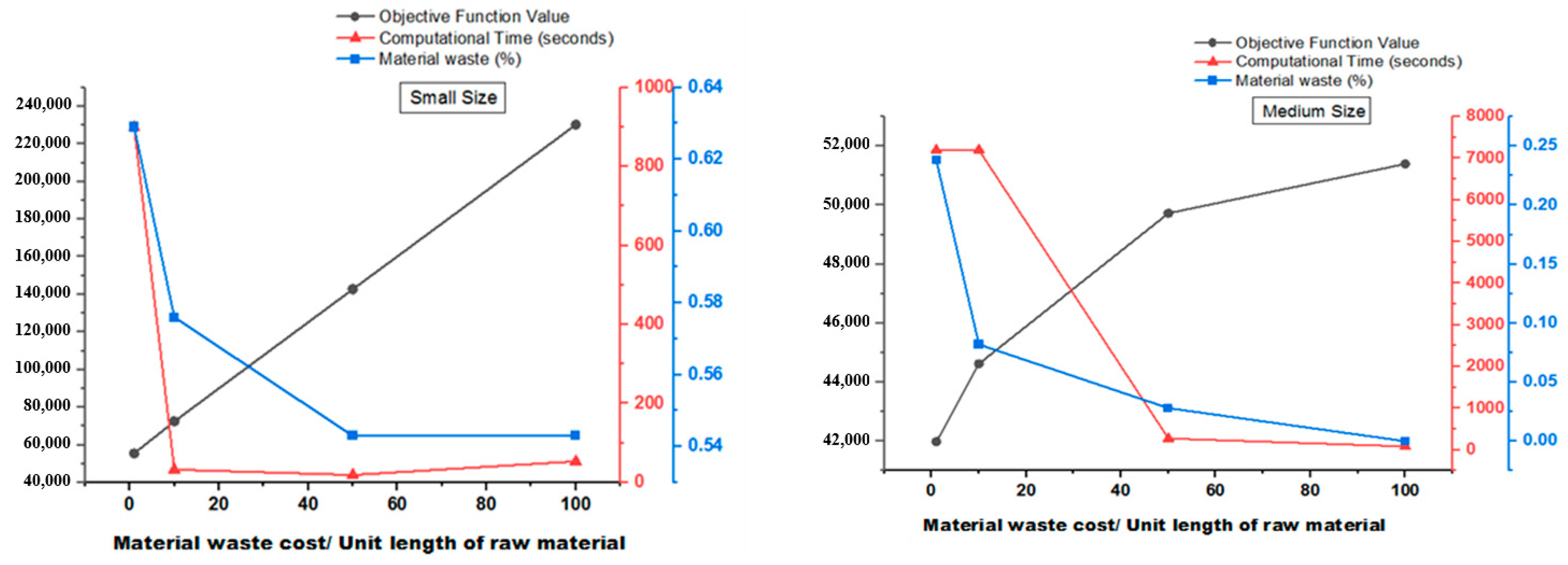
4.5.2. Studying Different Material Waste Cost
4.5.3. Studying Neglecting Setup Costs of Each Production Level
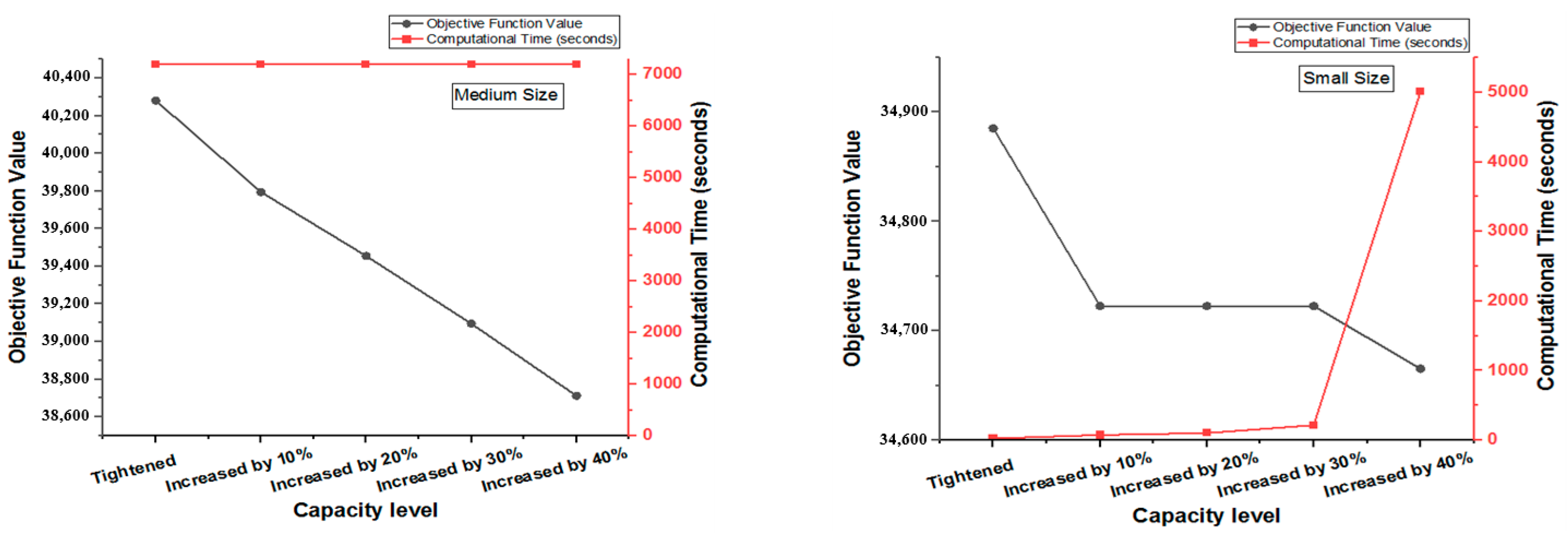
4.5.4. Studying Changing Capacity Levels
4.5.5. Studying Varying Inventory Holding Costs
4.6. Managerial Insights
- As changing items’ length with respect to object length showed an increase in material waste for large items’ length and resulted in more computational time for smaller items’ length. Then, managers should consider a leftover strategy in case of large items’ length to counter the increase in material waste. They should also balance material utilization with computational efficiency.
- Increasing material waste costs lead to decreased material waste percentage. Therefore, managers willing to achieve sustainability can increase material waste costs to reduce material waste.
- Neglecting setup costs for final products lowered the time consumed to solve the model. This gives insights to managers to neglect setup costs in case of having low setup costs, and in case of higher setup costs, they should focus on minimizing frequent changeovers and increasing batch sizes.
- Increasing capacity levels allowed for storing objects, items, and final products, which resulted in a decrease in total cost. Accordingly, managers should assess if expanding production capacity can provide long-term cost savings.
- Ignoring inventory cost for final products resulted in the lowest objective function value. Hence, managers should analyze the storage costs of their objects, items, and final products to decide on the optimal stocking strategies. In case of high storage costs for final products, they should prioritize storing items instead and assemble final products when needed.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Melega, G.M.; de Araujo, S.A.; Jans, R. Classification and literature review of integrated lot-sizing and cutting stock problems. Eur. J. Oper. Res. 2018, 271, 1–19. [Google Scholar] [CrossRef]
- Gramani, M.C.N.; França, P.M.; Arenales, M.N. A Lagrangian relaxation approach to a coupled lot-sizing and cutting stock problem. Int. J. Prod. Econ. 2009, 119, 219–227. [Google Scholar] [CrossRef]
- Gramani, M.C.N.; França, P.M.; Arenales, M.N. A linear optimization approach to the combined production planning model. J. Frankl. Inst. 2011, 348, 1523–1536. [Google Scholar] [CrossRef]
- Santos, S.G.; De Araujo, S.; Rangel, S. Integrated cutting machine programming and lot sizing in furniture industry. Pesqui. Oper. Para O Desenvolv. 2011, 3, 1–17. [Google Scholar]
- Alem, D.; Morabito, R. Risk-averse two-stage stochastic programs in furniture plants. OR Spectr. 2013, 35, 773–806. [Google Scholar] [CrossRef]
- José Alem, D.; Morabito, R. Production planning in furniture settings via robust optimization. Comput. Oper. Res. 2012, 39, 139–150. [Google Scholar] [CrossRef]
- Vanzela, M.; Melega, G.M.; Rangel, S.; Araujo, S.A.d. The integrated lot sizing and cutting stock problem with saw cycle constraints applied to furniture production. Comput. Oper. Res. 2017, 79, 148–160. [Google Scholar] [CrossRef]
- Vanzela, M.; Rangel, S.; De Araujo, S.A. The integrated lot sizing and cutting stock problem in a furniture factory. IFAC Proc. Vol. 2013, 46, 390–395. [Google Scholar] [CrossRef]
- Ayres, A.O.C.; Campello, B.S.C.; Oliveira, W.A.; Ghidini, C.T.L.S. A bi-integrated model for coupling lot-sizing and cutting-stock problems. OR Spectr. 2021, 43, 1047–1076. [Google Scholar] [CrossRef]
- Poltroniere, S.C.; Poldi, K.C.; Toledo, F.M.B.; Arenales, M.N. A coupling cutting stock-lot sizing problem in the paper industry. Ann. Oper. Res. 2007, 157, 91–104. [Google Scholar] [CrossRef]
- Poltroniere, S.C.; Araujo, S.A.; Poldi, K.C. Optimization of an integrated lot sizing and cutting stock problem in the paper industry. TEMA 2016, 17, 305. [Google Scholar] [CrossRef][Green Version]
- Valério de Carvalho, J.M. Exact solution of bin-packing problems using column generation and branch-and-bound. Ann. Oper. Res. 1999, 86, 629–659. [Google Scholar] [CrossRef]
- Leao, A.A.S.; Furlan, M.M.; Toledo, F.M.B. Decomposition methods for the lot-sizing and cutting-stock problems in paper industries. Appl. Math. Model. 2017, 48, 250–268. [Google Scholar] [CrossRef]
- Pierini, L.M.; Poldi, K.C. Optimization of the cutting process integrated to the lot sizing in multi-plant paper production industries. Comput. Oper. Res. 2023, 153, 106157. [Google Scholar] [CrossRef]
- Suliman, S.M.A. An algorithm for solving lot sizing and cutting stock problem within aluminum fabrication industry. In Proceedings of the 2012 International Conference on Industrial Engineering and Operations Management, Bali, Indonesia, 3–6 July 2012; pp. 783–793. [Google Scholar]
- de Lara Andrade, P.R.; de Araujo, S.A.; Cherri, A.C.; Lemos, F.K. The integrated lot sizing and cutting stock problem in an automotive spring factory. Appl. Math. Model. 2021, 91, 1023–1036. [Google Scholar] [CrossRef]
- Andrade, P.; De Araujo, S.; Cherri, A.; Lemos, F. A 3-level integrated lot sizing and cutting stock problem applied to a truck suspension factory. Top 2025, 33, 74–101. [Google Scholar] [CrossRef]
- Signorini, C.d.A.; de Araujo, S.A.; Melega, G.M. One-dimensional multi-period cutting stock problems in the concrete industry. Int. J. Prod. Res. 2022, 60, 2386–2403. [Google Scholar] [CrossRef]
- Kantorovich, L. Mathematical methods of organizing and planning production. Manag. Sci. 1960, 6, 366–422. [Google Scholar] [CrossRef]
- Gilmore, P.C.; Gomory, R. A linear programming approach to the cutting stock problem—Part II. Oper. Res. 1963, 11, 863–888. [Google Scholar] [CrossRef]
- Sanan, A.B.; Azizoglu, M. An integrated two dimensional cutting stock and lot sizing problem with two criteria. Eur. J. Ind. Eng. 2023, 17, 1. [Google Scholar] [CrossRef]
- Silva, E.; Alvelos, F.; Carvalho, J.M. Integrating two-dimensional cutting stock and lot-sizing problems. J. Oper. Res. Soc. 2013, 65, 108–123. [Google Scholar] [CrossRef]
- Melega, G.M.; Araujo, S.A.D.; Jans, R. Comparison of MIP models for the integrated lot-sizing and one-dimensional cutting stock problem. Pesqui. Oper. 2016, 36, 167–196. [Google Scholar] [CrossRef]
- Poldi, K.C.; de Araujo, S.A. Mathematical models and a heuristic method for the multiperiod one-dimensional cutting stock problem. Ann. Oper. Res. 2016, 238, 497–520. [Google Scholar] [CrossRef]
- Ma, N.; Liu, Y.; Zhou, Z. Two heuristics for the capacitated multi-period cutting stock problem with pattern setup cost. Comput. Oper. Res. 2019, 109, 218–229. [Google Scholar] [CrossRef]
- do Nascimento, D.N.; de Araujo, S.A.; Cherri, A.C. Integrated lot-sizing and one-dimensional cutting stock problem with usable leftovers. Ann. Oper. Res. 2022, 316, 785–803. [Google Scholar] [CrossRef]
- Curcio, E.; de Lima, V.L.; Miyazawa, F.K.; Silva, E.; Amorim, P. The integrated lot-sizing and cutting stock problem under demand uncertainty. Int. J. Prod. Res. 2022, 61, 6691–6717. [Google Scholar] [CrossRef]
- Khamis, N.; Fors, H.; Harraz, N. Optimization of integrated lot sizing and cutting stock problems considering three production levels. In Proceedings of the 2022 The 3rd International Conference on Industrial Engineering and Industrial Management, Barcelona, Spain, 12–14 January 2022; pp. 226–231. [Google Scholar]
- Gau, T.; Wäscher, G. CUTGEN1: A problem generator for the standard one-dimensional cutting stock problem. Eur. J. Oper. Res. 1995, 84, 572–579. [Google Scholar] [CrossRef]
- Trigeiro, W.; Thomas, L.; McClain, J. Capacitated lot sizing with setup times. Manag. Sci. 1989, 35, 353–366. [Google Scholar] [CrossRef]

| Characteristics | Reference | Poltroniere et al. [10] | Gramani et al. [2] | Gramani et al. [3] | Santos et al. [5] | Alem and Morabito [6] | Suliman [15] |
| Dimensionality | One-dimensional | • | • | ||||
| Two-dimensional | • | • | • | • | |||
| Object Type | One type | • | • | • | • | ||
| Several types | • | • (t) | |||||
| CSP Formulation | Gilmore and Gomory | ||||||
| Valerio de Carvalho | |||||||
| Other | • | • | • | • | • | • | |
| Type of Inventory | Objects | • | • | ||||
| Items | • | • | • | • | • | ||
| Residual pieces | |||||||
| Final products | • | • | • | • | |||
| Setup | Cost | • | • | • | |||
| Time | • | ||||||
| Capacity | Capacity level | • (o) | • (m) | • (m) | |||
| Decision Variables | Production quantity | • (o) | • (f) | • (f) | • (f) | • (i) | • (f) |
| Inventory | • (o&i) | • (f) | • (i&f) | • (f) | |||
| Setup | •(m) | • (i) | |||||
| No. of residual pieces | |||||||
| Number of Production Levels | Single level | • | • | ||||
| Multi level | • | • | • | • | |||
| Other LSP Considerations | Safety stock | ||||||
| Multiple machines | • | • | |||||
| Objective Function Elements | Production cost | • (o) | • (f) | • (f) | • (o) | • (o) | |
| Trim loss cost | • | • | • | • | • | ||
| Setup cost | • | • | • (m) | • | • | ||
| Storage cost | • (o&i) | • (i) | • (i&f) | • (i&f) | • (i) | ||
| Overtime | • | ||||||
| Non-fulfillment | • | ||||||
| Purchasing cost | • | ||||||
| Backlogging | • | ||||||
| Solution Approach | Exact | • | • | • | • | ||
| Heuristic | • | • | • | ||||
| Mathematical Model Type | ILP | ||||||
| MILP | • | • | • | • | • | ||
| INLP | • | ||||||
| Application | Paper industry | • | |||||
| Furniture | • | • | • | • | |||
| General | |||||||
| Others | • | ||||||
| Characteristics | Reference | Vanzela et al. [8] | Alem and Morabito [5] | Silva et al. [22] | Poldi and de Araujo [24] | Poltroniere et al. [11] | Melega et al. [23] |
| Dimensionality | One-dimensional | • | • | • | |||
| Two-dimensional | • | • | • | ||||
| Object Type | One type | • | • | • | |||
| Several types | • | • | • | • | |||
| CSP Formulation | Gilmore and Gomory | • | • | • | |||
| Valerio de Carvalho | • | • | • | ||||
| Other | • | • | • | • | |||
| Type of Inventory | Objects | • | • | ||||
| Items | • | • | • | • | • | • | |
| Residual pieces | • | ||||||
| Final products | • | ||||||
| Setup | Cost | • | • | ||||
| Time | • | • | |||||
| Capacity | Capacity level | • (m) | • (m) | • (o) | • (m) | • (i) | |
| Decision Variables | Production quantity | • (f) | • (i) | • (i) | • (o) | • (o) | • (i) |
| Inventory | • (i&f) | • (i) | • (f) | • (i) | |||
| Setup | • (i) | • (i) | |||||
| No. of residual pieces | • | ||||||
| Number of Production Levels | Single level | • | • | ||||
| Multi level | • | • | • | • | |||
| Other LSP Considerations | Safety stock | • | |||||
| Multiple machines | • | • | |||||
| Objective Function Elements | Production cost | • (f) | • (o) | • (o) | |||
| Trim loss cost | • | • | • | • | • | • | |
| Setup cost | • | • | |||||
| Storage cost | • (i&f) | • (i) | • (i) | • (o&f) | • (o&i) | • (i) | |
| Overtime | • | ||||||
| Non-fulfillment | |||||||
| Purchasing cost | |||||||
| Backlogging | • | ||||||
| Solution Approach | Exact | • | • | ||||
| Heuristic | • | • | • | • | |||
| Mathematical Model Type | ILP | • | |||||
| MILP | • | • | • | • | • | ||
| INLP | |||||||
| Application | Paper industry | • | |||||
| Furniture | • | • | |||||
| General | • | • | • | ||||
| Others | |||||||
| Characteristics | Reference | Vanzela et al. [7] | Leao et al. [13] | Ma et al. [25] | do Nascimento et al. [26] | Ayres et al. [9] | Andrade et al. [16] |
| Dimensionality | One-dimensional | • | • | • | • | • | |
| Two-dimensional | • | • | |||||
| Object Type | One type | • | |||||
| Several types | • (t) | • | • | • | • | • | |
| CSP Formulation | Gilmore and Gomory | • | • | • | • | ||
| Valerio de Carvalho | • | ||||||
| Other | • | • | • | ||||
| Type of Inventory | Objects | • | • | ||||
| Items | • | • | • | • | • | ||
| Residual pieces | • | ||||||
| Final products | • | • | • | ||||
| Setup | Cost | • | • | ||||
| Time | • | ||||||
| Capacity | Capacity level | • (m) | • (m) | • (o) | • (o&m) | ||
| Decision Variables | Production quantity | • (o) | • (o)&(i) | • (o) | • (i)&(f) | ||
| Inventory | • (f) | • (o)&(i) | • (i) | • (i)&(l) | • (o&i&f) | • (i)&(f) | |
| Setup | • (o) | • (p) | |||||
| No. of residual pieces | • | ||||||
| Number of Production Levels | Single level | • | • | • | |||
| Multi level | • | • | • | ||||
| Other LSP Considerations | Safety stock | • | |||||
| Multiple machines | • | • | • | ||||
| Objective Function Elements | Production cost | • (o&f) | • (o) | • (o) | |||
| Trim loss cost | • | • | • | • | • | ||
| Setup cost | • (o) | • | |||||
| Storage cost | • (i&f) | • (o)&(i) | • (i) | • (i)&(l) | • (o&i&f) | • (i)&(f) | |
| Overtime | |||||||
| Non-fulfillment | |||||||
| Purchasing cost | |||||||
| Backlogging | |||||||
| Solution Approach | Exact | ||||||
| Heuristic | • | • | • | • | • | • | |
| Mathematical Model Type | ILP | ||||||
| MILP | • | • | • | • | • | • | |
| INLP | |||||||
| Application | Paper industry | • | • | ||||
| Furniture | • | ||||||
| General | • | ||||||
| Others | • | ||||||
| Characteristics | Reference | Signorini et al. [18] | Curcio et al. [27] | Pierini and Poldi [14] | Sanan &Azizoglu [21] | Andrade et al. [17] | This Study |
| Dimensionality | One-dimensional | • | • | • | • | ||
| Two-dimensional | • | • | |||||
| Object Type | One type | • | • | ||||
| Several types | • | • | • | • | |||
| CSP Formulation | Gilmore and Gomory | • | |||||
| Valerio de Carvalho | • | ||||||
| Other | • | • | • | • | • | ||
| Type of Inventory | Objects | • | • | • | |||
| Items | • | • | • | • | • | • | |
| Residual pieces | |||||||
| Final products | • | • | |||||
| Setup | Cost | • | • | ||||
| Time | • | ||||||
| Capacity | Capacity level | • (o) | • (i) | • (m) | • (m) | • (o&i&f) | |
| Decision Variables | Production quantity | • (i) | • (i) | • (o&i) | • (o&i) | • (i&f) | • (o&i&f) |
| Inventory | • (i) | • (i) | • (o&i) | • (i) | • (o&i&f) | • (o&i&f) | |
| Setup | • (o) | • (m) | • (o&m&f) | ||||
| No. of residual pieces | |||||||
| Number of Production Levels | Single level | • | • | • | |||
| Multi level | • | • | • | ||||
| Other LSP Considerations | Safety stock | ||||||
| Multiple machines | • | • | |||||
| Objective Function Elements | Production cost | • (o) | • (o) | •(o) | • (o&i&f) | ||
| Trim loss cost | • | • | • | • | • | ||
| Setup cost | • (o) | • (o&m&f) | |||||
| Storage cost | • (i) | • (i) | • (o&i) | • (i) | • (o&i&f) | • (o&i&f) | |
| Overtime | |||||||
| Non-fulfillment | |||||||
| Purchasing cost | |||||||
| Backlogging | • | ||||||
| Solution Approach | Exact | • | • | ||||
| Heuristic | • | • | • | • | |||
| Mathematical Model Type | ILP | • | |||||
| MILP | • | • | • | • | • | ||
| INLP | |||||||
| Application | Paper industry | • | |||||
| Furniture | |||||||
| General | • | • | |||||
| Others | • | • | • |
| Parameter | Value/Interval |
|---|---|
| Object length (Lk) | [300, 1000] |
| Item length (li) | [0.1, 0.4] |
| Average object length ( | |
| Setup cost of object, machine, final product () | [100, 500] |
| Setup time of object, machine, final product () | [10, 50] |
| Production/purchasing cost of object ( | 0 |
| Production time of object () | 0.01 |
| Production cost of cutting an object on machine () | 0 |
| Production time of cutting an object on machine () | 0.02 |
| Production cost of final product () | 2 |
| Production time of final product () | 5 |
| Holding cost of object () | β |
| Holding cost of item () | α |
| Holding cost of final product () | γ max () × 10 |
| Inventory factors to calculate holding costs of object and item (α, β) | {0.0, 0.01, 0.1, 0.5} |
| Inventory factors to calculate holding cost of final product (γ) | {0.0, 0.5, 1.0, 5.0} |
| Unit length cost of raw material waste (cw) | 1 |
| Demand of final product () | [1, 50] |
| Number of required items for assembling final product () | [0, 2] |
| Number of cutting machines (m) | 2 |
| Instance | No. of Items | No. of Periods | No. of Objects | No. of Final Products | Instance | No. of Items | No. of Periods | No. of Objects | No. of Final Products |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 2 | 2 | 2 | 19 | 15 | 2 | 2 | 2 |
| 2 | 4 | 3 | 20 | 4 | 3 | ||||
| 3 | 6 | 4 | 21 | 6 | 4 | ||||
| 4 | 5 | 4 | 2 | 2 | 22 | 15 | 4 | 2 | 2 |
| 5 | 4 | 3 | 23 | 4 | 3 | ||||
| 6 | 6 | 4 | 24 | 6 | 4 | ||||
| 7 | 5 | 6 | 2 | 2 | 25 | 15 | 6 | 2 | 2 |
| 8 | 4 | 3 | 26 | 4 | 3 | ||||
| 9 | 6 | 4 | 27 | 6 | 4 | ||||
| 10 | 10 | 2 | 2 | 2 | 28 | 20 | 2 | 2 | 2 |
| 11 | 4 | 3 | 29 | 4 | 3 | ||||
| 12 | 6 | 4 | 30 | 6 | 4 | ||||
| 13 | 10 | 4 | 2 | 2 | 31 | 20 | 4 | 2 | 2 |
| 14 | 4 | 3 | 32 | 4 | 3 | ||||
| 15 | 6 | 4 | 33 | 6 | 4 | ||||
| 16 | 10 | 6 | 2 | 2 | 34 | 20 | 6 | 2 | 2 |
| 17 | 4 | 3 | 35 | 4 | 3 | ||||
| 18 | 6 | 4 | 36 | 6 | 4 |
| Instance | Objective Function Value | Gap (%) | Lower Bound | Computational Time (seconds) | Material Waste | Material Waste (%) | No. of Nodes |
|---|---|---|---|---|---|---|---|
| 1 | 19,724.7 | 0.00 | 19,722.7 | 371.51 | 219 | 0.199 | 10,192 |
| 2 | 17,181.6 | 0.00 | 17,181.6 | 89.24 | 81 | 0.089 | 1850 |
| 3 | 25,233.9 | 0.00 | 25,231.6 | 82.78 | 5 | 0.003 | 9632 |
| 4 | 22,800.4 | 0.00 | 22,799.4 | 339.38 | 576 | 0.496 | 7686 |
| 5 | 50,724.2 | 0.00 | 50,724.2 | 199.76 | 1044 | 0.358 | 4348 |
| 6 | 39,775.7 | 0.00 | 39,773.5 | 1897.12 | 206 | 0.096 | 27,193 |
| 7 | 14,253.9 | 0.00 | 14,253.9 | 49.68 | 469 | 0.801 | 524 |
| 8 | 52,542.7 | 0.17 | 52,452.3 | 7200.19 | 544 | 0.191 | 52,220 |
| 9 | 77,912.3 | 0.06 | 77,860.8 | 7200.24 | 1696 | 0.39 | 66,484 |
| 10 | 41,411.5 | 0.05 | 41,388.3 | 7201.67 | 623 | 0.249 | 500,964 |
| 11 | 18,640.9 | 0.00 | 18,640.9 | 178.27 | 362 | 0.358 | 1321 |
| 12 | 70,412.5 | 0.00 | 70,405.7 | 454.63 | 355 | 0.080 | 7075 |
| 13 | 43,840.9 | 0.01 | 43,836.5 | 6557.63 | 883 | 0.350 | 174,909 |
| 14 | 87,617.4 | 0.01 | 87,600.4 | 7202.69 | 759 | 0.141 | 186,336 |
| 15 | 116,252 | 0.01 | 116,230.7 | 7200.35 | 167 | 0.022 | 77,910 |
| 16 | 112,293 | 0.60 | 111,618.1 | 7200.13 | 1681 | 0.246 | 18,943 |
| 17 | 144,217 | 0.29 | 143,793.9 | 7200.48 | 407 | 0.045 | 16,339 |
| 18 | 181,211 | 0.24 | 180,767.6 | 7200.05 | 943 | 0.083 | 15,836 |
| 19 | 65,535.4 | 0.00 | 65,528.8 | 1123.81 | 1393 | 0.340 | 74,304 |
| 20 | 59,811.1 | 0.01 | 59,801.0 | 7200.29 | 12 | 0.003 | 114,555 |
| 21 | 97,321.1 | 0.00 | 97,312.8 | 660.10 | 31 | 0.004 | 1431 |
| 22 | 70,141.6 | 0.00 | 70,137.7 | 727.47 | 27 | 0.006 | 3033 |
| 23 | 143,671 | 0.00 | 143,657.8 | 4853.52 | 299 | 0.032 | 48,380 |
| 24 | 125,631 | 0.61 | 124,853.4 | 7200.08 | 61 | 0.007 | 4404 |
| 25 | 110,676 | 0.40 | 110,225.2 | 7200.12 | 27 | 0.003 | 11,645 |
| 26 | 160,181 | 0.29 | 159,710.8 | 7200.05 | 108 | 0.010 | 13,180 |
| 27 | 97,321.1 | 0.00 | 97,312.8 | 782.96 | 31 | 0.004 | 1431 |
| 28 | 30,261.6 | 0.01 | 30,257.8 | 7200.36 | 104 | 0.057 | 159,310 |
| 29 | 68,549.5 | 0.00 | 68,544.0 | 1062.46 | 28 | 0.006 | 1058 |
| 31 | 59,493 | 0.02 | 59,480.2 | 7200.61 | 857 | 0.239 | 192,541 |
| Instance Size | a | b | Average Object Length | Average Item Length | Objective Function Value | Gap (%) | Computational Time (seconds) | Material Waste | Material Waste (%) |
|---|---|---|---|---|---|---|---|---|---|
| Small | 0.02 | 0.1 | 479.0 | 38.6 | 11,034.8 | 0.00 | 1813.60 | 205 | 0.576 |
| 0.04 | 0.2 | 858.0 | 63.0 | 13,257.6 | 0.00 | 860.62 | 71 | 0.130 | |
| 0.08 | 0.4 | 640.0 | 156.6 | 47,820.1 | 0.00 | 158.38 | 678 | 0.245 | |
| 0.1 | 0.6 | 682.5 | 230.4 | 24,239 | 0.00 | 45.89 | 3817 | 3.769 | |
| Medium | 0.02 | 0.1 | 699.5 | 40 | 16,430.5 | 0.00 | 4032.60 | 0 | 0 |
| 0.04 | 0.2 | 571.0 | 84.3 | 22,657 | 3.82 | 7200.07 | 20 | 0.018 | |
| 0.08 | 0.4 | 756.0 | 185.8 | 62,717.8 | 0.07 | 7200.46 | 1605 | 0.441 | |
| 0.1 | 0.6 | 717.0 | 260.9 | 93,539.1 | 0.00 | 79.60 | 10,857 | 2.135 |
| Instance Size | cw | Objective Function Value | Gap (%) | Computational Time (seconds) | Material Waste (%) | Increased Total Cost (%) |
|---|---|---|---|---|---|---|
| Small | 1 | 55,430.7 | 0.00 | 899.27 | 0.629 | - |
| 10 | 72,493.4 | 0.00 | 32.63 | 0.576 | 30.7 | |
| 50 | 142,744.0 | 0.00 | 19.06 | 0.543 | 157.5 | |
| 100 | 230,293 | 0.00 | 53.58 | 0.543 | 315.4 | |
| Medium | 1 | 41,981.2 | 0.01 | 7201.28 | 0.238 | - |
| 10 | 44,623.2 | 0.02 | 7200.16 | 0.082 | 4.7 | |
| 50 | 49,726.3 | 0.00 | 274.02 | 0.028 | 13.9 | |
| 100 | 51,400.2 | 0.00 | 84.06 | 0 | 16.99 |
| Instance Size | Neglecting Setup Cost of | Objective Function Value | Gap (%) | Computational Time (seconds) | Total Objects Setup Cost | Total Machines Setup Cost | Total Final Products Setup Cost | Total Cost Reduction (%) |
|---|---|---|---|---|---|---|---|---|
| Small | - | 22,279.1 | 0.00 | 790.48 | 1014.0 | 856 | 1701 | - |
| Objects | 20,700.4 | 0.00 | 1556.71 | 0.0 | 856 | 1701 | 7.08 | |
| Cutting objects into items | 21,447.6 | 0.19 | 1579.90 | 1235 | 0.0 | 1701 | 3.73 | |
| Final products | 20,542.9 | 0.00 | 638.75 | 1356 | 856 | 0.0 | 7.79 | |
| Medium | - | 43,840.9 | 0.01 | 6557.63 | 650 | 580 | 1568 | - |
| Objects | 40,727.2 | 0.00 | 6904.24 | 0.0 | 580 | 1568 | 7.10 | |
| Cutting objects into items | 41,403.4 | 0.03 | 7200.18 | 650 | 0.0 | 1568 | 5.55 | |
| Final products | 40,413.2 | 0.01 | 4196.93 | 650 | 580 | 0.0 | 7.81 |
| Instance Size | Capacity Level | Objective Function Value | Gap (%) | Computational Time (seconds) | Material Waste (%) | Inventory Value of | ||
|---|---|---|---|---|---|---|---|---|
| Objects | Items | Final Products | ||||||
| Small | Tightened | 34,885.3 | 0.00 | 25.21 | 1.96 | 0 | 18 | 0 |
| Increased by 10% | 34,722.7 | 0.00 | 74.52 | 1.92 | 0 | 28 | 5 | |
| Increased by 20% | 34,722.7 | 0.00 | 102.96 | 1.92 | 0 | 28 | 5 | |
| Increased by 30% | 34,722.7 | 0.00 | 216.56 | 1.92 | 0 | 28 | 5 | |
| Increased by 40% | 34,665.3 | 0.00 | 5014.24 | 2.08 | 0 | 12 | 13 | |
| Medium | Tightened | 40,279.3 | 0.20 | 7200.36 | 0.112 | 0 | 21 | 0 |
| Increased by 10% | 39,794 | 0.36 | 7200.08 | 0.147 | 1 | 4 | 7 | |
| Increased by 20% | 39,455.1 | 0.17 | 7200.12 | 0.112 | 2 | 12 | 18 | |
| Increased by 30% | 39,095.6 | 0.02 | 7200.35 | 0.112 | 2 | 8 | 20 | |
| Increased by 40% | 38,712.6 | 0.03 | 7200.28 | 0.215 | 3 | 23 | 20 | |
| Objective Function Value | Gap (%) | Computational Time (seconds) | Material Waste | Objects Inventory Value | Avg. Object Inventory Cost/Unit | Items Inventory Value | Avg. Item Inventory Cost/Unit | Final Product Inventory Value | Avg. Final Products Inventory Cost/Unit | |
|---|---|---|---|---|---|---|---|---|---|---|
| β | Objects’ Inventory | |||||||||
| 0 | 21,617.7 | 0 | 378.87 | 346 | 30 | 0 | 37 | 0.67 | 62 | 6.56 |
| 0.01 | 21,652.7 | 0.00 | 281.61 | 576 | 0 | 5.6 | 19 | 0.67 | 63 | 6.56 |
| 0.1 | 21,652.7 | 0.00 | 1741.11 | 576 | 0 | 153.1 | 19 | 0.67 | 63 | 6.56 |
| 0.5 | 21,652.7 | 0.00 | 388.55 | 576 | 0 | 382.75 | 19 | 0.67 | 63 | 6.56 |
| α | Items’ Inventory | |||||||||
| 0 | 21,554.1 | 0.00 | 129.17 | 346 | 7 | 5.6 | 366 | 0 | 30 | 6.56 |
| 0.01 | 21,652.7 | 0.00 | 164.12 | 576 | 0 | 5.6 | 19 | 0.67 | 63 | 6.56 |
| 0.1 | 21,801.5 | 0.00 | 2411.6 | 576 | 0 | 5.6 | 4 | 6.7 | 68 | 6.56 |
| 0.5 | 21,818.2 | 0.00 | 219.2 | 474 | 8 | 5.6 | 0 | 98.25 | 71 | 6.56 |
| γ | Final products’ Inventory | |||||||||
| 0 | 21,216 | 0.00 | 275.85 | 576 | 0 | 5.6 | 4 | 0.67 | 68 | 0 |
| 0.5 | 21,441.6 | 0.00 | 160.47 | 576 | 0 | 5.6 | 4 | 0.67 | 68 | 3.27 |
| 1 | 21,652.7 | 0.00 | 153.1 | 576 | 0 | 5.6 | 19 | 0.67 | 63 | 6.56 |
| 5 | 22,462.8 | 0.03 | 7200.64 | 346 | 58 | 5.6 | 42 | 0.67 | 7 | 32.8 |
| Objective Function Value | Gap (%) | Computational Time (seconds) | Material Waste | Objects Inventory Value | Avg. Object Inventory Cost/Unit | Items Inventory Value | Avg. Item Inventory Cost/Unit | Final Product Inventory Value | Avg. Final Products Inventory Cost/Unit | |
|---|---|---|---|---|---|---|---|---|---|---|
| β | Objects’ Inventory | |||||||||
| 0 | 39,075.9 | 0.09 | 7200.43 | 257 | 2 | 0 | 8 | 1.96 | 20 | 22.28 |
| 0.01 | 39,095.6 | 0.02 | 7200.42 | 257 | 2 | 7.65 | 8 | 1.96 | 20 | 22.28 |
| 0.1 | 39,134.7 | 0.05 | 7201.05 | 257 | 0 | 76.5 | 16 | 1.96 | 20 | 22.28 |
| 0.5 | 39,136.2 | 0.15 | 7200.56 | 257 | 0 | 382.75 | 18 | 1.96 | 21 | 22.28 |
| α | Items’ Inventory | |||||||||
| 0 | 40,191.8 | 0.13 | 7200.1 | 567 | 2 | 7.65 | 82 | 0 | 0 | 22.28 |
| 0.01 | 40,279.3 | 0.20 | 7200.45 | 257 | 0 | 7.65 | 21 | 1.96 | 0 | 22.28 |
| 0.1 | 40,507.6 | 0.36 | 7200.28 | 335 | 0 | 7.65 | 6 | 19.65 | 0 | 22.28 |
| 0.5 | 40,740.8 | 0.25 | 7200.05 | 339 | 5 | 7.65 | 3 | 98.25 | 0 | 22.28 |
| γ | Final products’ Inventory | |||||||||
| 0 | 38,600.9 | 0.11 | 7200.16 | 257 | 0 | 7.65 | 11 | 0.67 | 22 | 0 |
| 0.5 | 38,878.6 | 0.16 | 7200.05 | 285 | 2 | 7.65 | 6 | 0.67 | 20 | 11.14 |
| 1 | 39,095.6 | 0.02 | 7200.24 | 257 | 2 | 7.65 | 8 | 0.67 | 20 | 22.28 |
| 5 | 39,634 | 0.14 | 7200.32 | 490 | 4 | 7.65 | 78 | 0.67 | 1 | 111.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khamis, N.; Harraz, N.; Fors, H. Minimizing Waste and Costs in Multi-Level Manufacturing: A Novel Integrated Lot Sizing and Cutting Stock Model Using Multiple Machines. Modelling 2025, 6, 56. https://doi.org/10.3390/modelling6030056
Khamis N, Harraz N, Fors H. Minimizing Waste and Costs in Multi-Level Manufacturing: A Novel Integrated Lot Sizing and Cutting Stock Model Using Multiple Machines. Modelling. 2025; 6(3):56. https://doi.org/10.3390/modelling6030056
Chicago/Turabian StyleKhamis, Nesma, Nermine Harraz, and Hadi Fors. 2025. "Minimizing Waste and Costs in Multi-Level Manufacturing: A Novel Integrated Lot Sizing and Cutting Stock Model Using Multiple Machines" Modelling 6, no. 3: 56. https://doi.org/10.3390/modelling6030056
APA StyleKhamis, N., Harraz, N., & Fors, H. (2025). Minimizing Waste and Costs in Multi-Level Manufacturing: A Novel Integrated Lot Sizing and Cutting Stock Model Using Multiple Machines. Modelling, 6(3), 56. https://doi.org/10.3390/modelling6030056