Evaluation of Neural Networks for Improved Computational Cost in Carbon Nanotubes Geometric Optimization

Abstract

Geometric optimization of carbon nanotubes (CNTs) is a fundamental step in computational simulations, enabling precise studies of their properties for various applications. However, this process becomes computationally expensive as the molecular structure grows in complexity and size. To address this challenge, this study utilized three deep-learning-based neural network architectures: Multi-Layer Perceptron (MLP), Bidirectional Long Short-Term Memory (BiLSTM), and 1D Convolutional Neural Networks (1D-CNNs). Simulations were performed using the CASTEP module in Material Studio to generate datasets for training the neural networks. While the final geometric optimization calculations were completed within Material Studio, the neural networks effectively generated preoptimized CNT structures that served as starting points, significantly reducing computational time. The results showed that the 1D-CNN architecture performed best for CNTs with 28, 52, 76, and 156 atoms, while the MLP outperformed others for CNTs with 84, 124, 148, and 196 atoms. Across all cases, computational time was reduced by 39.68% to 90.62%. Although the BiLSTM also achieved reductions, its performance was less effective than the other two architectures. This work highlights the potential of integrating deep learning techniques into materials science; it also offers a transformative approach to reducing computational costs in optimizing CNTs and presents a way for accelerated research in molecular systems.

1. Introduction

In materials science, geometric optimization is important in advancing the development of materials. Researchers can use computational simulations to explore a broad spectrum of geometric configurations and material properties with remarkable efficiency [1]. The primary goal of this process is to identify the most stable and energetically favorable configuration of a molecular structure [2]. Geometric optimization involves systematically adjusting atomic positions to minimize the system’s total energy, which is critical for conducting simulations that explain the fundamental properties and behaviors of materials.

Carbon nanotubes (CNTs) have emerged as a cornerstone in nanotechnology research due to their extraordinary physical and chemical properties. Geometric optimization of CNTs is particularly useful for understanding and enhancing their potential applications [3,4,5,6,7]. One of the most relevant representatives is hydrogen storage, which has direct implications for developing advanced energy storage technologies [8,9,10,11,12]. In this field, integrating computational simulation tools has proven to be a powerful strategy for innovation in the design and study of nanostructured materials [13,14,15].

However, the geometric optimization of CNTs is computationally intensive, with the processing time increasing substantially as the number of atoms in the system grows [16]. This computational challenge arises from the necessity to locate the global minimum energy state amidst numerous local minima [17]. For CNTs, this complexity can impede the feasibility of large-scale simulations, especially in scenarios involving intricate molecular structures. Thus, exploring innovative methods to accelerate geometric optimization without compromising accuracy is imperative.

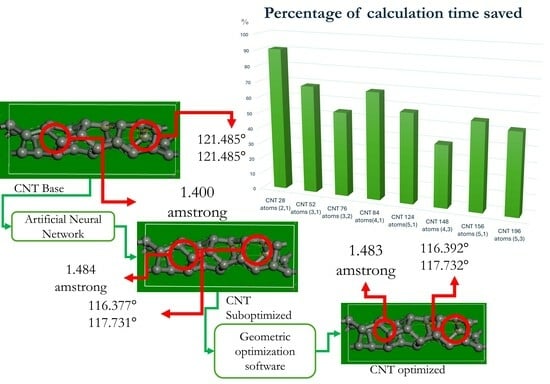
To address these challenges, this study investigates the potential of deep neural networks (DNNs) to reduce the computational cost associated with the geometric optimization of CNTs. The research focuses on a hybrid approach where DNNs generate preoptimized (suboptimal) configurations of CNTs, which serve as starting points for further optimization using the software BIOVIA Materials Studio^®, version 2024, CASTEP Module [18].

In this work, BIOVIA Materials Studio^® was used to construct and optimize the geometry of CNTs. This software is widely employed in materials science for its powerful molecular modeling tools and its support for universal force fields, including Lennard-Jones potentials [19]. The licensed availability of this tool at our institution facilitated its use. The generated CNT structures were used for data extraction and validating our artificial neural network (ANN) predictions.

In this sense, the methodology proposed in this work comprises three phases:

1.

Initial CNT configurations are generated using BIOVIA Materials Studio^®, which are then used to train DNN models.

2.

Suboptimal configurations of CNTs are produced using the trained DNNs. These configurations are subsequently refined through optimization in BIOVIA Materials Studio^®.

3.

The effectiveness of using DNNs as a precursor step to optimization in BIOVIA Materials Studio^® is evaluated.

The proposed approach contributes significantly to the geometric optimization of complex systems by introducing deep neural networks as a preprocessing step, thereby reducing the computational time required by BIOVIA Materials Studio^®. The reported time savings, ranging from 39.68% to 90.62%, are based on benchmark experiments carried out in this study, comparing conventional optimization procedures with the ANN-assisted approach across various CNT configurations.

Thus, this study demonstrates the viability of integrating artificial intelligence into materials science workflows, providing a more efficient exploration of CNT properties. The research aims to accelerate innovation in designing and applying advanced materials by addressing computational bottlenecks using deep learning tools.

2. Related Works

In recent years, advancements in artificial intelligence, particularly in artificial neural networks (ANNs), have revolutionized various research domains, including materials science [20,21]. In this field, ANNs have successfully contributed to developing new materials, such as carbon nanotubes, frequently studied through computational approaches to uncover their potential and utility in diverse applications. This section reviews notable studies highlighting the application of ANNs for improving and discovering new materials.

Vivanco et al. [22] examined machine learning techniques for modeling carbon nanotubes, emphasizing using ANNs, support vector machines (SVMs), and random forests to analyze these nanostructures. Valentina et al. [23] utilized multilayer perceptrons (MLPs) and One-Dimensional Convolutional Neural Networks (1D CNNs) to predict stress–strain curves in CNTs, achieving high accuracy in their predictions.

Similarly, Fakhrabadi et al. [24] applied an MLP neural network to predict fundamental vibrational frequencies in CNTs, while Kaushal et al. [25] developed an ANN-based model to forecast the yield and diameter of single-walled carbon nanotubes (SWCNTs) with over 90% accuracy. Akbari et al. [26] explored the impact of gas interactions on the conductivity of CNTs by employing ANNs and SVMs to model current–voltage (I-V) characteristics, finding that SVMs delivered superior predictions.

Marko [27] developed an ANN model to predict mechanical properties based on data derived from molecular dynamics simulations, showcasing the precision of deep learning techniques. Anderson et al. [28] integrated molecular simulations with ANN methods to analyze hydrogen storage in porous crystals, enabling rapid preassessment of storage capacities.

In predicting nanomaterial properties, Salah et al. [29] utilized an MLP system to achieve a remarkable 99.7997% accuracy in forecasting electromagnetic absorption in polycarbonate and CNT films. Nguyen et al. [30] reported a significant enhancement in the thermal conductivity of hybrid nanofluids, emphasizing their relevance in heat transfer applications and applied neural networks for precise modeling.

Despite these advancements, the computational time required for developing carbon structures has received limited attention. A notable exception is the study by Aci and Avci [31], which employed feedforward neural networks (FFNN) and generalized regression neural networks (GRNN) for the geometric optimization of structures. Their approach achieved an 85% reduction in the number of iterations required for calculations, underscoring the efficiency of these techniques in computational optimization and highlighting their potential for similar applications.

The successful application of deep learning neural networks in predicting properties and optimizing materials demonstrates their potential to significantly reduce simulation times. These advancements open new opportunities for accelerating research and development in advanced materials while making efficient ways of exploring nanostructures like CNTs and other innovative materials.

3. Theoretical Foundations

3.1. Carbon Nanotubes (CNTs)

Carbon nanotubes (CNTs) are one-dimensional materials composed of graphite planes rolled into cylindrical shapes with diameters at the nanometric scale. They can be classified as single-walled carbon nanotubes (SWCNTs) or multi-walled carbon nanotubes (MWCNTs). SWCNTs consist of a single graphene layer seamlessly rolled into a cylinder, while MWCNTs comprise multiple concentric cylindrical graphene layers [32].

Graphene sheets are planes of carbon (C) atoms arranged in a hexagonal lattice. Each carbon atom forms a covalent C-C bond with its nearest neighbors in this structure. The rolling of a graphene sheet to form a CNT is defined by a chiral vector ($\mathbf{Ch}$) that determines the direction along which the graphene sheet is rolled into a tubular structure, as ilustrated in Figure 1 [33]. This chiral vector is mathematically represented as depicted in Equation (1).

$$\mathbf{Ch}=n{\mathbf{a}}_1+m{\mathbf{a}}_2,$$

(1)

where n and m are integers referred to as the chiral indices and ${\mathbf{a}}_1$ and ${\mathbf{a}}_2$ are unit vectors of the graphene lattice. The pair $(n,m)$ uniquely describes an SWCNT and governs its geometry, primarily its diameter D and chiral angle $\theta$, as well as its physicochemical properties [33,34].

Due to the hexagonal symmetry of the graphene lattice and the chiral symmetry of the nanotubes $(n,m)$, the chiral angle for CNTs are limited to the range $0^{\circ }\le \theta \le {30}^{\circ }$. Depending on the value of $\theta$, CNTs are categorized into specific configurations: (1) zigzag nanotubes ($m=0$, and $\theta =0°$), resulting in a straight-line pattern along the tube circumference; (2) armchair nanotubes ($n=m$, and $\theta =30°$), forming a symmetric “chair-like” pattern; and (3) chiral nanotubes ($0^{\circ }<\theta <{30}^{\circ }$), which are asymmetrical configurations and represent the majority of possible nanotube structures [35].

3.2. Artificial Neural Networks

In this section, we explain the neural network architectures employed in this research to outline their fundamental characteristics, clarify their operational principles, and justify their selection in the context of the study.

3.2.1. Multilayer Perceptron

A Multilayer Perceptron (MLP) is a feedforward neural network composed of an input layer, one or more hidden layers, and an output layer. Each neuron computes a weighted sum of its inputs and applies a nonlinear activation function $\sigma$, enabling the network to model complex relationships and approximate continuous functions [36]. The output $y_j$ of a hidden neuron j is computed as:

$$s_j=\sum _{i=1}^n{w}_{ji}{x}_i+b_j,y_j=\sigma \left(s_j\right)$$

(2)

where $w_{ji}$ reflects the synaptic weights, $x_i$ represents the inputs from the previous layer, $b_j$ is the bias, and $\sigma$ can be ReLU, sigmoid, or tanh.

The output layer neuron k computes:

$$y_k=\sigma \left(\sum _{j=1}^m{w}_{kj}{y}_j+b_k\right)$$

(3)

MLPs are trained via supervised learning to minimize a loss function E using backpropagation and gradient-based optimization (e.g., SGD, Adam) [37]. The update rule for weights, given a learning rate $\eta$ is expressed as follows:

$$\Delta w_{ji}=-\eta {\displaystyle \frac{\partial E}{\partial w_{ji}}}$$

(4)

In this work, MLPs are selected for their proven ability to approximate complex functions, manage high-dimensional input data, and predict material properties efficiently. Their structure facilitates hierarchical feature extraction, making them suitable for the geometric optimization of carbon nanotubes.

3.2.2. Bidirectional Long Short-Term Memory Networks

Bidirectional Long Short-Term Memory Networks (BiLSTMs) are a powerful extension of Recurrent Neural Networks (RNNs) that process sequential data in both forward and backward directions, improving the modeling of long-range dependencies [38]. This dual context is particularly valuable when the output at each step depends on both past and future elements in the sequence.

A standard Long Short-Term Memory (LSTM) unit incorporates gating mechanisms to control the flow of information. At each time step t, the input gate $i_t$, forget gate $f_t$, output gate $o_t$, and cell state $C_t$ are described as follows:

$$i_t=\sigma (W_i{x}_t+U_i{h}_{t-1}+b_i)$$

(5)

$$f_t=\sigma (W_f{x}_t+U_f{h}_{t-1}+b_f)$$

(6)

$$o_t=\sigma (W_o{x}_t+U_o{h}_{t-1}+b_o)$$

(7)

$$C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t$$

(8)

where the candidate cell state ${\tilde{C}}_t$ is computed as:

$${\tilde{C}}_t=tanh(W_C{x}_t+U_C{h}_{t-1}+b_C)$$

(9)

and the hidden state ($h_t$) encodes the output of the LSTM at each time step, and it is expressed as:

$$h_t=o_t\odot tanh\left(C_t\right)$$

(10)

where $\sigma$ is the sigmoid activation function, ⊙ denotes element-wise multiplication, and $x_t$ and $h_t$ are the input and hidden state at time t, respectively, because in a BiLSTM, two separate LSTMs traverse the input sequence:

$$\overrightarrow{h_t}={\mathrm{LSTM}}_{\mathrm{fwd}}(x_t,\overrightarrow{h_{t-1}}),\overleftarrow{h_t}={\mathrm{LSTM}}_{\mathrm{bwd}}(x_t,\overleftarrow{h_{t+1}})$$

(11)

and their outputs are concatenated:

$$h_t=[\overrightarrow{h_t};\overleftarrow{h_t}]$$

(12)

This structure enables the network to capture comprehensive contextual information at each point in the sequence. The forward and backward LSTMs operate independently and do not share weights, increasing model flexibility and representational capacity [39,40].

In this study, BiLSTMs are employed to analyze CNT structures by capturing dependencies within their atomic configurations. This is particularly advantageous when processing chirality-encoded vectors, as structural features often rely on both preceding and succeeding elements in the CNT sequence.

3.2.3. Convolutional Neural Networks

Convolutional Neural Networks (CNNs) are a class of neural networks well-suited for identifying patterns in structured data such as images or sequences. Their architecture generally includes convolutional layers for feature extraction, followed by fully connected layers for classification or regression tasks [41,42,43].

In this study, CNNs are adapted to process vector-based representations of CNTs using one-dimensional (1D) convolutions. Each convolutional layer applies a set of filters $K^k$ across the input sequence x, with m being the offset (or index traversing the input), generating feature maps $f_{ij}^k$ as follows:

$$f_{ij}^k={(K^k\ast x)}_{ij}=\sum _m{K}_m^k{x}_{(i+m)}$$

(13)

Unlike traditional CNNs, pooling layers are omitted to preserve input dimensionality and retain all geometric and physical information during convolution.

The output of the convolutional layers is passed to fully connected layers, where each neuron $z_j$ computes:

$$z_j=\sum _i{w}_{ji}{a}_i+b_j$$

(14)

where $a_i$ denotes activations from the previous layer, $w_{ji}$ the synaptic weights, and $b_j$ the bias term.

The use of CNNs in this context enables efficient processing of CNT data by using local spatial correlations in the atomic structure. Their ability to automatically learn hierarchical representations makes them particularly effective for modeling the structural properties of CNTs. Moreover, by using 1D convolutions and excluding pooling layers, the network retains all relevant geometric and physical information during feature extraction, ensuring that critical details are preserved.

4. Experimental Design

The methodology of this study is divided into three phases to ensure a systematic analysis of the computational efficiency of the proposed ANN-based approach for CNT geometric optimization.

Phase I: Involves generating the dataset comprising initial and optimized CNT molecules. These structures are obtained using BIOVIA Materials Studio^® (CASTEP module), which performs first-principles simulations to optimize the geometric properties of the CNTs.

Phase II: Suboptimized CNT structures are generated using selected ANN architectures. Subsequently, these suboptimized structures are used as the starting point for geometric optimization via the CASTEP module.

Phase III: The computational times required for the geometric optimization of CNTs is analyzed. Two approaches are evaluated: one using the structures directly optimized in CASTEP module and the other using the suboptimized CNTs generated by the ANN as the initial input.

4.1. Phase I: Dataset Generation

The dataset for training the selected ANN models was generated by first constructing CNTs in BIOVIA Materials Studio^®, where key parameters such as atomic type (carbon) and bond length (1.42 Å as the default value) were specified. These initial structures were then subjected to geometric optimization using the CASTEP module, with the electronic energy tolerance parameter set to $1\times {10}^{-5}$ eV per atom to ensure high precision in the computational results.

All CNT structures in this study were optimized using energy minimization protocols at 0 K, as implemented by default in BIOVIA Materials Studio^®. This approach allows for the determination of equilibrium geometries without thermal noise.

While temperature effects are crucial in atomistic simulations involving molecular dynamics or thermal stability assessments, they were not considered here, as the objective was to evaluate the structural prediction accuracy of the ANN under idealized conditions. Moreover, since many CNT synthesis techniques aim for processes compatible with room temperature or mild conditions, the resulting geometries remain relevant for experimental applications [44].

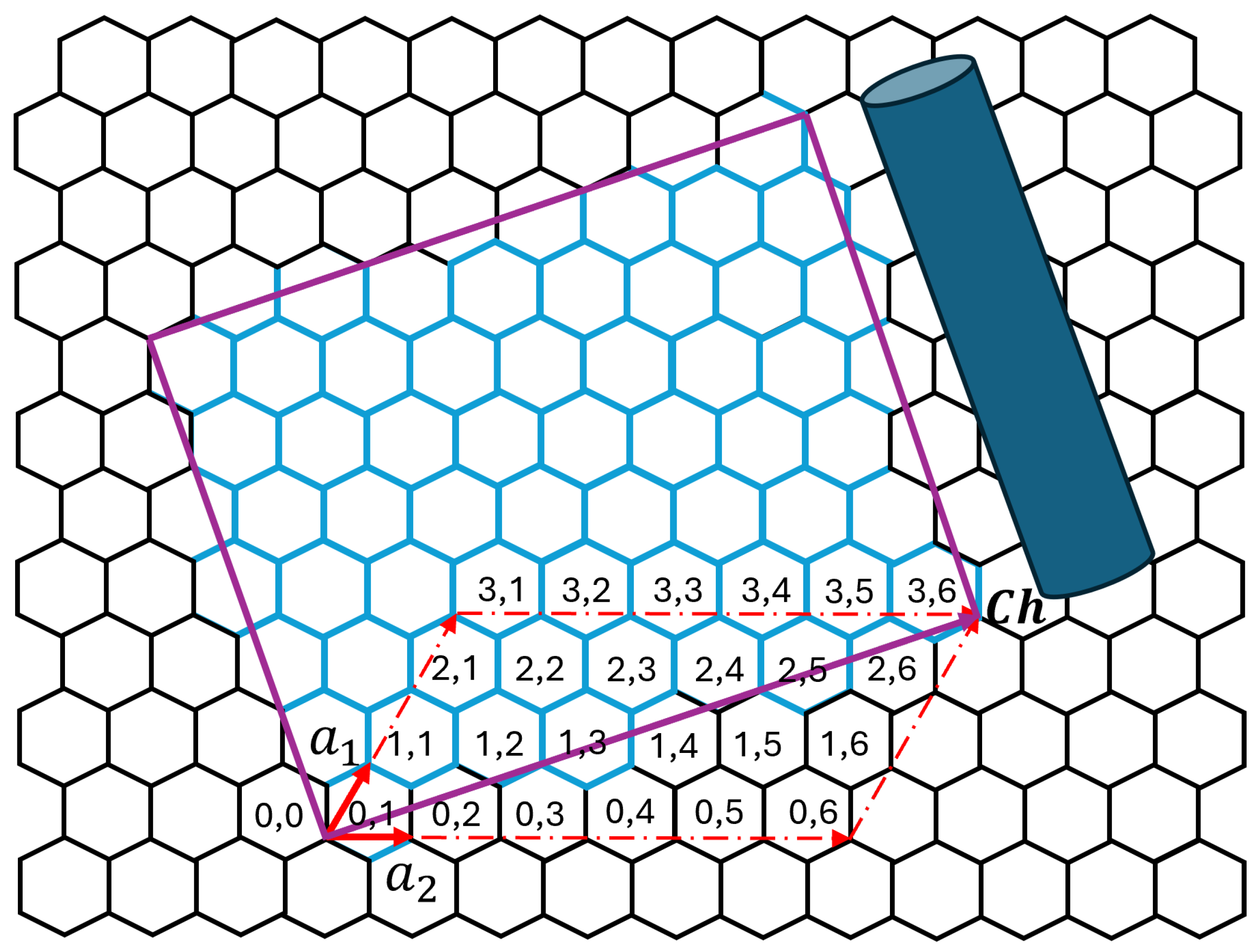
As a reference, Figure 2 illustrates a CNT with chirality $n=2$ and $m=1$. Chirality parameters define how the graphene sheet is rolled to form the nanotube. The specific CNT depicted contains 28 atoms, and its spatial coordinates (x, y, z) were used as inputs for the CASTEP module. After optimization, the corresponding coordinates ($x^{\prime }$, $y^{\prime }$, $z^{\prime }$) served as the output targets.

The number of atoms corresponds to the number of carbon atoms within the translational unit cell of the chiral CNT (2,1). This value results from the construction of the nanotube based on its chiral vector $\mathbf{Ch}=2{\mathbf{a}}_1+{\mathbf{a}}_2$, and the corresponding translational vector along the tube axis. Thus, the unit cell formed is the smallest repeating structure that fully captures the atomic arrangement of this chirality.

The number of atoms in the unit cell of a chiral carbon nanotube is given by the expression Equation (15) [45]:

$$N={\displaystyle \frac{n^2+nm+m^2}{d_R}}$$

(15)

where $d_R$ is the greatest common divisor of $2m+n$. Then, the (2,1) chirality yields $N=28$ atoms, corresponding to the minimal translational unit cell along the nanotube axis.

Table 1. Spatial coordinates of the atoms that make up the 28-atom CNT, with base (x, y, z) and optimized ($x^{\prime }$, $y^{\prime }$, $z^{\prime }$).

x	y	z	${\mathit{x}}^{\prime }$	${\mathit{y}}^{\prime }$	${\mathit{z}}^{\prime }$
0.716	0.646	0.114	0.755	0.671	0.113
0.601	0.720	0.209	0.624	0.756	0.209
0.286	0.440	0.066	0.253	0.432	0.067
0.331	0.538	0.185	0.306	0.538	0.184
0.284	0.354	0.280	0.255	0.332	0.281
0.676	0.703	0.328	0.710	0.744	0.328
0.505	0.694	0.423	0.517	0.733	0.423
0.601	0.720	0.542	0.615	0.761	0.542
0.409	0.629	0.637	0.393	0.655	0.637
0.716	0.646	0.780	0.745	0.668	0.781
0.676	0.703	0.995	0.705	0.728	0.995
0.399	0.280	0.042	0.385	0.240	0.043
0.591	0.371	0.137	0.607	0.345	0.137
0.495	0.306	0.256	0.505	0.280	0.256
0.669	0.462	0.352	0.701	0.456	0.353
0.286	0.440	0.399	0.255	0.434	0.398
0.324	0.297	0.471	0.295	0.273	0.471
0.284	0.354	0.614	0.245	0.329	0.613
0.399	0.280	0.709	0.376	0.244	0.709
0.505	0.694	0.756	0.495	0.720	0.756
0.331	0.538	0.544	0.299	0.544	0.544
0.409	0.629	0.645	0.393	0.655	0.637
0.591	0.371	0.971	0.743	0.932	0.970
0.495	0.306	0.789	0.557	0.893	0.889
0.669	0.462	0.873	0.702	0.891	0.868
0.286	0.440	0.345	0.257	0.246	0.314
0.324	0.297	0.475	0.245	0.288	0.445
0.714	0.560	0.830	0.718	0.758	0.898

details the spatial coordinates of the 28 atoms comprising the CNT. The first three columns represent the unoptimized CNT’s initial coordinates (x, y, z). In comparison, the last three columns list the optimized coordinates ($x^{\prime }$, $y^{\prime }$, $z^{\prime }$) after processing with the Materials Studio software. Then, eight CNTs with different chiralities were constructed, resulting in structures with varying numbers of atoms, as shown in

Table 2. Summary of the base CNT dataset used in this research.

Chirality (m,n)	Number of Atoms	Data Amount
(2, 1)	28	168
(3, 1)	52	312
(3, 2)	76	456
(4, 1)	84	504
(4, 3)	148	888
(5, 1)	124	744
(5, 2)	156	936
(5, 3)	196	1176

.

It is important to note that the carbon nanotubes analyzed in Table 2, especially those with chiral indices (2,1), (3,1), etc., correspond to structures with very small diameters (i.e., diameter < 0.5 nm). While valid from a theoretical standpoint, these geometries are known to present high curvature-induced strain, which can lead to reduced thermodynamic stability under ambient conditions.

Nonetheless, such ultra-small CNTs have been predicted and, in some cases, observed experimentally, particularly in confined environments or synthesized using specialized techniques [45]. One study by Zhao et al. [46] found that a stable 3 Å carbon nanotube can be grown inside a multi-walled carbon nanotube (MWNT) using high-resolution transmission electron microscopy. Density functional calculations indicated that this 3 Å CNT is the armchair CNT (2,2). While this study does not directly address the observation by Zhao et al. [46], it provides evidence that very small carbon nanotubes can be stable and observable under certain conditions.

The study of low chiralities CNTs remains relevant for understanding the limits of CNT structural stability and validating computational nanotube behavior models. Moreover, other studies suggest that carbon nanotubes with low chiralities should be studied because they exhibit unique electronic, optical, and mechanical properties, have a strong preference in growth processes, and are crucial for high-purity separation and specific applications [34,47,48].

The datasets created under conditions specified in Table 1 and Table 2 are grouped into three categories, as follows:

• CNT-BCO: Contains both the initial (random) and CNT data optimized by CASTEP module of BIOVIA Materials Studio^® software.
• CNT-BCO2: Includes the initial CNTs and those optimized twice using the CASTEP module to augment the data volume.
• CNT-BCO-ALL: A comprehensive dataset combining the first two datasets.

The three categories were generated based on the process in

Table 3. Composition of the three datasets generated after single and double processing in Materials Studio software.

Dataset	Input	Output
CNT-BCO	Base CNT	CNT optimized
CNT-BCO2	Base CNT	CNT optimized 2 times
CNT-BCO-ALL	Base CNT	CNT optimized
		CNT optimized 2 times

. First, we used the base CNT and the BIOVIA Materials Studio^® sofware to optimize the atom coordinates; then, an optimized CNT dataset was produced.

Afterward, we processed the base CNT in BIOVIA Materials Studio^® twice, thus creating a new augmented dataset (CNT-BCO2). The CNT-BCO-ALL contains the dataset from the two previous stages.

These datasets were the foundation for ANN training, enabling the models to learn from the initial and optimized CNT geometries. By incorporating diverse examples, the datasets ensured the robustness of the ANN predictions, ultimately enhancing the geometric optimization process of CNTs.

4.2. Phase II: Construction of Models for Generating Suboptimized CNTs

To generate suboptimized CNTs, the three ANN architectures explained in Section 3.2 were employed: a Multilayer Perceptron (MLP), a Bidirectional Long Short-Term Memory (BiLSTM) network, and a 1D Convolutional Neural Network (1D-CNN). These architectures were configured with the hyperparameters detailed in

Table 4. ANN parameter configuration summary.

Parameter	MLP	BiLSTM	1D-CNN
Layers	2	1	1
Neurons	50	25	200
Activation function	Gelu	Swish	Relu
Optimizer	Adamax	Adamax	Adamax
Epochs	1000	1000	1000
Batch	32	32	32
$\eta$	0.001	0.001	0.001

.

The datasets, previously presented in Table 3, were split into three subsets to ensure proper training, evaluation, and validation of the models: (a) 60% for training, used to adjust the model’s parameters during the learning phase, (b) 30% for testing, utilized to evaluate the model’s performance and prevent over-fitting, and (c) 10% for validation, applied during training to monitor generalization and fine-tune hyperparameters.

Each ANN was trained using a supervised learning approach. The Early Stopping criterion was implemented to optimize computational efficiency and ensure convergence. This mechanism halts training if the validation loss does not improve for ten consecutive epochs, thereby preventing over-fitting and excessive computation.

The primary goal of this phase was to generate suboptimized CNT structures that serve as intermediate geometries between the unoptimized and fully optimized states. These were later used in Phase III, allowing for a detailed comparison of computational efficiency in contrast with the original processed datasets (see Section 4.1).

This systematic approach ensured that each ANN architecture was rigorously tested and could reliably produce suboptimized CNTs, thus reducing the processing time in the final optimization process with Materials Studio software.

5. Results and Discussion

The results focus on Phase III, which evaluates the effectiveness of the neural network models as a preoptimization step for CNTs. After training the ANN models with the CNTs detailed in Table 2, suboptimized structures were generated. These were then used as initial inputs for geometric optimization via the CASTEP module (BIOVIA Materials Studio^®), aiming to assess the reduction in computational time.

Table 5. Best results in computational time savings in CASTEP geometric optimization of CNTs after BiLSTM suboptimization.

Chirality $(\mathit{m},\mathit{n})$	Atoms Number	Initial CASTEP Time (s)	Iterations Initial CNT	Iterations Suboptimized CNT	Computing Time (s)/Dataset	% Improved Time	Saved Time (s)
2,1	28	473.11	17	2	195.27/CNT-BCO2	58.72%	277.84
3,1	52	486.69	5	3	249.86/CNT-BCO	48.66%	236.83
3,2	76	479.55	5	3	348.19/CNT-BCO2	27.39%	131.36
4,1	84	1011.17	5	4	351.55/CNT-BCO2	65.23%	513.58
4,3	148	2525.23	5	4	2001.80/CNT-BCO2	20.72%	523.43
5,1	124	1946.78	5	4	1270.92/CNT-BCO2	34.71%	675.86
5,2	156	3573.41	5	3	2651.84/CNT-BCO2	25.78%	921.57
5,3	196	6342.31	5	3	6108.05/CNT-BCO2	3.69%	234.26

summarizes the results obtained using the BiLSTM network. It demonstrated a notable reduction in computation time, ranging from 3.69% for the CNT with 196 atoms to 65.23% for the CNT with 84 atoms. This trend indicates that the reduction percentage decreases as the number of atoms in the CNTs increases. Similar behavior was observed in the other neural network models, albeit to a lesser extent.

In

Table 6. Computational time savings in CASTEP geometric optimization of CNTs after 1D-CNN suboptimization. Chirality (5,3) was set for all cases.

Iterations Suboptimized CNT	Final CASTEP Time (s)	% Improved Time	Saved Time (s)
7	7116.17	-	-
6	6271.56	1.11%	70.75
3	3036.84	52.11%	3305.47
6	6322.44	0.31%	19.87
5	5070.62	20.05%	1271.69
3	3043.31	52.01%	3299

, results from six trials conducted on a CNT with chirality $n=5$, $m=3$ (196 atoms) are summarized. Identical hyperparameters were configured across tests; also, the used ANN was 1D-CNN, and the dataset for this experiment was CNT-BCO2. Five iterations in the initial CNT dataset were performed. The reference time for time-saving estimation was reported as 6342.31 s, which was the CASTEP module processing time without ANN preprocessing. Each trial represents the results of varying the iterations in the suboptimized CNT, as depicted in the first column.

It must be noted in Table 6 that the performance varied notably among the trials. For instance, in trial 2 (2nd row), the network achieved a modest 1.11% reduction in computational time, indicating limited learning effectiveness. In contrast, trials 3 and 6 (highlighted in bold) yielded substantial improvements, with up to 52.11% reduction in computational time. Also, please note that suboptimized CNT with 7 iterations (first row) increased the computational time.

Following this variability analysis, the most favorable results in terms of time reduction were selected for CNTs with varying chiralities. These are summarized in

Table 7. Best results in computational time savings in CASTEP geometric optimization of CNTs after 1D-CNN and MLP suboptimization.

Chirality $(\mathit{m},\mathit{n})$/ANN	Atoms Number	Initial CASTEP Time (s)	Iterations Initial CNT	Iterations Suboptimized CNT	Computing Time (s)/Dataset	% Improved Time	Saved Time (s)
2,1/1D-CNN	28	473.11	17	2	44.36/CNT-BCO	90.62%	428.75
3,1/1D-CNN	52	486.69	5	3	153.02/CNT-BCO2	68.55%	337.67
3,2/1D-CNN	76	479.55	5	3	221.14/CNT-BCO2	53.8%	254.41
4,1/MLP	84	1011.17	5	4	320.81/CNT-BCO	68.27%	690.36
4,3/MLP	148	2525.23	5	4	1523.19/CNT-BCO2	39.68%	1002.04
5,1/MLP	124	1946.78	5	4	827.48/CNT-BCO2	57.49%	1119.3
5,2/1D-CNN	156	3573.41	5	3	1574.78/CNT-BCO2	55.93%	1998.63
5,3/MLP	196	6342.31	5	3	3036.84/CNT-BCO2	52.11%	3305.47

, where the suboptimization with 1D-CNN and MLP architectures was also tested. Datasets CNT-BCO and CNT-BCO2 were used for this analysis.

For smaller CNTs (28, 52, and 76 atoms), the 1D-CNN architecture was the most effective overall. A notable exception was the CNT with chirality $n=4$ and $m=1$, where the MLP network outperformed others, achieving a remarkable 68.27% reduction in computational time. Notably, for the CNT with 28 atoms ($n=2$, $m=1$), the 1D-CNN achieved an outstanding 90.62% reduction, marking the highest efficiency in time cost improvement across all tested cases.

On the other hand, for larger CNTs (148, 124, and 196 atoms), the MLP architecture demonstrated superior efficiency in most scenarios. However, for the CNT with chirality $n=5$, $m=2$, the 1D-CNN surpassed the MLP, achieving a 55.93% reduction in computational time. From a general point of view, in many cases, computational time reductions exceeded 50%, demonstrating a significant enhancement in the optimization process’s efficiency in terms of saving time.

The results confirm that deep ANNs, particularly 1D-CNNs, and MLPs significantly reduce the computational time for geometric optimization by generating suboptimized CNT structures that serve as effective starting points for CASTEP. These reductions, reaching up to 90.62% (CNT with 28 atoms), represent a breakthrough in computational efficiency for material simulations. The demonstrated effectiveness of these ANN-based methods highlights their potential for accelerating similar processes in nanotechnology and materials science.

Nonetheless, as shown in Table 5, Table 6 and Table 7, the relative time savings achieved through neural network preprocessing decrease as the chirality indices increase (and thus, the number of atoms). This effect becomes more pronounced starting from chirality (5,3), where the computational overhead of the neural network inference and the subsequent geometric optimization in BIOVIA Materials Studio^® begins to surpass the initial speedup. This behavior is anticipated, as the scaling of the energy minimization process is highly sensitive to system size.

Despite this, exploring CNTs with a wide range of chiralities, including small-diameter variants, remains relevant. Small CNTs such as (2,2), (3,3), and (4,2), though less frequently synthesized, have been shown to exhibit mechanical stability under specific conditions. For example, Zhao et al. [46] reported that such structures can be stable despite higher strain energy than larger tubes. In other work, Peng et al. [49] found that CNTs with diameters as small as 0.33 nm can remain stable at temperatures exceeding 1000 °C. Including these cases in the analysis allows us to identify the threshold at which the preprocessing method begins to lose efficiency, providing valuable information for future scalability studies.

Therefore, while larger and more stable CNTs hold clear experimental and technological interest, the present work offers a broader perspective on how neural networks operate across various structural configurations, aiding in defining practical boundaries for their application in computational materials design.

6. Conclusions

This study has demonstrated that deep-learning-based artificial neural networks can reduce computational time for geometric optimization of CNTs by up to 90.62%, significantly improving the time consumed by CASTEP Materials Studio Software. It could extend this methodology to a broader range of carbon nanotube chiralities and possibly other molecular systems. With further refinement of ANN architectures and weight optimization, achieving even more significant reductions in computation time is plausible, particularly for more complex molecular structures. Moreover, once trained, these ANNs do not necessarily require retraining for similar tasks, further enhancing computational efficiency.

Unlike previous studies, such as the work of Aci and Avci [31], which focused on reducing the number of iterations using ANNs, this work implemented deep-learning-based ANNs, including MLP, BiLSTM, and 1D-CNN architectures. Experimental results indicate that these models demonstrate a more accurate learning ability for the numerical patterns that define the energy minimum of molecular structures. This improvement directly leads to a significant decrease in computational time related to geometric optimization.

One notable challenge identified is the dependence on proprietary software, specifically the Material Studio platform and its CASTEP module, for generating the dataset used in ANN training. This reliance presents limitations in scalability and accessibility for broader applications. Future research could explore alternative strategies, such as using unsupervised or reinforcement learning approaches. These methods could potentially eliminate dependency on specific simulation tools while maintaining or even improving the computational efficiency and accuracy of the optimization process.

To successfully implement these advanced methodologies, it would be important to consider the numerical methods and algorithms CASTEP utilizes during geometric optimization. By integrating these principles into the training process, future models could further enhance their ability to predict optimal configurations while reducing computational overhead.