Three-Dimensional Mathematical Modeling and Simulation of the Impurity Diffusion Process Under the Given Statistics of Systems of Internal Point Mass Sources
Abstract
1. Introduction
2. Materials and Methods
- Problem parameter interpreter module;
- Homogeneous concentration and Green’s function calculation module;
- Flux function evaluation module;
- Stochastic characteristics computation module;
- Two- and three-dimensional visualization module.
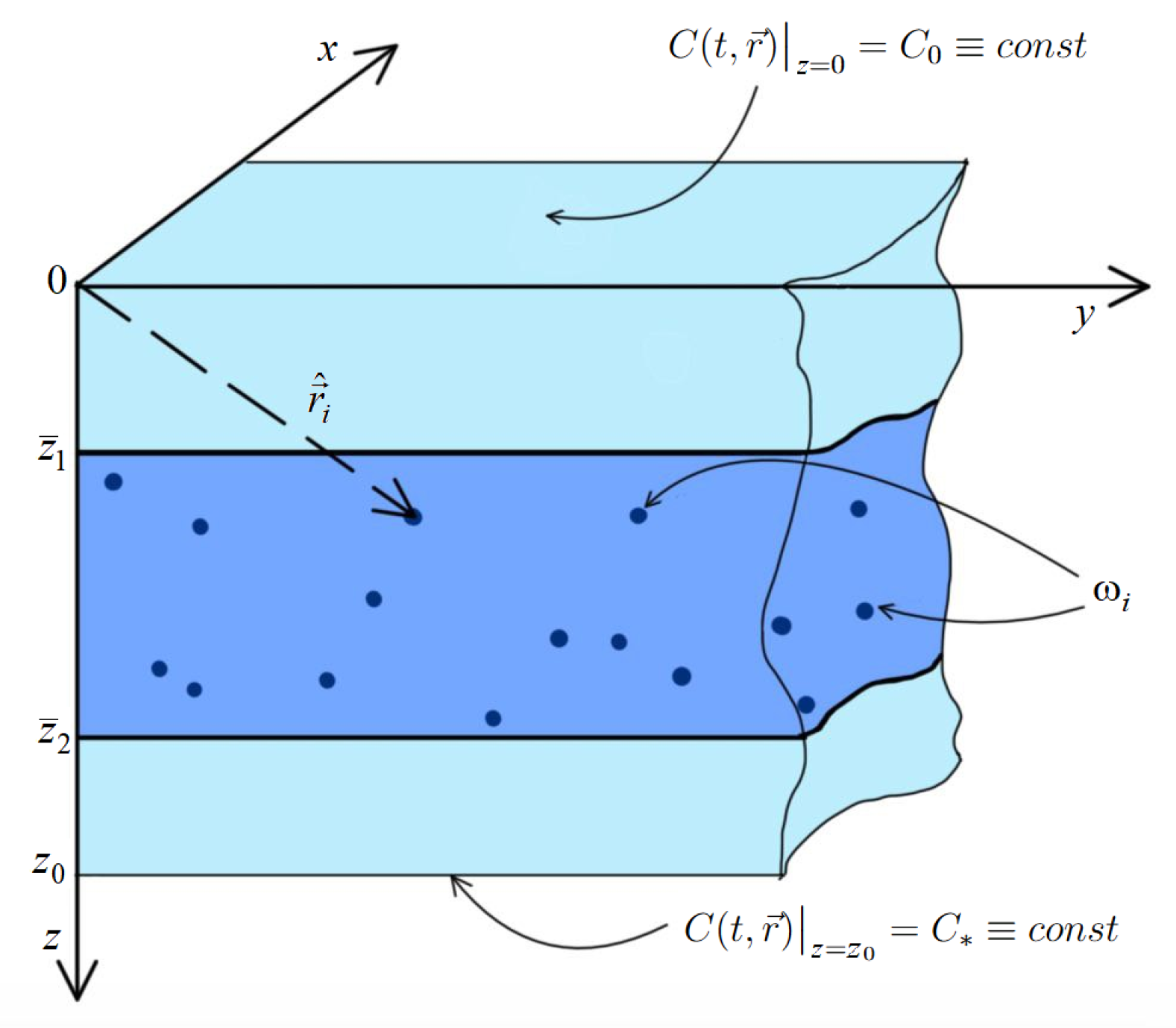
3. Mathematical 3D Model of Impurity Diffusion Influenced by Point Source System
3.1. Construction of the Mathematical Model
3.2. Formulation of the Initial–Boundary Value Problem for Diffusion
4. Construction of the Solution to the 3D Problem of Impurity Diffusion Influenced by the Stochastic Point Source System
4.1. Integral Transforms
4.2. Averaging the Concentration over the Random Source Locations
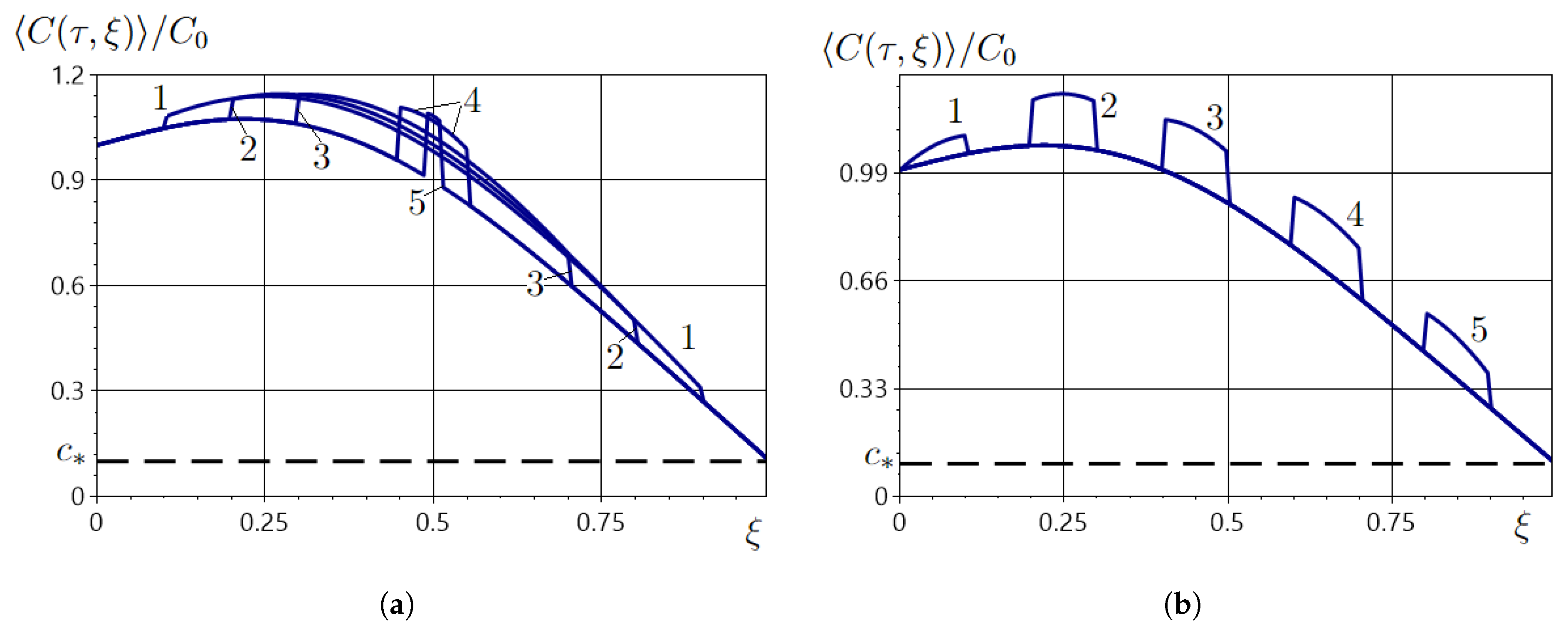
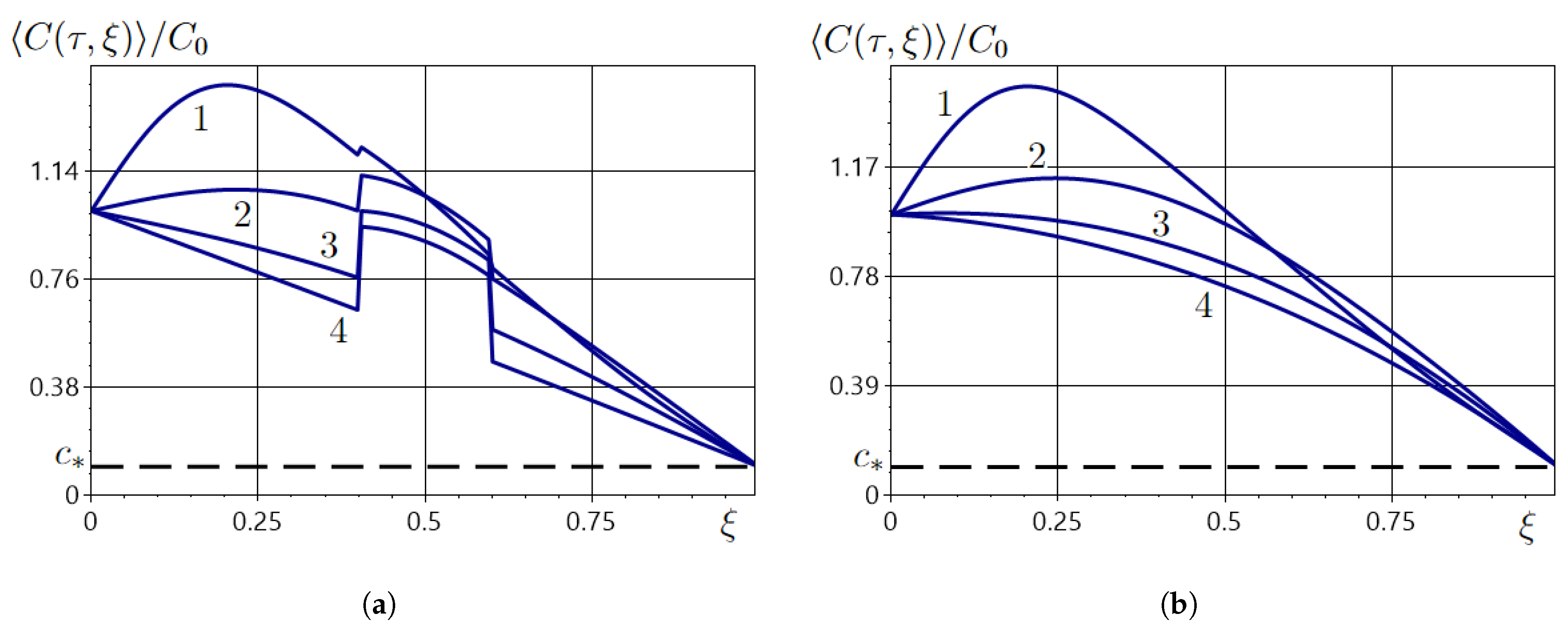
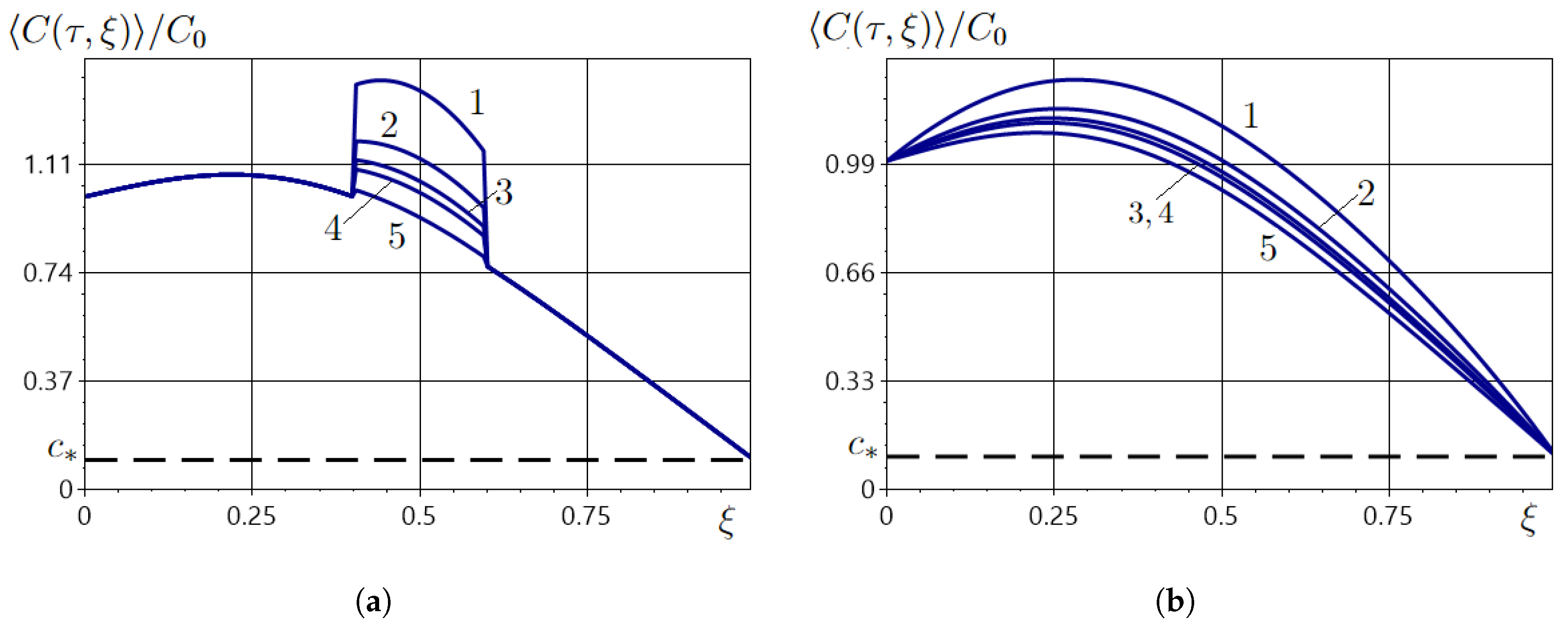
5. Results
5.1. Numerical Analysis of the Averaged Field of the Impurity Concentration
5.2. Second Moments of the Averaged Concentration Field
5.3. Numerical Analysis of the Variance and Correlation Function of the Concentration Field
5.4. Correlation Coefficient
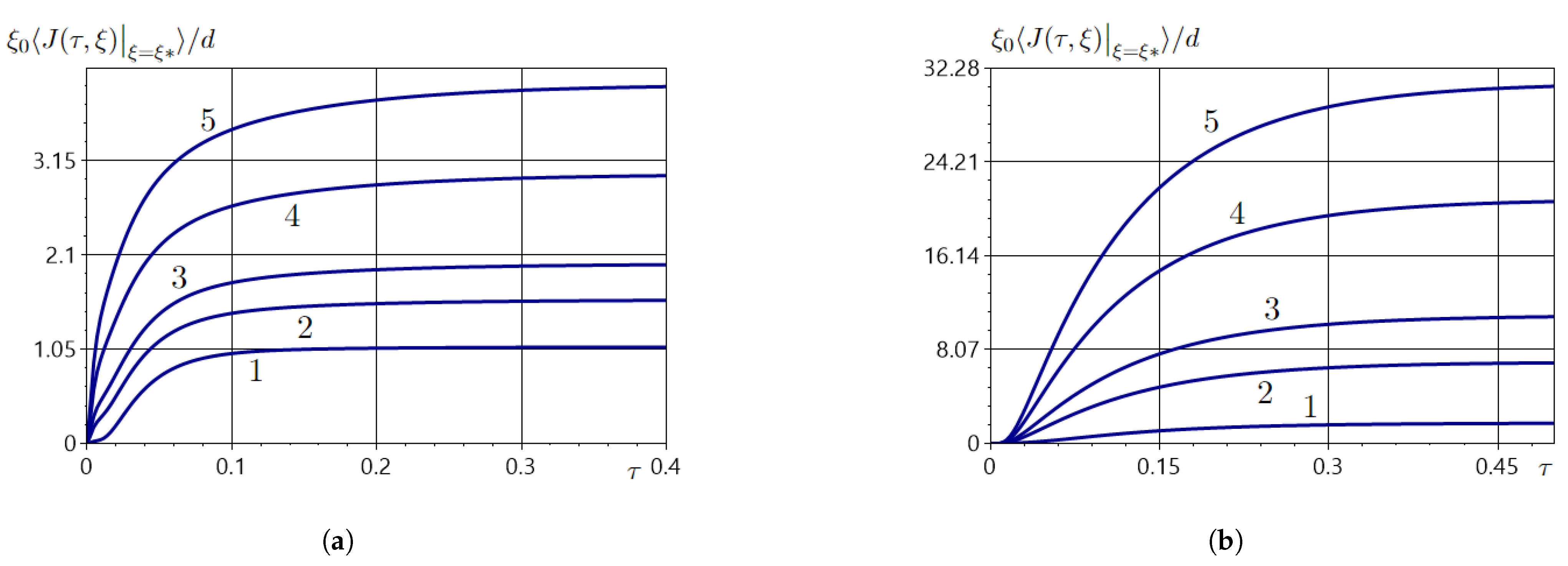
5.5. Diffusive Fluxes Affected by the System of Random Point Sources of Mass
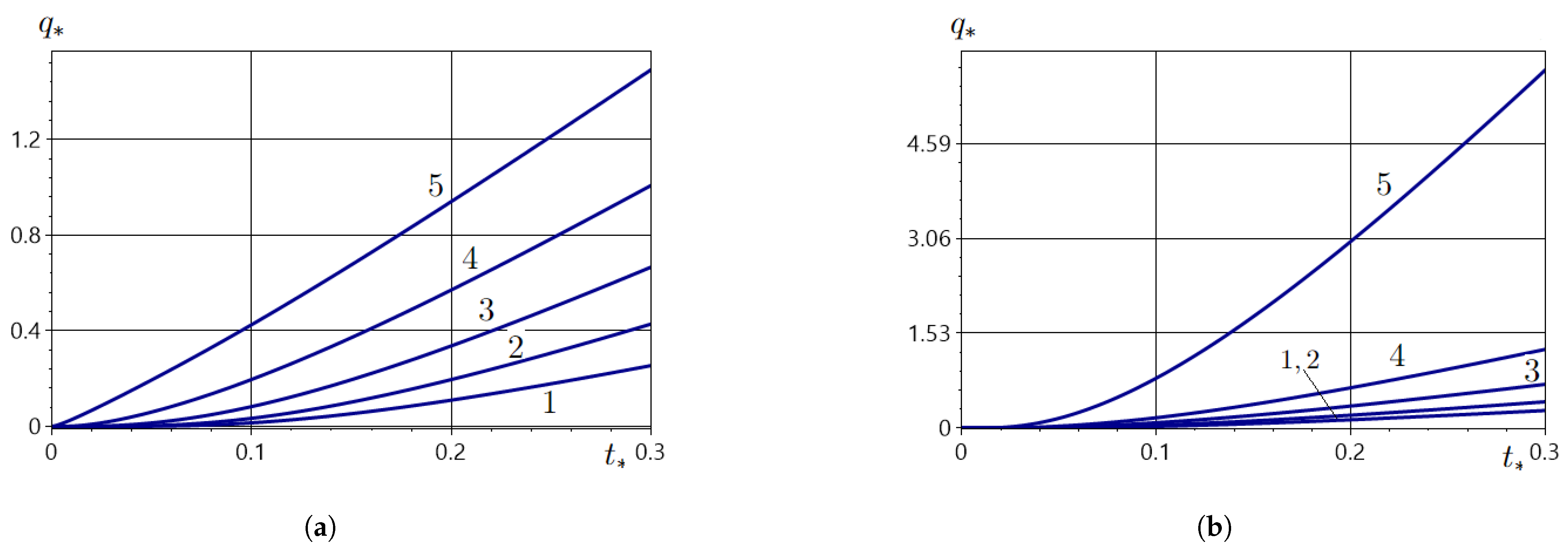
5.6. Amount of Substance Passed Through the Strip over Time
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martyniuk, P.; Ulianchuk-Martyniuk, O.; Herus, V.; Pryshchepa, O. Integral conjugation conditions for a discontinuous filtration flow via a geobarrer in the case of its biocolmatation. Int. J. Appl. Math. 2024, 37, 21–28. [Google Scholar] [CrossRef]
- Beck, F.R.; Mohanta, L.; Henderson, D.M.; Cheung, F.-B.; Talmage, G. An engineering stability technique for unsteady, two-phase flows with heat and mass transfer. Int. J. Multiph. Flow 2021, 142, 103709. [Google Scholar] [CrossRef]
- Mátyás, L.; Barna, I.F. Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon. Universe 2023, 9, 264. [Google Scholar] [CrossRef]
- Kovács, E. A class of new stable, explicit methods to solve the non-stationary heat equation. Numer. Methods Partial Differ. Equ. 2020, 37, 2469–2489. [Google Scholar] [CrossRef]
- Sen, S.; Kundu, S.; Absi, R.; Ghoshal, K. A Model for Coupled Fluid Velocity and Suspended Sediment Concentration in an Unsteady Stratified Turbulent Flow through an Open Channel. J. Eng. Mech. 2023, 149, 04022088. [Google Scholar] [CrossRef]
- Yu, Q.; Turner, I.; Liu, F.; Moroney, T. A study of distributed-order time fractional diffusion models with continuous distribution weight functions. Numer. Methods Partial Differ. Equ. 2023, 39, 383–420. [Google Scholar] [CrossRef]
- Chernukha, O.; Chuchvara, A.; Bilushchak, Y.; Pukach, P.; Kryvinska, N. Mathematical Modelling of Diffusion Flows in Two-Phase Stratified Bodies with Randomly Disposed Layers of Stochastically Set Thickness. Mathematics 2022, 10, 3650. [Google Scholar] [CrossRef]
- Gahn, M.; Neuss-Radu, M.; Pop, I.S. Homogenization of a reaction-diffusion-advection problem in an evolving micro-domain and including nonlinear boundary conditions. J. Differ. Equ. 2021, 289, 95–127. [Google Scholar] [CrossRef]
- Khoroshun, L. Mathematical Models and Methods of the Mechanics of Stochastic Composites. Int. Appl. Mech. 2000, 36, 1284–1316. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Münster, A. Chemische Thermodynamik; De Gruyter: Berlin, Germany, 1970. [Google Scholar]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Ahmed, A. Laplace transform solutions of Cauchy problem for the modified Korteweg-De Vries equation. Int. J. Appl. Math. 2024, 37, 447–454. [Google Scholar] [CrossRef]
- Schiff, J.L. The Laplace Transform: Theory and Applications; Springer: New York, NY, USA, 2013. [Google Scholar]
- Sneddon, I.N. Fourier Transforms; Dover Publications: New York, NY, USA, 1995. [Google Scholar]
- Rudin, W. Real and Complex Analysis, 3rd ed.; Mc Graw Hill International, Ed.; Mc Graw Hill International: New York, NY, USA, 1975; p. 428. [Google Scholar]
- Pukach, P.Y.; Chernukha, Y.A. Mathematical modeling of impurity diffusion process under given statistics of a point mass sources system. Math. Model. Comput. 2024, 11, 385–393. [Google Scholar] [CrossRef]
- Lykov, A.; Mikhailov, Y. Theory of Heat and Mass Transfer; Daniel Davey & Co., Inc.: New York, NY, USA, 1965. [Google Scholar]
- Breiman, L. Probability, First Thus Edition; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]


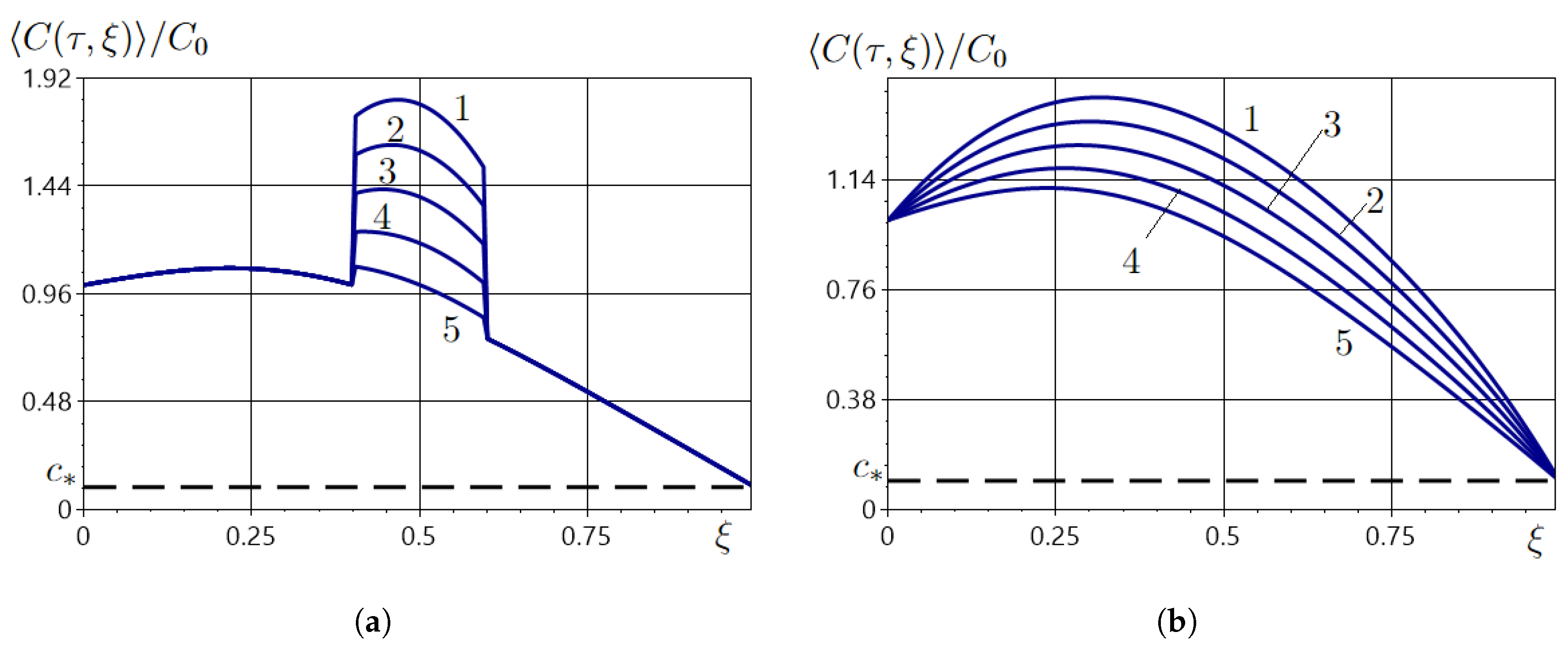
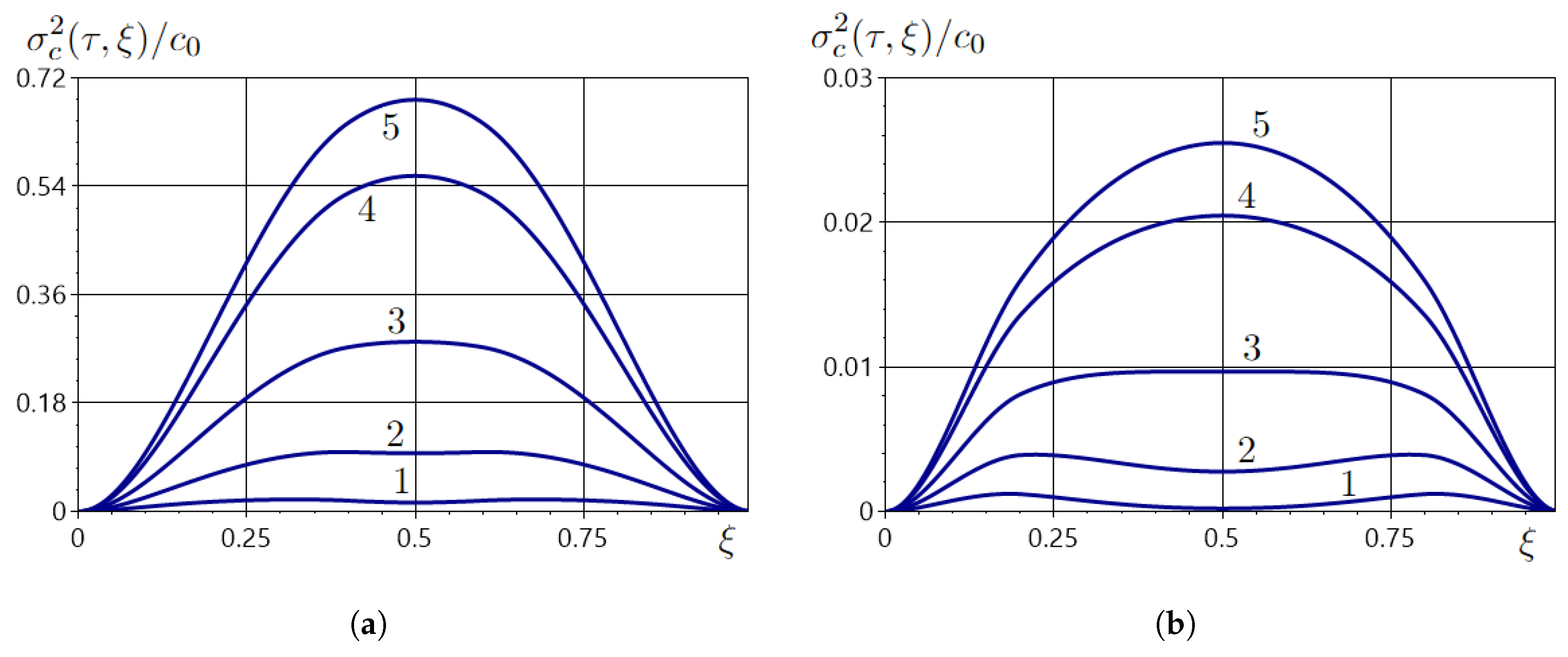

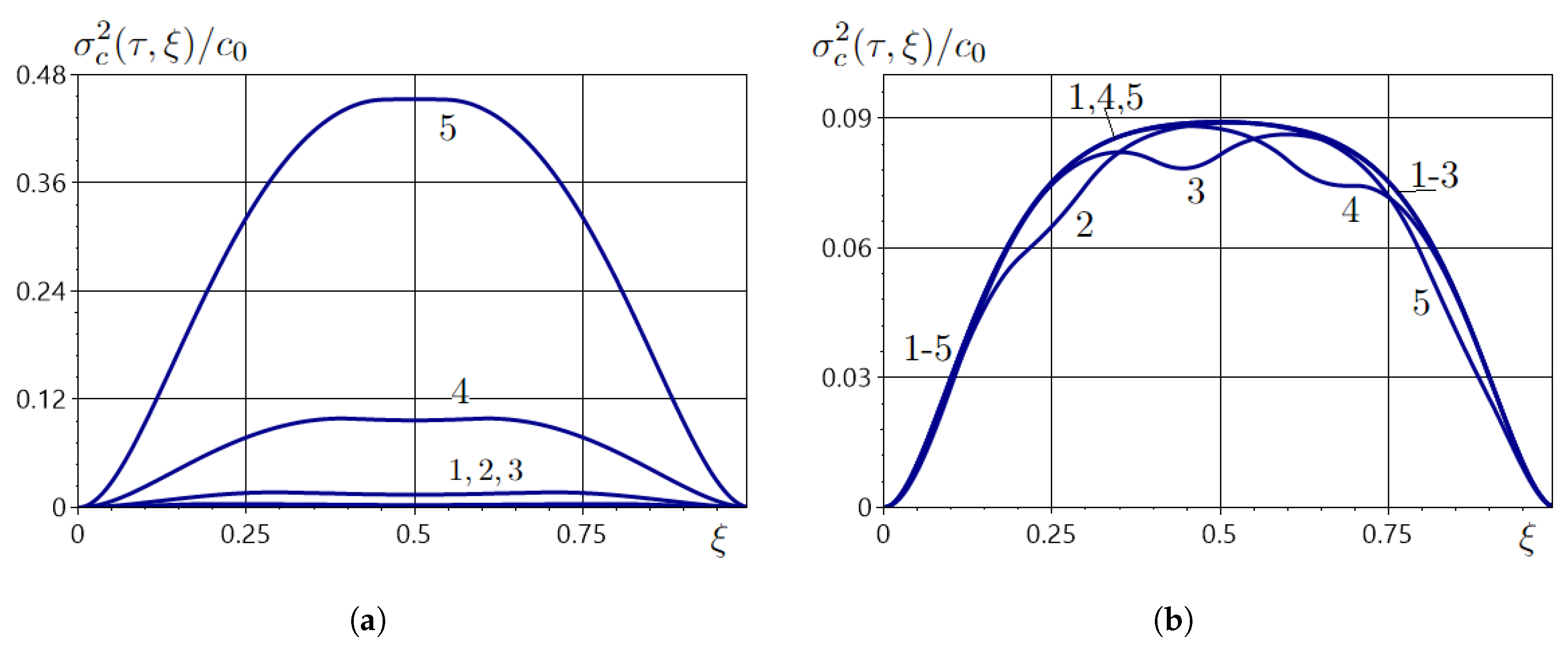
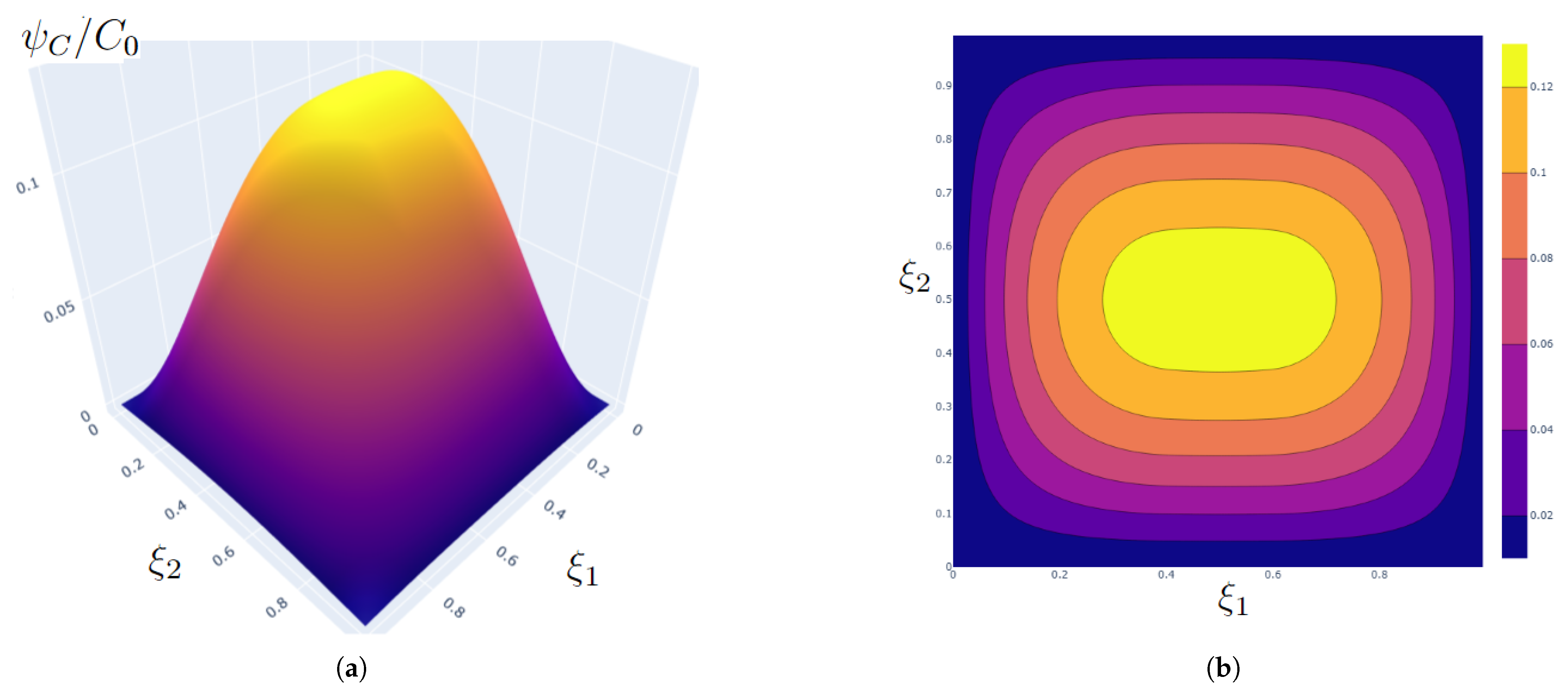
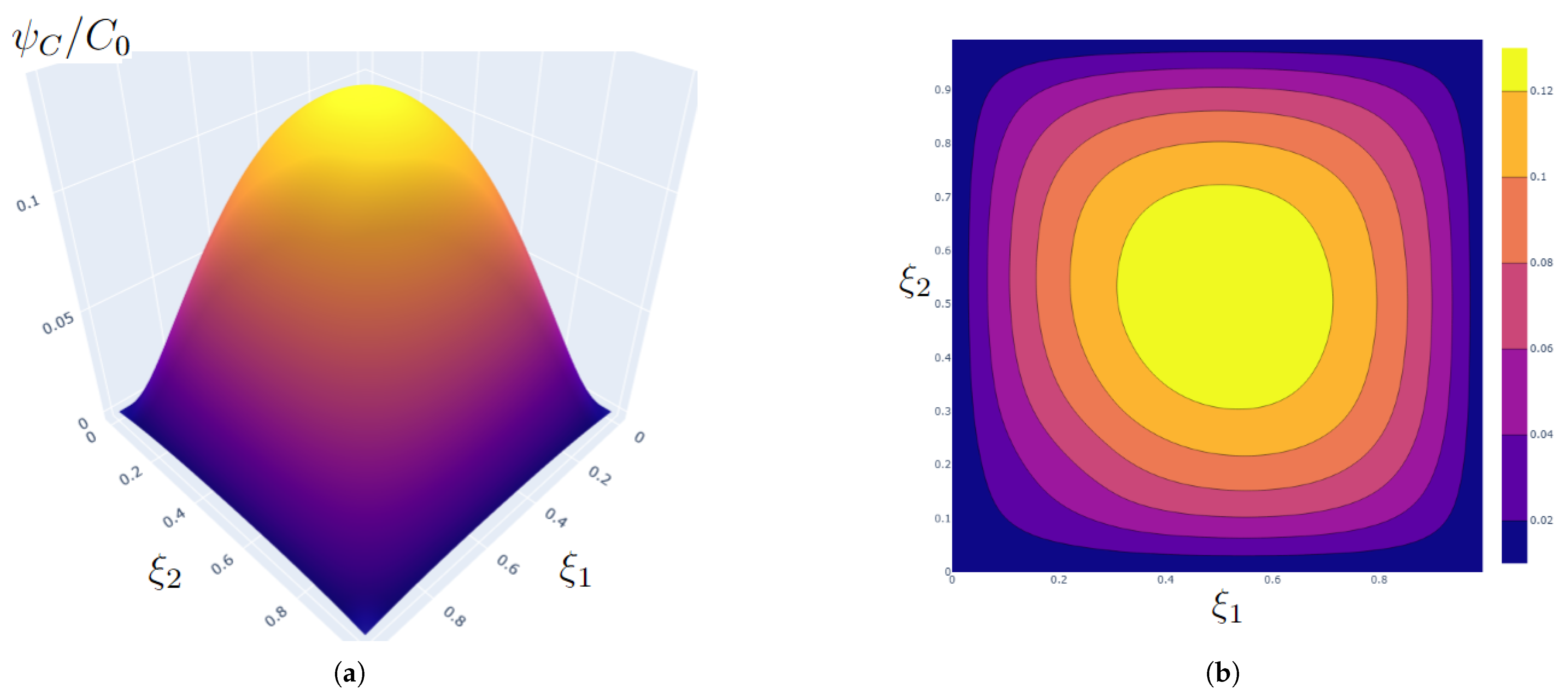



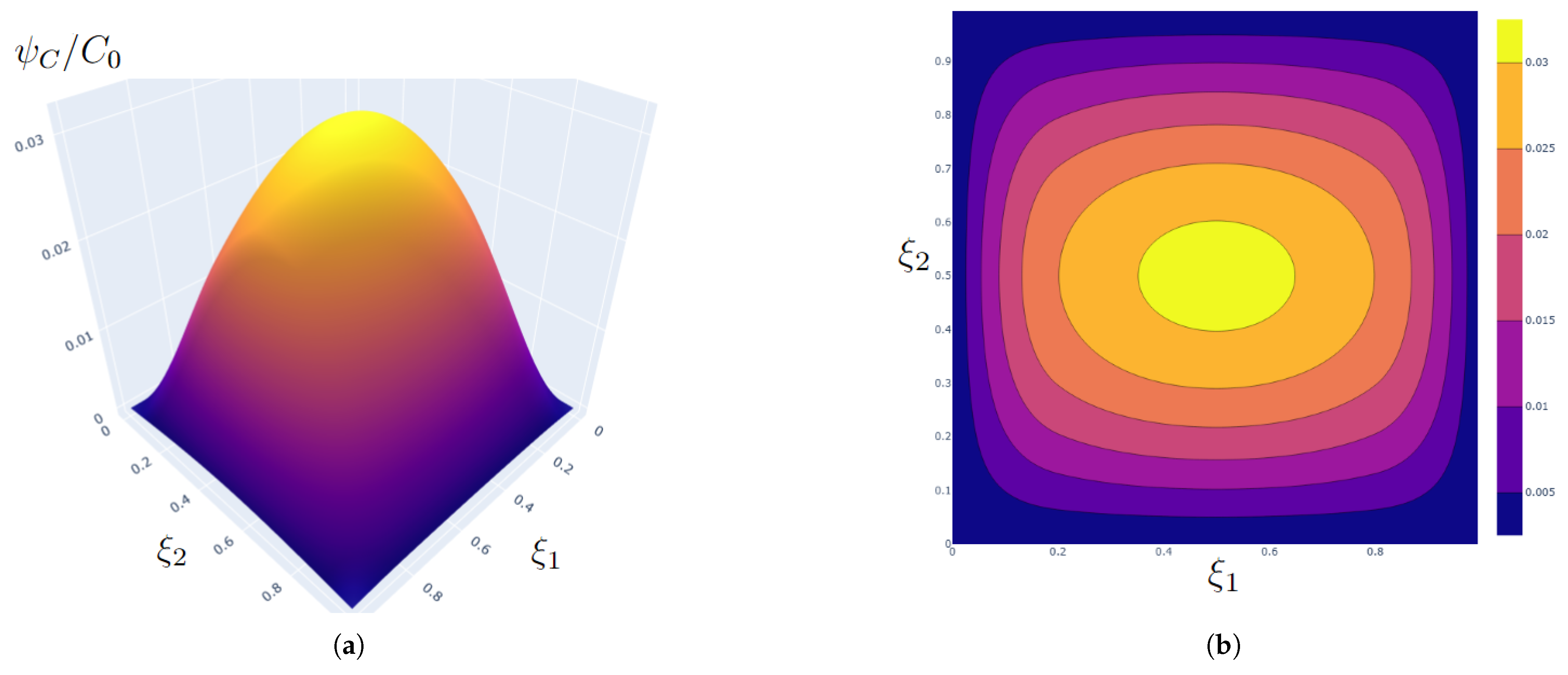
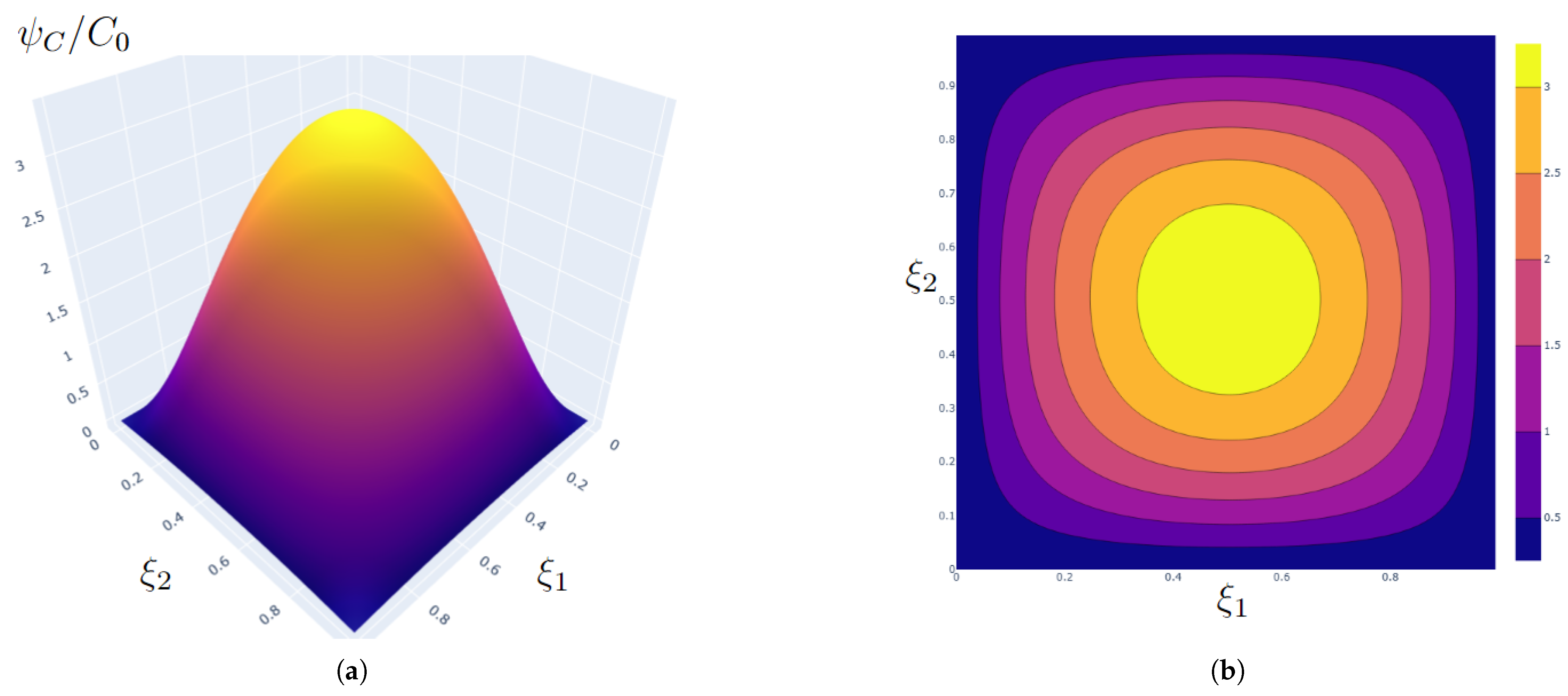

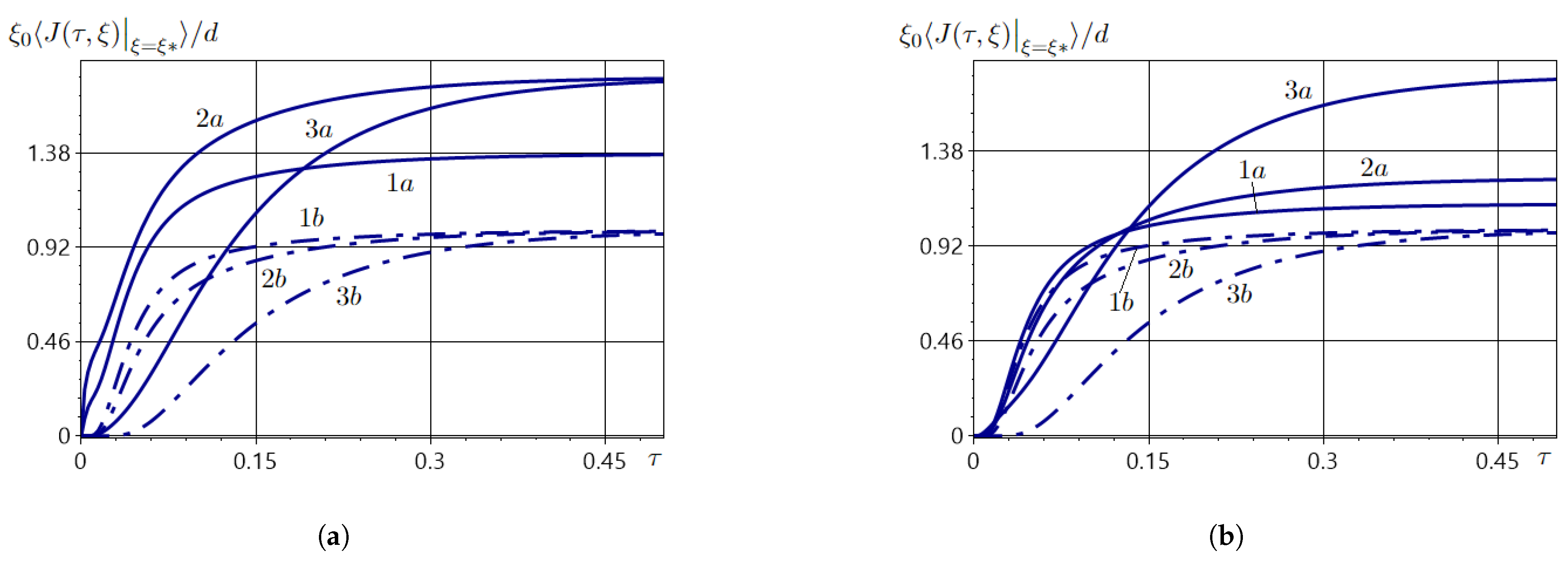

| 0.02 | 0.3237, 0.6763 | 0.0198 | 0.1850, 0.8150 | 0.0012 |
| 0.05 | 0.3931, 0.6069 | 0.0987 | 0.2197, 0.7803 | 0.0039 |
| 0.1 | 0.5 | 0.2817 | 0.4335, 0.5665 | 0.0097 |
| 0.2 | 0.5 | 0.5574 | 0.5 | 0.0205 |
| 0.3 | 0.5 | 0.6838 | 0.5 | 0.0225 |
| 0.1416 | 0.0620 | 0.5 | 0.45 | 0.8975 | 0.1416 | 0.0620 | 0.5 | 0.45 | 0.8013 |
| 0.1416 | 0.4956 | 0.5 | 0.45 | 0.8942 | 0.1416 | 0.4956 | 0.5 | 0.45 | 0.7532 |
| 0.0177 | 0.5044 | 0.5 | 0.45 | 0.8014 | 0.0177 | 0.5044 | 0.5 | 0.45 | 0.6137 |
| 0.7234 | 0.7123 | 0.5 | 0.45 | 0.9748 | 0.7234 | 0.7123 | 0.5 | 0.45 | 0.9647 |
| 0.1681 | 0.1062 | 0.05 | 0.06 | 0.8199 | 0.1681 | 0.1062 | 0.05 | 0.06 | 0.7076 |
| 0.1504 | 0.5044 | 0.05 | 0.06 | 0.7925 | 0.1504 | 0.5044 | 0.05 | 0.06 | 0.6069 |
| 0.0880 | 0.4956 | 0.05 | 0.06 | 0.7133 | 0.0880 | 0.4956 | 0.05 | 0.06 | 0.5121 |
| 0.2312 | 0.8612 | 0.05 | 0.06 | 0.8973 | 0.2312 | 0.8612 | 0.05 | 0.06 | 0.8661 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pukach, P.; Chernukha, O.; Chernukha, Y.; Vovk, M. Three-Dimensional Mathematical Modeling and Simulation of the Impurity Diffusion Process Under the Given Statistics of Systems of Internal Point Mass Sources. Modelling 2025, 6, 23. https://doi.org/10.3390/modelling6010023
Pukach P, Chernukha O, Chernukha Y, Vovk M. Three-Dimensional Mathematical Modeling and Simulation of the Impurity Diffusion Process Under the Given Statistics of Systems of Internal Point Mass Sources. Modelling. 2025; 6(1):23. https://doi.org/10.3390/modelling6010023
Chicago/Turabian StylePukach, Petro, Olha Chernukha, Yurii Chernukha, and Myroslava Vovk. 2025. "Three-Dimensional Mathematical Modeling and Simulation of the Impurity Diffusion Process Under the Given Statistics of Systems of Internal Point Mass Sources" Modelling 6, no. 1: 23. https://doi.org/10.3390/modelling6010023
APA StylePukach, P., Chernukha, O., Chernukha, Y., & Vovk, M. (2025). Three-Dimensional Mathematical Modeling and Simulation of the Impurity Diffusion Process Under the Given Statistics of Systems of Internal Point Mass Sources. Modelling, 6(1), 23. https://doi.org/10.3390/modelling6010023







