Bayesian and Non-Bayesian Parameter Estimation for the Bivariate Odd Lindley Half-Logistic Distribution Using Progressive Type-II Censoring with Applications in Sports Data
Abstract
1. Introduction
2. Overview of PrTIICS and the BOLiHL Distribution
2.1. Model Description
- Under this scheme, n units are tested at time zero and m failure and are recorded.
- After the first failure, or , discard items randomly from the remaining () items and continue the test.
- After the next failure, or , discard items randomly from the remaining items and continue the test.
- One would continue in this approach until observing the final failure, or , and then the remaining items are eliminated.
- The ith PrTII order statistic is denoted as or .
- We call the PrTIICS. In Type-II censoring, the censoring scheme R is fixed before the experiment.
- It can be seen that Type-II censoring is a particular case of PrTIICS, where the scheme is .
2.2. BOLiHL Distribution
3. Maximum Likelihood Estimation
4. Bayesian Estimation
- 1.
- Start with any initial values , , satisfying and uniform ; .
- 2.
- using the current value , sample a candidate point from the proposal distribution .
- 3.
- Given the candidate point , calculate the acceptance probability using this formula
- 4.
- Draw a value of u from the normal distribution.
- 5.
- Repeat steps 2–5 until a set N samples is generated.
- 6.
- Burn-in period (1000 iterations): Eliminate the first 1000 iterations to allow the Markov chain to converge to the stationary distribution and avoid bias from initial values.
- 7.
- Thinning (keep every 10th sample): After the burn-in period, keep every 10th sample to reduce auto correlation and improve the independence of the samples.
- 8.
- Storage of samples: Only store the samples after the burn-in period (1000 iterations) and thinning (keeping every 10th sample), which are then used for posterior inference.
- 9.
- Generally, the burn-in period is chosen to be 10–50% of the total number of iterations. In our case, we selected 10%, corresponding to 1000 iterations, as the chain converged within this period. Using 1000 iterations ensures reliable posterior estimates by eliminating the initial unstable values.
- 10.
- Compute the Bayesian estimate of with respect to the SELF is
- 11.
- The following formulas are used to calculate the bias, MSE, length of the CI and the length of the CrI for each model.where is the estimated value of .
- 12.
- Repeat this steps i time to obtain the Bayesian estimate of .
- 1.
- Arrange , , where L is the total number of simulations generated.
- 2.
- The symmetric CrI of become , and
5. Simulation Study
- 1.
- and
- 2.
- and
- 3.
- Step 1: Start with uniform random variables: Generate two sets of random variables and from the uniform distribution with the same sample size n. These uniform random variables will be used for transforming into BOLiHL-distributed variables.
- Step 2: Quantile function of the BOLiHL distribution: The bivariate random variables X and Y from the BOLiHL distribution are obtained using the following transformations:
- and are the scale parameters for X and Y, respectively.
- is the negative branch of the Lambert W-function.
- and are independent uniform random variables.
- Step 3: Transform uniform variables: For each and , apply the quantile function formulas to calculate X and Y.
- Step 4: Sort the samples: To prepare for PrTIICS, sort the transformed variables and in ascending order.
- Step 5: Apply the censoring scheme: Under PrTIICS:
- Retain only the first m smallest values for both variables. The remaining samples are addressed as censored.
- Let and .
- Step 6: Output the results: The uncensored observations, and , along with the censoring scheme R (which specifies the number of failures between successive observations), represent the PrTIICS bivariate sample.
- 1.
- The MSE and bias for the considered parameters decrease as the n increases.
- 2.
- The values of bias and MSE parameters of the BOLiHL distribution decrease as the m increases.
- 3.
- CI and CrI are also found for different sample sizes and failure times.
- 4.
- Based on the values of bias, MSE, and the length of CI, Bayesian estimation is the most effective method than MLE for estimating the parameters of the BOLiHL distribution.
- 5.
- Additionally, we observe that the Bayesian CrIs are better than asymptotic CIs.
- 6.
- In most of the cases, we observe that Bayesian estimates measures tend to be more accurate than MLE estimates.
| MLE | Bayesian | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (n,m) | CS(R) | Bias | MSE | LCI | UCI | Bias | MSE | LCrI | UCrI | |
| (30,25) | 1 | −0.3642 | 0.4801 | 0.9997 | 0.99973 | −0.0673 | 0.0045 | 0.3249 | 0.4968 | |
| −0.8651 | 1.0958 | 0.5730 | 1.4320 | −0.4946 | 0.2447 | 0.4293 | 0.6064 | |||
| −1.8629 | 3.8137 | 0.6843 | 1.9664 | −0.3584 | 0.1284 | 1.4299 | 1.8758 | |||
| 2 | −0.3674 | 0.4709 | 0.9995 | 0.99951 | −0.0667 | 0.0044 | 0.3455 | 0.4975 | ||
| −0.8672 | 1.1074 | 0.5260 | 1.1396 | −0.3862 | 0.1492 | 0.4976 | 0.7445 | |||
| −1.8604 | 3.8204 | 0.9759 | 2.9853 | −0.3235 | 0.1047 | 1.5222 | 1.8181 | |||
| 3 | −0.3689 | 0.4885 | 0.9992 | 0.9992 | −0.3290 | 0.1083 | 0.0447 | 0.2470 | ||
| −0.8651 | 1.0537 | 0.4771 | 1.2095 | −0.4063 | 0.1651 | 0.5081 | 0.7091 | |||
| −1.8603 | 3.8309 | 0.7914 | 2.7348 | −0.1042 | 0.0109 | 1.7215 | 2.0536 | |||
| (40,20) | 1 | −0.282 | 0.4541 | 0.99925 | 0.999259 | −0.0614 | 0.0037 | 0.3802 | 0.4976 | |
| −0.7747 | 0.9574 | 0.2406 | 0.4218 | −0.4521 | 0.2044 | 0.4689 | 0.6196 | |||
| −1.7868 | 3.5807 | 2.8145 | 9.3399 | −0.2504 | 0.0627 | 1.5343 | 1.9759 | |||
| 2 | −0.2616 | 0.3921 | 0.9990979 | 0.9990983 | −0.0587 | 0.0345 | 0.3845 | 0.4975 | ||
| −0.7655 | 0.9142 | 0.1496 | 0.2541 | −0.3844 | 0.1478 | 0.5317 | 0.7058 | |||
| −1.7815 | 3.5493 | 2.3302 | 6.1383 | −0.3149 | 0.0992 | 1.5172 | 1.8234 | |||
| 3 | −0.2692 | 0.4122 | 0.99913 | 0.99915 | −0.1149 | 0.0132 | 0.1962 | 0.5787 | ||
| −0.7646 | 0.9064 | 3.2562 | 0.4127 | −0.3924 | 0.1539 | 0.5186 | 0.6893 | |||
| −1.7709 | 3.4832 | 3.0197 | 9.3462 | −0.0877 | 0.0076 | 1.7457 | 2.1933 | |||
| (45,25) | 1 | −0.2577 | 0.3167 | 0.9998 | 0.99984 | 0.0440 | 0.0019 | 0.3972 | 0.4980 | |
| −0.7873 | 0.9397 | 0.1202 | 0.1915 | −0.4029 | 0.1623 | 0.5341 | 0.6737 | |||
| −1.773 | 3.4312 | 1.4845 | 3.68 | −0.1308 | 0.0171 | 1.7098 | 2.0147 | |||
| 2 | −0.2585 | 0.3301 | 0.9994 | 0.999482 | −0.057 | 0.00325 | 0.3953 | 0.4967 | ||
| −0.7548 | 0.8169 | 0.1753 | 0.2823 | −0.3804 | 0.1447 | 0.5389 | 0.7363 | |||
| −1.7814 | 3.4796 | 2.2968 | 6.1162 | −0.2768 | 0.0766 | 1.5696 | 1.8354 | |||
| 3 | −0.2675 | 0.3500 | 0.9995028 | 0.9995032 | 0.0514 | 0.0026 | 0.3438 | 0.8023 | ||
| −0.7332 | 0.7437 | 0.1899 | 0.3143 | −0.3402 | 0.1157 | 0.5972 | 0.7445 | |||
| −1.7351 | 3.2182 | 2.0135 | 6.1423 | −0.0207 | 0.0004 | 1.7639 | 2.2122 | |||
| (60,20) | 1 | −0.0954 | 0.2497 | 0.999491 | 0.999492 | −0.0384 | 0.0015 | 0.4069 | 0.4981 | |
| −0.6587 | 0.7638 | 0.1859 | 0.3182 | −0.3724 | 0.1387 | 0.5654 | 0.6938 | |||
| −1.5985 | 2.7838 | 3.5725 | 12.4408 | −0.069 | 0.0047 | 1.8305 | 2.0724 | |||
| 2 | −0.0963 | 0.2155 | 0.9996 | 0.999612 | −0.0414 | 0.0017 | 0.4029 | 0.4986 | ||
| 0.6870 | 0.8291 | 0.1361 | 0.2338 | −0.3241 | 0.1050 | 0.5642 | 0.7839 | |||
| −1.6657 | 3.1081 | 2.1189 | 7.7476 | −0.2549 | 0.0649 | 1.5998 | 1.9328 | |||
| 3 | −0.1688 | 0.3649 | 0.9995 | 0.99952 | 0.0273 | 0.00075 | 0.2609 | 0.9215 | ||
| −0.6299 | 0.6777 | 0.1714 | 0.2938 | −0.3403 | 0.1158 | 0.5904 | 0.7346 | |||
| −1.6642 | 3.0859 | 3.1415 | 10.8048 | 0.0092 | 0.000085 | 1.8192 | 2.3893 | |||
6. Real-Life Application
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burzykowski, T. Survival analysis: Methods for analyzing data with censored observations. Semin. Orthod. 2024, 30, 29–36. [Google Scholar] [CrossRef]
- Aggarwala, R. Ch. 13. Progressive censoring: A review. Handb. Stat. 2001, 20, 373–429. [Google Scholar]
- Oommen, N.P.; Gillariose, J. Review of Censoring Schemes: Concepts, Different Types, Model Description, Applications And Future Scope. Reliab. Theory Appl. 2024, 19, 287–300. [Google Scholar]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Springer Science & Business Media: New York, NY, USA, 2000. [Google Scholar]
- Mahmoud, M.R.; Muhammed, H.Z.; El-Saeed, A.R.; Abdellatif, A.D. Estimation of parameters of the GIE distribution under progressive Type-I censoring. J. Stat. Theory Appl. 2021, 20, 380–394. [Google Scholar] [CrossRef]
- Kundu, D. Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics 2008, 50, 144–154. [Google Scholar] [CrossRef]
- Tolba, A.H.; Almetwally, E.M.; Ramadan, D.A. Bayesian estimation of a one parameter Akshaya distribution with progressively type ii censord data. J. Stat. Appl. Probab. 2022, 11, 16. [Google Scholar]
- Ahmed, E.A. Bayesian estimation based on progressive Type-II censoring from two-parameter bathtub-shaped lifetime model: An Markov chain Monte Carlo approach. J. Appl. Stat. 2014, 41, 752–768. [Google Scholar] [CrossRef]
- Alshenawy, R.; Al-Alwan, A.; Almetwally, E.M.; Afify, A.Z.; Almongy, H.M. Progressive type-II censoring schemes of extended odd Weibull exponential distribution with applications in medicine and engineering. Mathematics 2020, 8, 1679. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Muhammed, H.Z.; Almetwally, E.M. Data analysis by adaptive progressive hybrid censored under bivariate model. Ann. Data Sci. 2024, 11, 507–548. [Google Scholar] [CrossRef]
- Muhammed, H.Z.; Almetwally, E.M. Bayesian and non-Bayesian estimation for the bivariate inverse weibull distribution under progressive type-II censoring. Ann. Data Sci. 2023, 10, 481–512. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Almetwally, E.M.; Muhammed, H.Z. Bayesian and non-bayesian estimation for the parameter of bivariate generalized Rayleigh distribution based on clayton copula under progressive type-II censoring with random removal. Sankhya A 2023, 85, 1205–1242. [Google Scholar] [CrossRef]
- Muhammed, H. Analysis of Dependent Variables Following Marshal-Olkin Bivariate Distributions in the Presence of Progressive Type II Censoring. Stat. Optim. Inf. Comput. 2023, 11, 694–708. [Google Scholar] [CrossRef]
- Polipu, S.; Gillariose, J. On a bivariate odd Lindley half logistic distribution from Farlie-Gumbel-Morgenstern copula. Afr. Mat. submitted for publication. 2024. [Google Scholar]
- Shamlan, D.; Baaqeel, H.; Fayomi, A. A Discrete Odd Lindley Half-Logistic Distribution with Applications. J. Phys. Conf. Ser. 2024, 2701, 012034. [Google Scholar] [CrossRef]
- Eliwa, M.; Altun, E.; Alhussain, Z.A.; Ahmed, E.A.; Salah, M.M.; Ahmed, H.H.; El-Morshedy, M. A new one-parameter lifetime distribution and its regression model with applications. PLoS ONE 2021, 16, e0246969. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hartmann, S. A remark on the application of the Newton-Raphson method in non-linear finite element analysis. Comput. Mech. 2005, 36, 100–116. [Google Scholar] [CrossRef]
- Akram, S.; Ann, Q.U. Newton raphson method. Int. J. Sci. Eng. Res. 2015, 6, 1748–1752. [Google Scholar]
- El-Sherpieny, E.S.A.; Muhammed, H.Z.; Almetwally, E.M. Bivariate Chen distribution based on copula function: Properties and application of diabetic nephropathy. J. Stat. Theory Pract. 2022, 16, 54. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Meintanis, S.G. Test of fit for Marshall–Olkin distributions with applications. J. Stat. Plan. Inference 2007, 137, 3954–3963. [Google Scholar] [CrossRef]
- Chesneau, C.; Tomy, L.; Gillariose, J. On a new distribution based on the arccosine function. Arab. J. Math. 2021, 10, 589–598. [Google Scholar] [CrossRef]

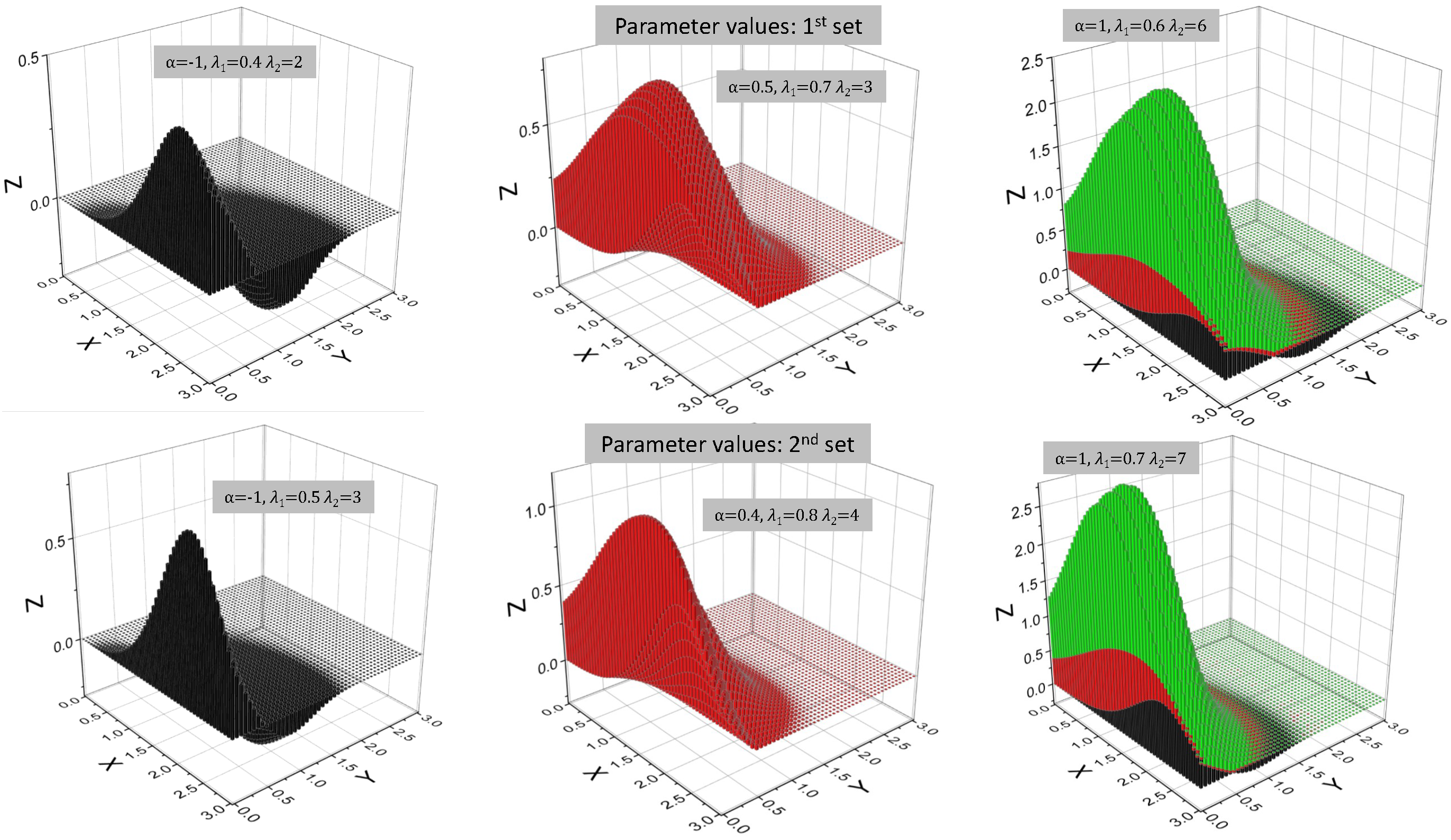
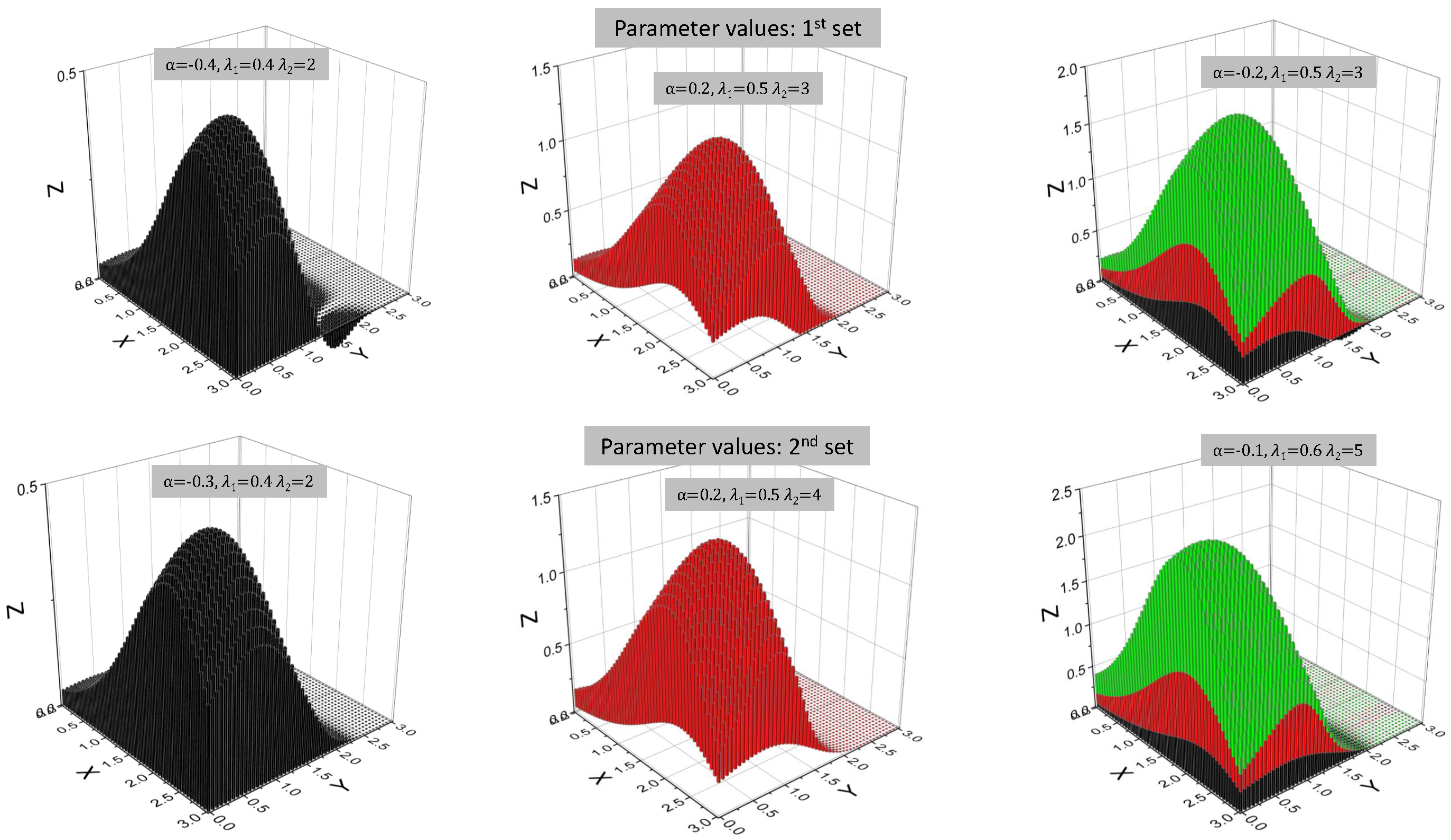

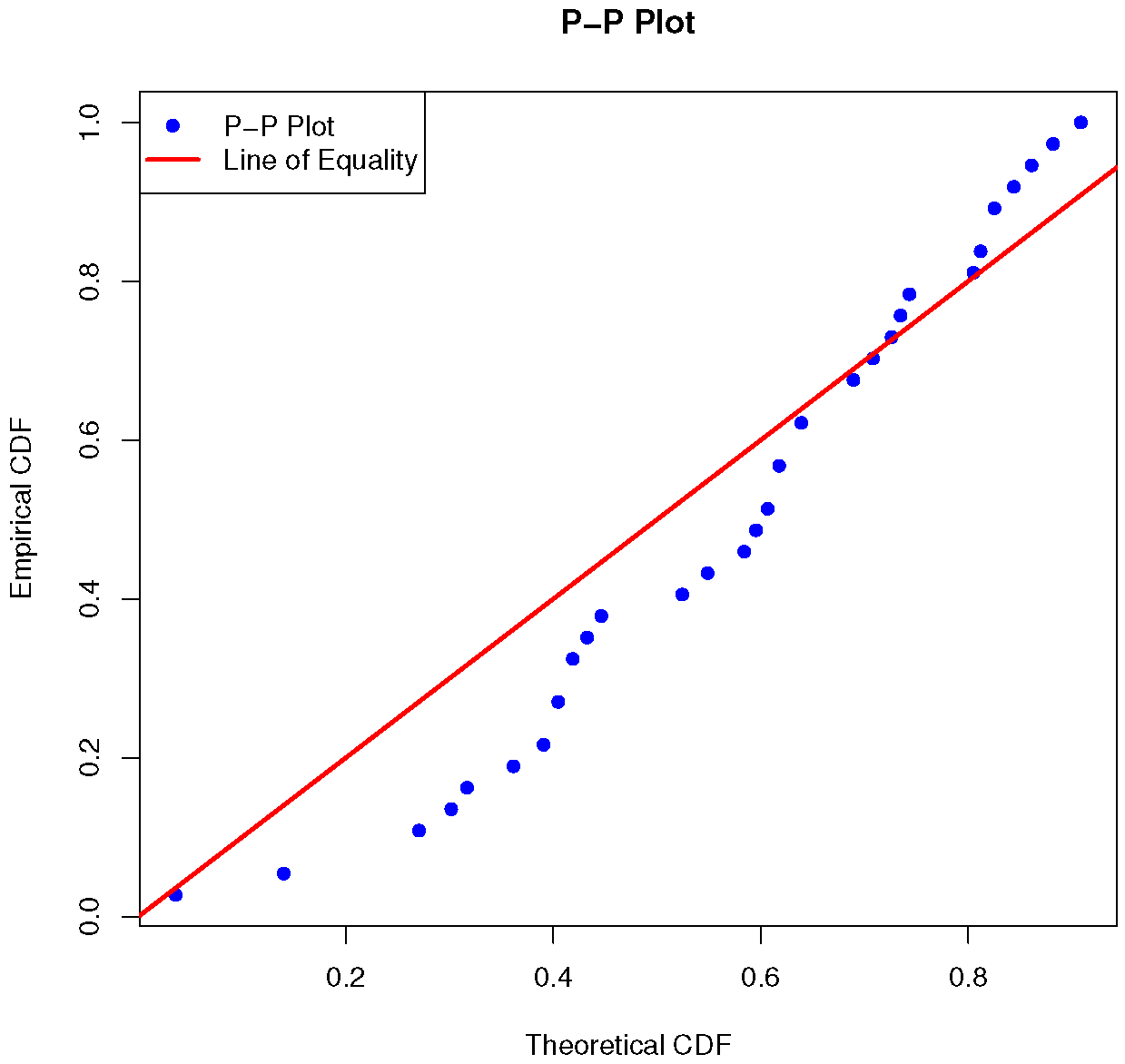


| Model | ||||||
|---|---|---|---|---|---|---|
| K-S | p-Value | LogL | K-S | p-Value | LogL | |
| BOLiHL | 0.2165 | 0.0623 | −1.64864 | 0.10292 | 0.8281 | −6.8581 |
| MLE | Bayesian | |||||||
|---|---|---|---|---|---|---|---|---|
| R | m | α | λ1 | λ2 | α | λ1 | λ2 | |
| 1 | 20 | Estimate | 0.9997 | 0.6369 | 8.3529 | 0.5307 | 1.3753 | 2.586 |
| SE | 1.084417 × 10−7 | 0.101102 | 2.6658 | 0.0049 | 0.0042 | 0.0057 | ||
| 25 | Estimate | 0.9991 | 0.7032 | 7.3782 | 0.3097 | 1.6926 | 2.365 | |
| SE | 1.083713 × 10−7 | 0.0963 | 1.8398 | 0.0319 | 0.0039 | 0.0054 | ||
| 30 | Estimate | 0.9994 | 0.8622 | 6.6041 | 0.9029 | 1.1961 | 2.4515 | |
| SE | 1.084084 × 10−7 | 0.1095 | 1.319 | 0.0029 | 0.0031 | 0.0052 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polipu, S.; Gillariose, J. Bayesian and Non-Bayesian Parameter Estimation for the Bivariate Odd Lindley Half-Logistic Distribution Using Progressive Type-II Censoring with Applications in Sports Data. Modelling 2025, 6, 13. https://doi.org/10.3390/modelling6010013
Polipu S, Gillariose J. Bayesian and Non-Bayesian Parameter Estimation for the Bivariate Odd Lindley Half-Logistic Distribution Using Progressive Type-II Censoring with Applications in Sports Data. Modelling. 2025; 6(1):13. https://doi.org/10.3390/modelling6010013
Chicago/Turabian StylePolipu, Shruthi, and Jiju Gillariose. 2025. "Bayesian and Non-Bayesian Parameter Estimation for the Bivariate Odd Lindley Half-Logistic Distribution Using Progressive Type-II Censoring with Applications in Sports Data" Modelling 6, no. 1: 13. https://doi.org/10.3390/modelling6010013
APA StylePolipu, S., & Gillariose, J. (2025). Bayesian and Non-Bayesian Parameter Estimation for the Bivariate Odd Lindley Half-Logistic Distribution Using Progressive Type-II Censoring with Applications in Sports Data. Modelling, 6(1), 13. https://doi.org/10.3390/modelling6010013






