Non-Linear Control and Numerical Analysis Applied in a Non-Linear Model of Cutting Process Subject to Non-Ideal Excitations

Abstract

This work presents a non-linear mathematical model of a machining system subjected to a non-ideal vibration source. Computer simulations have shown chaotic behavior for specific parameters of the proposed mathematical model. The chaotic behavior is proven using time histories, phase diagrams, bifurcation diagrams, and the Lyapunov exponent. Considering that cutting tool vibration in the machining process is one of the main problems of productivity and machining accuracy, the introduction of a magnetorheological damper was considered in the proposed model to reduce the vibration amplitudes of the cutting tool and suppress the chaotic behavior. Hysteresis was considered in the magnetorheological damper model and its application in the system as both a passive and active absorber. The active control strategy considered the application of two non-linear control signals: feedforward to maintain the vibration with a desired behavior and state feedback to drive the system to the desired behavior. The numerical results demonstrated that the proposed controls efficiently reduced the vibration amplitude by introducing the MR damper. Active control has proven effective in controlling the force of the MR damper by varying the electrical voltage applied to the damper coil.

1. Introduction

In machining processes, tool vibration control is critical for ensuring productivity, machining accuracy, and reducing tool wear [1]. According to [2], friction and regeneration effects are the main factors contributing to cutting tool vibration. Friction vibration is caused by the contact of the cutting tool and the machined workpiece. In contrast, regeneration vibration is caused by the variation of the cutting force, which depends on the current and past positions of the tool [2,3,4].

Machining processes mathematical models consider non-linear elements, such as non-linear forces, with the Duffing oscillator being one of the models considered due to its similarity to the regenerative cutting vibration system. In the cutting process, the regenerative force is represented by a cubic non-linearity [5]. Another representative component in the modeling is the eccentricity of the unbalanced mass of the part that has undergone turning and grinding [6]. In [7], it is demonstrated that using more flexible tools or those with a higher damping coefficient allows for better stability in the machining process.

It is necessary to develop vibration control techniques in the machining process to suppress the adverse effects of cutting tool vibration, increase the material removal rate, and solve a bottleneck in the manufacturing industry [8,9].

Among the control strategies, we can mention passive dampers that do not depend on external sources for their actuation or active dampers that depend on sensors and actuators. For passive dampers, we can highlight vibration absorbers, friction dampers, and adjusted mass dampers [10,11]. However, according to [12], even with the advantages of simplicity of implementation and low cost for implementing passive damping systems, their performance is limited due to the dynamic characteristics of the equipment in the machining process. One way to avoid the limitations of passive dampers is to use active dampers.

Active methods for vibration suppression consider using appropriate sensors and actuators in the cutting system, thus generating the desired active control forces and absorbing the energy generated by the vibration [13,14]. In [9], a model-free finite frequency band (MFFFB) H∞ control system is proposed to suppress the vibration of the turning process. Numerical and experimental results of an H∞ controller based on linear matrix inequality (LMI) are presented in [15], demonstrating the effectiveness of the proposed control. An optimal control system for vibration suppression in turning is proposed in [16,17]. A delay-dependent output feedback H∞ controller is proposed in [18] for the active control of regenerative vibration during internal turning. A turning position and vibration suppression controller are proposed in [13].

Considering the actuators considered to reduce the vibration of the cutting tool, we can highlight piezoelectric materials, magnetorheological or electrorheological magnetorheological dampers, and magnetorheological elastomers [19]. In [20], ER fluid is used in the chuck of the machining system to control the stiffness of the boring bar and reduce the vibration in the machining process. The electric field of the ER fluid is controlled by applying adaptive control.

The use of piezoelectric materials in the vibration control of the cutting tool in the machining process is considered in [21]. The authors considered the piezoelectric material with an active actuator and the vibration obtained by the variation of the voltage signal of an extensometer. The actuator control was considered using a feedback control that used the voltage of the extensometer as a control signal in the piezoelectric actuator. The experimental results demonstrate a significant reduction in the surface roughness of the machined part.

The use of magnetorheological fluids in the control of vibration in machining has been highlighted in the control of the vibration of the boring tube [22,23,24,25,26,27,28,29]. In [22], the magnetorheological fluid foams are proposed to reduce vibrations in the machining process. Using magnetorheological fluid foam aims to reduce vibration in boring, thus reducing vibration in the machining process. Experimental results are presented for different configurations of polyurethane foams and magnetorheological fluids, and the vibration reduction capacity is evaluated through finite element analysis. In [23], an ON/OFF control is proposed to control vibrations in the machining process. A single-tube boring damper with magnetorheological fluids is considered for vibration control in machining. To demonstrate the effectiveness of the proposed control, computational simulations were considered using Simulink and experimental validation in machining AISI 01 and AISI D2 steel. Experimental results demonstrate that vibration control enabled a better surface finish of the machined part as well as the useful life of the cutting tool. In [24], a boring tube containing magnetorheological fluid for vibration control was developed. The numerical results demonstrated that high electric currents with medium frequencies obtained the best results in controlling the vibration of the machined part. In [25], a linear quadradic regulator (LQR) controller was proposed to control the electric current applied to the magnetorheological fluid contained in the boring tube. In [26], a fuzzy controller was proposed to control the electric current applied to the magnetorheological fluid. In [27], it was found that using magnetorheological fluid in the boring tube can reduce the vibration of the cutting tool by up to 24%. In [28], a study was carried out with variations in the electric current and the percentage of magnetizable particles in the magnetorheological fluid to determine the best strategy for reducing the vibration of the boring tube. In [29], the use of parametric excitations was proposed to vary the electric current applied to the magnetorheological fluid contained in the boring tube, considering the van der Pol-Mathieu–Duffing oscillator to generate the excitations.

This work contributes to the application of numerical modeling systems and computational simulations in engineering science, presenting the investigation of the influence of the eccentricity of the machined mass, which is coupled to a DC motor, implying a non-ideal excitation source [30]. This paper introduces a magnetorheological damper perpendicular to the cutting tool displacement to suppress the chaotic behavior of the cutting tool tip and reduce its vibration amplitude. Two control strategies were considered: a passive one, in which the MR damper is not energized with electrical voltage; and another active control strategy, which controls the electrical voltage applied to the MR damper coil. The proposed active control considers two control strategies: a feedback control obtained by the state-dependent Riccati equation (SDRE) non-linear control method and a feedforward control that aims to compensate for external excitations. The non-linear control strategy SDRE control is well known and has been applied to several non-linear problems. The control method has become attractive due to its ability to provide non-linear feedback controls, including in its proposal the possibility of using non-linear terms in the system state matrix and adapting the state and control matrices to obtain controllable systems [31].

MR dampers have ferrous microparticles suspended in the damper fluid, and when magnetized, they align when subjected to a magnetic field, thus increasing the fluid’s viscosity. The magnetic properties of the MR fluid allow it to be used as a voltage or electric current-controlled damper. Due to electromagnetic residuals, MR dampers have a dynamic hysteresis behavior, maintaining a residual force even after depolarization, similar to that observed in viscoelastic systems. According to [31], the LuGre model is the most suitable for representing the force of the MR damper when its applications in control systems are considered.

This paper is organized as follows: In Section 2, the mathematical modeling for the turning system with a non-ideal excitation source is presented, as well as the dynamic analysis of the system for variations in the damping coefficient and cubic stiffness. In Section 3, the turning system with a non-ideal excitation source with the introduction of the MR damper is presented, as well as the dynamic analysis for variations in the total force of the damper and the variation of the electrical voltage applied to the MR damper coil. In Section 4, the active control proposal is presented, using the SDRE control to control the voltage of the MR damper. Finally, the conclusions are summarized in Section 5.

2. Mathematical Model

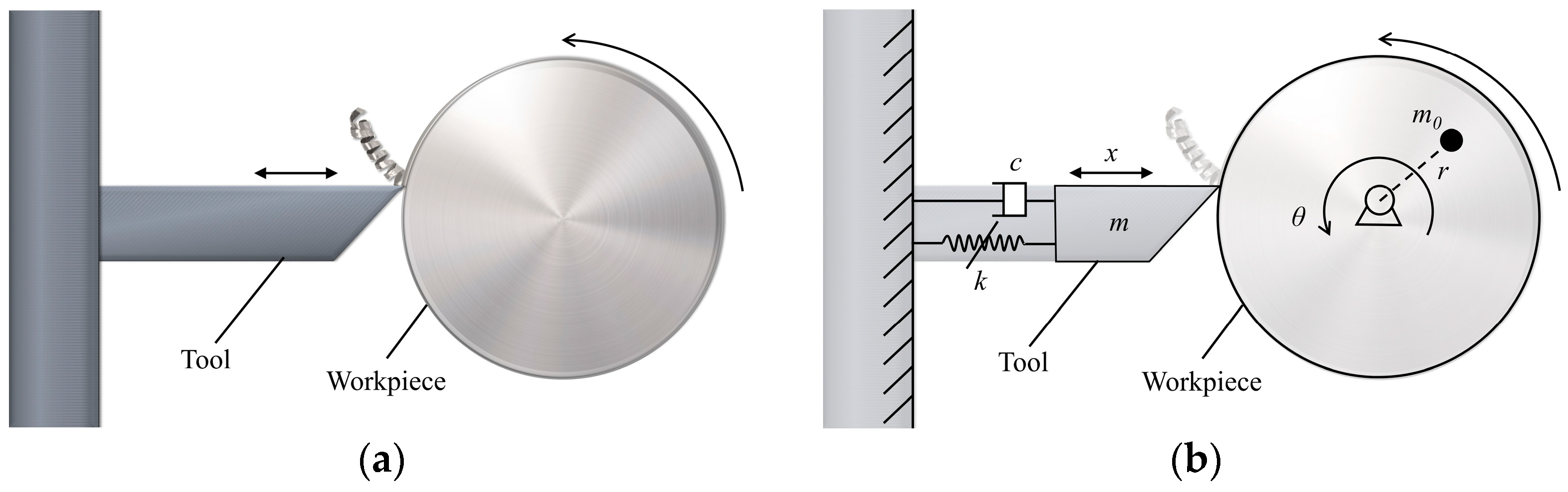
Figure 1 illustrates a basic physical model of single-degree-of-freedom orthogonal vibration and rotation machining with mass eccentricity and a non-ideal excitation source (induction motor).

• where $x$ is the tool chatter amplitude, $m$ is cutting tool mass, $c$ is damping, $k$ and $k_{nl}$ are the linear and non-linear stiffness, $m_0$ is the unbalanced mass of the motor, and $r$ is the eccentricity of the unbalanced mass.

In this paper, the Lagrangian equation (Equation (1)) is considered to obtain the mathematical model of Figure 1:

$$L=T-V,$$

(1)

where $T$ is the kinetic energy, and $V$ is the potential energy.

The mathematical model is obtained from the following:

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial {\dot{Q}}_i}}\right)-{\displaystyle \frac{\partial L}{\partial Q_i}}={\mathfrak{I}}_i,$$

(2)

where i = 1, 2, …, N. N is the degree of freedom system, ${\mathfrak{I}}_i$ are non-conservative forces, and $Q_i$ are generalized coordinates, being that $Q_1=x$ and $Q_2=\theta$.

Disregarding the gravitational force, the non-ideal system considered in Figure 1 presents the following potential energy:

$$V={\displaystyle \frac{1}{2}}{k}_l{x}^2+{\displaystyle \frac{1}{4}}{k}_{nl}{x}^4.$$

(3)

Kinetic energy is obtained from the following:

$$T={\displaystyle \frac{1}{2}}m{\dot{x}}^2+{\displaystyle \frac{1}{2}}J{\dot{\theta }}^2+{\displaystyle \frac{1}{2}}{m}_0\left({\dot{x}}^2+r^2{\dot{\theta }}^2-2r\dot{x}\dot{\theta }\sin \left(\theta \right)\right).$$

(4)

Non-conservative energies are obtained from the following:

$$\begin{array}{l}{\mathfrak{I}}_1=-c\dot{x}\\ {\mathfrak{I}}_2=V_1-V_2\dot{\phi }\end{array}.$$

(5)

Considering the substitution of (3) and (4) in (1), and substitution of (1) and (5) in (2), the following mathematical model is obtained:

$$\begin{array}{l}m\ddot{x}+c\dot{x}+k_{l}x+k_{nl}{x}^3=m_{0}r\ddot{\theta }\sin (\theta )+m_{0}r{\dot{\theta }}^2\cos (\theta )\\ \left(J+r^2{m}_0\right)\ddot{\theta }-m_{0}r\ddot{x}\sin \left(\theta \right)=V_1-V_2\dot{\theta }\end{array},$$

(6)

where $J$ is the moment of inertia for the motor, and $V_1-V_2\dot{\phi }$ is the motor’s torque, where $V_1$ is the voltage and $V_2$ is a constant [30].

Considering the following substitutions: $\tau =\omega t$, $\omega =\sqrt{{\displaystyle \frac{k_l}{m}}}$, $x_1={\displaystyle \frac{x}{x^{*}}}$, $x_2=\dot{x}$, $x_3={\displaystyle \frac{\theta }{{\theta }^{*}}}$, $x_4={\dot{x}}_3$, $I=J+r^2{m}_0$, ${\alpha }_1={\displaystyle \frac{c}{\omega m}}$, ${\alpha }_2={\displaystyle \frac{k_{nl}}{{\omega }^{2}m}}$, ${\alpha }_3={\displaystyle \frac{k_l}{{\omega }^{2}m}}$, ${\delta }_1={\displaystyle \frac{m_{0}r}{m}}$, ${\delta }_2={\displaystyle \frac{m_{0}r}{\omega m}}$, ${\beta }_1={\displaystyle \frac{m_{0}r}{I}}$, ${\beta }_2={\displaystyle \frac{V_1}{{\omega }^{2}I}}$, and ${\beta }_3={\displaystyle \frac{V_2}{\omega I}}$. The system (6) is obtained in dimensionless form the following:

$$\begin{array}{l}\ddot{x}=-{\alpha }_1\dot{x}-{\alpha }_{3}x-{\alpha }_2{x}^3+{\delta }_1\ddot{\phi }\sin (\phi )+{\delta }_2{\dot{\phi }}^2\cos (\phi )\\ \ddot{\theta }={\beta }_1\ddot{x}\sin \left(\theta \right)+{\beta }_2-{\beta }_3\dot{\theta }\end{array}.$$

(7)

The following system can represent the system (7):

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2={\displaystyle \frac{1}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\left(-{\alpha }_1{x}_2-{\alpha }_3{x}_1-{\alpha }_2{x_1}^3+{\beta }_2{\alpha }_3\sin (x_3)-{\beta }_3{\delta }_1{x}_4\sin (x_3)+{\delta }_2{x_4}^2\cos (x_3)\right)\\ {\dot{x}}_3=x_4\\ {\dot{x}}_4={\displaystyle \frac{1}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\left(\begin{array}{l}-{\alpha }_1{\beta }_1{x}_2\cos \left(x_3\right)+x_1{\beta }_1\cos \left(x_3\right)-{\alpha }_2{x_1}^3{\beta }_1\cos \left(x_3\right)\\ +{\delta }_2{x_4}^2\cos \left(x_3\right){\beta }_1\cos \left(x_3\right)+{\beta }_2-{\beta }_3{x}_4\end{array}\right)\end{array}.$$

(8)

System Dynamic Analysis

The fourth-order Runge–Kutta method with integration step (h = 0.01) is considered for numerical simulations with the following parameters: ${\alpha }_3=-1$, ${\delta }_1=8.373$, ${\delta }_2=0.25$, ${\beta }_1=0.05$, ${\beta }_2=100$, ${\beta }_3=200$, ${\alpha }_1=\left[0.01:0.3\right]$, and ${\alpha }_2=\left[0.01:0.5\right]$, along with the initial condition $x_{1_0}=x_{2_0}=x_{3_0}=x_{4_0}=0$. To obtain the bifurcation diagram and largest Lyapunov exponents, the algorithms available in [32] are considered.

Figure 2 presents the bifurcation diagrams and largest Lyapunov exponents, considering the parameter ${\alpha }_1=\left[0.01:0.3\right]$ and ${\alpha }_2=0.2$.

We can observe in Figure 2 that the cutting tool enters into chaotic behavior for different variations of the damping coefficient (${\alpha }_1$), being chaotic for ${\alpha }_1\cong \left[0.01:0.107\right]$ and ${\alpha }_1\cong \left[0.14:0.224\right]$.

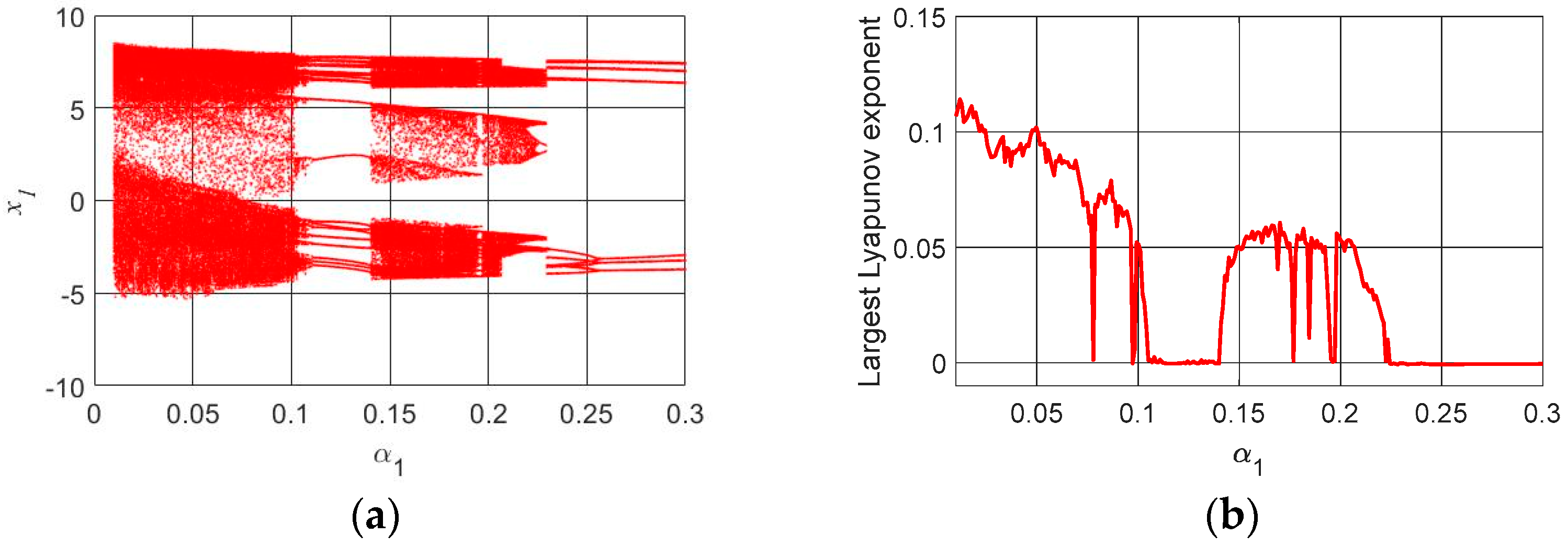
Figure 3 presents the bifurcation diagrams and largest Lyapunov exponents, considering the parameter ${\alpha }_2=\left[0.01:0.5\right]$ and ${\alpha }_1=0.1$.

Analyzing Figure 3, we can observe that the vibration of the cutting tool is sensitive to variations in the cubic stiffness coefficient. It is possible to observe a significant variation of chaotic and periodic behaviors. The following are the most significant variations of ${\alpha }_2$ that lead the system to chaotic behavior: ${\alpha }_2\cong \left[0.01:0.013\right]$, ${\alpha }_2\cong \left[0.018:0.025\right]$, ${\alpha }_2\cong \left[0.032:0.036\right]$, ${\alpha }_2\cong \left[0.038:0.055\right]$, ${\alpha }_2\cong \left[0.097:0.105\right]$, ${\alpha }_2\cong \left[0.114:0.143\right]$, ${\alpha }_2\cong \left[0.168:0.211\right]$, and ${\alpha }_2\cong \left[0.238:0.254\right]$.

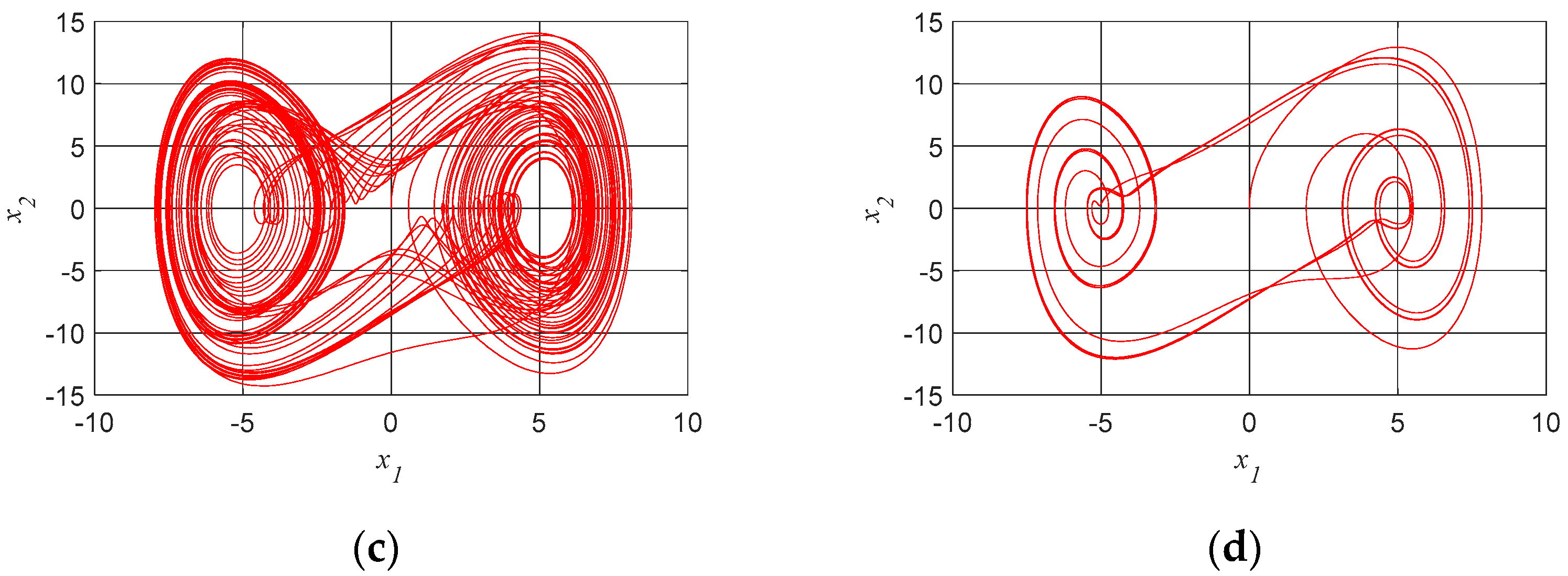
In Figure 4, we present the vibrations in time for $x_1$ and the phase diagram of $x_1$ versus $x_2$ for the following parameters: ${\alpha }_1=0.1$, ${\alpha }_2=0.2$, ${\alpha }_3=-1$, ${\delta }_1=8.373$, ${\delta }_2=0.25$, ${\beta }_1=0.05$, ${\beta }_2=100$ and ${\beta }_3=200$.

Analyzing Figure 4, one can see the dynamics of the chaotic behavior of the cutting tool. Considering the results presented in Figure 2 and Figure 3, we have the following Lyapunov exponents for Figure 4: ${\lambda }_1=0.053727$, ${\lambda }_2=-0.001$, ${\lambda }_3=-0.198$, and ${\lambda }_4=-178.182$.

Considering that large displacements of the cutting tool are undesirable and impair the machined part’s finishing quality, this paper will consider the case in which it is possible to include additional damping in the structure of the cutting tool. The use of magnetorheological damping is considered. The damping coefficient is controlled by the variation of the electrical voltage applied to the damper coil.

3. Mathematical Model with the Inclusion of MR Damping

Due to the non-linear friction mechanism, magnetorheological dampers have hysteresis effects. The LuGre friction model, which was initially developed to describe non-linear friction phenomena, has been successfully used and is expressed as follows [31]:

$$\begin{array}{l}{F}_{mrd}={\sigma }_{a}z+{\sigma }_{0}z\nu +{\sigma }_1\dot{z}+{\sigma }_2\dot{x}+{\sigma }_b\dot{x}\nu \\ \dot{z}=\dot{x}-{\sigma }_0{a}_0\left|\dot{x}\right|z\end{array},$$

(9)

where $F_{mrd}$ is the damping force, $\nu$ is the input voltage, $z$ is the internal state variable, and $\dot{x}$ is the velocity of the damper piston; ${\sigma }_0$, ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_a$, ${\sigma }_b$, and $a_0$ are constant values.

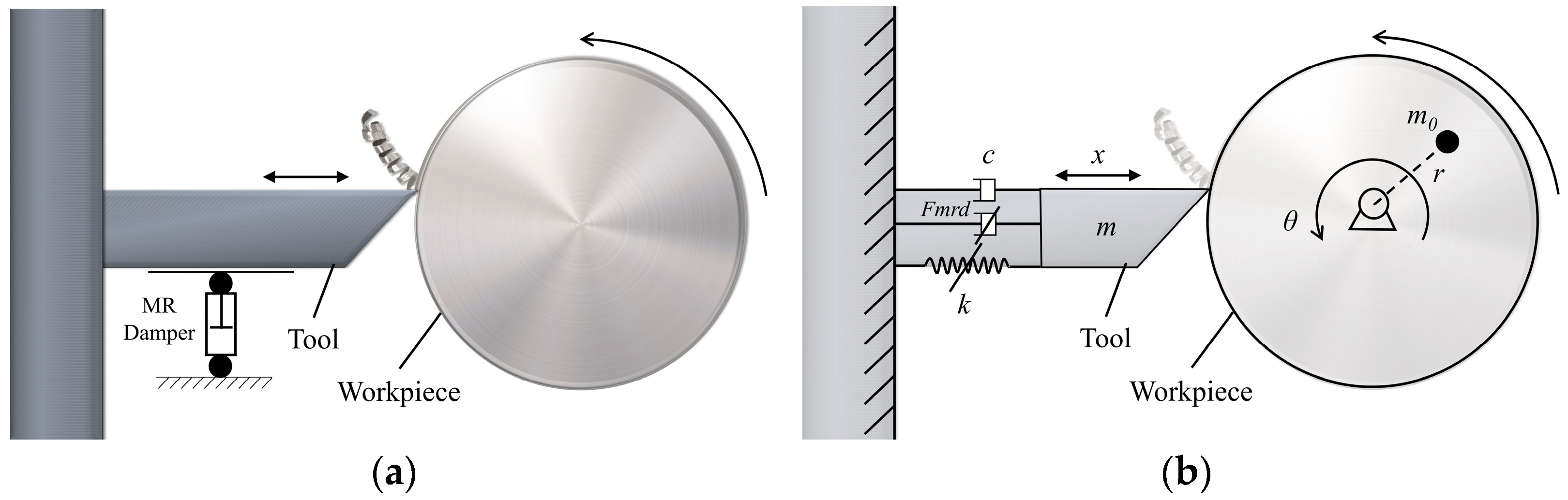
Figure 5 shows the kinematic diagram of the system for the inclusion of the magnetorheological (MR) damper.

Considering the inclusion of the damper force MR (Equation (9)) in Equation (8), we obtain Equation (10), which represents the system shown in Figure 5.

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2={\displaystyle \frac{1}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\left(-{\alpha }_5{F}_{mrd}-{\alpha }_1{x}_2-{\alpha }_3{x}_1-{\alpha }_2{x_1}^3+{\beta }_2{\alpha }_3\sin (x_3)-{\beta }_3{\delta }_1{x}_4\sin (x_3)+{\delta }_2{x_4}^2\cos (x_3)\right)\\ {\dot{x}}_3=x_4\\ {\dot{x}}_4={\displaystyle \frac{1}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\left(\begin{array}{l}-{\alpha }_5{F}_{mrd}-{\alpha }_1{\beta }_1{x}_2\cos \left(x_3\right)-{\delta }_1{x}_1{\beta }_1\cos \left(x_3\right)-{\alpha }_2{x_1}^3{\beta }_1\cos \left(x_3\right)\\ +{\delta }_2{x_4}^2\cos \left(x_3\right){\beta }_1\cos \left(x_3\right)+{\beta }_2-{\beta }_3{x}_4\end{array}\right)\\ {\dot{x}}_5=x_2-{\sigma }_0{a}_0\left|x_2\right|x_5\end{array},$$

(10)

where ${\alpha }_5$ is the MR damping parameter in the system.

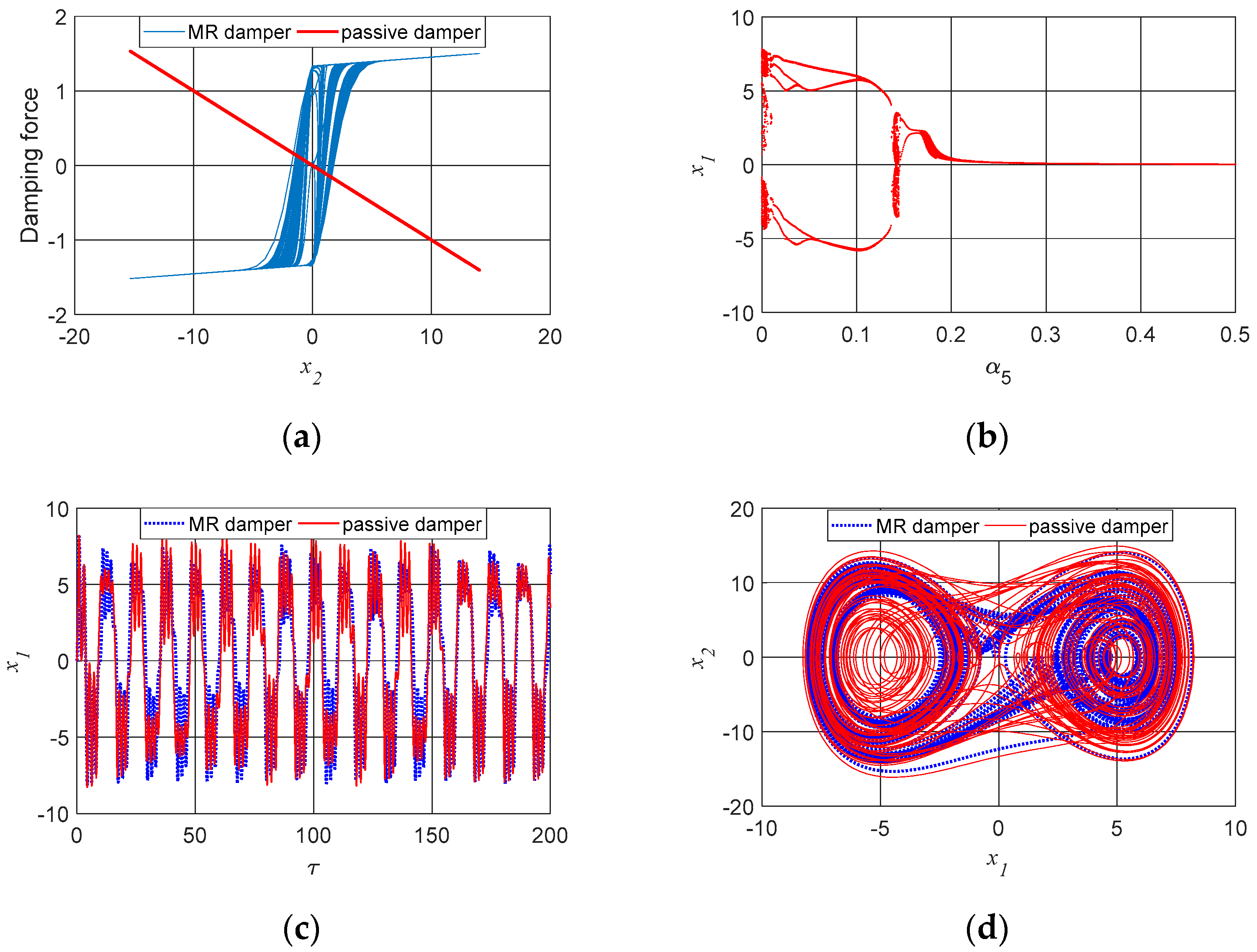
For numerical simulations, Equation (10) was considered with the following fixed initial parameters: ${\alpha }_1=0.1$, ${\alpha }_2=0.2$, ${\alpha }_3=-1$, ${\delta }_1=8.373$, ${\delta }_2=0.25$, ${\beta }_1=0.05$, ${\beta }_2=100$ and ${\beta }_3=200$, ${\sigma }_0=8000$, ${\sigma }_1=16$, ${\sigma }_2=1.5$, ${\sigma }_a=4000$, ${\sigma }_b=8$, $a_0=0.003$, $\nu =\left[0:2.5\right]$, and ${\alpha }_5=\left[0:0.1\right]$.

Figure 6 presents the bifurcation diagrams and largest Lyapunov exponents, considering the parameters ${\alpha }_5=\left[0:0.1\right]$ and $\nu =0$.

We can observe in Figure 6 that as the damping force of the MR shock absorber is increased, the system becomes periodic, which is expected behavior. However, in cases in which it is not possible to use high damping, the system will remain chaotic for the following ${\alpha }_5$ values: ${\alpha }_5\cong \left[0:0.003\right]$, ${\alpha }_5\cong \left[0.0017:0.0056\right]$ and ${\alpha }_5\cong \left[0.0084:0.0107\right]$.

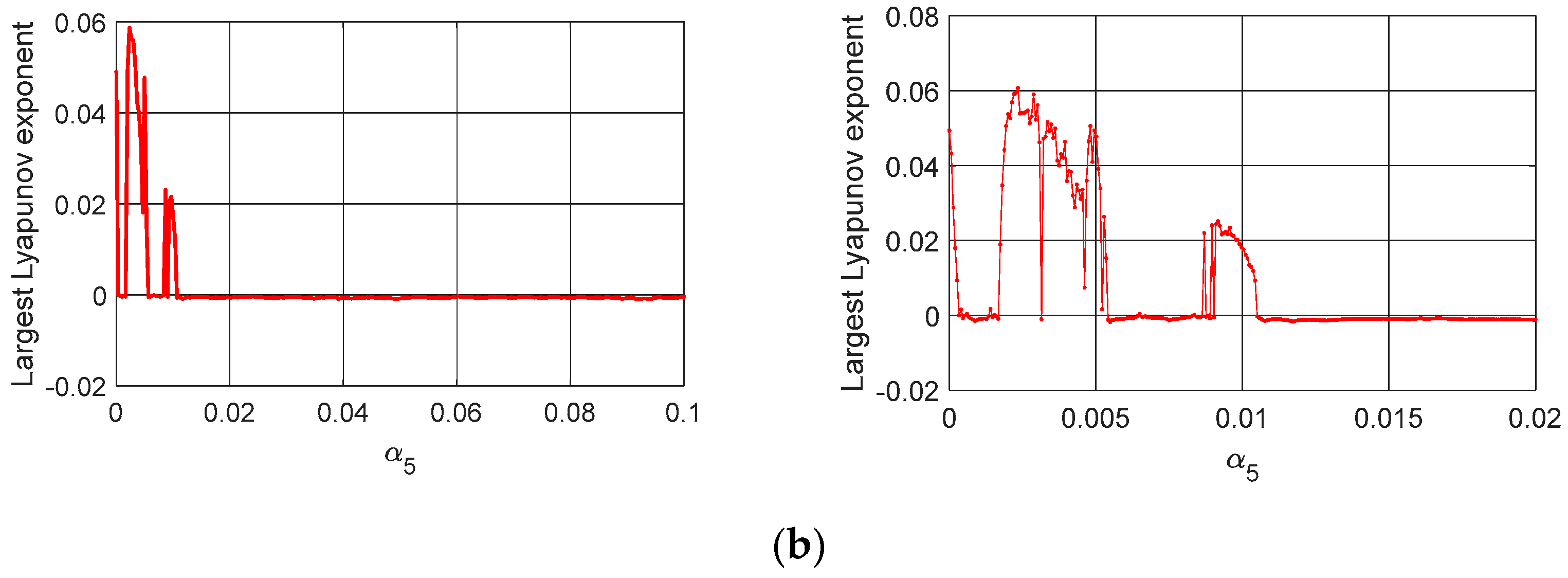
Figure 7 presents the bifurcation diagrams and largest Lyapunov exponents, considering the parameter $\nu =\left[0:2.5\right]$ and ${\alpha }_5=0.005$.

We can observe in Figure 7 that as the electrical voltage in the MR damper coil increases, the system becomes periodic while remaining chaotic for the following $\nu$ values: $\nu \cong \left[0:0.04\right]$ and $\nu \cong \left[0.37:0.48\right]$.

In analyzing Figure 6 and Figure 7, we can see that it is possible for the system to adopt a periodic behavior for small electrical voltages and a low damping coefficient.

In Figure 8, show that the vibration of the cutting tool for the case of $\nu =0$, ${\alpha }_5=0.005$, and ${\alpha }_5=0.02$.

As shown in Figure 8, the system remains chaotic for small values of ${\alpha }_5$ (${\alpha }_5=0.005$) and changes to periodic behavior when we increase the value of ${\alpha }_5$ (${\alpha }_5=0.02$).

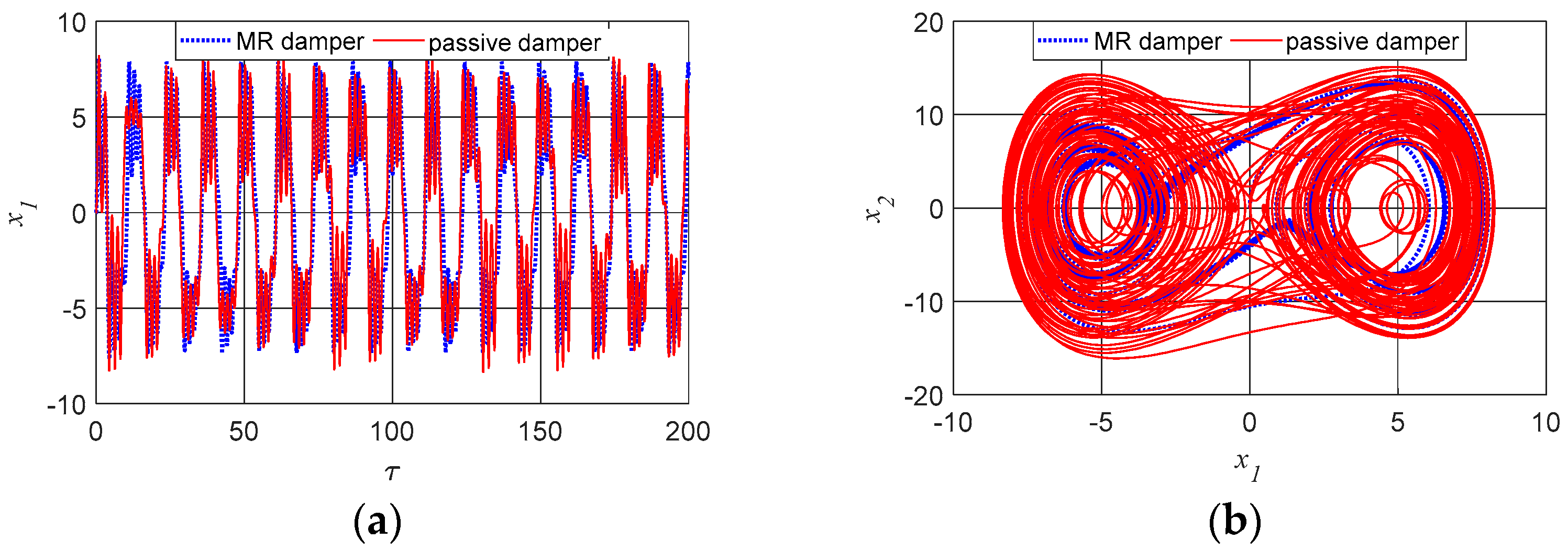
Figure 9 shows the case where the system has only passive damping (${\alpha }_1=0.1$ and ${\alpha }_5=0$) and only non-linear damping related to MR (${\alpha }_1=0$ and ${\alpha }_5=0.008$).

In Figure 10, we analyze the case of the combination of the two dampings (${\alpha }_1=0.1$ and ${\alpha }_5=0.008$) in the case of $\nu =0$.

The results of Figure 9 and Figure 10 show that the cutting tool displacements are not significantly altered in the case of being purely MR or the combination of the two damping forces (${\alpha }_1=0.1$ and ${\alpha }_5=0.008$), thus demonstrating the dominance of the MR damper force in the system dynamics.

4. Proposal of the Control Strategy by SDRE Control

The control proposed in this article aims to reduce the vibration amplitudes of the cutting tool by controlling the electrical voltage applied to the MR damper coil. The proposed control strategy considers using two controls, one of which is a state feedback control associated with a feedforward control. The state feedback control aims to lead the system to a desired behavior, and the state feedback control.

Since the main objective is to control the vibration of the cutting tool, the variables of interest are $x_1$ and $x_2$, so the variables $x_3$, $x_4$, and $x_5$ will be considered only as disturbances of the system, a proposal similar to that used in [33,34].

Thus, the control proposal can be applied to the following system:

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2={\displaystyle \frac{1}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\left(-{\alpha }_{5}U-{\alpha }_1{x}_2-{\alpha }_3{x}_1-{\alpha }_2{x_1}^3+{\beta }_2{\alpha }_3\sin (x_3)-{\beta }_3{\delta }_1{x}_4\sin (x_3)+{\delta }_2{x_4}^2\cos (x_3)\right)\end{array},$$

(11)

where $U=F_{mrd}$.

Substituting $U$ in Equation (9), we can observe that it is possible to control the shape $F_{mrd}$ by controlling the electrical voltage $\nu$ as follows:

$$\nu ={\displaystyle \frac{U-{\sigma }_{a}z-{\sigma }_1\dot{z}-{\sigma }_2\dot{x}}{{\sigma }_{0}z+{\sigma }_b\dot{x}}}.$$

(12)

As can be seen in Equation (12), the electrical voltage $\nu$ is obtained from the control signal $U$. Considering that negative electrical voltage is not used, and that the maximum voltage (${\nu }_{max}$) is also considered, we can define the following rule for calculating the electrical voltage:

$$\nu =\left\{\begin{array}{ccc}if \nu <0& \to & \nu =0\\ if 0<\nu <v_{\max }& \to & \nu ={\displaystyle \frac{U-{\sigma }_{a}z-{\sigma }_1\dot{z}-{\sigma }_2\dot{x}}{{\sigma }_{0}z+{\sigma }_b\dot{x}}}\\ if \nu >v_{\max }& \to & \nu =v_{\max }\end{array}\right..$$

(13)

System (11) can be represented in the following matrix form [33,34]:

$$\dot{X}=AX+BU+G,$$

(14)

where A is the state matrix, B is the control matrix, $U=u_{fd}+u_{fw}$, $u_{fd}$ is the feedback control, $u_{fw}$ is the feedforward control, and $G$ are the terms that do not contain the states $x_1$ and $x_2$.

The feedback control is obtained from the following [33,34]:

$$U=-R^{-1}{B}^{\mathrm{T}}Pe,$$

(15)

where $\mathrm{e}=\left[\mathrm{X}-{\mathrm{X}}^{\mathrm{*}}\right]$, $\mathrm{X}$ is the states of the system, and ${\mathrm{X}}^{\mathrm{*}}$ the desired states.

The matrix $\mathrm{P}$ is obtained from the following [33,34]:

$$A^{T}P+PA-PB{R}^{-1}{B}^{T}P+Q=0.$$

(16)

The functional cost considered for the $u_{fd}$ is given by the following [33,34]:

$$J={\displaystyle \frac{1}{2}}{\displaystyle \underset{t_0}{\overset{\infty }{\int }}(e^{T}Qe+U^{T}RU)}dt,$$

(17)

where Q and R are positive definite matrices.

Rewriting the system (Equation (11)) in the form (Equation (14)), we obtain the system (Equation (11)) in the following matrix form:

$$\begin{array}{l}\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{-{\alpha }_3-{\alpha }_2{x_1}^2}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}& {\displaystyle \frac{-{\alpha }_1}{1-\delta {\beta }_1\sin {(x_3)}^2}}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ {\displaystyle \frac{-{\alpha }_5}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\end{array}\right]U\\ +\left[\begin{array}{c}0\\ {\displaystyle \frac{{\beta }_2{\delta }_1\sin (x_3)-{\beta }_3{\delta }_1{x}_4\sin (x_3)+{\delta }_2{x_4}^2\cos (x_3)}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\end{array}\right]\end{array}$$

(18)

where $A=\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{-{\alpha }_3-{\alpha }_2{x_1}^2}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}& {\displaystyle \frac{-{\alpha }_1}{1-\delta {\beta }_1\sin {(x_3)}^2}}\end{array}\right]$, $B=\left[\begin{array}{c}0\\ {\displaystyle \frac{-{\alpha }_5}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\end{array}\right]$, and $G=\left[\begin{array}{c}0\\ {\displaystyle \frac{{\beta }_2{\delta }_1\sin (x_3)-{\beta }_3{\delta }_1{x}_4\sin (x_3)+{\delta }_2{x_4}^2\cos (x_3)}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\end{array}\right]$.

Replacing $e=\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]=\left[\begin{array}{c}{x}_1-x_1^{*}\\ x_2-x_2^{*}\end{array}\right]$ in Equation (18), we have the error-dependent system:

$$\dot{e}=Ae+BU+G,$$

(19)

where $A=\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{-{\alpha }_3-{\alpha }_2\left({e_1}^2+3e_1{x}_1^{*}+3{x_1^{*}}^2\right)}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}& {\displaystyle \frac{-e_2}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\end{array}\right]$, $B=\left[\begin{array}{c}0\\ {\displaystyle \frac{-{\alpha }_5}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}\end{array}\right]$, and $G=\left[\begin{array}{c}0\\ {\displaystyle \frac{{\beta }_2{\delta }_1\sin (x_3)-{\beta }_3{\delta }_1{x}_4\sin (x_3)+{\delta }_2{x_4}^2\cos (x_3)-{\alpha }_3{x}_1^{*}-{\alpha }_2{x}_1^{{*}^3}-x_2^{*}}{1-{\delta }_1{\beta }_1\sin {(x_3)}^2}}-{\dot{x}}_2^{*}\end{array}\right]$.

Where $u_{fd}=-R^{-1}{B}^{\mathrm{T}}Pe$ and $u_{fw}=-G$.

As can be observed in the system (Equations (18) and (19)), the matrix depends on the states $x_1$ and $x_2$. Thus, the SDRE (state-dependent Ricatti equation) control strategy will be considered to obtain the feedback control signal. The control generally involves parameterizing the variables in an array of states $x_1$ and $x_2$. Thus, the SDRE control captures the system non-linearities with the state coefficient matrix SDC (state-dependent coefficient) matrices A and B [33,34].

To determine the desired states, oscillations at the same dominant frequencies as the uncontrolled system and a reduction of at least the vibration amplitude of the cutting tool will be considered in this investigation.

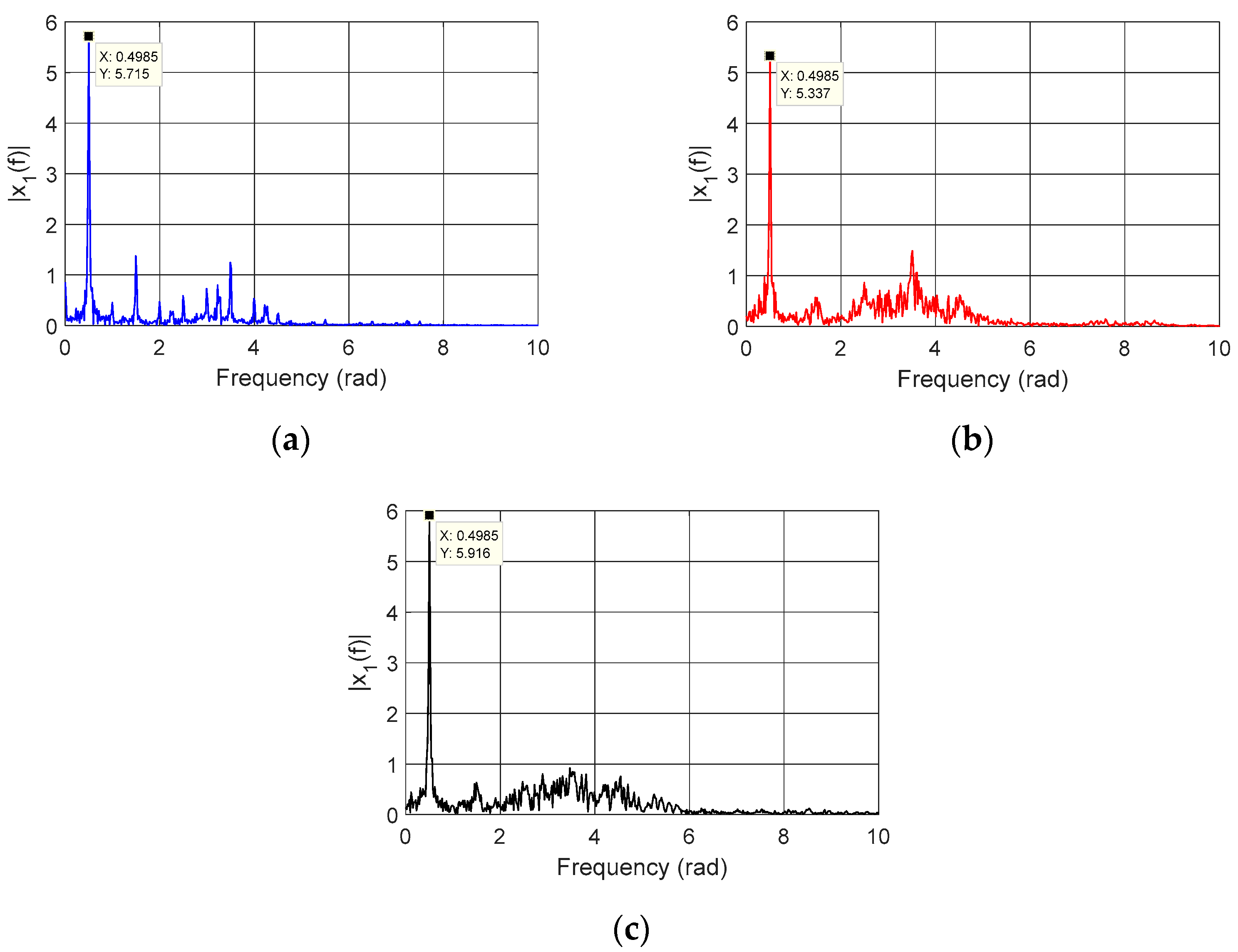
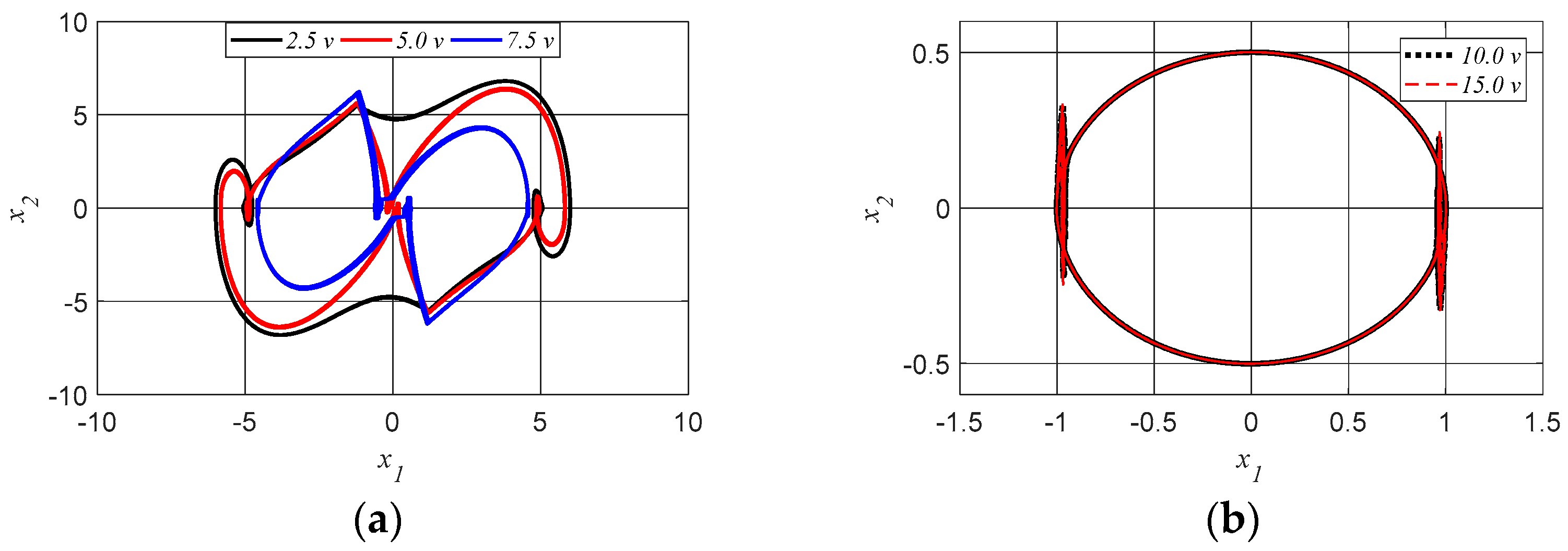
Figure 11 shows the FFTs of the system with and without the MR damper.

As can be seen from the results of Figure 11, the dominant frequency is $0.4985$ radians, the average frequency of the angular speed of the motor. We can also see in Figure 8, Figure 9 and Figure 10 that we have the maximum displacement for the system with MR and passive damping ($x_{1_{max}}=8.0553$), the system with only passive damping ($x_{1_{max}}=8.2695$), and the system with only MR damping ($x_{1_{max}}=8.1593$). Thus, the following states are defined as desirable: ${x_1}^{*}=\sin \left(0.4985\tau \right)$, ${x_2}^{*}=0.4985\cos \left(0.4985\tau \right)$, and ${{\dot{x}}_2}^{*}={-0.4985}^2\sin \left(0.4985\tau \right)$. And we define the matrices as follows: $Q={10}^5\left[\begin{array}{cc}{10}^3& 0\\ 0& 1\end{array}\right]$ and $R=\left[{10}^{-3}\right]$.

In Figure 12, Figure 13, Figure 14 and Figure 15, the results of the system with the proposed control, considering the maximum permitted electrical voltages ${\nu }_{max}=2.5$, ${\nu }_{max}=5$, ${\nu }_{max}=7.5$, ${\nu }_{max}=10.0$, and ${\nu }_{max}=15.0$, are presented.

As can be seen in the results presented, the proposed control of the voltage $v$ enables a significant reduction in the vibration amplitude of the cutting tool (Figure 12), and the desired amplitude can be achieved when ${\nu }_{max}=10.0$, there is no need for values much higher than this. We can also observe that for values of ${\nu }_{max}=2.5$, the control provided a good reduction in the displacement amplitude.

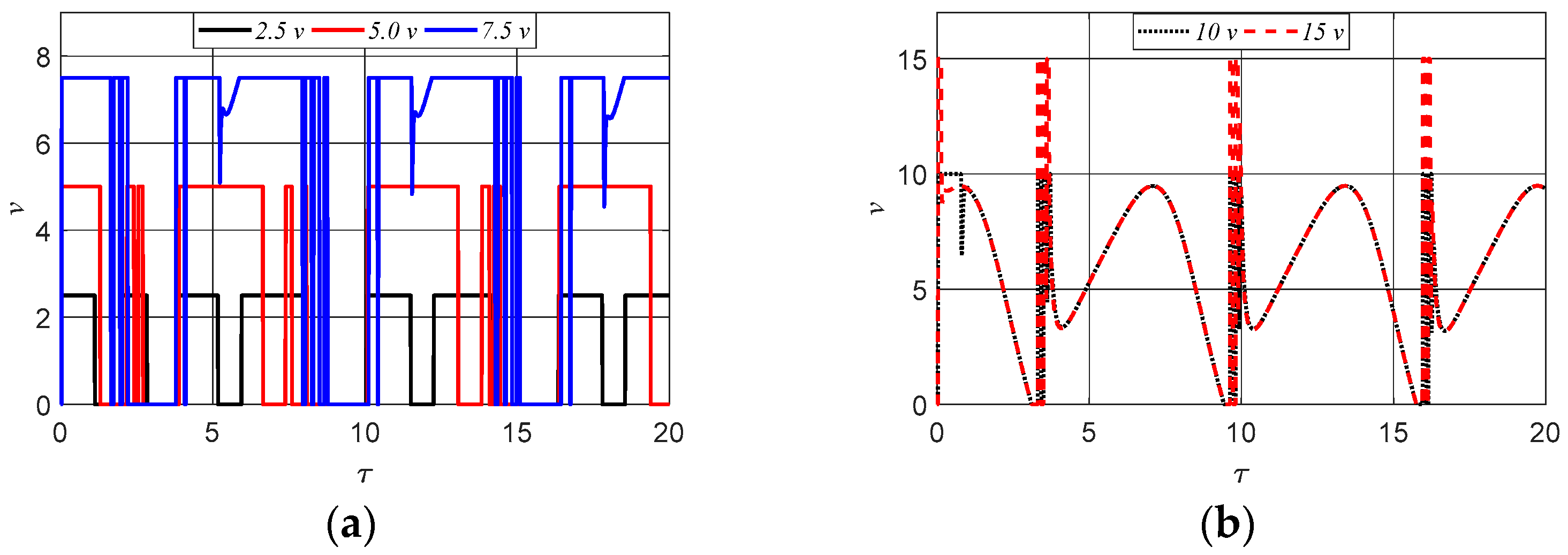
The results show that there is a significant change in the hysteresis behavior of the MR damper when the switching proposed in Equation (13) is considered, acquiring a more complex behavior than that observed for the unrestricted system. This result contributes to the continuity of investigations into the behavior of the MR damper.

5. Conclusions

By including the electric motor in the mathematical model that represents the machining process, it was possible to obtain a more realistic model, including in the dynamics of the system the interaction of the cutting tool, the workpiece that is undergoing roughing, and the motor responsible for the rotational movement of the workpiece. By using the non-ideal Duffing oscillator model, it was possible to obtain chaotic behavior for variations in the cubic stiffness parameters of the cutting tool and for its dissipative damping. Introducing the MR damper in the system’s dynamics provided richer dynamics. Its application as both a passive and active absorber proved to be efficient in attenuating the vibration of the cutting tool. The active control strategy also proved efficient in controlling the voltage applied to the MR damper coil.

The numerical results demonstrated that the proposed controls, through the introduction of the MR damper, were efficient in reducing the vibration amplitude and that the active control proved to be effective in controlling the force of the MR damper, varying the electrical voltage applied to the damper coil.

Considering the restrictions on the maximum voltage that can be applied to the coil of MR dampers, this paper presents new results on the hysteresis movement of the MR damper (Figure 14 and Figure 15), contributing to the study of the use of the MR damper in the vibration control of a portal frame, where the saturations of the electrical voltage were not considered [34]. Regarding vibration control in a machining system, this paper contributes to the proposal of including an MR damper perpendicular to the cutting tool, a strategy not found by the authors in other bibliographic sources. We can also highlight that this paper enables future studies to validate the numerical results, mainly in assembling an experimental apparatus. The dynamic analysis of the system for variations of the unbalanced mass $m_0$ and its eccentricity $r$, variations that should occur when machining the material, can also be considered in future work. Regarding the MR damper, future work may consider the dynamic analysis of the system in fractional order, thus including memory in the MR damper model.