Specific Characteristics of Numerical Simulation of Mechatronic Systems with PWM-Controlled Drives

Abstract

This paper explores the features of numerical simulation used to analyze the dynamic behaviour of drives controlled by pulse-width modulators. Modern motor control systems commonly employ pulse-width modulation. Effective numerical modelling of such systems presents unique challenges because the models employed are continuous-event and have hybrid behaviour due to the presence of nonlinear links with discontinuities of the first kind. Therefore, it is essential to have special integration methods with variable steps, which should be factored in when developing the model. This paper shows how these problems are solved when modelling an electric drive with a DC motor using the SimInTech software.

1. Introduction

With advancements in power electronics technology, pulse-width modulation (PWM)-controlled converters have become widely utilized in applications requiring high precision and efficiency, such as communications and industrial equipment control [1,2,3]. A substantial amount of research is devoted to the mathematical modelling of PWM. Practical issues regarding the applicability of individual methods and implementations of approaches to PWM simulation are especially acute.

When developing software for controllers of modern pulse converters, it is important to take into account nonlinear processes occurring in the controlled device. This is necessary from the point of view of selecting circuitry and parameters of key elements, as well as from the point of view of assessing electromagnetic compatibility and control accuracy parameters. Modelling PWM by the averaging method is not fully suitable for this, since it does not allow for the assessment of small-scale dynamic processes in the system. Direct modelling of the system allows more correct selection of filtering algorithms for signals coming from sensors to the controller.

The principles for control of a linear resonant drive with PWM are the main focus of [4]. Three methods are tested to convert force to PWM, two of which show linear correlation (>0.7) with the original data. The correlation between PWM commands and the generated acceleration was found to be highly linear across all three methods with a minimum coefficient of 0.85.

The effects of (low) switching frequency and delays (associated with digital control implementation) on PWM-powered DC servos are examined in [5]. A modelling procedure and analytical formulas are presented to quantify deviations from standard (idealized) fixed-gain models.

Another area of PWM application in radio communication problems is considered in [6]. To solve the problem of real-time system performance limitations caused by time resolution, the phase shift control principle is used to constrain the output pulse state.

In [7], a mathematical input–output model is initially designed by constructing equations and transforming d-q coordinates. A voltage and current double closed-loop simulation model is then built in MATLAB/Simulink, and the control effect is analyzed. Based on these findings, a new voltage-setting strategy is developed to reduce the output voltage overload of the PWM rectifier during startup.

In studies [8,9], the main goal of control in the proposed inverter is to regulate current in the network with a low level of total harmonic distortion while compensating for load power components. The proposed control and switching methods aim to achieve voltage balance on the DC side and the lowest switching losses.

Approaches using pulse-width modulation necessary for regulating the power supply of multiphase AC drives are presented in [10,11]. These studies by colleagues provide comparisons and methods for enhancing, shaping, and modulating control to improve the quality of output power converters.

An elevator system presented in [12] provides energy supply inside the elevator car by eliminating the need for running cable and using a low-capacity energy storage. The study [13] presents results on designing the PWM control algorithms.

To effectively combat the effects of both matched and mismatched power disturbances in a three-phase PWM rectifier, a robust direct power control method with a single-loop control structure is proposed in [14,15].

The paper [16] presents a study of traditional propulsion systems used for ships. These systems include diesel and turbo-electric drives with a cycloconverter technology used for speed regulation. The main disadvantage of the cycloconverter technology is the characteristic output voltage waveform, which is non-sinusoidal and produces harmonic-laden currents, which negatively affect power factor and efficiency.

The paper [17] presents the use of the Butterworth approach for the design and control of a PWM rectifier based on an LCL filter with power quality functions. By using the linear portion of the system, this approach reduces the number of variables involved in the control scheme. This approach differs from previous methods in that it does not use nonlinear controllers, dq–transformations, or double control loops. Thus, this approach simplifies the design and control of power converters through the use of polynomial synthesis, while also enhancing the system performance in complex scenarios.

PWM control algorithms for wireless charging stations are presented in [18]. This study considers a topology with PWM-controlled switched impedance.

The focus of [19] is on AC/DC converters, with an interleaved full bridge chosen as the topology due to its flexibility and ability to increase system power. To ensure high performance, various PWM techniques are analyzed for this converter.

A study of simulation models of a motor, inverter, speed detection circuit, and controller is presented in [20].

Models of the dynamics of electric drives are usually defined using a system of differential-algebraic equations. In this case, to ensure accurate modelling, it is essential to carefully select an appropriate integration step for the model. This will enable the pulse-width modulator model to correctly process the events where the value of the reference PWM signal is exceeded relative to the modulating signal. To meet this requirement, it is necessary to select an integration step that is smaller than the frequency of the PWM counter, or to build the model of the pulse-width modulator to account for the precise timing of events where the values of these signals intersect. In the first case, the model will require a significant increase in the number of integration steps. The algorithm for detecting the intersection of the PWM modulating signal with the reference signal allows for the reduction of the total number of integration steps by introducing intermediate integration steps.

The problem of PWM modelling is of practical importance for industry. It should be noted that modelling of renewable energy facilities, where inverter equipment operating on power IGBT modules is implemented [21,22], is of particularly growing interest. Moreover, the frequency-controlled electric drives, which also function based on PWM, is becoming increasingly widespread in industry. Thus, adequate modelling of PWM is has become a pressing scientific task.

2. Problem Statement

Let us consider an example of using PWM when implementing the simplest servo drive [23], the structure of which is shown in Figure 1.

The abstract model of such a servo drive with a symmetrical pulse-width modulator can be described by the following system of equations

$$\left\{\begin{array}{c}{\displaystyle \frac{d\omega }{dt}}=k_{\omega }f\left(u-k\omega -\phi ,t\right)\\ {\displaystyle \frac{d\phi }{dt}}=\omega \\ \omega \left(0\right)={\omega }_0,\phi \left(0\right)={\phi }_0\end{array}\right.,$$

(1)

where $\omega$ is the angular velocity with the initial value ${\omega }_0$; $k_{\omega }={\displaystyle \frac{1}{J}}{M}_{nom}$ is the speed gain; $J$—is the moment of inertia or rotor; $M_{nom}$—nominal drive moment; $u$ is the control action; $k$ is the damping coefficient; $\phi$ is the angle of rotation with initial value ${\phi }_0$; and ${f:R}^3\times R\to R$ is the PWM function.

If we assume the value of the PWM modulating signal to be $x=u-k\omega -\phi$, then

$$f\left(x,t\right)=sign\left(x\right)·z(x,t),$$

(2)

where

$$sign\left(x\right)=\left\{\begin{array}{cc}\hfill -1,& x<0\hfill \\ \hfill 0,& x=0\hfill \\ \hfill 1,& x>0\hfill \end{array}\right.,$$

(3)

Finally, we find the function z(x, t) from (2) in the form

$$z\left(x,t\right)=\left\{\begin{array}{c}{1,k}_{pwm}\left|x\right|\ge saw\left(t\right)\\ {0,k}_{pwm}\left|x\right|<saw\left(t\right)\end{array}\right.,$$

(4)

where $k_{pwm}$ is the PWM coefficient.

In this case, the source of the reference sawtooth signal in this model is calculated as

$$saw\left(t\right)=t-⌊{\displaystyle \frac{t}{T_{pwm}}}⌋·T_{pwm},$$

(5)

where $T_{pwm}$ is the PWM period in seconds.

As seen from the above equations, this model includes three nonlinearities with discontinuities of the first kind: (3)—sign function, (4)—ideal relay, (5)—fractional part. This leads to corresponding computational difficulties, for example, stiffness in certain modes [23], which are associated with the need to correctly determine the integration step when the values of the modulating and reference signals intersect [24], and to use appropriate integration methods [25]. In this case, it is crucial to determine the time of the transition point for nonlinearity (4), which determines the pulse duration.

To do this, we introduce the intersection function

$${v\left(x,t\right)=k}_{pwm}\left|x\right|-saw\left(t\right),$$

(6)

and from the condition

$$v\left(x^{*},t^{*}\right)\approx 0$$

(7)

we will limit the integration step ${h_{i+1}=t_{i+1}-t}_i$, $0\le i\le N$ so that it corresponds to the condition

$$\left|t^{*}-t_{i+1}\right|\le \epsilon ,$$

(8)

where $t^{*}$ is the exact time at which condition (7) is satisfied, $t_{i+1}$ is the value of the model time at the next integration step, $t_i$ is the value at the current step, $\epsilon$ is the specified temporal accuracy of intersection detection, and $i\in [0,N]$ is the integration step number.

The block diagram of the PWM submodel in the SimInTech software [26] is shown in Figure 2.

In addition to the main comparison operator (4), the system of equations also indicates that there are at least 2 nonlinearities, described in (3) and (5). In this case, the nonlinear Equation (5), which generates the reference sawtooth signal, depends only on the model time variable. This means that in order to specify the shape of the sawtooth signal, it is also necessary to accurately calculate the times at which this function takes on zero and maximum values. This greatly affects the quality of the transient process modelling. For the nonlinear Equation (5), the values of the points where this function takes on the minimum and maximum values are a priori set by the PWM period parameter $T_{pwm}$.

The values of the time when the events of reaching the minimum and maximum occur are equivalent to zeros or ones of the event function $g\left(t\right)$, which has the form demonstrated in [27]

$$g_{saw}\left(t\right)=sign\left({\displaystyle \frac{t}{T_{pwm}}}-⌊{\displaystyle \frac{t}{T_{pwm}}}⌋\right),$$

(9)

and is related to the generator function of a sawtooth signal as follows

$$g_{saw}\left(t\right)=sign\left({\displaystyle \frac{saw\left(t\right)}{T_{pwm}}}\right).$$

(10)

By combining condition (7) with the one-sidedness condition, we can formulate an event function [27] that describes the intersection of the reference and modulating signal values

$$g_{intersect}\left(x,t\right)=\left|v\left(x,t\right)\right|.$$

(11)

In order to correctly specify the step for blocks with precisely known times of occurrence of events in blocks of signal sources and blocks with a given discrete time (discrete blocks, timers, delays), the required integration step of the occurrence of an event is calculated, and the formula for calculating the required steps may vary for different types of blocks. As a result, the integration method takes the minimum possible required step from all such blocks. For blocks with a priori known response times, which do not depend on the values of dynamic state variables, iterations are not required and the size for the next step can be immediately calculated.

The intersection detection algorithm includes two components: the integration method itself and the intersection detection algorithm that interacts with it. The intersection detection algorithm is as follows:

• Calculate the function (6) of intersections at the trial step:

  $$v_i{=k}_{pwm}\left|x_i\right|-saw\left(t_i\right).$$

  (12)
• Numerically calculate the increment of function (5) at the current i trial step:

  $${∆v}_i=v_i-v_{i-1}.$$

  (13)
• Determine a predicate for the presence of an event of a given type $p_e$ (increase, decrease, both) at the current trial step. For an increase, the predicate is defined as:

  $$p_e=(\left(v_{i-1}\le 0\right)\wedge \left(v_i>0\right)).$$

  (14)
  For a decrease, the predicate is defined as:

  $$p_e=(\left(v_{i-1}>0\right)\wedge \left(v_i\le 0\right)).$$

  (15)
• Calculate the upper limit of the step at the k+1 trial iteration of the integration method

  $${hmax}_{k+1}=\left\{\begin{array}{c}{p}_e,max(k_h{h}_k\left|v_{i-1}\right|/(\left|v_{i-1}\right|+\left|v_i\right|)-\epsilon ,\hspace{1em}max(h_{min},\epsilon \left)\right)\\ \neg p_e,{max(hextr}_{k+1},max(h_{min},\epsilon )),\end{array}\right.$$

  (16)

  where $k_h$ is the step reduction factor at iterations, taken equal to 0.55; $h_k$ is the integration step at the current trial step; $v_{i-1}$ is the value of function (5) at the previous accepted integration step; $h_{min}$ is the minimum specified integration step; ${hextr}_{k+1}$ is the step obtained by extrapolation method, if the event is not recorded at the intermediate step, which is calculated as

  $${hextr}_{k+1}=\mathit{min}\left(h_k,h1\right),$$

  (17)

  where the extrapolation estimate of the integration step is calculated by the formula

  $$h1=\left\{\begin{array}{c}{h}_e+0.5\epsilon ,h_e<3\epsilon \\ h_e-0.5\epsilon ,h_e>4\epsilon \\ 3.5\epsilon ,\left(\right(h_e\ge 3\epsilon )\vee (h_e\le 4\epsilon \left)\right)\end{array}\right.,$$

  (18)

  where

  $$h_e=-v_i*h_k/{∆v}_i$$

  (19)
  The step correction is performed based on considerations of gradual approach to the intersection point on the left and conjugation of the predicted step with the integration methods used.
• If the integration step at the next trial step satisfies the calculated upper constraint and exceeds the minimum specified integration step, then the integration method stops executing trial steps and performs the accepted step, provided that the specified accuracy in the dynamic and algebraic state variables is satisfied. If the specified accuracy is not met, the algorithm performs a trial integration step with the calculated limitations.

One of the disadvantages of intersection detection algorithms for arbitrary nonlinearities is the need to perform an additional trial step for the interpolation stage of the algorithm (i.e., when an event occurs between two trial steps). This leads to a slight increase in computational cost, resulting in enhanced modelling accuracy.

To take into account intersection events in the models that require this (for example, a PWM model), a comparison block with intersection detection is utilized instead of a standard comparison block.

3. Testing the Detection Algorithm

The intersection detection algorithm is tested using a model of a PWM-based servo drive (Figure 1) as an example, with the following calculation settings: the integration method used is ARK32v1, which is an explicit adaptive Runge–Kutta type method of order 3 for non-stiff problems and that of order 2 for stiff problems [28,29,30,31,32]. The minimum integration step is $10^{-5}$ s, maximum step for the reference model without intersection detection of $10^{-5}$ s, for tested models without detection and with detection of only intersections 0.1 s, for a model with additional refinement by period of sources and discrete blocks, and detection of intersections 1 s. The model parameters assumed are: $k=0.1$, $k_{\omega }=100$, $k_{pwm}=0.1$, $T_{pwm}=0.1$ s, initial conditions: ${\omega }_0=0$, ${\phi }_0=0$, the control action is taken as a constant $u=1$, time detection accuracy $\epsilon =10^{-5}$ s. The accuracy settings of the integration method are as follows: relative error of no more than 0.001, and absolute error of no more than $10^{-10}$. The standard deviation of the output signal was calculated over the full modelling interval, using linear interpolation of the data calculated for the reference model. The numerical simulation results are shown in Figure 3 and Figure 4. Figure 3 shows that the reference value matches the value calculated using the variable step integration method with zero-crossing detection enabled and source signal refinement.

4. Cross-Verification of the Intersection Detection Algorithm

In order to cross-verify the presented intersection detection algorithm, a model of a simple servo drive with PWM was developed in the ISMA 2007 modelling and simulation environment, aimed at calculating hybrid dynamic systems.

The block diagram built in the ISMA 2007 is shown in Figure 5. Diagram parameters are: $k=0.1$ (amplifier on the right side of the diagram), $k_{\omega }=100$ (amplifier to the right of the PWM block), $k_{pwm}=0.1$ (amplifier to the left of the PWM block), $T_{pwm}=0.1$ s (set in the PWM text block). The initial conditions are ${\omega }_0=0$, ${\phi }_0=0$, the control action is taken as a constant $u=1$ (the constant signal source on the left side of the diagram).

The text component of the model, which implements pulse control (error pulse signal) is presented in Figure 6. Here, $x$ is the value of the signal received at the PWM block input, $st$ is the output of the block (PWM signal). The reference sawtooth signal is generated by integrating the $saw’=1$ equation reset upon reaching a $saw$ value greater than the PWM period ($m=0.1$). The model can be in four states: $st1a$ meets the condition $z(x,t)=1\mathrm{a}\mathrm{n}\mathrm{d}x>0$; $st1b$ fulfills the condition $z(x,t)=0$; $st1c$ satisfies the condition $z(x,t)=1\mathrm{a}\mathrm{n}\mathrm{d}x<0$; while the fourth state $st2$ is necessary to reset the value of the saw variable when a sawtooth signal is generated.

Parameters of the computational experiment are: calculation interval $t\left[0,2.5\right];$ STEKS integration algorithm, accuracy $\epsilon ={10}^{-3}$, initial step $h_0=0.01$ s; switching detection algorithm based on the Runge–Kutta method with parameter $\gamma =0.6$.

The computational experiment required 1285 integration steps, with the average step size being approximately ${1.9\times 10}^{-3}$ s, and 6425 calculations of the right-hand side of the Cauchy problem.

The simulation modelling results are presented in Figure 7 and Figure 8. The results obtained were qualitatively compared with the graphs generated for the model in SimInTech. This comparison did not show any differences in the graphs of the rotation angle φ(t) for the models in ISMA and SimInTech with refinement of intersection events.

The performance characteristics and accuracy of the resulting solution for various calculation options in SimInTech and ISMA are shown in

Table 1. Simulation performance characteristics.

Parameter	ISMA 2007	SimInTech Reference	SimInTech without Detection	SimInTech with Intersection Refinement	SimInTech with Intersection Refinement and Specification of Step for Discrete Blocks
Integration method	STEKS	ARK32v1
Number of function calls	6425	3028	2195	1630	1865
Number of integration steps	1285	1109	479	330	377
Number of trial steps	n/a	169	202	22	22
Standard deviation	n/a	0	0.03011187	0.015199124	0.0000393341

.

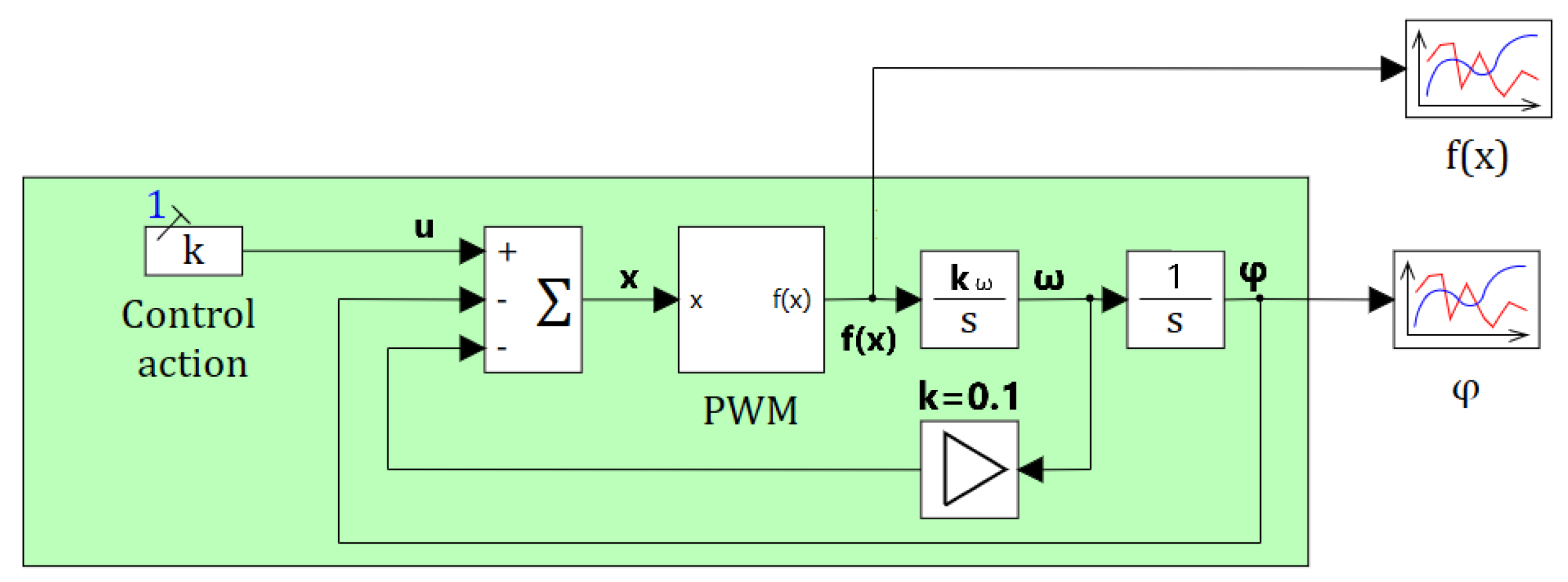
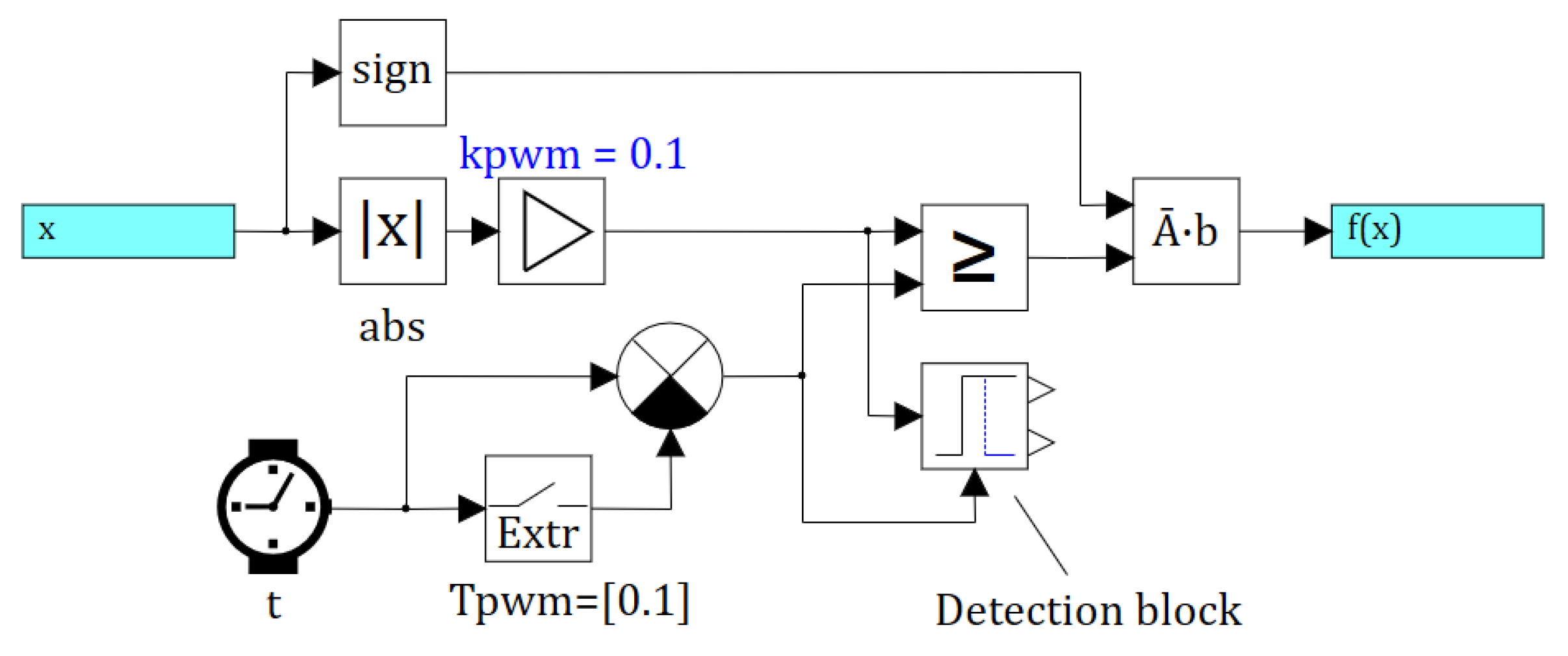
5. A Complex Electric Drive Model

A block diagram of a computer model of a drive with a brushless DC motor [26] is shown in Figure 9. A block diagram of control is shown in Figure 10. The PWM model is included in the drive model and generates control signals for the inverter model that controls the motor. The PWM modulating signal is generated in another model, calculated in parallel with the motor model, with a constant integration step equal to the PWM period.

When simulating PWM and a motor with an inverter in one project, it is essential to focus on the correct operation of the motor and inverter model. PWM typically controls the transistor port of a converter, with a small (from fractions of a microsecond to several microseconds) guard interval between on-states. Its duration must also be taken into account when choosing a step. In the SimInTech software, delays are implemented using an on-delay block that manages step control. Generally, the Euler method is chosen for modelling, with a step size less than or equal to the guard interval. For models of conventional motors, a step of $10^{-6}$ s is usually sufficient.

The model was calculated using the Euler integration method with a constant integration step equal to $h_{min}=10^{-6}$ s (while, in the model, the electrical part is calculated by the implicit Shikhman method [27]), as well as the ARK21 method with a variable step with settings of $h_{min}=10^{-6}$ s and $h_{max}=10^{-4}$ s. The model used a PWM algorithm with detection of intersections with an acceptable time accuracy set equal to the minimum integration step.

The modelling results are shown in Figure 11 and Figure 12. The numerical simulation of the system using various integration methods resulted in identical graphs.

Table 2. Simulation performance characteristics for complex model.

Method	Euler	ARK21 with Detection	SimInTech without Detection
Position at the end of the modelling	0.00999914934636218	0.0100026831685805	0.0100020459415512
$N_f$	4,530,403	1,701,481	1,133,284
$T$, s	60.7	18.29	11.98

shows the numerical characteristics for the integration methods with and without the intersection detection, $N_f$ is the number of calculations of the right side of the ordinary differential equation, and $T$ is the physical calculation time in seconds.

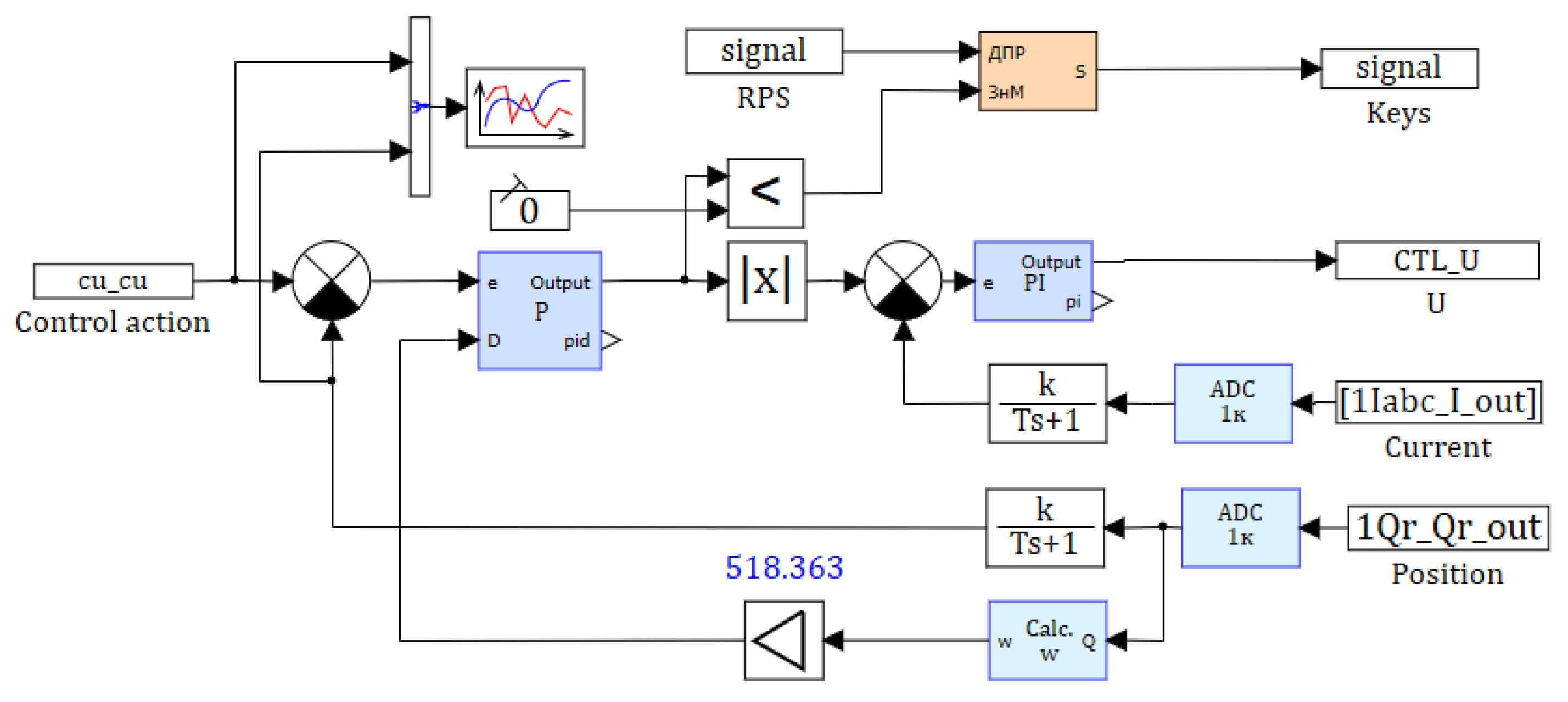
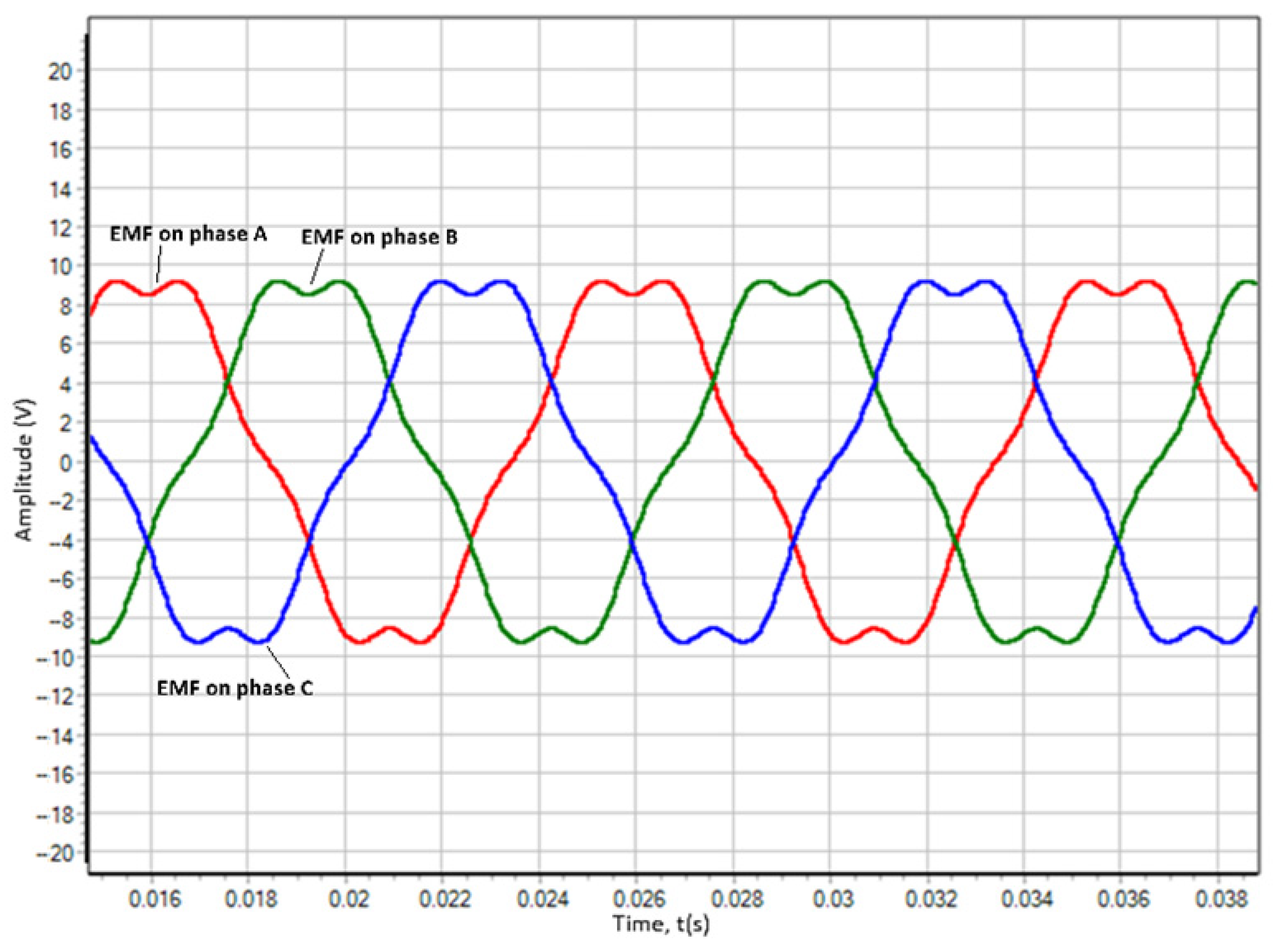
6. Experimental Verification of the Electric Drive Model

The electric drive model used in the calculations was verified to ensure compliance.

The experimental prototype included an electric drive with a screw transmission with a brushless DC motor. The motor control system was developed on the basis of the MILANDR 1986VE1T controller and programmed using the SimInTech code generation module. The motor was loaded using a linear loading machine. The experimental prototype corresponds to the given structural diagram of the dynamics model.

The model consists of three main parts:

• Inverter model;
• Electric motor model;
• Mechanical transmission model.

The parameters of the electric motor model are shown in

Table 3. Electric motor model parameters.

Parameter	Value
Winding resistance	0.3 ohm
Winding inductance	0.00027 H
Rotor flux linkage	0.0137 Wb
Number of pole pairs	2
Moment of inertia	4.45 × 10 −6 kg m2

.

The model verification was conducted in two stages. The first stage involved verification of the motor model. In this case, the motor was disconnected from the mechanical transmission of the electric drive. The following experiments were carried out:

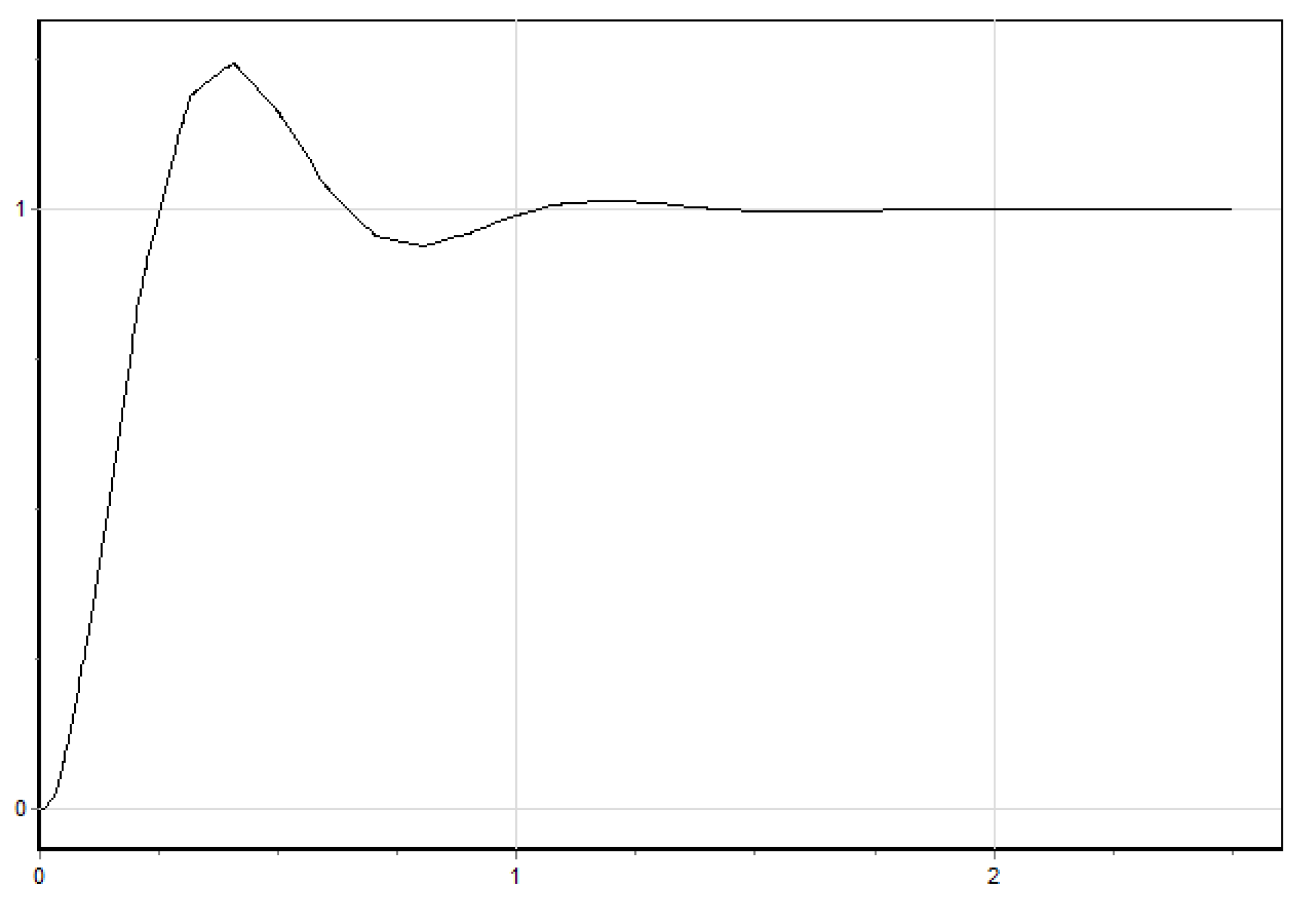
• No-load test:
  • An unloaded motor controlled by rotor position sensor (RPS), with a nominal power supply (54.5 V), accelerated to real idle speed.
  • The motor phase speed and current were measured.
  • Similar conditions were simulated in SimInTech and the modelling results were compared with the experiment.
• Static load test:
  • The RPS controlled motor was loaded to its nominal value using a load machine, with a nominal power supply (54.5 V).
  • The motor phase speed and current were measured.
  • Similar conditions were modelled in SimInTech and the modelling results were compared with the experiment.
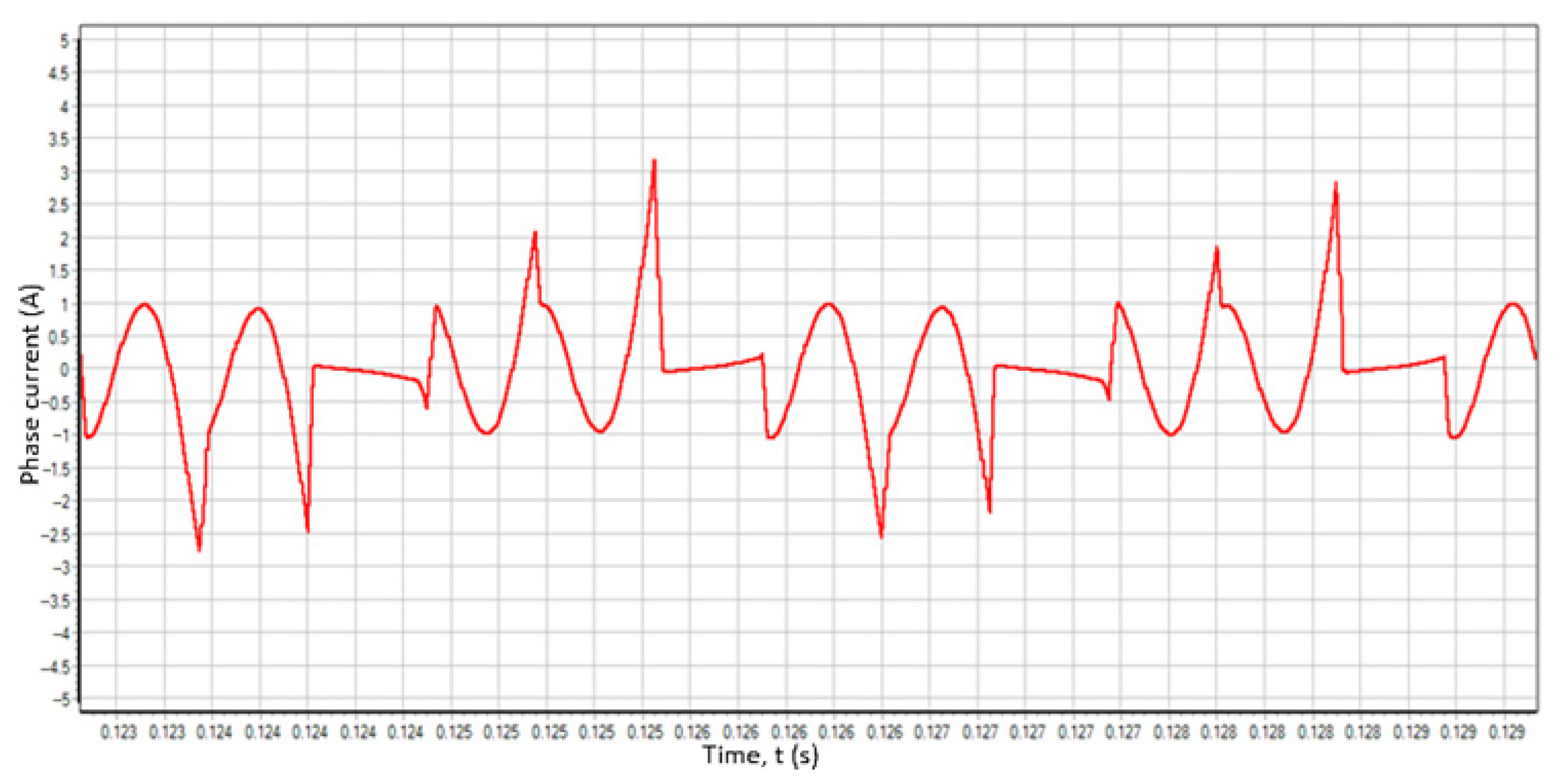
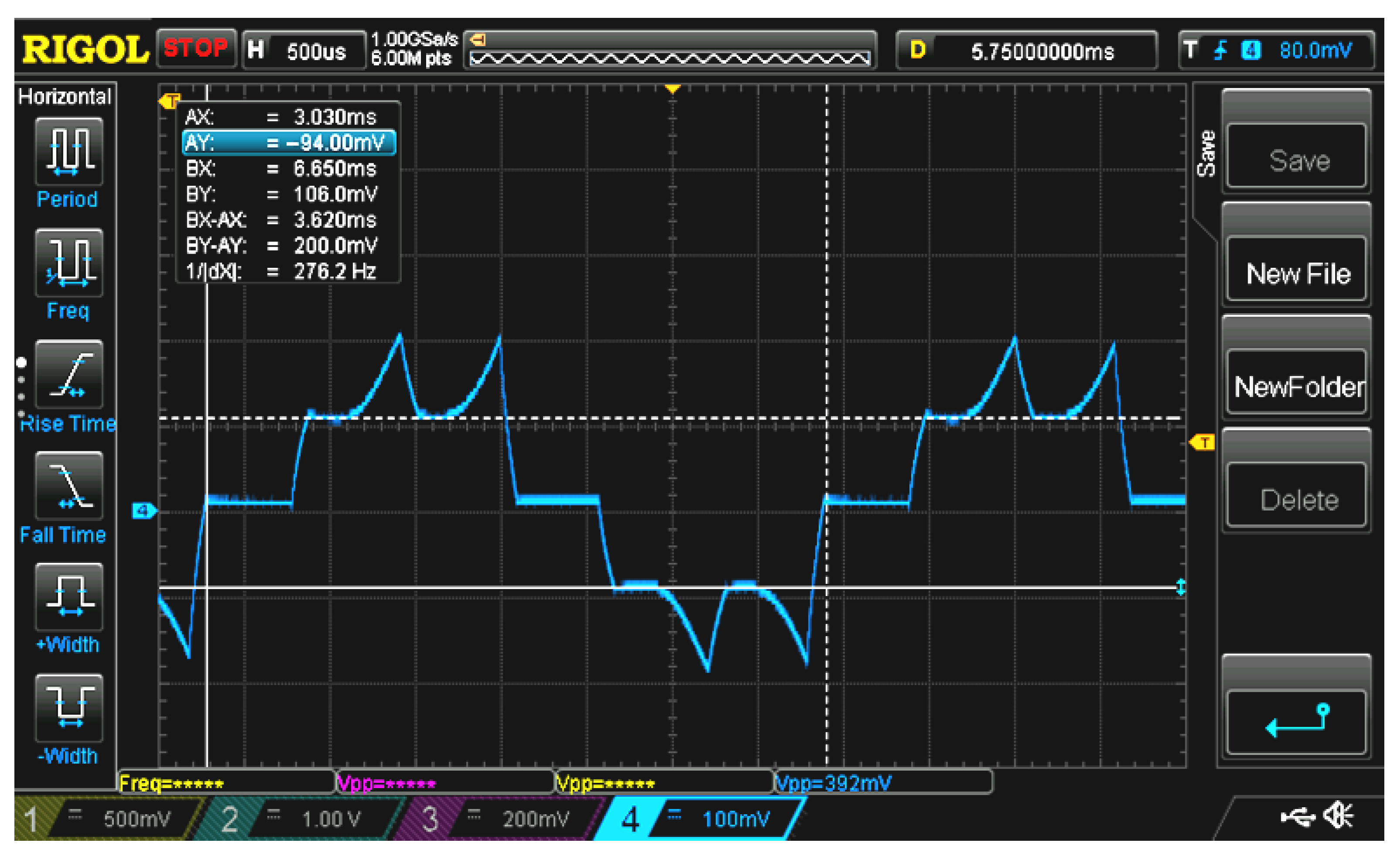
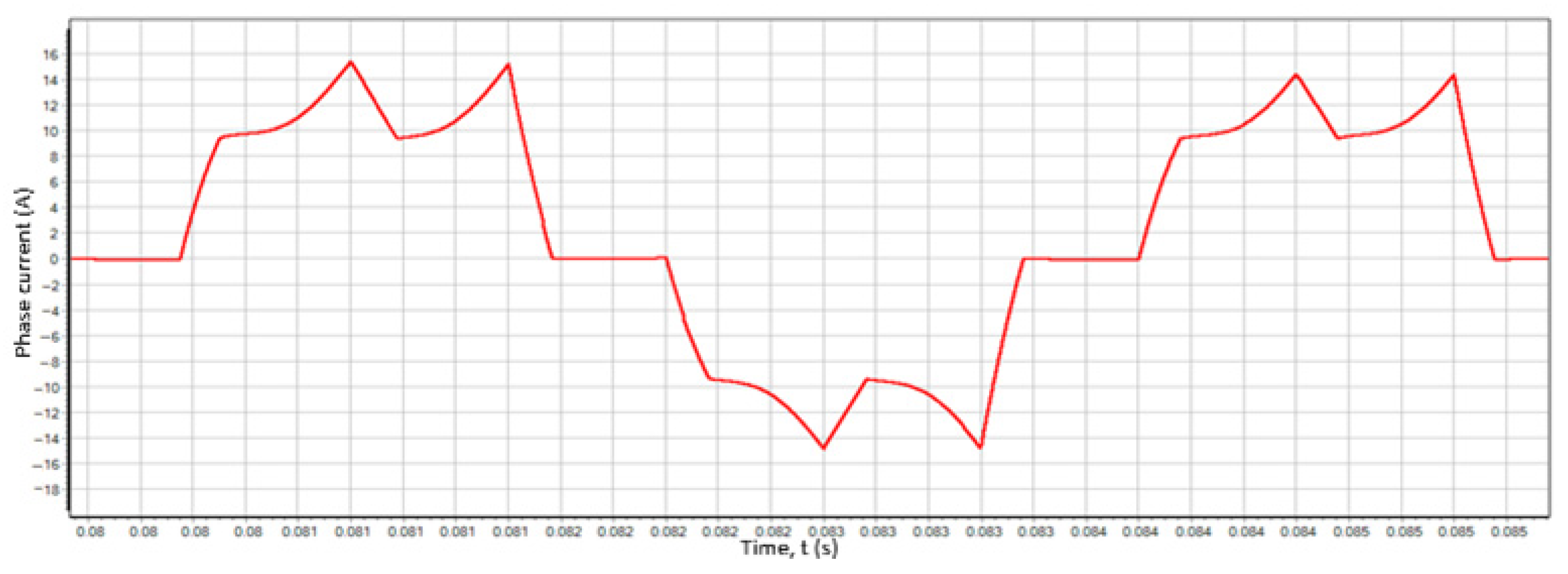
• At the second stage, the mechanical transmission model was verified. The motor was connected to the mechanical transmission of the electric drive, and the dynamic impact response experiment was performed:
  • The inverter was powered with a voltage of 54.5 V.
  • A torque command was issued to an RPS-controlled motor in the form of a bipolar square wave of maximum amplitude of various frequencies.
  • The position of the output rod of the electric drive and the inverter shunt current were measured.
  • Similar conditions were simulated in SimInTech and the modelling results were compared with the experiment.

For simulation, SimInTech v.2.24 software was used with a common library, electrical drive library, and 1D-mechanic library. SimInTech is software for one-dimensional modelling of the dynamics of complex technical systems, such as: power plants, mobile objects of various purposes, electric drives, and others. The control system model used the Euler integration method. The electrical drive model used the ARK21 integration method.

The model of the control system is shown in Figure 13.

This structure consists of standard SimInTech modules and implements valve control of a motor using RPS. The electric drive model used for verification is shown in Figure 14.

The EMF of the simulated motor differs significantly from the trapezoidal one. The actual EMF, experimentally measured at a speed of 3000 rpm, is shown in Figure 15.

Figure 16 shows a graph of the model EMF that matches the experimental model in amplitude and shape.

Steel losses were taken into account following the agreement with the motor designer through an active resistance connected in parallel to the winding. This resistance varied in inverse proportion to the frequency of the motor field to the power of 1.5.

The parameters of the mechanical transmission model are given in

Table 4. Mechanical transmission model parameters.

Parameter	Value
Friction coefficient on the motor shaft	0.00001
Motor—gearbox backlash	0.013 (rad)
Gearbox moment of inertia	0.00000276 kg m2
Gearbox transmission ratio	3.3
Gearbox—ball screw backlash	0.0063
Ball screw moment of inertia	0.00000914 kg m2
Ball screw transmission ratio	1 571

.

Figure 17 depicts the graph of the experimentally measured phase current in idle mode at a motor speed of 10,500 rpm (1099 1/s).

Figure 18 presents the graph of the model phase current at a motor model speed of 10,500 rpm (1140 1/s), K tr = 0.0001.

The experimentally measured phase current at a motor speed of 8300 rpm and a torque of 0.52 Nm is shown in Figure 19.

Viscous friction with a coefficient of Kfr = 0.00056 was used as the motor load in the model. In this case, the average value of the electromagnetic torque at a speed of 8300 rpm corresponds to a value of 0.49 Nm. The graph of the model phase current is shown in Figure 20.

The experimentally measured position of the shaft and the shunt current of converter are shown in Figure 21.

The model position of the shaft and the inverter shunt current are presented in Figure 22.

The model showed strong agreement with the experimental results. Discrepancies in the values of the inverter shunt current in the experiment of the dynamic impact response can be caused by: inaccuracy of speed measurement in the no-load and on-load experiments, inaccuracy of torque measurement in the load experiment, inaccurately set inductance and resistance of the motor winding in the model, and non-ideal correspondence between the operating parameters of the model inverter and real-world electric drive inverter.

7. Conclusions

The graphs and tables presented provide clear evidence that the intersection refinement process, taking into account the step from both discrete blocks and source blocks in the model, ensures the highest level of accuracy. In this case, there are no skipped PWM periods and the number of trial steps for the integration method is minimized. The refinement of intersections and the consideration of the periods of discrete blocks allow for minimizing the number of trial steps in the integration method and calculating the dynamics of such systems as accurately as possible, with coarse tuning of the maximum integration step. The above intersection refinement algorithm can also work if the input value of the refinement block is quantized. However, this may result in a decrease in accuracy.

The use of the adaptive integration method ARK21 in a complex drive model can reduce the number of function calculations by more than 2.6 times compared to the Euler method with a constant integration step (Euler with step $10^{-6}$ s: 4,530,403; ARK21 with variable step and zero-crossing detection: 1,701,481). Moreover, the modelling results are almost identical for all methods. Enabling intersection refinement increases the number of function calculations and brings about a modest improvement in modelling accuracy. However, in this model, the impact on accuracy is negligible, as the electric circuit modelling kernel and the motor model itself influence the integration step. There is some benefit associated with increased accuracy when enabling intersection refinement in the PWM model. Since it is imperative to correctly consider the guard interval during modelling, it is also advisable to use the intersection refinement block in the PWM model and include refinement of a priori specified delays for signal sources and delay blocks.

In the simulation modelling, the use of numerical methods alongside an adaptive numerical scheme combined with an intersection refinement algorithm allows for a significant increase in the integration step necessary for modelling mechatronic systems while maintaining the desired level of accuracy. This capability reduces physical modelling time and enhances performance when modelling large-scale systems.