Numerical Analysis of Flow Structure Evolution during Scour Hole Development: A Case Study of a Pile-Supported Pier with Partially Buried Pile Cap
Abstract
1. Introduction
2. Numerical Model
3. Validation Test Cases
3.1. Turbulent Channel Flow
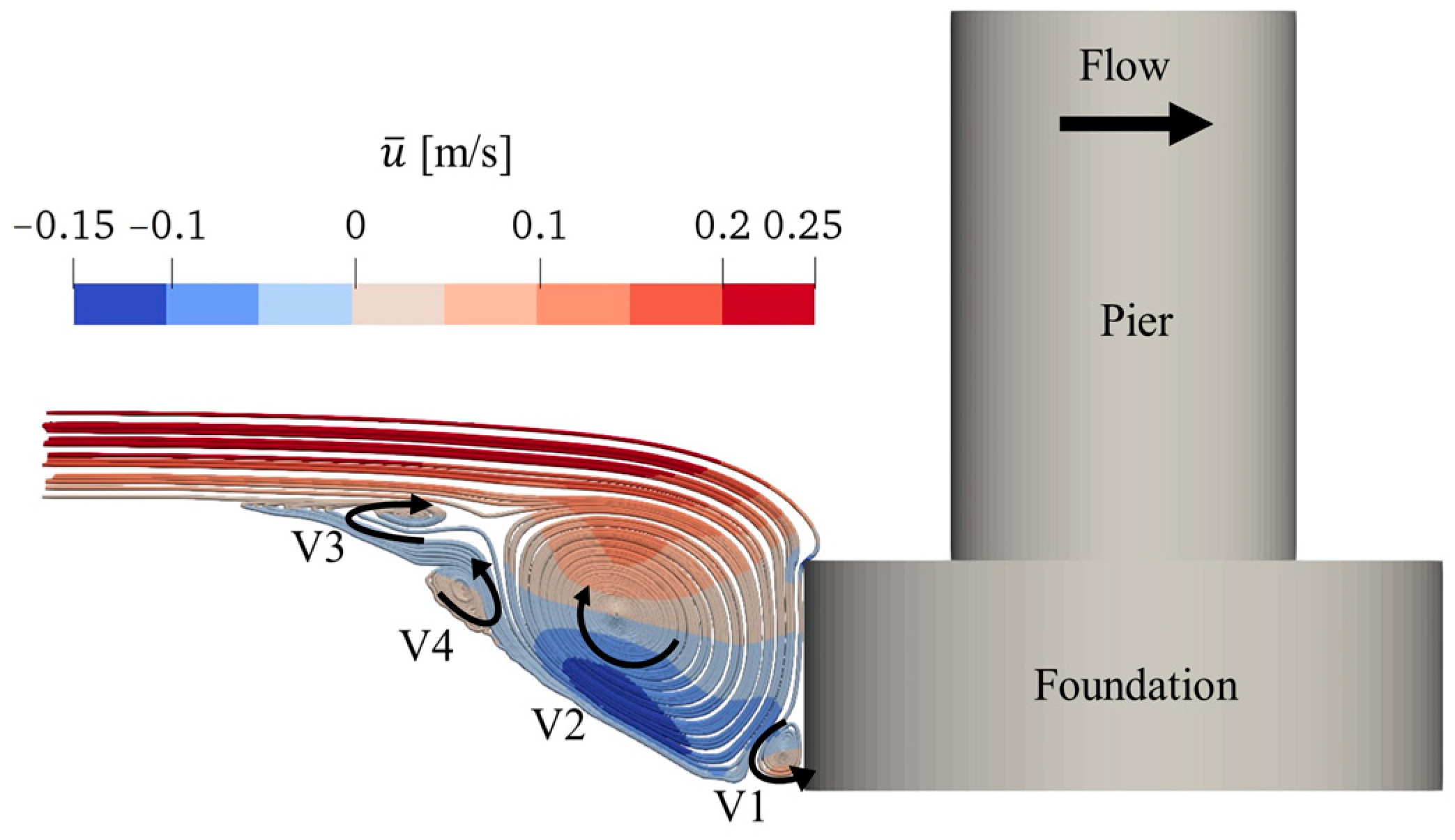
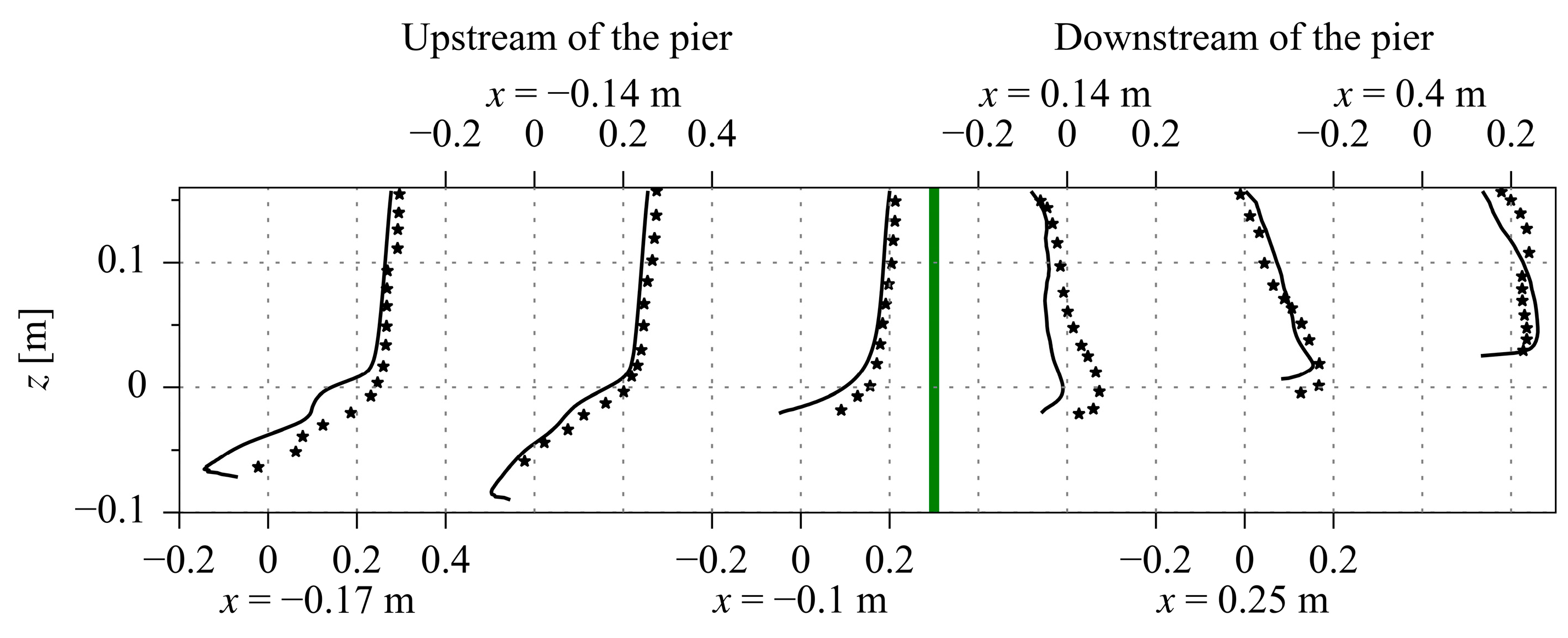
3.2. Compound Pier Flow
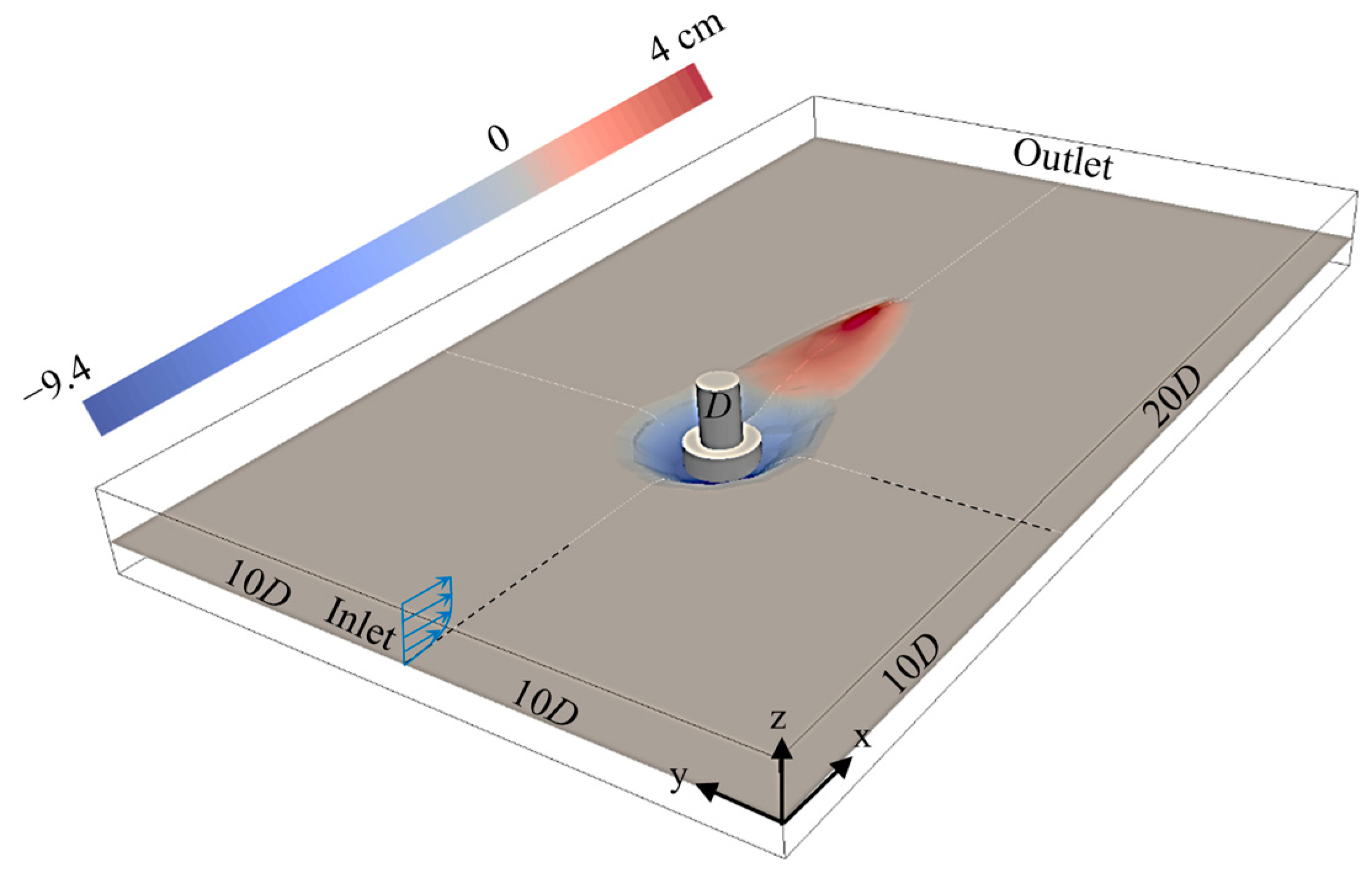
4. Model Setup for the Pile-Supported Pier Case
5. Results and Discussion
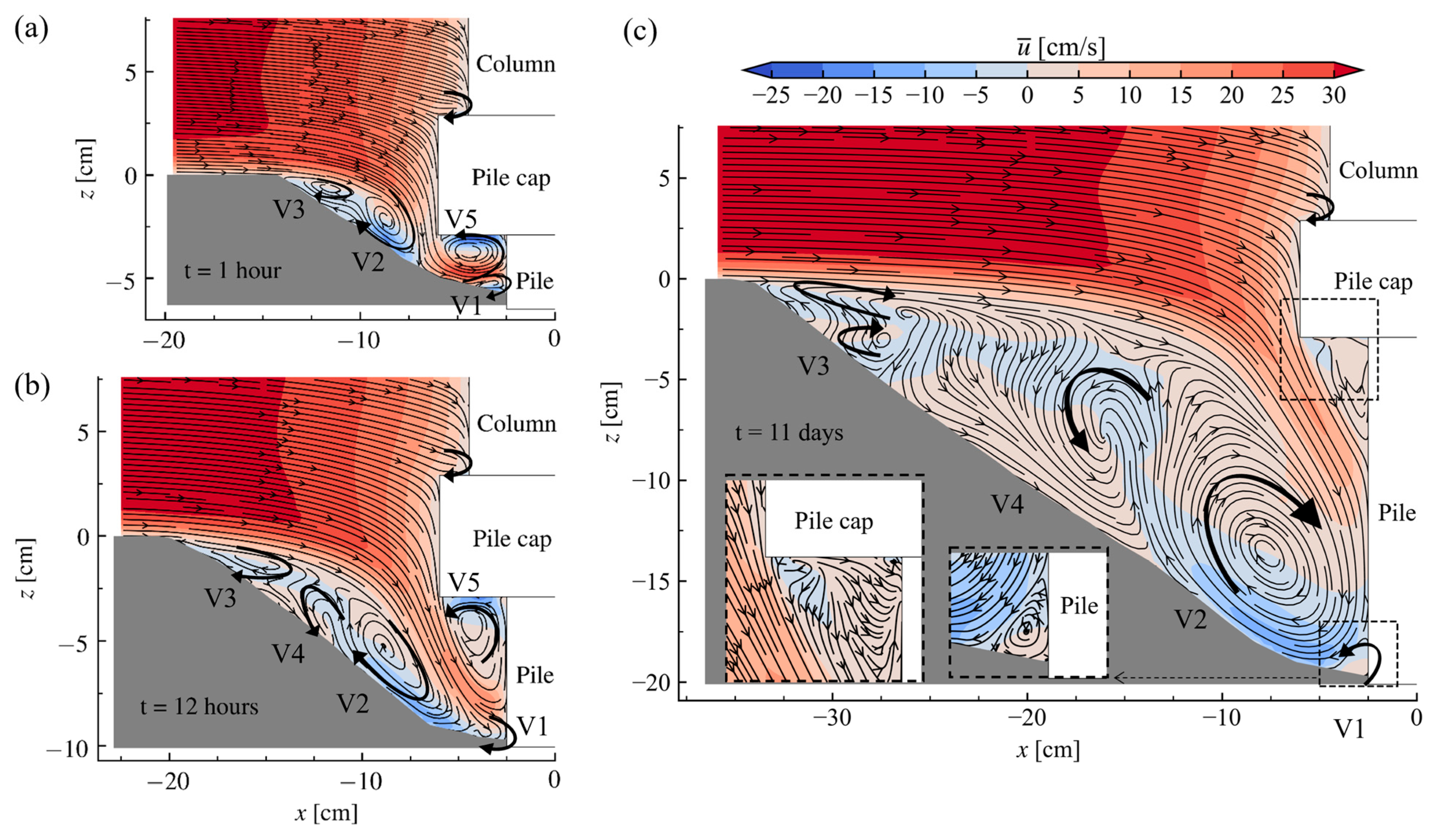
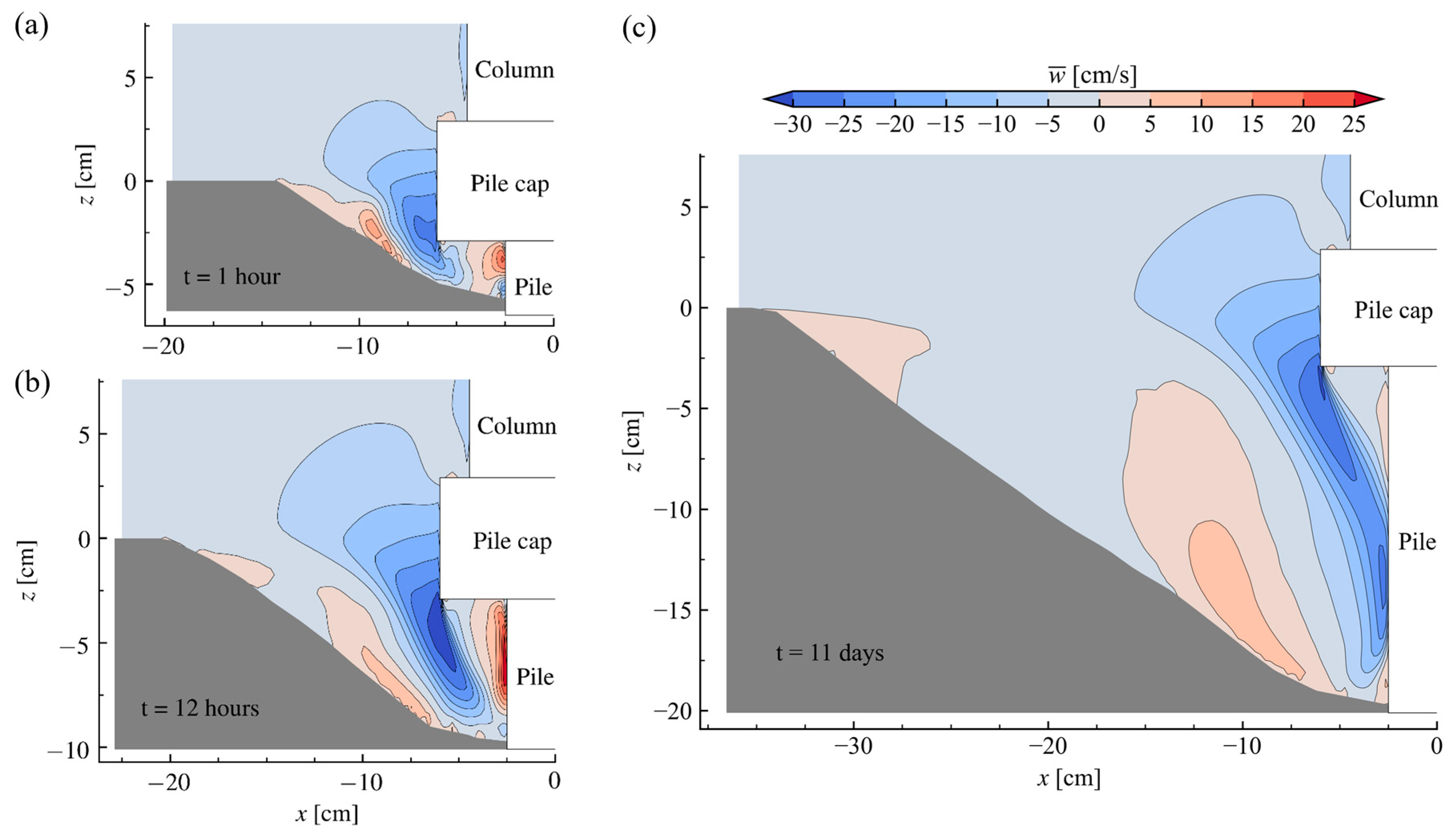
5.1. Flow Velocities and Streamline Patterns
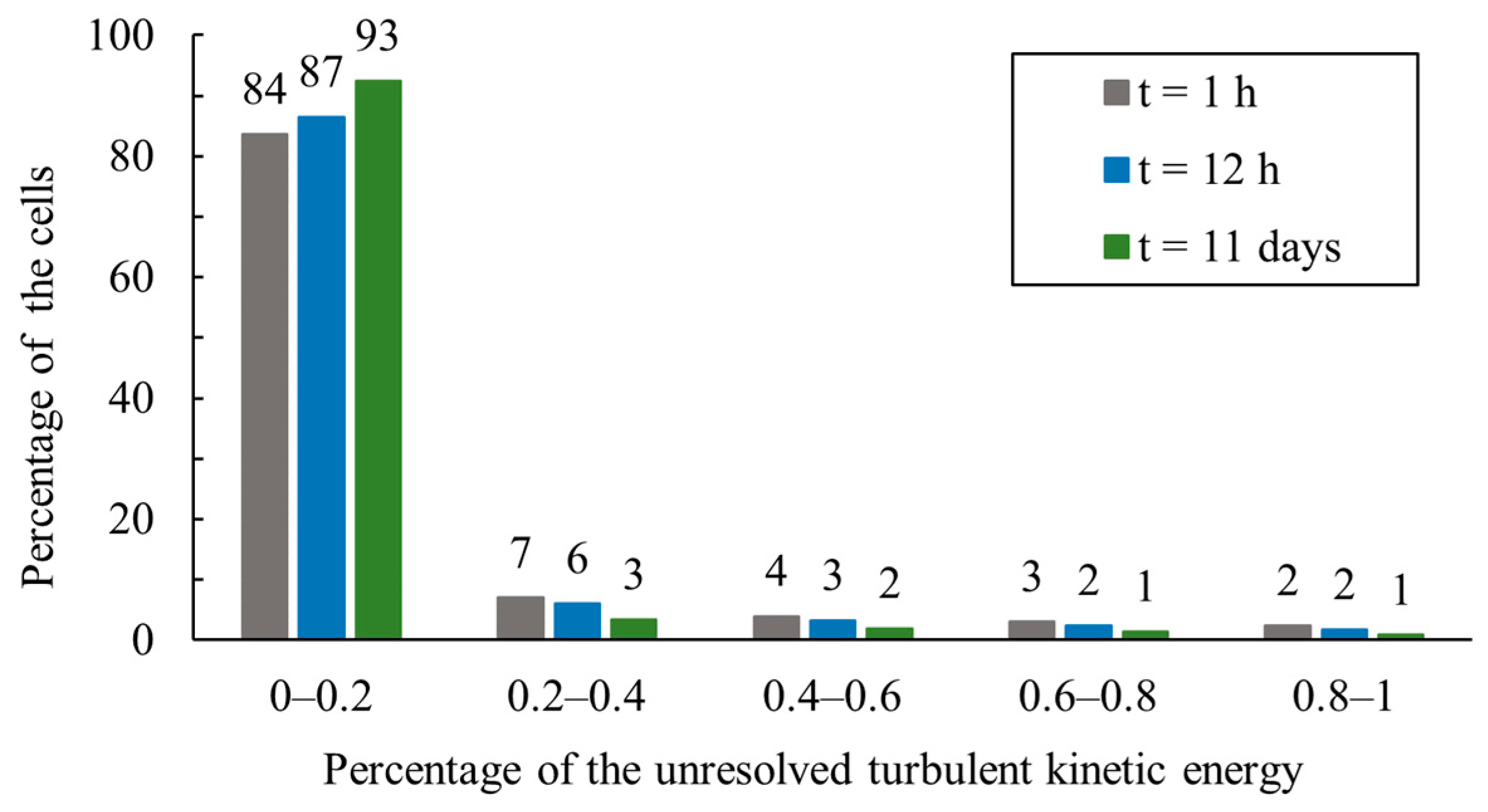
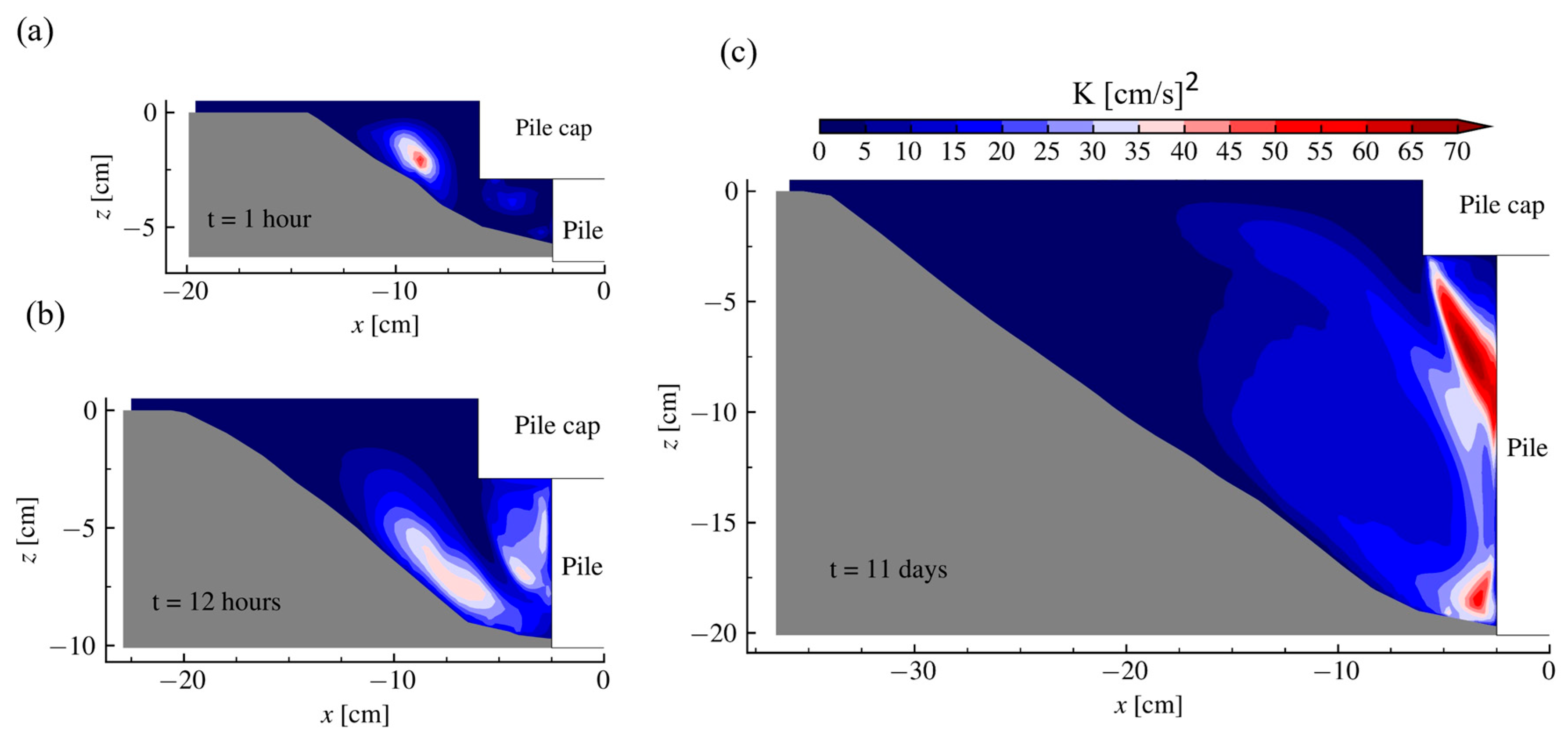
5.2. Turbulent Kinetic Energy
5.3. Reynolds Shear Stress
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Diameter or square side length |
| Fr | Froude number |
| h | Flow depth or channel half-height |
| Hcap | Pile cap height |
| Bed layer depth | |
| Pier Reynolds number () | |
| Reynolds number based on h | |
| Friction Reynolds number () | |
| Time | |
| Mean approach velocity | |
| Friction velocity | |
| Pile cap width | |
| x,y,z | Longitudinal, transverse, and vertical directions |
| u,v,w | Velocity components in the x, y and z directions |
| , | Velocity components fluctuations |
| Kinematic viscosity | |
| CBC | Convective Boundary Condition |
| DNS | Direct Numerical Simulation |
| HV | Horseshoe Vortex |
| LES | Large-eddy simulation |
| RSS | Reynolds shear stress |
| TKE | Turbulent kinetic energy (K) |
References
- Unger, J.; Hager, W.H. Down-Flow and Horseshoe Vortex Characteristics of Sediment Embedded Bridge Piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Dargahi, B. The Turbulent Flow Field around a Circular Cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Alemi, M.; Pêgo, J.P.; Maia, R. Numerical Investigation of the Flow Behavior around a Single Cylinder Using Large Eddy Simulation Model. Ocean. Eng. 2017, 145, 464–478. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, S.G.; Ettema, R. Coherent Structures in the Flow Field around a Circular Cylinder with Scour Hole. J. Hydraul. Eng. 2008, 134, 572–587. [Google Scholar] [CrossRef]
- Guan, D.; Chiew, Y.-M.; Wei, M.; Hsieh, S.-C. Characterization of Horseshoe Vortex in a Developing Scour Hole at a Cylindrical Bridge Pier. Int. J. Sediment Res. 2019, 34, 118–124. [Google Scholar] [CrossRef]
- Muzzammil, M.; Gangadhariah, T. The Mean Characteristics of Horseshoe Vortex at a Cylindrical Pier. J. Hydraul. Res. 2003, 41, 285–297. [Google Scholar] [CrossRef]
- Okhravi, S.; Gohari, S.; Alemi, M.; Maia, R. Numerical Modeling of Local Scour of Non-Uniform Graded Sediment for Two Arrangements of Pile Groups. Int. J. Sediment Res. 2023, 38, 597–614. [Google Scholar] [CrossRef]
- Helmi, A.M.; Shehata, A.H. Three-Dimensional Numerical Investigations of the Flow Pattern and Evolution of the Horseshoe Vortex at a Circular Pier during the Development of a Scour Hole. Appl. Sci. 2021, 11, 6898. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Characteristics of Horseshoe Vortex in Developing Scour Holes at Piers. J. Hydraul. Eng. 2007, 133, 399–413. [Google Scholar] [CrossRef]
- Beheshti, A.A.; Ataie-Ashtiani, B. Experimental Study of Three-Dimensional Flow Field around a Complex Bridge Pier. J. Eng. Mech. 2010, 136, 143–154. [Google Scholar] [CrossRef]
- Beheshti, A.A.; Ataie-Ashtiani, B. Scour Hole Influence on Turbulent Flow Field around Complex Bridge Piers. Flow Turbulence Combust 2016, 97, 451–474. [Google Scholar] [CrossRef]
- Gautam, P.; Eldho, T.I.; Mazumder, B.S.; Behera, M.R. Experimental Study of Flow and Turbulence Characteristics around Simple and Complex Piers Using PIV. Exp. Therm. Fluid Sci. 2019, 100, 193–206. [Google Scholar] [CrossRef]
- Alemi, M.; Pêgo, J.P.; Maia, R. Characterization of the Turbulent Flow around Complex Geometries Using Wall-Modeled Large Eddy Simulation and Immersed Boundary Method. Int. J. Civ. Eng. 2020, 18, 279–291. [Google Scholar] [CrossRef]
- Moreno, M.; Maia, R.; Couto, L. Effects of Relative Column Width and Pile-Cap Elevation on Local Scour Depth around Complex Piers. J. Hydraul. Eng. 2016, 142, 04015051. [Google Scholar] [CrossRef]
- Alemi, M. Numerical Simulation of the Flow Behavior around Bridge Piers. Ph.D. Thesis, University of Porto, Porto, Portugal, 2018. Available online: https://repositorio-aberto.up.pt/bitstream/10216/117225/2/301519.pdf (accessed on 11 July 2024).
- Alemi, M.; Pêgo, J.P.; Maia, R. Numerical Simulation of the Turbulent Flow around a Complex Bridge Pier on the Scoured Bed. Eur. J. Mech. B Fluids 2019, 76, 316–331. [Google Scholar] [CrossRef]
- Ramos, P.X.; Bento, A.M.; Maia, R.; Pêgo, J.P. Characterization of the Scour Cavity Evolution around a Complex Bridge Pier. J. Appl. Water Eng. Res. 2016, 4, 128–137. [Google Scholar] [CrossRef]
- Hinterberger, C.; Fröhlich, J.; Rodi, W. 2D and 3D Turbulent Fluctuations in Open Channel Flow with Re τ = 590 Studied by Large Eddy Simulation. Flow Turbul. Combust 2008, 80, 225–253. [Google Scholar] [CrossRef]
- Moser, R.D.; Kim, J.; Mansour, N.N. Direct Numerical Simulation of Turbulent Channel Flow up to Reτ=590. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Kumar, A.; Kothyari, U.C. Three-Dimensional Flow Characteristics within the Scour Hole around Circular Uniform and Compound Piers. J. Hydraul. Eng. 2012, 138, 420–429. [Google Scholar] [CrossRef]
- Pope, S.B. Ten Questions Concerning the Large-Eddy Simulation of Turbulent Flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Gautam, P.; Eldho, T.I.; Behera, M.R. Effects of Pile-Cap Elevation on Scour and Turbulence around a Complex Bridge Pier. Int. J. River Basin Manag. 2023, 21, 283–297. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G. Flow and Turbulence Structure around an In-stream Rectangular Cylinder with Scour Hole. Water Resour. Res. 2010, 46, 2010WR009336. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemi, M.; Pêgo, J.P.; Okhravi, S.; Maia, R. Numerical Analysis of Flow Structure Evolution during Scour Hole Development: A Case Study of a Pile-Supported Pier with Partially Buried Pile Cap. Modelling 2024, 5, 884-900. https://doi.org/10.3390/modelling5030046
Alemi M, Pêgo JP, Okhravi S, Maia R. Numerical Analysis of Flow Structure Evolution during Scour Hole Development: A Case Study of a Pile-Supported Pier with Partially Buried Pile Cap. Modelling. 2024; 5(3):884-900. https://doi.org/10.3390/modelling5030046
Chicago/Turabian StyleAlemi, Mahdi, João Pedro Pêgo, Saeid Okhravi, and Rodrigo Maia. 2024. "Numerical Analysis of Flow Structure Evolution during Scour Hole Development: A Case Study of a Pile-Supported Pier with Partially Buried Pile Cap" Modelling 5, no. 3: 884-900. https://doi.org/10.3390/modelling5030046
APA StyleAlemi, M., Pêgo, J. P., Okhravi, S., & Maia, R. (2024). Numerical Analysis of Flow Structure Evolution during Scour Hole Development: A Case Study of a Pile-Supported Pier with Partially Buried Pile Cap. Modelling, 5(3), 884-900. https://doi.org/10.3390/modelling5030046






