Estimation Approach for a Linear Quantile-Regression Model with Long-Memory Stationary GARMA Errors

Abstract

The aim of this paper is to assess the significant impact of using quantile analysis in multiple fields of scientific research . Here, we focus on estimating conditional quantile functions when the errors follow a GARMA (Generalized Auto-Regressive Moving Average) model. Our key theoretical contribution involves identifying the Quantile-Regression (QR) coefficients within the context of GARMA errors. We propose a modified maximum-likelihood estimation method using an EM algorithm to estimate the target coefficients and derive their statistical properties. The proposed procedure yields estimators that are strongly consistent and asymptotically normal under mild conditions. In order to evaluate the performance of the proposed estimators, a simulation study is conducted employing the minimum bias and Root Mean Square Error (RMSE) criterion. Furthermore, an empirical application is given to demonstrate the effectiveness of the proposed methodology in practice.

1. Introduction

Linear regression is one of the most common and well understood techniques for modeling the relationship between one or more covariates or predictor variables, X, and the conditional mean $E\left(Y\right|X=x)$ of the response variable Y, given $X=x$. The conditional mean minimizes the expected squared error: $E\left(Y\right|X=x)=arg\underset{\mu }{min}E\left[{(Y-\mu )}^2\right|X=x]$. If the conditional mean of Y, given x, is linear and expressed as $\mu \left(x\right)=x^{\prime }\beta$, then $\beta$ can be estimated by solving $\underset{\beta }{min}\sum {(y_i-x^{\prime }\beta )}^2$, which is the ordinary least squares solution of the linear regression model.

However, inference from this model requires that specific assumptions be made about the distribution of the error (i.e., linearity, homoscedasticity, independence, or normality). In contrast, quantile regression, as introduced by Koenker and Bassett [1], aims to extend these ideas to the estimation of conditional quantile function models wherein the quantiles of the conditional distribution of the response variable are expressed as functions of observed covariates. For a pair of observed values $(x,y)$ of random vector $(X,Y)$, a quantile regression has the form $q_{\tau }\left(x\right)=inf\{y:P(Y\le y|x)\ge \tau \}$, where $\tau$ indicates that the specific quantile of Y is the smallest value of y denoted by $P(Y\le y|x)=E\left({\mathbb{1}}_{\{Y\le y\}}\right|X=x)$, given without making assumptions about the distribution of the error. In the case of classical quantile regressions, we can assume that these quantiles of the conditional distribution have a linear form,

$$q_{\tau }\left(x\right)=x^{\prime }{\beta }_{\tau },$$

(1)

where ${\beta }_{\tau }$ is a parameter vector (a vector of regression coefficients).

For the following, it may be useful to note that this expression can be written in an equivalent way: $Y=x^{\prime }{\beta }_{\tau }+{ϵ}_{\tau }$, with $q_{\tau }\left({ϵ}_{\tau }\right|x)=0$. Condition 1 is similar to that carried out in the standard linear regression, in which the conditional mean of the variable of interest Y is modelled as a linear expression of the explanatory variables X. One difference is that here we allow the coefficients to differ from quantile to quantile. This provides additional information not apparent from simple linear regression.

In the parameter estimation problem, the form of the quantile regression function is known, but it contains unknown parameters, ${\beta }_{\tau }$. The most intuitive way to calculate the standard estimator, ${\widehat{\beta }}_{\tau }$, consists of ordering these n variables, the quantile of order $\tau$ being provided by the ($n{\tau }^{th}$) observation where [$n\tau$] is the smallest integer greater than or equal to $n\tau$. However, it is more useful to notice that the popular method for estimating the unknown parameters, ${\beta }_{\tau }$, in a quantile-regression function is by solving the estimating equation

$${\widehat{q}}_{\tau }\left(Y\right)=\underset{{\beta }_{\tau }}{min}\sum {\rho }_{\tau }{(y_i-x^{\prime }{\beta }_{\tau })}^2,$$

(2)

where ${\widehat{q}}_{\tau }(.)$ is the check function defined by ${\rho }_{\tau }\left(u\right)=u(\tau -I(u<0))$ for some $\tau \in (0,1)$. Here, $I(.)$ is an indicator function that takes the value of unity when $I(.)$ is true and zero otherwise, and here $u=y_i-x_i^{\prime }{\beta }_{\tau }$. However, this function is not differentiable at zero, and clear solutions to minimization problems are unobtainable [2,3]. In quantile-regression methods, linear programming is frequently implemented for parameter estimation.

The Expectation-Maximization (EM) algorithm and the Alternating Least Squares (ALS) algorithm are both iterative optimization techniques commonly employed in statistical modeling to estimate parameters iteratively. In quantile regression, aimed at estimating conditional quantiles of a response variable given covariates, the selection between EM and ALS relies on several considerations.

Opting for EM in quantile regression over ALS is justified due to its capability in managing latent variables and accommodating diverse error distributions, and its alignment with the objectives of quantile regression. Additionally, EM avoids the swapping effect by updating parameters sequentially rather than alternately, enhancing stability in estimation. However, it is essential to note that the bias in EM hinges on factors such as sample size and model assumptions.

Despite potential variations in speed, where the speed of EM varies depending on the complexity of the model and convergence criteria, EM’s advantages in handling latent variables and error distributions make it a favorable choice in many quantile-regression applications.

There are numerous articles about the parameter estimation of quantile-regression models with the EM algorithm. Tian et al. [4] proposed a new method based on the Expectation-Maximization algorithm for a linear quantile-regression model with symmetric Laplace error distribution. Furthermore, Tian et al. [5] used this method for a linear quantile-regression model with autoregressive errors. Zhou et al. [6] developed the EM algorithm and GEM algorithm for calculating the quantiles of linear and non-linear regression models.

All of these results are only for the errors that are modeled by short-memory, time-series models. However, long-memory models are very important; they are used in various fields, such us hydrology, chemistry, and economics; see, for example Hurst [7], Jeffreys [8], Student [9].

The most commonly used long-memory model, which deals with the modeling of cyclic behavior, is The Generalized Autoregressive Moving Average model (GARMA). It was proposed by Gray et al. [10] to deal with non-additivity, non-normality, and heteroscedasticity in real time-series data.

This behavior has attracted considerable attention, prompting extensive research efforts over recent decades. For instance, Darmawan et al. [11] utilized a GARMA model to predict COVID-19 data trends in Indonesia, Albarracin et al. [12] analyzed the structure of GARMA models in practical scenarios, while Huntet al. [13] introduced an R package, ‘garma’, specifically tailored for fitting and forecasting GARMA models in R (Version R-4.4.0).

The foundations of the methods for independent data have now been consolidated, and some computational commands for the analysis of such data are provided by most of the available statistical software (e.g., R (Version 4.4.1 R. Ross Ihaka and Robert Gentleman’s creation in Vienna, Austria)/Python (Version 3.13. Guido van Rossum’s creation, in Wilmington, DE, USA).

In this paper, we will consider a linear quantile-regression model with Generalized Autoregressive Moving Average error, defined as follows:

$$y_t=x_t^{\prime }{\beta }_{\tau }+{ϵ}_t,\mathit{t}=\mathit{1},\mathit{2},\dots ,\mathit{n}\mathit{with}{q}_{\tau }\left(y_t\right|x_t)=x_t^{\prime }{\beta }_{\tau },$$

(3)

where $y_t$ is the t-th observation of the response variable, $x_t={(x_{t,1},\dots ,x_{t,M})}^{\prime }$ is a $M\times 1$ covariate, ${\beta }_{\tau }={({\beta }_{\tau ,1},\dots ,{\beta }_{\tau ,M})}^{\prime }$ is a regression parameter vector, and $\{{ϵ}_t,t\in \mathbb{Z}\}$ is a stationary long-memory process generated by the GARMA(p,0) model, as follows:

$${\mathrm{\Phi }}_p\left(L\right){(1-2\eta L+L^2)}^d{ϵ}_t={\xi }_t,$$

(4)

where ${\mathrm{\Phi }}_p\left(L\right)=1-{\displaystyle \sum _{k=1}^p}{\varphi }_k{L}^k$ with $\mathrm{\Phi }={({\varphi }_1,\dots ,{\varphi }_p)}^{\prime }$ is the autoregressive parameter vector, L is the Backshift operator defined by $L{X}_t=X_{t-1}$, ${(1-2\eta L+L^2)}^d$ represent the long-memory Gegenbauer component, and $\{{\xi }_t,t\in \mathbb{Z}\}$ is an iid process.

In this work, we aim to estimate the parameters of our models with the EM algorithm (see [14]) based on the method of Tian et al. [4]. However, we will derive the asymptotic properties of our estimators.

The outline of this paper is organized as follows: In Section 2, we provide the likelihood function, and Section 3 deals with the estimation of our parameters by the EM algorithm. In Section 4, we derive the asymptotic properties of the estimators under some mild conditions. Some simulation results will be provided in Section 5, and finally a real data example is provided in Section 6.

2. Estimation Procedure via EM Algorithm

The maximum-likelihood method is a technique that is widely recognized for deriving estimators. One of the principal reasons for the wide popularity of the maximum-likelihood method is that the resulting estimator has many interesting properties. However, in some complicated problems maximum-likelihood estimators are unsuitable or do not exist. This method estimates the parameters of various statistical models, including quantile-regression models. In such cases, to estimate the $q_{\tau }\left(y_t\right|x_t)$ at model (1), it is natural to simultaneously estimate the regression coefficients and the GARMA parameters using quantile regression. Hence, in this section we focuses on the estimation of the parameter vector of models (3) and (4) by ${({\beta }_{\tau }^{\prime },{\mathrm{\Phi }}^{\prime },\sigma )}^{\prime }$. It is also worth noting that maximum-likelihood estimation is related to other optimization techniques. In particular, if we assume a normal distribution then it is equivalent to the ordinary least squares method. In practice, the normality assumption of the random error may be abandoned for many reasons, such as outliers, contaminated data, and heavy-tailed distributions. The Laplace distribution is a good robust alternative in this case [15]. Yu and Moyeed [16] found that minimizing the expression (1) is equivalent to maximizing a likelihood function formed by combining the independently distributed asymmetric Laplace error distribution (see [17]). In this work, we adopt a similar idea to build a likelihood function; the distribution of the process $\{{\xi }_t,t\in \mathbb{Z}\}$ in model (3) is assumed to be a symmetric Laplace distribution with zero mean, scale parameter $\sigma >0$, and skewness parameter $\tau \in (0,1)$. Let ${\xi }_t\sim ALD(0,\sigma ,\tau )$, as follows:

$$f\left({\xi }_t\right)=\frac{\tau (1-\tau )}{\sigma }exp\left\{-{\rho }_{\tau }\left(\frac{{\xi }_t}{\sigma }\right)\right\},$$

(5)

where ${\rho }_{\tau }\left(u\right)=u(\tau -{\mathbb{1}}_{[u<0]})$ is the quantile check function.

The mean and the variance of this distribution are given by: $E\left({\xi }_t\right)=\sigma {\displaystyle \frac{1-2\tau }{\tau (1-\tau )}}$ and $Var\left({\xi }_t\right)={\sigma }^2{\displaystyle \frac{(1-2\tau +2{\tau }^2)}{{(1-\tau )}^2{\tau }^2}}.$ (See [18]).

The Laplace distribution was chosen for the error term in the GARMA model due to several advantages it offers. Firstly, it offers robustness to outliers. The Laplace distribution, also referred to as the double-exponential distribution, has heavier tails compared to the normal distribution. This implies that it is more robust to outliers in the data. In a GARMA error model, which aims to capture the time-series behavior of a process, having robustness to outliers is essential for precise estimation and prediction. Secondly, unlike the normal distribution, the Laplace distribution is symmetric and has the capability to capture skewness in the data. In time-series analysis, it is common to encounter data that exhibit asymmetric patterns. By using the Laplace distribution as the error term in the GARMA model, we align the model’s assumptions with the potential skewness in the data, thus improving its ability to capture the underlying patterns. Additionally, the Laplace distribution possesses straightforward mathematical properties that enhance its computational efficiency. This characteristic can be beneficial when fitting the GARMA model to extensive datasets or when performing simulations for different scenarios.

Under such circumstance, the maximum-likelihood estimates for the parameters ${\beta }_{\tau }$, $\mathrm{\Phi }$, and $\sigma$ are obtained by maximizing the marginal density, $f\left(y_t\right|{\beta }_{\tau },\mathrm{\Phi },\sigma )$, which is obtained by replacing ${\xi }_t$ with ${\mathrm{\Phi }}_p\left(L\right){(1-2\eta L+L^2)}^d(y_t-x_t^{\prime }{\beta }_{\tau })$ in Equation (3), that is,

$$L({\beta }_{\tau },\sigma ,\tau )={\left(\frac{\tau (1-\tau )}{\sigma }\right)}^{n}exp\left\{\sum _{t=1}^n{\rho }_{\tau }\left(\frac{{\mathrm{\Phi }}_p\left(L\right){(1-2\eta L+L^2)}^d(y_t-x_t^{\prime }{\beta }_{\tau })}{\sigma }\right)\right\}.$$

(6)

The maximization of (4) is equivalent to the maximization of the logarithm of the likelihood function:

$$log\left(L({\beta }_{\tau },\sigma ,\tau )\right)=nlog\left(\frac{\tau (1-\tau )}{\sigma }\right)-\sum _{t=1}^n{\rho }_{\tau }\left(\frac{{\mathrm{\Phi }}_p\left(L\right){(1-2\eta L+L^2)}^d(y_t-x_t^{\prime }{\beta }_{\tau })}{\sigma }\right).$$

(7)

Clearly, the objective function has no closed form. Hence, it is not possible the estimate the quantile-regression coefficients because this objective function is non-convex with respect to ${\beta }_{\tau }$ and the differentiation (the function ${\rho }_{\tau }(.)$ is not differentiable at 0). Therefore, to overcome this problem we suggest the use of the property of the asymmetric Laplace, combining a normal distribution conditional on an exponential distribution, proposed by Yu and Moyeed [16], as follows:

$${\xi }_t=\theta z_t+\omega \sqrt{\sigma z_t}{u}_t,$$

(8)

where $u_t\sim \mathcal{N}(0,1)$, $z_t\sim exp\left(\frac{1}{\sigma }\right)$, $\theta =\frac{1-2\tau }{\tau (1-\tau )}$ and ${\omega }^2=\frac{2}{\tau (1-\tau )}$.

This proposal should be seen as a ratification to the previous objective function, using the Gegenbauer polynomials ($C_i^{(-d)}\left(\eta \right)$, $i\in \mathbb{Z}$), defined by:

$${(1-2\eta L+L^2)}^d=\sum _{i=0}^{\infty }{C}_i^{(-d)}\left(\eta \right)L^i.$$

(9)

(See [19]).

Then, under the previous results, Equations (3), (8) and (9) lead to the following explicit expression:

$$y_t=\sum _{i=0}^{\infty }{C}_i^{(-d)}\left(\eta \right)L^i{y}_t-{(1-2\eta L+L^2)}^d(\sum _{k=1}^p{\varphi }_k{L}^k{y}_t-{\mathrm{\Phi }}_p\left(L\right)x_t^{\prime }{\beta }_{\tau })+\theta z_t+\omega \sqrt{\sigma z_t}{u}_t$$

(10)

Therefore, we can conclude that $y_t$ is conditionally normally distributed (see [5] for more details). Then, the quantile-regression model here is represented as a normal regression model. The full joint density for $y=(y_1,\dots ,y_n)$ is given by:

$$f(y/z,{\beta }_{\tau })=\prod _{t=1}^n\frac{1}{\sqrt{2\pi }\omega \sqrt{\sigma z_t}}exp\left\{-\frac{{({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })-\theta z_t)}^2}{2{\omega }^2{z}_t\sigma }\right\},$$

(11)

with $z=(z_1,\dots ,z_n)$ and $P\left(L\right)={(1-2\eta L+L^2)}^d$.

The estimators of the unknown quantile-regression parameters, ${\beta }_{\tau }$, the scale $\sigma$, and the vector parameters of the GARMA model, $\mathrm{\Phi }$, may be obtained by maximizing the likelihood function:

$$L({\beta }_{\tau },\mathrm{\Phi },\sigma /y,x,z)=\prod _{t=1}^n\frac{1}{\sqrt{2\pi }\omega \sqrt{\sigma z_t}}exp\left\{-\frac{{({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })-\theta z_t)}^2}{2{\omega }^2{z}_t\sigma }\right\}\frac{1}{\sigma }exp(-\frac{z_t}{\sigma }).$$

(12)

The corresponding log-likelihood function is given by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill log(L({\beta }_{\tau },\mathrm{\Phi },\sigma /y,x,z)& =-nlog\left(\sqrt{2\pi }\tau \omega \right)-\frac{3n}{2}log\left(\sigma \right)-\frac{1}{2}\sum _{t=1}^{n}log\left(z_t\right)\hfill \\ \hfill & -\sum _{t=1}^n\frac{{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\right)}^2}{2{\omega }^2\sigma }{z}_t^{-1}+2\sum _{t=1}^n\frac{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\theta }{2{\omega }^2\sigma }\hfill \\ \hfill & -\sum _{t=1}^n(\frac{{\theta }^2}{2{\omega }^2\sigma }+\frac{1}{\sigma })z_t\hfill \end{array}.\end{array}$$

(13)

Due to the unobserved variables, $z_t$, the maximum likelihood becomes intractable. In this case, solving Equation (2) requires an iterative algorithm. The EM algorithm (see [20]) is a broad method of finding the maximum-likelihood estimates of the parameters of a fundamental distribution from a provided dataset that has missing values. In the next section, we present the Expectation-Maximization (EM) algorithm, which is derived from likelihood optimization.

2.1. EM Algorithm

The Expectation-Maximization (EM) algorithm [14] is a commonly utilized method for finding maximum-likelihood estimates in statistical models that rely on missing data or unobservable latent variables. A latent variable is a variable that affects our observed data but in ways that we cannot know directly. The EM algorithm is an iterative approach that alternates between two modes. The first mode attempts to estimate the missing or hidden variables; this is known as the estimation-step or E-step. The second mode attempts to optimize the parameters of the model to provide the best explanation of the data; this is known as the maximization-step or M-step.

In the model (10), the EM iterations are based on regarding the random variable ($z_t=(z_1,\dots ,z_n)$) as a set of unobserved latent variables or missing values. We seek to estimate our model by maximizing the complete-data log likelihood, which is then denoted in Equation (12), $log(L({\beta }_{\tau },\mathrm{\Phi },\sigma /y,x,z)$, where $\vartheta ={({\beta }_{\tau }^{\prime },{\mathrm{\Phi }}^{\prime },\sigma )}^{\prime }$ are the unknown parameter vectors for which we wish to find the MLE. To apply the EM algorithm for estimation, we must first find the conditional pdf of the unobserved variable $z_t$, in order to estimate the missing variables in the dataset. Indeed, since $z_t$, in Equation (8), is assumed to be $exp\left(\frac{1}{\sigma }\right)$ and $u_t\sim \mathcal{N}(0,1)$, it can be observed that the conditional distribution of $z_t$, given y, $\left(z_t\right|y)$ is given by:

$$\begin{array}{cc}\hfill f(z_t/y,x)& \backsimeq \frac{1}{\sqrt{\sigma z_t}}exp\left\{-\frac{{({\mathrm{\Phi }}_p\left(L\right){(1-2\eta L+L^2)}^d(y_t-x_t^{\prime }{\beta }_{\tau })-\theta z_t)}^2}{2{\omega }^2{z}_t\sigma }\right\}\frac{1}{\sigma }exp(-\frac{z_t}{\sigma })\hfill \\ & \backsimeq \frac{1}{\sqrt{{\sigma }^3}}{z}_t^{\frac{1}{2}-1}exp\left\{-\frac{{({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })-\theta z_t)}^2}{2{\omega }^2{z}_t\sigma }\right\}exp(-\frac{z_t}{\sigma })\hfill \\ & \backsimeq \frac{1}{\sqrt{{\sigma }^3}}{z}_t^{\frac{1}{2}-1}exp\left\{-\frac{1}{2}\left[\frac{{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\right)}^2{z}_t^{-1}}{{\omega }^2\sigma }+(\frac{{\theta }^2}{{\omega }^2\sigma }+\frac{2}{w<\sigma })z_t\right]\right\}\hfill \\ & \backsim GIG\left(\frac{1}{2},\frac{{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\right)}^2}{{\omega }^2\sigma },(\frac{{\theta }^2}{{\omega }^2\sigma }+\frac{2}{\sigma })\right)\hfill \end{array},$$

where GIG is the Generalized Inverse Gaussian distribution, a three parameter distribution introduced by Good, [21] that has been applied in a variety of fields of statistics. More recently, Sánchez et al. [22] used the GIG distribution as a mixing distribution to estimate the parameters of quantile-regression models. Furthermore, note that the r-th moment of $z_t\sim GIG(\alpha ,\gamma ,\delta )$ is given by:

$$E\left(z^r\right)={\left(\frac{\gamma }{\delta }\right)}^{\frac{r}{2}}\frac{K_{\alpha +r}\left(\sqrt{\gamma \delta }\right)}{K_{\alpha }\left(\sqrt{\gamma \delta }\right)}$$

(14)

and

$$E\left(log\left(z\right)\right)=\frac{dE\left(z^r\right)}{dr}{|}_{r=0},$$

(15)

where K is a modified Bassel function of the second kind (see [23] for more details). The above relations (14) and (15) will be useful in calculating the conditional expectation of the log-likelihood function, with respect to the conditional distribution of $z_t$ given y, when applying the following two EM steps, described as follows:

• Step E

To applying EM to model (10) (with GARMA errors), we start by writing down the expected complete log-likelihood, given by Equation (2), known as the Q-function, $Q(\vartheta /{\vartheta }^{\left(h\right)})=E(log(\vartheta /y,z)/y,{\vartheta }^{\left(h\right)})$, where $E_{{\vartheta }^{\left(h\right)}})[.]$ means that the expectation is being affected using ${\vartheta }^{\left(h\right)}$ for $\vartheta$, with respect to the unknown data z given the observed data y and the current parameter estimates ${\vartheta }^{\left(h\right)}$, which is the estimated value of the h-th iteration. Calculating this expectation at the ($h-1$)-th iteration yields

$$Q({\beta }_{\tau },\mathrm{\Phi },\sigma /y,{\vartheta }^{\left(h\right)})=E(log\left(L({\beta }_{\tau },\mathrm{\Phi },\sigma /y,x,z)\right)/y,{\vartheta }^{\left(h\right)}).$$

Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill Q({\beta }_{\tau },\mathrm{\Phi },\sigma /y,{\vartheta }^{(h-1)})& =-nlog\left(\sqrt{2\pi }\tau \omega \right)-\frac{3n}{2}log\left(\sigma \right)-\frac{1}{2}\sum _{t=1}^n{\lambda }_t\hfill \\ \hfill & -\sum _{t=1}^n\frac{{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\right)}^2}{2{\omega }^2\sigma }{\mu }_t+2\sum _{t=1}^n\frac{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\theta }{2{\omega }^2\sigma }\hfill \\ \hfill & -\sum _{t=1}^n(\frac{{\theta }^2}{2{\omega }^2\sigma }+\frac{1}{\sigma }){\nu }_t\hfill \end{array},\end{array}$$

(16)

where we have defined the pseudo-values ${\lambda }_t=E(log\left(z_t\right)/y,{\vartheta }^{(h-1)})$, ${\mu }_t=E(z_t^{-1}/y,{\vartheta }^{(h-1)})$, and ${\nu }_t=E(z_t/y,{\vartheta }^{(h-1)})$.

For evaluating (2), it is necessary to compute ${\lambda }_t$, ${\mu }_t$, and ${\nu }_t$, as in (14) and (15), which will depend of the conditional pdf of z in Equation (11).

These expressions are straightforward to derive using Equations (14) and (15), as discussed in Eberlein and Hammerstein [24]. The elements of the partial derivatives of the t-th moment of $z_t$ evaluated at ${\vartheta }^{(h-1)}$ are as follows:

${\lambda }_t=\frac{dE(z^a/y,{\vartheta }^{(h-1)})}{da}{|}_{a=0}$

${\mu }_t=\frac{\sqrt{{\theta }^2+2{\omega }^2}}{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })}$

${\nu }_t=\frac{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })}{\sqrt{{\theta }^2+2{\omega }^2}}\times \frac{K_{\frac{3}{2}}\left(\frac{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })}{{\omega }^2{\sigma }^{(t-1)}}\right)}{K_{\frac{1}{2}}(\frac{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })}{{\omega }^2{\sigma }^{(t-1)}}}$.

We can calculate ${\nu }_t$ explicitly by applying the well-known recursion formula defined by $x{K}_{a-1}\left(x\right)-x{K}_{a+1}\left(x\right)=-2a{K}_a\left(x\right)$, resulting in the following expression:

$${\nu }_t=\frac{{\omega }^2{\sigma }^{(t-1)}}{{\theta }^2+2{\omega }^2}+\frac{{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })}{\sqrt{{\theta }^2+2{\omega }^2}}.$$

• Step M (Maximization)

The above E-step of the EM algorithm simply uses $L\left(y\right|x,z,{\vartheta }^{(h-1)})$ to calculate the expectation of the unobservable information, z, given the observed data $(y,x)$ and the existing estimates of unknown parameters ${\vartheta }^{(h-1)}$.

In the M-step, the parameters are re-estimated by maximizing the Q-function to find the new estimate ${\vartheta }^{\left(h\right)}$ by solving the ${\left(h\right)}^{th}$ step; the M-step procedures is as follows:

$${\vartheta }^{\left(h\right)}=arg\underset{\vartheta }{max}Q(\vartheta ,{\vartheta }^{(h-1)})=arg\underset{\vartheta }{max}Q(\vartheta ,({\beta }^{(h-1)},{\mathrm{\Phi }}^{(h-1)},{\sigma }^{(h-1)})),$$

where each estimate parameter can be acquired by partially maximizing the objective Q-function:

(A.1)

${\beta }_{\tau }^{\left(h\right)}=arg\underset{\beta }{max}Q({\vartheta }^{\left(h\right)},(\beta ,{\mathrm{\Phi }}^{(h-1)},{\sigma }^{(h-1)}))$

(A.2)

${\mathrm{\Phi }}^{\left(h\right)}=arg\underset{\mathrm{\Phi }}{max}Q({\vartheta }^{\left(h\right)},({\beta }^{\left(h\right)},\mathrm{\Phi },{\sigma }^{(h-1)}))$

(A.3)

${\sigma }^{\left(h\right)}=arg\underset{\sigma }{max}Q({\vartheta }^{\left(h\right)},({\beta }^{\left(h\right)},{\mathrm{\Phi }}^{\left(h\right)},\sigma ))$.

In this regard, starting values, ${\vartheta }^{\left(0\right)}={({\beta }_{\tau }^{{\left(0\right)}^{\prime }},{\mathrm{\Phi }}^{{\left(0\right)}^{\prime }},{\sigma }^{\left(0\right)})}^{\prime }$, are necessary in order to initiate the iterative procedure. These can be obtained from the Least Squares Estimates (LSE) method (see [25]).

An estimate of $\vartheta ={({\beta }_{\tau }^{\prime },{\mathrm{\Phi }}^{\prime },\sigma )}^{\prime }$ can be obtained by equating the score vector, including the first-order partial derivatives of $Q\left(\vartheta \right)$ with respect to each parameter, denoted by $\frac{\partial \mathbf{Q}\left(\vartheta \right)}{\partial \vartheta }=(\frac{\partial \mathbf{Q}}{\partial \sigma },\frac{\partial \mathbf{Q}}{\partial {\varphi }_1},\dots ,\frac{\partial \mathbf{Q}}{\partial {\varphi }_p},\frac{\partial \mathbf{Q}}{\partial \sigma })$, to zero vector, leading to Q-function equations. In particular, we have the following explicit expressions:

2.1.1. Estimator of ${\beta }_{\tau }$

Let ${\beta }_{\tau }$ be the parameter value at a local maximum of the Q-function in Equation (2). Differentiating the previous expression in respect to ${\beta }_{\tau }$, we find

$$\begin{array}{cc}\hfill \frac{\partial \mathbf{Q}}{\partial {\beta }_{\tau }}=0& \iff \frac{1}{{\omega }^2\sigma }\sum _{t=1}^n{\mu }_t{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)\right)}^2(y_t-x_t^{\prime }{\beta }_{\tau })x_t-\frac{\theta }{{\omega }^2\sigma }\sum _{t=1}^n{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)x_t=0\hfill \\ & \iff \sum _{t=1}^n{\mu }_t{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)\right)}^2{x}_t^{\prime }{x}_t{\beta }_{\tau }=\sum _{t=1}^n{\mu }_t{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)\right)}^2{y}_t{x}_t-\theta \sum _{t=1}^n{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)x_t.\hfill \end{array}$$

In matrix form, we have:

$$X{\mathrm{\Gamma }}^{(h-1)}{X}^{\prime }{\beta }_{\tau }=X{\mathrm{\Gamma }}^{(h-1)}Y-X\mathrm{\Theta },$$

where:

• $X=({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)x_1,\dots ,{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)x_n)$
• $Y={({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)y_1,\dots ,{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)y_n)}^{\prime }$
• ${\mathrm{\Gamma }}^{(h-1)}=diag({\mu }_1,\dots ,{\mu }_n)$ and $\mathrm{\Theta }={(\theta ,\dots \theta )}^{\prime }$

Denoting:

$$\widehat{X}=({\widehat{\mathrm{\Phi }}}_p^{(h-1)}\left(L\right)P\left(L\right)x_1,\dots ,{\widehat{\mathrm{\Phi }}}_p^{(h-1)}\left(L\right)P\left(L\right)x_n)$$

$$\widehat{Y}={({\widehat{\mathrm{\Phi }}}_p^{(h-1)}\left(L\right)P\left(L\right)y_1,\dots ,{\widehat{\mathrm{\Phi }}}_p^{(h-1)}\left(L\right)P\left(L\right)y_n)}^{\prime }$$

We obtain the h-th iteration estimator of the parameter ${\beta }_{\tau }$ as follows:

$${\widehat{{\beta }_{\tau }}}^{\left(h\right)}={\left(\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }\right)}^{-1}(\widehat{X}{\mathrm{\Gamma }}^{(h-1)}\widehat{Y}-\widehat{X}\mathrm{\Theta }).$$

(17)

2.1.2. Estimator of $\mathrm{\Phi }$

Now, we apply the same procedure for our parameters ${\varphi }_1$, …,${\varphi }_p$:

For $k\in \{1,\dots ,p\}$, we have:

$$\begin{array}{cc}\hfill & \frac{\partial \mathbf{Q}}{\partial {\varphi }_k}=0\hfill \\ \hfill & \iff \frac{1}{{\omega }^2\sigma }\sum _{t=1}^n{\mu }_{t}P{\left(L\right)}^2(y_{t-k}-x_{t-k}^{\prime }{\beta }_{\tau }){\mathrm{\Phi }}_p\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })-\frac{\theta }{{\omega }^2\sigma }\sum _{t=1}^{n}P\left(L\right)(y_{t-k}-x_{t-k}^{\prime }{\beta }_{\tau })=0\hfill \\ & \iff \sum _{t=1}^n{\mu }_{t}P{\left(L\right)}^2(y_{t-k}-x_{t-k}^{\prime }{\beta }_{\tau })\left((y_t-x_t^{\prime }{\beta }_{\tau })-\sum _{j=1}^p{\varphi }_j(y_{t-j}-x_{t-j}^{\prime }{\beta }_{\tau })\right)-\theta \sum _{t=1}^{n}P\left(L\right)(y_{t-k}-x_{t-k}^{\prime }{\beta }_{\tau })=0\hfill \\ & \iff \sum _{j=1}^p{\varphi }_j\sum _{t=1}^n{\mu }_{t}P{\left(L\right)}^2(y_{t-k}-x_{t-k}^{\prime }{\beta }_{\tau })(y_{t-j}-x_{t-j}^{\prime }{\beta }_{\tau })=\sum _{t=1}^{n}P\left(L\right)(y_{t-k}-x_{t-k}^{\prime }{\beta }_{\tau })\left({\mu }_{t}P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })-\theta \right).\hfill \end{array}$$

Then, we write the matrix form as follows:

$$\left(E^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}E\right)\mathrm{\Phi }=E^{\prime }({\mathrm{\Gamma }}^{\left(h\right)}J-\mathrm{\Theta }),$$

where:

$E={\left(E_{i,j}\right)}_{p\times p}$, $E_{i,j}=P\left(L\right)(y_{i-j}-x_{i-j}^{\prime }{\beta }_{\tau })$ and $J={(J_1,\dots ,J_n)}^{\prime }$, $J_i=P\left(L\right)(y_i-x_i^{\prime }{\beta }_{\tau })$ for $i=1,\dots ,n$

Therefore, the h-th iteration estimators of the parameters ${\varphi }_j$ are given by:

$${\widehat{\mathrm{\Phi }}}^{\left(h\right)}={\left({\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{E}\right)}^{-1}\left({\widehat{E}}^{\prime }({\mathrm{\Gamma }}^{\left(h\right)}\widehat{J}-\mathrm{\Theta })\right).$$

(18)

2.1.3. Estimator of $\sigma$

Finally, for $\sigma$, we have:

$$\begin{array}{c}\frac{\partial \mathbf{Q}}{\partial \sigma }=0\hfill \\ \iff \frac{3n}{2\sigma }=\frac{1}{{\omega }^2{\sigma }^2}\left({\displaystyle \sum _{t=1}^n}{\left({\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\right)}^2{\mu }_t+{\displaystyle \sum _{t=1}^n}({\theta }^2+2{\omega }^2){\nu }_t-2\theta {\displaystyle \sum _{t=1}^n}{\mathrm{\Phi }}_p\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\beta }_{\tau })\right).\hfill \end{array}$$

Then, we get:

$${\widehat{\sigma }}^{\left(h\right)}=\frac{{\displaystyle \sum _{t=1}^n}{\widehat{\mathrm{\Phi }}}_p^{\left(h\right)}\left(L\right)P\left(L\right){(y_t-x_t^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)})}^2{\mu }_t+{\displaystyle \sum _{t=1}^n}({\theta }^2+2{\omega }^2){\nu }_t-2\theta {\displaystyle \sum _{t=1}^n}{\widehat{\mathrm{\Phi }}}_p^{\left(h\right)}\left(L\right)P\left(L\right)(y_t-x_t^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)})}{3n{\omega }^2}.$$

(19)

3. Consistency and Asymptotic Normality

In this section, we establish the consistency and asymptotic results of our estimators in Equations (17)–(19). We will begin by stating and discussing a set of basic notations and some assumptions that will be used throughout the remaining parts of this paper.

For the derivation of asymptotic normality of the estimator of ${\beta }_{\tau }$, we need consistency and some additional assumptions. Because we try to show the asymptotic normality of $\sqrt{n}(\widehat{{\beta }_{\tau }}-{\beta }_{\tau })$, it is convenient to apply the notation introduced in (1)–(2) and make the following assumptions of regularity conditions:

C1:

$W:=E\left({\left({\widehat{\mathrm{\Phi }}}_p^{(h-1)}\left(L\right)P\left(L\right)x_1\right)}^2{\mu }_1^{(h-1)}\right)<\infty$

C2:

$T:=E({\widehat{\mathrm{\Phi }}}_p^{(h-1)}\left(L\right)P\left(L\right)x_1{\mu }_1^{(h-1)}-\theta x_1)<\infty$.

While condition (C1) is needed in order to apply the ergodic theorem, condition (C2) allows us to apply the martingale central limit theorem of Billingsley [26]. Then, we have the following theorem:

Theorem 1.

Let ${\widehat{{\beta }_{\tau }}}^{\left(h\right)}$ the EM estimator of ${\beta }_{\tau }$. Under (C1) and (C2) we have:

$$\sqrt{n}({\widehat{{\beta }_{\tau }}}^{\left(h\right)}-{\beta }_{\tau })\underset{n\to +\infty }{⟶}\mathcal{N}(0,W^{-1}TW).$$

(20)

Proof. 

Note that:

$${\widehat{{\beta }_{\tau }}}^{\left(h\right)}-{\beta }_{\tau }={\left(\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }\right)}^{-1}(\widehat{X}{\mathrm{\Gamma }}^{(h-1)}\widehat{Y}-\widehat{X}\mathrm{\Theta })-{\beta }_{\tau }.$$

Then

$$\begin{array}{cc}\hfill \sqrt{n}({\widehat{{\beta }_{\tau }}}^{\left(h\right)}-{\beta }_{\tau })& ={\left({\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }}{n}}\right)}^{-1}\left({\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}\widehat{Y}-\widehat{X}\mathrm{\Theta }}{\sqrt{n}}}\right)-\sqrt{n}{\beta }_{\tau }\hfill \\ & ={\left({\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }}{n}}\right)}^{-1}\left({\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}\widehat{Y}-\widehat{X}\mathrm{\Theta }-\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }{\beta }_{\tau }}{\sqrt{n}}}\right)\hfill \\ & ={\left({\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }}{n}}\right)}^{-1}\left({\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}\widehat{\xi }-\widehat{X}\mathrm{\Theta }}{\sqrt{n}}}\right)-\sqrt{n}{\beta }_{\tau }(\widehat{\xi }=\widehat{Y}-{\widehat{X}}^{\prime }{\beta }_{\tau })\hfill \\ & =A_n^{-1}{B}_n,\hfill \end{array}$$

where

$$A_n={\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}{\widehat{X}}^{\prime }}{n}}\mathrm{and}{B}_n={\displaystyle \frac{\widehat{X}{\mathrm{\Gamma }}^{(h-1)}\widehat{\xi }-\widehat{X}\mathrm{\Theta }}{\sqrt{n}}}.$$

Under (C1) and using the ergodic theorem, we find that:

$$A_n\underset{n\to +\infty }{\stackrel{a.s}{⟶}}W.$$

Furthermore, using the martingale central limit theorem of Billingsley [26] and (C2), we find that:

$$B_n\stackrel{d}{⟶}\mathcal{N}(0,T).$$

Finally, we have:

$$\sqrt{n}({\widehat{{\beta }_{\tau }}}^{\left(h\right)}-{\beta }_{\tau })=A_n^{-1}{B}_n\underset{n\to +\infty }{⟶}\mathcal{N}(0,W^{-1}TW).$$

□

To obtain the asymptotic convergence of the EM estimator of $\mathrm{\Phi }$, let:

$${\left(G_t\right)}_{p\times p},{\left(G_t\right)}_{i,j}=P\left(L\right)(y_{t-i}-x_{t-i}^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)})P\left(L\right)(y_{t-j}-x_{t-j}^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)})$$

and

$$H_t={(P\left(L\right)(y_{t-1}-x_{t-1}^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)}),\dots ,P\left(L\right)(y_{t-p}-x_{t-p}^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)}))}^{\prime },$$

and consider the conditions

C3:

$G:=E\left({\mu }_1^{\left(h\right)}{\widehat{G}}_1\right)<\infty$

C4:

$H:=E\left(({\mu }_1^{\left(h\right)}({\widehat{y}}_1-{\widehat{x}}_1^{\prime }{\widehat{{\beta }_{\tau }}}^{\left(h\right)})-\theta ){\widehat{H}}_1\right)<\infty$.

As well as conditions (C1) and (C2), we will use condition (C3) to apply the ergodic theorem and condition(C4) for the martingale central limit theorem of Billingsley [26]. Thus, we have the following theorem:

Theorem 2.

Let ${\widehat{\mathrm{\Phi }}}^{\left(h\right)}$ the EM estimator of Φ. Under (C3) and (C4), we have:

$$\sqrt{n}({\widehat{\mathrm{\Phi }}}^{\left(h\right)}-\mathrm{\Phi })\underset{n\to +\infty }{⟶}\mathcal{N}(0,G^{-1}HG).$$

(21)

Proof. 

Note that $\widehat{\xi }=\widehat{J}-\widehat{E}\mathrm{\Phi }$, we have:

$\begin{array}{cc}\hfill \sqrt{n}({\widehat{\mathrm{\Phi }}}^{\left(h\right)}-\mathrm{\Phi })& ={\left({\displaystyle \frac{{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{E}}{n}}\right)}^{-1}\left({\displaystyle \frac{{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{J}-{\widehat{E}}^{\prime }\mathrm{\Theta }}{\sqrt{n}}}\right)-\sqrt{n}\mathrm{\Phi }\hfill \\ & ={\left({\displaystyle \frac{{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{E}}{n}}\right)}^{-1}\left({\displaystyle \frac{{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{J}-{\widehat{E}}^{\prime }\mathrm{\Theta }-{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{E}\mathrm{\Phi }}{\sqrt{n}}}\right)\hfill \\ & ={\left({\displaystyle \frac{{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{E}}{n}}\right)}^{-1}\left({\displaystyle \frac{{\widehat{E}}^{\prime }{\mathrm{\Gamma }}^{\left(h\right)}\widehat{\xi }-{\widehat{E}}^{\prime }\mathrm{\Theta }}{\sqrt{n}}}\right)\hfill \\ & =C_n^{-1}{D}_n.\hfill \end{array}$

Similarly to Proof 1, we found that:

$$\sqrt{n}({\widehat{\mathrm{\Phi }}}^{\left(h\right)}-\mathrm{\Phi })=C_n^{-1}{D}_n\underset{n\to +\infty }{⟶}\mathcal{N}(0,G^{-1}HG).$$

□

4. Simulation

In this section, we present a simulation study in order to illustrate the performance of our proposed estimation procedure of $\vartheta ={({\beta }_{\tau }^{\prime },{\mathrm{\Phi }}^{\prime },\sigma )}^{\prime }$ under different scenarios. This study was performed based on the QR model with GARMA errors, designed with two covariates each measuring n samples. The response variable, $y_t$, is generated from the following equation:

$$y_t=x_t^{\prime }\beta +{ϵ}_t={\beta }_1{x}_{t,1}+{\beta }_2{x}_{t,2}+{ϵ}_t,\mathit{t}=\mathit{1},\mathit{2},\dots ,\mathit{n}\mathit{with}(1-\varphi L){(1-2\eta L+L^2)}^d{ϵ}_t={\xi }_t.$$

The simulation scenario considers the following setting:

The sample size (n) is fixed at $n=50$, $n=100$, and $n=200$ and combinations of the vector of the true values for the parameters stated as $\eta =-0.9$, $d=-0.4$, $\varphi =-0.5$, $\beta ={({\beta }_1,{\beta }_2)}^{\prime }={(3,2)}^{\prime }$$\sigma =1$, including different degrees of asymmetry considered by choosing $\tau =0.25$, $0.5$, and $0.75$ as the quantile points for estimation, with 500 Monte Carlo replications for each n.

The covariate values for $x_t={(x_{t,1},x_{t,2})}^{\prime }$, $t=1,2,\dots ,n$ are i.i.d random vectors generated from the standard normal distribution. The data for the error term, ${ϵ}_t$, are also generated by taking the different distributions, density-Gaussian, $\mathcal{N}(0,1)$, density function for Student distribution with $k=3$ degrees of freedom ($t_3$), and the density function for the skewed t distribution with $k=5$ degrees of freedom ($s{t}_5$). The performance and recovery of the estimators are assessed by the bias and Root Mean Square Error (RMSE) to ensure that the parameters estimated have small bias and small variance, which are stated, respectively, by:

$$RMSE=\sqrt{E\left({({\beta }_{\tau }-{\widehat{{\beta }_{\tau }}}^{\left(h\right)})}^2\right)}$$

and

$$Bias\left({\widehat{{\beta }_{\tau }}}^{\left(h\right)}\right)=E\left({\widehat{{\beta }_{\tau }}}^{\left(h\right)}\right)-{\beta }_{\tau },$$

where ${\beta }_{\tau }$ and ${\widehat{{\beta }_{\tau }}}^{\left(h\right)}$ are the true parameter value and its respective $h-th$ maximum-likelihood estimate using the EM algorithm. The Monte Carlo simulation experiments were performed using the R software (version 4.4.1); see www.r-project.org, accessed on 31 October 2023.

The results derived from simulation studies are presented in

Table 1. The estimation results for the Standard Normal distribution (out of 500 replications).

Parameter	$\mathit{\tau }$		n = 50	n = 100	n = 200
${\beta }_1$	$0.25$	Bias	0.094	0.029	0.021
		RMSE	0.341	0.233	0.087
	$0.5$	Bias	0.149	0.052	−0.014
		RMSE	0.242	0.225	0.104
	$0.75$	Bias	−0.071	−0.023	−0.016
		RMSE	0.328	0.291	0.124
${\beta }_2$	$0.25$	Bias	0.121	−0.083	−0.030
		RMSE	0.317	0.226	0.136
	$0.5$	Bias	−0.131	0.065	−0.017
		RMSE	0.342	0.225	0.085
	$0.75$	Bias	0.113	0.005	0.002
		RMSE	0.317	0.203	0.139
$\varphi$	$0.25$	Bias	0.132	0.095	0.074
		RMSE	0.344	0.222	0.176
	$0.5$	Bias	0.092	0.015	0.012
		RMSE	0.324	0.175	0.109
	$0.75$	Bias	−0.070	−0.067	0.036
		RMSE	0.330	0.212	0.154

,

Table 2. The estimation results for the Student ($t_3$) distribution (out of 500 replications).

Parameter	$\mathit{\tau }$		n = 50	n = 100	n = 200
${\beta }_1$	$0.25$	Bias	0.0692	0.034	−0.012
		RMSE	0.361	0.257	0.155
	$0.5$	Bias	0.095	0.027	0.017
		RMSE	0.238	0.164	0.080
	$0.75$	Bias	0.095	-0.083	0.049
		RMSE	0.330	0.215	0.085
${\beta }_2$	$0.25$	Bias	0.057	0.041	−0.002
		RMSE	0.290	0.133	0.062
	$0.5$	Bias	0.065	0.038	0.025
		RMSE	0.337	0.237	0.174
	$0.75$	Bias	0.088	0.040	0.039
		RMSE	0.299	0.215	0.088
$\varphi$	$0.25$	Bias	0.125	−0.043	0.038
		RMSE	0.245	0.134	0.094
	$0.5$	Bias	0.067	0.053	0.025
		RMSE	0.283	0.192	0.085
	$0.75$	Bias	0.104	−0.033	0.001
		RMSE	0.269	0.136	0.062

and

Table 3. The estimation results for the Skew Student ($s{t}_5$) distribution (out of 500 replications).

Parameter	$\mathit{\tau }$		n = 50	n = 100	n = 200
${\beta }_1$	$0.25$	Bias	0.0822	0.049	−0.011
		RMSE	0.327	0.287	0.124
	$0.5$	Bias	0.086	-0.068	0.050
		RMSE	0.271	0.184	0.097
	$0.75$	Bias	0.083	0.069	−0.040
		RMSE	0.332	0.269	0.113
${\beta }_2$	$0.25$	Bias	0.109	0.034	−0.007
		RMSE	0.359	0.213	0.096
	$0.5$	Bias	0.091	0.075	0.020
		RMSE	0.334	0.280	0.137
	$0.75$	Bias	−0.017	0.040	−0.007
		RMSE	0.292	0.169	0.085
$\varphi$	$0.25$	Bias	−0.113	−0.063	0.020
		RMSE	0.310	0.193	0.100
	$0.5$	Bias	0.098	0.032	−0.025
		RMSE	0.231	0.182	0.086
	$0.75$	Bias	0.109	0.071	−0.052
		RMSE	0.325	0.223	0.090

. A look at the results in all these tables allows us to conclude that, as expected, in general, as the sample size increases, the bias and RMSE of the estimators decrease for all values of quantile points ($\tau$) considered. Moreover, $\widehat{{\beta }_1}$, $\widehat{{\beta }_2}$, and $\widehat{\varphi }$ all seem to be consistent and asymptotically normally distributed.

5. Real Data Example

In this work, to evaluate our proposed quantile-regression model with GARMA errors formulated in this paper, we used a dataset called Engel (Engel food expenditure data), sourced from the R package quantreg. Koenker and Bassett [27] utilized this dataset to exemplify the application of quantile regression in R using authentic, real-world data.

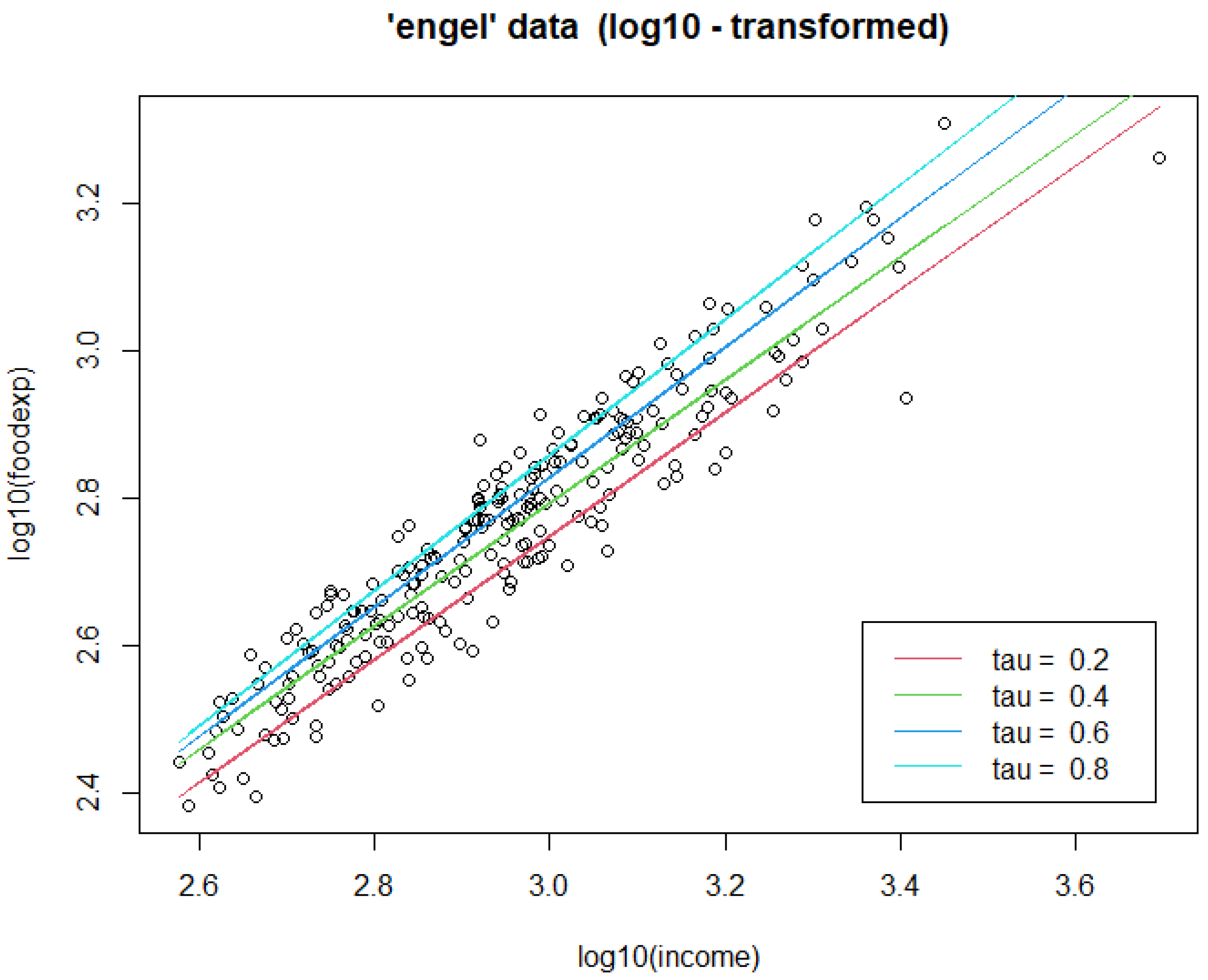
In Figure 1, displayed below, Koenker and Bassett show the scatter plot of the original data on double log axes. Fitted regression quartile lines are superimposed on the same figure. The estimated slope parameters (Engel elasticities), 0.8358, 0.8326, 0.8780, and 0.9170, for the quartiles corresponding to the 20th, 40th, 60th, and 80th percentiles, respectively. It is interesting to note in this example that the fitted quartile lines indicate an increasing conditional scale effect.

To investigate the influence of the GARMA error model’s “significance” in quantile-regression models, we suggest the following approach with the GARMA errors expressed as:

$$y_t=\beta +x_{1,t}{\beta }_1+{ϵ}_t,\mathit{t}=\mathit{1},\mathit{2},\dots ,\mathit{n},$$

with

$$(1-{\varphi }_{1}L-{\varphi }_2{L}^2){(1-2\eta L+L^2)}^d{ϵ}_t={\xi }_t,$$

where:

• $y_t$ is the food expenditure of observation t;
• $x_{1,t}$ is the income of observation t;
• $d=0.35$ and $\eta =-0.8.$

Our methodology commences by estimating the parameters $\beta$, ${\beta }_1$, ${\varphi }_1$, and ${\varphi }_2$ at the quartiles 0.2, 0.4, 0.6, and 0.8 via our method described in Section 2 with the R software (version 4.4.1).

Table 4. Estimated parameters for Engel data with expectation-maximization algorithm.

Estimate		0.2	0.4	0.6	0.8
	τ
Intercept		96.35	94.8	86.94	76.60
Income		0.58	0.59	0.62	0.63
${\varphi }_1$		−0.35	−0.27	−0.22	−0.23
${\varphi }_2$		−0.09	−0.12	−0.14	−0.06
Prediction for observation 235		721.6	723.27	736.9	744.35

shows the estimated coefficients (Estimate) and the corresponding predictions at four quantile levels, $\tau :0.2,0.4,0.6$, and $0.8$.

Upon examination of Table 4, the estimates associated with the covariate “income” consistently escalate as $\tau$ increases, in accordance with our expectations. Moreover, the values of prediction are close to the true value, which is $750.32$, and tend to increase as $\tau$ increases, as expected.

This closeness to the true value not only validates the efficacy of our method but also underscores its reliability in making accurate predictions. Moreover, akin to the estimates, the predicted values also manifest a tendency to increase with escalating $\tau$, a phenomenon that aligns seamlessly with our anticipated behavior of the model.

6. Conclusions

In this article, we have used the maximum-likelihood estimation method and the EM algorithm to estimate the unknown parameters of the quantile regression model with Generalized Autoregressive Moving Average error. To asses the performance of our estimators, we conducted a simulation study. The results were promising, demonstrating that our parameter estimates closely approximate the true values. Additionally, we provide a practical illustration using real data.