Numerical Simulation of the Interaction between a Planar Shock Wave and a Cylindrical Bubble
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Level Set Coupled with Volume of Fluid
2.3. Spatial and Temporal Discretisation
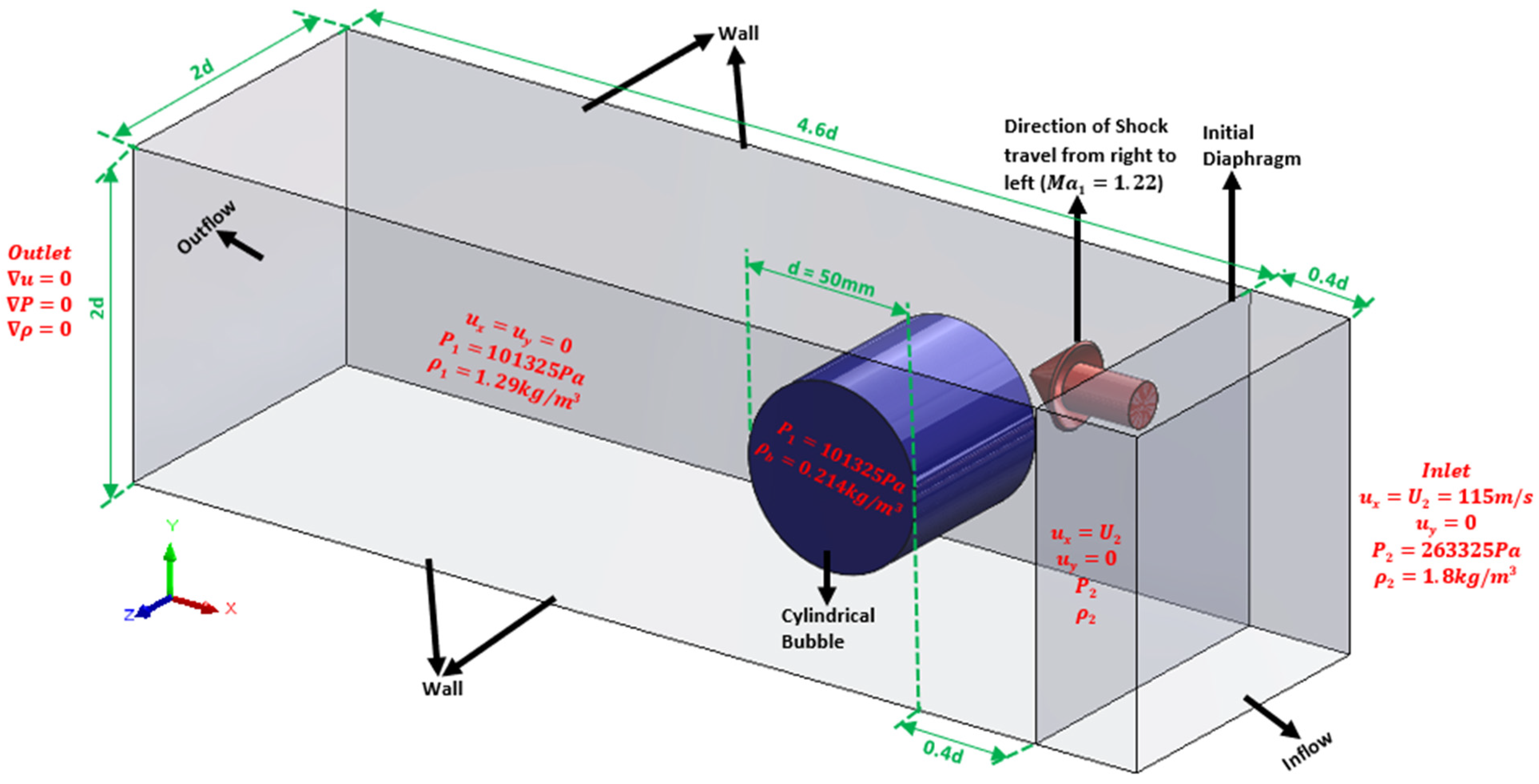
2.4. Computational Details
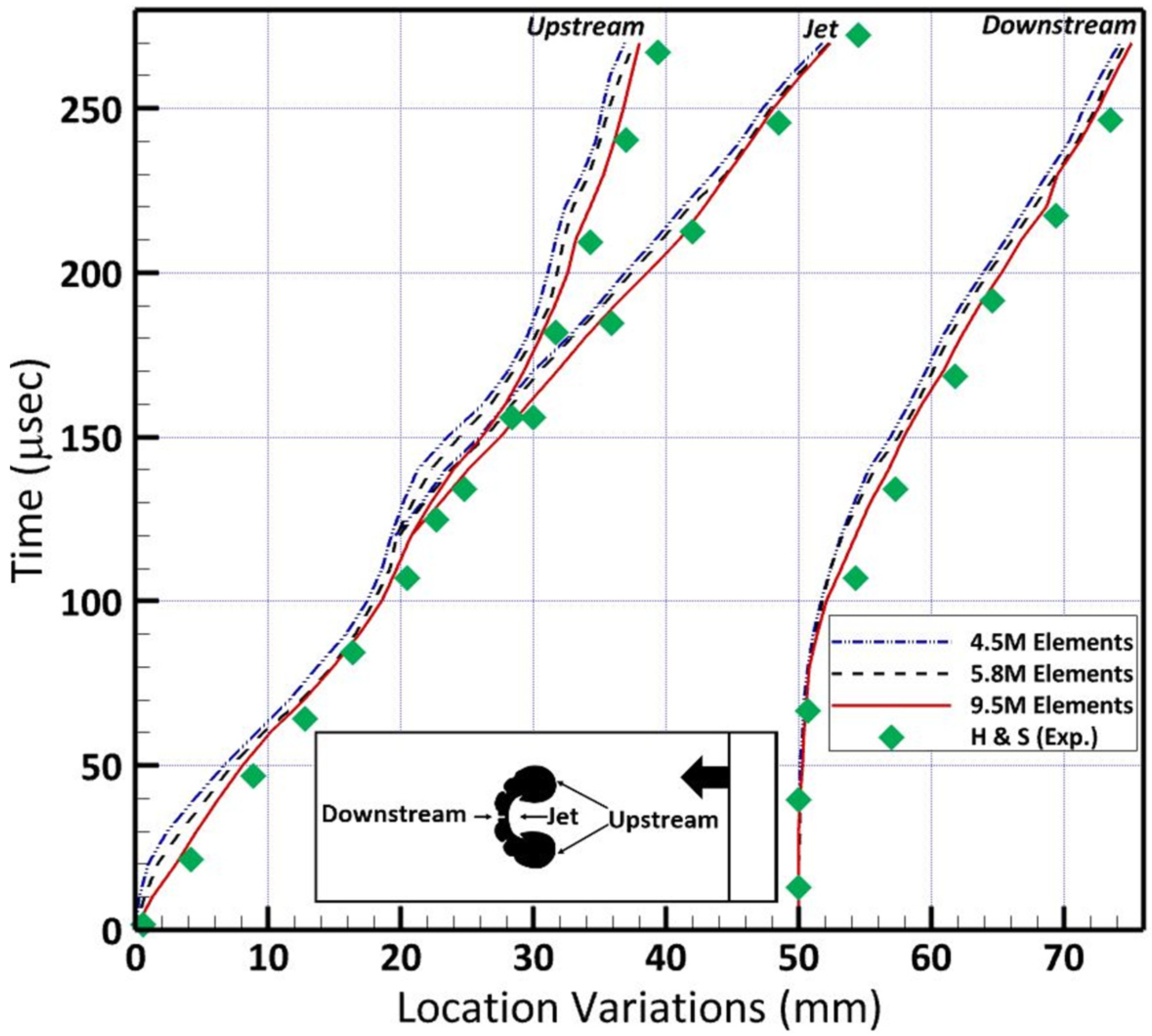
2.5. Mesh Independence Study
2.6. Turbulence Model Selection
3. Results
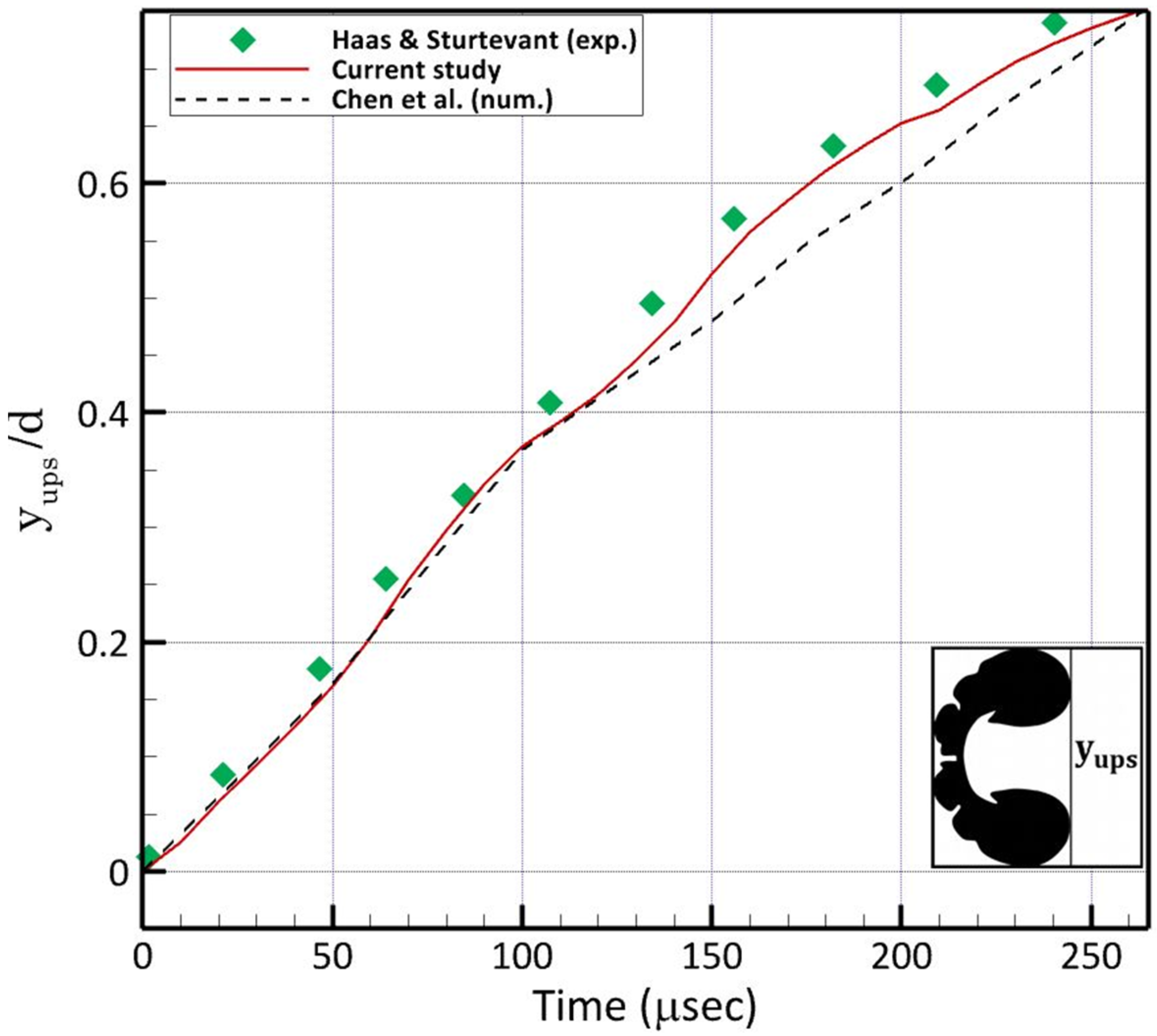
3.1. Comparison between the Measured and Predicted Velocities
3.2. Air Displacement, Bubble Acceleration, and Vortex Formation
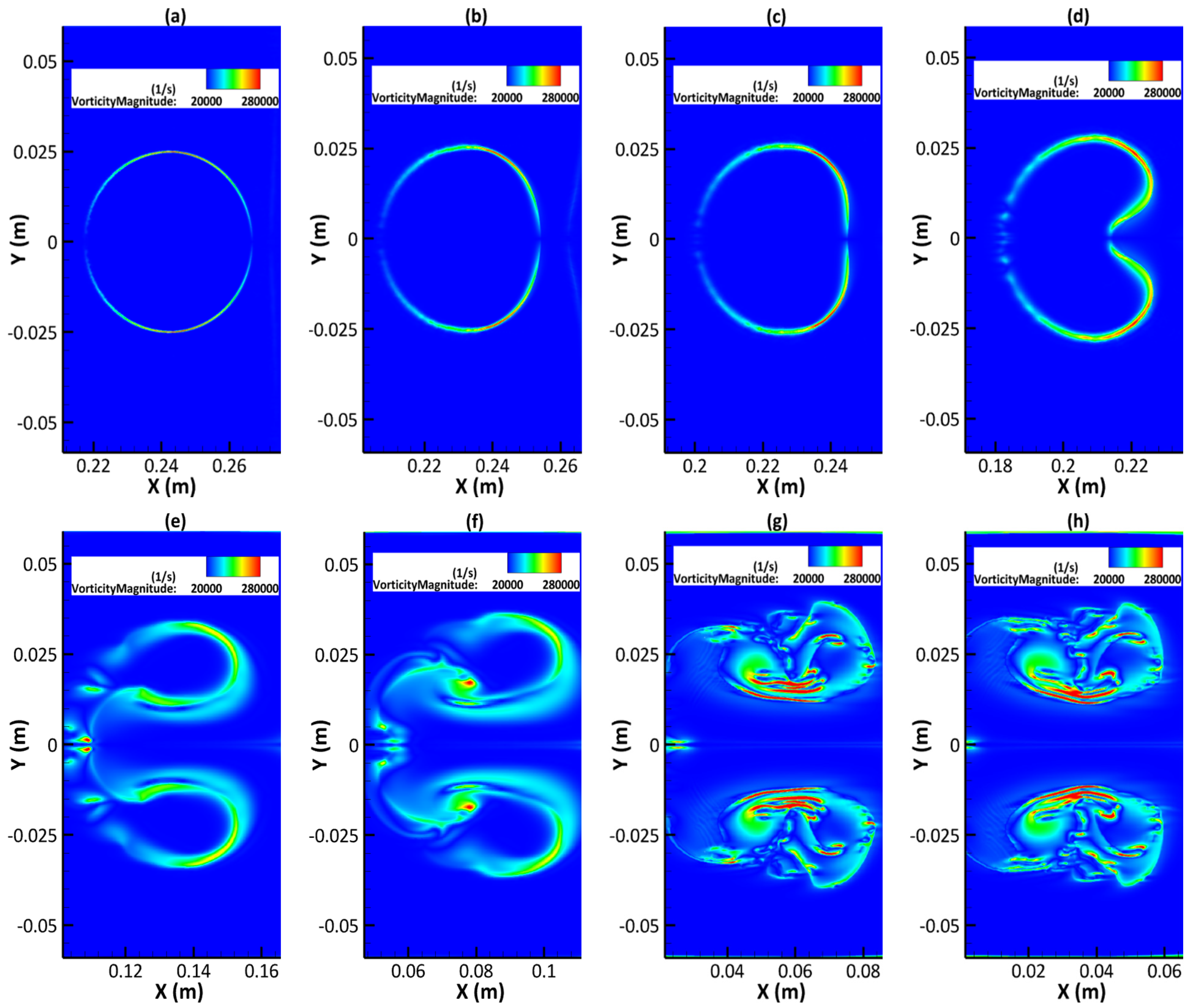
3.3. Distortion and Evolution of the Interface
3.4. Shock–Bubble Interaction Process on a 2D Plane
3.5. Vorticity Generation
3.6. Shock–Bubble Interaction Process in 3D
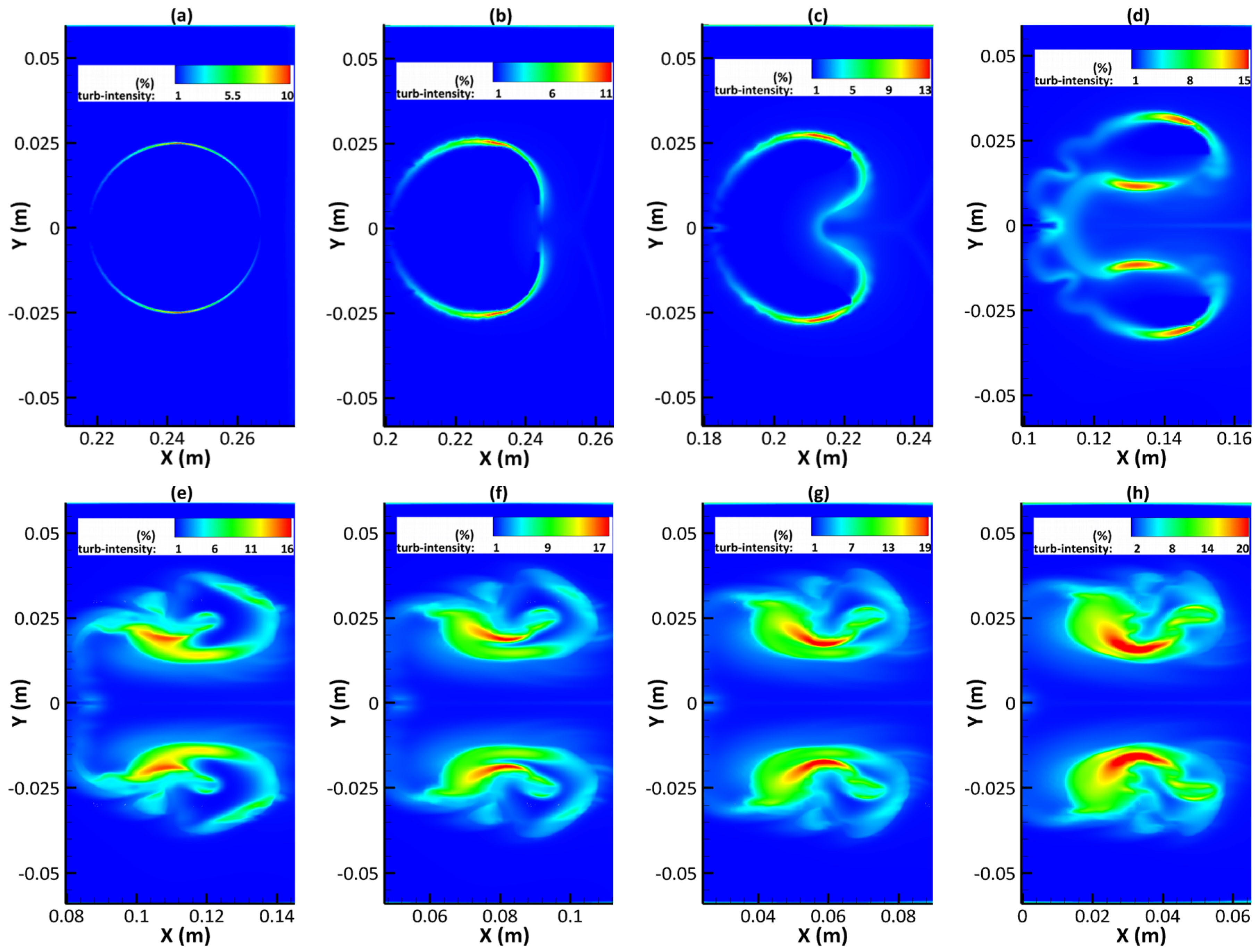
3.7. Turbulence Generation and Development
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols and Acronyms
| A | Atwood number |
| d | Bubble diameter (mm) |
| P | Pressure (Pa) |
| ρ | Density (kg/m3) |
| α | Volume fraction |
| UNDb | Non-dimensional bubble velocity |
| UNDv | Non-dimensional vortex velocity |
| ux | Velocity in the horizontal direction (m/s) |
| uy | Velocity in the vertical direction (m/s) |
| uAJ | Velocity of air-jet head (m/s) |
| uI | Velocity of incident shock wave (m/s) |
| uIU | Velocity of initial upstream interface (m/s) |
| uID | Velocity of initial downstream interface (m/s) |
| uFU | Velocity of final upstream interface (m/s) |
| uR | Velocity of refracted wave (m/s) |
| uT | Velocity of transmitted wave (m/s) |
| uIU | Velocity of initial upstream interface (m/s) |
| AMP | Adaptive mesh refinement |
| CFD | Computational fluid dynamics |
| DNS | Direct numerical simulation |
| FVM | Finite volume method |
| LE | Level set |
| LES | Large-eddy simulation |
| LSVOF | Level set coupled with volume of fluids |
| Ma | Mach number |
| MUSCL | Monotone upstream-centered schemes for conservation laws |
| SBI | Shock–bubble interaction |
| URANS | Unsteady Reynolds-averaged Navier–Stokes |
| VOF | Volume of fluids |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| aj | Air-jet |
| de | Downstream interface |
| hbs | Helium bridge structure |
| iw | Incident shock wave |
| pts | Primary transmitted wave |
| rfw | Reflected wave |
| rs | Refracted wave |
| t | Non-dimensional time |
| ue | Upstream interface |
| vf | Vortex filament |
References
- Niederhaus, J.H.J.; Greenough, J.A.; Oakley, J.G.; Ranjan, D.; Anderson, M.H.; Bonazza, R. A computational parameter study for the three-dimensional shock-bubble interaction. J. Fluid Mech. 2008, 594, 85–124. [Google Scholar] [CrossRef]
- Layes, G.; Jourdan, G.; Houas, L. Distortion of a spherical gaseous interface accelerated by a plane shock wave. Phys. Rev. Lett. 2003, 91, 174502. [Google Scholar] [CrossRef] [PubMed]
- Layes, G.; Jourdan, G.; Houas, L. Experimental investigation of the shock wave interaction with a spherical gas inhomogeneity. Phys. Fluids 2005, 17, 028103. [Google Scholar] [CrossRef]
- Layes, G.; Le Metayer, O. Quantitative numerical and experimental studies of the shock accelerated heterogenous bubbles motion. Phys. Fluids 2007, 19, 042105. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Zeng, S.M. Shock cavity implosion morphologies and vortical projectile generation in axisymmetric shock-spherical fast/slow bubble interactions. J. Fluid Mech. 1998, 362, 327–346. [Google Scholar] [CrossRef]
- Haas, J.F.L.; Sturtevant, B. Interaction of weak shock waves with cylindrical and spherical inhomogeneities. J. Fluid Mech. 1987, 181, 41–76. [Google Scholar] [CrossRef]
- Jacobs, J.W. Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 1992, 234, 629–649. [Google Scholar] [CrossRef]
- Jacobs, J.W. The dynamics of shock accelerated light and heavy gas cylinders. Phys. Fluids 1993, A5, 2239–2247. [Google Scholar] [CrossRef]
- Marquina, A.; Mulet, P. A flux-split algorithm applied to conservative models for multicomponent compressible flows. J. Comput. Phys. 2003, 185, 120–138. [Google Scholar] [CrossRef]
- Henderson, L.F. On the refraction of shock waves. J. Fluid Mech. 1989, 198, 365–386. [Google Scholar] [CrossRef]
- Henderson, L.F.; Colella, P.; Puckett, E.G. On the refraction of shock waves at a slow-fast gas interface. J. Fluid Mech. 1991, 224, 1–27. [Google Scholar] [CrossRef]
- Rudinger, G.; Somers, L.M. Behavior of small regions of different gases carried in accelerated gas flows. J. Fluid Mech. 1960, 7, 161–176. [Google Scholar] [CrossRef]
- Ding, J.; Si, T.; Chen, M.; Zhai, Z.; Lu, X.; Luo, X. On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 2017, 828, 289–317. [Google Scholar] [CrossRef]
- Picone, J.M.; Boris, J.P. Vorticity generation by shock propagation through bubbles in a gas. J. Fluid Mech. 1988, 189, 23–51. [Google Scholar] [CrossRef]
- Quirk, J.J.; Karni, S. On the dynamics of a shock–bubble interaction. J. Fluid Mech. 1996, 318, 129–163. [Google Scholar] [CrossRef]
- Bagabir, A.; Drikakis, D. Mach number effects on shock-bubble interaction. Shock Waves 2001, 11, 209–218. [Google Scholar] [CrossRef]
- Taniguchi, N.; Furuhata, R.; Sou, A.; Abe, A. Numerical simulation of shock wave bubble interaction for ballast water treatment. In Proceedings of the 3rd International Symposium of Maritime Sciences, Kobe, Japan, 10–14 November 2014. [Google Scholar]
- Hayashi, K.; Sou, A.; Tomiyama, A. A volume tracking method based on non-uniform subcells and continuum surface force model using a local level set function. Comput. Fluid. Dyn. J. 2006, 15, 95–101. [Google Scholar]
- Yee, H.C.; Warming, R.F.; Harten, A. Implicit total variation diminishing (TVD) schemes for steady-state calculations. J. Comput. Phys. 1985, 57, 327–360. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, B.; Chen, H.; Zhang, B.; Liu, H. Scaling vortex breakdown mechanism based on viscous effect in shock cylindrical bubble interaction. Phys. Fluids 2018, 30, 126103. [Google Scholar] [CrossRef]
- Chen, J.; Qu, F.; Wu, X.; Wang, Z.; Bai, J. Numerical study of interactions between shock waves and a circular or elliptic bubble in air medium. Phys. Fluids 2021, 33, 043301. [Google Scholar] [CrossRef]
- Singh, S.; Battiano, M.; Myong, R.S. Impact of bulk viscosity on flow morphology of shock accelerated cylindrical light bubble in diatomic and polyatomic gases. Phys. Fluids 2021, 33, 066103. [Google Scholar] [CrossRef]
- Onwuegbu, S.; Yang, Z. Numerical analysis of shock interaction with a spherical bubble. AIP Adv. 2022, 12, 025215. [Google Scholar] [CrossRef]
- Shyue, K.M. An efficient shock-capturing algorithm for compressible multicomponent problems. J. Comput. Phys. 1998, 142, 208–242. [Google Scholar] [CrossRef]
- Serthian, J.A.; Smereka, P. Level set methods for fluid interfaces. Ann. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G.; Zahedi, S. A Conservative Level Set Method for Two Phase Flow II. J. Comput. Phys. 2007, 225, 785–807. [Google Scholar] [CrossRef]
- Van Leer, B. Toward the Ultimate Conservative Difference Scheme. V. A Second Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Holleman, R.; Fringer, O.; Stacey, M. Numerical diffusion for flow-aligned unstructured grids with application to estuarine modelling. Int. J. Numer. Methods Fluids 2013, 72, 1117–1145. [Google Scholar] [CrossRef]
- Zubair, M.; Abdullah, M.Z.; Ahmad, K.A. Hybrid mesh for nasal airflow studies. Comput. Math. Methods Med. 2013, 2013, 727362. [Google Scholar] [CrossRef] [PubMed]
- Ingram, D.M.; Causon, D.M.; Mingham, C.G. Developments in Cartesian cut cell methods, Math. Comput. Simul. 2013, 61, 561–572. [Google Scholar] [CrossRef]
- Johnson, M.W. A novel Cartesian CFD cut cell approach. Comput. Fluids 2013, 79, 105–119. [Google Scholar] [CrossRef]
- Taylor, G.I. Formation of a vortex ring by giving an impulse to a circular disk and then dissolving it away. J. Appl. Phys. 1953, 24, 104–105. [Google Scholar] [CrossRef]







| Bubble Gas | Helium |
|---|---|
| Ambient gas | Air |
| Ma number | 1.22 |
| Atwood number | −0.715 |
| Experimental Data | Current Study | |
|---|---|---|
| 410 | 403.3 | |
| 900 | 894.6 | |
| 393 | 388.8 | |
| 170 | 166.5 | |
| 113 | 110 | |
| 145 | 141.3 | |
| 230 | 2226.7 | |
| 128 | 122.2 |
| Theoretical Values | Experimental Data | Current Study | |
|---|---|---|---|
| 1.692 | 1.37 | 1.345 | |
| 1.14 | 1.12 | 1.068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onwuegbu, S.; Yang, Z.; Xie, J. Numerical Simulation of the Interaction between a Planar Shock Wave and a Cylindrical Bubble. Modelling 2024, 5, 483-501. https://doi.org/10.3390/modelling5020026
Onwuegbu S, Yang Z, Xie J. Numerical Simulation of the Interaction between a Planar Shock Wave and a Cylindrical Bubble. Modelling. 2024; 5(2):483-501. https://doi.org/10.3390/modelling5020026
Chicago/Turabian StyleOnwuegbu, Solomon, Zhiyin Yang, and Jianfei Xie. 2024. "Numerical Simulation of the Interaction between a Planar Shock Wave and a Cylindrical Bubble" Modelling 5, no. 2: 483-501. https://doi.org/10.3390/modelling5020026
APA StyleOnwuegbu, S., Yang, Z., & Xie, J. (2024). Numerical Simulation of the Interaction between a Planar Shock Wave and a Cylindrical Bubble. Modelling, 5(2), 483-501. https://doi.org/10.3390/modelling5020026






