On Mechanical and Chaotic Problem Modeling and Numerical Simulation Using Electric Networks
Abstract
1. Introduction
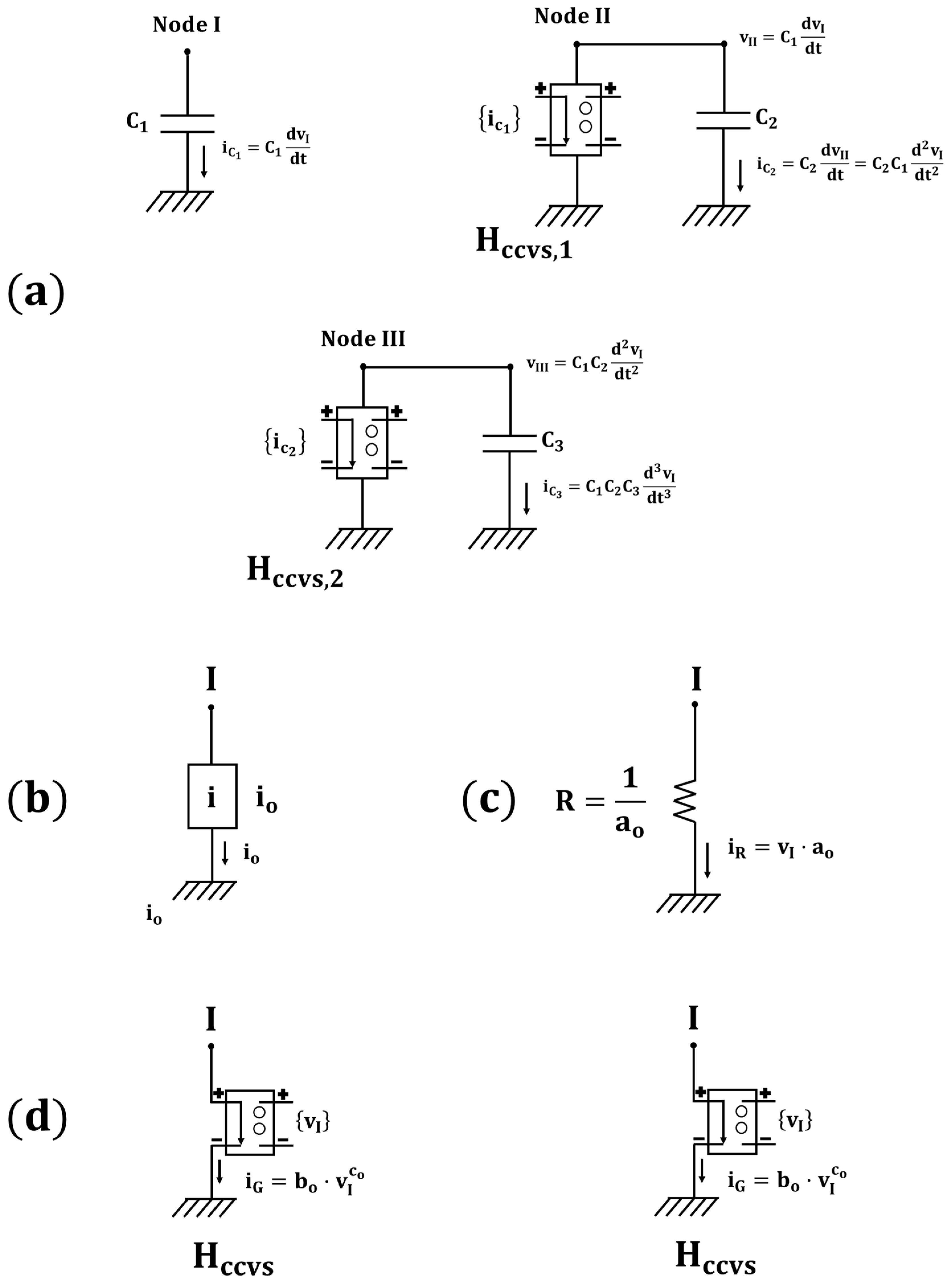
2. Design of the Network Models—The Electrical Components of the Model
2.1. Basic Circuits
2.2. Text Files
3. Applications and Simulation
3.1. Mass Falling in Air or Viscous Fluid
- *Solution of ordinary differential equations
- *Governing equation: m × g − (γ) × () − m × a = 0.
- G1 I 0 VALUE = {m × g}
- Gcccs,3 I 0 VALUE = {γ × }
- Gcccs,2 0 I VALUE = {m × a}
- Gvccs,1 II 0 VALUE = {V(I)}
- C1 II 0 1
- Gcccs,1 III 0 VALUE = {iC1}
- C2 III 0 1
- Vtime 100 0 PWL(0,0 500,500)
- .TRAN 1 s 1.5 s 0 UIC
- .END
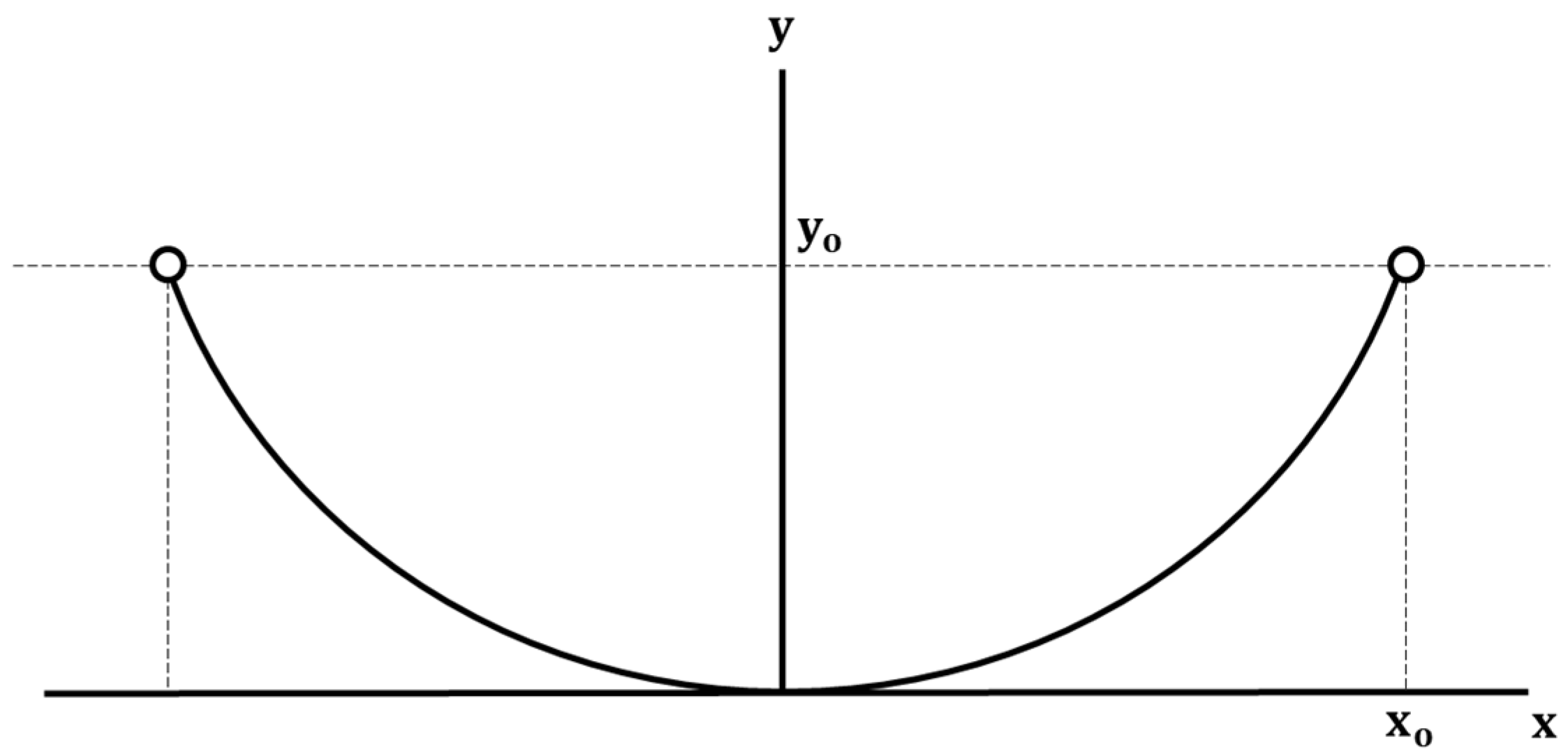
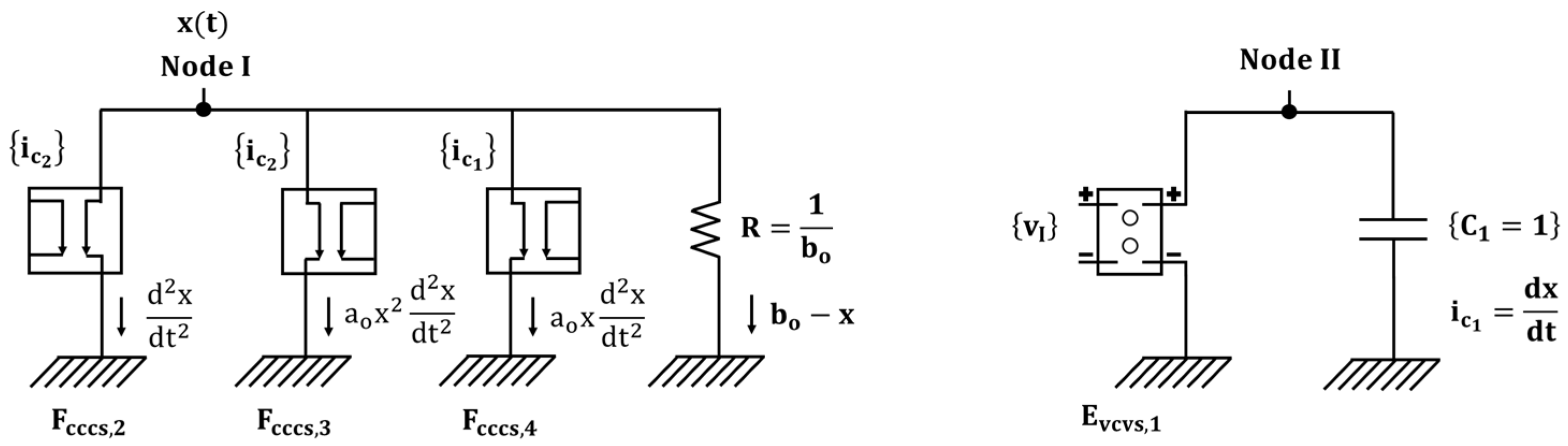
3.2. Crimped Bead Sliding on a Parabolic Shaped Wire
- *Solution of ordinary differential equations
- *Governing equation:
- Gcccs,2 I 0 VALUE = {}
- Gcccs,3 I 0 VALUE = {}
- Gcccs,4 I 0 VALUE = {}
- R 1 0 bo−1
- Gvcvs,1 II 0 VALUE = {V(I)}
- C1 II 0 1
- Gvccs,1 III 0 VALUE = {iC1}
- C2 III 0 1
- .TRAN 1 s 50 s 0 UIC
- .END
3.3. The van der Pol Oscillator
4. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| acceleration (m2/s) | |
| constants | |
| capacitor | |
| constant current generator | |
| voltage controlled voltage source | |
| voltage controlled current source | |
| current controlled voltage source | |
| current controlled current source | |
| force (Newtons) | |
| gravitational acceleration (m2/s) | |
| current through a capacitor | |
| out current of a constant current generator () | |
| input current of a current controlled source | |
| output current of a controlled current source | |
| current through a resistor | |
| masa (Kg) | |
| weight (Newtons) | |
| resistor | |
| time (s) | |
| velocity (m/s) | |
| constant, initial velocity (m/s) | |
| voltage at the ends of a capacitor | |
| input voltage of a voltage-controlled source | |
| voltage at the ends of a resistor | |
| voltage at the output of a controlled voltage source | |
| solution to the equation (voltage at node I) | |
| spatial coordinates (m) | |
| constant, initial location (m) | |
| constant | |
| τ | period (s) |
| Subscripts | |
| ini | refers to initial values |
| max | refers to maximum values |
| time | refers to time-dependent sources |
| I, II… | nodes of the network model (I: main node) |
| 1, 2, 3 | defines each component of the same type in the network |
References
- Kirchhoff, S. Ueber den Durchgang eines elektrischen Stromes durch eine Ebene, insbesondere durch eine kreisförmige. Ann. Phys. 1845, 140, 497–514. [Google Scholar] [CrossRef]
- Kayan, C.F. An electrical geometrical analogue for complex heat flow. Trans. Am. Soc. Mech. Eng. 1945, 67, 713–716. [Google Scholar] [CrossRef]
- Arvinti, B.; Toader, D.; Vesa, D.; Costache, M. Experimental and Analytical Study of the Electric Potential using Lagrange Polynomials. In Proceedings of the 2020 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 5–6 November 2020; IEEE: New York, NY, USA, 2020. [Google Scholar]
- Paschkis, V.; Heisler, M.P. The Influence of Through-Metal on the Heat Loss From Insulated Walls. Trans. Am. Soc. Mech. Eng. 1944, 66, 653–661. [Google Scholar] [CrossRef]
- Karplus, W.J.; Soroka, W.W. Analog Methods: Computation and Simulation; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Horno, J.; González-Caballero, F.; González-Fernández, C.F. A network thermodynamic method for numerical solution of the Nernst-Planck and Poisson equation system with application to ionic transport through membranes. Eur. Biophys. J. 1990, 17, 307–313. [Google Scholar] [CrossRef] [PubMed]
- López-García, J.J.; Moya, A.A.; Horno, J.; Delgado, A.; González-Caballero, F. A network model of the electrical double layer around a colloid particle. J. Colloid Interface Sci. 1996, 183, 124–130. [Google Scholar] [CrossRef]
- López-García, J.J.; Horno, J.; Delgado, A.V.; González-Caballero, F. Use of a network simulation method for the determination of the response of a colloidal suspension to a constant electric field. J. Phys. Chem. B 1999, 103, 11297–11307. [Google Scholar] [CrossRef][Green Version]
- Chen, M.; Rosendahl, L.A.; Bach, I.; Condra, T.; Pedersen, J.K. Transient behavior study of thermoelectric generators through an electro-thermal model using SPICE. In Proceedings of the 2006 25th International Conference on Thermoelectrics, Vienna, Austria, 6–10 August 2006; IEEE: New York, NY, USA, 2006. [Google Scholar]
- Meca, A.S.; Alhama, F.; Fernandez, C.G. An efficient model for solving density driven groundwater flow problems based on the network simulation method. J. Hydrol. 2007, 339, 39–53. [Google Scholar] [CrossRef]
- Bég, O.A.; Zueco, J.; Bhargava, R.; Takhar, H.S. Magnetohydrodynamic convection flow from a sphere to a non-Darcian porous medium with heat generation or absorption effects: Network simulation. Int. J. Therm. Sci. 2009, 48, 913–921. [Google Scholar] [CrossRef]
- Serna, J.; Velasco, F.J.S.; Meca, A.S. Application of network simulation method to viscous flows: The nanofluid heated lid cavity under pulsating flow. Comput. Fluids 2014, 91, 10–20. [Google Scholar] [CrossRef]
- Cánovas, M.; Alhama, I.; Trigueros, E.; Alhama, F. Numerical simulation of Nusselt-Rayleigh correlation in Bénard cells. A solution based on the network simulation method. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 986–997. [Google Scholar] [CrossRef]
- Cánovas, M.; Alhama, I.; García, G.; Trigueros, E.; Alhama, F. Numerical simulation of density-driven flow and heat transport processes in porous media using the network method. Energies 2017, 10, 1359. [Google Scholar] [CrossRef]
- García-Ros, G.; Alhama, I.; Cánovas, M. An electrical analogy to compute general scenarios of soil consolidation. WSEAS Trans. Circuits Syst. 2017, 16, 131–140. [Google Scholar]
- Rossi, C.; Buccella, P.; Stefanucci, C.; Sallese, J.M. SPICE modeling of photoelectric effects in silicon with generalized devices. IEEE J. Electron Devices Soc. 2018, 6, 987–995. [Google Scholar] [CrossRef]
- Akram, S.; Bertilsson, K.; Siden, J. LTspice electro-thermal model of joule heating in high density polyethylene optical fiber microducts. Electronics 2019, 8, 1453. [Google Scholar] [CrossRef]
- Yaqoob, S.J.; Obed, A.A. Modeling, simulation and implementation of PV system by proteus based on two-diode model. J. Tech. 2019, 1, 39–51. [Google Scholar] [CrossRef]
- Garratón, M.C.; del Carmen García-Onsurbe, M.; Soto-Meca, A. A new Network Simulation Method for the characterization of delay differential equations. Ain Shams Eng. J. 2023, 14, 102066. [Google Scholar] [CrossRef]
- Lineykin, S.; Kuperman, A.; Sitbon, M. Estimation of the power of a thermoelectric harvester for low and ultra-low temperature gradients using a dimensional analysis method. In Proceedings of the 2023 IEEE 17th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Estonia, Tallinn, 14–16 June 2023; pp. 1–6. [Google Scholar]
- Sánchez-Pérez, J.F.; Marín-García, F.; Castro, E.; García-Ros, G.; Conesa, M.; Solano-Ramírez, J. Methodology for Solving Engineering Problems of Burgers–Huxley Coupled with Symmetric Boundary Conditions by Means of the Network Simulation Method. Symmetry 2023, 15, 1740. [Google Scholar] [CrossRef]
- Horno, J. Network Simulation Method; Research Signpost: Trivandrum, India, 2002. [Google Scholar]
- PSPICE. Version 6.0: Microsim Corporation. 20 Fairbanks, Irvine, California 92718. 1994. Available online: https://www.pspice.com (accessed on 23 December 2023).
- Nagel, L.W. SPICE2: A Computer Program to Simulate Semiconductor Circuits; College of Engineering, University of California: Berkeley, CA, USA, 1975. [Google Scholar]
- Wing, O. Classical Circuit Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 773. [Google Scholar]
- Guckenheimer, J. Dynamics of the van der Pol equation. IEEE Trans. Circuits Syst. 1980, 27, 983–989. [Google Scholar] [CrossRef]






| Authors | Year | Model | Problem |
|---|---|---|---|
| Kirchhoff [1] | 1845 | Electrolytic tank | Electrical currents on conductive surfaces |
| Paschkis and Heisler [4] | 1944 | Resistors and capacitors (laboratory) | Heat transfer |
| Kayan [2] | 1945 | Graphite paper | Heat fluxes |
| Karplus and Soroka [5] | 1959 | Resistors and capacitors (laboratory) | Heat and mass transfer |
| Horno et al. [6] | 1990 | Network method (Pspice) | Transport through membranes |
| López-García et al. [7] | 1996 | Network method (Pspice) | Colloidal systems |
| López-García et al. [8] | 1999 | Network method (Pspice) | Thermodynamic colloidal systems |
| Chen et al. [9] | 2006 | Pspice | Heat transfer |
| Meca et al. [10] | 2007 | Network method (Pspice) | Flow and salt transport |
| Bég et al. [11] | 2009 | Network method (Pspice) | Magnetohydrodynamic systems |
| Serna et al. [12] | 2014 | Network method (Pspice) | Lid cavity problem |
| Cánovas et al. [13] | 2015 | Network method (Pspice) | Flow and heat transport |
| Cánovas et al. [14] | 2017 | Network method (Pspice) | Density driven flow |
| García-Ros et al. [15] | 2017 | Network method (Pspice) | Soil consolidation systems |
| Rossi et al. [16] | 2018 | Network models | Semiconductors |
| Akram et al. [17] | 2019 | Network models (LTspice) | Thermal heating |
| Yaqoob and Obed [18] | 2019 | Semiconductor networks (Proteus) | Photovoltaic |
| Arvinti et al. [3] | 2020 | Electrical resistors (laboratory) | Electrostatic |
| Garratón et al. [19] | 2023 | Network models (Pspice) | Delay differential equations |
| Lineykin et al. [20] | 2023 | Electric analogy | Thermoelectric harvest equipment |
| Sánchez-Pérez et al. [21] | 2023 | Network method (Ngspice) | Burgers-Huxley problems |
| Component | Symbol | Constitutive Equation |
|---|---|---|
| Resistor | 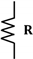 | |
| Capacitor |  | |
| Constant voltage source |  | |
| Constant current source | 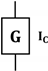 | |
| Voltage-controlled voltage-source |  | |
| Voltage-controlled current-source |  | |
| Current-controlled voltage-source | 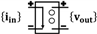 | |
| Current-controlled current-source |  |
| Component | Sentence | |||
|---|---|---|---|---|
| Symbol | Connection Nodes | Value | ||
| Input | Output | |||
| Resistor | ||||
| Capacitor | ||||
| Constant voltage source | ||||
| Constant current source | ||||
| Voltage-controlled voltage-source | ||||
| Voltage-controlled current-source | ||||
| Current-controlled voltage-source | ||||
| Current-controlled current-source | ||||
| 4.00 | 4.00 | 4.00 | 1.00 | 2.00 | 3.00 | |
| 1.00 | 2.00 | 3.00 | 1.00 | 1.00 | 1.00 | |
| (m) | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 |
| (m) | 100.00 | 100.00 | 100.00 | 25.00 | 50.00 | 75.00 |
| (m·s−1) | 22.53 | 31.77 | 39.00 | 22.53 | 22.53 | 22.53 |
| τ (s) | 8.15 | 6.48 | 5.28 | 4.76 | 6.57 | 7.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aráez, P.; Jiménez-Valera, J.A.; Alhama, I. On Mechanical and Chaotic Problem Modeling and Numerical Simulation Using Electric Networks. Modelling 2024, 5, 410-423. https://doi.org/10.3390/modelling5020022
Aráez P, Jiménez-Valera JA, Alhama I. On Mechanical and Chaotic Problem Modeling and Numerical Simulation Using Electric Networks. Modelling. 2024; 5(2):410-423. https://doi.org/10.3390/modelling5020022
Chicago/Turabian StyleAráez, Pedro, José Antonio Jiménez-Valera, and Iván Alhama. 2024. "On Mechanical and Chaotic Problem Modeling and Numerical Simulation Using Electric Networks" Modelling 5, no. 2: 410-423. https://doi.org/10.3390/modelling5020022
APA StyleAráez, P., Jiménez-Valera, J. A., & Alhama, I. (2024). On Mechanical and Chaotic Problem Modeling and Numerical Simulation Using Electric Networks. Modelling, 5(2), 410-423. https://doi.org/10.3390/modelling5020022






