Using Discrete-Event Simulation to Balance Staff Allocation and Patient Flow between Clinic and Surgery

Abstract

We consider the problem of system-level balanced scheduling in a pediatric hospital setting. A hospital clinic has a queue for patients needing care. After being seen in clinic, many require follow-up surgery, for which they also wait in a queue. The rate-limiting factor is physician availability for both clinic visits and surgical cases. Although much existing work has been done to optimize clinic appointments, as well as to optimize surgical appointments, this novel approach models the entire patient journey at the system level, through both clinic and surgery, to optimize the total patient experience. A discrete-event simulation model of the system was built based on historic patient encounter data and validated. The system model was then optimized to determine the best allocation of physician resources across the system to minimize total patient wait time using machine learning. The results were then compared to baseline.

1. Introduction and Background

1.1. Statement of the Problem

This study proposes a novel discrete event simulation model to study physician allocation between clinic and surgery to minimize patient wait time. As an extension of classical queuing theory, many studies have been done to optimize the clinic scheduling aspect of the patient journey, or the surgery scheduling aspect [1]; however, this study is distinctive in considering how allocation of resources for one service affect the other and vice versa, as well as how to optimize the allocation between them to minimize total, holistic patient wait time. This is explained further in the literature review below. The variables in the analysis will be physician allocation; that is, what is the effect of changing the amount of time in clinic seeing new patients versus the amount of time in surgery on the total indirect wait time for the total patient population? A secondary variable will be patient scheduling, both in the clinic and in surgery, though these will be changed as a result of physician allocation and not true independent variables.

The study examines a mid-sized (300+ bed) pediatric teaching hospital that serves a regional population of approximately 3,000,000 people (1,000,000 children). It features a Level IV neonatal intensive care unit (NICU), a pediatric intensive care unit (PICU), a burn center (which treats both pediatric and adult patients), and a Level I pediatric trauma center. In addition to the 14 inpatient units, it also has 35 outpatient primary care and specialty care clinics, with over 500 physicians, 200 residents, and more than 4000 nurses and ancillary support staff. The outpatient clinics treat over 220,000 patients per year, while over 55,000 are seen in the Emergency Department [2].

Routine visits, such as primary care, may happen at one of the hospital’s primary care clinics, or at a community provider. For specific ailments, or if the ailment is outside the scope of primary care, those patients may need to be seen in one of the specialty clinics. For example, stomach problems are seen in the Gastroenterology Clinic, while seizures are treated in the Neuroscience Clinic. Appointments in specialty clinics are typically via referral from a primary care physician [3]. After a referral, the patient will typically have to wait until an available appointment slot opens which matches the patient’s schedule, physician availability, and acuity priority [4]. This delay in care from need identified until care is provided is called indirect wait time. This is opposed to direct wait time, which is the delay in care from arrival on the scheduled day to service. Direct wait time is the most visible type of waiting, though it is a small fraction of the total wait time. Indirect wait time can be orders of magnitude greater than direct wait times [5]. The indirect wait time is shown as Delay nodes in the process map in Figure 1.

Once seen in the specialty clinic, the diagnosis and treatment of the underlying ailment can begin. Such treatments sometimes involve a surgical procedure. If surgery is needed, then the search for an available surgical slot that fits within the patient’s schedule is conducted. When a match is found, the surgery is scheduled. There is typically a delay between the time that the need for a surgery is identified and when an available surgical appointment is open. This is another instance of an indirect wait for care, also shown in Figure 1.

The delays in this process, both from the referral to the initial visit, and from the visit to the surgery, adversely affect patients. Delays in appointments are delays in diagnosis and delays in care. Every day between the referral and the initial specialty visit is another day with an undiagnosed, untreated condition. Every day between the diagnosis and the surgery is an extra day the patient is living with the condition that could be treated. The goal of clinics is to treat the condition effectively and safely, but also in a timely manner.

A contributing factor to these delays is the requirement for physicians to perform multiple tasks within the process [6]. Physicians see patients in the clinic as well as perform required surgeries. Many of them also have teaching and research obligations, which will constrain clinic and surgical availability. Seeing patients in the clinic clears the clinic referral backlog. A certain percentage of those clinic visits will also need surgery, which will fill the surgical backlog. Performing surgeries will clear the surgical backlog. However, in either case, time spent in one activity is time away from the other.

Compounding this is the patient mix seen by different physicians. Each physician has a sub-specialty, which sees a slightly different patient population. These different populations have clinic visits of varying lengths, and generate different types of surgeries of varying complexities. It is not uncommon to have a long clinic visit result in a relatively short surgery, or a short clinic visit uncover the need for a complex surgery. Finally, different patient populations require surgeries at varying rates. As such, different physicians generate surgery cases at different rates [7].

The availability of surgical appointments is limited by operating room (OR) time. There are a limited number of ORs available, which must be shared by different specialties. An eight-hour shift in a single operating room is commonly referred to as a “block”. Different services are allocated different numbers of blocks per week (or per month) based on a heuristic considering the number of cases performed, the backlog of cases, the duration of cases, and the average block utilization (i.e., how much of an eight-hour OR day is spent with active surgical patients, versus how much is unfilled). This varies from an “open booking” schedule, in which time in ORs is available to services/surgeons on a first-come, first-served basis [8].

Within that assigned block, physicians often prefer to group similar procedures together. This leverages economies of scale and reduces turnover time between procedures. Depending on the volume and make-up of cases, it is not always possible to group “like” cases. For some specialists, the variation in cases is such that each is unique, both in procedure and duration. Variability in case duration is a leading cause of unfilled block time.

At the hospital of interest, there are just over 500 physician specialists across 35 outpatient specialty clinics and 14 in-patient units. This study proposes to examine one specialty clinic, Otolaryngology (colloquially known as the Ear, Nose, and Throat [ENT] Clinic). The ENT clinic employs 14 specialty physicians. It operates its clinic five days per week. It is allocated 15 surgical blocks per week (three per day, five days per week). In calendar year 2019, the clinic saw 19,649 patients in office visits. Of those clinic visits, 5307 resulted in surgical cases. The median time from referral to being seen in the clinic was 35 days, with a mean and standard deviation of 40.5 and 43.3 days. This spread indicates a high degree of variation with some significant outliers. The median time from being seen in the clinic to the surgery date was 41 days, with a mean of 64.4 days and standard deviation of 64.3 days, again implying high variation with significant outliers. The ENT service would like to minimize the time from referral to completion of the patient encounter (either a clinic visit without surgical procedure, or the total length with surgical procedure); i.e., they seek to minimize the total indirect wait time.

1.2. Related Works

A prior systematic literature review we conducted per the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) framework [9] identified 933 unique articles related to discrete event simulation in healthcare published in calendar years 2017–2021. From the systematic review, no articles related to this unique intersection of scheduling both patients and staff across both clinic and surgery were found. However, those related to scheduling either patients or staff, in either clinic or surgery, are worth further consideration.

1.2.1. Staff Scheduling

Surgery Scheduling

Lamprecht et al. [10] studied staffing patterns and work breakdown structures and how they affect patient wait times and process durations. Considering an emergency surgical center, it was shown that a significant fraction of the physicians’ time (up to 31%) was spent in documentation. At baseline levels, nursing resources were used at an average rate of 53% capacity, while physicians were used at 79% of capacity, and were the rate-limiting resource. A simulation was built that added another employee resource type, the Medical Documentation Assistant (MDA), who was responsible for performing the physicians’ documentation tasks. The simulation showed that adding the MDA resource reduced the average physician use to 63% of capacity. In addition to staffing benefits, the average patient visit duration was reduced by 50%, from almost 400 min to just under 200. This simulation shows the value of resource optimization in a constrained setting, as well as the effect of resource optimization on patient time in system. However, it focused on only one aspect of the total patient experience, surgery, while keeping clinic wait out of scope.

Clinic Scheduling

Chalk [11] studied staffing patterns in an ambulatory emergency center (sometimes called “urgent care clinic” in the U.S., to indicate a lower level of care required than a traditional emergency room). Arrival patterns were identified from historic data, and throughput rate as a function of staff availability was calculated. With those inputs, a model was built to compare different staffing patterns. The objective function was the number of patients that required transfer to the medical assessment unit (MAU) of the hospital. Different configurations of operating hours, staffing levels, and days of operation were simulated. Based on historical arrival data, there was more benefit from extending operating hours than in adding additional staff to the current hours. This study optimized staff allocation across a clinic, with patient wait time being examined in proxy by the number of transfers. However, downstream staff allocations were outside the scope of the model.

A study by Qureshi et al. [12] looked at the effects of staffing levels via the nurse to patient ratio. A simulation modeled the typical tasks performed by a nurse during a given shift. The frequency and duration of each was defined. The simulation measured how many tasks were in the nurse’s queue. This was a proxy measure for mental workload. More tasks in the queue meant that the nurse had to spend more of his/her mental attention resources prioritizing and routing. Unsurprisingly, a higher number of patients per nurse resulted in more tasks in queue, longer queue time, and more missed tasks. This study did not seek to find an optimum allocation of resources, only to compare different staffing levels on efficiency. Additionally, downstream staff allocation was outside its scope.

A real-world detail often overlooked in healthcare simulation models is the allocation of specific tasks in a workflow between different resources. Zhong et al. [13] studied the allocation of various tasks involved in a clinic visit to find the optimal distribution to minimize patient visit length. The physician workload is typically the limiting factor in patient throughput. Finding ways to distribute tasks to other staff members frees the physician to focus on patient care and eliminate bottlenecks. This resulted in the shortest patient visit length. While the study did use optimization to minimize patient visit length, it did so by evaluating task allocation, rather than staff allocation; additionally, downstream staff allocation was outside its scope.

Patient arrival patterns are a prime driver of staffing requirements. Most clinics try to schedule patient arrivals to plan staff levels accordingly. However, irregular arrivals can be difficult to plan for accurately. Zimmerman et al. [14] studied a general practice clinic in Canada. Actual patient arrival rates were modeled. Scheduled patients were given priority over walk-up patients. With the objective of minimizing patient wait time while maintaining existing staffing levels, an optimal staffing pattern was developed. This allowed the clinic management to reallocate staff without adversely affecting either staffing rates or worked hours while improving patient access. While this is a prime example of optimizing staff allocation to minimize patient wait time, downstream and indirect wait times are outside of its scope.

1.2.2. Patient Scheduling

Surgery Scheduling

Yip et al. [15] studied surgery scheduling in a multi-theater surgery center with inpatient prep and recovery in Hong Kong. The center had eight operating rooms in the surgical suite. It operated on a block allocation, with a block being a half-day; this resulted in 16 blocks per day (112 per week), divided between 13 different surgical services. Pre-op preparation and post-op recovery occurred in four different inpatient wards. Different surgeries in different services generated post-op stays of varying lengths. A simulation was built to study pre- and post-op inpatient unit occupancy as a function of surgery schedule. The master schedule was optimized to minimize variation in recovery ward volume. This helped to ensure constant patient flow and level staffing. This study has valuable implications for block scheduling of patient surgery times. However, clinic scheduling and staff allocation were outside its scope.

Samudra et al. [16] studied scheduling surgical patients to try to meet target dates. At their surgical hospital in Belgium, a goal is set to complete all surgeries before their due date. As a baseline, 65.4% of surgeries were completed before their due date and 34.6% were completed after the due date. Twelve percent were 28 or more days after their due date, and six percent were 28 or more days before the due date. This wide variance in completion times left some patients very satisfied with quick service, while others waited more than a month beyond when they should have been scheduled. The surgical block allocation rules in place constrained how much the scheduling rules could be changed. The simulation model found that a mix of first-come, first-served combined with a waiting list for unclaimed slots was the ideal balance. This model varied staff allocation primarily, with patient schedule as a dependent variable. However, clinic scheduling was outside its scope.

Bovim et al. [17] studied not simply surgery scheduling optimization, but the master surgery schedule. Most hospitals use a master surgery schedule to allocate surgical blocks to the different surgical specialties. Each surgical specialty is then responsible for scheduling individual surgeries within its own block. Within this framework, some OR space and time must be set aside for emergency surgeries. These must be performed nearly immediately, and the demand rate is variable. However, under heavy demand, emergency surgery requirements may exceed the allocated space, and therefore require last-minute cancellation of scheduled surgeries. Based on historic baseline data from a hospital in Norway, a model was built to optimize the surgical block allocation. The objective was to maximize the elective surgical block allocation and minimize elective surgery cancellations. The model was iterated until an optimal schedule was found. This model has implications for surgery staff allocation as well as meta-level surgical block allocation. However, clinic scheduling was outside the scope of this study.

Clinic Scheduling

Peres et al. [18] studied patient scheduling in an outpatient bariatric clinic. Their study focused on minimizing total cost—that is, the combined wait time of the patients and idle time of the physician. In many situations, there is a trade-off between patient wait time and physician idle time. Minimizing physician idle time by having many patients available increases patient wait time. Conversely, minimizing patient wait time can increase physician idle time, especially in real-world situations that consider patient no-shows or late appointment arrivals. This study created a model that considered both no-show rates and appointment arrival patterns (both early and late) in its simulation. With the objective of minimizing total cost, the variable in the simulation was the patient arrival schedule. A series of defined arrival patterns and overbooking strategies were simulated. An increasing-interval clustering rule with 30% overbooking was found to be the best pattern of those considered, though not necessarily mathematically optimal. Of note, this study only considered clinic visit scheduling. It did not analyze surgical scheduling patterns or the interaction between them and physician availability, nor did it find a true optimum.

In many outpatient clinics, there is variation in the types of patients seen and their visit lengths and requirements. Clinics allot slots in their schedules for patient types in certain mixes in advance. For example, there may be a set number of appointments for new patients, a set number for follow-ups, a set number for referrals, etc. Laana et al. [19] considered a Dutch oncology clinic schedule allocation. Using a simulation model, they compared various scheduling rules in an effort to minimize patient wait time and maximize slot utilization. They found that a dynamic scheduling scheme, which changed the allocation of patient appointment types throughout the year, was superior to a static schedule. Treating the patient schedule as the independent variable and staff allocation as the dependent variable differs from many other simulations. Additionally, surgery allocation was outside the scope of the study.

1.2.3. Other Areas of Research

Beyond direct application of discrete event simulation, there are other areas of research that need consideration. As a service system [20], other methods have been explored for application to problems in this category. Petri nets can also be used to model and analyze healthcare systems. For example, Kang et al. [21] used a Petri net model paired with mixed-integer linear programming to optimize staff allocation in an outpatient clinic to minimize patient wait times. Generalized nets are another potential alternative for modeling health systems, as demonstrated by Stefanova-Pavlova et al., who used the tool to model and optimize staff resources in a diabetic telemedicine setting [22].

2. Materials and Methods

2.1. Designing the Simulation Model with Real Baseline Data, Constraints, and Assumptions

This study uses a discrete event simulation model to study the effects of physician allocation between clinic and surgery on the total indirect patient wait time between clinic referral and clinic visit, and between clinic visit and surgical procedure. The primary variable in the analysis is physician allocation; that is, what is the effect of changing the amount of time in clinic seeing new/follow-up patients versus the amount of time in surgery on the total indirect wait time for the total patient population? A secondary variable is patient scheduling, both in the clinic and in surgery, though this will be changed as a result of physician allocation and is not truly independently variable. Specifically, as a physician’s availability varies between clinic and surgery, the time available for patients for each activity is changed as a result.

One calendar year of real data was analyzed to establish baseline patterns to use in defining the details of the simulation model. Calendar year 2019 was considered “typical”, in that it did not suffer from pandemic-induced volume fluctuations. The data were studied to establish the breakdown of visit type by provider, the percentage of visits by provider that generate surgeries, and the breakdown of surgery types by provider. Additionally, time distributions for both visit type and surgery type were established. Data for clinic visit allocation, surgical case allocation, and time distributions for each physician (anonymized) are shown in

Table 1. Allocation and duration of clinic and surgical case per physician.

Physician	Clinic Visits	Avg Time/Visit (Minutes)	Clinic Visits	Surgery Cases	Visits to Surgery	Avg Time/Surgery (Minutes)	Std Dev (Minutes)	Cases to Surgery
1	2412	19.90	12.28%	865	35.86%	46.60	86.16	16.30%
2	1788	26.85	9.10%	711	39.77%	37.74	160.91	13.40%
3	2381	20.16	12.12%	815	34.23%	47.42	113.59	15.36%
4	2034	23.60	10.35%	889	43.71%	51.80	158.87	16.75%
5	1333	18.00	6.78%	625	46.89%	35.15	69.17	11.78%
6	2259	21.25	11.50%	820	36.30%	33.04	79.19	15.45%
7	1943	24.70	9.89%	582	29.95%	51.93	63.25	10.97%
8	2157	33.38	10.98%
9	1427	84.09	7.26%
10	796	60.30	4.05%
11	288	83.30	1.47%
12	601	119.80	3.06%
13	115	104.35	0.59%
14	115	105.26	0.59%

. Note, of the 14 clinic physicians, only seven perform surgeries.

The current rate of clinic referrals was assumed to remain constant. With an annual volume of 19,649 visits per year, 52 weeks per year, 5 days per week, and 9 clinic hours per day, this gives an average arrival rate of one patient entering the clinic queue every 7.15 min. There is a mix of patient visits in the ENT clinic, depending on the chief complaint, for example, cleft lip/palate, hearing loss, breathing difficulty, fever/swelling/pain, etc. The arrival rate of new requests remains constant, but the rate at which different visit/patient types clear the queue varies based on physician allocation.

This model assumes that surgical availability is limited only by block allocation and physician availability. It does not consider limitations outside ENT resources, such as surgical nurses, sedation or anesthesia resources, or post-operative care resources. This model does not affect the time allocated to physicians for teaching or research. Only the time allocation between clinic and surgery was varied.

One aspect of total patient wait time is patient preference. In many cases, even if a surgical slot is immediately available, the patient will prefer to wait for a later slot, due to scheduling conflicts, such as arranging time off from work. This model takes two different approaches to that aspect of the total wait. For baseline model validation, a minimum voluntary wait time was modeled, based on discussions with members of the Family Advisory Board, a group of parents and caregivers of patients and former patients at the hospital who meet regularly with hospital leadership as a sounding board for hospital policy and practice. These discussions found that patients will voluntarily wait an average of 20 days, distributed normally with a standard deviation of 20 days. For optimization, the minimum voluntary wait time was removed, and the model assumed that if a clinic or surgical appointment slot is available, the patient will accept the first available slot. After the optimized allocation is found, the schedule was checked with the minimum voluntary wait time for an “apples-to-apples” comparison.

Total wait time is the dependent variable to be minimized. This is defined as the difference between when a patient enters the system and when a patient leaves the system. The patient enters the system in two ways: upon referral from an outside physician, or as a follow-up visit to a prior visit in the ENT clinic. These events “start the clock”. A patient exits the system upon completion of their needed care. This could happen in two ways: the clinic visit could resolve their case, or a surgical visit could resolve the case. These events “stop the clock” (Either of these could potentially require a follow-up visit. If so, that would be considered a new encounter, and the clock would reset and the process repeat). The time is measured in days between referral and final encounter (either clinic visit, if no surgery is required, or surgical case).

Physician allocation between clinic and surgery is the independent variable to be changed. The ENT clinic sees patients five days per week. However, not every physician sees clinic patients every day. Physicians see clinic patients on a set schedule. This is typically in half-day blocks. A full day consists of two half-day blocks, morning and afternoon. The first part of the independent variable is how many half-day blocks are allocated to each physician to see patients in clinic. The ENT clinic operates six clinic rooms, five days per week. These blocks clear the clinic visit referral backlog, which addresses the first half of the patient wait time. They also generate new surgical cases. The rate of surgical case generation is determined by the historic data, driven by visit type. The ENT service is allocated fifteen full-day surgical blocks per week. That is, three operating rooms per day, five days per week, are reserved for ENT patients. Not each physician performs surgery in each block. Much like clinic visits, physicians typically work a number of half-day blocks, morning or afternoon, throughout the week. It is possible to mix the block allocation—to see clinic patients in the morning and surgical patients in the afternoon (or vice versa)—but this is not preferred as it runs the risk of delays in one block cascading into the next block. The allocation of clinic and surgery block allocation is varied in the model. Each physician has a set number of half-day blocks available. The theoretical maximum is ten (morning and afternoon, five days per week), but in practice, most physicians serve fewer blocks than the maximum. Each has duties outside clinic and surgery, such as in-patient care, teaching, and research. The baseline allocation of physician resources between clinic and surgery (anonymized) is shown in

Table 2. Baseline physician allocation between clinic and surgery by day of week.

Physician	Mon	Tue	Wed	Thu	Fri	Total
1	Clinic		Surgery	Clinic	Surgery	8
2	Clinic	Surgery	Clinic		Surgery	8
3	Surgery	Clinic		Surgery	Clinic	8
4	Clinic	Surgery		Clinic	Surgery	8
5	Surgery		Surgery	Clinic		6
6	Surgery	Clinic		Surgery	Clinic	8
7	Clinic	Surgery	Clinic	Surgery		8
8	Clinic	Clinic	Clinic			6
9	Clinic	Clinic	Clinic	Clinic	Clinic	10
10		Clinic			Clinic	4
11					Clinic	2
12		Clinic	Clinic	Clinic		6
13			Clinic (AM)			1
14			Clinic (PM)			1
Surgery	6	6	4	6	6	28
Clinic	12	12	12	10	10	56

.

The number shown in the “Total” column is how many half-day blocks each resource has available. A goal is to keep the total resource usage consistent; only the allocation between clinic and surgery is subject to change. The numbers in the “Clinic” and “Surgery” rows indicate how many half-day blocks are allocated to each per day. These are subject to change based on the optimization, subject to constraints on maximum utilization.

2.2. Baseline Model Validation

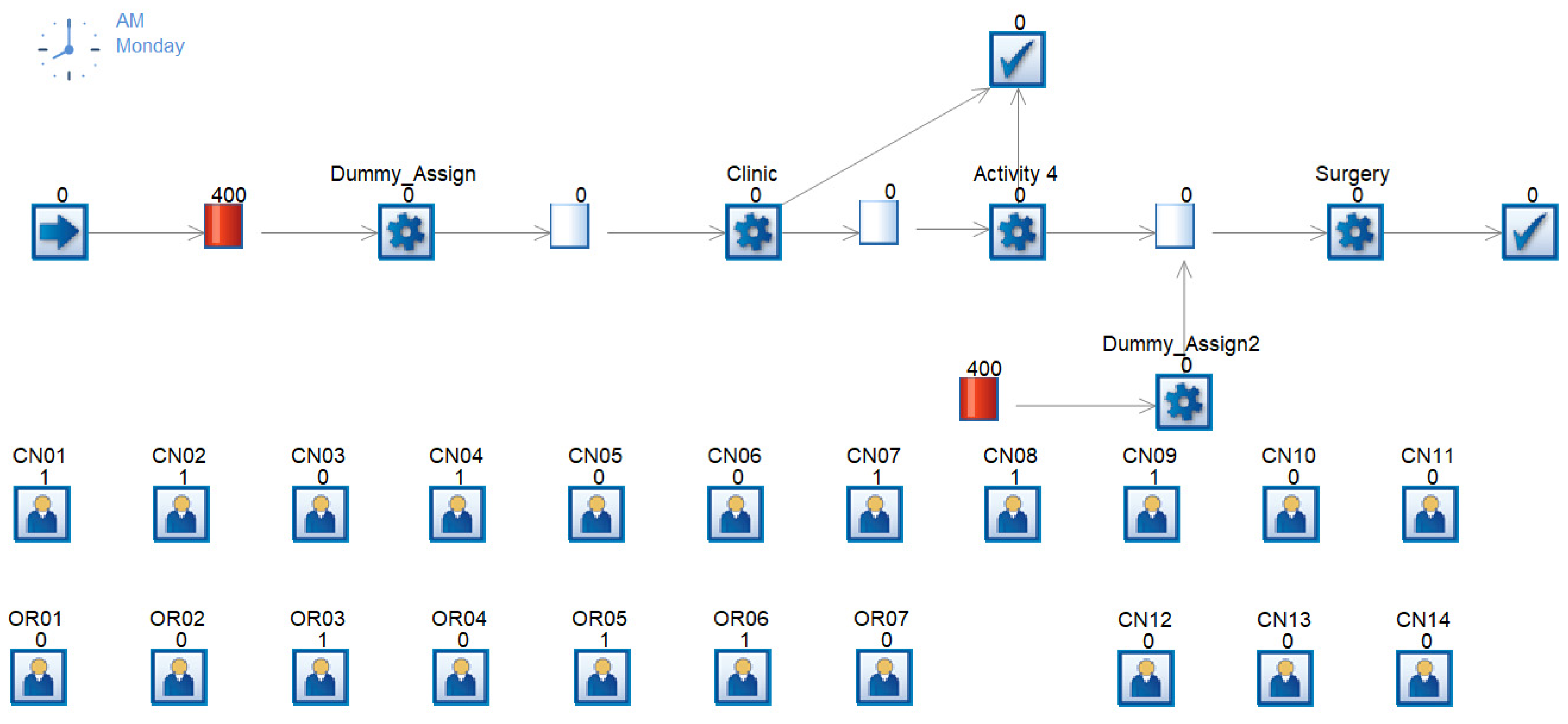
The model was built in the Simul8 2022 Professional discrete event modeling software, shown in Figure 2. For more specific detail on the Simul8 model construction, please refer to the Supplementary Materials.

The model is a high-level representation of the patient flow through the ENT clinic and surgical visit. Patients arrive at the start point with an average arrival rate of 1 every 7.15 min. Next is a queue with an initial volume of 400 patients. This is to front-load the simulation to account for steady-state operation and avoid beginning with a completely empty system, which would artificially speed the patient through, since they would not be waiting for prior patients to clear. Next is a “dummy” activity. This activity is assigned a duration of 0 min and is the step that assigns which physician will be seen by each patient. The probability of seeing any given physician is based on the historic data, as shown in Table 1.

Next the patient enters the queue for the clinic visit. This is the traditional start of the patient journey. Here the patient waits for their clinic visit. This wait is determined by two factors: the minimum voluntary wait time and the physician availability. This minimum voluntary wait time is modeled as a distribution based on discussions with the Family Advisory Board. Many patients are willing and able to be seen almost immediately, but others have various social needs that necessitate a longer wait. As per the family feedback, the minimum wait time was modeled as a normal distribution with a mean and standard deviation of 4 weeks.

Next the patients are seen by their assigned physician. This task is replicated 6 times to account for the number of available exam rooms. Each physician is modeled as a separate resource, which can be assigned to either the clinic or surgery. If physician #1 is in clinic, the resource “CN01” equals 1, while resource “OR01” must equal 0, since the physician cannot be in both at the same time. This resource availability is defined in the Simul8 Resource Schedule tool, as per the defined baseline schedule from Table 2. Each day and each physician are modeled separately.

The workflow is a “first in, first out” selection from the queue, once the minimum wait time has elapsed. This ensures that patients with extended visits or complex diagnoses are not made to wait an unreasonable amount of time. The minimum wait time models the probability of a longer wait for a more complex or less-common case, and avoids modeling in such a way that patients languish in the queue.

The clinic visit length is modeled per physician, as per the data from Table 1. Based on the physician label assigned earlier in the flow, the average clinic visit time is assigned.

After the clinic visit, a series of activities determine which patients exit the system. Those patients seen by physicians 8 through 14 exit the system, as those physicians do not perform surgeries. Those seen by physicians 1 through 7 have a certain percentage exit the system, while the complement proceeds to the queue for surgery. The probability of a physician’s patient proceeding to surgery is as per the probability in Table 1.

Also entering the queue for surgery is a prior queue with a set volume and another dummy activity. This is similar to the earlier dummy activity, seeding the surgical queue with patients so as to reach steady-state condition. The dummy activity assigns patients to a surgeon based on the probability in Table 1.

When in the queue for surgery, much like the queue for clinic, there is a minimum voluntary wait time based on patient preference. This distribution was much more flexible than that for clinic, as a surgical visit entails a greater time commitment than a clinic visit, and therefore more advance planning. The minimum voluntary wait distribution was modeled as a normal distribution with a mean and standard deviation of 10 weeks.

Finally, the patient is seen by the assigned physician (surgeon). This activity is replicated three times, to account for the three operating rooms available for ENT surgeries each day. Much like clinic availability, surgical availability is modeled using the Resource Scheduler. Also as with clinic visits, the queue is a “first in, first out” selection, after the minimum wait time is reached. Surgery duration per physician is modeled from the data in Table 1.

With the baseline model built, it was validated against historic data. In order to ensure a discrete event simulation model gives statistically significant results, multiple trials with different random variables must be run. This prevents encountering a fluke scenario that is statistically improbable (but still possible) and outside statistical limits. Simul8 has a Trial Calculator feature that evaluates how many trials are necessary to return a statistically significant result. Based on the baseline model running for one year, the number of independent trials required to reach a significant result for total patient time in system is 4, as shown in Figure 3.

The baseline model was validated against historic performance data. A trial of four runs was conducted and the composite results compared to existing baseline data.

From historic baselines, the mean wait time for a clinic visit is 40.5 days with a standard deviation of 43.3 days. The simulation results gave a mean clinic wait time of 40.7 days with a standard deviation of 32.4 days. Similarly, the mean wait time for a surgical procedure historically was 64.4 days with a standard deviation of 64.3 days. The simulation results have a surgery wait time of 65.2 days with a standard deviation of 48.4 days. As will be discussed in Section 3, the simulation results are not statistically significantly different from historic data. From these two results, it can be concluded that the results from the simulation are an accurate reflection of actual system performance, and that any changes from the simulation can reasonably be expected to predict actual system performance changes.

2.3. Schedule Optimization

Next, the OptQuest for Simul8 (ver 7.0) tool was integrated with the Simul8 model to find the optimal physician schedule in a constraint-reduced feasible region search. OptQuest is an optimization plug-in that integrates with many discrete event simulation tools. It uses a proprietary machine learning algorithm to optimize (minimize or maximize) an outcome variable given a set of input variables and optional constraints. OptQuest then uses the variables and constraints and runs various trials of the simulation model, studying and learning how the input variables affect the output variable, seeking an optimal solution. It should be noted that unless one is willing to exhaust all possible combinations of input variables, it is not possible to absolutely guarantee a global optimum over the input variable set. However, the machine learning tools it employs increase the likelihood of finding a solution that is close to optimal. The number of trials necessary to reach a satisfactory solution is dependent on several factors, but the one with the largest impact is the number of input variables. From the software developer, as the number of input variables increases, so too does the minimum number of required trials, as shown in

Table 3. Simulation trials needed by number of decision variables (adapted from [23]).

Number of Decision Variables	Minimum Number of Simulation Trials
Less than 10	100
Between 10 and 25	500
Between 25 and 100	2500
More than 100	5000

[23].

The OptQuest optimization program interfaces with the simulation model and variables defined in Simul8. The first step in the optimization process is defining all the variables, as well as the minimum, maximum, and suggested values for each. For this, the total number for each physician resource was defined as a variable. The clinic-only physicians had their minimum, maximum, and suggested values set to be the same value. This ensured that the clinic-only physicians do not have their allocations affected. For the clinic and surgery physicians, their minimum for both surgery and clinic was set to 1. That is, they must have at least one half-day in each. The maximum was set to their total work time minus 1; that is, they cannot be fully assigned to either. The Suggested Value was the baseline allocation, an even split between clinic and surgery.

After defining the variables, the constraints must be defined. For this project, the sum of the clinic allocation and surgery allocation cannot exceed the total allocation. If physician #1 has 8 total blocks available, then the sum of clinic allocation and surgery allocation cannot exceed 8. For this model, the constraint was set to “equal to” ensuring that no physician will lose any work compared to the baseline allocation. Additionally, the total number of clinic blocks cannot exceed the maximum number of clinic rooms, and the total number of surgical blocks cannot exceed the maximum number of operating rooms.

Finally, the objective function is selected. This project used Total Time in System. This is the complete patient experience time, from entry in the queue for clinic, through clinic visit, to queue for surgery, to finally exiting the system after surgery. This combines all aspects of the patient journey, including the two primary indirect and voluntary wait times, clinic wait and surgery wait, into one simplified variable. This was set to be minimized.

OptQuest then runs the simulation for either a set time, a set number of trials, or until all feasible input variable combinations have been tested. This project was set to run for 1,000,000 simulated minutes. This arbitrarily long time will allow the tool to complete enough trials to reach a reasonable conclusion, as discussed in [18]. The number of simulation runs per trial is variable. This project used four runs per trial, as per the results of the Trial Calculator discussed previously.

OptQuest begins with the Suggested Value for each variable, runs the simulation trial, and records the value of the output variable. It then systematically begins new trials with variables set to extreme (minimum or maximum) values and studies the effect on the output variable. Proprietary machine learning algorithms in the tool find patterns in the input variables and begin to hone in on an optimum solution. Each “best” solution is logged as it proceeds, and the value for each input variable is recorded.

Mathematically, the analysis is a constraint-reduced feasible region. The objective function of the search is:

$$min\frac{{{\displaystyle \sum }}_{n=1}^n(WCn+WSn)}{\mathrm{n}}$$

(1)

Subject to the following constraints:

$${{\displaystyle \sum }}_{i=1}^{10}BCim+BSim=TBim, TBm \le 10 \mathrm{for} \mathrm{each} m$$

(2)

$${{\displaystyle \sum }}_{m=1}^{m}BCim \le 6 \mathrm{for} \mathrm{each} i$$

(3)

$${{\displaystyle \sum }}_{m=1}^{m}BSim \le 3 \mathrm{for} \mathrm{each} i$$

(4)

$$BCim \ne BSim \mathrm{for} \mathrm{each} i; \mathrm{for} \mathrm{each} m$$

(5)

$${\displaystyle \sum }_{m=1}^m {\displaystyle \sum }_{i=1}^{10} BCim\le 60$$

(6)

$${\displaystyle \sum }_{m=1}^m {\displaystyle \sum }_{i=1}^{10} BSim\le 30$$

(7)

where:

WCn = Wait time from referral to clinic visit for patient n

WSn = Wait time from clinic visit to surgery for patient n

n = patient index, the nth patient

n = total number of patients visiting the clinic

m = physician index, the mth physician

i = index for half-day block, 1–10 (1 = Monday morning, 2 = Monday afternoon, 3 = Tuesday morning, … 10 = Friday afternoon)

BCim = binary variable, is the mth physician booked in the clinic during the ith block

BSim = binary variable, is the mth physician booked in surgery during the ith block

TBm = total blocks allocated to physician m

Equation (1) is the objective function of the search. It seeks to minimize the average total wait time experienced by a patient in the ENT clinic. Equation (2) limits the total number of blocks available to each physician. There are 10 half-day blocks in a week. The absolute maximum number of blocks that can be assigned is 10. However, each physician has a different number of total blocks available. They have time reserved for research, teaching, in-patient care, etc., that reduces the time available to see patients in clinic and surgery, and that time available is physician-specific. Equations (3) and (4) set limits on how many physicians can be in clinic or surgery in one block. There can be a maximum of 6 physicians in clinic at any one time, and a maximum of 3 physicians in surgery. Equation (5) ensures that a physician is not double-booked into both clinic and surgery during the same block. Equations (6) and (7) limit the total number of clinic and surgery blocks in a given week.

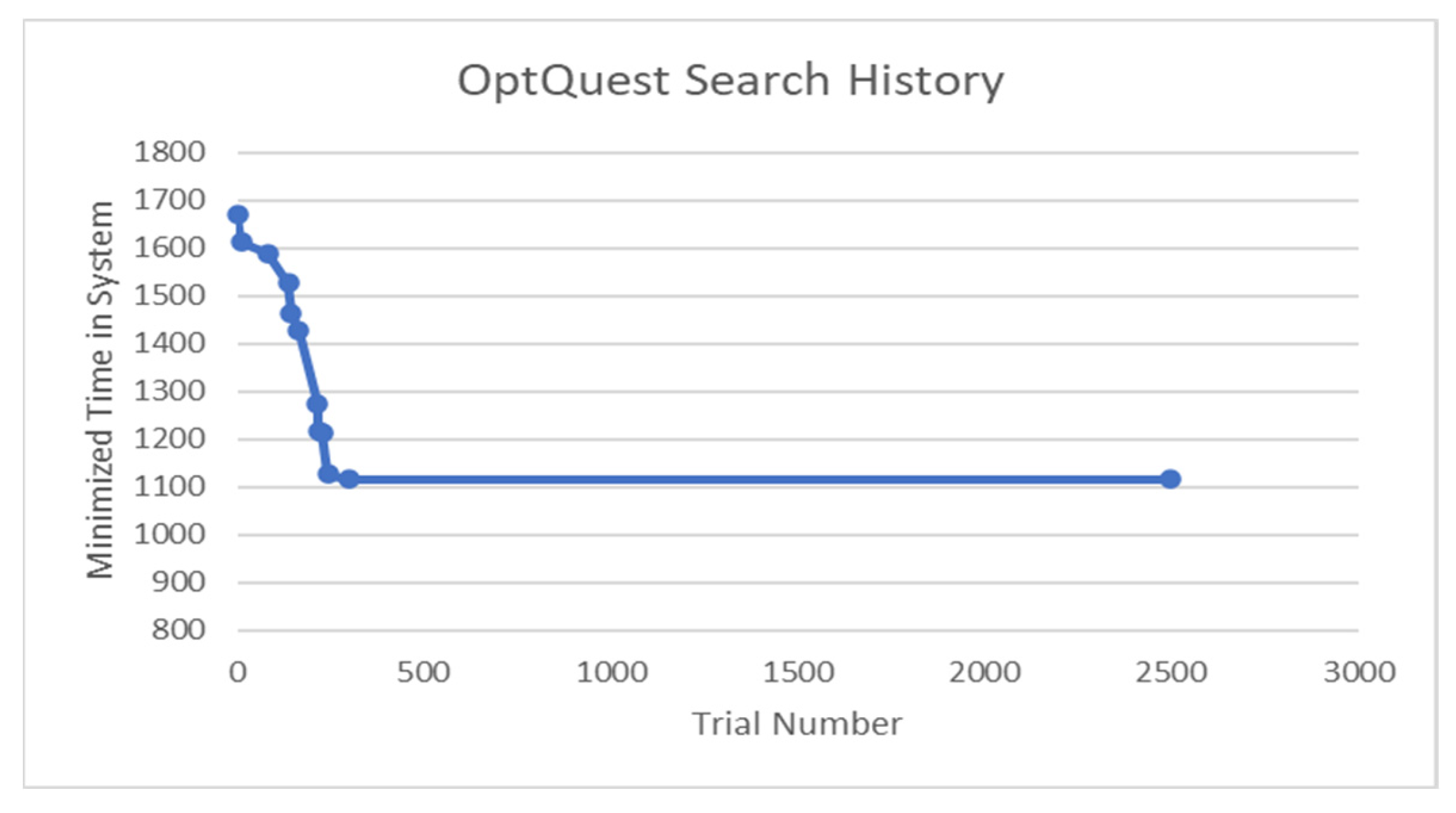
After 2500 trials, the optimization was terminated. As per [18], this would be well over the minimum number of trials required. With 7 decision variables, the minimum recommended number of trials is 100. Therefore, 2500 trials would be sufficient for over 25 decision variables. The search took 8.5 days to complete, with an average of 4.9 min per trial. The search history is shown in Figure 4.

As the OptQuest tool iterated, it recorded the total time in the system, studied the results, changed the input variables based on its internal machine learning algorithm, and continued the search. If the resultant time was less than the previous “best” those input variables were recorded and that trial became the new basis for comparison. The overall best trial was trial number 299. No combination of input variables gave a better result for over 2000 more trials. Therefore, while this result cannot be guaranteed to be a global optimum, it is the best that was found over the space of input variables in a large number of simulation trials, and superior to the baseline scenario. The optimized output compared to baseline is shown in

Table 4. OptQuest resource allocation.

Physician	Clinic Blocks—Baseline	Clinic Blocks—Optimized	Surgery Blocks—Baseline	Surgery Blocks—Optimized
4	4	3	4	5
2	4	1	4	7
3	4	7	4	1
4	4	7	4	1
5	2	2	4	4
6	4	4	4	4
7	4	3	4	5
8	6	6	N/A	N/A
9	10	10	N/A	N/A
10	4	4	N/A	N/A
11	2	2	N/A	N/A
12	6	6	N/A	N/A
13	1	1	N/A	N/A
14	1	1	N/A	N/A

.

2.4. Results Validation: Weekly Schedule, Optimized

There are many mathematically equivalent weekly schedules that match the total block allocation given by the OptQuest results. One such schedule is shown in

Table 5. Potential optimized weekly schedule.

Physician		Mon	Tue	Wed	Thu	Fri
1	AM	Surgery	Surgery	Clinic	Clinic
	PM	Surgery	Surgery	Surgery	Clinic
2	AM	Surgery	Surgery	Surgery	Surgery
	PM	Surgery	Surgery	Surgery	Clinic
3	AM	Clinic	Clinic		Clinic	Clinic
	PM	Clinic	Clinic		Surgery	Clinic
4	AM	Clinic	Clinic	Surgery		Clinic
	PM	Clinic	Clinic	Clinic		Clinic
5	AM	Clinic		Surgery	Surgery
	PM	Clinic		Surgery	Surgery
6	AM	Surgery	Surgery		Clinic	Clinic
	PM	Surgery	Surgery		Clinic	Clinic
7	AM		Clinic	Clinic	Surgery	Surgery
	PM		Clinic	Surgery	Surgery	Surgery
8	All Day		Clinic	Clinic	Clinic
9	All Day	Clinic	Clinic	Clinic	Clinic	Clinic
10	All Day	Clinic				Clinic
11	All Day					Clinic
12	All Day		Clinic	Clinic	Clinic
13	AM		Clinic AM
14	PM		Clinic PM

.

This schedule was put back into the original model. The simulation gave a clinic wait time of 43.7 days with a standard deviation of 34.7 days compared to the historic baseline of 40.5 days with a standard deviation of 43.3 days. The surgical wait time was 51.3 days with a standard deviation of 44.2 days; compared to the baseline of 64.4 days with standard deviation of 64.3 days. Finally, the model gives a total wait time of 94.8 days with a standard deviation of 52.3 days, compared to the baseline total wait time of 105.4 days with standard deviation of 54.8. This shows that the optimized schedule gives a total patient wait time below that of the historic baseline.

3. Results

At present, the median time from referral through clinic visit to completed surgery is over 70 days. Wide variation leaves several outliers that can take over twice as long. Physician availability is a leading bottleneck to clearing these queues and reducing the wait time, as well as the most readily adjusted lever. Determining the optimal allocation can reduce the time from diagnosis to treatment, improving patient quality of life and outcome satisfaction.

For a simulation model to be useful in making predictions about alternate scenarios, it must first be validated to accurately reflect current reality and model baseline scenarios in alignment with historic data. Using the key performance indicators of clinic wait time and surgery wait time, a two-tailed t-test for significance was conducted on the simulation. The null hypothesis, h0, is that there is no significant difference between the historic data and the simulation results. The test hypothesis, h1, is that the simulation is different than historic baseline. As shown in

Table 6. Baseline simulation statistical analysis.

	Clinic Wait Time		Surgery Wait Time
	Historic	Simulation	Historic	Simulation
mean	40.5	40.7	64.4	65.2
std dev	43.3	32.4	64.3	48.4
t-value	0.5467		1.3166
p-value	0.5486		0.1880
Conclusion	Fail to reject		Fail to reject

, in both cases we fail to reject the null hypothesis.

The baseline simulation model gave an accurate reflection of current-state patient journey length, not statistically different than historic data (t-value of 0.5467, p-value of 0.5848). This demonstrates the validity of discrete event simulation as a tool for trialing “what-if” scenarios to affect journey length.

The baseline model was then optimized by reallocating physician resources to minimize to minimize the total patient wait. Again, two-tailed t-tests were conducted on the historic key performance indicators versus the simulation results, with the same null and test hypotheses. In all three cases, we reject the null hypothesis and conclude that the optimized values are different than baseline, as shown in

Table 7. Optimized simulation statistical analysis.

	Clinic Wait Time		Surgery Wait Time		Total Patient Wait
	Historic	Simulation	Historic	Simulation	Historic	Simulation
mean	40.5	43.7	64.4	51.3	105.4	94.8
std dev	43.3	34.7	64.3	44.2	54.8	52.3
t-value	7.94		11.91		19.22
p-value	<<0.001		<<0.001		<<0.001
Conclusion	Reject null hypothesis		Reject null hypothesis		Reject null hypothesis

.

The optimized simulation demonstrated a reduction in total patient journey length, from 105.4 days to 94.8 days. This is a reduction of 10.6 days (just over two weeks, weekdays only) or 10.1%. This indicates real opportunity to reduce patient visit journey by changing physician resource allocation as per the results of the simulation optimization.

4. Discussion and Conclusions

As demands on the system increase, healthcare resources are becoming increasingly taxed. Staff are required to do more, with less, on a shorter time frame. “Thus, specialty clinics face the difficult task of simultaneously guaranteeing quick access for high-priority cases and realizing high utilization of the specialist’s time” [7]. As payment models change in the U.S., these pressures will further compound. This is already being seen in adult settings, and is coming to pediatrics.

Various heuristics are currently used to allocate those limited healthcare resources. However, many were developed when resources were more plentiful and demand was lower. Administrators would benefit from knowing in advance if any revised paradigms are beneficial.

Discrete event simulation (DES) has been used for several years across a variety of applications. Its use in healthcare has continued to increase through recent years. It has been used in a wide variety of healthcare applications, to assist in making many different decisions. While most often thought of as a tool to make operational decisions, it is also used frequently to model population health and economics. In addition to spreading into different applications, its use is spreading to countries and health systems all over the world. It has proven to be a valuable tool for solving vast numbers of healthcare problems.

While DES has seen growth in its use, there are some applications where it lags. In particular, pediatrics has been relatively poorly represented in DES models. Pediatrics is a small percentage of the overall healthcare system, and the wide variety in pediatric patients can make the modeling more difficult. However, pediatric patients are some of the most vulnerable, and need as many tools as possible to find ways to provide quality health care.

Many simulation models have been made of sections of the patient journey. Clinic scheduling optimization models are abundant. Surgery optimization models are not uncommon, with many of them being variations on clinic optimization models. However, the interrelation between the clinic portion and the surgery portion of the patient journey is still poorly studied. Yet, the two affect one another. Optimizing one may have deleterious effects on the other. Only by studying both parts together, as in this study, can we optimize the entire flow. To explore this direction further, our work in the pediatric domain could be used to illuminate other medical domains as well, because while the underlying motivation applies across medical domains, the specifics and the advantages may differ. Future work is needed to investigate this.

Many scheduling models focus only on patient arrival, keeping physician/provider availability as a constant. Again, these two are interrelated, and changing one will affect the other. Modeling the complex interaction between all four facets—clinic, surgery, patient, physician—is a unique opportunity to truly optimize the system as a whole. Here again, our work in the pediatric domain could be tested on other medical domains as well.

An interesting outcome of the optimization process was the trade-off between clinic wait time and surgical wait time. While the optimized solution reduced total time by ten days, clinic wait time actually increased by three days, with surgical wait time decreased by 13 days. This result would require further discussion with the stakeholders to determine if this trade-off is acceptable. The fact that fully half of the clinic physicians’ allocations were unchanged, and therefore should see no change in their patients’ wait time, means that the patients whose physicians also perform surgeries see their clinic wait times increase even more. Whether that increase in clinic wait, offset by the decrease in surgery wait, is acceptable is a question for the decision makers. Further work is required to answer these important questions.

This result may be explained by the impact that voluntary wait times have on total visit wait times. The difference in clinic wait time without the voluntary wait was over 30 days. Only approximately three days of clinic visit wait time was due to system inefficiencies, versus 20 for surgery wait time. This indicates an allocation already disposed to favor clinic access at the expense of surgery access. The optimized schedule results in a closer to balanced wait time for both parts of the journey. This seems counterintuitive—the original allocation of physicians between clinic and surgery was almost evenly balanced. However, variation in case length and arrival rate between clinic and surgery result in more of the unnecessary wait in the surgery half. The optimized schedule moved many physicians to more time in surgery and less in clinic, resulting in a more balanced patient flow.

Another aspect of the optimization that would require consultation with the stakeholders is the use of half-day split schedules. Under current practice, physicians spend the whole day in either clinic or in surgery. There is the perception or concern that delays in the first half of the day will be exacerbated further by changing workflows mid-day. For example, assume a physician is scheduled in the clinic in the morning and in surgery in the afternoon. If the clinic gets behind schedule for some reason, then the surgical half of the day would start off behind schedule, in addition to the physician having to switch from a clinical-diagnostic mindset to a surgical-treatment mindset. This also does not factor in travel time between clinic and surgery, nor the time changing into (or out of) surgical attire. As such, the split-schedule optimization is a best-case scenario.

We used this novel model to look at the meta-level interaction between clinic visit scheduling and surgery visit scheduling, how changing one affects the other, and how to optimally balance the two. This approach has not been tried before, and the model shows promise for continued application. These techniques can be applied to other multi-stage patient journey encounters, particularly those who see limited resources spread across the different facets of the journey. Other clinic/surgical services would benefit from similar analyses, including orthopedics, gastroenterology, and neurology.

Additionally, this technique could be applied at a higher level, to allocate not just physician resources, but rather to balance clinic and surgical allocation to entire services to optimize whole-hospital patient flow. A model could be built of total hospital clinic space and total hospital surgical space. The variables could be which services operate clinics, which services receive surgical blocks, and the numbers of each. This would be a more computationally complex model, therefore requiring more rigor in building the model parameters and more computational time. However, the potential benefit to the hospital as a whole is great. Such a model could be further expanded, incorporating in-patient bed availability (which varies day by day as a result of weekly and seasonal changes in emergency department admissions volume) as a constraint equation.