Optimising Maintenance Workflows in Healthcare Facilities: A Multi-Scenario Discrete Event Simulation and Simulation Annealing Approach
Abstract
1. Introduction
1.1. Background
- Predicting or detecting opportunities for optimisation of service levels, technical resourcing, spare parts management and servicing costs, as well as service times;
- Forecasting optimisation based on changes in healthcare service demand or system shocks, such as due to the COVID-19 pandemic.
1.2. State of Maintenance Management of Healthcare Facilities in Low-Income Economies
1.3. Research Question
- what is the level of spares parts that must be maintained in the store;
- what is the number of technicians that must be hired; and
- what is the service frequency rate
2. Literature Review
2.1. Challenges in Maintenance of Facilities
2.2. Existing Tools and Techniques Developed within Maintenance Management Research
2.3. Operational Contexts
2.4. Previous Approaches
2.5. DES-Based Tools Applied within Healthcare
3. Methodology
3.1. Approach and Research Tools
3.2. Modelling Framework
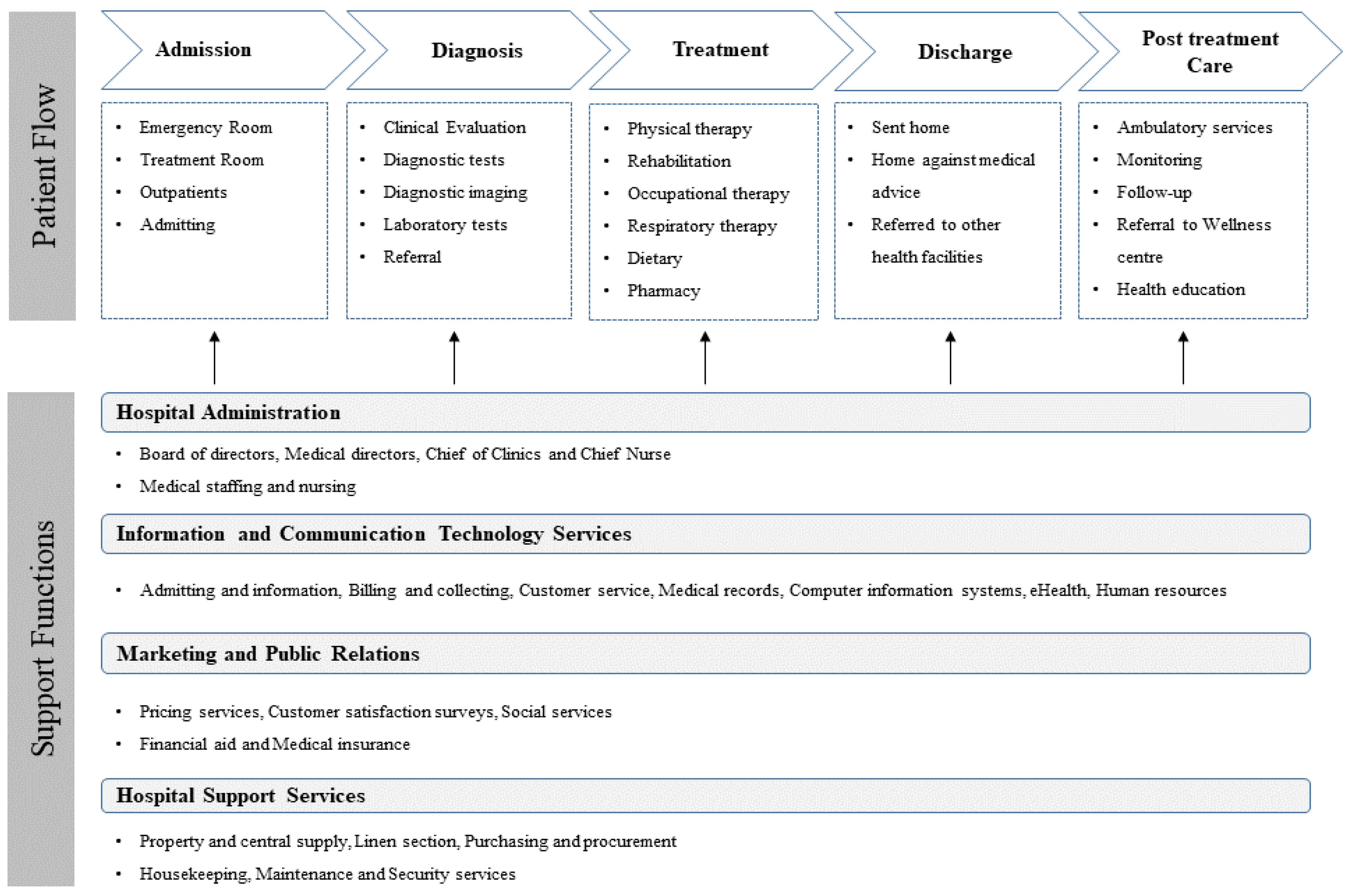
3.2.1. Define Scope
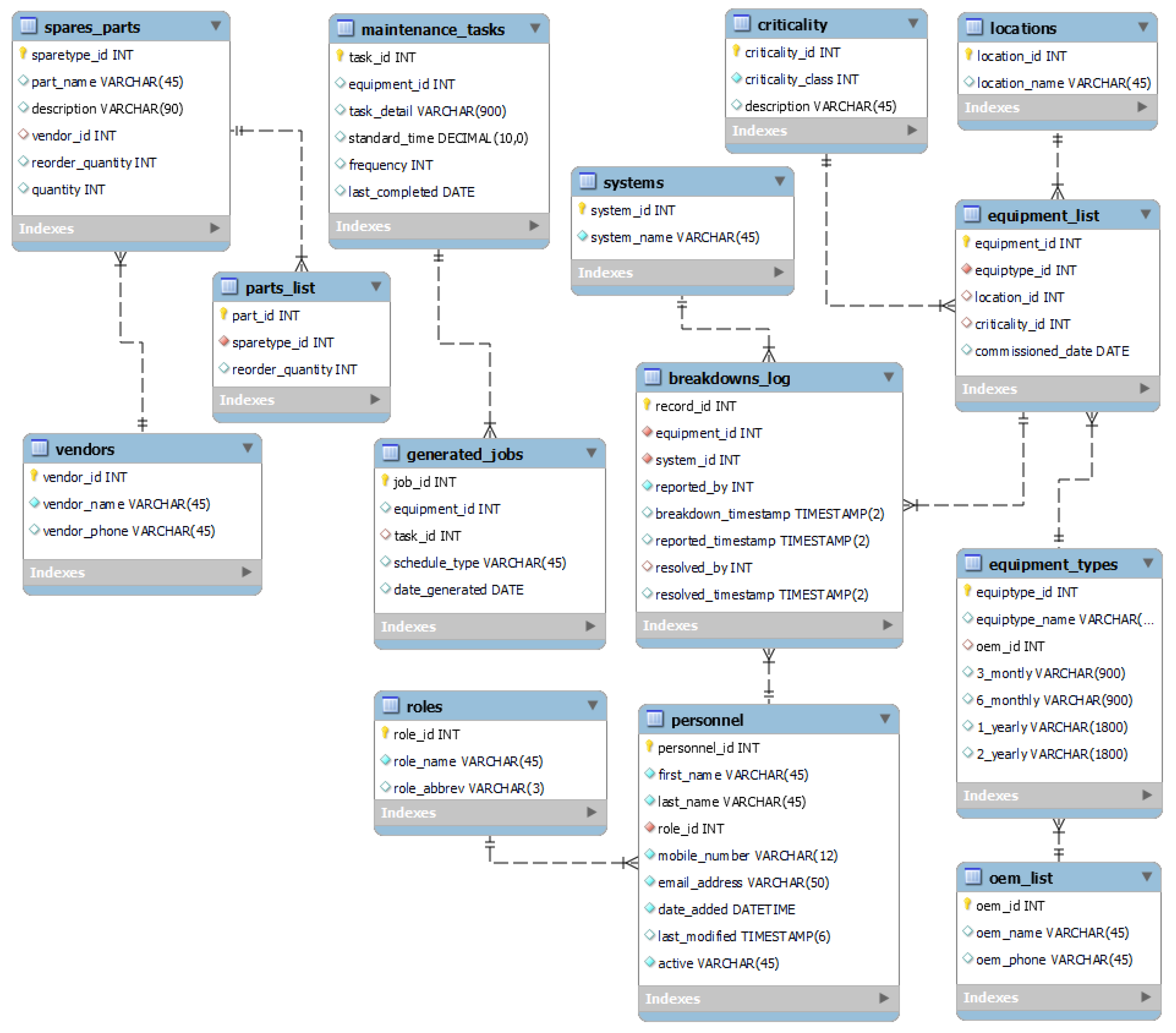
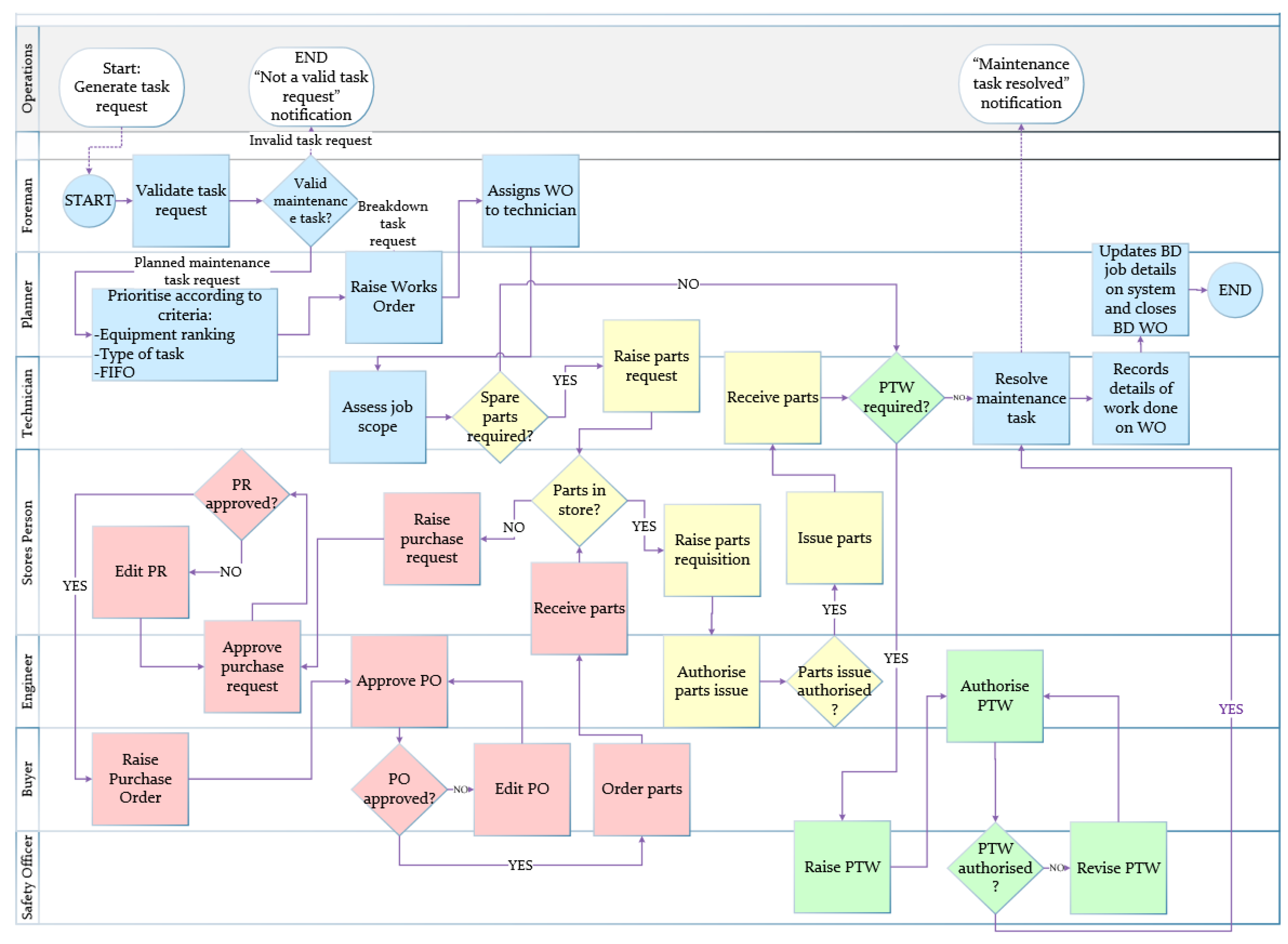
3.2.2. Build Process Model and Translate to Digital Model
3.2.3. Define System Variables
- maintenance strategy per equipment group (that is, maintenance type and frequency);
- spares inventory stocking and replenishment policy; and
- human resources.
3.2.4. Define Bounds and Constraints
3.2.5. Formulate Objective Function
- is the mean time to repair asset of type k, including queuing time;
- is the mean time to execute a preventive schedule on asset of type k, including any waiting; and
- is the mean time to execute a preventive maintenance schedule on asset of type k, including queuing time.
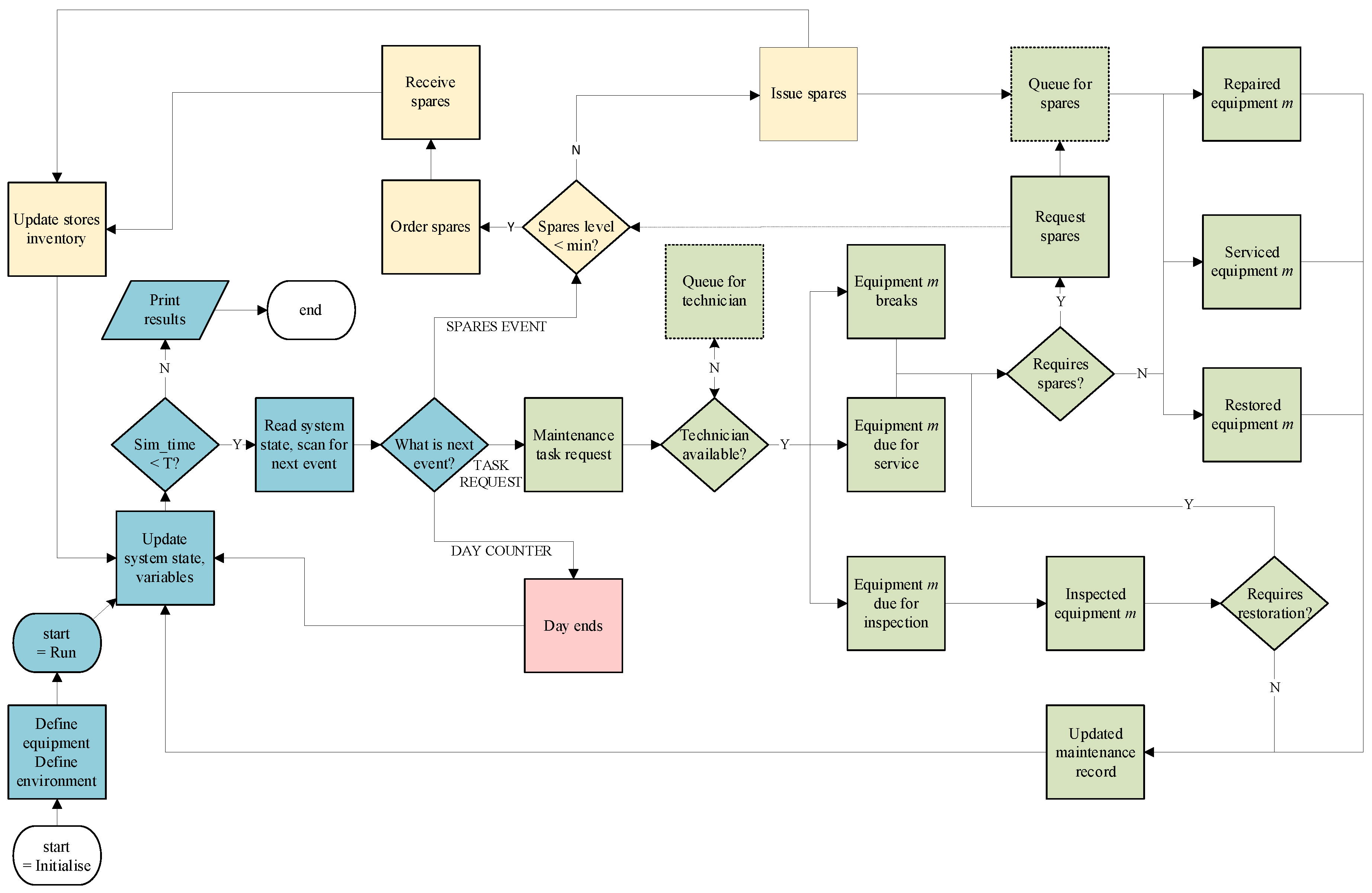
3.2.6. Set Up the Discrete Event Simulation
3.2.7. Set Parameters for Simulated Annealing
3.2.8. Execution
4. Results
4.1. Initial Conditions
4.2. Output
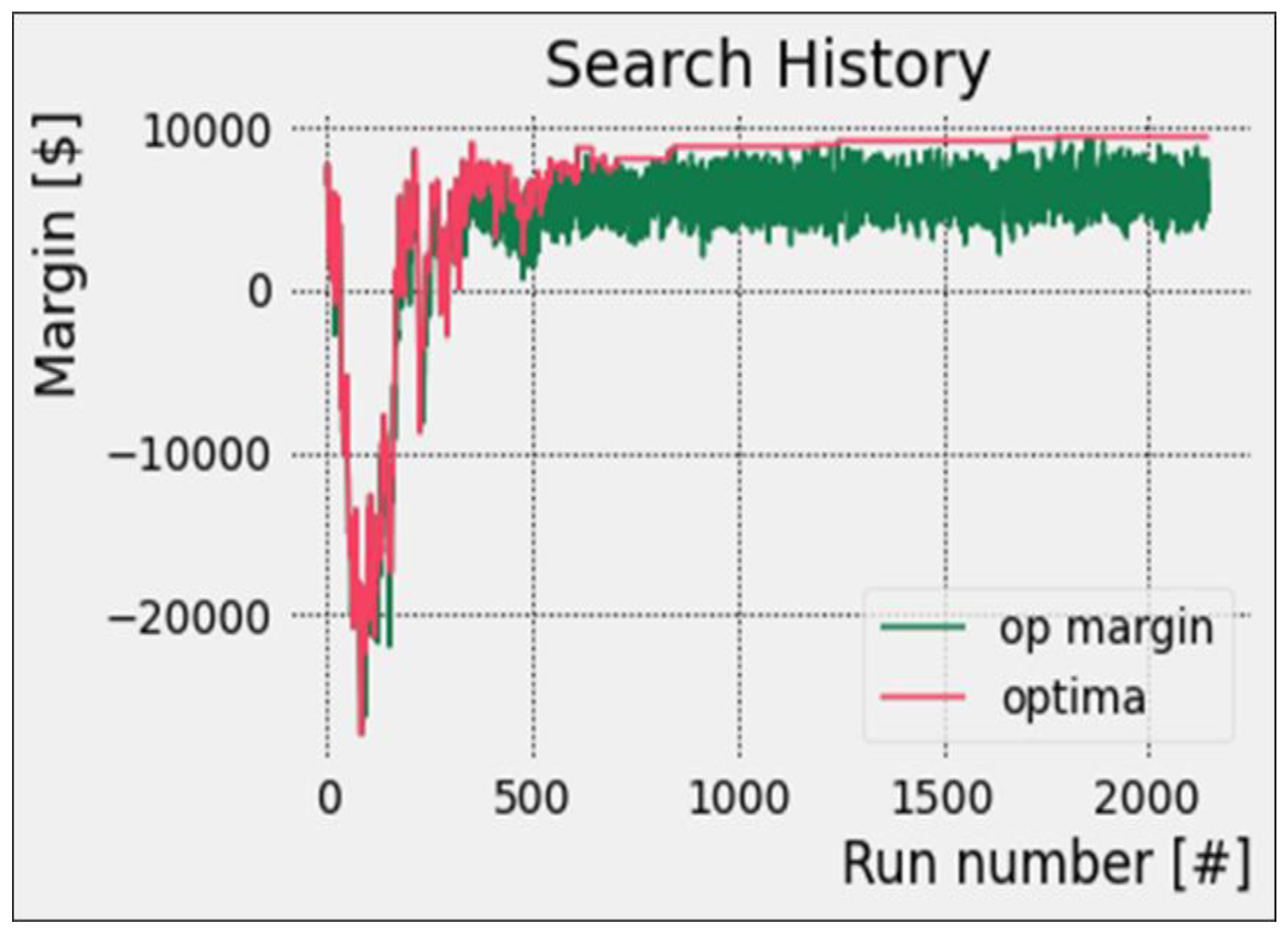
4.3. Search History
4.4. Analysis
5. Discussion
- determine what the input parameters must be in order to ensure optimal performance, not just of the maintenance function but of the health facility in general, including operating margin and customer service level;
- determine the optimum frequency for preventive maintenance activities on a given asset;
- show visual outputs that can be studied for insights and that may reveal hidden relationships among variables;
- give information that can assist managers to formulate a store’s spares policy that is in sync with operations and maintenance;
- provide what-if analysis feedback that managers can use to improve the quality of strategic and tactical decision making; and
- work in any facility with discrete assets without any further customisation.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABS | Agent-based simulation |
| DES | Discrete event simulation |
| KPI | Key performance indicator |
| MTBF | Mean time between failures |
| MTTR | Mean time to repair |
| SD | System dynamics |
| SSR | Solution space reduction |
References
- Ebekozien, A.; Duru, O.S.; Dako, O.E. Maintenance of public hospital buildings in Nigeria—An assessment of current practices and policy options. J. Facil. Manag. 2021, 20, 120–143. [Google Scholar] [CrossRef]
- Ran, Y.; Zhou, X.; Lin, P.; Wen, Y.; Deng, R. A Survey of Predictive Maintenance: Systems, Purposes and Approaches. arXiv 2019, arXiv:1912.07383. [Google Scholar] [CrossRef]
- Yousefli, Z.; Nasiri, F.; Moselhi, O. Healthcare facilities maintenance management: A literature review. J. Facil. Manag. 2017, 15, 352–375. [Google Scholar] [CrossRef]
- Yongkui, L.; Yilong, H.; Jianjun, W. Development of a Conceptual Benchmarking Framework for Healthcare Facilities Management: Case Study of Shanghai Municipal Hospitals. J. Constr. Eng. Manag. 2020, 146, 05019016. [Google Scholar] [CrossRef]
- Valamede, L.S.; Akkari, A.C. Lean 4.0: A New Holistic Approach for the Integration of Lean Manufacturing Tools and Digital Technologies. Int. J. Math. Eng. Manag. Sci. 2020, 5, 851–868. [Google Scholar] [CrossRef]
- Ma, Z.; Ren, Y.; Xiang, X.; Turk, Z. Data-driven decision-making for equipment maintenance. Autom. Constr. 2020, 112, 103103. [Google Scholar] [CrossRef]
- Pargar, F.; Kauppila, O.; Kujala, J. Integrated scheduling of preventive maintenance and renewal projects for multi-unit systems with grouping and balancing. Comput. Ind. Eng. 2017, 110, 43–58. [Google Scholar] [CrossRef]
- Rodríguez-Padial, N.; Marín, M.; Domingo, R. An Approach to Integrating Tactical Decision-Making in Industrial Maintenance Balance Scorecards Using Principal Components Analysis and Machine Learning. Complexity 2017, 2017, 3759514. [Google Scholar] [CrossRef]
- Yousefli, Z.; Nasiri, F.; Moselhi, O. Maintenance workflow management in hospitals: An automated multi-agent facility management system. J. Build. Eng. 2020, 32, 101431. [Google Scholar] [CrossRef]
- Azzalin, M.; Massimo, L. A Maintenance Management Model. Upgrading and Experimentation. In Proceedings of the XV International Conference on Durability of Building Materials and Components, Barcelona, Spain, 25 September 2020. [Google Scholar]
- García-Sanz-Calcedo, J.; Gómez-Chaparro, M. Quantitative analysis of the impact of maintenance management on the energy consumption of a hospital in Extremadura (Spain). Sustain. Cities Soc. 2017, 30, 217–222. [Google Scholar] [CrossRef]
- Arab-Zozani, M.; Imani, A.; Doshmangir, L.; Dalal, K.; Bahreini, R. Assessment of medical equipment maintenance management: Proposed checklist using Iranian experience. BioMedical Eng. Online 2021, 20, 49. [Google Scholar] [CrossRef] [PubMed]
- Małgorzata, J.-K.; Stanislaw, L.; Piotr, K. Maintenance 4.0 technologies—New opportunities for sustainability driven maintenance. Manag. Prod. Eng. Rev. 2020, 11, 74–87. [Google Scholar] [CrossRef]
- Morag, I.; Chemweno, P.; Pintelon, L.; Sheikhalishahi, M. Identifying the cause of human error in maintenance work in developing countries. Int. J. Ind. Ergon. 2018, 6, 222–230. [Google Scholar] [CrossRef]
- Alrabghi, A.; Tiwari, A. A novel approach for modelling complex maintenance systems using discrete event simulation. Reliab. Eng. Syst. Saf. 2016, 154, 160–170. [Google Scholar] [CrossRef]
- Jimenez, J.J.; Sébastien Schwartz, R.V. Towards multi-model approaches to predictive maintenance: A systematic literature survey on diagnostics and prognostics. J. Manuf. Syst. 2020, 56, 539–557. [Google Scholar] [CrossRef]
- Bakri, A.; Alkbir, M.; Awang, N.; Januddi, F.; Ismail, M.; Ahmad, A.N.; Zakaria, I.H. Addressing the Issues of Maintenance Management in SMEs: Towards Sustainable and Lean Maintenance Approach. Emerg. Sci. J. 2021, 5, 367–379. [Google Scholar] [CrossRef]
- Wakiru, J.M.; Pintelon, L.; Muchiri, P.; Chemweno, P. A comparative analysis of maintenance strategies and data application in asset performance management for both developed and developing countries. Int. J. Qual. Reliab. Manag. 2021, 39, 961–983. [Google Scholar] [CrossRef]
- Fotovatfard, A.; Heravi, G. Identifying key performance indicators for healthcare facilities maintenance. J. Build. Eng. 2021, 42, 102838. [Google Scholar] [CrossRef]
- Scheidegger, A.P.; Pereira, T.F.; Oliveira, M.L.; Banerjee, A.; Montevechi, J.A. An introductory guide for hybrid simulation modelers on the primary simulation methods in industrial engineering identified through a systematic review of the literature. Comput. Ind. Eng. 2018, 124, 474–492. [Google Scholar] [CrossRef]
- Barlas, Y.; Özgün, O. Queuing systems in a feedback environment: Continuous versus discrete-event simulation. J. Simul. 2018, 12, 144–161. [Google Scholar] [CrossRef]
- Iannino, V.; Mocci, C.; Vannocci, M.; Colla, V.; Caputo, A.; Ferraris, F. An Event-Driven Agent-Based Simulation Model for Industrial Processes. Appl. Sci. 2020, 10, 4343. [Google Scholar] [CrossRef]
- Rebs, T.; Brandenburg, M.; Seuring, S. System dynamics modeling for sustainable supply chain management: A literature review and systems thinking approach. J. Clean. Prod. 2019, 208, 1265–1280. [Google Scholar] [CrossRef]
- Warrington, L.; Jones, J.A.; Davis, N. Modelling of maintenance, within discrete event simulation. In Proceedings of the Annual Reliability and Maintainability Symposium, 2002 Proceedings (Cat. No.02CH37318), Seattle, WA, USA, 28–31 January 2002; pp. 260–265. [Google Scholar] [CrossRef]
- Ahmed, R.; Nasiri, F.; Zayed, T. A novel Neutrosophic-based machine learning approach for maintenance prioritization in healthcare facilities. J. Build. Eng. 2021, 42, 102480. [Google Scholar] [CrossRef]
- Carnero, M.; Gómez, A. A Multicriteria Model for Optimization of Maintenance in Thermal Energy Production Systems in Hospitals: A Case Study in a Spanish Hospital. Sustainability 2017, 9, 493. [Google Scholar] [CrossRef]
- Sleptchenko, A.; Hanbali, A.A.; Zijm, H. Joint planning of service engineers and spare parts. Eur. J. Oper. Res. 2018, 271, 97–108. [Google Scholar] [CrossRef]
- Ulugbek, F.; Buyun, S.; Zheng, X.; Ismael, T. A reliability-based preventive maintenance methodology for the projection spot welding machine. Manag. Sci. Lett. 2018, 8, 497–506. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J.; Guo, P.; Lin, X. The booking problem of a diagnostic resource with multiple patient classes and emergency interruptions. Comput. Ind. Eng. 2017, 105, 277–286. [Google Scholar] [CrossRef]
- Salah, M.; Osman, H.; Hosny, O. Performance-Based Reliability-Centered Maintenance Planning for Hospital Facilities. J. Perform. Constr. Facil. 2018, 32, 04017113. [Google Scholar] [CrossRef]
- Zhang, X. Application of discrete event simulation in health care: A systematic review. BMC Health Serv. Res. 2018, 18, 687. [Google Scholar] [CrossRef]
- Pegoraro, F.; Santos, E.A.; Loures, E.D. A support framework for decision making in emergency department management. Comput. Ind. Eng. 2020, 146, 106477. [Google Scholar] [CrossRef]
- Petroodi, S.E.; Eynaud, A.B.; Klement, N.; Tavakkoli-Moghaddam, R. Simulation-based optimization approach with scenario-based product sequence in a reconfigurable manufacturing system (RMS): A case study. IFAC Conf. Pap. Arch. 2019, 56, 2638–2643. [Google Scholar] [CrossRef]
- Lee, M.J.; Moon, S.M.; Kim, B.; Park, S.Y.; Park, J.Y.; Koo, H.; Lee, H.; Song, K.-H.; Lee, H.; Park, J.S.; et al. Status of antimicrobial stewardship programmes in Korean hospitals including small to medium-sized hospitals and the awareness and demands of physicians: A nationwide survey in 2020. J. Glob. Antimicrob. Resist. 2021, 26, 180–187. [Google Scholar] [CrossRef] [PubMed]
- Weissinger, R. Economic Benefits of Standards—ISO Methodology 2.0; International Organisation for Standardisation (ISO): Geneva, Switzerland, 2014. [Google Scholar] [CrossRef]
- Bedeley, R.T.; Iyer, L.S. Examining the Role of Business Analytics in Healthcare Value Chain. In Proceedings of the 2016 Pre-ICIS SIGDSA/IFIP WG8.3 Symposium: Innovations in Data Analytics, Dublin, Ireland, 11 December 2016. [Google Scholar]
- Matloff, N. Introduction to Discrete-Event Simulation and the Simpy Language; University of California, Dept. of Computer Science: Davis, CA, USA, 2008. [Google Scholar]
- van der Ham, R. salabim; discrete event simulation and animation in Python. J. Open Source Softw. 2018, 3, 767. [Google Scholar] [CrossRef]
- Pascual, R.; Meruane, V.; Rey, P. On the effect of downtime costs and budget constraint on preventive and replacement policies. Reliab. Eng. Syst. Saf. 2008, 93, 144–151. [Google Scholar] [CrossRef]
- Sánchez-Barroso, G.; Sanz-Calcedo, J.G. Application of Predictive Maintenance in Hospital Heating, Ventilation and Air Conditioning Facilities. Emerg. Sci. J. 2019, 3, 337–343. [Google Scholar] [CrossRef]
- Doostparast, M.; Kolahan, F.; Doostparast, M. Optimisation of PM scheduling for multi-component systems–a simulated annealing approach. Int. J. Syst. Sci. 2015, 46, 1199–1207. [Google Scholar] [CrossRef]
- Salama, M.; Srinivas, S. Adaptive neighborhood simulated annealing for sustainability-oriented single machine scheduling with deterioration effect. Appl. Soft Comput. 2021, 110, 107632. [Google Scholar] [CrossRef]
- Song, W.; Kang, J.; Wu, J.; Jia, H.; Chang, H. Research on Flexible Equipment Maintenance Process Scheduling Problems Based on HNSGSA Algorithm. Math. Probl. Eng. 2021, 2021, 7912754. [Google Scholar] [CrossRef]
- Ali, M.; Törn, A.; Viitanen, S. A direct search variant of the simulated annealing algorithm for optimization involving continuous variables. Comput. Oper. Res. 2002, 29, 87–102. [Google Scholar] [CrossRef]
- Peprah, A.K.; Appiah, S.K.; Amponsah, S.K. An Optimal Cooling Schedule Using a Simulated Annealing Based Approach. Appl. Math. 2017, 8, 1195–1210. [Google Scholar] [CrossRef]
- Mahesh, A.; Sushnigdha, G. A novel search space reduction optimization algorithm. Soft Comput. 2021, 25, 9455–9482. [Google Scholar] [CrossRef]
- El Afia, A.; Lalaoui, M.; Chiheb, R. A Self Controlled Simulated Annealing Algorithm using Hidden Markov Model State Classification. Procedia Comput. Sci. 2019, 148, 512–521. [Google Scholar] [CrossRef]
- Ben-Ameur, W. Computing the initial temperature of simulated annealing. Comput. Optim. Appl. 2004, 29, 369–385. [Google Scholar] [CrossRef]
- Zheng, Q.; Feng, B.-W.; Chang, H.-C.; Liu, Z.-Y. Dynamic space reduction optimization framework and its application in hull form optimization. Appl. Ocean. Res. 2021, 114, 102812. [Google Scholar] [CrossRef]





| Variable Groups | Independent | Dependent | Control |
|---|---|---|---|
| People related |
|
|
|
| Spares related |
|
|
|
| Equipment related |
|
|
|
| Operations related | - |
|
|
| Simulation related |
|
|
|
| Simulation Parameter | Value | Explanation |
|---|---|---|
| Dynamic 20 0.75 |
|
| 50 |
|
| Asset Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Units per group | 4 | 4 | 3 | 6 | 5 | 7 | 10 | 2 | 8 | 0 |
| MTBF [weeks] | 30 | 10 | 32 | 9 | 23 | 22 | 29 | 10 | 17 | 8 |
| Preventive maintenance interval [weeks] | 52 | 52 | 52 | never | never | never | never | never | never | never |
| Predictive maintenance interval [weeks] | 13 | 13 | 13 | 13 | 26 | 26 | 26 | 26 | 26 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mwanza, J.; Telukdarie, A.; Igusa, T. Optimising Maintenance Workflows in Healthcare Facilities: A Multi-Scenario Discrete Event Simulation and Simulation Annealing Approach. Modelling 2023, 4, 224-250. https://doi.org/10.3390/modelling4020013
Mwanza J, Telukdarie A, Igusa T. Optimising Maintenance Workflows in Healthcare Facilities: A Multi-Scenario Discrete Event Simulation and Simulation Annealing Approach. Modelling. 2023; 4(2):224-250. https://doi.org/10.3390/modelling4020013
Chicago/Turabian StyleMwanza, Joseph, Arnesh Telukdarie, and Tak Igusa. 2023. "Optimising Maintenance Workflows in Healthcare Facilities: A Multi-Scenario Discrete Event Simulation and Simulation Annealing Approach" Modelling 4, no. 2: 224-250. https://doi.org/10.3390/modelling4020013
APA StyleMwanza, J., Telukdarie, A., & Igusa, T. (2023). Optimising Maintenance Workflows in Healthcare Facilities: A Multi-Scenario Discrete Event Simulation and Simulation Annealing Approach. Modelling, 4(2), 224-250. https://doi.org/10.3390/modelling4020013