Abstract
A population balance model for the aggregation of iron oxide nanoflowers (IONfs) is presented. The model is based on the fixed pivot technique and is validated successfully for four kinds of aggregation kernels. The extended Derjaguin, Landau, Verwey, and Overbeek (xDLVO) theory is also employed for assessing the collision efficiency of the particles, which is pertinent to the total energy of the interaction. Colloidal stability experiments were conducted on IONfs for two dispersant cases—aqueous phosphate buffered saline solution (PBS) and simulated body fluid (SBF). Dynamic light scattering (DLS) measurements after 24-h of incubation show a significant size increase in plain PBS, whereas the presence of proteins in SBF prevents aggregation by protein corona formation on the IONfs. Subsequent simulations tend to overpredict the aggregation rate, and this can be attributed to the flower-like shape of IONfs, thus allowing patchiness on the surface of the particles that promotes an uneven energy potential and aggregation hindering. In silico parametric study on the effects of the ionic strength shows a prominent dependency of the aggregation rate on the salinity of the dispersant underlying the effect of repulsion forces, which are almost absent in the PBS case, promoting aggregation. In addition, the parametric study on the van der Waals potential energy effect—within common Hamaker-constant values for iron oxides—shows that this is almost absent for high salinity dispersants, whereas low salinity gives a wide range of results, thus underlying the high sensitivity of the model on the potential energy parameters.
1. Introduction
The stability of colloids is a very important aspect that may affect pertinent applications of the synthetic nanoparticles, and therefore an understanding of the aggregation mechanisms and subsequent time-frames of a specific suspension is crucial. In particular, inorganic nanoparticles exhibit a tendency towards aggregation when dispersed in saline solutions. In addition, with the ion’s specific effects, there is a significant influence of charge, shape, and surface functional groups on the aggregation of different colloidal particles [1,2,3]. Although experimental studies are usually used for defining the time-dependent particle size distribution (PSD) of nanoparticles in a particular dispersant, in silico methods are emerging as an easy-to-use and cost-effective alternative. Based on the Smoluchowski’s coagulation equation that describes the population balance of the particles in conjunction with the process and kinetics of aggregation, several methods have been developed for numerically simulating these mechanisms by discretizing the size distribution range into consecutive sections and solving the aforementioned equations successively for each section. An extensively used method is the one developed by Hounslow et al. [4], which discretizes the range into consecutive volume sections, each of which is double in size in terms of volume compared to the previous. The equations are expressed in such a way so as to ensure the correct prediction of the total number of particles and, in addition, a correction parameter was introduced so as to ensure conservation of mass. The limiting factor of having sections of predefined volume was overcome by Kumar and Ramkrishna [5], who introduced a method of discretizing the volume range in sections of an arbitrary size, thus providing the flexibility to focus on the behavior and outcome at certain volumes of the spectrum, which was also capable of correctly evaluating two different moments of the distribution. An extensive review of the solution methods of the population balance equations (PBE) is given by Vanni [6].
There has since been a wide utilization of the aforementioned methods for modeling aggregation in liquid solutions. Biggs et al. [7] applied the method developed by Hounslow et al. [4] for modelling activated sludge flocculation, providing a good approximation of the change in mean floc size with time. The flocculation of colloidal suspensions by salts and polymers was studied by Runkana et al. [8], also by applying the method by Hounslow et al. [4], this time in a more sophisticated model encompassing the Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory. The model predictions are in close agreement with the experimental results for the flocculation of colloidal hematite suspensions in the presence of KCl and polyacrylic acid at different concentrations. Atmuri et al. [9] performed a combined experimental and modelling study to explore aggregation in concentrated attractive colloidal suspensions using a PBE model in conjunction with the DLVO theory for describing the interparticle potential. Although the model is reported to predict much faster aggregation rates than those observed experimentally, the authors argue that it is the first PBE model that can successfully predict stable aggregate size and aggregation regimes of charged colloidal particles over a range of salt concentrations and particle concentrations. Liang et al. [10] used the Kumar and Ramkrishna [5] method, also taking into account the DLVO theory, for studying the aggregation behavior of submicron-sized particles of praseodymium-doped zirconium silicate, a ceramic pigment, in an aqueous suspension. The model was modified to predict the stable state of the aggregation by introducing the volume mean size of the aggregate to the stability ratio. In this study, experiments were also performed for investigating the aggregation of the particles in an aqueous suspension in the presence of sodium dodecyl benzene sulfonate or potassium chloride, and the authors report that the predicted data were in reasonable agreement with the experimental results, with an exception regarding predictions for certain levels of suspension concentrations. A similar study employing the same model was performed by Huang et al. [11], who studied the dispersion/aggregation behavior of colloidal particles in the suspension under different conditions by a modified population balance model (PBM). The colloidal system consisted of a dispersion of praseodymium-doped zirconium silicate pigment in an aqueous suspension by modified hydroxyl copolymer and an experimental study was also performed, with the authors ultimately reporting that predicted data are similar to the experimental results.
Iron oxide nanoparticles (IONps) are a prominent class of nanostructures, with impactful medical applications owing to their intrinsic magnetic properties. IONps lay on the superparamagnetic regime, allowing them to be used as contrast agents in magnetic resonance imaging (MRI), as well as nanoheaters for the magnetic hyperthermia treatment of cancer [12]. The shape and size of IONps dictates their colloidal stability, magnetic properties, and the corresponding biomedical application [13,14]. Several synthetic methodologies have been reported for the preparation of IONps, the most common of which is the “co-precipitation method” due to its high yield and low cost. The main disadvantages of this method are increased polydispersity of the final ferrofluid, sedimentation after prolonged storage, and aggregation effects. To overcome these limitations, a shift of interest has been noted towards the “polyol method”, where IONps are prepared in hydrophylic polyol solvents that act both as reducing and capping agents [15]. Through this method, IONps with narrow size distributions, controllable shape, and exceptional colloidal stability in aqueous solutions can be formulated. The formation of citrate coated high crystallinity iron oxide nanoflowers (IONfs) can be achieved via polyol synthesis by controlling the ratio on the polyols used, as reported by Hugounenq et al. [16]. The multicore IONf shape yields superior magnetic properties than the plain spherical nanoparticles, rendering them suitable for biomedical applications [17]. The aim of the current study is three-fold: (i) to carry out case-specific experiments on the colloidal stability of IONfs and specify the effects of using citrate coating, (ii) to develop an in silico model for simulating colloidal stability taking into account the xDLVO theory, and (iii) to study by simulation the effects on the colloidal stability of parameters such as ionic strength and van der Waals forces.
2. Materials and Methods
2.1. Numerical Model
The population balance equation (PBE) [18] is a basic tool in the field of colloidal science for the description of interparticle behavior and for the subsequent prediction of the evolution particle aggregation and consequent size distribution with time. Based on this, a discretized form of the PBE for aggregation of particles is given as [10,11]:
where i represents a particle-size section; is the number concentration of particles in section ; and is the aggregation kernel, which is a combination of collision frequency k and collision efficiency λ, and is expressed as
The first term on the right-hand side of (1) describes the loss of particles of size i because of their aggregation with other particles, whereas the second term represents the addition of particles of size i by their formation due to the aggregation of smaller particles.
The part of the aggregation kernel that corresponds to collision frequency is pertinent to the Brownian motion of the particles, i.e., perikinetic aggregation, and is given by the equation developed by Smolukowski [18], assuming the collision of two particles of diameters:
where is Boltzmann’s constant, is the absolute temperature, and is the fluid viscosity.
The part of the aggregation kernel that corresponds to collision efficiency is pertinent to the total energy of interaction, which is a function of the forces acting between surfaces, and includes van der Waals force, electrostatics, short range repulsion by hydration, long range hydrophobic attraction, magnetic forces, steric forces or bridging due to adsorbed polymer, etc. [19]. This term is generally assumed to be the inverse of the Fuchs’ stability ratio, W, and is given by the following equation [20]:
where is the total interaction energy and R is the center-to-center distance between the particles. Based on the classic and extended DLVO theory, the total interaction energy concerning the present case is given by the following:
where is the energy due to van der Waals forces, is due to the electrical double layer, and is due to the magnetic forces. In the Hamaker theory, the van der Waals energy of attraction for two spheres is given by the following:
where A represents the Hamaker constant [10]. For estimating the electrical double layer repulsion between two spherical particles having surface potentials and , the following analytical expression used in the past [8,10] is employed:
where is the elementary charge; is the valence of the counter ions; and are the dielectric constants of vacuum and the solvent, respectively; and represents the surface potential of the particles. The Debye−Hückel parameter is a function of the salt concentration , the valence of electrolyte ions, and temperature :
where is the Avogadro number. The magnetic energy between two particles that behave as magnetic dipoles and are oriented in a head-to-tail configuration is given by the following [21]:
where M is the magnetization of the material and is the permeability of the vacuum.
According to the method by Kumar and Ramkrishna [5], the size range can be divided into consecutive sections of arbitrary volume sizes (also referred to as size bins) from x1 to xK of arbitrary size (Figure 1), and (1) thereby becomes:
where is the Kronecker delta. The method indicates that when the collision two of particles of volume xj and xk form a particle of volume υ = between preset grid volumes xi-1 and xi (Figure 1), then this is arithmetically split between these neighboring grid volumes. For the preservation of numbers and mass within the whole spectrum, this split is defined by in (10) as follows:

Figure 1.
Computational grid.
For the numerical solution of (10), a FORTRAN code is developed with exploitation of the ODEPACK solver [22].
2.2. Experimental Procedure
All of the reagents were purchased from Sigma-Aldrich Co. (St. Louis, MO, USA) and the solvents were purchased from Fischer Scientific (Waltham, MA, USA, HPLC grade). Fetal Bovine serum (FBS) was obtained from PAN Biotech GmbH (Aidenbach, Germany). All of the other chemicals and materials were commercially available and of high grade, and are described below. Citrate coated IONfs were synthesized through the polyol method according to Hugounenq et al. [16]. The final ferrofluid was an aqueous colloidal solution of 15 nm IONfs, measured by transmission electron microscopy (TEM) (Figure 2), with a maghemite crystal structure, assessed through X-ray diffraction spectroscopy (XRD). The volume magnetization (M) of the IONfs was determined at 0.735 A/m via SQUID-based magnetometry. To assess their colloidal stability in terms of aggregation, size measurements were conducted in a Malvern Zetasizer Nano ZS dynamic light scattering (DLS) instrument.
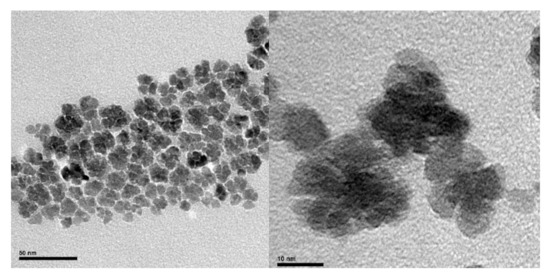
Figure 2.
TEM images of IONfs at two different magnifications Scale bars are at 50 nm (left) nm and 10 nm (right).
IONfs were dispersed in an aqueous phosphate buffered saline solution (PBS) at a 1000μM concentration of iron content. Separate measurements for the same iron concentration were conducted in PBS supplemented with 10% v/v fetal bovine serum (FBS) to use as the simulated body fluid (SBF). FBS is a biofluid containing over 3700 different proteins, among them albumin represents ~60% and globulins ~40%, while the rest is ~1% [23]. The samples were first treated at 37 °C (mean physiological temperature) and measured in 15 consecutive cycles with 30 s duration and 30 s time gap. Two time points were selected for the measurement, the first (t0) was within 3 min after mixing the IONfs with PBS or SBFand the second (t24) after 24-h of incubation at 37 °C.
3. Results and Discussion
3.1. Model Validation
Validation of the model was carried out based on analytical expressions for three kinds of collision frequency kernels and where the collision-efficiency effect was not considered, i.e., λ = 1. For this purpose, the PBE equation was expressed in non-dimensionalised form, as follows:
where , , and is initial number of particles, i.e., the number of particles at t=0. In addition, is the volume used for non-dimensionalisation of the particle volumes and, in this case, it is assumed as the median of the size bins. The discretization was carried out assuming and 21 size bins. The benchmark analytical solutions from the literature are provided for the number−density function n, the relation of which with the number concentration function is given in discretized form as follows:
and its non-dimensionalised form is .
3.1.1. Constant Kernel
This kernel is given as and therefore, and . The analytical solution for the initial condition
where , is given by Gelbard and Seinfeld [24]:
Using (13), we obtain the benchmark solution for the number concentration, and the comparison with the numerical solution is shown in Figure 3a.
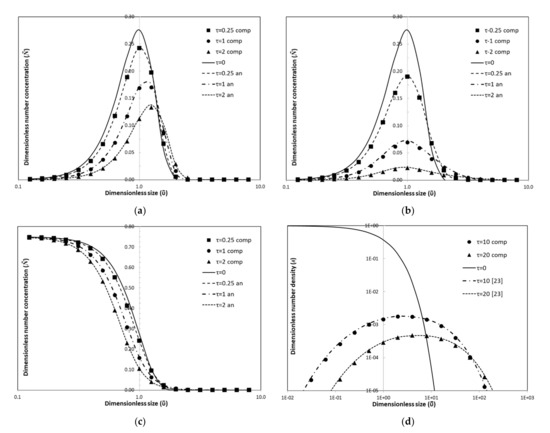
Figure 3.
Validation of the model by comparison with the analytical expressions for (a) constant kernel, (b) linear kernel, (c) quadratic kernel, and (d) Brownian kernel. Comp—computational results; an—analytical expressions.
3.1.2. Linear Kernel
This kernel is given as , and therefore and where . The initial condition is again taken as in (14), the analytical solution of which is given by Gelbard and Seinfeld [24]:
where and I1 is the modified Bessel function of first class and order one. Using (13), we obtain the benchmark solution for the number concentration, and the comparison with the numerical solution is shown in Figure 3b.
3.1.3. Quadratic Kernel
This kernel is given as , therefore and . For this case, the initial condition is used, the analytical solution of which is given by Ernst et al. [25]:
where
and I1 is the modified Bessel function of first class and order one. It is important to point out that for this kernel, the mass is not conserved for due a loss of mass from finite size clusters (sol particles) to the infinite cluster (gel or super particle) [25]. Using (13), we obtain the benchmark solution for the number concentration, and the comparison with the numerical solution is shown in Figure 3c.
3.1.4. Brownian Kernel
Taking into account Equation (3), this kernel can be expressed as , therefore and , where . The initial condition employed is given in (14) and the results obtained when solving (13) are given in Figure 3d and are compared with past results [26].
It can be seen that there is a very good agreement between the numerical and analytical solutions for all four cases for all of the time instances considered. This yields even for in the case of the quadratic kernel, meaning that the model is also capable of taking into account the loss of mass.
3.2. Aggregation Experiments
The IONfs in an aqueous dilution right after synthesis demonstrated a hydrodynamic radius (by number) of 16.56 ± 4.53 nm, whereas after one year, no significant alterations were observed (17.75 ± 4.70 nm), indicating a colloidally stable solution free of sedimentation or aggregation. The storage condition was refrigeration at 2–4 °C.
The measurements corresponding to simulated body fluids in terms of salinity (PBS) and the presence of proteins (SBF) are discussed for t0 and t24. The average size value by number of 15 consecutive measurements of IONfs in PBS at t0 and t24 are 16.22 ± 8.034 nm and 79.60 ± 19.25 nm, respectively. A significant increase in size was reported after 24-h incubation in PBS, dictated by the presence of salts in the colloidal solution (Figure 4a). For the sample of IONfs dispersed in SBF at t0, the average size value by number is 25.80 ± 9.01 nm, whereas at t24 it is at 35.62 ± 11.71 nm. It is worth mentioning that the presence of FBS adds a second peak in these measurements, which was determined at 5.22 ± 1.43 nm, by measuring the plain SBF without IONfs. Again, there is an apparent increase in size that corresponds to the formation of protein corona (PC), but not that substantial to indicate aggregation. This can be confirmed by the ζ-potential decrease before and after treatment with 10% FBS in PBS from −27 mV to −19 mV. The latter can be attributed to the attractive interactions induced between the carboxylic acid of IONfs and the protein’s functional groups present in FBS (e.g., NH2). PC forms when nanoparticles are in close contact with proteins, such as albumins, which adsorb on their surface, further stabilizing them in the medium [27]. According to our data, IONfs seem to aggregate more in plain PBS than in SBF; this behavior can be attributed to the formation of PC, which averts the adsorption of the salts due to the higher affinity for the proteins rather than the salt counter ions [28]. In low nanoparticle concentrations, like the one used in our research, aggregation phenomena stemming from the PC formation are minimal (Figure 4b). FBS is a biological fluid that contains more than 3700 different proteins, with 12 orders of magnitude differences in their relative concentrations. Among all of the proteins in the serum, albumin represents the most abundant fraction and accounts for ~60% mass of the total proteins in the solution (1 mM), with globulins being the second most abundant (~40%) and all the rest representing less than 1% [23]. The observation of aggregation blocking due to PC is consistent with previous studies [29].
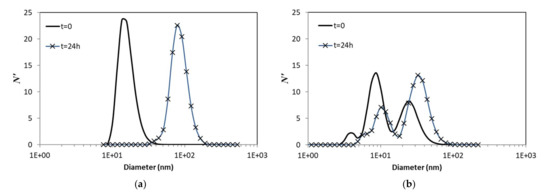
Figure 4.
Initial and 24-h size distribution of IONfs in (a) PBS and (b) SBF.
3.3. Simulations
In the present case and according to the discrete measurements by the dynamic light scattering (DLS) analyzer, the computational grid included 28 size bins, i.e., K = 28 in (10), corresponding exactly to the aforementioned discretization obtained from the experiments. The values of the parameters involved in the equations are given in Table 1.

Table 1.
Parameters used in the simulations.
The PBS results highlight the progress regarding the percentage number concentration , where with showing the total number of particles at the current time instant. Simulations show a fair agreement with the experimental results (Figure 5a). The observed deviation from the experiments can be attributed to the uncertainty regarding the Hamaker constant, but also to the balance between the potential energies, as it seems that when the ionic strength is low, then the der Waals forces are dominant and can affect the aggregation mechanism. With respect to the physics of aggregation, a higher aggregation rate in simulations compared to experiments has also been reported in the past [9]. The effect of patchiness of the particles can be significant in the case of nanoflowers, as these particles deviate markedly from perfect spheres and therefore there can be important differences in the surface potential, which cause the particles to have a reversible aggregation, i.e., they also undergo breakup. In addition, the fact that the particles do not coalesce but retain their shape forming fractal aggregates, the shape of which is far from a perfect sphere, may therefore cause the corresponding kernel to not exactly represent this differentiated phenomenology of aggregates. Therefore, this effect is difficult to be accounted in the PBE model. Next, the magnitude of potentials is studied. It should be noted that in the experiments, no magnetic field was applied, so there is no magnetic potential. However, this is taken into account in the simulations, so as to study its effect when a magnetic field is assumed and to confirm its negligibility [30]. The magnitude of the potentials as a function of the dimensionless distance between the particle surfaces is shown in Figure 5b. It can be seen that the magnetic potential is the least effective of the potentials considered, and therefore has the lowest contribution in the total potential energy even in its most prominent effect, which is the head-to-tail configuration of particles, as assumed in (9), and which would anyway not be possible in the present case where IONfs aggregate in near spherical clusters. In view of this, the effects of the ionic strength and van der Waals forces were further studied.
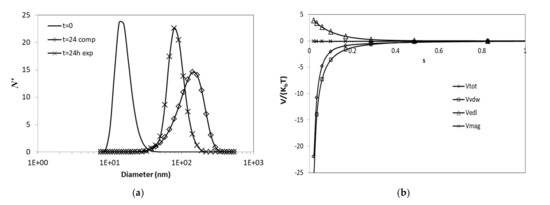
Figure 5.
Simulations for a 24 h period (a) comparison with experimental results and (b) potential energies. Tot—total; vdw—van der Walls; edl—electric double layer; mag—magnetic; comp—computational; exp—experiment.
3.3.1. Effects of Ionic Strength
Various cases of ionic strength are considered, namely the aforementioned PBS case and cases that are usually used in experiments [31] involving 1:1 electrolyte (e.g., NaCl or KCl) with a molarity of 1 mM and 10 mM, whereas a case of no electric double layer (EDL) potential energy was also considered. The van der Walls potential energy corresponds to A = 3.1 × 10−20 J. It can be seen that, as expected, the introduction of dispersants of a higher molarity weakens the effects of EDL, as the Debye length increases and consequently imposes exponential decreasing of the EDL potential. Therefore, attractive forces (Van der Waals) remain dominant, as in the case of PBS, where the total potential energy remains negative for all distance values (Figure 6b). Consequently, the aggregation rate is higher in the cases of a higher molarity, and the PBS case is almost identical to having no EDL potential, as also observed in the past [32]. In addition, molarities as low as 1 mM induce lower aggregation rates than in the experiment (Figure 6a).
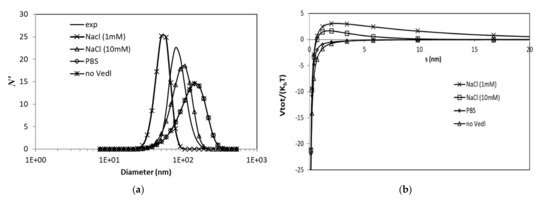
Figure 6.
Effects of ionic strength on (a) particle size distribution and (b) total potential energy.
3.3.2. Effects of van der Waals Forces
Van der Waals potential energy effect on the aggregation rate is calculated for two cases of ionic strengths. The Hamaker constant value was used as a parameter and the range of values considered were obtained from the literature. These values can be as low as n 2 × 10−20 J for IONps [33], and reach values of up to 4.5 × 10−20 J especially for maghemite NPs [34]. In the case of PBS, it seems that the changes within the range of Hamaker constants studied are marginal, i.e., there is no apparent change in the aggregation rate and the results after 24 h are almost identical (Figure 7a). In this case, the total potential energy is again dominated by van der Waals forces and shows no repulsive effects for any surface distance (Figure 7b).
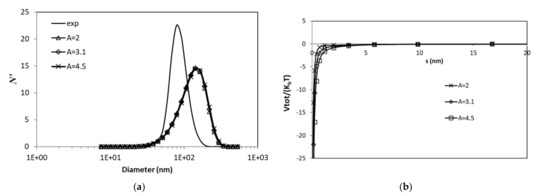
Figure 7.
Effects of Hamaker constant for PBS on (a) particle size distribution; (b) total potential energy (values of A are in 10−20 J).
Conversely, the total potential energy for lower molarities such as 10 mM solution induces dominant repulsive effects within the surface distance range (Figure 8b). In this case, there are differences in the effect of the Hamaker constant values on the aggregation rate within the studied range (Figure 8a), and this seems to be pertinent to the balance between repulsive and attractive potentials, which consequently makes the integral of the total potential with respect to the NP surface distance very sensible to variations. The rates are lower than the previous case and for A = 2, the result for a 24-h period is almost identical to the experimental observations.
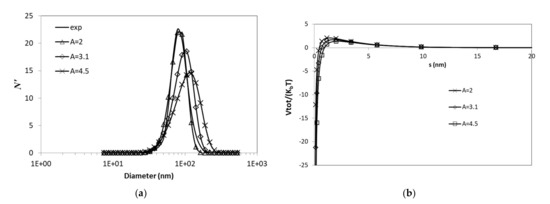
Figure 8.
Effects of Hamaker constant for NaCl (10 mM) on (a) particle size distribution; (b) total potential energy (values of A are in 10−20 J).
4. Conclusions
IONfs were synthesized using the polyol method and their colloidal stability in terms of aggregation was assessed by DLS measurements in both a PBS and an SBF suspension. In the first case, a significant increase in the size is observed after 24-h incubation, whereas in the second case, the presence of proteins induces the formation of a protein corona in the IONfs, thereby preventing aggregation, as also confirmed by the DLS measurements. Simulations using a validated in silico model for solving the particle balance equation in conjunction with the xDLVO theory show a slight overprediction of the aggregation rate. This can be attributed to the patchiness on the NP surface or the fractal nature of aggregates that cannot be considered in the present model. Further study on the effects of the ionic strength shows a scarcity of repulsion forces with increasing salinity, thereby inducing a higher aggregation rate, whereas the PBS case is almost identical as having no EDL effects. In addition, the range of Hamaker constant values for IONs seem to have no effect on the aggregation rate in the case of the PBS, whereas for lower salinity, the experimental case can even be predicted exactly, thus underlying the high sensitivity of aggregation models on the potential energy parameters.
Author Contributions
Conceptualization, P.N.; methodology, P.N. and E.K.E.; validation, P.N., M.T. and M.G.K.; formal analysis, P.N.; data curation, P.N. and M.T.; writing—original draft preparation, P.N. and M.T.; writing—review and editing, M.G.K. and E.K.E.; visualization, M.T. and M.G.K.; supervision, P.N. and E.K.E.; project administration, E.K.E.; funding acquisition, E.K.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Programme «Human Resources Development, Education and Lifelong Learning 2014–2020» in the context of the project “Development of innovative nanotechnology through magnetic nanoflowers for atherosclerosis” (MIS 5048150).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge N. Boukos and E. Sakellis from the Institute of Nanoscience and Nanotechnology, National Center for Scientific Research “Demokritos”, Greece, for providing the TEM images. PN acknowledges the aid by A. Skiadopoulos in implementing ODEPACK.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hegedűs, T.; Takács, D.; Vásárhelyi, L.; Szilágyi, I.; Kónya, Z. Specific Ion Effects on Aggregation and Charging Properties of Boron Nitride Nanospheres. Langmuir 2021, 37, 2466–2475. [Google Scholar] [CrossRef]
- Yu, W.; Du, N.; Gu, Y.; Yan, J.; Hou, W. Specific Ion Effects on the Colloidal Stability of Layered Double Hydroxide Single-layer Nanosheets. Langmuir 2020, 36, 6557–6568. [Google Scholar] [CrossRef] [PubMed]
- Katana, B.; Takács, D.; Csapó, E.; Szabó, T.; Jamnik, A.; Szilagyi, I. Ion Specific Effects on the Stability of Halloysite Nanotube Colloids-Inorganic Salts versus Ionic Liquids. J. Phys. Chem. B 2020, 124, 9757–9765. [Google Scholar] [CrossRef] [PubMed]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Vanni, M. Approximate Population Balance Equations for Aggregation–Breakage Processes. J. Colloid Interface Sci. 2000, 221, 143–160. [Google Scholar] [CrossRef]
- Biggs, C.A.; Lant, P.A. Modelling activated sludge flocculation using population balances. Powder Technol. 2002, 124, 201–211. [Google Scholar] [CrossRef]
- Runkana, V.; Somasundaran, P.; Kapur, P.C. Mathematical modelling of polymer-induced flocculation by charge neutralization. J. Colloid Interface Sci. 2004, 270, 347–358. [Google Scholar] [CrossRef]
- Atmuri, A.K.; Henson, M.A.; Bhatia, S.R. A population balance equation model to predict regimes of controlled nanoparticle aggregation. Colloids Surf. A Physicochem. Eng. Asp. 2013, 436, 325–332. [Google Scholar] [CrossRef]
- Liang, L.; Wang, Y.; Pan, Z. Prediction of sedimentation behavior of submicron-sized particles of praseodymium-doped zirconium silicate in aqueous suspension by population balance model. Particuology 2016, 25, 83–92. [Google Scholar] [CrossRef]
- Huang, G.; Pan, Z.; Wang, Y. Dispersion of praseodymium-doped zirconium silicate pigment in aqueous suspension by modified hydroxyl copolymer. Chem Eng. Res. Des. 2020, 154, 86–100. [Google Scholar] [CrossRef]
- Arias, L.S.; Pessan, J.P.; Vieira, A.P.M.; Lima, T.M.T.; Delbem, A.C.B.; Monteiro, D.R. Iron Oxide Nanoparticles for Biomedical Applications: A Perspective on Synthesis, Drugs, Antimicrobial Activity, and Toxicity. Antibiotics 2018, 7, 46. [Google Scholar] [CrossRef] [Green Version]
- Guardia, P.; Labarta, A.; Batlle, X. Tuning the Size, the Shape, and the Magnetic Properties of Iron Oxide Nanoparticles. J. Phys. Chem. C. 2011, 115, 390–396. [Google Scholar] [CrossRef]
- Hemery, G.; Keyes, A.C., Jr.; Garaio, E.; Rodrigo, I.; Garcia, J.A.; Plazaola, F.; Garanger, E.; Sandre, O. Tuning Sizes, Morphologies, and Magnetic Properties of Monocore Versus Multicore Iron Oxide Nanoparticles through the Controlled Addition of Water in the Polyol Synthesis. Inorg. Chem. 2017, 56, 8232–8243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fievet, F.; Lagier, J.P.; Blin, B.; Beaudoin, B.; Figlarz, M. Homogeneous and heterogeneous nucleations in the polyol process for the preparation of micron and submicron size metal particles. Solid State Ionics 1989, 32–33, 198–205. [Google Scholar] [CrossRef]
- Hugounenq, P.; Levy, M.; Alloyeau, D.; Lartigue, L.; Dubois, E.; Cabuil, V.; Ricolleau, C.; Roux, S.; Wilhelm, C.; Gazeau, F.; et al. Iron Oxide Monocrystalline Nanoflowers for Highly Efficient Magnetic Hyperthermia. J. Phys. Chem. C 2012, 116, 15702–15712. [Google Scholar] [CrossRef]
- Hemery, G.; Genevois, C.; Couillaud, F.; Lacomme, S.; Gontier, E.; Ibarboure, E.; Lecommandoux, S.; Garanger, E.; Sandre, O. Monocore vs multicore magnetic iron oxide nanoparticles: Uptake by glioblastoma cells and efficiency for magnetic hyperthermia. Mol. Syst. Des. Eng. 2017, 2, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Von Smoluchowski, M. Versucheiner mathematischen theorie der koagulations kinetic kolloider losungen. Z. Phys. Chem. 1917, 92, 129–168. [Google Scholar]
- Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population balance modelling to describe the particle aggregation process: A review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Somasundaran, P.; Runkana, V. Modeling flocculation of colloidal mineral suspensions using population balances. Int. J. Miner. Process. 2003, 72, 33–55. [Google Scholar] [CrossRef]
- De Vicente, J.; Delgado, A.V.; Plaza, R.C.; Duran, J.D.G.; Gonzalez-Caballero, F. Stability of cobalt ferrite colloidal particles: Effect of pH and applied magnetic fields. Langmuir 2000, 16, 7954–7961. [Google Scholar] [CrossRef]
- Hindmarsh, A.C. ODEPACK: “Ordinary Differential Equation Solver Library”. Astrophysics Source Code Library 2019. Available online: https://ui.adsabs.harvard.edu/#abs/2019ascl.soft05021H/abstract (accessed on 6 November 2021).
- Piella, J.; Bastus, N.G.; Puntes, V. Size-Dependent Protein–Nanoparticle Interactions in Citrate-Stabilized Gold Nanoparticles: The Emergence of the Protein Corona. Bioconjug. Chem. 2017, 28, 88–97. [Google Scholar] [CrossRef]
- Gelbard, F.; Seinfeld, J.H. Numerical solution of the dynamic equation for particulate systems. J. Comput. Phys. 1978, 28, 357–375. [Google Scholar] [CrossRef]
- Ernst, M.H.; Ziff, R.M.; Hendriks, E.M. Coagulation processes with a phase transition. J. Colloid Interface Sci. 1984, 97, 266–277. [Google Scholar] [CrossRef]
- Liu, A.; Rigopoulos, S. A conservative method for numerical solution of the population balance equation, and application to soot formation. Combust. Flame 2019, 2015, 506–521. [Google Scholar] [CrossRef]
- Barbero, F.; Russo, L.; Vitali, M.; Piella, J.; Salvo, I.; Borrajo, M.L.; Busquets-Fité, M.; Grandori, R.; Bastús, N.G.; Casals, E.; et al. Formation of the Protein Corona: The Interface between Nanoparticles and the Immune System. Semin. Immunol. 2017, 34, 52–60. [Google Scholar] [CrossRef]
- Lima, T.; Bernfur, K.; Vilanova, M.; Cedervall, T. Understanding the Lipid and Protein Corona Formation on Different Sized Polymeric Nanoparticles. Sci. Rep. 2020, 10, 1129. [Google Scholar] [CrossRef]
- Zhanov, V.P. Nanoparticles without and with protein corona: Van der Waals and hydration interaction. J. Biol. Phys. 2019, 45, 307–316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faure, B. Particle Interactions at the Nanoscale. Ph.D. Thesis, Stockholm University, Stockholm, Sweden, 2012. [Google Scholar]
- Antonopoulou, E.; Rohmann-Shaw, C.F.; Sykes, T.C.; Cayre, O.J.; Hunter, T.N.; Jimack, P.K. Numerical and experimental analysis of the sedimentation of spherical colloidal suspensions under centrifugal force. Phys. Fluids 2018, 30, 030702. [Google Scholar] [CrossRef]
- Galli, M.; Sáringer, S.; Szilágyi, I.; Trefalt, G. A Simple Method to Determine Critical Coagulation Concentration from Electrophoretic Mobility. Colloids Interfaces 2020, 4, 20. [Google Scholar] [CrossRef]
- Li, W.; Liu, D.; Wu, J.; Kim, C.; Fortner, J.D. Aqueous Aggregation and Surface Deposition Processes of Engineered Superparamagnetic Iron Oxide Nanoparticles for Environmental Applications. Environ. Sci. Technol. 2014, 48, 11892–11900. [Google Scholar] [CrossRef] [PubMed]
- Ezzaier, H.; Marins, J.A.; Claudet, C.; Hemery, G.; Sandre, O.; Kuzhir, P. Kinetics of Aggregation and Magnetic Separation of Multicore Iron Oxide Nanoparticles: Effect of the Grafted Layer Thickness. Nanomaterials 2018, 8, 623. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).