Electrochemical Model-Based Investigation of Thick LiFePO₄ Electrode Design Parameters

Abstract

The electrification of the powertrain requires enhanced performance of lithium-ion batteries, mainly in terms of energy and power density. They can be improved by optimising the positive electrode, i.e., by changing their size, composition or morphology. Thick electrodes increase the gravimetric energy density but generally have an inefficient performance. This work presents a 2D modelling approach for better understanding the design parameters of a thick LiFePO₄ electrode based on the P2D model and discusses it with common literature values. With a superior macrostructure providing a vertical transport channel for lithium ions, a simple approach could be developed to find the best electrode structure in terms of macro- and microstructure for currents up to 4C. The thicker the electrode, the more important are the direct and valid transport paths within the entire porous electrode structure. On a smaller scale, particle size, binder content, porosity and tortuosity were identified as very impactful parameters, and they can all be attributed to the microstructure. Both in modelling and electrode optimisation of lithium-ion batteries, knowledge of the real microstructure is essential as the cross-validation of a cellular and lamellar freeze-casted electrode has shown. A procedure was presented that uses the parametric study when few model parameters are known.

1. Introduction

Rechargeable batteries are ubiquitous in everyday life. Especially lithium-ion batteries are nowadays some of the most used energy storage solutions, e.g., in mobile phones, laptops, household aids and consumer electronics, making them an essential player for the digitalisation of our society. Continuous progress in research leads to higher capacities, energies and power densities. This development opens new markets and fields of application. With the transformation of society to green energy, the local storage of electric energy becomes more and more important. To answer the demand for e-mobility and affordable large-scale stationary energy storage, research is now widely focused on the electrification of the powertrain and stationary energy storages which single out lithium-ion batteries as the world-leading technology.

These batteries working principle is based on reversible intercalation of lithium ions in electrode materials. The material of the cathode depends on the field of application and consists of transition metals (e.g., cobalt, manganese, nickel) or lithium iron phosphate (LiFePO₄), shortform LFP. The anode is typically graphite. Lithium-ion accumulators are characterised by a high efficiency and energy density, a good cycle stability and a satisfying operating life. They can be used in a wide temperature range (243–333 K) and have a low self-discharge [1]. However, the electrification of the powertrain is limited by the relatively low energy and power density of lithium-ion batteries compared to fossil fuels. In addition to a high specific capacity, the electrodes must provide a fast charging capability, a low price and excellent safety. On the material level of the cathode, LFP could be one of the promising candidates [2]. Besides the continuous improvement of cathode materials, electrolytes [3] and separators [4,5] or the replacement of graphite by metal anodes [6], the cathode structure could be an essential factor to achieve these goals. In general, porous electrodes with low tortuosity provide efficient ion flow and ensure uniform replenishment of the lithium supply, especially at high discharge rates [7]. The charge and discharge cycles can also be stabilised by a porous structure with small particles [8]. In order to gain a deep scientific understanding of physical and electrochemical processes associated with the material structure, extensive data or simulations are required [9]. Without this prior knowledge, the search for a suitable material composition and structure (e.g., porosity, tortuosity, thickness or mass loading) is like the fabled search for the needle in a haystack. Simulations can provide a quick insight into problems or processes and save resources, time and effort.

Lithium-ion models can basically be classified into two types, i.e., empirical and electrochemical models. Empirical models such as equivalent circuit models are mostly based on impedance spectroscopy measurements of single cells [10,11]. These models are highly abstracted and simplified for estimating parameters such as the State-of-Charge (SoC) or State-of-Health (SoH) under different operating conditions. They are particularly used in the design of battery management systems (BMS) due to their usually fast computing time and easy integration [12]. The disadvantage of these models is often the lack of physical interpretability and the non-transferability to other battery types, even those of the same cell chemistry.

Electrochemical models are less abstract and are based on electrochemical transport and reaction equations, but they are mostly not suitable for real-time applications due to the complexity and the high computing time requirements [13]. One of the most common modelling approaches for lithium-ion batteries, known as Pseudo-two-Dimensional (P2D) model, was developed by Doyle, Fuller and Newman [14,15,16]. The P2D model, which has proven to be very accurate [13], combines the porous electrode theory consisting of spherical particles [17], the concentrated solution theory and the kinetics equations. This approach enables the simulation of several material properties and the prediction of battery performance under various design parameters. New approaches try to use the high precision of the P2D model by simplification [18,19] or by coupling it with an equivalent circuit model in order to apply it to real-time applications [20,21,22].

Many numerical studies that are mainly based on the P2D model have been carried out for LFP electrodes [23,24,25,26,27,28,29,30,31,32,33,34]. In the studies, various approaches were analysed with regard to optimising the electrode structure. It was found that a high porosity of an LFP electrode close to the separator can reduce the heat generation [35] and that a lower porosity inhibits the ion transport. For an optimised ion conductivity of a dense electrode, consisting of spherical particles, an optimal porosity of 0.6 was determined [36]. It was pointed out that there is a trade-off between thick and dense electrodes, which theoretically have a high volumetric and gravimetric capacity, and very thin and porous electrodes, which provide high energy efficiency and power density [23,36]. Besides the porosity, the importance of the tortuosity was mentioned [25]. A low tortuosity leads to better diffusion and activation of the electrode and results in higher power densities [37]. Only few studies deal with the real microstructure of electrodes that depends on manufacturing and additives. They pointed to inhomogeneities that lead to non-uniform lithiation within the electrode, resulting in limited capacities [30,38]. This could explain the reason for the discrepancies between theoretical models and experimental measurements.

All studies have in common that they are very specialised on one or two parameters, which leads to a large uncertainty with the number of free parameters within the modelling approach presented here, when only a few model parameters are known. This uncertainty was first discussed theoretically using the example of a thick porous LFP electrode and then using the example of a cellular and lamellar freeze-casted electrode [39]. In this paper, the modelling approach is mainly based on the P2D approach under the extension of different experimental concepts regarding the concentration dependency and the material properties. The geometry of the cell components and especially the thickness of the electrode refer to preliminary work on freeze-casted LFP electrodes [39]. The porous electrode structure consists of well-distributed and equally sized spherical particles. The optimisation of the electrode design parameters was tested through a variety of models, where the parameters were extracted and compared with each other. The parameters worth highlighting include the diffusion and ionic conductivity for both the electrolyte and the electrode, pore volume, particle radius, filler volume fraction, electrode height and, in broad terms, the tortuosity. The lithiation along the LFP electrode after reaching the cut-off voltage of 2.5 V and the voltage curve over the specific capacity were used as quality criteria. A procedure for determining suitable model parameters was presented that takes advantage of the visual parameter study for finding suitable parameters when only few model inputs are given or the uncertainty of these is high. On the one hand, the procedure provides good results, and on the other hand, it demonstrates where the large deviations in the model parameters within the literature originate from. This work enhances the existing models and optimisation strategies especially with regard to electrodes thicker than 150 µm.

2. Model Development

Figure 1 illustrates the electrochemical cell used in this study. The cell is divided into three main areas: the current collector, the porous LFP electrode and the separator. The LFP electrode and the separator (polyethylene, shortform PE) are soaked with lithium hexafluorophosphate (LiPF₆) electrolyte in a mixture of propylene carbonate, ethylene carbonate and dimethyl carbonate (PC/EC/DMC, 10:27:63 by volume). The lithium zone is modelled as a boundary condition. During the discharge process, shown in Figure 1, lithium ions diffuse from the lithium electrode through the separator into the electrolyte and finally the LiFePO₄ electrode.

2.1. Electrochemical Model

The electrochemical battery model is mainly based on the P2D approach [14,15] and now refined by different experimental concepts regarding the temperature- and concentration-dependent coefficients and the material properties [27,28,31,40,41]. The underlying equations were solved numerically using the commercial software COMSOL Multiphysics 5.5. First, a stationary solution for the initial values was calculated and then passed to a fully coupled time-dependent solver. The stationary solution improves the convergence of the time-dependent solver, since both the electrolyte and the electrode potential as well as the solid phase and electrolyte salt concentration are solved under the steady-state assumption and passed to the time-dependent solver as new initial values. The cut-off voltage of 2.5 V was implemented as a termination criterion for the time-based calculation.

2.2. Electrolyte Equations

The mass transport in the electrolyte can be described by diffusion, migration and convection. All these processes are summarised in the Nernst–Planck-Equation given by

$$J_{l,i}=-D_{l,i}\nabla c_{l,i}-z_i{c}_{l,i}F\cdot \frac{D_{l,i}}{RT}\cdot \nabla {\varphi }_l-c_{l,i}u,$$

(1)

where $J_{l,i}$ is the diffusion flux density of the ion sort i, $D_{l,i}$ is the electrolyte diffusivity, $c_{l,i}$is electrolyte concentration, ${\sigma }_{l,i}$ is the ionic conductivity, $z_i$ is the valence of the ionic species, $F$ is the Faraday constant, $R$ is the universal gas constant, ${\varphi }_l$ is the electric potential and $u$ is the velocity of the fluid. Since the dimensions are small and the electrolyte is confined in the separator and in the porous electrode, the convection can be neglected. In case of an electroneutral binary 1:1 lithium-based electrolyte, it is sufficient to solve Equation (1) only for a single ionic species, because the second species is directly obtained from the electroneutral condition. This is often expressed by the ${\mathrm{Li}}^{+}$ ions, with the corresponding transport number $t_{+}$ and the mean molar activity coefficient $f_{\pm }$. Equation (1) can now be reformulated as follows, considering the Nernst–Einstein relation and including both species:

$$J_l=\frac{2\cdot {\sigma }_l RT}{z F^2}\left(1+\frac{\partial \ln \left(f_{\pm }\right)}{\partial \ln \left(c_l\right)}\right)\left(1-t_{+}\right)\nabla \ln \left(c_l\right)-\frac{{\sigma }_l}{z F}\nabla {\varphi }_l,$$

(2)

where ${\sigma }_l$ defines the electrolyte conductivity and $c_l$ denotes both the ${\mathrm{Li}}^{+}$ and the ${\mathrm{PF}}_6^{-}$ concentration. The multiplication with the valence of ionic species $z$ and the Faraday constant $F$ yields the electrolyte current density $j_l=z\cdot F\cdot J_l$. The electrolyte equations for conductivity (3), activity (4) and diffusivity (5) can be obtained from [41]:

$$\begin{array}{ll}{\sigma }_l\left(c_l,T\right)={\mathsf{\sigma }}_{LiPF6}& \\ & \cdot c_l(-10.5+0.074T-6.96\times {10}^{-5}{T}^2\\ & +c_l\left(0.668-0.0178T+2.8\times {10}^{-5}{T}^2\right)\\ & +c_l^2\left(0.494-8.86\times {10}^{-4}T\right)){}^2,\end{array}$$

(3)

$$\ln \left(f_{\pm }\left(c_l,T\right)\right)=\frac{-0.48c_l^{0.5}+0.6546\left(1-0.0052\left(T-293\right)\right)c_l^{1.5}}{1-t_{+}},$$

(4)

$${\log }_{10}\left(D_l\left(c_l,T\right)\right)={\log }_{10}\left(D_{LiPF6}\right)\cdot \left(-4.43-\frac{54}{T-\left(229+5c_l\right)}-0.22c_l\right) ,$$

(5)

where ${\sigma }_{LiPF6}$, and $D_{LiPF6}$ are dimensionless prefactors, which are equal to 1 in [41]. In case of a closed system, the electric charge and mass conservation are applied:

$$\frac{\partial {\rho }_q}{\partial t}+\nabla j_l=0 ,$$

(6)

$$\frac{\partial c_l}{\partial t}+\nabla J_l=S_{sum},$$

(7)

where $p_q$ is the charge density with ${\rho }_q=0$in terms of electroneutral condition. The term $S_{sum}$ is the reaction rate or production of any homogeneous chemical reactions in the electrolyte. Here, all homogeneous reactions are electrically balanced, and the term is mentioned to be zero.

2.3. Electrode Equations

The porous electrode is considered as a superposition of two continua, one representing the electrolyte solution and the other the solid matrix. For the liquid phase in the porous electrode and the separator (a network of non-uniform micro pores), the above given ionic transport equations are used, but extended by the Bruggeman estimation of a corrected diffusivity and ionic as well as electric conductivity:

$$D_{l,eff}={\epsilon }_l^{\alpha }{D}_l ,$$

(8)

$$D_{l,eff}={\epsilon }_l^{\alpha }{D}_l ,$$

(9)

$${\sigma }_{LFP,eff}={\epsilon }_s^{\alpha }{\sigma }_{LFP} ,$$

(10)

where ${\epsilon }_l$ and ${\epsilon }_s$are the volume fractions of the electrolyte and solid content in the porous structure, ${\sigma }_{LFP}$ is the electrical conductivity of the electrode and $\alpha$ is the Bruggeman coefficient equalling 1.5 for spherical particles [40]. In the porous electrode, the void space is filled with electrolyte, so the electrolyte volume fraction is equal to the porosity ${\Phi }_{LFP}={\epsilon }_l$. Since the microstructures of the porous electrodes are often unknown, this value provides a high uncertainty [23,24,28,29,30,31,32,42].

The mass balance, related to Equation (7), is also adapted with the electrolyte volume fraction and considers the intercalation reaction into the solid electrode (see Equation (11)):

$${\epsilon }_l\frac{\partial c_l}{\partial t}=\nabla \cdot D_{l,eff}\nabla c_l-\frac{\nabla j_l t_{+}}{z\cdot F}+a_v\cdot J_{in}\cdot \left(1-t_{+}\right)$$

(11)

The charge transport within the solid phase of the porous electrode takes place through electron transport. By adding conductive additives during the production of the LFP electrode, it is considered as a metallic conductor. The electron transport is then described by Ohm’s law:

$$j_s=-{\sigma }_{LFP,eff} \nabla {\varphi }_s .$$

(12)

Here, $j_s$ is the electrical current density, ${\sigma }_{LFP,eff}$ the electrical conductivity and ${\varphi }_s$ the electrode potential. Both current densities are conserved by the electroneutrality condition that any charge, leaving the solid electrode, must enter the electrolyte phase $\nabla j_s+\nabla j_l=0$.

The interface between the solid electrode and the electrolyte in the porous electrode hosts the charge transfer reaction, which converts the ionic current to an electrical current. This charge transfer can be understood as a finite reaction rate, which leads to the activation overpotential $\eta$:

$$\eta ={\varphi }_s-{\varphi }_l-E_{eq} .$$

(13)

This overpotential is related to the electrode potential ${\varphi }_s$, the electrolyte potential ${\varphi }_l$ and the equilibrium potential $E_{eq}$. The equilibrium potential depends proportionally on the entropy change, which can be approximated by Taylor’s first expansion with $T_{ref}=298.15$ K [31]:

$$E_{eq}=E_{0,ref}+\frac{\partial E_{eq}}{\partial T}\cdot \left(T-T_{ref}\right).$$

(14)

For LiFePO₄ at room temperature, the standard equilibrium potential $E_{0,ref}$ and the entropy change $\frac{\partial E_{eq}}{\partial T}$ were found to be approximations of the State-of-Lithiation (SoL) [28]:

$$E_{0,ref}=3.399+{\displaystyle \sum }_{i=1}^3{k}_i\cdot \exp (l_i{\left(1-SoL\right)}^{m_i}),$$

(15)

$$\frac{\partial E_{eq}}{\partial T}={\displaystyle \sum }_{j=0}^8{g}_j\cdot So{L}^j .$$

(16)

The parameter set for Equation (15) is given in

Table 1. Parameter set for the standard equilibrium potential taken from [28].

$\mathit{i}$	${\mathit{k}}_{\mathit{i}}$	${\mathit{l}}_{\mathit{i}}$	${\mathit{m}}_{\mathit{i}}$
1	−1.239	−7.903	0.3821
2	$3.644\times {10}^{-10}$	21.12	30.37
3	$8.249\times {10}^{-12}$	22.39	1.56

and the coefficients for Equation (16) are given in

Table 2. Parameter set of the entropy change taken from [28].

${\mathit{g}}_0$	${\mathit{g}}_1$	${\mathit{g}}_2$	${\mathit{g}}_3$	${\mathit{g}}_4$	${\mathit{g}}_5$	${\mathit{g}}_6$	${\mathit{g}}_7$	${\mathit{g}}_8$
$1.9186\times {10}^{-5}$	0.0032158	−0.046272	0.28857	−0.98716	1.9635	−2.2585	1.3902	−0.35376

.

The $SoL$ is defined as the relation between the solid electrode lithium concentration $c_s$ and the total concentration of lithium in the solid electrode $c_{s,max}$:

$$SoL=\frac{c_s}{c_{s,max}} .$$

(17)

The local electrode current density $j_{loc}$ is a function of the overpotential described by the Butler–Volmer equation:

$$j_{loc}=j_0\left(\exp \left(\frac{{\alpha }_{\mathrm{a}}F}{RT}\eta \right)-\exp \left(\frac{-{\alpha }_{\mathrm{c}}F}{RT}\eta \right)\right) ,$$

(18)

where $j_0$ is the exchange current density, $R$ is the universal gas constant, $F$ is the Faraday constant, and ${\alpha }_{\mathrm{a},\mathrm{c}}$are the charge transfer coefficients of the anodic (a) and cathodic (c) reaction.

The exchange current density is substance-specific and depends on the anodic and cathodic rate constants $k_{a,c}$, the charge transfer coefficients ${\alpha }_{\mathrm{a},\mathrm{c}}$with ${\alpha }_a+{\alpha }_c=1$, the lithium concentration in the solid electrode $c_s$ and the possible maximum value $c_{s,max}$ as well as the concentration in the electrolyte $c_l$ in respect to the reference concentration $c_{l,ref}$. It can be described by

$$j_0=F\cdot {\left(k_c\right)}^{{\alpha }_a}{\left(k_a\right)}^{{\alpha }_c}{\left(c_{s,max}-c_{s,k}\right)}^{{\alpha }_a}{\left(c_{s,k}\right)}^{{\alpha }_c}{\left(\frac{c_l}{c_{l,ref}}\right)}^{{\alpha }_a} .$$

(19)

The rate constants are affected by the SoL and the temperature. They can be described by the Arrhenius equation [27] with the specific activation energy $E_a$:

$$k_a=3\times {10}^{-11}\exp \left(\frac{E_a}{R}\left(\frac{1}{T}-\frac{1}{298.15}\right)\right),$$

(20)

$$k_c=1.4\times {10}^{-12}\exp \left(-3\cdot SoL\right)\exp \left(\frac{E_c}{R}\left(\frac{1}{T}-\frac{1}{298.15}\right)\right).$$

(21)

The local exchange current density is equal to the intercalation flux (or pore wall flux) $J_{in}$ with regard to the specific electrode surface $a_v$ and yields to the conservation of charge:

$$-\nabla \cdot j_s=a_v\cdot j_{loc}=a_v\cdot z\cdot F\cdot J_{in} ,$$

(22)

where $a_v$ is calculated from the geometric factor $m$ ($m$ = 3 for spherical particles), the relation factor between active material and porous electrode ${\epsilon }_s$ and the particle radius $r_p$:

$$a_v=\frac{m\cdot {\epsilon }_s}{r_p}.$$

(23)

In the solid material of the electrode, diffusion of the charge carrier lithium takes place only, and it is defined in the Fick’s 2nd Law as long as no volume changes and the transport number is constant:

$$\frac{\partial c_s}{\partial t}=\nabla \cdot \left(D_s\nabla c_s\right) ,$$

(24)

where $c_s$ is the concentration of lithium and $D_s$ is the diffusivity of the intercalated particles with the following boundary conditions:

$$\mathrm{particle}\mathrm{surface}:D_s\frac{\partial c_s}{\partial r}=J_{in} {│}_{r=r_p} ,$$

(25)

$$\mathrm{within}\mathrm{particle}:\frac{\partial c_s}{\partial r}=0 {│}_{r=0} .$$

(26)

The diffusion coefficient depends on the lithiation of the porous LFP electrode [32]. The dynamic temperature dependency can be described by applying the Arrhenius equation [27]:

$$D_s=\frac{D_{LFP}}{{\left(1+SoL\right)}^{1.6}}\cdot \exp \left(-\frac{E_s}{R}\left(\frac{1}{T}-\frac{1}{298.15}\right)\right) ,$$

(27)

where $D_{LFP}$ is a dimensionless prefactor. The lithium electrode was assumed to be ideal, leading to a simpler Butler–Volmer equation:

$$j_{loc,Li}=c_{ref,Li}\cdot F\cdot k_{Li}{\left(\frac{c_l}{c_{ref,Li}}\right)}^{{\alpha }_{Li}}\left(\exp \left(\frac{\left(1-{\mathsf{\alpha }}_{\mathrm{Li}}\right)\cdot F}{RT}\eta \right)-\exp \left(\frac{-{\alpha }_{Li}\cdot F}{RT}\eta \right)\right),$$

(28)

The applied constant discharge current is obtained from the theoretical gravimetric capacity $Q_m\approx 170$ mAh g⁻¹ and the mass of the active material:

$$i_{DC}=\left({\epsilon }_s{\rho }_{LFP}{V}_{LFP}\right)\cdot C_{rate}\cdot Q_m.$$

(29)

It should be mentioned here that real LFP cells have a lower gravimetric capacity depending on their condition and the materials used.

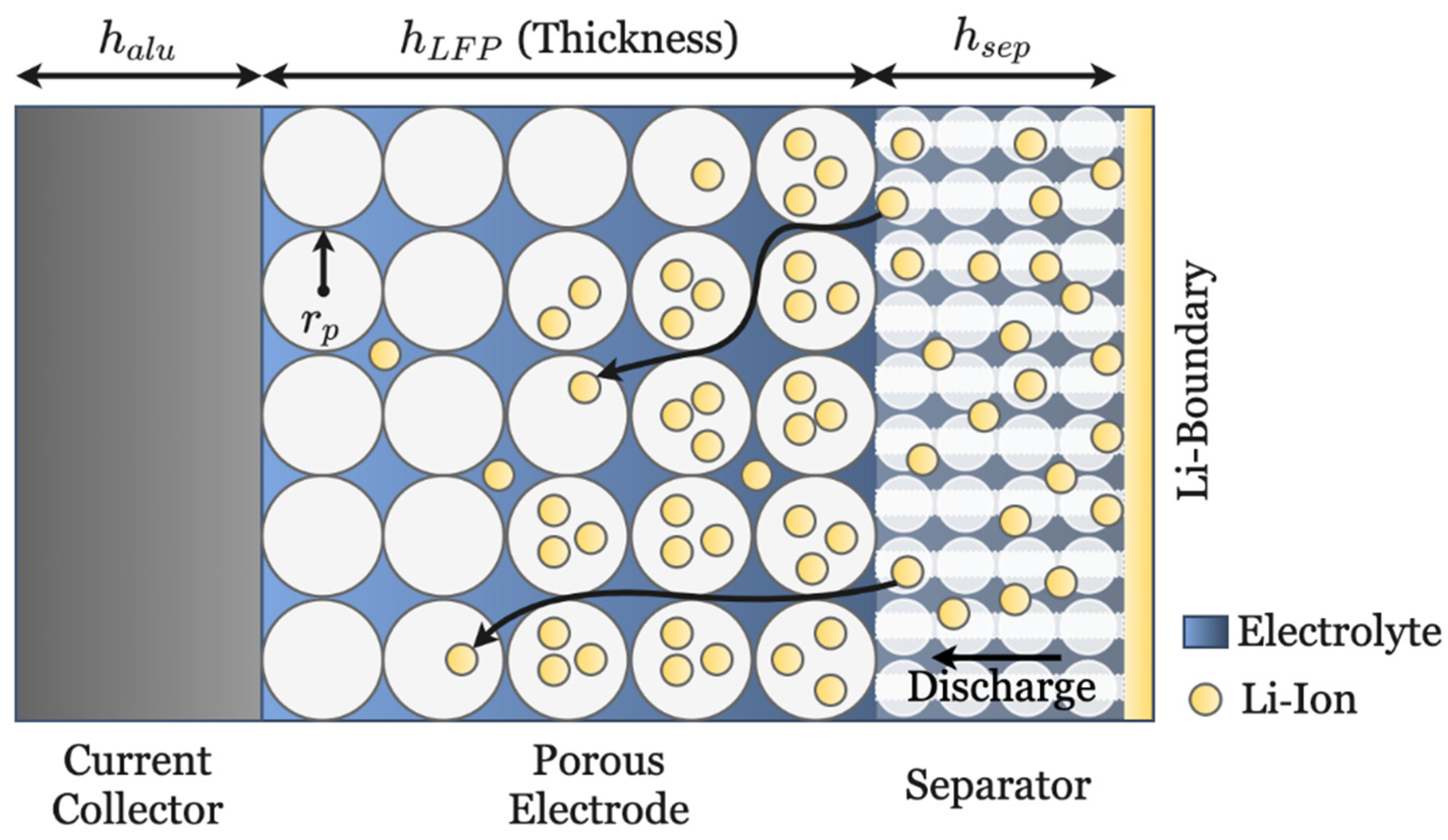
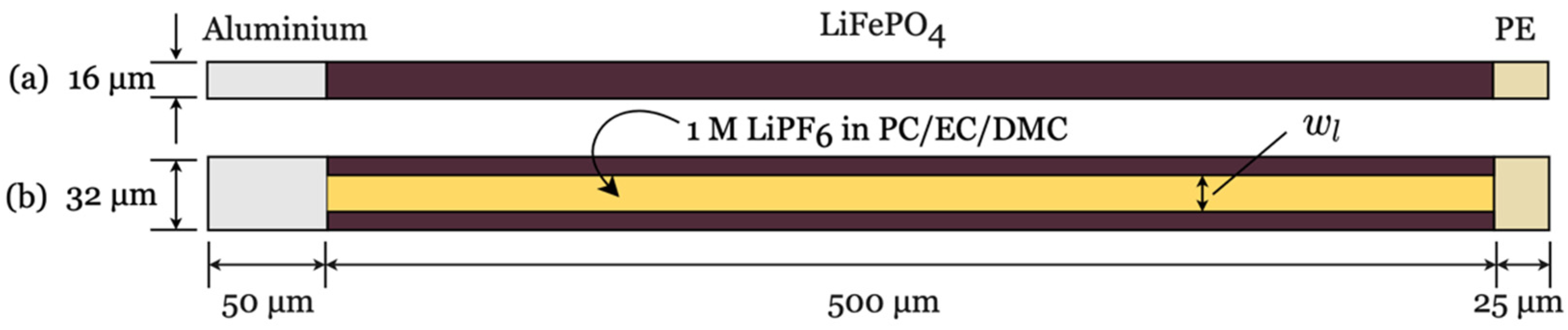
2.4. Material and Geometric Properties

The geometric dimensions of the model development are based on the preliminary work of Zavareh et al. [39]. LFP electrodes were produced by freeze-casting, which form both lamellar and cellular structures depending on the suspension. This technique seems to be very suitable for electrode optimisation as it offers many adjustment parameters for the structure [43,44,45,46]. Here, based on the lamellar structure, which had an electrode wall thickness up to $w_{LFP}=16$ µm, exactly one lamella was considered for the model design over the maximum length of the coin cell diameter of $l_{LFP}=$10 mm. Assuming that (1) the mass and charge transport from the lithium to the LFP electrode follows an approximately straight path, (2) the lithiation is radially symmetric and (3) the geometry is axis symmetric, the 3D structure can be reduced to a 2D problem neglecting the length, as shown in Figure 2.

The thickness of the electrode is defined as the height with $h_{LFP}=500$ µm. The current collector (aluminium) has a height of $h_{alu}=50$ µm, and the separator has a height of $h_{sep}=25$ µm. The lithium electrode is considered as an infinite reservoir of lithium supply without any dimension.

Table 3. Applied parameters for this work.

Parameter	Value	Unit	Reference
electrolyte
$D_l$	(5)	cm2 s−1	[41]
$D_{LiPF6}$	1	-	[41]
${\sigma }_l$	(3)	mS cm−1	[41]
${\mathsf{\sigma }}_{LiPF6}$	1	-	[41]
$f$	(4)	-	[41]
$t^{+}$	0.38	-	[41]
$c_{l,ref}$	1000	mol m−3	[47]
electrode
$D_s$	(27)	m2 s−1	[27]
$D_{LFP}$	$1.18\times {10}^{-18}$	-	[32]
${\sigma }_{LFP}$	0.5	S m−1	[27]
$E_{eq}$	(12)	V	[31]
$c_{s,max}$	16,481	mol m−3	calculated
$c_{ref,Li}$	1	mol m−3	assumed
$So{L}_{min}$	0.01	-	assumed
$So{L}_{\max }$	0.99	-	assumed
$r_p$	$1.25\times {10}^{-7}$	m	[39]
${\epsilon }_s$	0.4	-	calculated
${\epsilon }_l$	0.6	-	[36]
$\alpha$	1.5 (spherical)	-	[40]
${\rho }_{LFP}$	2.6	g cm−3	[39]
electrode kinetics
${\alpha }_a$	0.5	-	[32]
${\alpha }_c$	0.5	-	[32]
$k_a$	(17)	m s−1	[27]
$k_c$	(18)	m s−1	[27]
$k_{Li}$	$1\times {10}^{-4}$	m s−1	assumed
$E_a$	30	kJ mol−1	[27]
$E_c$	20	kJ mol−1	[27]
$E_s$	35	kJ mol−1	[27]
z	1	-	assumed
m	spherical: = 3	-	assumed
separator
${\epsilon }_{l,sep}$	0.724	-	[24]
current collector
${\sigma }_{alu}$	$-0.0325T^3+37.07T^2-1.5\times {10}^{4}T+2.408\times {10}^6$	S cm−1	[29]

contains all other necessary parameters with regard to the reproducibility of the model development.

It is very common to use the same properties for the separator and for the electrolyte. The properties of the electrolyte in a pore structure are assumed to correspond to the Bruggeman correction for spherical particles. However, according to Zahn et al. the ionic conductivity is much lower than assumed by Bruggeman, i.e., 0.053 S m⁻¹ [48].

3. Results and Discussion

For the theoretical performance analysis and identification of various influencing parameters, literature values were used. The model parameters from Table 3 were applied as the initial parameters and compared with other literature values. A wide range of values was established in order to visually represents the governing equations. The name identifier for the literature values in the figures can be found in

Table A1. Simulation parameters and name identifier related to the literature values.

Name Identifier	Parameter	Value	Source
Haverkort	${\epsilon }_s$	0.4	[36]
Saw et al.	${\sigma }_{LFP}$	0.04 S m−1	[24]
	$D_{LFP}$	$8\times {10}^{-14}$
	$r_p$	1 µm
Li et al.	${\sigma }_{LFP}$	0.5 S m−1	[27]
	$D_{LFP}$	$1.18\times {10}^{-18}$
	$r_p$	3.5 µm
	$D_l$	$3.2\times {10}^{-10}$ m2 s−1
Mastali et al.	${\sigma }_{LFP}$	6.75 S m−1	[31]
	$D_{LFP}$	$5.5\times {10}^{-18}$
	$r_p$	320 nm
Yu et al.	${\sigma }_{LFP}$	11.8 S m−1	[23]
	$D_{LFP}$	$6\times {10}^{-18}$
	$D_l$	$3\times {10}^{-10}$ m2 s−1
Huang et al.	${\sigma }_{LFP}$	91 S m−1	[49]
	$r_p$	8 µm
	$D_l$	$7.5\times {10}^{-11}$ m2 s−1
Delacourt et al.	${\sigma }_{LFP}$	16 S m−1	[51]
Kashkooli et al.	$D_{LFP}$	$7\times {10}^{-18}$	[30]
Srinivasan et al.	$D_{LFP}$	$8\times {10}^{-18}$	[34]
	$r_p$	52 nm
Maheshwari et al.	$D_{LFP}$	$2.2\times {10}^{-14}$	[28]
	$D_l$	$1.3\times {10}^{-10}$ m2 s−1
	${\sigma }_l$	0.77 S m−1
Zavareh et al.	$r_p$	125 nm	[39]
Thorat et al.	$D_l$	$1.5\times {10}^{-10}$ m2 s−1	[26]
Prada et al.	${\sigma }_l$	0.25 S m−1	[65]
Valøen et al.	${\sigma }_l$	1.2 S m−1	[41]
Wu et al.	${\sigma }_l$	1.4 S m−1	[57]

. For the purpose of finding a suitable and well performing thick electrode, the best value for each parameter variation was identified and carried over to the next parameter study, as long as the parameter was not given by the preliminary study [39]. The discharge curve and the normalised Li-ion concentration in the particles (lithiation) along the electrode when reaching the cut-off voltage were considered as quality criteria. Since many literature values are based on model fits, the suitability was critically examined for some parameters, especially with regard to thick electrodes.

3.1. Investigation of Electrode Design Parameters

All investigated electrode design parameters were examined at 298.15 K and a C-rate of 1C, which corresponds to a current of $i_{DC}=1.31\times {10}^{-5}$ A.

3.1.1. Influence of the Electrode Volume Fraction

The electrode volume fraction ${\epsilon }_s$ defines the ratio between the solid content of the active mass to the entire electrode. In the case where the electrode consists only of active mass and does not contain any additives, binders etc., the relation ${\Phi }_{LFP}=1-{\epsilon }_s$ defines the porosity of the electrode. Haverkort investigated the effect of electrode thickness and porosity on the electrode overpotential and ionic conductivity [36]. The highest energy efficiency assuming an optimised electrode thickness was achieved for a porosity of 0.6 in an electrode consisting of spherical particles with a Bruggeman correction of 1.5. This value implies a solid content of 40%, which is not common in the models considered, where this value is either below 20–30% or above 55–75% [23,24,28,30,31,34,49,50]. Based on Equations (12) and (23), this value has a linear influence on the specific electrode surface and on the electrode potential. The assumed relation between solid and electrolyte volume fraction $1={\epsilon }_l+{\epsilon }_s$ contributes indirect to the transport equations of the electrolyte within the porous structure (cf. Equations (8), (9) and (11)).

For a spherical particle electrode, an optimal solid content of 30–40% was found in terms of ohmic overpotential and more homogenous lithiation along the electrode (see Figure 3), which corresponds very well to Haverkort’s results. Figure 3b reveals that an increase in the volume fraction from 0.5 leads to a decrease in lithiation in the direction of the current collector at a Depth-of-Discharge (DoD) equalling 1.

3.1.2. Influence of the Electrode Conductivity

The terminology of conductivity in the field of intercalating battery materials must be differentiated into electrical (movement of electrons) and ionic conductivity (movement of ions). In this context, most common work on electrode optimisation for LFP deal with the improving of the electrical conductivity, which is very low for pure LFP ($~{10}^{-9}$ S cm⁻¹) [51]. Delacourt et al. proposed LFP to be coated with carbon, which forms a conductive network that improves electrical conductivity depending on the carbon amount, especially at high current rates [51]. A correlation between electrical and ionic conductivity was observed, with higher electrical conductivity possibly creating a space charge region leading to better ionic conductivity. Byles et al. emphasised the importance of the relationship between the two conductivities and, contrary to the prevailing opinion, showed the importance of the ionic conductivity using the example of manganese oxide [52]. Nevertheless, the ionic conductivity is usually expressed only in terms of the Li-ion diffusion coefficient [52], as was also assumed in this modelling approach and only the electrical conductivity was examined.

Figure 4 illustrates the influence of the electrical conductivity on the cell voltage in relation to the specific discharge capacity. According to Ohm’s law Equation (12), electrical conductivity has a direct influence on the electrode potential, with lower-quality conductors causing a higher potential. The lowest electrical conductivity of 0.005 S m⁻¹ by Srinivasan et al. [34] in combination with the chosen default values was not applicable to the model and led to an insufficient gravimetric capacity. Thorat et al. pointed out the difference between wet (electrolyte-flooded) and dry (bulk) electrical conductivity, with dry electrical conductivity being ten times higher [26]. A more precise specification was nowhere to be found in any further modelling approach. The comparatively low values of 0.03 S m⁻¹ determined by Kashkooli et al. [30] and 0.04 S m⁻¹ determined by Saw et al. [24] also hindered the full activation of the LFP electrode. It is noticeable that the lithiation for low conductivities (<10⁻¹ S m⁻¹) is strongly inhomogeneous and depends on the height of the electrode (cathode thickness). The value of Li et al., i.e., 0.5 S m⁻¹, was already sufficient for activating the entire thickness of the electrode [27]. However, this value still increases the ohmic overpotential. Only values above >10⁻⁰ S m⁻¹ no longer show any noticeable changes. The value of 16 S m⁻¹, which corresponds to a carbon content of 4.75% within the LFP [51], was chosen to be the best because the investigated freeze-casted electrodes have a similar carbon content of 5%. Higher values seem to be implausible when comparing all the examined values. Since the majority of the most models assume an electrode thickness between 50 and 75 µm, the massive deviations in the values are obviously not significant. It is thus questionable to use this parameter for model fitting.

However, worth mentioning is the general shift in lithiation at higher electrical conductivities, which is attributed to better lithiation near the anode due to the improved electron transport within the porous electrode. At low conductivities, the electrode is first lithiated near the current collector and then, with increasing lithiation, also near the anode. At higher conductivities, the lithiation starts constantly near the anode and moves sequentially up the entire electrode to the current collector, as is depicted in Figure A1.

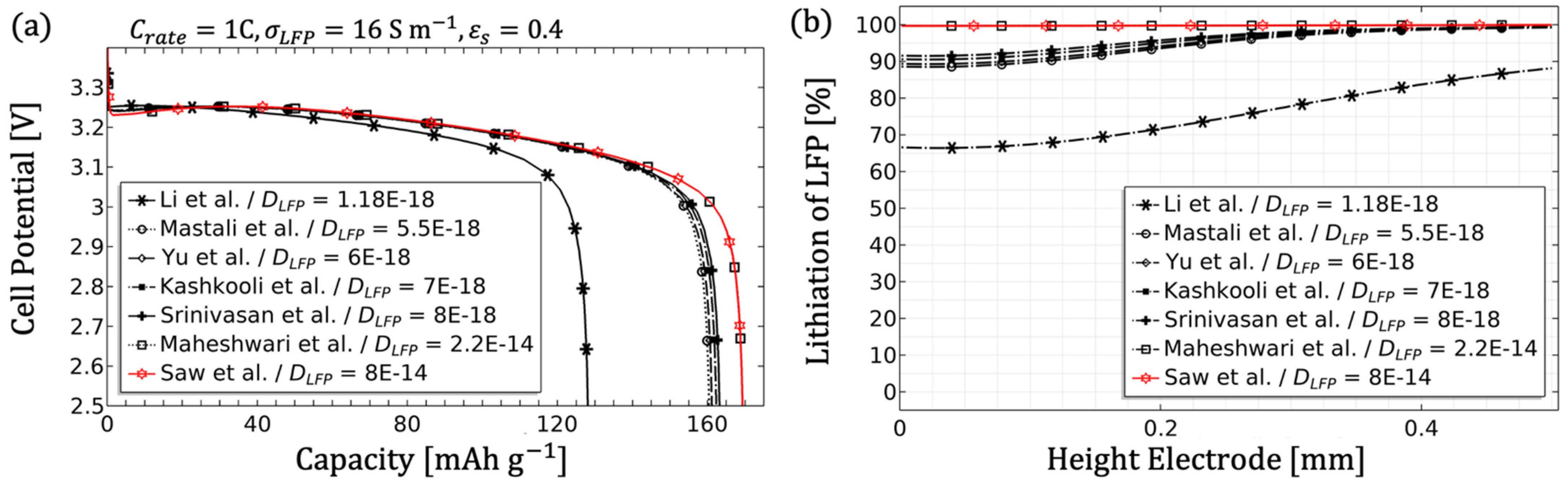
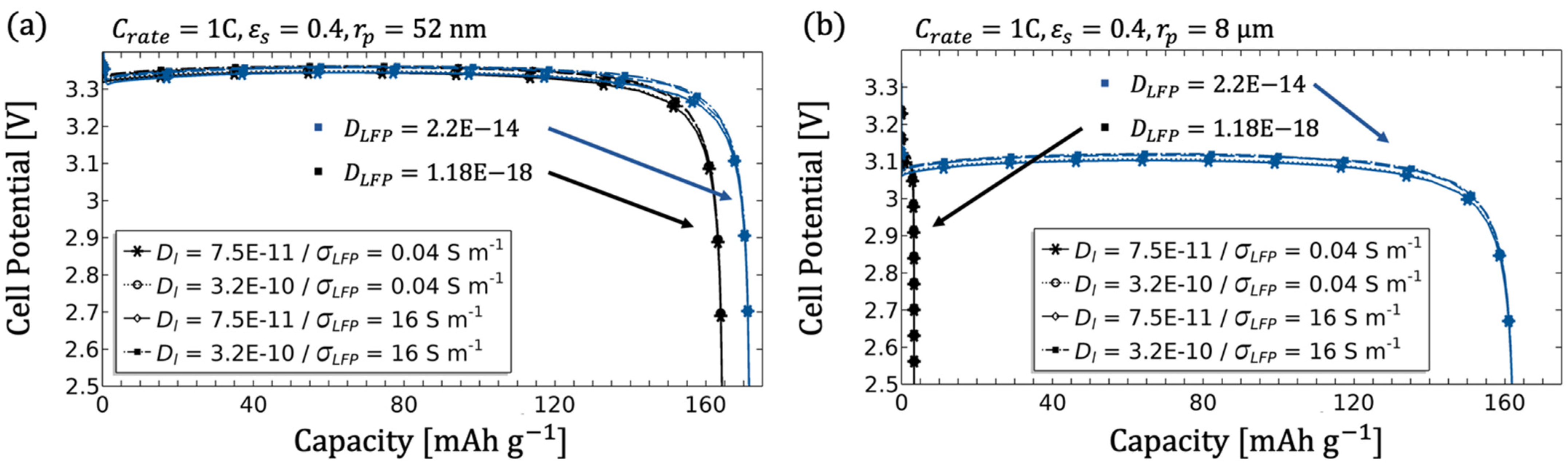
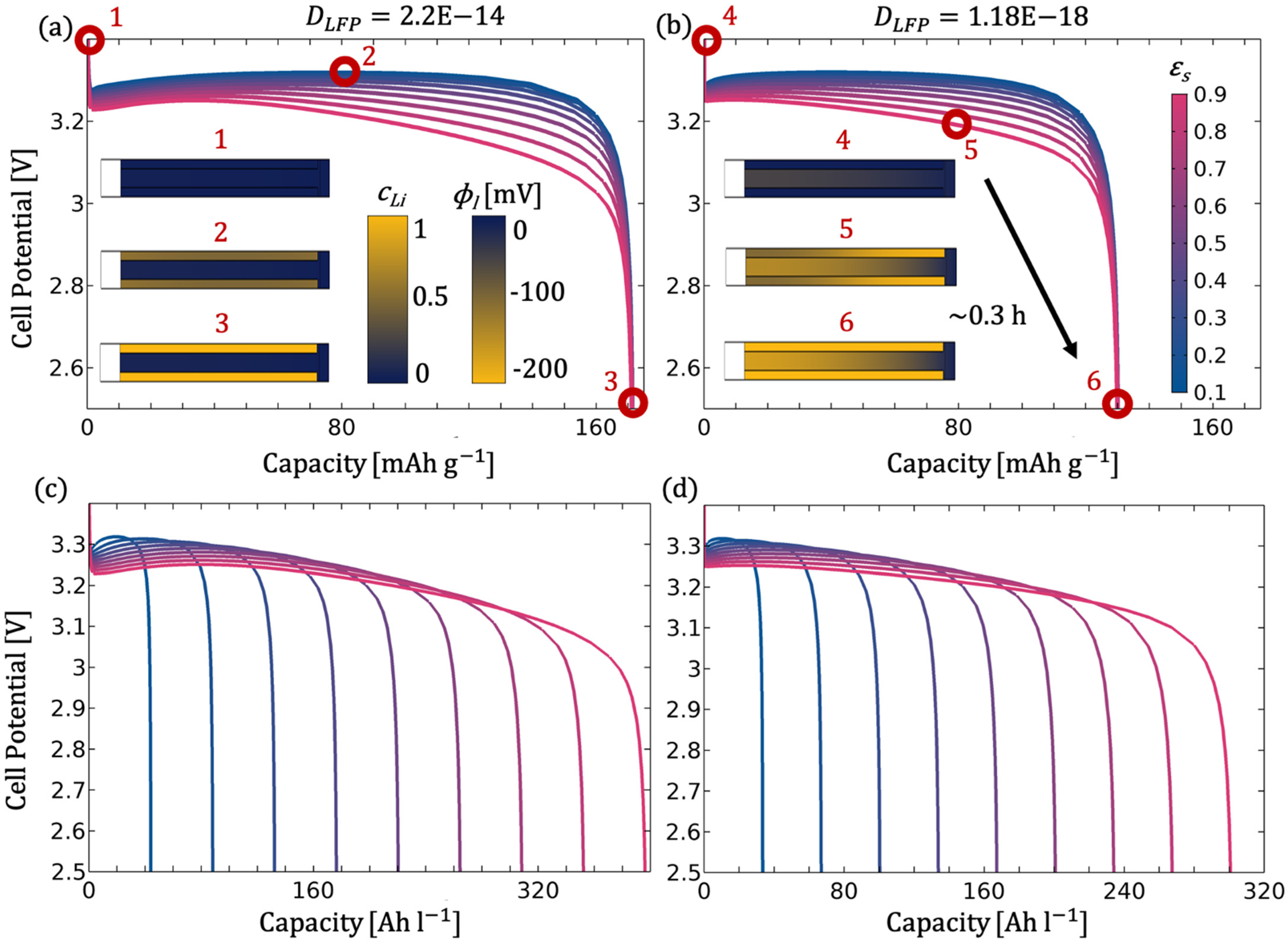
3.1.3. Influence of the Electrode Diffusion Coefficient

The diffusion coefficient of the LFP electrode is a measure of the mobility of the lithium ions in the solid phase. Theoretically, a higher diffusion coefficient allows an improved penetration depth per time into the material as a result of Equation (24). Consequently, an unfavourable combination of current rate and material thickness can lead to limited lithiation of the electrode and can reduce the capacity. In addition, the diffusion coefficient is far from constant and can lead to further limitations depending on the condition, like particle size and shape, concentration or temperature. This was first implemented by Srinivasan and Newman as a concentration-depended diffusion coefficient based on the core-shell theory [53]. This model assumed a growing shell, the so-called lithium rich phase, and a shrinking core (lithium poor phase) during discharge. This approach was extended by Safari and Delacourt [32] to simulate discharging as well as charging. Further approaches are presented in [54]. The reported magnitudes of the diffusion coefficient differ greatly for the same material, partly due to the problematic determination of the diffusion coefficient [55]. In the models, this parameter was often approximated by fitting, which may also account for the discrepancy [29,31,32]. Here, the temperature and $So$L dependent formula of Li et al. [27] is implemented and the prefactor of $1.18\times {10}^{-18}$ was replaced with the values found in literature.

When comparing Figure 5b or Figure 4b, it can be observed that a sufficient solid diffusion coefficient ensures a complete lithiation (see Equation (17)) of the electrode.

Insufficient values reduce the penetration depth (see Equation (24)) and lead to an increase in the lithium-ion concentration at the surface over time, resulting in a massive electrolyte overpotential caused by the intercalation flux (see Equation (25)). The lowest prefactor, i.e., $1.18\times {10}^{-18}$, of Li et al. [27] at 1C reduces the theoretically achievable specific capacity of 170 mAh g⁻¹ by approx. 25%. Increasing the prefactor 4.66 times ($~5.5\times {10}^{-18}$ from [31]) leads the limitation to decrease to approx. 6%. The effect of the prefactor is most pronounced in this range. Maheshwari et al. [29] and Saw et al. [24], presenting values situated four orders of magnitude above the previously considered values, utilise the full potential of the electrode. For further consideration in this work, the prefactor of $2.2\times {10}^{-14}$ was chosen, since this value is sufficient for completely activating the electrode and higher values have no additional influence on the performance. Based on the problem of determining the diffusion coefficient [56], this value is a reasonable fitting parameter for the capacity of a model, as there is no significant impact on other parameters.

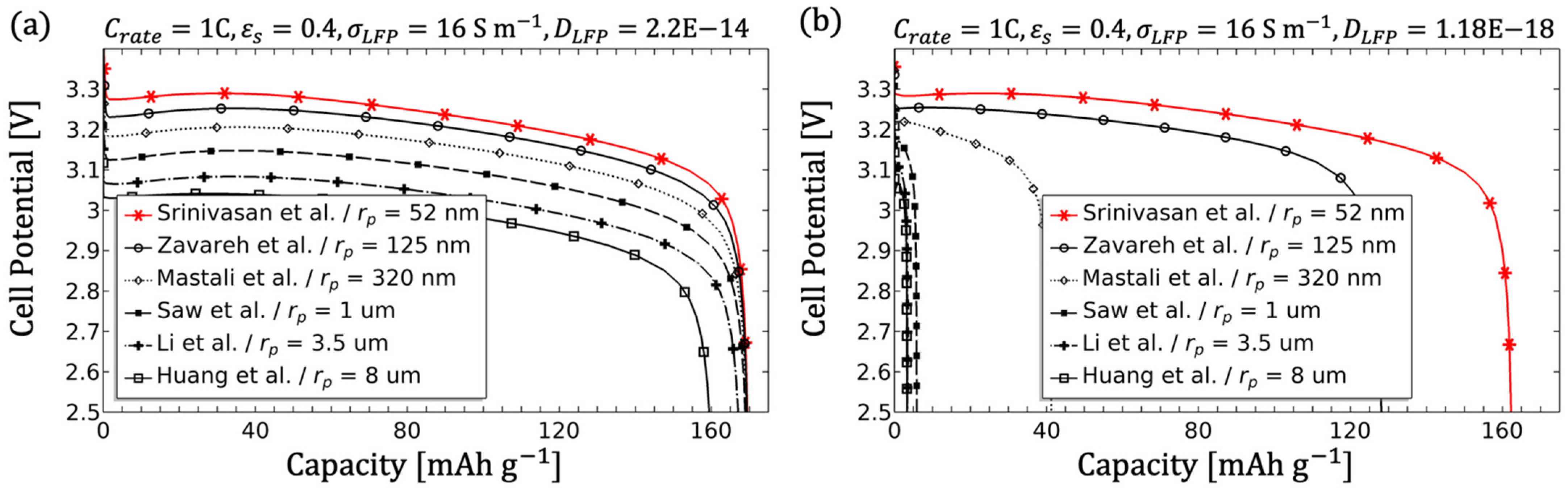
3.1.4. Influence of the Particle Radius

Both in this work and in almost all investigated literature models, a uniform spherical particle distribution was assumed and thus the particle radius has a direct influence on the specific electrode surface (see Equation (23)). A larger diameter of the particles reduces the surface area, which leads to a diminished intercalation flux (see Equation (25)) and thus a higher overpotential (see Equation (13)). Maheshwari et al. used this parameter to simulate the different charge and discharge behaviour of LFP instead of the diffusion coefficient or the reaction rate [29]. Srinivasan and Newman used a particle distribution with two sizes to improve the simulation of the discharge behaviour at different C-rates, as the approach of a concentration-dependent diffusion coefficient was not sufficient [53]. Farkhondeh and Delacourt also used this idea but with four particle sizes, which improved the reliability of the model at increasing current rates [54]. Garcia et al. halved the particle size of the random one-sized particle distribution, which resulted in a more homogeneous concentration distribution at 4C discharge rate [37]. Wu et al. found that limited performance related to a low electrode diffusion coefficient can be improved by reducing the particle size [57]. They also found that smaller particles are not always better performing, as larger particles showed better performance at medium current rates.

As shown in Figure 6a, at a constant current rate of 1C, an increasing particle radius from 52 nm up to 8 µm results in a logarithmic growth of the ohmic overpotential by approx. 240 mV as long as diffusivity through the electrode is guaranteed. The larger the particles, the smaller the influence of porosity, as solid diffusion predominates over diffusion in the electrolyte. Consequently, as illustrated in Figure 6b, using the smallest reported diffusion prefactor of $1.18\times {10}^{-18}$, it results in reduced electrode utilisation. The particle radius is mainly linked to Equations (22) and (25) and can influence both the ohmic overpotential and the specific capacity in connection with the solid diffusion coefficient. Since a uniform particle size distribution is unusual in real samples, it should be considered when modelling and, in the best case, be described by a real particle size distribution [53]. Although the value of Srinivasan et al. [34], i.e., 52 nm, gives the best performance, an average particle radius of 125 nm was taken for further consideration since it was derived from preliminary measurements [39].

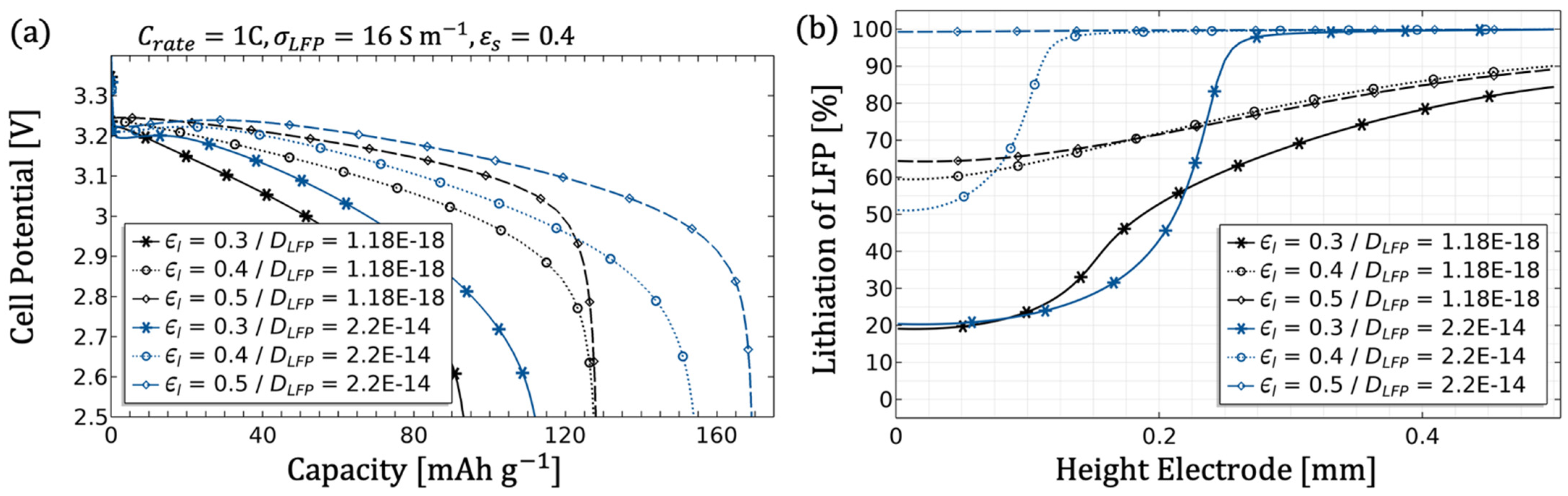
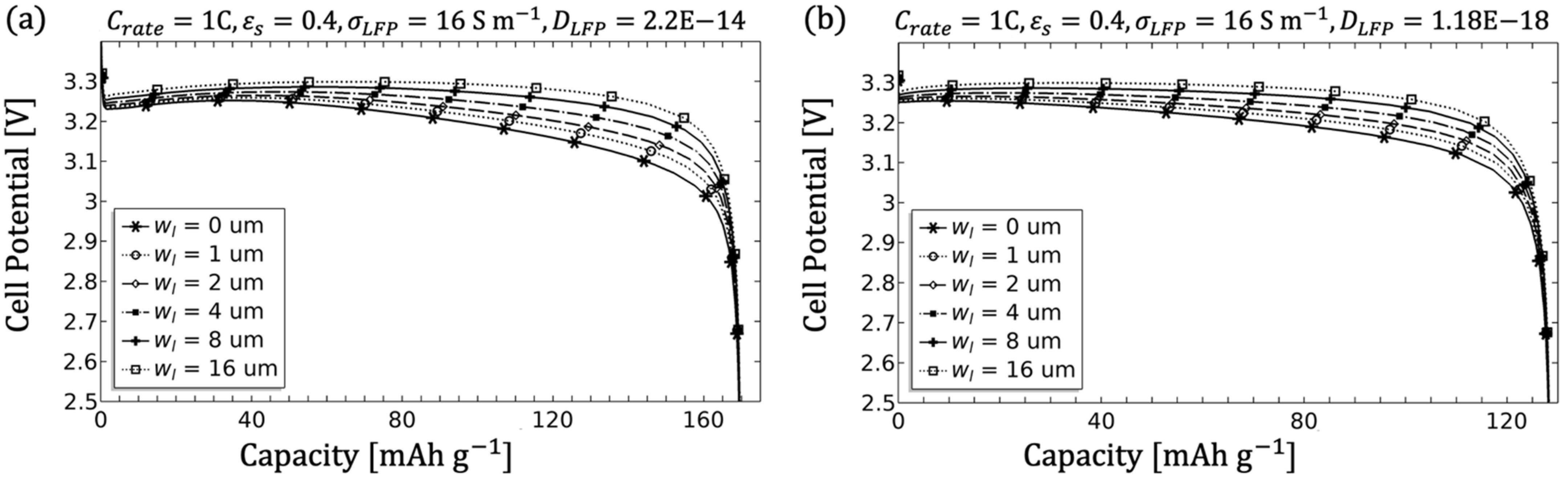
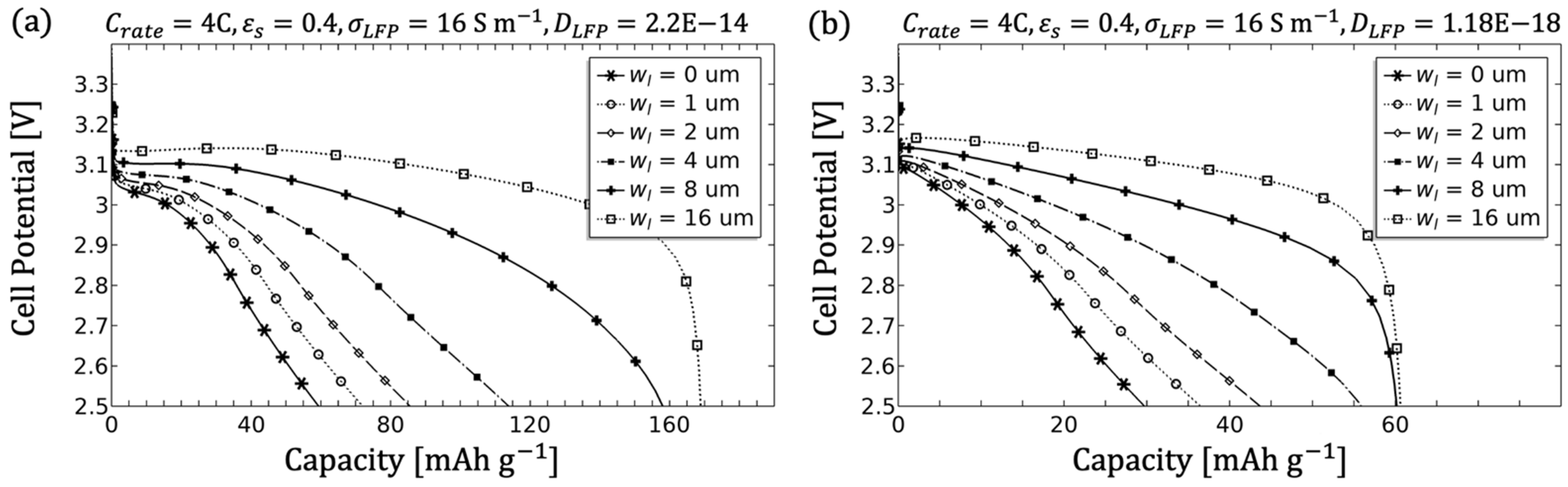
3.1.5. Influence of the Filler Content

The filler (e.g., binder) is an electrochemically inactive material within the solid electrode and has its own microstructure. In most models, it is only considered as a volume fraction-reducing constant of the pores $1={\epsilon }_l+{\epsilon }_s+{\epsilon }_{filler}$. Landesfeind et al. showed that the amount and type of binder, in addition to reducing the pore size, can also significantly increases the tortuosity, resulting in a lower charge capacity and higher overpotential [58]. Hu et al. demonstrated that the material of the binder can also participate in ion transport [59]. The more amorphous and the lower the glass transition temperature, the better the Li ions can penetrate the material and thus have less of a passivating effect. So far, only Lu et al. and Daemi et al. have developed a 3D model for NMC using a dual-scan superimposition technique that reveals both the microstructure of the binder and the structure of the electrode [38,60]. The heterogeneous structure of the electrode caused an unbalanced charge transport and a non-uniform intercalation behaviour [38]. This finding indicates that modelling based on the volume fraction only can be erroneous. However, this parameter was used to show the influence for the majority of the models by keeping the solid fraction constant and reducing the volume fraction of the electrolyte.

Reducing the pore volume decreases the amount of electrolyte inside the porous electrode, which consequently diminishes the lithium-ion transport in the liquid phase (see Equation (11)) and the diffusivity (see Equation (8)) and the ionic conductivity (see Equation (9)) of the electrolyte. The effects of the latter two parameters will be discussed in the next subsection. The filler content changes the transport equations in several ways, i.e., the influence is not immediately obvious. In simple terms: A higher filler content reduces the diffusion length from the separator towards the current collector, which can lead to a lower utilisation of the electrode depending on the thickness, as depicted in Figure 7b.

3.1.6. Influence of the Electrolyte

The electrolyte is not a direct parameter for electrode optimisation. However, due to the porous electrode structure, it is inevitably omnipresent at the phase boundary and plays a decisive role as a supplier in the charge transport through the electrode and in the distribution of the Li ions within the electrode. Therefore, it is obvious that the properties of the electrolyte have a significant influence on the cell performance. Unfortunately, there are only a few approaches or complete characterisations for the multitude of possible electrolytes [61], which makes a universal model impossible. Some of the investigated models assumed no transport limitations, resulting in a constant diffusion coefficient [14,24,49,62]. Others take into account a concentration dependence, in which the diffusion coefficient falls exponentially with increasing concentration [26,53,54]. According to Lundgren et al. the concentration dependency is not sufficient and must be supplemented by an additional temperature dependency, which is challenging due to the lack of data [61]. Valøen and Reimers have done an extensive study on the electrolyte LiPF₆ in a mixture of PC/EC/DMC, in a temperature range between 263 and 333 K and in a concentration range between of $7.7\times {10}^{-6}$ M and 3.9 M [41]. The empirical-analytical form for the diffusivity and for the ionic conductivity has been successfully used in many models [27,28,31,47]. Valøen and Reimers have also pointed out that the magnitude of the diffusion coefficient for their composition are similar to those of EC/EMC and EC/DEC, which makes an adaptation evident [41]. The results of Berhaut et al. confirm and extend this statement to the mixture of EC/DMC [63]. However, pure EC and DMC have very different properties in combination with Li ions [64], meaning that the formula cannot cover all combinations of solvents and an adaptation is necessary. This work uses the formulas given by the Equations (3)–(5), which were modified to obtain the reported values at 1 M and 298.15 K.

Figure 8a,b show that the default value ($3.2\times {10}^{-10}$ m² s⁻¹ at 298.15 K and 1 M from [27]) allows full activation of the electrode. Halving the prefactor, which corresponds to an electrolyte diffusion coefficient of about $1.5\times {10}^{-10}$ m² s⁻¹ reported in [26], shows a considerable loss of energy in which the entire length of the electrode is not sufficiently supplied with lithium ions. Even lower values intensify this effect and, in addition to a massive loss of specific capacity, also lead to a drop in cell potential. The electrolyte diffusion coefficient influences the diffusion term in Equation (11) and thus the Li-ion transport in the liquid phase. The already mentioned filler content scales Equation (11) not only in terms of diffusivity. Since the simulation of both parameters produces similar results, this implies that transport by diffusion is the dominant process. As already mentioned in the subsection on electrode conductivity, this effect may not be noticeable in most models, as it only occurs at a penetration depth of 100 µm, even with a low diffusion coefficient, as depicted in Figure 8b. However, it should be critically noted that the electrode has already been optimised for pore volume at this point.

Besides the diffusion coefficient, the ionic conductivity, the activity and the transport number are properties of the electrolyte. The transport number is often reported as 0.363 for all concentrations and temperatures [23,26,29,41,50]. Maheshwari et al. justified a constant value by the fact that there are no significant changes up to 5 C discharge current [28], which the simulations confirm. Nevertheless, a concentration and temperature expression can be obtained from Li et al. [27] or Lundgren et al. [61] for further investigations. Slight changes of the transport number have no effect on the discharge curve, as shown in Figure 9a.

Like the diffusion coefficient, the ionic conductivity depends on the solvent mixture, temperature and concentration (see Equation (3)). Prada et al. demonstrated that the maximum value of the ionic conductivity at 1 M can vary by a factor of five based on the data found for different compositions of the solvents [65]. In most of the literature, the analytical form of Valøen and Reimers was used or modified [41]. The same goes for this work: the formula given by Valøen and Reimers was implemented and linearly scaled to match the reported data at 298.15 K and 1 M.

The ionic conductivity mainly relates to the migration term in Equation (1), and it is a measure of ion movement through an electrical solution by applying an external electrostatic field. Since migration has a minor influence on the ion transport, values above 0.77 S m⁻¹ have no influence on the lithiation and almost none on the voltage curve, as depicted in Figure 9. In contrast, the lowest value of 0.25 S m⁻¹ strongly flattens the voltage plateau with increasing discharge capacity, but practically no capacity loss occurs. This effect could be an interesting fitting parameter due to the uncertainty of using different electrolyte compositions.

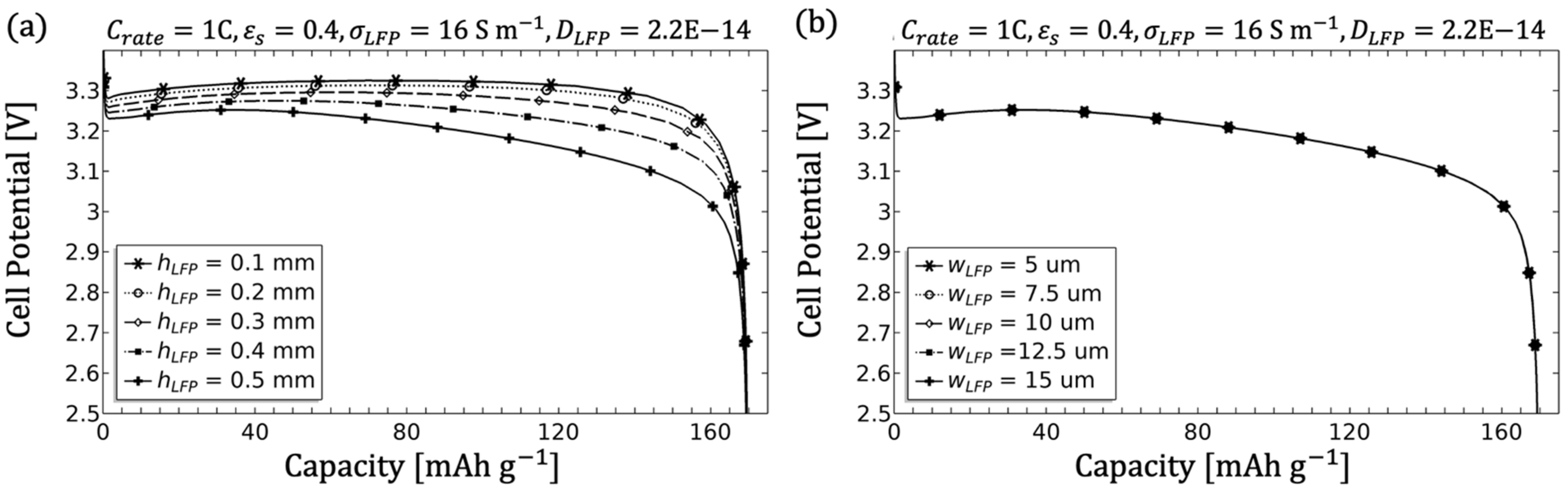
3.1.7. Influence of the Geometry

According to the fact that most models and commercial products work with very thin electrodes, the aforementioned assumptions on the influence of the electrode thickness and its width are validated below. In theory, an increase in electrode thickness and density leads to an enhanced specific capacity, while the proportion of cell dimension remains the same. Thus, a logical conclusion would be that thick and dense electrodes would lead to the highest measurable values. However, this is not the case, as ion transport can have a limiting effect on the specific capacity beyond a thickness of ~100 µm [66].

Srinivasan and Newman studied this effect on discharging to achieve the best specific energy and proposed thin electrodes of 135 µm with a solid content of 66% for high C-rates and thick electrodes of 550 µm with a solid content of 85% for low C-rates [34]. Zheng et al. investigated the thickness of both LFP and NMC electrodes and discovered for both materials an increasing capacity loss over the number of cycles with increasing electrode thickness due to higher internal resistance and stress accumulation [67]. Finally, Haverkort has developed a general approach for determining the optimal thickness according to the overpotential as a function of the current rate, Tafel slope and ionic as well as electrical conductivity [36]. In contrast to this extensive analysis, in this study all parameters remain constant and only the height and width were varied with an adjusted current.

As expected, the width of the electrode has no influence on the cell performance (see Figure 10b), since the mass transport is mainly assumed along the electrode height direction. This statement is not generally valid and should be examined for heterogeneous electrodes or other boundary conditions. The increase of thickness mainly influences the diffusion length through the porous medium in Equation (11). Figure 10a shows the already optimised electrode, in which the change in height has a marginal impact on the overpotential and thus on the energy density, but it confirms the tendency towards a lower energy density with an increasing height.

As mentioned previously, thick electrodes are rather uncommon, so in the following the identified critical parameters for Li-ion transport were verified for thin electrodes. This has been done by applying the best and the worst performing values of both electrode and electrolyte diffusivity, the electrode conductivity and the particle radius to a 50 µm thick electrode.

Figure 11a demonstrates that an electrical conductivity of 0.04 S m⁻¹ and a diffusion coefficient of $1.18\times {10}^{-18}$ of LFP, as well as the lowest electrolyte diffusion peak of $7.5\times {10}^{-11}$, have practically no effect on the cell performance for thin electrodes as long as the particle radius is small. Figure 11b shows that with bigger particle radius the associated type of ion transport (solid or liquid phase) has a tremendous influence, even on thin electrodes. It can be deduced that in the investigated models, the particle size distribution (PSD) in combination with the diffusion coefficient of the electrode is decisive for the achievable capacities.

Consequently, it is questionable how useful it is to consider the conductivity and diffusion coefficient of the electrolyte as fitting parameters for thin electrodes, as there may be a large deviation to achieve a perceptible effect.

3.1.8. Influence of the Tortuosity

The tortuosity describes how straight a transported element, for example electrons or ions, passes through a porous electrode. A tortuosity of one represents a path that leads straight through the entire thickness of the electrode without any bypasses. Every redirection through the electrode increases the value. With respect to diffusivity and conductivity in porous electrodes, a practical approach has been established by Bruggeman, an approach which states that the less porous the electrode, the more inhibited the mass transfer due to increasing tortuosity. For a uniform spherical particle distribution, the volume fraction values are weighted with an exponent of ~1.5 (see Equations (8)–(10)) and seems to be very popular in battery simulations. Thorat et al. have shown that the Bruggeman relationship between porosity and tortuosity provides a good approximation, but the determined tortuosities were a factor of two larger than expected from this approach [25]. Landesfeind et al. explained the deviation due to the additional inactive materials, with a higher binder content leading to higher tortuosities [58]. Furthermore, using graphite electrodes as an example, they emphasise that the tortuosity can have different values even if the porosity remains the same. Tjaden et al. have discussed the limitations of Bruggeman’s relation and have repeatedly shown by X-ray tomography that the real tortuosity in heterogeneous materials deviates significantly from the estimated values by Bruggeman [40]. Besides the fact that the tortuosity is often underestimated [68], Forouzan et al. studied the influence of the tortuosity by using a quasi-heterogeneous electrode model with three different porosity and tortuosity zones [69]. They underline the importance of a low tortuosity and a homogeneous structure for fast chargeability. For high energy density, a close-packed array of ordered particles with a stronger focus near the counter electrode was evaluated by Vijayaraghavan et al. using a Gaussian PSD [7]. Such a hybrid structure can be realised by horizontally aligned electrolyte channels through the entire electrode [66,70]. To investigate the influence of tortuosity in more detail, the electrode was divided in the middle (illustrated in Figure 2b), creating an electrolyte channel with an adjustable width $w_l$ and a tortuosity of one, which generated a superior macrostructure, while all other parameters were kept constant.

The curve in Figure 12a shows a slight improvement of the ohmic overpotential. In comparison, the improvement is also observable with a reduced diffusion coefficient of the electrode as shown in Figure 12b. The creation of a growing electrolyte channel has the same effect as reducing the electrode height (cf. Figure 10a). The impact on the transport equation of the lithium ions in the electrolyte (Equation (11)), however, is of a different nature. In the former, the transport is facilitated by a reduced diffusion length, in the latter, by the elimination of the dependency of the electrolyte volume fraction. However, solid diffusion keeps dominating and even with the additional transport path, the electrode cannot be completely activated at 1C.

Considering higher current rates (as in Figure 13 with 4C), the ion transport can be improved by the electrolyte channel and the ohmic overpotential can be reduced. This positive effect is particularly impressive if the solid diffusion is also optimised (see Figure 13a). In this case, a channel with a ratio 2:1 can completely lithiate the entire electrode even at 4C. It has been revealed that the microstructure correlated with a macrostructure has enormous potential for optimising electrode materials. Conversely, this means that transport paths that are not well aligned in the electrodes can lead to a macroscopic loss of performance [7]. In addition, as already shown in Figure 6, the performance is strongly dependent on the solid diffusion and thus also on the particle radius. If the complete activation of the active material is hindered by a poor solid diffusion, the capacity of the electrode can be better utilised by a reduced particle radius (cf. Section 3.1.4). This effect is independent of the macrostructure and has a scaling effect on the discharge curves in Figure 13b, as shown in Figure 6b. If the electrode can already be fully activated, the particle radius only has an effect on the reduction of the ohmic overpotential, as shown in Figure 6a, which is also independent of the macrostructure.

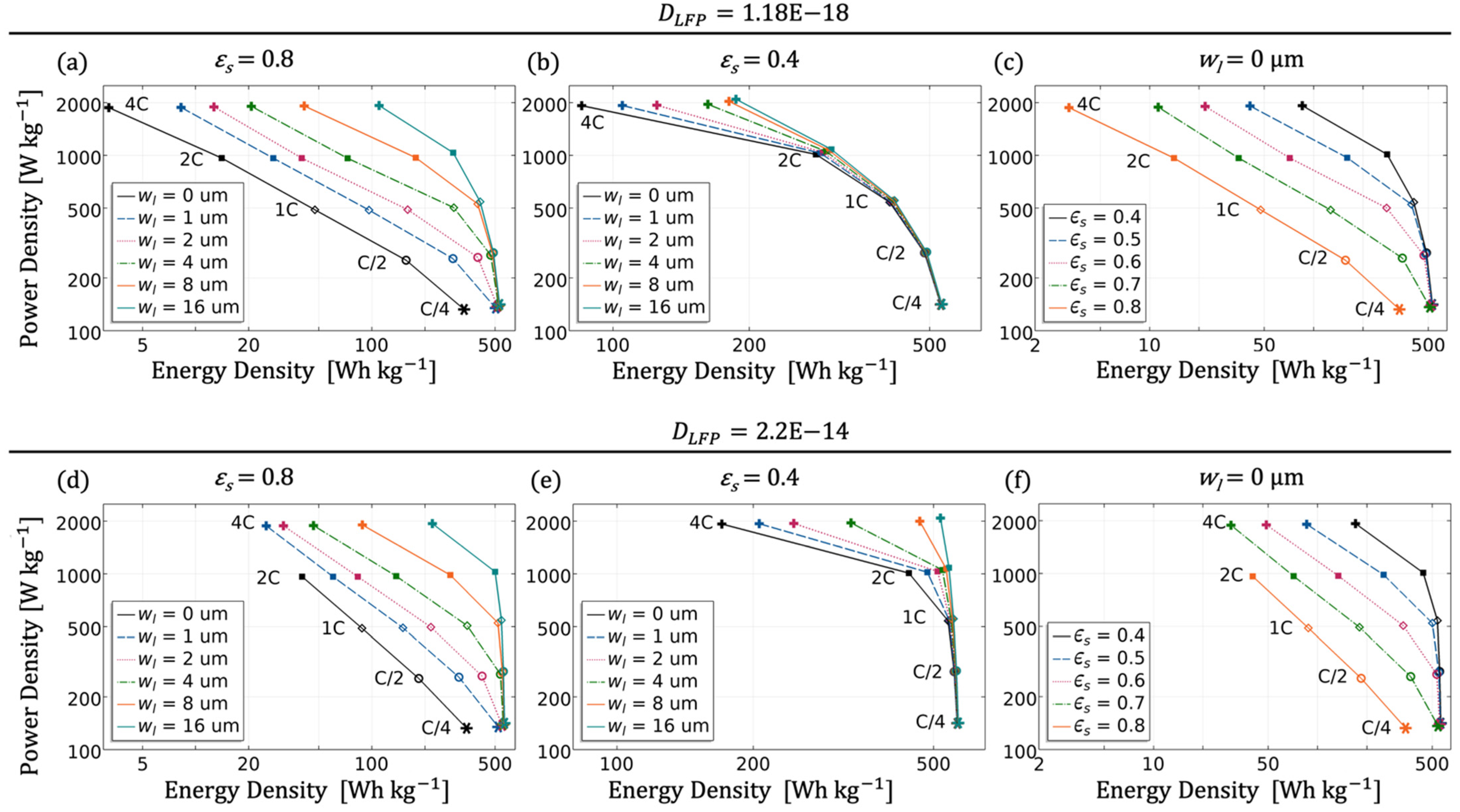
3.2. Performance Tests

The performance of the battery depends not only on the design parameters but also on external circumstances such as the charge/discharge current or the temperature. Consequently, it is advisable to define the desired operating range of the battery first and then to determine the best possible parameters within the limits. As the main purpose here is to show tendencies, which should be taken into account in modelling and optimisation, a comparatively selected small current range between C/4 and 4C was used (for comparison: the smallest current in the LFP models noted C/25 [62] and the largest 50C [67]). As for the temperature, the range was limited to the parameters studied by Valøen [41].

The single-structured electrode related to Figure 2a, containing only spherical particles, was analysed in Figure 14. The applied currents are coupled by the electroneutrality condition and influence both the electrode current density governed by Ohm’s law and the electrolyte current density and thus smaller currents show a better performance (shown in Figure 14a). Moreover, higher currents lead to non-uniform lithiation with a stronger incidence near the separator, which increasingly inhibits the flow of ions into the electrode and finally results in a loss of capacity. As discussed for LCO by Kumaresan et al. using Valøen’s approach, the temperature cannot be neglected due to its influence on transport kinetics in both the electrolyte and the electrode [71]. Although there is a macroscopic influence of the temperature (see Figure 14b), some models disregard this dependence for the electrolyte [14,24,26,49,53,54,62]. This is possibly due to the small effect of ~25 mV difference in the ohmic overpotential between 298 and 313 K (shown in Figure 14b), which includes all temperature dependencies for the P2D approach. Li et al. emphasised the heat generation of a cylindrical 26650 LFP cell during discharge, which is mainly driven by the positive electrode [27]. At 1C, the average cell temperature increased from 298 to 310 K and at an applied current of 5C, the temperature exceeded 333 K. This is outside the comfortable range between 288 and 308 K and can lead to rapid degradation and other unwanted side effects [72], and the models are expected to result in unrealistic behaviour without appropriate temperature dependencies. Temperatures below 298 K decrease the ionic conductivity and diffusivity in both the electrolyte and in the electrode, resulting in visibly reduced capacity and average cell potential (depicted in Figure 14b).

Since a significant influence of macrostructure and microstructure was noticeable during the simulation of the individual parameters, especially with regard to the optimisation of the LFP electrode, the parameter combination of porosity and electrolyte channel width is discussed in more detail below.

By reducing the porosity from 0.9 to 0.1, the simple relationship ${\epsilon }_s=1-{\Phi }_{LFP}$ proportionally increases the solid content of the electrode, when the filler content, e.g., binder, additives, etc., is neglected. More active mass means a higher capacity, but in theory and contrary to Figure 3, the gravimetric energy density related to the active mass is not influenced. If the volume of the electrode does not change and the increase in material results from densification, an increase in volumetric capacity follows, as illustrated in the simulation in Figure 15c,d). The loss of gravimetric capacity can be explained on the basis of the C-rate. In order to achieve 1C, the current is set by the amount of active material and increases accordingly with more LFP content. Thick and dense electrodes, however, are unsuitable for higher currents [70], which leads to the aforementioned capacity loss by reducing the porosity (microstructure). Furthermore, an increased current also results in a higher ohmic overpotential (cf. Figure 14a). By using a superimposed macrostructure, such as the given example of two lamellae, the latter can be completely lithiated for both a poor (Figure 15b-6) and a good (Figure 15a-3) solid diffusion coefficient. The microstructure with a solid content of 90% (Figure 15b-5) further affects the uniformity of lithiation from the separator to the electrode, creating a concentration gradient in the electrolyte, which leads to an increase in overpotential up to 200 mV. The gravimetric capacity, however, remains unaffected due to the additional transport channel for Li ions.

The effect of the higher-level macrostructure is particularly evident when a specific performance of an application is required. If sufficient ion transport is ensured through the electrode or if adequate replenishment zones exist, densification of the active material in the substructure can even increase the performance and the capacity in relation to the cell area (see Figure 16a,c).

However, in relation to the area or volume, a superimposed structure causes an increase in the porosity of the entire electrode (here at $w_l=16$ µm this corresponds to ${\mathsf{\Phi }}_{LFP}\approx 0.5$). As shown in Figure 16b, a single structure with optimised parameters and a solid content of approx. 50% can even slightly improve the surface capacity (Figure 16d), and the gravimetric capacity reaches the same value. Although the surface area is halved compared to the two-structure electrode, the surface capacity is not doubled. The effects on performance are more difficult to estimate, and the influence of tortuosity increases, which leads to additional uncertainty [7,40].

When looking for the best electrode in terms of cost optimisation, the potential of the active material should be fully utilised. In terms of the cell, this means a high power and energy density and, in the best case, a higher stability against higher current rates. Only for LFP, the possible achievable gravimetric capacity is about 170 mAh g⁻¹. With a nominal cell voltage of 3.2 V, this results in a formal energy density of 544 Wh kg⁻¹ and at 4C in a power density of 2176 W kg⁻¹. In the following, the time average of the voltage curve was used to calculate the power and energy density instead of considering the nominal cell voltage.

Analysing Figure 17, it is noticeable that at low currents of 0.25C the parameter variations of macrostructure and microstructure are negligible. A special case is the single structure ($w_l=0$) with very high density (${\epsilon }_s=0.8$), which has both lower power and lower energy density. A higher porosity ensures better Li-ion transport in the electrolyte due to the reduction of tortuosity within the electrode, and consequently higher currents can be applied without any loss of power [7]. In case of the thick single electrode with a porosity of 60%, currents up to 2C cause an energy loss of ~20%, and at 4C the loss is even ~70%. The situation becomes more dramatic if, in addition, the lithiation is hindered by a lower solid diffusion, which means a loss of 85% at 4C. The best performance was identified for the lamellar structure with the widest electrolyte channel and a solid content of 40%, resulting in an overall porosity of 80%. The combination of the two structures enables an almost constant energy density (510~550 Wh kg⁻¹) with increasing current up to 4C, provided there is sufficient solid diffusion. As already discussed, a high content of active material leads to a reduction in power and energy density. The electrolyte channel can counteract this in a similar way, e.g., through increasing the porosity in the single structure. Thus, a lamellar structure offers more adjustment parameters for designing an optimised electrode especially intended for high currents. For small currents up to 1C, it is rather unimportant whether the necessary increase in porosity for a good performance with thick electrodes occurs through the macrostructure or through the microstructure, as long as the overall porosity remains approximately the same (as depicted in Figure 17a,c). This statement could be relativised in that sense as real tortuosities are used for the microstructure, and they are often significantly larger [25]. The validation in the next subsection also shows the limitation of the idealised P2D approach, since although the cellular structure presented, i.e., comparable to a highly porous electrode, had a similar porosity to the lamellar structure, the performance of the lamellar structure was significantly better.

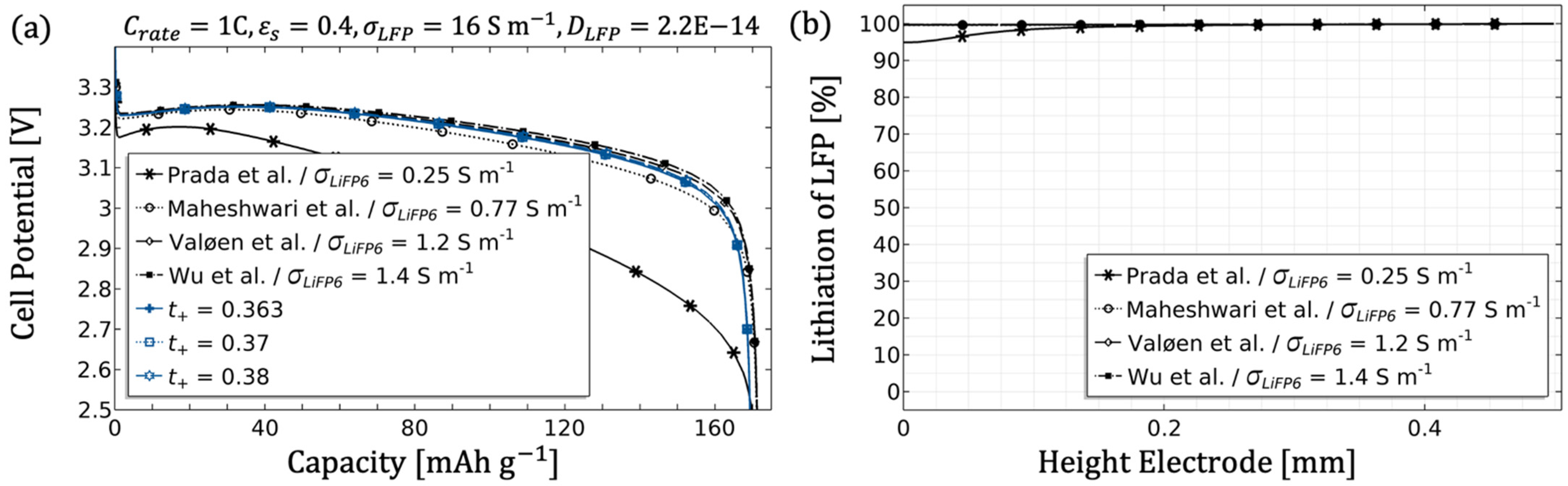
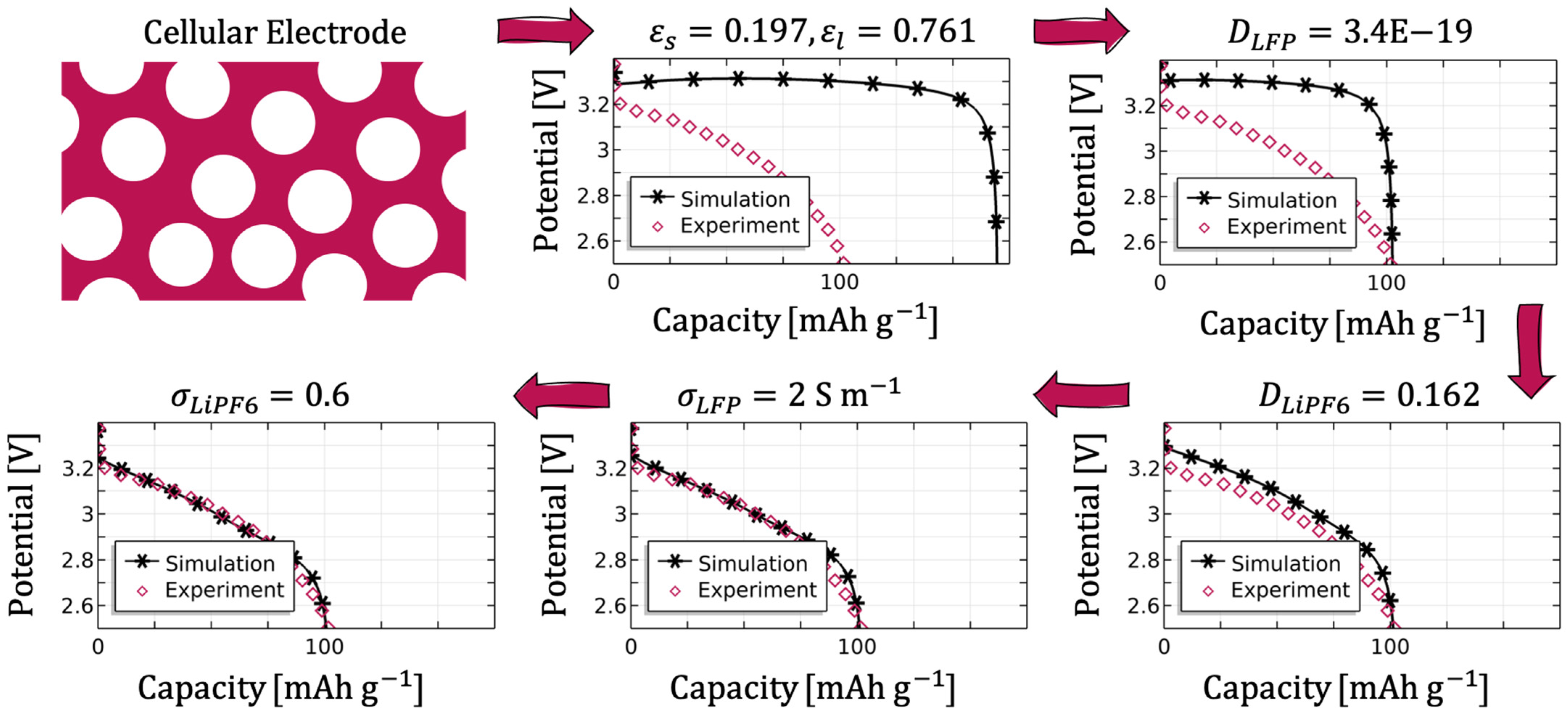
3.3. Validation and Usability

The geometric modelling was based on preliminary studies in which two LFP electrode structures (cellular and lamellar) were fabricated by freeze casting [39]. The two structures showed different discharge performances. Those structures were classified only by the total porosity and the achievable gravimetric capacity, which makes modelling difficult due to the many degrees of freedom. In the following, a procedure is proposed on how to use the already shown simulations to approximate the modelling and the experiment when the uncertainty of the model parameters is high and only geometric values are given:

• All physical parameters that are verified, e.g., by the manufacturer’s specifications or experiments, must be taken into account.
• The best parameter set related to the theoretical study should be chosen for the undetermined parameters in order to start without any limitations.
• The external circumstances such as the discharge or charging current and the temperature must be clearly defined.
• The electrode diffusion coefficient should be determined to scale the achievable capacity (see Figure 5).
• An adjustment of the inhomogeneities can be done by the diffusivity as well as the conductivity of the electrolyte. Since in the porous electrode these two parameters are influenced by the microstructure (see Equations (8) and (9)), an adjustment of the microstructure would likewise be target-oriented (see Figure 7, Figure 8 and Figure 9).
• By reducing the conductivity of the electrode (see Figure 4) or the particle radius (see Figure 6), the ohmic overpotential can be adjusted.

Figure 18 shows the usability of the procedure for the cellular structure from [39]. The geometric approach from Figure 2a was taken for this purpose, the height of the electrode was adjusted to 800 µm, and the values for the calculated solid and electrolyte volume fractions were used. The remaining parameters were taken from the evaluated parameter set, and the discharge current was set to 0.5C at 298 K. First, the solid diffusion prefactor was determined as $D_{LFP}=3.4\times {10}^{-19}.$ Next, the electrolyte diffusion prefactor was reduced until the shape of the discharge curve was achieved. The ohmic overpotential was subsequently fine-tuned by means of the conductivity of both the electrode and the electrolyte.

For the validation of the obtained parameters, the parameter set was applied to the lamellar structure using the geometric model from Figure 2b with an electrolyte channel width of $w_l=10$ µm. Figure 19 shows that the parameters are generally applicable, but the solid diffusion prefactor was chosen insufficiently to achieve the higher gravimetric capacity of ~120 mAh g⁻¹. Hence, a new solid diffusion prefactor was determined with $D_{LFP}=4.5\times {10}^{-19}$. Nevertheless, the measurement compared to the simulation reveals that the mass transport is hindered with decreasing State-of-Charge. According to the procedure, it is obvious to fit the curve next by the electrolyte diffusion coefficient. However, this would counteract the idea of the proposed procedure, as the lamellar and cellular parameter set would no longer be validated among each other. Therefore, it is more obvious to make an adjustment via the microstructural parameters, which are different for the lamellar structure as shown in [39]. The obtained parameter set A is shown in

Table 4. Set of parameters for sets A and B in Figure 19.

Set	${\mathit{D}}_{\mathit{L}\mathit{F}\mathit{P}}$	${\mathit{D}}_{\mathit{L}\mathit{i}\mathit{P}\mathit{F}6}$	${\mathit{\epsilon }}_{\mathit{s}}$	${\mathit{\epsilon }}_{\mathit{l}}$
A	$4.5\times {10}^{-19}$	0.162	0.4	0.35
B	$4.2\times {10}^{-19}$	0.3	0.6	0.35

. Due to the measured porosities, an even higher solid content in the lamella is assumed (see Table 4 parameter set B), and the solid diffusion prefactor had to be modified. This in turn reiterates the importance of microstructure, which has already been emphasised several times, as it has a significant influence on validation.

For more accurate simulations, the microstructure should either be modelled, or the tortuosity and spherical particle assumption should be corrected by appropriate methods or measurements.

4. Conclusions

A two-dimensional electrochemical model was developed for a thick LiFePO₄ electrode to study the design parameters of the electrode. For this purpose, the discharge curves at different parameters and the lithiation of the electrode were examined in more detail in order to understand more about the underlying processes in a visual way. The parameters were taken from a variety of other studies and discussed.

The large deviations in the literature values for both the diffusion coefficient of the electrolyte and the LFP electrode and the electrical conductivity of the LFP electrode have shown almost no effect on the performance or capacity of very thin and porous electrodes up to 100 µm at 1C. Although these parameters are often used as fitting parameters for model validation, the study shows that the nature of the electrode itself has a much greater influence. However, as only little is known about the actual microstructure and how it relates to the performance, major discrepancies between model and experiment can arise. This was shown by a procedure for determining suitable model parameters of a lamellar and a cellular LFP electrode. Valid model parameters could be found for the cellular structure, which are partly applicable to the lamellar structure. Generally, the most important influencing parameters of the microstructure are the particle size, the porosity, the filler content and finally the tortuosity. Especially the tortuosity within the microstructure is characterised by a large uncertainty. By shaping a superior macrostructure, which creates an electrolyte channel with the tortuosity $\tau =1$, the high-current capability is improved. Another positive effect of a wide transport channel is the homogenisation of the lithiation along the electrode.

The value of the electrolyte volume fraction and electrode volume fraction models the microstructure of the electrode. The higher the electrolyte volume fraction, the better the porosity within the electrode. Simulations with barely any macrostructure (solid body) are more affected than electrodes with distinctive electrolyte channels. The diffusion in the electrolyte is still better than in the solid electrode. This is the reason for the poor performance of solid electrodes with low porosity, where the solid diffusion dominates. It leads to a loss of capacity and a linear decrease of the cell voltage with falling State-of-Charge as well as a strong inhomogeneous lithiation along the electrode. An ideal electrode for currents up to 4C discharge and with a thickness of 500 µm therefore has a 16 µm transport channel, a porosity of the macrostructure of 60%, resulting in a total porosity of 80%, a particle size in the nanometre range and sufficiently good solid diffusion to ensure a full activation of the electrode.

However, a limitation of the P2D approach was identified. For a good performance up to 1C, the lamellar structures are negligible as long as the porosity of the whole electrode is the same. The experimental data showed that although the porosity of the cellular structure is similar to the lamellar structure, the lamellar structure has significantly better performance. Real microstructures would support refining the procedure and improving the simulation.

The model used in this work can be applied to a variety of ion insertion battery electrodes to obtain the best parameters for the positive electrode. Both the presented procedure for identifying suitable model parameters and the parameter studies can be used as a tool when few physical parameters are available for an experiment or to critically validate one’s model with the experimental data.