On the Application of the Particle Swarm Optimization to the Inverse Determination of Material Model Parameters for Cutting Simulations

Abstract

The manufacturing industry is confronted with increasing demands for digitalization. To realize a digital twin of the cutting process, an increase of the model reliability of the virtual representation becomes necessary. Thereby, different models are required to represent the experimental behavior of the workpiece material or frictional interactions. One of the most utilized material models is the Johnson–Cook material model. The material model parameters are determined either by conventional or by non-conventional material tests, or inversely from the cutting process. However, the inverse parameter determination, where the model parameters are iteratively modified until a sufficient agreement between experimental and numerical results is reached, is not robust and requires a high number of iterations. In this paper, an approach for the inverse determination of material model parameters based on the Particle Swarm Optimization (PSO) is presented. The approach was investigated by the inverse re-identification of an initial parameter set. The conducted investigations showed that a material model parameter set can be determined within a small number of iterations. Thereby, the determined material model parameters resulted in deviations of approximately 1% in comparison to their target values. It was shown that the PSO is suitable for the inverse material parameter determination from cutting simulations.

1. Introduction

The process design, such as the design of the tool or the choice of the process parameters, of most of the state-of-the-art cutting processes depends on experimental studies that base on “trial-and-error” approaches. This procedure of process design is expensive and time consuming [1,2]. Further, this practice does not meet today’s demands for a digital twin [3,4]. Due to major improvements in computer technology within the last three decades [5], modeling of cutting processes by means of numerical techniques is well established in research today [6]. Among the numerical techniques, the Finite Element Method (FEM) has become one of the most applied techniques to model the cutting process [7]. The advantage of the FEM, especially in comparison to the experimental process design, is given in the capability to predict state variables, such as temperature fields, strains, and strain rates, which are difficult or even impossible to measure during the cutting process [8,9].

When modeling the cutting process by means of FE simulations, various input models are required. Among these input models, an accurate material and friction model was reported to be essential for the success and reliability of the simulated results [10]. The importance of the material model that describes the plastic material behavior is given, since the calculation of many process observables (e.g., cutting force or chip form) can be traced back to the quality of the applied flow stress data [11]. Additionally, the use of an accurate flow stress model is important for further scopes of research by FEM-simulations. The research scope of simulations is extended by using a variety of models and sub-models to expand the calculation of cutting simulations to specific aspects, such as surface integrity, tool wear, or chip breakage [12,13,14].

In the state-of-the-art, different material models are used for cutting simulations. These models can be classified into empirical/phenomenological, semi-empirical, and physical-based constitutive models [15]. Phenomenological material models rely solely on observations, whereas physical-based material models take physical phenomena of the material into account [13], such as micro-structural aspects of plastic deformation [16]. Even though physical-based material models are more appealing in comparison to the non-physical-based models, each physical mechanism brings more parameters into the model, which increases the number of model parameters to be determined [17]. Due to the high efforts when using physical-based material models, empirical models have found more application in FE cutting simulations. The empirical material models often describe the flow stress as function of the strain, strain rate, and temperature and can take effects such as hardening, viscosity, or loading history into account [18].

The approaches used to determine the material model parameters can be categorized into two different groups: direct and inverse determination. When using the direct determination, the model parameters are fitted with experimental data from conventional quasi-static and/or dynamic material tests, such as the Split Hopkinson Pressure Bar (SHPB) test. Since the achievable thermo-mechanical loads in terms of strains, strain rates, and temperatures during these tests are lower than those occurring in the metal cutting process, extrapolation into the cutting regime becomes necessary [19,20,21,22]. The problem of extrapolation can be circumvented when using inverse techniques. The inverse technique was suggested by Venuvindo and Jin as one of the first [23]. Thereby, the cutting process is utilized as a material test itself, and simulations of the corresponding experiments are conducted while varying the material model parameters until the results of the simulations match those of the experimental cutting investigations [24,25]. The match between simulations and experiments is assessed by different process results, such as the cutting force or the chip form. These process results are called from here on process observables.

One of the first attempts for the inverse determination of material model parameters from the cutting process was presented by Özel and Altan, who utilized flow stress data from low strains and strain rates as starting points for their simulations of the orthogonal cutting process [26]. The agreement between experiments and simulations was evaluated by means of the cutting force, whereby a deviation lower than 10% was achieved. Later, Shrot and Bäker presented an inverse approach to re-identify material model parameters that were taken initially from the literature [27,28,29]. The authors employed the Levenberg–Marquardt algorithm in order to re-determine the material model parameters. The re-identification of the material model parameters finished successfully after a low number of iterations. Albeit, the authors focused on the re-identification of two material model parameters. The influence of the two material model parameters on the flow stress, especially in comparison to the remaining parameters, remains questionable. Further, the re-determined material model parameters can directly be obtained from quasi-static material tests.

A procedure for the inverse determination of material and damage model parameters of AISI 316L was presented by Klocke et al. [30]. The approach is based on the calibration using a lower and an upper value that underestimates and overestimates the target values, assuming a linear relation for the parameters. However, the underlying material model is non-linear and small variations in the material models can cause distinct differences in the modeled flow stress. Later, the authors used this approach for the inverse identification of the material model parameters of AISI 1045 and Inconel 718 [11].

Albeit that there are advantages of the inverse parameter determination from machining experiments, such as the avoidance of extrapolation of flow stress data into the regime of metal cutting, different drawbacks were reported. One challenge of the inverse determination is given by the non-uniqueness of the material model parameters for the domain of investigation [31]. Further, the inverse iterative identification can be time-consuming and might need a large number of iterations [32].

To reduce the number of iterations and to increase the accuracy of the determined model parameter, optimization strategies were used in solving manufacturing optimization problems. For example, in the field of laser cutting Sibalija et al. utilized Particle Swarm Optimization to determine the optimal combination of process parameters to achieve tolerable characteristics of the cut area [33]. Thereby, the authors optimized a cost function that evaluates the relationship between the process parameters and their process measures. Chaparro et al. compared, in their study, a genetic algorithm, a gradient-based algorithm, and combination of both to identify material model parameters for sheet metal forming inversely [24]. The authors showed that both kinds of algorithm were able to fit the numerical with the experimental data. In the field of metal cutting, optimization algorithms were applied to determine process parameters, with respect to surface finish, dimensional deviations, tool wear, or the occurring cutting forces. Chandrasekaran et al. and Yusup et al. published a broad literature review on the application of optimization strategies in these fields of machining [34,35].

To determine material model parameters in the field of metal cutting, Özel and Karpart utilized Particle Swarm Optimization for optimizing the Johnson–Cook (JC) parameters [36]. Therefore, the authors used an experimental database obtained from SHPB tests. Since data from SHPB tests were used and not experimental data from cutting tests, this approach cannot be considered as an inverse approach, but rather as a method for curve fitting. Denkena et al. utilized Particle Swarm Optimization in conjunction with Oxley’s machining theory [37]. Therefore, the widely reported drawbacks resulting from the assumptions and simplifications of Oxley’s machining theory underlie this approach [38]. Since the iterative procedure aimed to match the experimental forces by adjusting the JC-material model as input for Oxely’s machining theory, the procedure used the intermediate step of the analytical model.

Bergs et al. utilized the Downhill Simplex Algorithm (DSA) for the inverse material model parameter determination from FE cutting simulations. At first, the general applicability was investigated by the inverse re-identification of an initial material model parameter set that was taken from the literature [39]. Therefore, a close match between the target and the simulated process observables was achieved within a low number of iterations. Later, the authors applied this approach to experimental data from AISI 1045, which resulted in a close agreement for different process observables [40]. However, the parametric investigation on the application of the DSA to the inverse problem of material model parameter determination from FE-cutting simulations revealed some drawbacks, which were associated with the characteristics of the algorithm and its exploitation characteristics [41].

In this study, a methodology that is based on Particle Swarm Optimization is developed to inversely re-determine material model parameters from orthogonal cutting simulations. Thereby, the use of the PSO as the evolutionary algorithm is reasoned by its wide application to engineering problems and the possibility to transition the inverse determination from the exploitation of the DSA [41] into an exploration. The application of the algorithm to simulation data instead of experimental data is justified by the possibility to evaluate the determined parameter set in comparison to the target set as well as by the ideal representation of the material behavior because of the utilized material model. When using an experimental database, the parameter set is unknown and can, therefore, not be compared with the one determined inversely. Further, the real material behavior does not exactly follow the ideal theoretic description of the constitutive model, which results in remaining deviations between experiments and simulations.

In Section 2, the material model that is utilized within this paper is outlined, followed by the theoretical background of Particle Swarm Optimization. Thereafter, the FE model of orthogonal cutting, which underlies the simulations of this study, is described (Section 3). Further, the theory of Particle Swarm Optimization is applied to the inverse problem of material model parameter determination from orthogonal cutting simulations (Section 4). The results of the inverse material model parameter determination are presented in Section 5, followed by a discussion of the results in Section 6. Concluding the presented research, a summary of the obtained results will be given and conclusions will be drawn in Section 7.

2. Material Model to Describe the Constitutive Material Behavior

Within this study, the JC-material model is utilized to describe the constitutive material behavior. The JC model is one of the most utilized material models in FE-cutting simulations and is expressed by three multiplicative terms: Equation (1) [42]. The three terms express the effects of strain hardening, strain rate hardening, and thermal softening. In comparison to other material models, the influence of the strain, strain rate, and temperature are modeled uncoupled by the JC model [43,44]. In an uncoupled material model, the strain rate sensitivity is independent of the temperature. In the JC material model, $A$, $B$, $n$, $C$, and $m$ are the material model parameters, ${\dot{ϵ}}_0$ the reference strain rate, $T_0$ the reference temperature, and $T_m$ the melting temperature of the material.

$${\sigma }_F=\left(A+B\cdot {ϵ}^n\right)\cdot \left(1+C\cdot \ln \left(\frac{\dot{ϵ}}{{\dot{ϵ}}_0}\right)\right)\cdot \left(1-{\left(\frac{T-T_0}{T_m-T_0}\right)}^m\right)$$

(1)

The choice of the material model for the conducted research of this paper is reasoned by the wide application of the JC model. However, a transfer to other material models is expected, since the underlying optimization procedure does not take the formulation of the model into account.

The aim of this study is to investigate the applicability of Particle Swarm Optimization (PSO) for the inverse parameter determination. Therefore, it is aimed to re-identify a target set of material model parameters. As target set, a set of material model parameters is taken from the literature [11] (

Table 1. Johnson–Cook material model parameters of AISI 1045 used for the inverse re-identification [11].

Material	AISI 1045 (Normalized)
$A$/MPa	546
$B$/MPa	487
$n$/-	0.25
$m$/-	0.631
$C$/-	0.027
${\dot{ϵ}}_0$/s−1	0.002
$T_0$/°C	20
$T_m$/°C	1500

). The target parameter set is utilized to simulate the process observables, which are later used for the inverse re-identification. If being applied to experimental results, the same process observables could be determined from orthogonal cutting experiments and could therefore be used for the methodology. During the re-identification of this study, the target parameter set is handled as if it is unknown, as it would be the case for the inverse identification of the material model parameters from experimental cutting tests. Within this study, the machining process of AISI 1045 is simulated within a certain cutting parameter range, with cutting speeds between 50 and 150 m/min and an un-deformed chip thickness of 0.05 mm. Within this domain of process parameters, the produced chips of AISI 1045 are continuous and have no chip segmentation [40]. Therefore, a damage model is not incorporated into the simulations.

3. Particle Swarm Optimization

The PSO is an algorithm for the minimization of non-linear functions and was initially developed by Kennedy and Eberhardt in 1995 [45]. The general idea of the algorithm is based on the social behavior, which a population of individuals adapts to the environment by returning to regions of interest that were identified previously [46]. The fundamental principle goes back to the hypothesis of the social biologist Wilson, according to whom an individual member of a population can profit from discoveries and experiences from all other members of the population [47]. That theory being transferred to the PSO algorithm means that the initial population of particles within the hyperspace of the design variables, to which the velocity operators are applied to, simulates individual cognitive abilities and social interactions [48].

In the beginning of the algorithm, the initial population $p^0$ of particles $p_n^0$, Equation (2), and their initial velocities $v^0$, Equation (3), are randomly defined within the hyperspace.

$$p^0=\left[p_1^0, p_2^0, \dots , p_m^0,\dots , p_n^0\right]$$

(2)

$$v^0=\left[v_1^0, v_2^0, \dots , v_m^0,\dots , v_n^0\right]$$

(3)

The individual particles $p_m^k$ of a population $p^k$ contain the coordinates $n_p$ of the parameters to be optimized. Therefore, an individual particle $m$ with the particle position and particle velocity is defined in the initial iteration as:

$$p_m^k={\left[p_1^k, p_2^k, \dots , p_j^k,\dots , p_{n_p}^k\right]}^T$$

(4)

$$v_m^k={\left[v_1^k, v_2^k, \dots , v_j^k,\dots , v_{n_p}^k\right]}^T$$

(5)

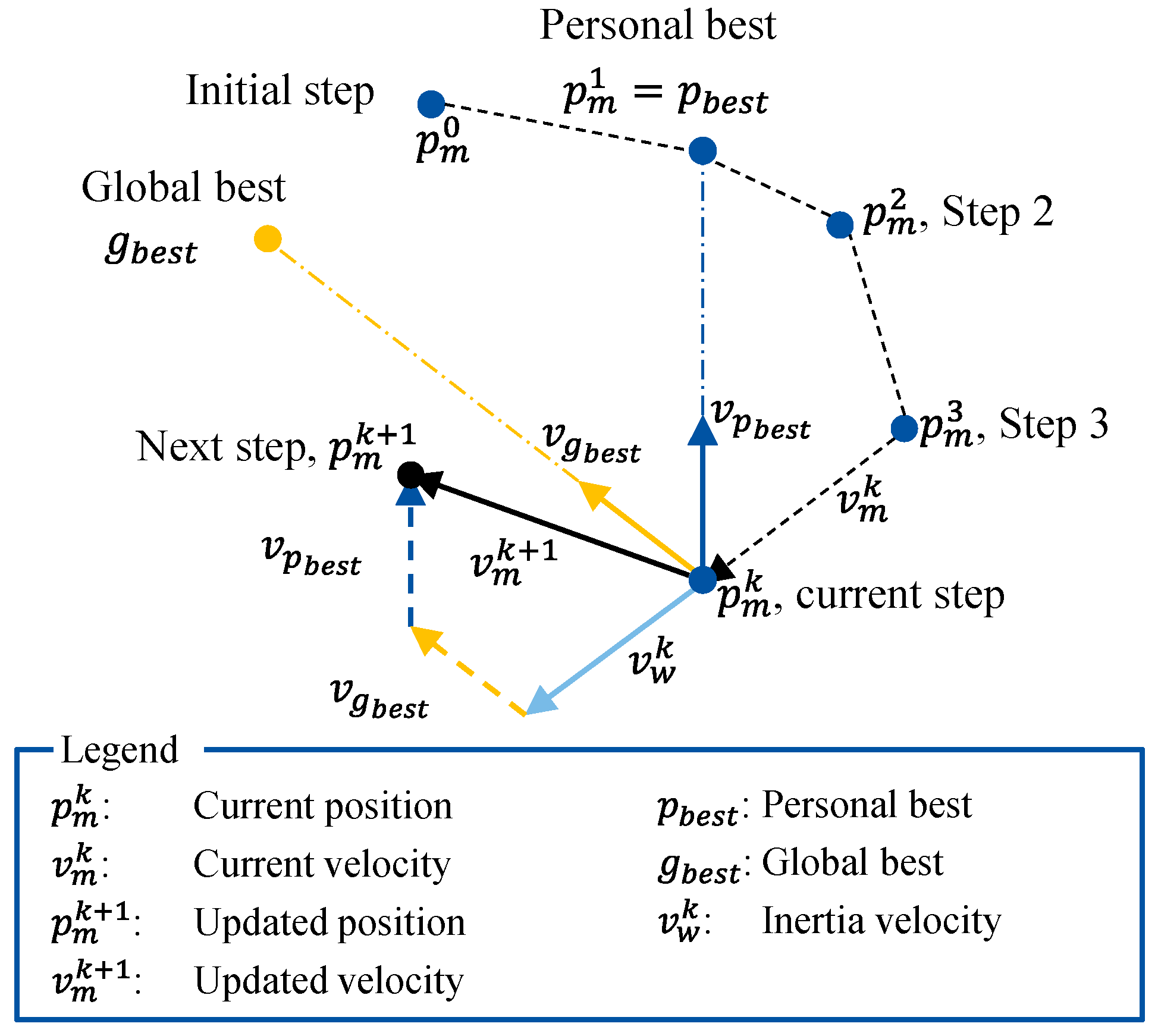
In the following steps, the velocities of the particles are modified based on the inertia, the personal history, and the effects of the neighbor particles, as illustrated in Figure 1 for the case of an optimization within a two-dimensional hyperspace. The particle’s inertia takes into account that a particle follows along the initial direction and the personal history accounts for the individual particle’s best position. In comparison to the personal history, the effect of the neighbor particles modifies the particle velocity based on the global best position of all particles. The general form of the updated velocity is given in Equation (6), where the subscript of $v_w$ indicates the inertia parameter, $v_{p_{best}}$ the individual, and $v_{g_{best}}$ the global best position that was identified so far. The formulation of the single influences on the velocity is given in Equation (7), where w is the inertia coefficient, $C_1$ the personal acceleration coefficient, and $C_2$ the social acceleration coefficient. $rand()$ represents random numbers within a predefined interval. The calculation of the updated particle position is given in Equation (8).

$$v^{k+1}=v_w^k+v_{p,best}^k+v_{g,best}^k$$

(6)

$$v_i^{k+1}=w^k\cdot v_i^k+C_1\cdot rand()\cdot \left(p_{best}{}_i^k-p_m^k\right)+C_2\cdot rand()\cdot \left(g_{best}^k-p_m^k\right)$$

(7)

$$p^{k+1}=p^k+v^{k+1}$$

(8)

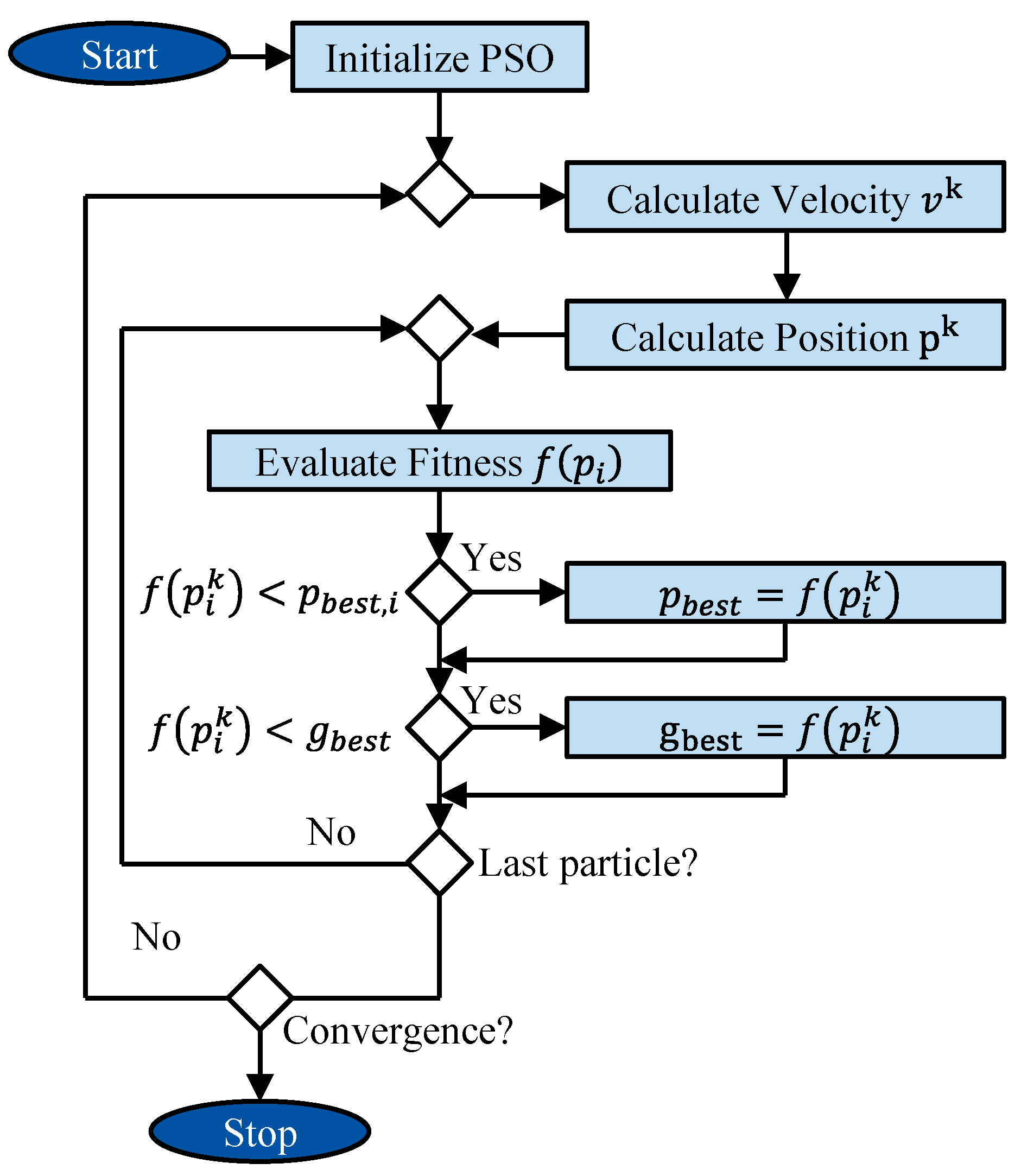
The procedure of the PSO algorithm is shown in a flowchart in Figure 2. After the initialization of the initial particles $p^0$ and their corresponding velocities $v^0$, the individual particles are evaluated regarding their personal $p_{best}$ and regarding the global best particle $g_{best}$. The results of the particles are evaluated in terms of the function to be minimized, which is called a fitness function. Depending on the results of each particle of the current iteration, the particle’s position is updated. If the result of the fitness function of a single particle during the iteration $k$ is lower than the previous results of the particle, the personal best $p_{best}$ is updated. If the resulting fitness function value of the particle during step $k$ is lower than all previous results of all the particles of the population, the global best $g_{best}$ is updated. This procedure is done for all particles of the population during one iteration. Thereafter, the global best $g_{best}$ is evaluated regarding a pre-defined value, which has to be undercut to stop the algorithm. If the results of the fitness function of the global best $g_{best}$ is larger than the pre-defined value, the velocities are updated, the position of each particle is calculated, and the procedure is repeated.

Since its development, the PSO algorithm found wide application in multiple optimization problems, such as in scheduling, task assignment, neural network training or in engineering problems [49]. A broad summary on conducted research in this field is given by Blum and Li [49], Poli et al. [50], and Schutte and Groenwold [51].

4. Finite Element Model of Orthogonal Cutting

To model the chip formation, the orthogonal cutting process was simulated within this study. The simulation of the chip formation process was the focus of several studies [19,52,53,54]. Among the variants of cutting, the orthogonal cutting is the most elementary case [55]. To determine the material model parameters inversely from the cutting process, the orthogonal cutting process was utilized in multiple studies [56,57,58,59].

Besides others, the models of the chip formation process deviate in terms of the formulation. The two most utilized formulations are the Eulerian and the Lagrangian formulation. In the Eulerian formulation, the material can flow freely through the fixed mesh within the domain [60,61]; whereas, in the Lagrangian formulation the deformation of the material is associated with the movement of the mesh [62]. However, both of these formulations have some drawbacks, which were reported by Bäker [63] and Arrazola et al. [19]. The drawbacks of the two formulations led to the development of hybrid formulations. Among these, the Arbitrary Lagrangian Eulerian (ALE) formulation and the Coupled Eulerian–Lagrangian (CEL) formulation are the most common used alternatives to the Lagrangian and Eulerian formulations [59,60,61,62]. Within this study, a CEL model of the orthogonal cutting process is utilized. The CEL formulation was initially introduced by Ducobu et al. [64] and Puls et al. 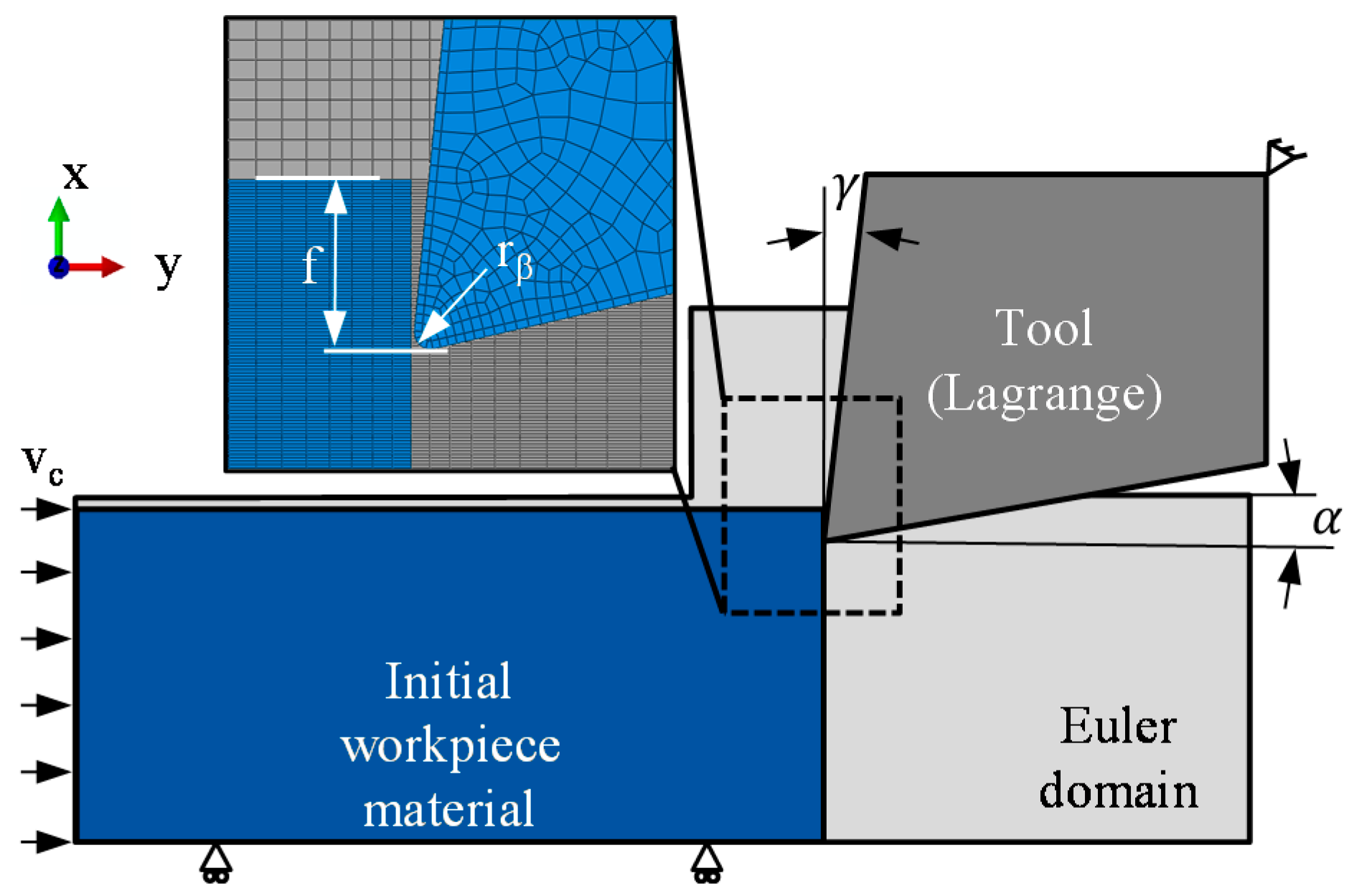[65]. In the CEL formulation, the tool is discretized by the Lagrangian formulation and the workpiece by the Eulerian formulation. The utilized set-up of the simulation model underlying this paper is illustrated in Figure 3. The set-up of the FE model of chip formation is in agreement with the model of a previous study by the authors [40], where its potential to accurately model the orthogonal cutting process was verified.

As boundary condition of the FE-model, an inflow of the workpiece material into the Euler domain is used to simulate the cutting speed. The inflowing workpiece material leaves the Euler domain either in form of the chip or in form of machined workpiece material. To enable the formation of the chip, an additional area is meshed by the Eulerian formation. Therefore, the resulting chip can be evaluated within the steady state. The Euler domain was meshed by EC3D8RT elements within the simulation software ABAQUS/Explicit. Since the EC3D8RT elements are three-dimensional, a three-dimensional model of the orthogonal cutting process was used. The number of elements in the z-direction was set to one, and, therefore, the model can be considered as a quasi-two-dimensional model of the orthogonal cutting process. To discretize the Euler domain, elements with a mesh size between $0.005 \mathrm{and} 0.1 \mathrm{mm}$ were used, whereby the smaller mesh sizes were used in the region of chip formation. On the other side, for the Lagrangian discretization of the tool elements of type C3D4T with a mesh size between $0.005 \mathrm{and} 0.05 \mathrm{mm}$ were utilized. A further detailed description of the model and the utilized parameters can be found in [40].

Besides the material model, the utilized friction model and the thermo-mechanical properties of the tool and workpiece have a crucial impact on the simulated results. To obtain realistic results, the temperature-dependent friction model according to Puls et al. was utilized [66]. The underlying friction model parameters were kept constant for all simulations presented within this paper. Further, the thermo-mechanical properties of the workpiece material and the cutting tool material were taken from the literature [67,68,69].

The simulations were run on a virtual machine, of which the specifications are given in

Table 2. Specification of the virtual machine used for the simulations.

Memory	64 GB
CPU	Intel® Xeon® E5-2637 v2 @3.5 GHz
Parallelization	Domain parallelization
No. of CPU	16

. In order to lower the computational time of the simulations, mass scaling was used, wherefore the material density and the specific heat was artificially increased and decreased, respective. By using a mass scaling factor of $1000$ it was possible to define a time increment $1.6\cdot {10}^{-8} \mathrm{s}$. For all the simulations, the same cutting length of $l_c=0.33 \mathrm{mm}$ was used for the simulations. This cutting length showed to be sufficient to reach the steady state within the simulations. By using the virtual machine, the computational time of a single simulation with a cutting time of $t_c= 0.002 \mathrm{s}$ was approximately 1:40 h.

5. Application of the Particle Swarm Optimization to the Inverse Material Model Parameter Re-Identification

Fundamental for the application of the PSO algorithm to the inverse (re-) identification of material model parameters from machining simulations is the definition of a fitness function. The fitness function evaluates the deviation between the target values and the iterative simulation results. In this study, different process observables are considered in the fitness function. Therefore, the optimization presented here can be considered as a multi-response optimization. Multiple process observables are considered, since just taking the averaged cutting force as the only or main verification parameter into account was reported in the literature to be not sufficient [63]. The process observables that are considered in the fitness function within this study are the cutting force $F_c$, thrust force $F_D$, maximum tool temperature $T_{T,max }$, and chip thickness $h\prime$. Generally, different formulation of the cost function for the multi-response optimization appear to be conceivable. In the state-of-the-art, different mathematical formulations were used for the multi-response optimization. According to Sibalija, the formulations of the objective functions can be divided into two types [70]:

• Type 1: For this type, the objective function is known, as it is the case for minimizing the machining time by determining the cutting parameters.
• Type 2: For this type, the objective function is unknown. A feasible way to formulate the objective function is to apply regression techniques to experimental data.

For further information on the used formulations for the multi-response optimization, the authors refer to the review of Sibalija et al. [70] and Venkato Rao et al. [71].

For this study, the cost function to be optimized can be classified as Type 2. To use a regression model for the inverse determination of the material model parameters, the conduction of a vast number of simulations with small step variation of the material model parameters would be necessary.

Here, the cost function is formulated based on the sum of the weighted relative deviations of the considered process observables (Equation (9)). Thereby, the utilized formulation is in agreement with the formulation of a previous study [40], and, therefore, the results of these approaches can be compared. The definition of the weighting factors based on a pairwise comparison, whereby the dependence of the process observables on the material model was evaluated on the basis of empirical values and experience. Their values were set to ${\omega }_{F_c}=0.30$, ${\omega }_{F_{cN}}=0.15$, ${\omega }_{T_{T,max}}= 0.35$, and ${\omega }_h^{\prime }=0.20$. The choice of the weighting factors is based on empirically established values and takes the dependence of the process observables on the material model parameters into account, determined from a pairwise comparison. For example, the thrust force was weighted less than the cutting force because the thrust force was found in several investigations to be strongly dependent on the friction model [72,73,74,75,76,77]. However, it has to be stated that the error function used for the optimization here depends on the weighting factors. Varying the weighting factors can result in distinct differences in the determined results. Their impact need to be evaluated in future studies.

$$\xi ={\displaystyle \sum }_{i=1}^N{\omega }_i\cdot \left|\frac{x_i^{target}-x_i^{sim}}{x_i^{target}}\right|\cdot 100\%$$

(9)

For the PSO, the three hyper-parameters $C_1$, $C_2$, and $w$ have to be properly selected in order to provide the global optimum within a decent number of iterations [70]. The determination of the optimal PSO parameters requires fine tuning of these parameters, which has to be done specifically for the optimization problem the PSO is applied to [70,78]. However, an adequate determination of the PSO parameters for the inverse parameter determination would require a vast number of simulations and with it countless computational times. This is why the determination of the most suitable PSO parameters is beyond the scope of this study. In order to utilized reasonable PSO parameters for the present multi-response problem, PSO parameters were taken from the scientific literature [70,79]. Therefore, the inertia coefficient was set to $w=1$, the personal acceleration coefficient to $C_1=2$, and the social acceleration coefficient to $C_2= 2$.

Additional to the inertia coefficient, a damping factor $w_{damp}$ was multiplied to the inertia velocity that reduces the inertia coefficient after each iteration, Equation (10). Thereby, the damping factor was set to $w_{damp}=0.99$. The definition of this value bases on the assumption that the step size is reduced after each iteration in order to achieve a finer search with increasing number of iterations. However, values that were too low would affect the step size after a few iterations to a large extent, which might cause higher number of iterations. The used value was further determined based on preliminary tests conducted by the authors.

However, it is important to state that the coefficients used for the PSO do not necessarily represent the optimum values. Instead, the values were identified to be practical for applying the PSO to the inverse problem. In order to determine the best PSO parameters, extensive investigations are required, considering the application case. These investigations are left for future research activities.

$$v_w^k=w_{damp}\cdot w^k\cdot v^k$$

(10)

A further important factor that affects the results of the PSO is the initial population. In the scientific literature, different techniques were utilized for the initialization of the particles. These techniques can be divided into those where the initial particles are randomly assigned and those where the initialization technique follows a defined scheme [78]. In this context, however, it should be noted that computers cannot specify truly random numbers. Within the investigations of the present paper, the position of the initial particles was “randomly” determined. The random positions were normally distributed with a mean of zero and a standard deviation of one. As for the other boundary conditions of the PSO, the choice of the initial particle is entirely problem specific [78].

The PSO algorithm was implemented into a MATLAB to generate and to update the particles of the population. The calculated material model parameters were inserted into the FEM chip formation simulation using ABAQUS/Explicit 6.14–6. The simulation results were extracted and used as input in the MATLAB program. Thereby, the valuated cutting force components were evaluated in their steady state, the maximum tool temperature was evaluated from the same region, and the chip thickness was averaged from five manual measurements that were done in the post-processor of ABAQUS.

In this study, the PSO algorithm was used to re-identify the five JC material model parameters $A$, $B$, $C$, $n$, and $m$. The domain of the parameters to be identified were limited within physical meaningful boundaries. The upper and lower value of the parameter domains are summarized in

Table 3. Parameter domains of the Johnson–Cook material model parameters to be identified.

JC-Parameter	Lower Limit	Upper Limit
$A$/MPa	300	700
$B$/MPa	350	750
$n$/-	0.10	0.90
$m$/-	0.10	0.85
$C$/-	0.005	0.150

. In case the algorithm calculates a parameter outside of the pre-defined domain, the parameter is set to a value close to the boundary. The dynamic boundaries, defined by Equations (11) and (12), were modeled according to Adewumi et al. [80].

$$If x_i<x_{min}:x_i\leftarrow x_{min}+\left(x_{min}-x_i\right)\cdot random\left(0,1\right)$$

(11)

$$If x_i>x_{min}:x_i\leftarrow x_{max}-\left(x_i-x_{max}\right)\cdot random\left(0,1\right)$$

(12)

To investigate the applicability and performance of the PSO, different approaches were conducted and are outlined in the following subchapters. The approaches address both the underlying cutting conditions as well as the boundary conditions of the PSO. The characteristics of the approaches are summarized in

Table 4. Cutting conditions and PSO characteristics used for the investigated approaches of this study.

Approach	Cutting Conditions		Particle-Swarm-Optimization
	Cutting Speed ${\mathit{v}}_{\mathit{c}}$/m/min	Un-Deformed Chip Thickness h/mm	Number of Particles	Velocity Step ${\mathit{v}}^{\mathit{n}+\mathbf{1}}$
1	100	0.05	6	≤7.5
2	100	0.05	6	≤40
3	50, 150	0.05	4	≤7.5

. The reasons using these boundary conditions will be discussed in the following subchapters, where the results of the three approaches will be presented.

For the PSO, three criteria for termination were defined:

• Error criteria: the error values of all investigated cutting conditions for one particle of a single iteration are smaller than ${\xi }_{\lim }\le 1\%$.
• Convergence criterion I: the iteratively determined parameter sets deviate by less than $1\%$ in terms of the individual parameters between two iterations following one another.
• Convergence criterion II: the resulting error values differ by less than $\Delta \xi \le 0.1\%$ for two consecutive iterations.

5.1. Approach 1

Within the first approach, a single cutting condition with a cutting speed of $v_c= 100 \mathrm{m}/\min$ and an un-deformed chip thickness of $h=0.05 \mathrm{mm}$ was utilized for the inverse parameter re-identification. For the PSO, six different particles were utilized, which were randomly assigned. The values of the initially assigned parameters are summarized in

Table 5. Initial particles and their randomly assigned material model parameters used for the investigated approaches.

Particle	$\mathit{A}$/MPa	$\mathit{B}$/MPa	$\mathit{n}$/-	$\mathit{C}$/-	$\mathit{m}$/-
1	625.89	712.32	0.202	0.097	0.785
2	339.02	461.40	0.538	0.145	0.818
3	363.05	738.24	0.866	0.121	0.464
4	356.75	518.70	0.833	0.144	0.694
5	562.30	364.28	0.779	0.013	0.801
6	603.10	647.25	0.414	0.030	0.592

. The velocity parameter of the PSO algorithm was limited to an upper value of $v_{max}^{n+1} =7.5\%$. This was done in order to limit the step size of the particles, since pre-runs showed that too high velocity parameters result in the tendency of the particles to reach and remain at the boundary of the parameter domain. The choice of the step size within a reasonable area (see also Approach 2) was arbitrary.

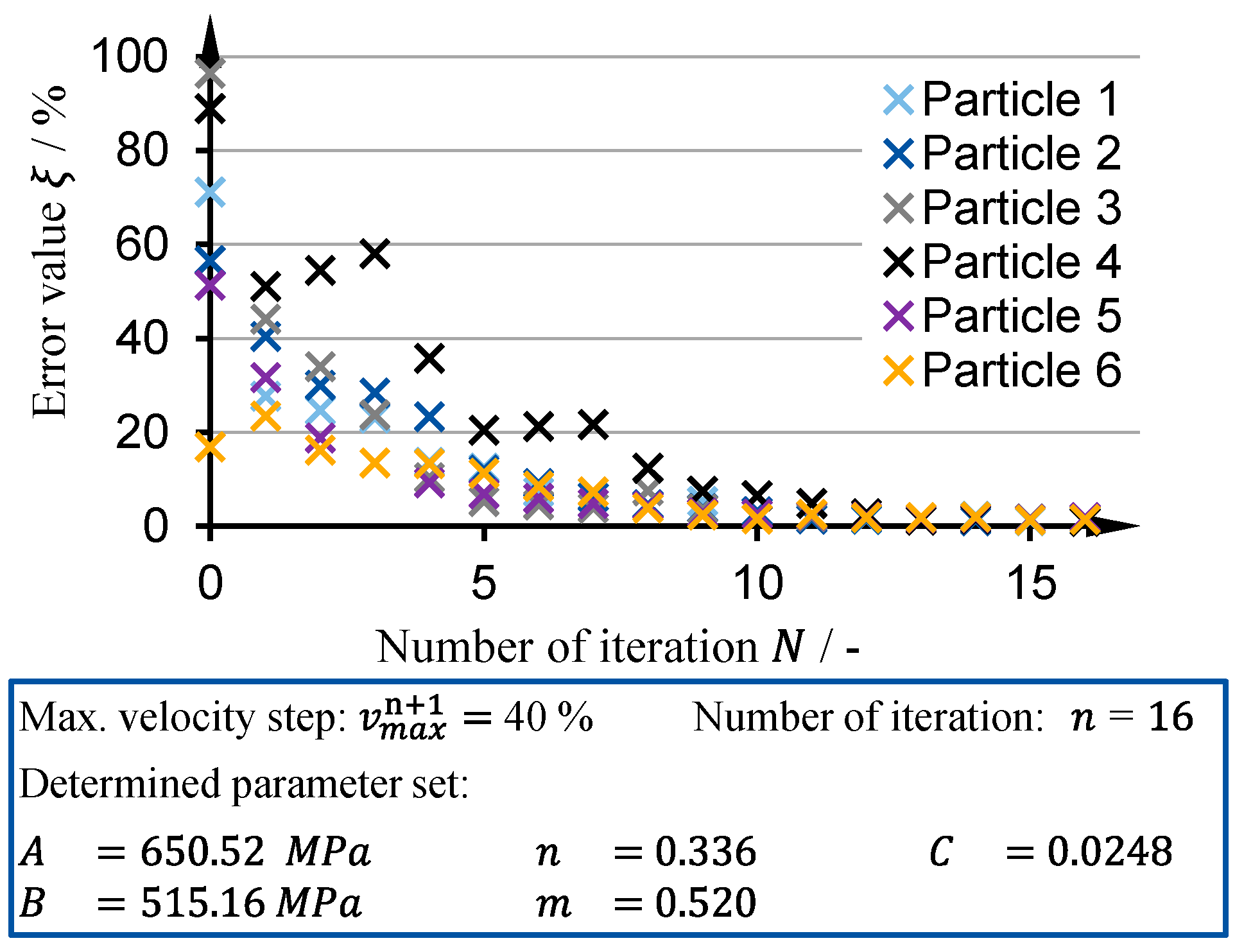
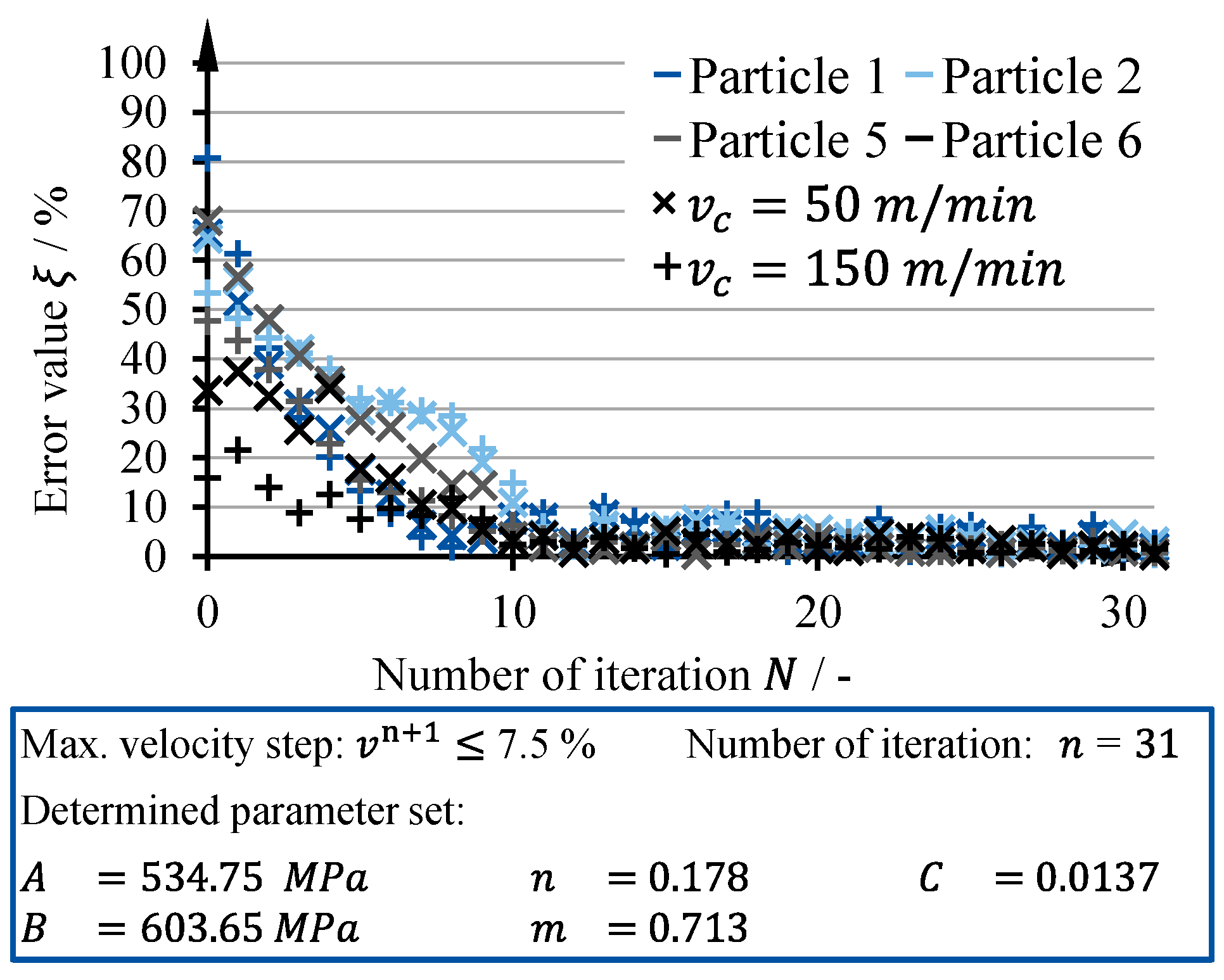
The results of the first approach are illustrated in Figure 4, showing the resulting error value of each of the particles over the number of iterations. The approach was terminated after 36 iterations, whereby the error criteria was the abortion criteria. The error value in this case was ${\xi }_1=0.96\%$. The evolution of the error value for the individual particles shows a distinct initial decrease, which flattens out after approximately ten iterations. For the initial, randomly assigned particles, Particle 6 resulted in the lowest error value, which represents for this iteration the global best value. This is why the other initial particles that resulted in a higher error value tend into the direction of Particle 6. In the second iteration the error value of Particle 6 increases, whereas the error values of the other particles decrease. In the third iteration, the error value of Particle 6 decreases and develops into the reverse direction due the experience of the particle. For the further iterations, all particles tend to decrease to an error value below ${\xi }_{max}<10\%$ within ten iteration. However, for this approach 26 more iterations were necessary to fulfill one of the abortion criteria.

The determined parameter set of Approach 1, given in

Table 6. Determined parameter sets of the conducted approaches in comparison to the target parameter set.

Parameter Set	$\mathit{A}$/MPa	$\mathit{B}$/MPa	$\mathit{n}$/-	$\mathit{C}$/-	$\mathit{m}$/-
Target set	546.0	487.0	0.250	0.027	0.631
Approach 1	593.2	459.1	0.299	0.021	0.672
Approach 2	650.5	515.2	0.336	0.025	0.520
Approach 3	534.8	603.7	0.178	0.014	0.713

, deviates from the target parameter set. This observation can be attributed to the existence of multiple local minima within the domain of investigation as identified in previous studies [69]. The comparison of the individual parameters shows a close agreement for the JC parameters $A$, $B$, and $m$, whereas the deviation for the parameters $n$ and $C$ are around $20\%$. It is assumed that the parameters and their influence on the materials flow stress compensate each other, which results in turn in comparable simulation results for the domain of investigation.

One crucial factor that has to be taken into account when evaluating inverse approaches is the computational effort. The computational effort is evaluated in this study by means of the computational time. For the first approach, 216 simulations were conducted, which resulted in a computational time of over 23 days. The relatively high number of required simulations, especially in comparison to previously conducted approaches where the Downhill Simplex Algorithm was used [39,40,41], is attributed to the number of particles that are used for the PSO.

5.2. Approach 2

The maximum PSO velocity parameter in Approach 1 was limited to $v_{max}^{n+1}=7.5\%$. During the iterative parameter determination, the upper value for the PSO velocity parameter was reached in three iterations. In Approach 2, the maximum PSO velocity parameter was increased to $v_{max}^{n+1}=40\%$. Further, the calculation of the PSO velocity parameter for a particle was related to the results of the error value of the previous iteration. Thereby, the PSO velocity parameter was linked in a linear relationship to the error value, Equations (13) and (14). This results in an PSO velocity parameter of $v_{max}^{n+1}=40\%$ for an error value of $\xi =100\%$. With a reduction of the error value, the velocity parameter also decreases. This procedure was implemented into the algorithm in order to increase the step size for high error values and decrease the step size for small error values. However, a drawback of this procedure could be that the search space is reduced to the vicinity of a local minimum. Small PSO velocity parameters, as a result of small error values, could mean that the particles cannot search outside this region. Therefore, the particles might not reach the global minimum. On the other hand, by using this modification of the PSO, it is expected that a parameter set can be determined in a reduced number of iterations. The results of the Approach 2 are shown in Figure 5, where the error value of each particle is plotted over the number of iterations.

$$\mathrm{For} \xi \le 100\%: v^{n+1}=0.4\cdot {\xi }^n$$

(13)

$$\mathrm{For} \xi >100\%: v^{n+1}=40\%$$

(14)

Approach 2 was terminated after 16 iterations due to the fulfilment of the error criteria. Therefore, a total of 96 simulations were conducted, which resulted in a computational time of more than 9 days. For Iteration 16, the error value was $\xi =0.99\%$. Therefore, by increasing the PSO velocity parameter it was possible to decrease the number of iterations by more than the half in comparison to Approach 1. The comparison between the development of the error value over the number of iterations for Approach 1 and Approach 2 shows similarities in terms of the characteristic asymptotical evolution. Further, both approaches show a rapid initial decrease of the error value. However, for Approach 2, the flattened area of the error value development is much less pronounced. This can be ascribed to the adaptive PSO velocity parameter, which allows the algorithm to proceed with a step size that depends on the current error value. Albeit, the risk of overstepping a local minimum has to be considered when selecting the PSO velocity parameter.

The Approach 2 resulted in a parameter set, given in Table 6, which deviated distinctively from the target parameter set and from the parameter set of Approach 1. The large deviation can be ascribed to the following factors: the non-uniqueness of the material model parameters [41], to the single cutting condition that underlies the inverse re-identification, and to the error function that evaluates the deviation of the simulated results from their target values.

5.3. Approach 3

For Approach 3, the procedure of the PSO was extended to evaluate two cutting conditions per particle per iteration. The extension to consider multiple cutting conditions was done in order to extend the domain of occurring thermo-mechanical loads within the chip formation process. In the scientific literature, it was reported that extending the domain of cutting conditions increases the reliability and validity of the determined material model parameters [31,81]. In this approach, the same un-deformed chip thickness as in the previous two approaches was used in combination with two cutting speeds, as summarized in Table 4. This allows the critical analysis of the validity of the determined material model parameters to cut conditions within the domain of calibration.

To decrease the computational effort, the number of the initial particles was reduced to four, whereby the particles 1, 2, 5, and 6 were used, Table 5. In order to compare the results of this approach with Approach 1, the maximum PSO velocity parameter was limited to $v_{max}^{n+1}=7.5\%$ as well. The results of Approach 3 are illustrated in Figure 6.

Approach 3 was terminated after 31 iterations since the algorithm determined a parameter set, which resulted in an error value of ${\xi }_{50}=0.92\%$ and ${\xi }_{150}=0.82\%$. The development of the error value over the number of iterations is in close agreement with the development of Approach 1, albeit the two determined material parameter sets deviate from each other. The close agreement between the two approaches is attributed to the same maximum PSO velocity parameter as well as to the partly same particles that were used. For both approaches, Particle 1 was used, which resulted in the lowest error value for the first iteration. Therefore, the other particles tend to evolve into the direction of Particle 1 and the development of Particle 1 is solely influenced by its personal best and its inertia. Further, the lower maximum error values for Approach 3 in comparison to those of the Approach 1 are due to the selected particles. In the Approach 1, the highest error values were calculated for Particle 3 and Particle 4. These particles were not considered in Approach 3.

For high error values, it was found that a parameter set resulted in a significantly lower value for one cutting speed than for the other cutting speed. In contrast, a parameter set that resulted in a low mean error value describes both cutting speeds well. This shows that a good parameter set describes both cutting speeds reasonable well.

For Approach 3, the computational time added up to 30 days. Due to multi-threading of the simulation and parallel simulations of the different cutting conditions, the time to determine the material model parameter set was reduced to approximately 23 days. Since the same cutting length of $l_c=3.33 \mathrm{mm}$ was used for the simulations underlying this study, the highest computational times occurred for the lowest cutting speed. For the cutting speed of $v_c=50 \mathrm{m}/\min$ the average computational time was approximately 4:15 h. In comparison to Approach 1, two cutting conditions and four particles were used in this approach. Due to this, it is not reasonable to compare the computational time of Approach 3 with the other two approaches.

6. Discussion

When comparing the results of the three conducted approaches regarding their determined parameter sets, distinct differences are obvious. The determined parameter sets and the target parameter set are summarized in Table 6. Although the order of magnitude of the individual model parameters is the same, the values differ from each other by up to 48%. The deviations of the individual material models and their parameters from the target set are not uniform. For example, as for Parameter set 3, one model parameter can deviate by only 2%, while other model parameter deviates by almost 50%.

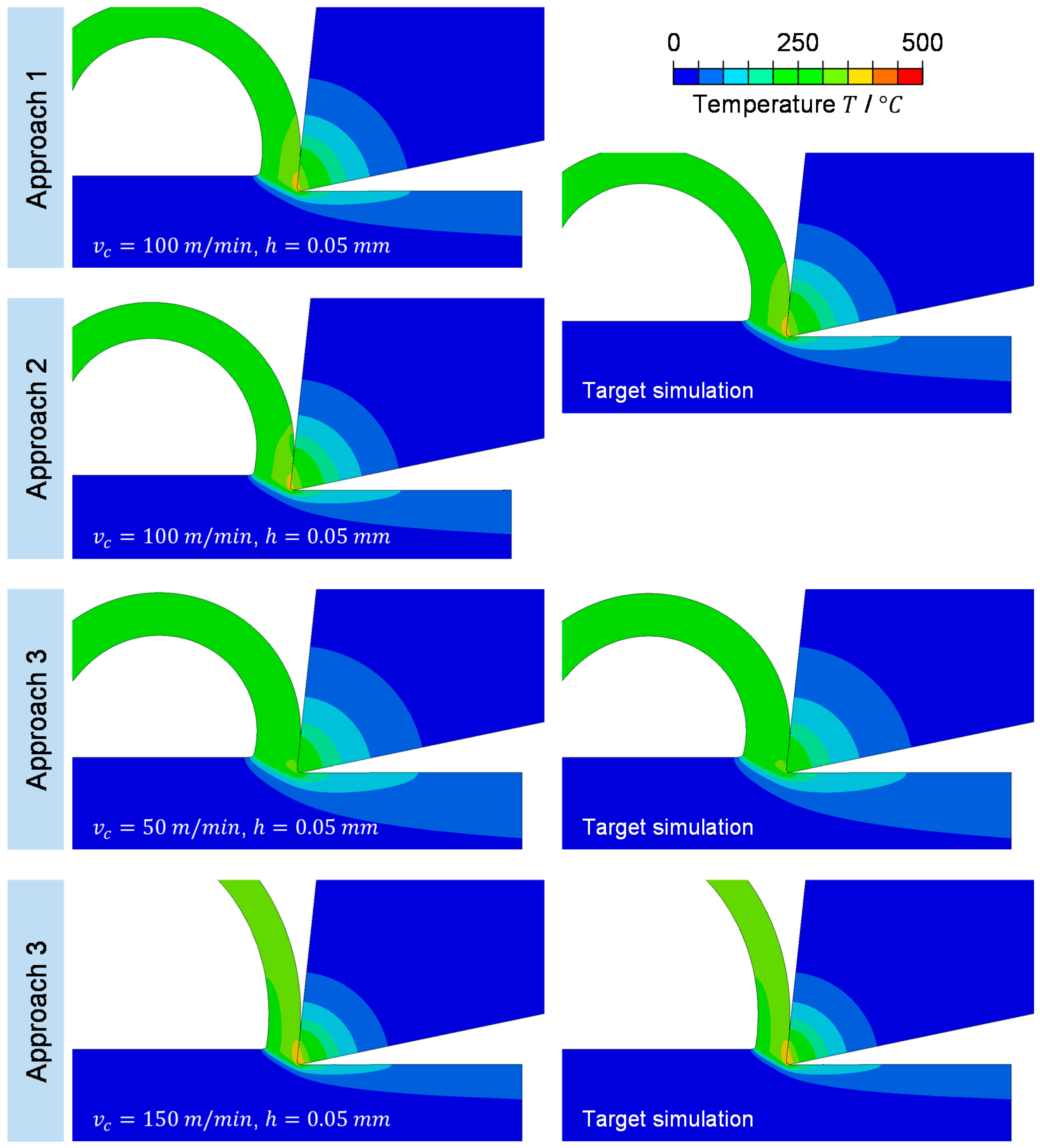
However, because of the small error values after the iterative parameter determination, it can be stated that the determined parameter sets result in a close agreement in terms of the evaluated process observables. For comparison, the results after the iterative procedure are contrasted to their target counterparts, Figure 7. It can be seen that simulations of the iterative parameter determination result in a very close agreement in terms of the temperature field, and the chip form. However, the chip form shows slight deviations regarding the chip radius. For one part, these differences can be attributed to the error function, which did not consider the chip form as a process observable. Based on the comparison of the simulated results with their target simulations it can be concluded that even though the inverse parameter determination resulted in partly significant different material model parameters, a close agreement in terms of the evaluated process observables for the underlying cutting conditions was achieved.

The mismatch between the determined material model parameter sets and the target parameter set can be attributed, to some extent, to the utilized optimization algorithm and its boundary conditions. The influence of the boundary conditions was discussed in Section 5. Besides that, the investigated domain and the underlying material model can affect the results of the inverse optimization. In terms of the model, one can expect a mutual compensation of the considered effects. In the JC material model the effects of strain hardening, strain rate hardening, and thermal softening are considered. For a certain domain of occurring thermo-mechanical loads, it is possible that the hardening effects can be compensated by the softening effect and vice versa. This suggests the existence of multiple local minima within the investigated parameter domain. A possible approach to reduce that effect could be the extension of the domain of investigation, by taking a broader range of cutting conditions into account. A further possibility would be to take results from established material tests into account.

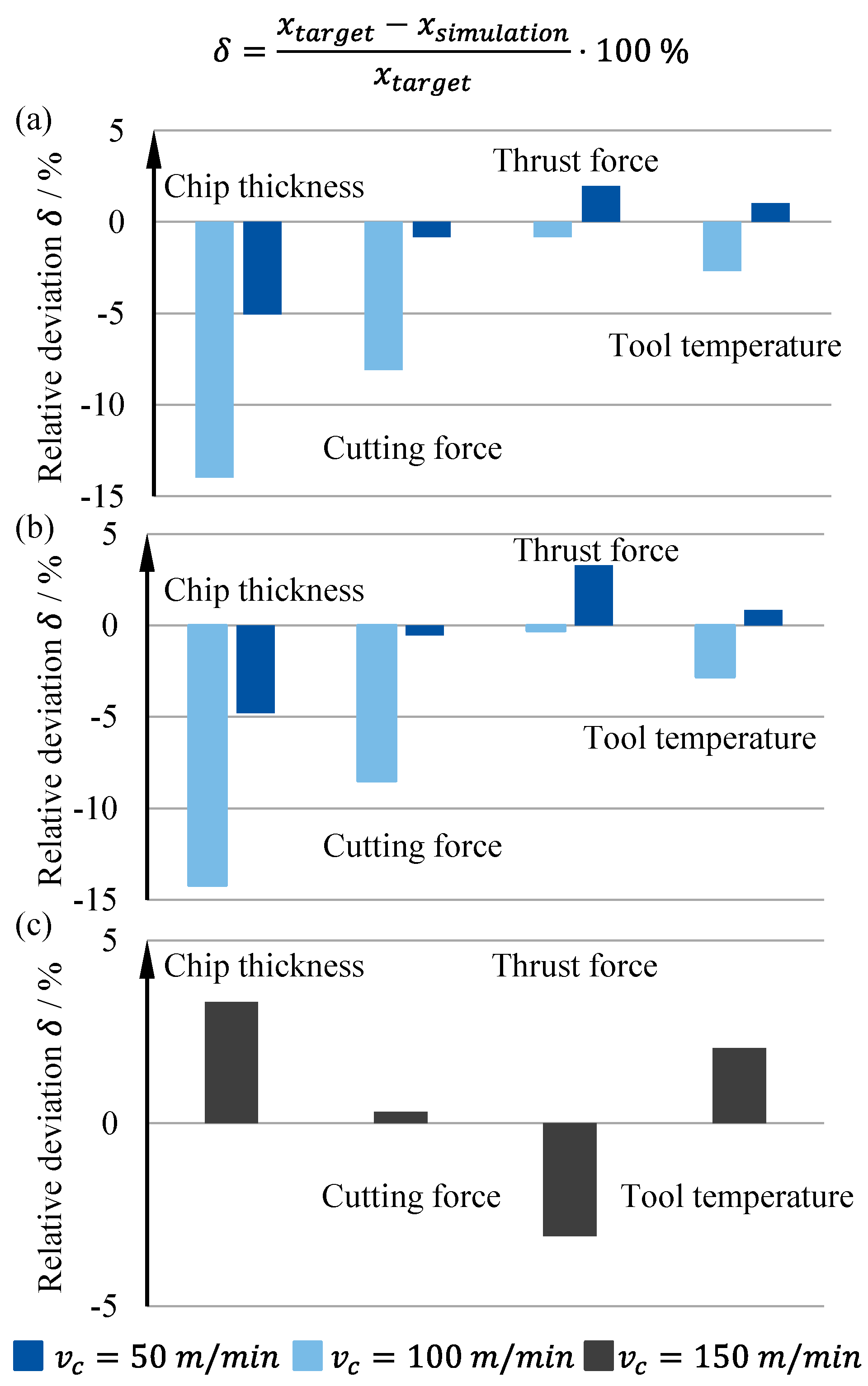
Since the material model parameters of this paper were calibrated for different cutting speeds, there are uncertainties regarding the suitability of these parameter sets to adequately represent the material behavior for other cutting conditions. Within this paper, two different sets of cutting conditions were used for the inverse re-identification of material model parameters. In Approach 1 and Approach 2, a single cutting condition was used. The parameter sets that were determined for this cutting condition are utilized to simulate cutting conditions outside of the domain of calibration. Therefore, the cutting conditions of Approach 3 are used. Conversely, the parameter set of Approach 3 is used to examine how well it can describe a cutting condition within the domain of calibration. The results of this investigation are illustrated in Figure 8.

For the parameter set of Approach 1 and Approach 2, the simulations outside the domain of calibration were shown to result in larger deviations in comparison to the results with the target parameter set. The deviations from the target values are the highest for the cutting force and the chip thickness. This can be attributed to the strong dependence of these process observables on the material model and its parameters. The thrust force on the other side depends strongly on the friction model [72]. For the parameter set of Approach 1, the simulations outside the domain of calibration resulted in an error value of ${\xi }_{50,PS1}=6.29\%$ for $v_c=50 \mathrm{m}/\min$ and ${\xi }_{150,PS1}=1.91\%$ for $v_c=150 \mathrm{m}/\min$, Figure 8a. The parameter set of Approach 2 resulted in an error value of ${\xi }_{50,PS2}=6.43\%$ for $v_c=50 \mathrm{m}/\min$ and ${\xi }_{150,PS2}=1.91\%$ for $v_c=150 \mathrm{m}/\min$, Figure 8b. Besides the large differences in terms of the material model parameter sets of Approach 1 and Approach 2, both parameter sets resulted in similar error values for the investigated cutting conditions outside the domain of calibration.

In deviation to the parameter set of Approach 1 and Approach 2, the parameter set of Approach 3 resulted in an error value that was comparably low. However, the error value within the domain of calibration is higher than the error value of the cutting conditions that were used for the calibration, Figure 8c. The error value of the investigated cutting condition was ${\xi }_{100,PS3}=1.94\%$. The results of the simulations indicate that the calibration range of the material model parameters has a distinct influence on the range of validity. Therefore, in order to increase the range of validity, a wide range of cutting parameters should be used for the inverse parameter determination.

7. Summary, Conclusion, and Outlook

In this study, an approach for the inverse determination of material model parameters was presented, which is based on the application of the Particle Swarm Optimization (PSO) algorithm. In order to apply the well-established PSO to the present inverse optimization problem, a multi-response formulation was utilized. Further, the PSO was modified by using dynamic boundaries in order to keep the parameters to be determined within physical meaningful boundaries. To investigate the applicability of the algorithm and to evaluate the determined parameter sets, the algorithm was used for the inverse re-identification of material model parameters. The findings of this study can be summarized as follows:

• The applicability of the PSO algorithm to the inverse material model parameter determination was successfully realized.
• When using the PSO algorithm, material model parameters can be calculated within less than 40 iterations while taking various process observables that can be measured from cutting experiments into account.
• The maximum PSO velocity parameter influences the number of required iterations distinctively and has to be selected carefully.
• The drawback of the existence of multiple local minima was further revealed for the domain of investigation. However, the comparison of the simulation results revealed only small differences in terms of the process observables as well as regarding the local temperature field.
• The validity of the determined material model parameters is a crucial factor for the inverse parameter determination and has to be considered when using the material model parameters outside the range of calibration.

Based on the results of this paper, considering the obtained results as well as the required computation time, it can be concluded that the PSO provides an efficient way for the inverse material model parameter determination. By applying this methodology, material model parameters can be determined with high reliability in a relatively short computation time in the future. In addition, the determination of model parameters for materials of small batches can be achieved in a cost-efficient way. Therefore, the presented methodology presents an attractive tool to be applied in industry.

In the future, further investigations regarding the influencing factors on the PSO, such as the number of particles, the maximum PSO velocity parameter, or the PSO parameters, will be investigated. To investigate the algorithm over a wide range of conditions, the algorithm will be implemented into a fully automatized program that is capable of analyzing the results and conducting iterations user-independently.

In comparison to the previously applied Downhill Simplex Algorithm [40,41], the PSO resulted in a smaller number of iterations and was characterized by a more pronounced regressive trend. However, due to the number of particles, the PSO resulted in higher total numbers of simulations and, therefore, in higher computational efforts. A combination of the DSA and the PSO, i.e., a hybrid algorithm, appears to be a possible way to utilize the advantages of both algorithms.