1. Introduction
Membranes are an ideal choice for filtering of fluids because they can create highly selective barriers that can retain particles due to various processes such as size-exclusion (straining), electro-chemical and other effects [
1]. As a result, membrane filtration has become the method of choice in various applications for separations, not only due to its economic advantage over other separation techniques due to lower energy costs, but also because it is better suited to preserve the quality of the product in the food and beverage industry than other purification processes [
2]. Applications in industry range from small-scale (protein filtration, virus removal) to large-scale (wastewater treatment) processes. Classical modes of operation include dead-end and cross-flow filtration, depending on whether the filter membrane surface is, respectively, either perpendicular or parallel to the flow direction [
3].
There are two main different ways in which the particles in the fluid can be retained by the membrane. In the first, which is characterised by the particles being small compared to the membrane pores, retention occurs inside the membrane, while in the second, which is characterised by the particles being bigger than the membrane pores, retention occurs by particles forming an additional layer on top of the membrane, usually referred to as a cake. In this work, we will refer to the whole device comprising a filter (the membrane) and a cake as a filtercake. Modelling of cake formation during both dead-end and cross-flow filtration has been studied extensively in the literature (see, for example, King & Please [
4] and Sanaei et al. [
5]).
Early core work on the build-up of a cake at a membrane surface comprised studies in compressional rheology. In the pioneering paper by Buscall & White [
6], the authors developed a theory of sedimentation in the form of a two-phase model, which forms the basis of many subsequent modelling efforts. A notable feature of this paper that permeates subsequent work is the concept of a yield stress of the cake, which is estimated using experimental data. The resulting model comprises a one-dimensional nonlinear diffusion equation for the volume fraction with a moving boundary denoting the free surface of the cake. The diffusion coefficient depends on both the permeability of the cake and the yield stress. In Landman et al. (1995) [
7], the authors showed how the framework developed by Buscall & White [
6] can be reconciled with simpler rheological relationships in the context of pressure filtration. In particular, the authors show how the growth of the cake layer can be predicted for a given applied pressure difference.
Applications of the compressional rheology theory to particular filtration processes are studied further in Landman et al. (1997) [
8], with the objective of using optimal control to maximise the processing rate. In this case they reduce the nonlinear diffusion equation derived in Buscall & White [
6] to a linearised version to facilitate a more tractable analysis. Similarly, Kapur et al. [
9] consider a simplified version of the model of Buscall & White [
6] to speed up computation.
Dewatering is an important application in which cake build-up is a key feature. In this process, water is removed from solid material or soil with the target product being the solid material. Stickland et al. (2016) [
10] study the dewatering process using the ideas of compressional rheology in a case where optimisation is the primary objective in forming the cake layer. Stickland et al. (2018) [
11] also show how compressional rheology models may be used to describe the specific case of wastewater treatment. Hewitt et al. [
12] show how the use of a compressive yield stress is a crucial component in accurately capturing the dewatering process. They validate their theory using experiments and demonstrate how the product that is being filtered plays a key role in the behaviour, finding that their model does not fit the behaviour for the filtration of cellulose. Finally, Eaves et al. [
13] study the dewatering process for paper and slurries. Again the key concept here is the modelling of water flow through a deforming consolidating material, however the main novelty in this paper is the more complicated physical configuration of the filtration process that is considered.
Vacuum filtration is another industrial process in which the build-up of cake is an important characteristic. A notable differentiating feature of this process to those aforementioned is that desaturation effects must be taken into account to model the air–liquid capillary imbibition (see for example Stickland et al. (2010) [
14]).
While there is an extensive body of literature that focuses on the accurate modelling of the formation and growth of a cake layer on a membrane, there has been much less work done to examine how mechanical deformation of both the cake and the underlying filter material, and the interplay between the two, might affect the behaviour of the entire system, and it is this question that forms the focus of this study.
We consider an elastic-response model to describe both the membrane and cake behaviour, which will allow for both a suitable characterisation of the membrane dynamics while enabling a direct comparison between the behaviour of the two materials. When a fluid flows through a porous medium, it exerts forces on the porous matrix, inducing deformations. These deformations in turn affect the local permeability of the material, which then influences the fluid flow. This coupling between the fluid flow and porous medium deformation is often modelled using poroelasticity theory, developed in the first half of the 20th century by Terzaghi and Biot [
15,
16] and since then applied in a plethora of industrial as well as biological applications [
17,
18,
19,
20,
21,
22].
To our knowledge, the first attempt to explicitly model the effects of elastic deformation on the local permeability of the porous medium was presented in Parker et al. [
18]. Authors extended a one-dimensional steady-state poroelastic model—comprising Darcy’s law for fluid flow, the Navier equation (equipped with a pressure gradient term arising from Terzaghi’s principle) for deformation and a conservation equation for fluid—by assuming a variety of constitutive assumptions relating local strain and permeability. In Köry et al. [
23], the analytic solution under the linear constitutive assumption from Parker et al. [
18] was used to obtain explicit conditions for porous-medium shutdown (deformation leading to locally zero permeability, which allows no flow through the medium). The analysis was then extended to the case of non-uniform rest-state permeability, i.e., permeability in the absence of any flow, with a special emphasis on applications to filtration processes.
Other models introduce more realistic descriptions of flow-deformation coupling either via power-law constitutive assumptions or using explicitly multi-phase frameworks (see Lee & Wang [
24]), but these are both less intuitive and less amenable to analytical progress, and become computationally challenging as the number of model parameters increases. A more complicated model consisting of a poroelastic model (with a more advanced relationship between the local permeability and deformation) and a fouling model (modelling the effects of caking and intra-membrane clogging separately) has recently been employed to explain the observed pressure–time signatures in direct-flow filtration under constant flux [
25].
In this work, we extend the simple poroelastic framework from Köry et al. [
23] to model cake filtration in a dead-end filter. The key objective of this work is to understand how deformations in both the filter and the cake interact with one another and affect the behaviour of the overall filtration process. We continue to assume the elastic response is instantaneous on the time scale of filtration, however the problem is time dependent due to the cake formation which takes the form of a moving boundary problem. In
Section 2, we formulate the model for a compressible filtercake including the boundary and interface conditions. We choose to model the system using a linearised theory in order to elucidate the concept of the interplay between the compression of the cake and the underlying membrane; the modelling ideas we lay out here readily generalise to more complex nonlinear theories. We nondimensionalise the system and then find the conditions required to both ensure the validity of small-deformations assumptions and avoid filter shutdown. We then derive the resulting caking filtration law (Equation (
30)). The caking law depends on the time-dependent pressure drop across the filtercake and two dimensionless material parameters, reflecting the behaviour of the two porous media (the filter and the cake; c.f. Köry et al. [
23]).
In
Section 3, we study the implications of the theory to three industrially relevant operating conditions, namely constant flux, maximising flux, and constant pressure-drop filtration, placing an emphasis on optimal filter design in each case. We conclude in
Section 4 by summarising the most important outcomes of our analysis and identifying areas in which the proposed theoretical framework could be improved and extended.
3. Industrial Applications
We now apply the theoretical framework that we have developed so far to industrially relevant problems. Specifically, we study three commonly employed filtration regimes—constant flux, greedy (where one wishes to achieve maximum total amount of fluid processed, or throughput, at any given time) and constant pressure drop. In each case, we aim to find the material properties of the filter (represented by the dimensionless parameter ) that optimise a given industrial goal for given material properties of the contaminant to be filtered (represented by the dimensionless parameter ).
3.1. Adaptive Pressure Drop to Obtain Constant Flux
A common operating regime in industry is to filter fluids at a constant flux. Enforcing a constant flux
, we find, using (
29), that
The solution to the cake-evolution Equation (
30) that satisfies the initial condition
is then
It can then be shown (see
Appendix C) that the time evolution of the transmembrane pressure difference across the entire filtercake is given by
We note that in the limit of an incompressible filter,
, which gives
in (
35), while (
37) reduces to
We see that the transmembrane pressure difference rises with time, to maintain the constant flux as a result of the increased resistance offered by the build-up of the cake. Eventually the pressure will become sufficiently large such that, at a point in either the filter or the cake, the permeability will reach zero. Beyond this point, no further fluid may be processed while maintaining constant flux. In practice, filtration is conducted only until some threshold pressure (<1/) is reached.
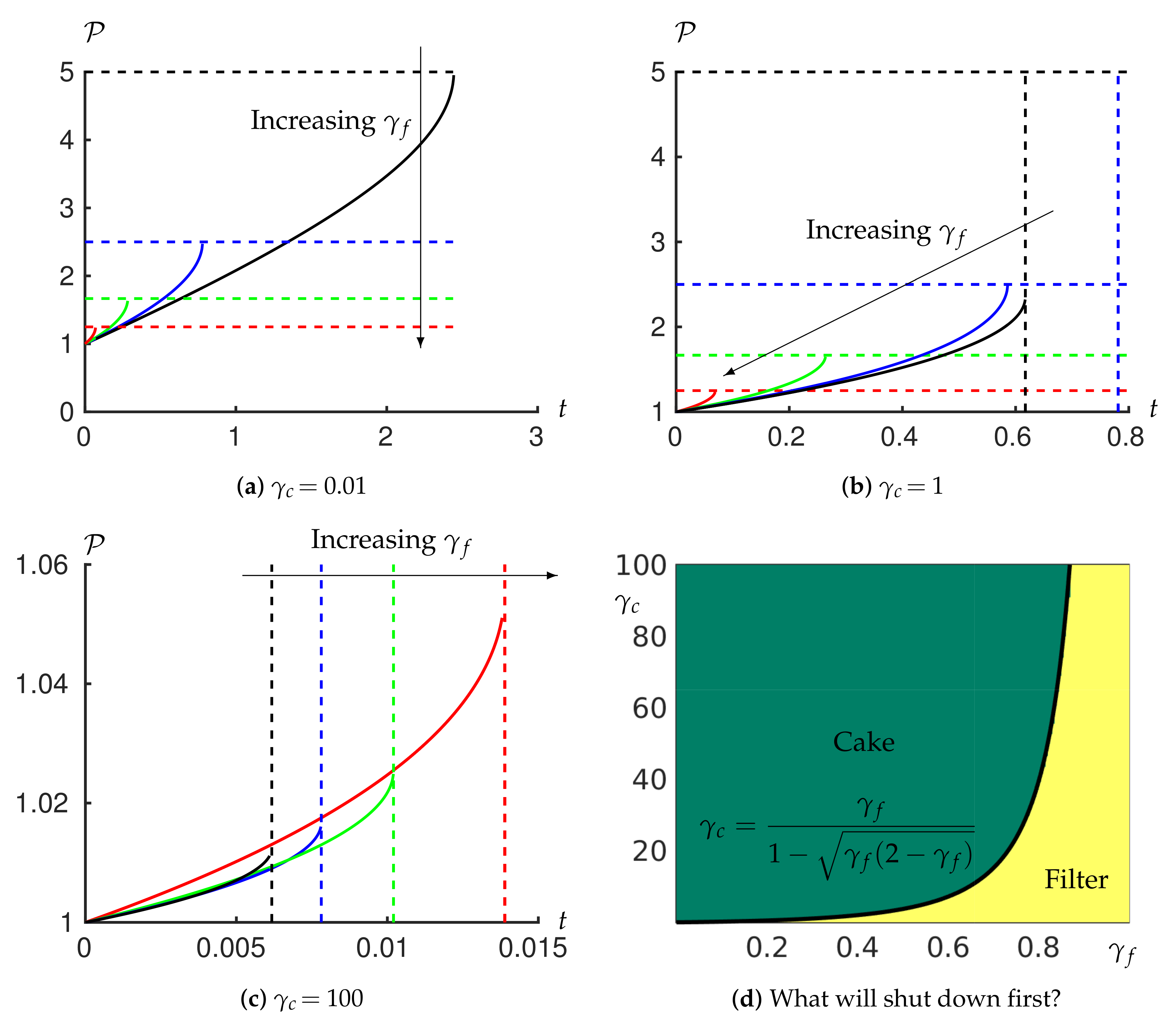
3.1.1. Observations
We now consider the behaviour of the system when it is operated in a constant flux regime using the model we have developed. For weakly compressible cakes (
,
Figure 2a) the higher the value of
the sooner the shutdown occurs. The shutdown is first reached within the filter for any value of
here. For a moderately compressible cake (
,
Figure 2b), while shutdown is reached in the filter for higher values of
, we now find that shutdown occurs in the cake if
is sufficiently low (
). When the cake is very compressible (
,
Figure 2c) the shutdown always occurs in the cake. Furthermore, in this case, while the behaviour for different values of
is similar at early time, at some point the pressure difference for the lowest value of
(
, black) overtakes that of the higher values of
(0.4 and 0.6, blue and green curves respectively). This reflects the fact that the cake resistance is becoming the limiting factor (
Figure 2c).
Note that, while in the case of incompressible filtercake, one needs to linearly increase pressure drop with time to maintain constant flux (cf. bottom-left subfigure of
Figure 3 in Ripperger et al. [
27]), when compression effects are taken into account, a superlinear growth of pressure drop is needed.
Inspired by these observations, we now examine whether the shutdown under constant-flux filtration first occurs in the cake or in the filter.
3.1.2. Where and When Does the Shutdown Take Place?
To determine whether the shutdown occurs in the filter or the cake, and the time
at which this occurs, we must first evaluate the strain and this can be determined from the strain field (
26) using
from (
35) and
. Using the results (
35) and (
36) as well as the definitions of dimensionless parameters from (
28), this gives
Provided
(which is required to avoid filter shutdown at
, see (
20)) the maximum strain within the filter continues to occur at
(the porous grid) where it attains the value
Within the cake the maximum strain occurs at
where the value
is attained. It is easy to see that both the maximum compression within the filter and that within the cake increase with time. We conclude that the shutdown might either occur in the filter at time
satisfying
(provided we have not yet reached shutdown in the cake) or in the cake at time
satisfying
provided we have not yet reached shutdown in the filter. After some algebraic manipulations of (
40) and (
41) (see
Appendix D) we conclude that the boundary separating shutdown in the cake and in the filter can be expressed as a critical value for the cake properties,
for given filter properties given by
We conclude that if
, shutdown occurs in the cake, while if
, shutdown occurs in the filter (see
Figure 2d). Inverting (
42) provides the critical filter properties that separate cake or filter shutdown for a given cake properties given by
Finally the analysis in
Appendix D gives that the maximum operating time given by
The total throughput,
, is obtained by multiplying this quantity by the flux, given by (
35), so that
3.1.3. Optimisation
We now use the expressions (
35), (
44) and (
45) to determine optimal values for
and
for the system operating at constant flux. We start by allowing the system to run until it shuts down and consider how the throughput might be maximised.
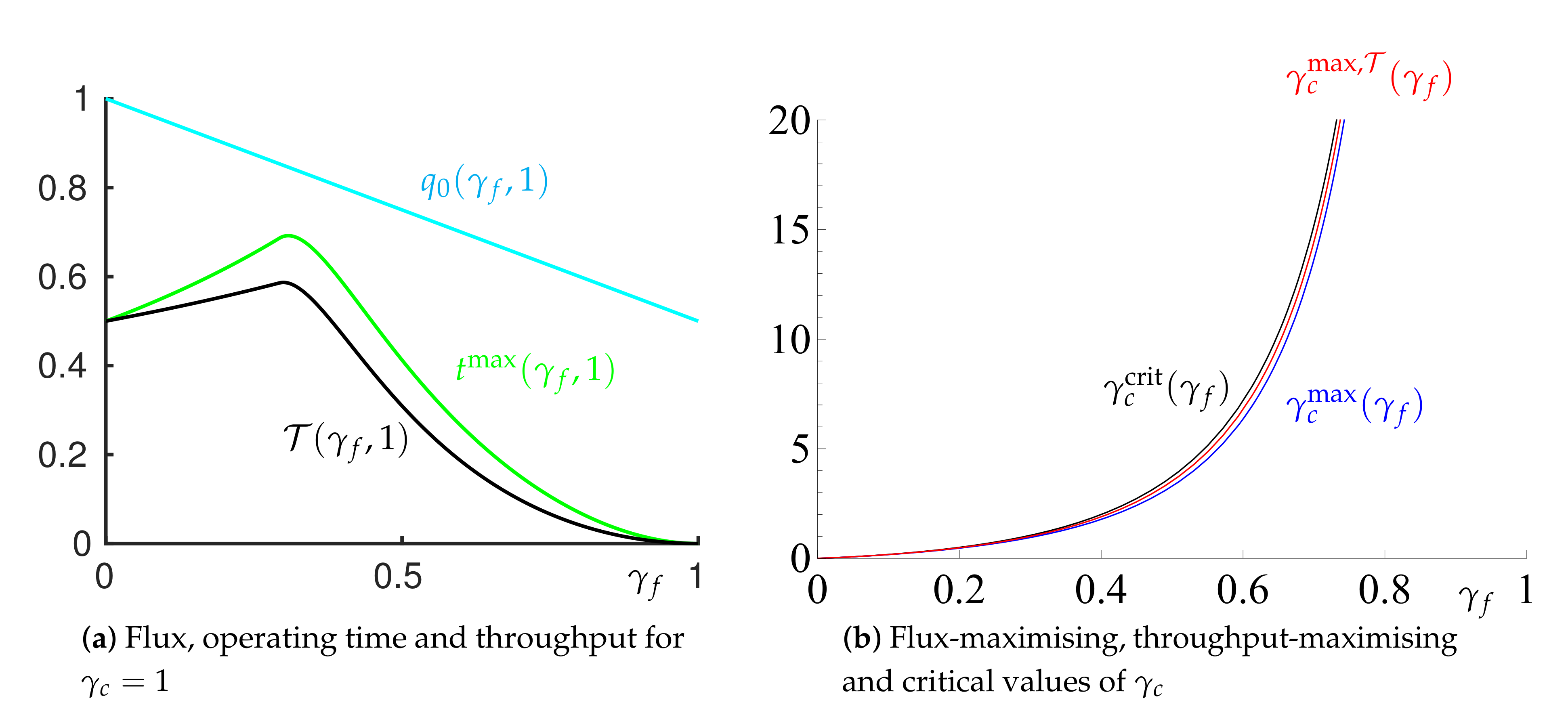
Figure 3a shows that, for a given contaminant, characterised by
, for small
we can increase the time before shutdown by increasing
. At the same time the flux decreases as
increases. However this penalty does not outweigh the advantages gained by the increased operating time, and so the total throughput, given by (
45) also increases with increasing
(
Figure 3a).
This increase in throughput is due to the more compressible filter acting as a ‘mattress’, taking up some of the pressure drop and compression that would otherwise be carried by the cake and preventing the cake from shutting down. However, if we increase
too far then the filter becomes too compressible and shuts down before the cake, leading to a reduction in total processing time.
Figure 3a indicates that for
both the total throughput and the maximum operating time are maximised at
.
We can further determine expressions for the filter properties that lead to the corresponding maximisations. First, the value of
that maximises the operating time can be obtained by differentiation of (
44), equating the resulting expression to zero and solving for
. This gives
Second, the value of
that maximises the total throughput can similarly be shown to satisfy
In
Figure 3b it can be seen that, for a given
, both the time-maximising and the throughput-maximising values of
are in the filter-shutdown region and very close to the critical value at which the filter and cake shut down simultaneously. These observations suggest that choosing a filter compressibility that is close to that for which we would observe simultaneous filter and cake shutdown would lead to maximum throughput before shutdown.
From these relationships we confirm that, for given cake properties (characterised through
), a filter with properties (characterised by
) that correspond to the threshold between cake and filter shutdown leads to a system that is very close to that which maximises both the operating time and the total throughput (
Figure 3b). This does indeed confirm that, given a particular material to filter, choosing the filter properties such that both the cake and filter shut down at the same time (given by (
43)), will lead to a system that is close to maximising the total operating time and final throughput. This offers a simple way of identifying an optimal filter selection.
3.1.4. Minimising Power Expenditure
Previously we discussed maximising throughput but another desirable industrial outcome is to minimise the total energy used per unit area of membrane required to generate a given flux. The total power per unit membrane cross-sectional area expended on the filtration is the product of the flux
q (here
) and the pressure difference
. A measure of the total energy,
, used at time
t, is the time integral of this:
This may be evaluated using (
44), (
35) and (
37), but while the result is analytic, it is cumbersome so we do not write it here.
Setting
yields filter shutdown at
, resulting in
, which trivially minimises the power expenditure. Therefore, we cannot minimise the expended power while maximising the throughput, and we thus consider trade-offs similar to those described in Köry et al. [
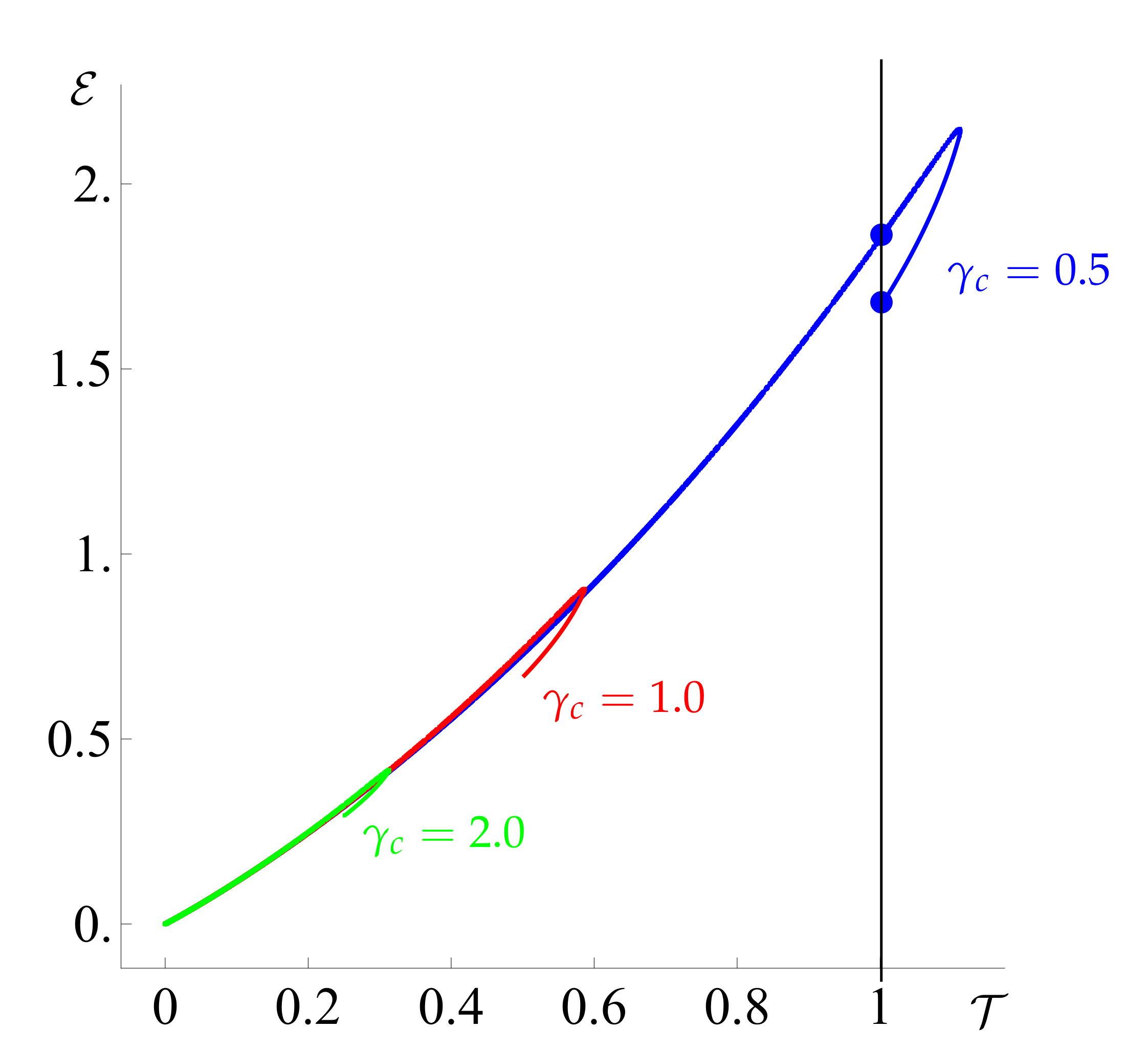
23]. However, for a given
, we find that varying
leads to a multi-valued energy
when plotted versus the throughput
(see
Figure 4). This indicates that, in some cases, the same final throughput can be achieved for less energy by choosing a more rigid filter, that is, one with a lower value of
.
3.2. Adjusting the Pressure Drop to Achieve Maximum Throughput at All Times
Let us now consider the operational regime where we want to filter a given amount of fluid as quickly as possible and we can vary the flux by changing the applied pressure. At any given instant in time, the transmembrane pressure must be below a critical value to avoid shutdown of the system. Here, we will derive an expression for the transmembrane pressure difference that maximises the flux at any time, noting that avoiding shutdown of the system requires us to be below the pressure that causes shut down of both the filter and the cake. We expect that maximising the flux at each time will maximise the throughput. We will assume that we are constrained initially to avoid shutdown in the filter and then check if and when shutdown in the cake becomes the limiting constraint.
To begin with, when the cake thickness is small, we will always be limited by the critical pressure that induces filter shutdown. This is given by
from (
31). Note from (
12) that
, which means that
here needs to be understood as an instantaneous switch of the dimensionless pressure drop from 1 to
at
. Substituting this into the cake-evolution Equation (
30) and simplifying the resulting expression, the cake evolution equation takes the form
Upon rewriting and integrating, we obtain an implicit relation for the cake thickness at a given time
t,
where we have applied
. We continue operating with
unless we reach shutdown in the cake. Substituting the right-hand side from the cake-evolution Equation (
30) for
q into the cake-shutdown condition (
34), we find that there are no positive solutions for
when
and one positive solution,
for
. Substituting (
51) into (
50) provides the transition time before which the system is on the brink of shutdown in the filter and after which the cake deformation limits the pressure drop. We conclude that, if
, continuing indefinitely with a transmembrane pressure of
will provide the maximum flux. In this case, it follows from (
50) that the cake size will increase unboundedly. This is because we have
here, and the condition for avoiding cake shutdown (
32) is thus always satisfied. If
, however, the constant transmembrane pressure
would cause the cake to grow, the filter–cake interface pressure to decrease, and eventually the cake to shut down (i.e., condition (
32) would cease to be true in finite time). In such a case, we maximise the flux at any given time by applying a transmembrane pressure
until the cake size reaches the value given by (
51), following which we enter a second phase where we decrease the pressure drop
in such a way that the flux is given by (
34) to ensure that the cake does not shut down.
Using the cake-evolution Equation (
13) and substituting for
q from (
34), we conclude that the cake evolution equation during this second phase reads
Solving this subject to the condition
gives
In order to determine how one should vary
to achieve the maximum flux at any time for
after the critical value of
from (
51), we equate the right-hand side of the cake-evolution equation (
30) and that of (
52) and solve for
to get
where we chose the appropriate solution of the quadratic for which
so that we do not have shutdown in the filter. Substituting (
53) into (
54) gives the maximum pressure that we can apply without the system shutting down for times
when the cake (rather than the filter) deformation begins to constrain the pressure drop. Substituting (
53) into (
52) gives the corresponding flux
q.
As a special case, note that for an incompressible filter (
), we find that, for all
,
and
. An incompressible filter maximises the throughput that can be achieved by any filter up to any positive time. Finally, note that whenever
, as
(i.e.,
), we get
. This is consistent with Equation (
32)), which ensures we do not reach shutdown in the cake, because
must be non-negative. Note further that as
under the throughput-maximising strategy, the cake size increases without bounds so the resistance of the filter becomes negligible compared to that of the cake, which (provided
for all times) results in
. This explains why
must converge to
as
.
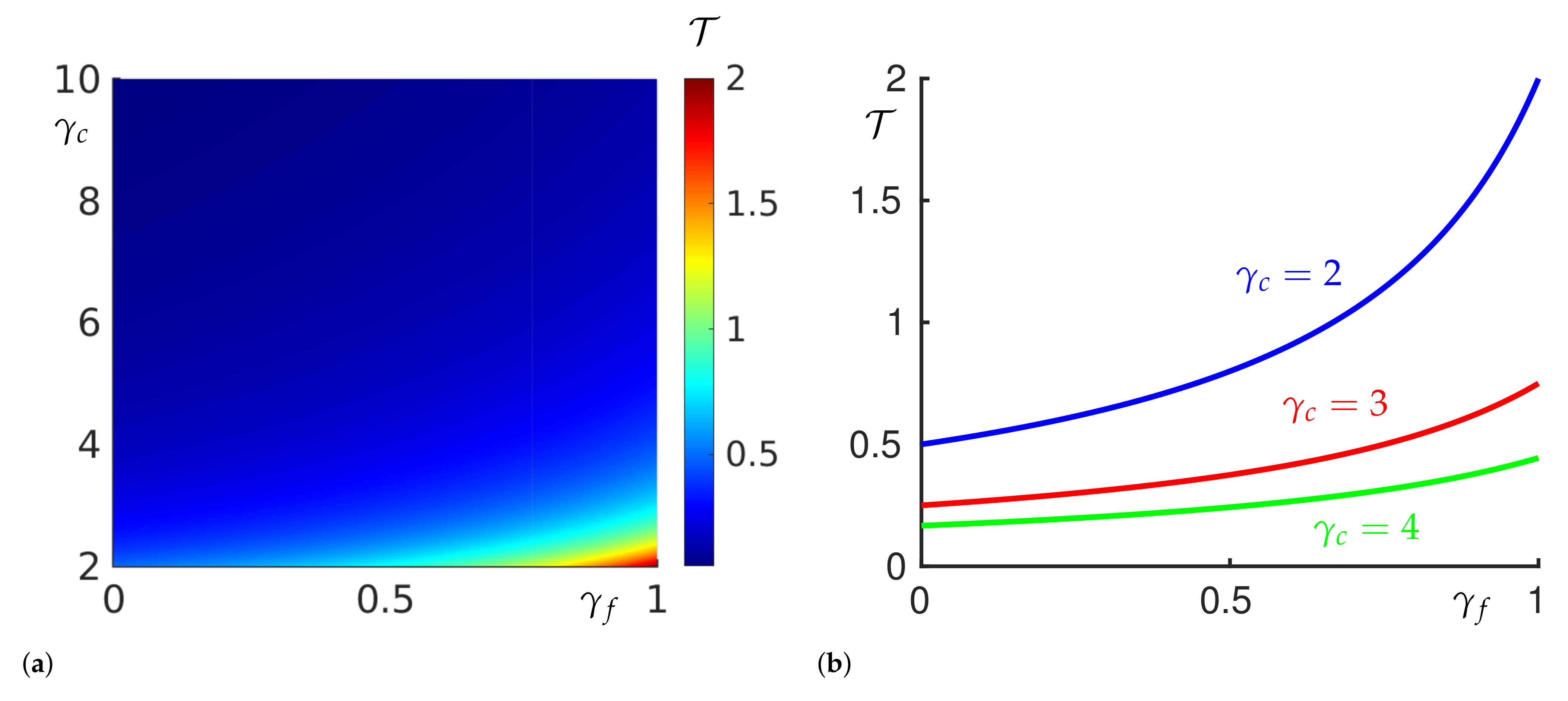
In
Figure 5a,b we show the evolution of
and
q as functions of cake size
, which acts as a proxy for time, for different values of
and
. We find that, for any
, one reaches any given value of
(and thus filters any given amount of fluid) in the shortest time by choosing an incompressible filter,
.
3.3. Behaviour for Fixed Pressure Drop
Finally, we study the operational regime where a constant pressure drop is applied across the filtercake and the flux therefore changes. We have already shown that for the threshold pressure drop can be maintained for all positive times t, so it follows that any constant pressure drop below this value (including ) can also be maintained indefinitely. Thus, we solely concentrate on the case where , for which the threshold pressure drop would result in finite-time cake shutdown.
In a similar manner to the previous section, we can find an implicit relationship for the dependence of cake size
on time
t. The expression is, however, rather cumbersome, and so instead we focus on the cake shutdown. Substituting
into the right-hand side of the cake-evolution Equation (
30), equating this expression with the cake shutdown condition for the flux (
34) and solving for
, we get (assuming
) no finite positive solutions
for
and one positive solution
for
. This implies that for
one can maintain such pressure drop indefinitely, while for
, the filtration under constant pressure drop ends in finite time. It follows from (
55) that, for any chosen
, one achieves maximal throughput by designing a filter with the largest possible
so that filter shutdown is avoided, that is,
. With such
, the throughput from (
55) becomes
This observation is confirmed in
Figure 6, where we find that, if one wishes to maximise the total throughput
before shutdown for arbitrary
, then it is best to choose a filter with
, and the result (
56) provides an upper bound on the expected throughput.
Finally, note that while the throughput at any time is given by
(provided we avoid shutdown), the power expended on such filtration process up to time
t is given by
This explicitly states the trade-off between the minimisation of power expenditure and the maximisation of throughput.
4. Discussion
In this paper we considered fouling of filters due to cake formation during dead-end filtration. We focused on the particular idea that both the cake and the underlying membrane may deform elastically during a filtration process and thus the interplay between the two may play an important role during filtration processes. We applied a poroelastic model introduced in Parker et al. [
18] and further studied in Köry et al. [
23] to the caking process. Both the filter and the cake were considered to be compressible porous media, where their permeabilities were assumed to vary linearly with the local strain, and the flow and deformations were taken to be one dimensional.
Using analytical methods, we determined the condition for filter shutdown (
31) and derived an equation for the growth of the cake that depended on only the pressure drop and two dimensionless parameters that measured the mechanical sensitivities of the cake and filter. This provides a novel cake-filtration law as the flux
through the filtercake is given explicitly as a function of the pressure drop
. Even though the equation for the growth of the cake layer cannot be solved for a general pressure drop, we made considerable analytical progress by considering three industrially relevant operating regimes of constant flux, maximising flux, and constant pressure-drop filtration.
To maintain a constant flux through the filtercake it is necessary to increase the applied pressure drop gradually. At some point the pressure drop will be such that either the filter or the cake will shut down. We found the required evolution of the pressure drop to maintain a constant flux and subsequently identified the parameter dependence that leads to either filter or cake shutdown. We proceeded to study the maximum operating time and throughput achievable and showed that, for given cake properties, the largest throughput is achieved with a slightly compressible filter, which acts as a mattress, taking some of the pressure drop and compression away from the cake. The effective elastic coefficients,
and
, of the optimal filter must be chosen slightly below the coefficients that cause the filter and the cake to shut down simultaneously. We concluded the constant-flux analysis by considering a minimisation of the power costs. Here, we noticed that, even though we can obtain higher throughput by allowing the filter to be compressible, it comes at the cost of significantly increased power expenditure, so trade-offs between throughput and power consumption, similar to those studied in Köry et al. [
23], should be taken into account.
We then analysed the operational regime where we maximise the flux (and thus throughput) at every time during the filtration process, regardless of power expenditure. We derived an implicit relationship for the cake size as a function of filtration time. We found that, if the compressibility of the filter was at least as large as that of the cake, a constant pressure drop (just below that which causes filter shutdown) could be maintained indefinitely without reaching shutdown in the cake. If the filter is more rigid than the cake, however, the maximum pressure that can be applied without the filtercake shutting down falls with time and we found an explicit expression for this dependence. For any cake properties, choosing an incompressible filter was shown to maximise throughput at all times.
Finally, we studied the operational regime of a constant applied pressure drop. We found that, for given material properties, there exists a critical pressure below which we can operate a system indefinitely without the filtercake shutting down. If we wish to maximise throughput for given cake properties at a pressure drop above this critical value, it is optimal to choose a filter that is highly compressible so that it is able to take some of the pressure drop and compression from the cake.
The work in this paper demonstrates how the resistance and deformation of both the cake and the underlying filter medium can play an important role when thinking about optimising the process of dead-end filtration with cake build-up. The main objective of this work was to present a simple model that was able to demonstrate the type of behaviour that can be exhibited in a system comprising a membrane and cake that both deform elastically. A key next step in this work would be to generalise the ideas to account more accurately for the filtration of specific materials. Specifically, this would involve using nonlinear compressional rheology modelling. In doing so, the system may be described by an elastic membrane with a plastically deforming cake. It would also be interesting to account for particle trapping in the interior of the filter medium. In addition it would be of interest to study the case where the particles that build up to form the cake remain free so that if the flow is switched off the cake can deplete. In this scenario, one would also need to model the effects of concentration polarisation. Finally, experiments need to be conducted to validate or disprove the implications of this theory.