Experimental Modelling of a Solar Dryer for Wood Fuel in Epinal (France)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Modelling
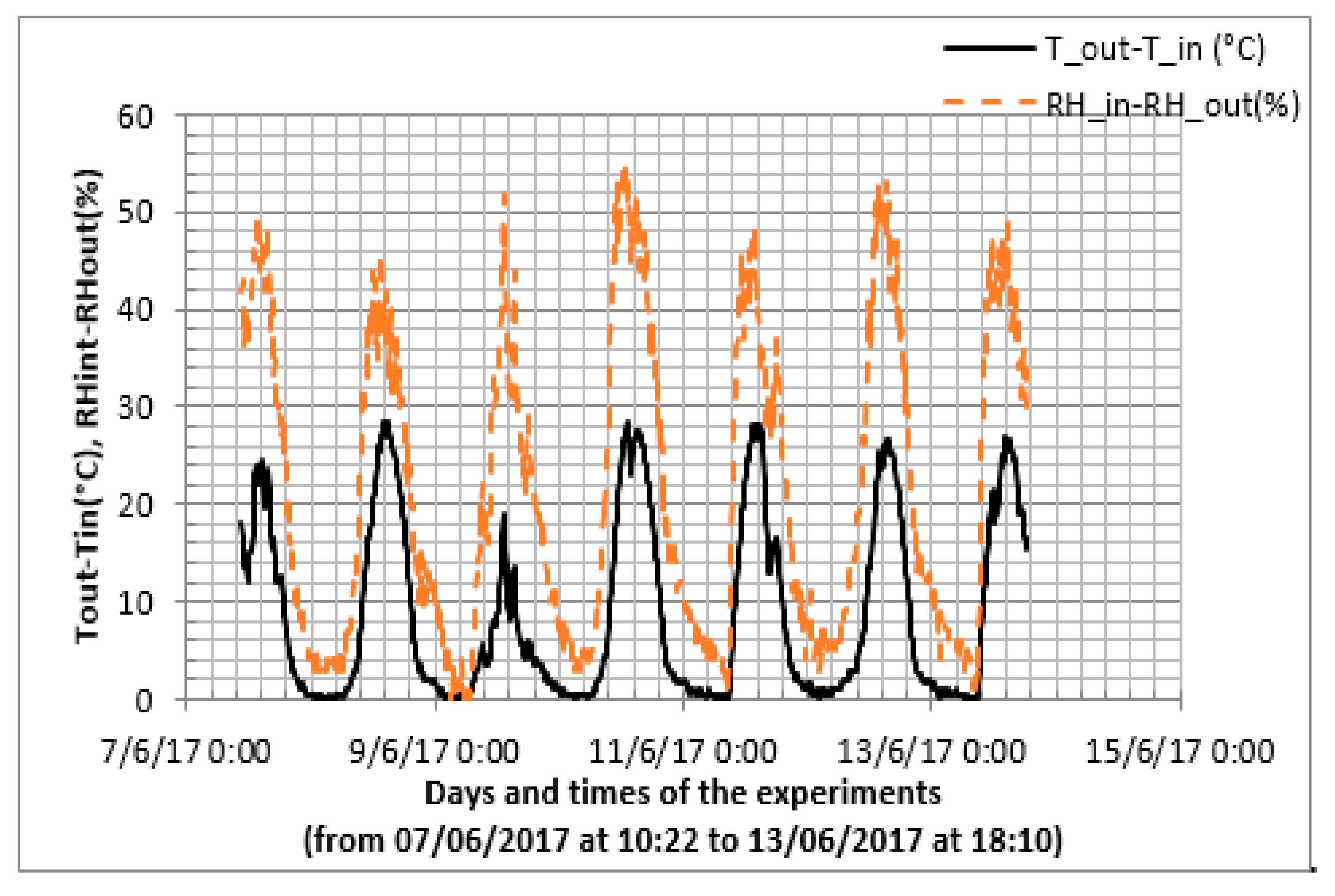
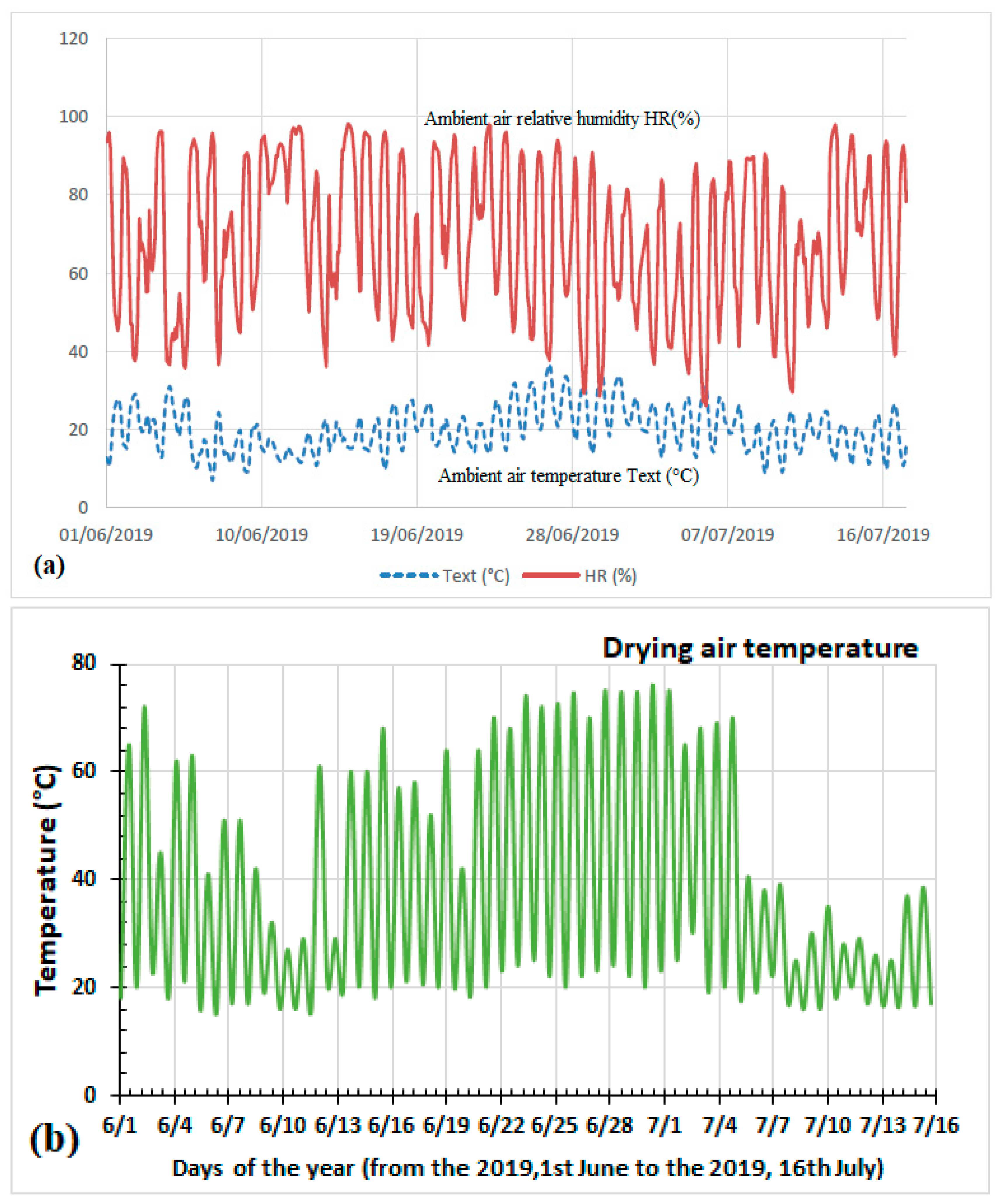
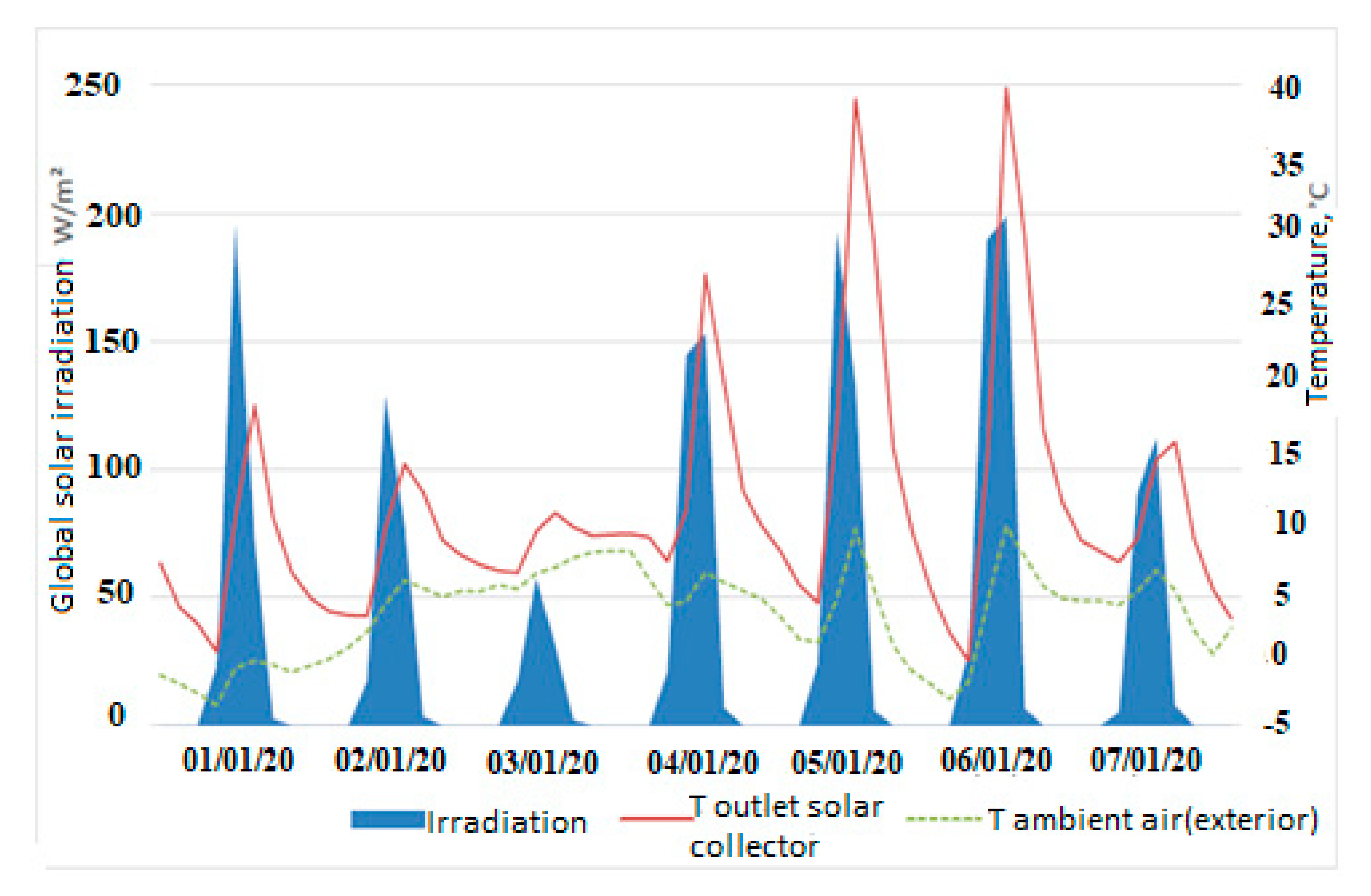
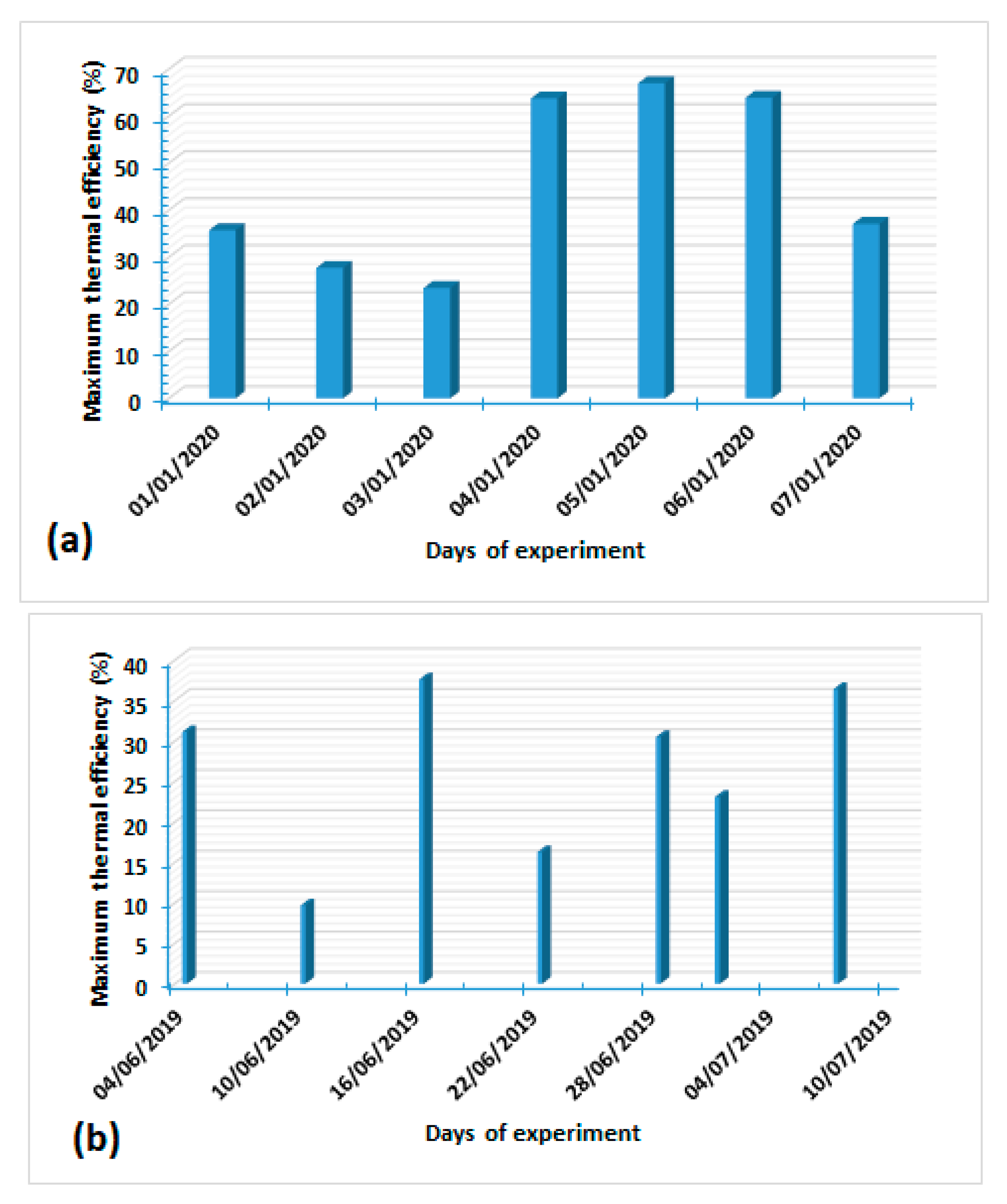
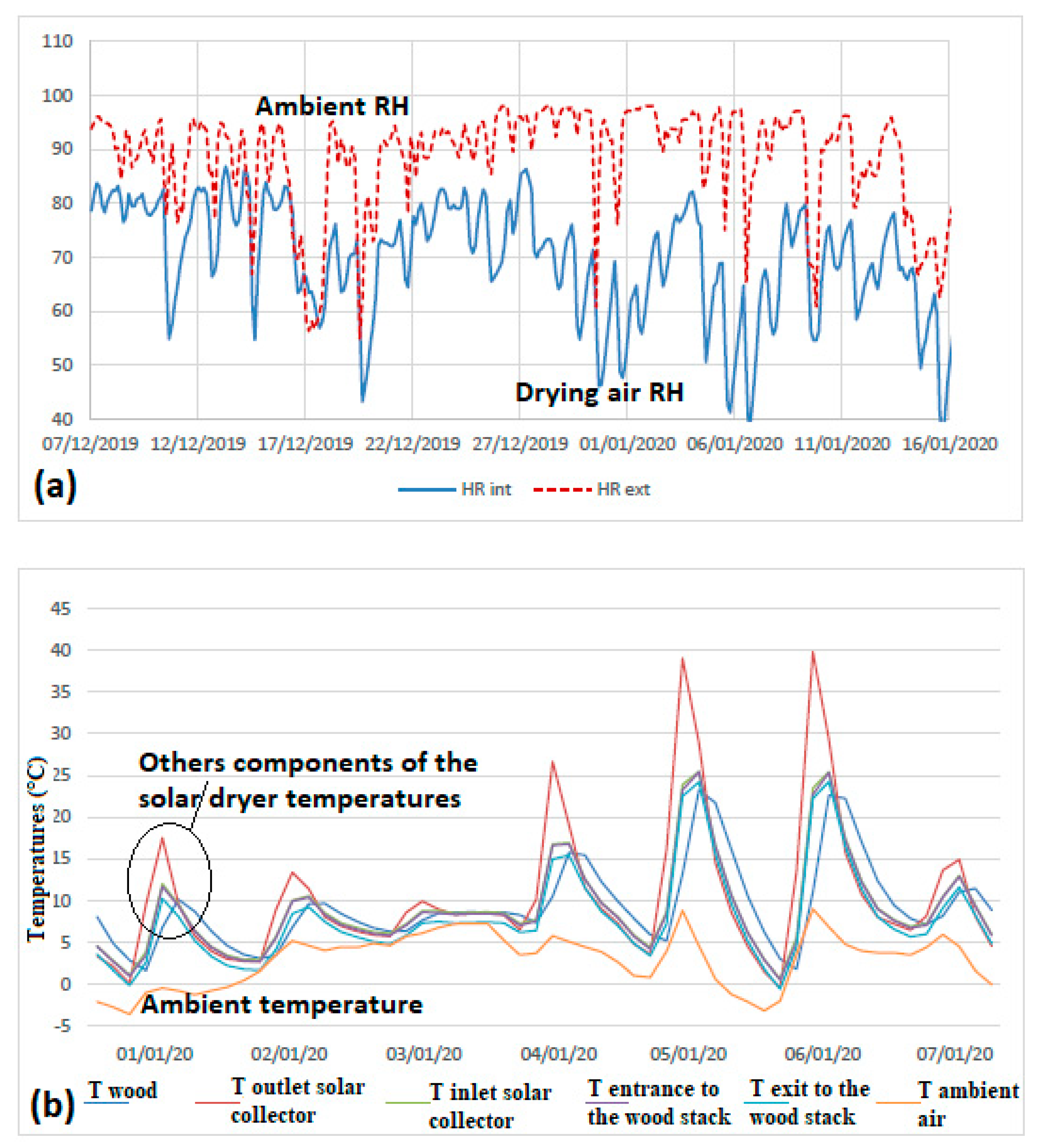
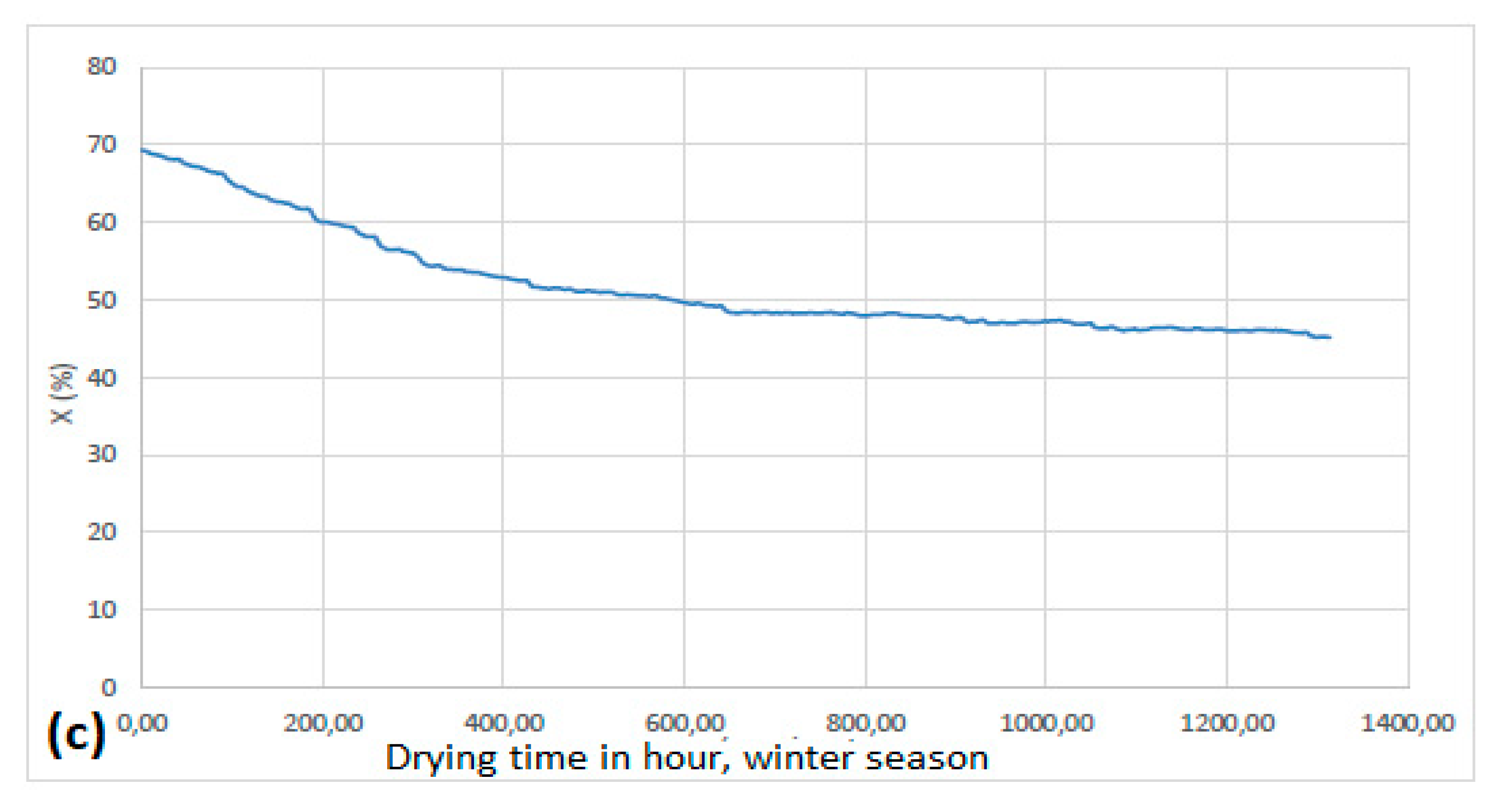
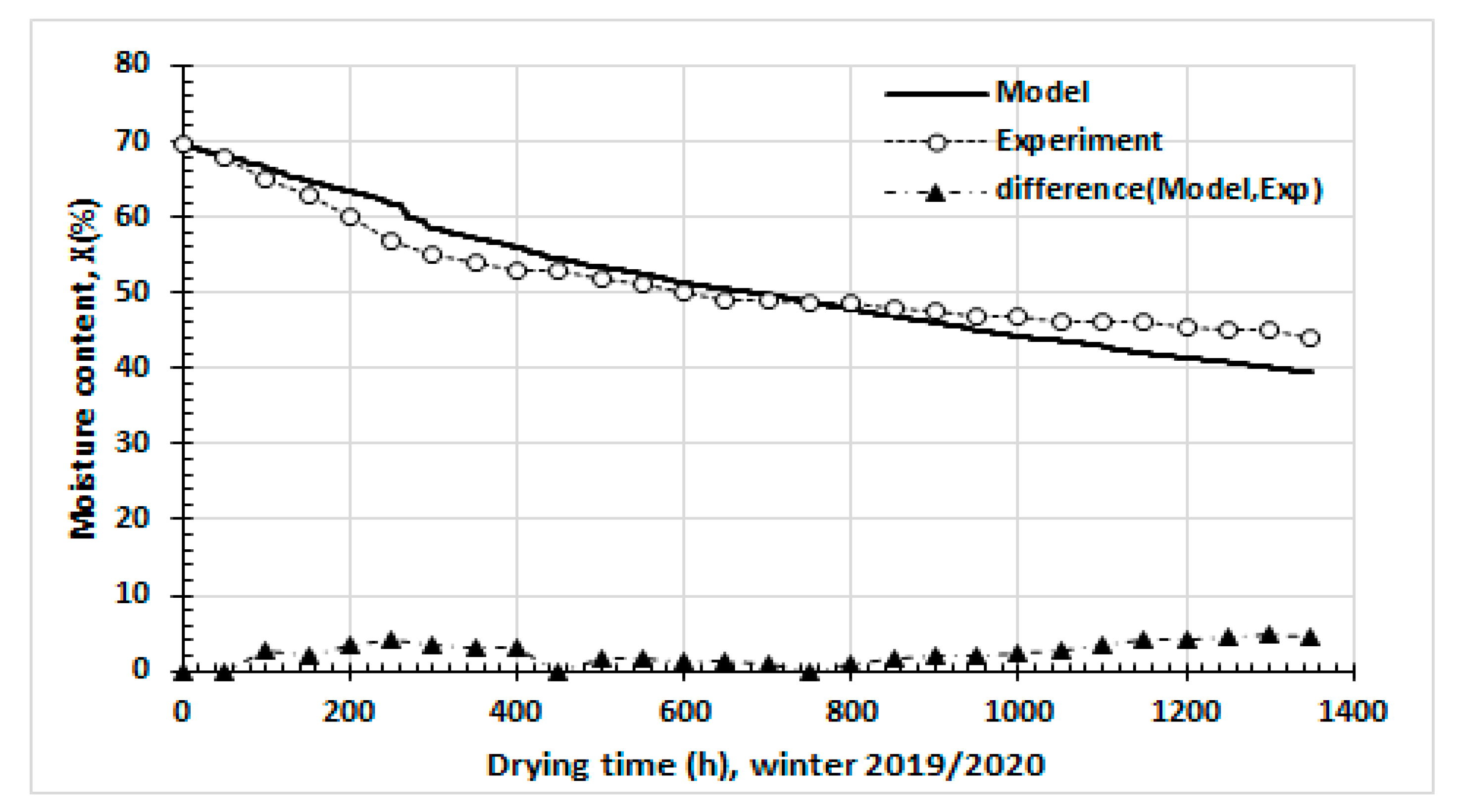
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Les Avis de L’ADEME: Le Chauffage Domestique au Bois (Mai 2019). Available online: https://www.connaissancedesenergies.org/sites/default/files/pdf-actualites/avis-ademe-chauffage-domestique-bois-2019.pdf (accessed on 16 July 2020).
- Tout Savoir Sur L’utilisation du Bois énergie en France. Available online: https://www.total-proxi-energies.fr/particuliers/actualites/tout-savoir-sur-lutilisation-du-bois-energie-en-france (accessed on 16 July 2020).
- Académie D’Agriculture de France. Available online: https://www.academie-agriculture.fr/sites/default/files/agenda/rapportsurlapollutiondelacombustiondubois.pdf (accessed on 16 July 2020).
- Energie et Rénovation de L’habitat: Les Chiffres du Logement en France. Available online: https://www.preservationdupatrimoine.fr/blog/environnement/energie-renovation-habitat-chiffres/ (accessed on 16 July 2020).
- Construction, Les Chiffres de L’année 2018. Available online: https://www.cherche-chantier.fr/chiffres-btp-2018/ (accessed on 16 July 2020).
- Bell, M.; Carrington, G.; Lawson, R.; Stephenson, J. Social-technical barriers to the use of energy-efficient timber drying technology in New Zealand. Energy Policy 2014, 67, 747–755. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Simo-Tagne, M.; Abam, F.I.; Onwuka, O.S.; Prince, S.; Bennamoun, L. Exergy, environmental and economic analysis of hybrid solar-biomass dryer integrated with copper tubing as heat exchanger. Heliyon 2020, 6, e03401. [Google Scholar] [CrossRef] [PubMed]
- Ndukwu, M.C.; Bennamoun, L. Potential of integrating Na2SO4·10H2O pellets in the solar drying system. Dry. Technol. 2018, 36, 1017–1030. [Google Scholar] [CrossRef]
- Simo-Tagne, M. Simple solar dryers adapted to the social, climatic and economic context can help increase the value of tropical timber (Fellowship Report). ITTO Trop. For. Update 2018, 27, 25–27. [Google Scholar]
- Awadalla, H.S.F.; El-Dib, A.F.; Mohamad, M.A.; Reuss, M.; Hussein, H.M.S. Mathematical modelling and experimental verification of the wood drying process. Energy Convers. Manag. 2004, 45, 197–207. [Google Scholar] [CrossRef]
- Bentayeb, F.; Bekkioui, N.; Zeghmati, B. Modelling and simulation of a wood solar dryer in a Moroccan climate. Renew. Energy 2008, 33, 501–506. [Google Scholar] [CrossRef]
- Loureiro, D.; Martis, M.J.; Santos, J.A.; Nogueira, A.; Pestana, L.; Costa, C.; Ramalho, A. Towards a competitive use of solar driers: A case study for the lumber industry. IEEES 2007, 3, 1–9. [Google Scholar]
- EECA. Summary of 9 Sawmill Energy Audits; Energy Efficiency and Conservation Authority: Wellington, New Zealand, 2005.
- Simo-Tagne, M.; Bennamoun, L. Numerical study of timber solar drying with application to different geographical and climatic conditions in Central Africa. Sol. Energy 2018, 170, 454–469. [Google Scholar] [CrossRef]
- Bekkioui, N.; Zoulalian, A.; Hakam, A.; Ez-Zahraouy, H. Using a parametric study to analyse the performance of wood solar dryers with glazed walls. Maderas Cienc. Tecnol. 2017, 19, 463–470. [Google Scholar] [CrossRef] [Green Version]
- Bekkioui, N.; Rachadi, A.; Ez-Zahraouy, H. One-year simulation of a solar wood dryer with glazed walls in a Moroccan climate. Renew. Energy 2020, 155, 770–782. [Google Scholar] [CrossRef]
- Khouya, A.; Draoui, A. Computational drying model for solar kiln with latent heat energy storage: Case studies of thermal application. Renew. Energy 2019, 130, 796–813. [Google Scholar] [CrossRef]
- Khouya, A. Effect of regeneration heat and energy storage on thermal drying performance in a hardwood solar kiln. Renew. Energy 2020, 155, 783–799. [Google Scholar] [CrossRef]
- Lamrani, B.; Khouya, A.; Draoui, A. Energy and environmental analysis of an indirect hybrid solar dryer of wood using TRNSYS software. Sol. Energy 2019, 183, 132–145. [Google Scholar] [CrossRef]
- Lamrani, B.; Khouya, A. Thermal performance and economic analysis of an indirect solar dryer of wood integrated with packed-bed thermal energy storage system: A case study of solar thermal applications. Dry. Technol. 2020. [Google Scholar] [CrossRef]
- Lamrani, B.; Khouya, A. Modelling and simulation of a hybrid solar-electrical dryer of wood integrated with latent heat thermal energy storage system. Therm. Sci. Eng. Prog. 2020, 18, 100545. [Google Scholar] [CrossRef]
- Lamrania, B.; Khouya, A.; Zeghmati, B.; Draoui, A. Mathematical modelling and numerical simulation of a parabolic trough collector: A case study in thermal engineering. Therm. Sci. Eng. Prog. 2018, 8, 47–54. [Google Scholar] [CrossRef]
- Luna, D.; Nadeau, J.P.; Jannot, Y. Model and simulation of a solar kiln with energy storage. Renew. Energy 2010, 36, 2533–2542. [Google Scholar] [CrossRef] [Green Version]
- Simo-Tagne, M.; Zoulalian, A.; Remond, R.; Rogaume, Y.; Bonoma, B. Modeling and simulation of an industrial indirect solar dryer for iroko wood (Chlorophora excelsa) in a tropical environment. Maderas Cienc. Tecnol. 2017, 19, 95–112. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Zoulalian, A.; Remond, R.; Rogaume, Y. Mathematical modelling and numerical simulation of a simple solar dryer for tropical wood using a collector. Appl. Therm. Eng. 2018, 131, 356–369. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Bonoma, B.; Bennamoun, L.; Monkam, L.; Léonard, A.; Zoulalian, A.; Rogaume, Y. Modeling of coupled heat and mass transfer during drying of ebony wood using indirect natural convection solar dryer. Dry. Technol. 2019, 37, 1863–1878. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Bennamoun, L.; Abam, F.I. Experience of solar drying in Africa: Presentation of designs, operations and models. Food Eng. Rev. 2018, 10, 211–244. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Remond, R.; Rogaume, Y.; Zoulalian, A.; Perre, P. Characterization of sorption behaviour and mass transfer properties of four central Africa tropical woods: Ayous, Sapele, frake, lotofa. Maderas Cienc. Tecnol. 2016, 18, 207–226. [Google Scholar]
- Delaunay, L.; Bourgaut, T. Décentraliser le Séchage Artificiel de Bois-Bûches. Master’s Thesis, ENSTIB, Epinal, France, 2020. [Google Scholar]
- Simo-Tagne, M.; Rémond, R.; Rogaume, Y.; Zoulalian, A.; Bonoma, B. Modeling of coupled heat and mass transfer during drying of tropical woods. Int. J. Therm. Sci. 2016, 109, 299–308. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Bennamoun, L.; Léonard, A.; Rogaume, Y. Modeling, numerical simulation and validation of a convective dryer in steady conditions: Case study of tropical woods. Int. J. Model. Simul. 2020, 40, 143–161. [Google Scholar] [CrossRef]
- Ananías, R.A.; Mougel, E.; Zoulalian, A. Introducing an overall mass-transfer coefficient for prediction of drying curves at low temperature drying rates. Wood Sci. Technol. 2009, 43, 43–56. [Google Scholar] [CrossRef]
- Chrusciel, L.; Mougel, E.; Zoulalian, A.; Meunier, T. Characterization of water transfer in a low-temperature convective wood drier: Influence of the operating parameters on the mass transfer coefficient. Holz. Roh. Werkst. 1999, 57, 439–445. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Rémond, R.; Rogaume, Y.; Zoulalian, A.; Bonoma, B. Sorption behavior of four tropical woods using a dynamic vapor sorption standard analysis system. Maderas. Cienc. Tecnol. 2016, 18, 403–412. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Bennamoun, L.; Léonard, A.; Rogaume, Y. Determination and modeling of the isotherms of adsorption/desorption and thermodynamic properties of obeche and lotofa using nelson’s sorption model. Heat Mass Transf. 2019, 55, 2185–2197. [Google Scholar] [CrossRef]
- Simpson, W.T.; TenWolde, A. Physical properties and moisture relations of wood. In Wood Handbook; Forest Products Laboratory: General technical report FPL; GTR-113; 1999; pp. 3.1–3.24. Available online: https://www.fpl.fs.fed.us/documnts/fplgtr/fplgtr113/ch03.pdf (accessed on 20 July 2020).
- Ndukwu, M.C.; Bennamoun, L.; Abam, F.I.; Eke, A.B.; Ukoha, D. Energy and exergy analysis of a solar dryer integrated with sodium sulfate decahydrate and sodium chloride as a thermal storage medium. Renew. Energy 2017, 113, 1182–1192. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Simo-Tagne, M.; Bennamoun, L. Solar drying research of medicinal and aromatic plants: An African experience with assessment of the economic and environmental impact. Afr. J. Sci. Technol. Innov. Dev. 2020. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Onyenwigwe, D.; Abam, F.I.; Eke, A.B.; Dirioha, C. Development of a low-cost wind-powered active solar dryer integrated with glycerol as thermal storage. Renew. Energy 2020, 154, 553–568. [Google Scholar] [CrossRef]
- Fuwape, I.A.; Fuwape, J.A. Construction and evaluation of a timber-drying solar kiln. Bioresour. Technol. 1995, 52, 283–285. [Google Scholar] [CrossRef]
- Séchage du Bois-Wood Drying. Available online: https://fr.qwe.wiki/wiki/Wood_drying (accessed on 20 July 2020).


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simo-Tagne, M.; Ndukwu, M.C.; Azese, M.N. Experimental Modelling of a Solar Dryer for Wood Fuel in Epinal (France). Modelling 2020, 1, 39-52. https://doi.org/10.3390/modelling1010003
Simo-Tagne M, Ndukwu MC, Azese MN. Experimental Modelling of a Solar Dryer for Wood Fuel in Epinal (France). Modelling. 2020; 1(1):39-52. https://doi.org/10.3390/modelling1010003
Chicago/Turabian StyleSimo-Tagne, Merlin, Macmanus Chinenye Ndukwu, and Martin Ndi Azese. 2020. "Experimental Modelling of a Solar Dryer for Wood Fuel in Epinal (France)" Modelling 1, no. 1: 39-52. https://doi.org/10.3390/modelling1010003
APA StyleSimo-Tagne, M., Ndukwu, M. C., & Azese, M. N. (2020). Experimental Modelling of a Solar Dryer for Wood Fuel in Epinal (France). Modelling, 1(1), 39-52. https://doi.org/10.3390/modelling1010003






