Kinetic Energy and the Free Energy Principle in the Birth of Human Life
Abstract
1. Introduction
2. Materials and Methods
2.1. Patients
2.2. Image Capturing Method
2.3. Vector Data Acquisition
2.4. Kinetic Energy Calculation
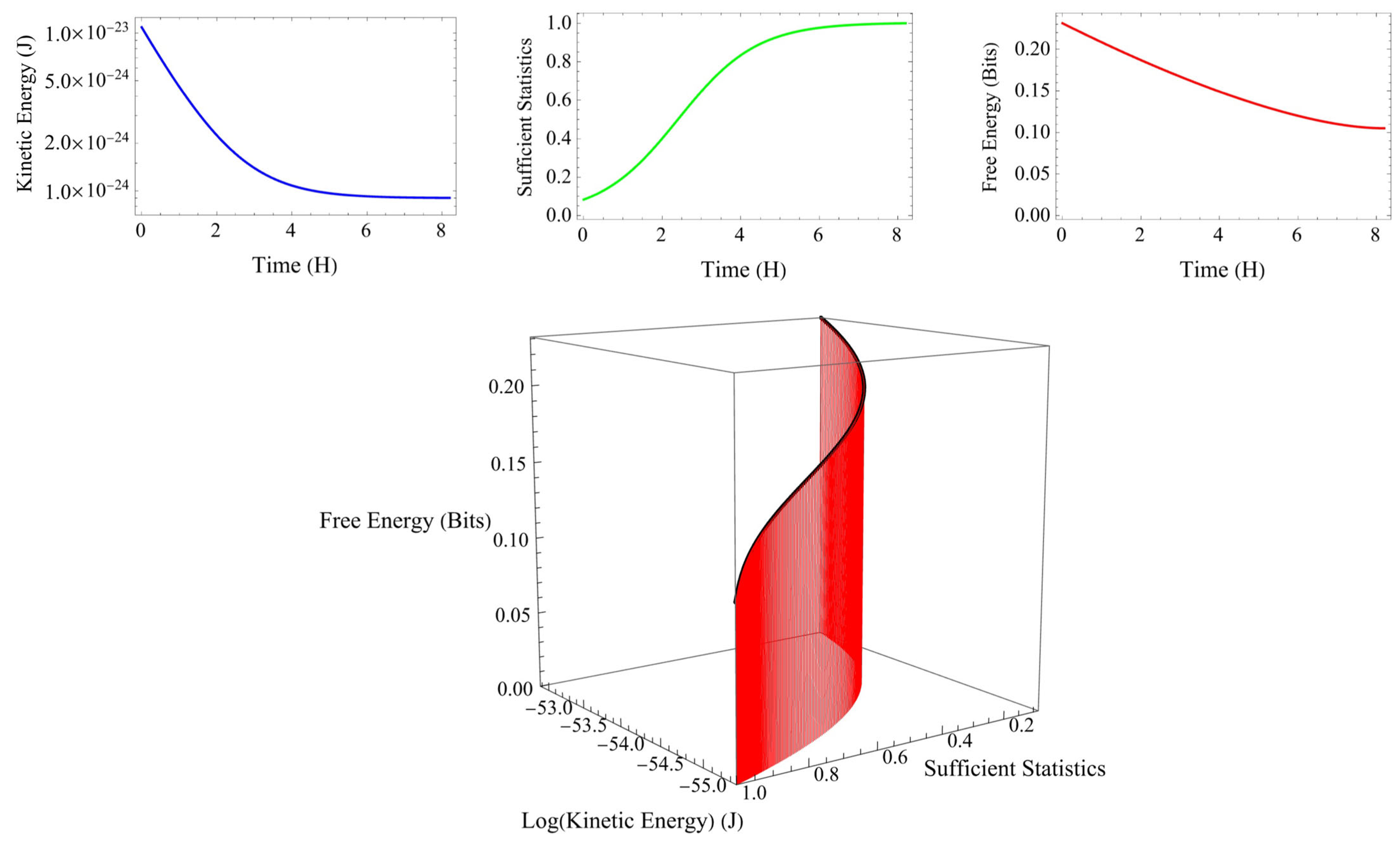
2.5. Application of the Free Energy Principle
2.6. Statistical Analysis
3. Results
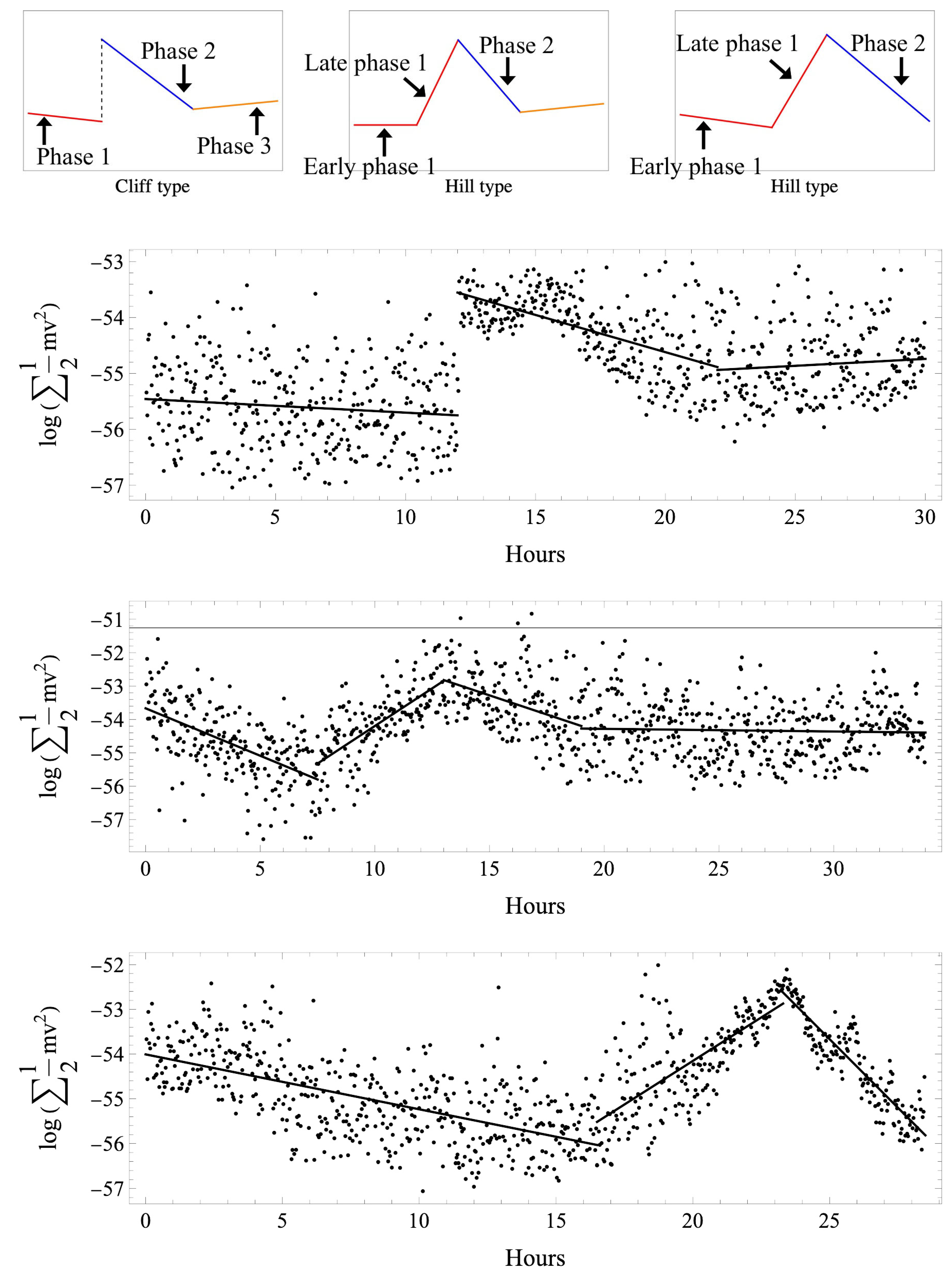
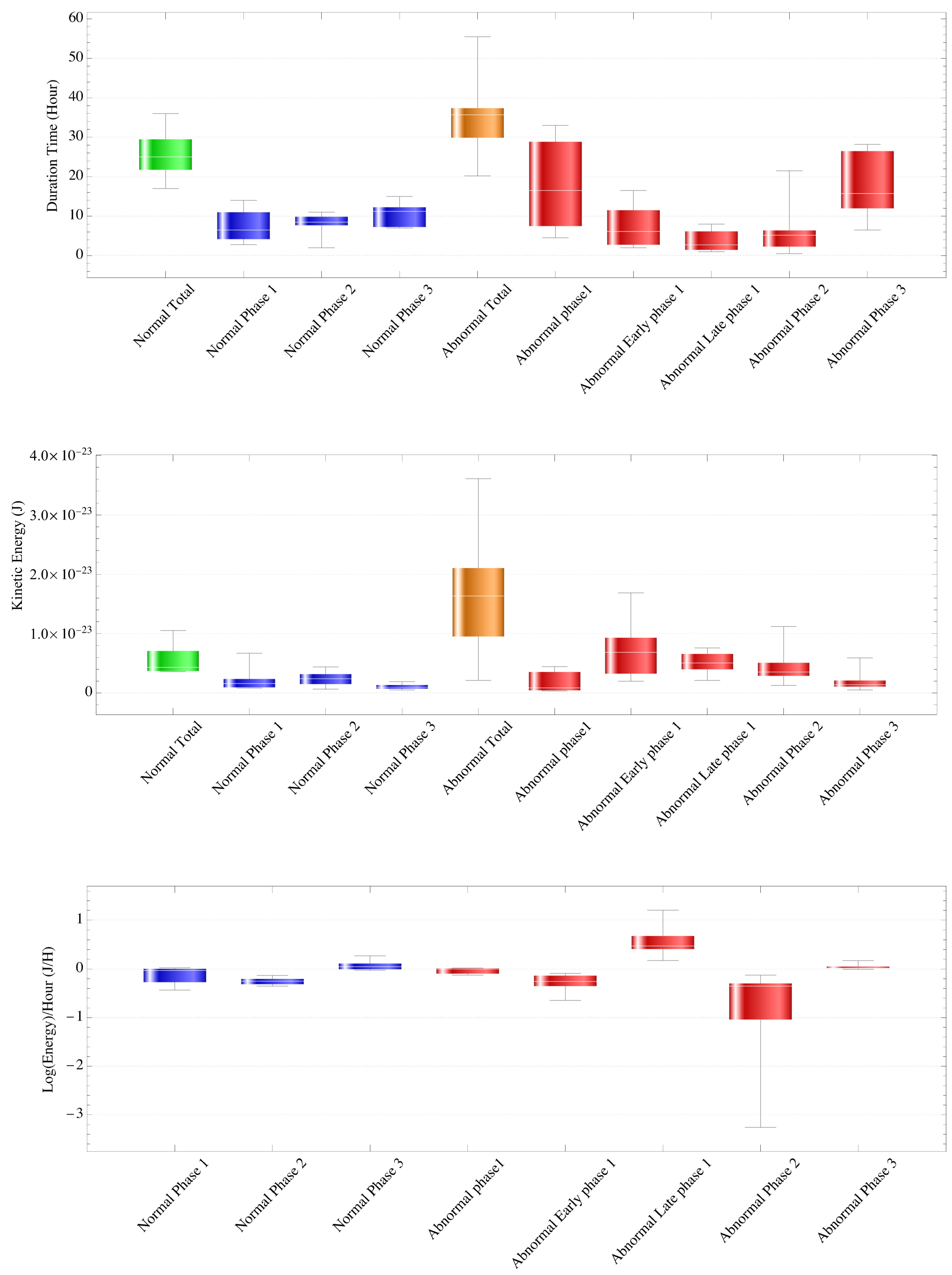
3.1. Analysis in Normal Cases
3.1.1. Time
3.1.2. Kinetic Energy Value
3.1.3. Regression Function
3.2. Analysis in Abnormal Cases
3.2.1. Time
3.2.2. Kinetic Energy Value
3.2.3. Regression Function
Comparison of Normal and Abnormal Cases
3.3. Comparison of Normal and Abnormal Cases in Phase 2
3.4. Kinetic Energy and Free Energy Principle
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koshland, D.E.; Goldbeter, A.; Stock, J.B. Amplification and adaptation in regulatory and sensory systems. Science 1982, 217, 220–225. [Google Scholar] [CrossRef] [PubMed]
- Ajduk, A.; Ilozue, T.; Windsor, S.; Yu, Y.; Bianka Seres, K.; Bomphrey, R.J.; Tom, B.D.; Swann, K.; Thomas, A.; Graham, C.; et al. Rhythmic actomyosin-driven contractions induced by sperm entry predict mammalian embryo viability. Nat. Commun. 2011, 2, 417. [Google Scholar] [CrossRef] [PubMed]
- Graham, C.F.; Windsor, S.; Ajduk, A.; Trinh, T.; Vincent, A.; Jones, C.; Coward, K.; Kalsi, D.; Zernicka-Goetz, M.; Swann, K.; et al. Dynamic shapes of the zygote and two-cell mouse and human. Biol. Open 2021, 10, bio059013. [Google Scholar] [CrossRef] [PubMed]
- Swann, K.; Windsor, S.; Campbell, K.; Elgmati, K.; Nomikos, M.; Zernicka-Goetz, M.; Amso, N.; Lai, F.A.; Thomas, A.; Graham, C. Phospholipase C-ζ-induced Ca2+ oscillations cause coincident cytoplasmic movements in human oocytes that failed to fertilize after intracytoplasmic sperm injection. Fertil. Steril. 2012, 97, 742–747. [Google Scholar] [CrossRef] [PubMed]
- Milewski, R.; Szpila, M.; Ajduk, A. Dynamics of cytoplasm and cleavage divisions correlates with preimplantation embryo development. Reproduction 2018, 155, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Bui, T.T.H.; Belli, M.; Fassina, L.; Vigone, G.; Merico, V.; Garagna, S.; Zuccotti, M. Cytoplasmic movement profiles of mouse surrounding nucleolus and not-surrounding nucleolus antral oocytes during meiotic resumption. Mol. Reprod. Dev. 2017, 84, 356–362. [Google Scholar] [CrossRef]
- Yi, K.; Unruh, J.R.; Deng, M.; Slaughter, B.D.; Rubinstein, B.; Li, R. Dynamic maintenance of asymmetric meiotic spindle position through Arp2/3-complex-driven cytoplasmic streaming in mouse oocytes. Nat. Cell Biol. 2011, 13, 1252–1258. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Kilner, J.; Harrison, L. A free energy principle for the brain. J. Physiol. Paris. 2006, 100, 70–87. [Google Scholar] [CrossRef]
- Friston, K.J. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Isomura, T.; Shimazaki, H.; Friston, K.J. Canonical neural networks perform active inference. Commun. Biol. 2022, 5, 55. [Google Scholar] [CrossRef]
- Miyagi, Y.; Hata, T.; Miyake, T. Fetal brain activity and the free energy principle. J. Perinat. Med. 2023, 51, 925–931. [Google Scholar] [CrossRef] [PubMed]
- Miyagi, Y.; Hata, T.; Bouno, S.; Koyanagi, A.; Miyake, T. Artificial intelligence to understand fluctuation of fetal brain activity by recognizing facial expressions. Int. J. Gynecol. Obstet. 2023, 161, 877–885. [Google Scholar] [CrossRef] [PubMed]
- Mio, Y. Morphological analysis of human embryonic development using time-lapse cinematography. J. Mamm. Ova Res. 2006, 23, 27–36. [Google Scholar] [CrossRef]
- Mio, Y.; Maeda, K. Time-lapse cinematography of dynamic changes occurring during in vitro development of human embryos. Am. J. Obstet. Gynecol. 2008, 199, 660.e1–660.e5. [Google Scholar] [CrossRef] [PubMed]
- Payne, D.; Flaherty, S.P.; Barry, M.F.; Matthews, C.D. Preliminary observations on polar body extrusion and pronuclear formation in human oocytes using time-lapse video cinematography. Hum. Reprod. 1997, 12, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Kyogoku, H.; Kitajima, T.S. Large cytoplasm is linked to the error-prone nature of oocytes. Dev. Cell 2017, 41, 287–298. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Joyce, J.M. Kullback-Leibler Divergence. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 720–722. [Google Scholar]
- Inui, T. The free-energy principle: A unified theory of brain functions. Nihon Shinkei Kairo Zassi 2018, 25, 123–134. [Google Scholar] [CrossRef]
- Friston, K.J. The free-energy principle: A rough guide to the brain? Trends Cogn. Sci. 2009, 13, 293–301. [Google Scholar] [CrossRef]
- Lan, G.; Sartori, P.; Neumann, S.; Sourjik, V.; Tu, Y. The energy–speed–accuracy trade-off in sensory adaptation. Nat. Phys. 2012, 8, 422–428. [Google Scholar] [CrossRef]
- Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi, N. New methods for comparing embryo selection methods by applying artificial intelligence: Comparing embryo selection AI for live births. Br. J. Healthc. Med. Res. 2022, 9, 36–44. [Google Scholar]
- Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi, N. Predicting a live birth by artificial intelligence incorporating both the blastocyst image and conventional embryo evaluation parameters. Artif. Intell. Med. Imaging 2020, 1, 94–107. [Google Scholar] [CrossRef]
- Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi, N. Feasibility of deep learning for predicting live birth from a blastocyst image in patients classified by age. Reprod. Med. Biol. 2019, 18, 190–203. [Google Scholar] [CrossRef] [PubMed]
- Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi, N. Feasibility of predicting live birth by combining conventional embryo evaluation with artificial intelligence applied to a blastocyst image in patients classified by age. Reprod. Med. Biol. 2019, 18, 344–356. [Google Scholar] [CrossRef] [PubMed]
- Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi, N. Feasibility of artificial intelligence for predicting live birth without aneuploidy from a blastocyst image. Reprod. Med. Biol. 2019, 18, 204–211. [Google Scholar] [CrossRef]
- Miyagi, Y.; Habara, T.; Hirata, R.; Hayashi, N. Deep Learning to predicting live births and aneuploid miscarriages from images of blastocysts combined with maternal age. Int. J. Bioinfor Intell. Comput. 2022, 1, 10–21. [Google Scholar] [CrossRef]

| Total | Phase 1 | Early Phase 1 | Late Phase 1 | Phase 2 | Phase 3 | |
|---|---|---|---|---|---|---|
| Normal Case 1 | 17 | 8 | N/A | N/A | 2 | 7 |
| Normal Case 2 | 30 | 12 | N/A | N/A | 10 | 8 |
| Normal Case 3 | 25 | 2.8 | N/A | N/A | 11 | 11.2 |
| Normal Case 4 | 36 | 14 | N/A | N/A | 9.5 | 12.5 |
| Normal Case 5 | 21 | 6.5 | N/A | N/A | 7.5 | 7 |
| Normal Case 6 | 24 | 4 | N/A | N/A | 8.5 | 11.5 |
| Normal Case 7 | 28 | 4.7 | N/A | N/A | 8.3 | 15 |
| Mean | 25.857 | 7.429 | N/A | N/A | 8.114 | 10.314 |
| SD | 6.203 | 4.201 | N/A | N/A | 2.937 | 3.062 |
| Q1/4 | 21 | 4 | N/A | N/A | 7.5 | 7 |
| Med | 25 | 6.5 | N/A | N/A | 8.5 | 11.2 |
| Q3/4 | 30 | 12 | N/A | N/A | 10 | 12.5 |
| Min | 17 | 2.8 | N/A | N/A | 2 | 7 |
| Max | 36 | 14 | N/A | N/A | 11 | 15 |
| Abnormal Case 8 | 55.5 | 33 | N/A | N/A | 6 | 16.5 |
| Abnormal Case 9 | 37 | 16.5 | N/A | N/A | 8.5 | 12 |
| Abnormal Case 10 | 37.5 | 4.5 | N/A | N/A | 6.5 | 26.5 |
| Abnormal Case 11 | 28.5 | N/A | 16.5 | 6.8 | 5.2 | N/A |
| Abnormal Case 12 | 36.5 | N/A | 15 | 8 | 5 | 8.5 |
| Abnormal Case 13 | 23.16 | N/A | 2.5 | 1.5 | 0.5 | 18.66 |
| Abnormal Case 14 | 20.2 | N/A | 3 | 1 | 1.7 | 14.5 |
| Abnormal Case 15 | 34 | N/A | 7.5 | 5.5 | 6 | 15 |
| Abnormal Case 16 | 38.5 | N/A | 8 | 2.5 | 21.5 | 6.5 |
| Abnormal Case 17 | 35.5 | N/A | 2 | 3 | 4 | 26.5 |
| Abnormal Case 18 | 35.7 | N/A | 4.8 | 1.4 | 1.3 | 28.2 |
| Mean | 34.733 | 18 | 7.412 | 3.713 | 6.018 | 17.286 |
| SD | 9.206 | 14.309 | 5.609 | 2.691 | 5.685 | 7.644 |
| Q1/4 | 28.5 | 4.5 | 2.5 | 1.4 | 1.7 | 12 |
| Med | 35.7 | 16.5 | 4.8 | 2.5 | 5.2 | 15 |
| Q3/4 | 37.5 | 33 | 8 | 5.5 | 6.5 | 26.5 |
| Min | 20.2 | 4.5 | 2 | 1 | 0.5 | 6.5 |
| Max | 55.5 | 33 | 16.5 | 8 | 21.5 | 28.2 |
| Total | Phase 1 | Early Phase 1 | Late Phase 1 | Phase 2 | Phase 3 | |
|---|---|---|---|---|---|---|
| Normal Case 1 | 3.670 × 10−24 | 2.548 × 10−24 | N/A | N/A | 6.395 × 10−25 | 5.083 × 10−25 |
| Normal Case 2 | 6.304 × 10−24 | 9.569 × 10−25 | N/A | N/A | 3.441 × 10−24 | 1.907 × 10−24 |
| Normal Case 3 | 3.721 × 10−24 | 8.320 × 10−25 | N/A | N/A | 1.932 × 10−24 | 9.574 × 10−25 |
| Normal Case 4 | 3.617 × 10−24 | 1.599 × 10−24 | N/A | N/A | 1.358 × 10−24 | 6.595 × 10−25 |
| Normal Case 5 | 1.053 × 10−24 | 6.702 × 10−24 | N/A | N/A | 2.418 × 10−24 | 1.410 × 10−24 |
| Normal Case 6 | 4.321 × 10−24 | 9.727 × 10−25 | N/A | N/A | 2.405 × 10−24 | 9.441 × 10−25 |
| Normal Case 7 | 7.337 × 10−24 | 1.781 × 10−24 | N/A | N/A | 4.393 × 10−24 | 1.163 × 10−24 |
| Mean | 5.647 × 10−24 | 2.199 × 10−24 | N/A | N/A | 2.369 × 10−24 | 1.078 × 10−24 |
| SD | 2.599 × 10−24 | 2.076 × 10−24 | N/A | N/A | 1.255 × 10−24 | 4.720 × 10−25 |
| Q1/4 | 3.696 × 10−24 | 9.570 × 10−25 | N/A | N/A | 1.358 × 10−24 | 6.590 × 10−25 |
| Med | 4.321 × 10−24 | 1.599 × 10−24 | N/A | N/A | 2.405 × 10−24 | 9.570 × 10−25 |
| Q3/4 | 7.337 × 10−24 | 2.548 × 10−24 | N/A | N/A | 3.441 × 10−24 | 1.410 × 10−24 |
| Min | 3.617 × 10−24 | 8.320 × 10−25 | N/A | N/A | 6.390 × 10−25 | 5.080 × 10−25 |
| Max | 1.053 × 10−23 | 6.702 × 10−24 | N/A | N/A | 4.393 × 10−24 | 1.907 × 10−24 |
| Abnormal Case 8 | 5.404 × 10−24 | 8.491 × 10−25 | N/A | N/A | 3.230 × 10−24 | 1.326 × 10−24 |
| Abnormal Case 9 | 2.125 × 10−24 | 3.232 × 10−25 | N/A | N/A | 1.275 × 10−24 | 5.266 × 10−25 |
| Abnormal Case 10 | 9.050 × 10−24 | 4.444 × 10−24 | N/A | N/A | 3.161 × 10−24 | 1.445 × 10−24 |
| Abnormal Case 11 | 1.145 × 10−23 | N/A | 1.988 × 10−24 | 4.733 × 10−24 | 4.733 × 10−24 | N/A |
| Abnormal Case 12 | 1.634 × 10−23 | N/A | 1.031 × 10−23 | 2.104 × 10−24 | 2.713 × 10−24 | 1.219 × 10−24 |
| Abnormal Case 13 | 1.097 × 10−23 | N/A | 3.533 × 10−24 | 3.579 × 10−24 | 2.784 × 10−24 | 1.071 × 10−24 |
| Abnormal Case 14 | 1.985 × 10−23 | N/A | 8.334 × 10−24 | 6.963 × 10−24 | 3.540 × 10−24 | 1.017 × 10−24 |
| Abnormal Case 15 | 2.146 × 10−23 | N/A | 2.990 × 10−24 | 5.375 × 10−24 | 9.351 × 10−24 | 3.745 × 10−24 |
| Abnormal Case 16 | 3.611 × 10−23 | N/A | 1.686 × 10−23 | 6.223 × 10−24 | 1.122 × 10−23 | 1.802 × 10−24 |
| Abnormal Case 17 | 1.958 × 10−23 | N/A | 5.475 × 10−24 | 7.603 × 10−24 | 4.398 × 10−24 | 2.109 × 10−24 |
| Abnormal Case 18 | 2.376 × 10−23 | N/A | 8.234 × 10−24 | 4.392 × 10−24 | 5.226 × 10−24 | 5.910 × 10−24 |
| Mean | 1.601 × 10−23 | 1.872 × 10−24 | 7.215 × 10−24 | 5.121 × 10−24 | 4.694 × 10−24 | 2.017 × 10−24 |
| SD | 9.598 × 10−24 | 2.243 × 10−24 | 4.878 × 10−24 | 1.813 × 10−24 | 2.997 × 10−24 | 1.625 × 10−24 |
| Q1/4 | 9.050 × 10−24 | 3.232 × 10−25 | 2.990 × 10−24 | 3.579 × 10−24 | 2.784 × 10−24 | 1.071 × 10−24 |
| Med | 1.634 × 10−23 | 8.491 × 10−25 | 6.854 × 10−24 | 5.054 × 10−24 | 3.540 × 10−24 | 1.385 × 10−24 |
| Q3/4 | 2.146 × 10−23 | 4.444 × 10−24 | 8.334 × 10−24 | 6.223 × 10−24 | 5.226 × 10−24 | 2.109 × 10−24 |
| Min | 2.125 × 10−24 | 3.232 × 10−25 | 1.988 × 10−24 | 2.104 × 10−24 | 1.275 × 10−24 | 5.266 × 10−25 |
| Max | 3.611 × 10−23 | 4.444 × 10−24 | 1.686 × 10−23 | 7.603 × 10−24 | 1.122 × 10−23 | 5.910 × 10−24 |
| Case No. | Phase 1 | Early Phase 1 | Late Phase 1 | Phase 2 | Phase 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (H) | ± SE | ± SE | Time (H) | ± SE | ± SE | Time (H) | ± SE | ± SE | Time (H) | ± SE | ± SE | Time (H) | ± SE | ± SE | |
| 1 | 0–8 | −52.852 ± 0.090 a | −0.4308 ±0.018 a | N/A | N/A | N/A | N/A | N/A | N/A | 8–10 | −52.726 ± 1.067 a | −0.352 ± 0.118 c | 10–17 | −56.724 ± 0.245 a | 0.047 ± 0.018 d |
| 2 | 0–12 | −55.458 ± 0.079 a | −0.024 ± 0.011 d | N/A | N/A | N/A | N/A | N/A | N/A | 12–22 | −51.951 ± 0.187 a | −0.133 ± 0.011 a | 22–30 | −55.484 ± 0.467 a | 0.025 ± 0.018 ¶ |
| 3 | 0–2.8 | −56.106 ± 0.224 a | 0.024 ± 0.137 ¶ | N/A | N/A | N/A | N/A | N/A | N/A | 2.8–13.8 | −52.810 ± 0.094 a | −0.266 ± 0.010 a | 13.8–25 | −58.150 ± 0.213 a | 0.130 ± 0.011 a |
| 4 | 0–14 | −54.752 ± 0.093 a | −0.084 ± 0.011 a | N/A | N/A | N/A | N/A | N/A | N/A | 14–23.5 | −51.655 ± 0.291 a | −0.199 ± 0.015 a | 23.5–36 | −55.681 ± 0.393 a | −0.026 ± 0.013 d |
| 5 | 0–6.5 | −52.722 ± 0.115 a | −0.333 ± 0.030 a | N/A | N/A | N/A | N/A | N/A | N/A | 6.5–14 | −52.616 ± 0.345 a | −0.249 ± 0.033 a | 14–21 | −60.091 ± 0.443 a | 0.272 ± 0.025 a |
| 6 | 0–4 | −55.562 ± 0.149 a | −0.029 ± 0.064 ¶ | N/A | N/A | N/A | N/A | N/A | N/A | 4–12.5 | −52.871 ± 0.137 a | −0.215 ± 0.016 a | 12.5–24 | −55.340 ± 0.240 a | −0.017 ± 0.013 ¶ |
| 7 | 0–4.7 | −55.157 ± 0.142 a | 0.0131 ± 0.053 ¶ | N/A | N/A | N/A | N/A | N/A | N/A | 4.7–13 | −51.222 ± 0.114 a | −0.327 ± 0.012 a | 13–28 | −56.837 ± 0.169 a | 0.064 ± 0.008 a |
| Mean | −54.659 | −0.123 | −52.265 | −0.249 | −56.901 | 0.070 | |||||||||
| SD | 1.343 | 0.182 | 0.653 | 0.075 | 1.718 | 0.103 | |||||||||
| Q1/4 | −55.510 | −0.208 | −52.768 | −0.296 | −57.494 | 0.004 | |||||||||
| Med | −55.158 | −0.029 | −52.616 | −0.249 | −56.724 | 0.047 | |||||||||
| Q3/4 | −53.803 | −0.006 | −51.803 | −0.207 | −55.582 | 0.097 | |||||||||
| Min | −56.106 | −0.431 | −52.871 | −0.352 | −60.091 | −0.026 | |||||||||
| Max | −52.722 | 0.024 | −51.222 | −0.133 | −55.340 | 0.272 | |||||||||
| 8 | 0–33 | −55.808 ± 0.046 a | 9.661 × 10−06 ± 0.002 ¶ | N/A | N/A | N/A | N/A | N/A | N/A | 33–39 | −42.949 ± 1.056 a | −0.321 ± 0.029 a | 39–55.5 | −56.303 ± 0.305 a | 0.022 ± 0.006 b |
| 9 | 0–16.6 | −56.949 ± 0.053 a | 0.0181 ± 0.006 c | N/A | N/A | N/A | N/A | N/A | N/A | 16.5–25 | −48.123 ± 0.152 a | −0.352 ± 0.007 a | 25–37 | −61.593 ± 0.237 a | 0.172 ± 0.008 a |
| 10 | 0–4.5 | −53.696 ± 0.101 a | −0.125 ± 0.039 c | N/A | N/A | N/A | N/A | N/A | N/A | 4.5–11 | −52.283 ± 0.209 a | −0.289 ± 0.026 a | 11–37.5 | −56.091 ± 0.099 a | 0.028 ± 0.004 a |
| 11 | N/A | N/A | N/A | 0–16.5 | −54.008 ± 0.065 a | −0.123 ± 0.007 a | 16.5s–23.3 | −61.936 ± 0.509 a | 0.389 ± 0.025 a | 23.3–28.5 | −38.327 ± 0.596 a | −0.614 ± 0.023 a | N/A | N/A | |
| 12 | N/A | N/A | N/A | 0–15 | −52.3388 ± 0.111 a | −0.244 ± 0.013 a | 15–23 | −58.327 ± 0.471 a | 0.175 ± 0.025 a | 23–28 | −46.234 ± 0.942 a | −0.328 ± 0.037 a | 28–36.5 | −55.886 ± 0.592 a | 0.013 ± 0.018 ¶ |
| 13 | N/A | N/A | N/A | 0–2.5 | −53.892 ± 0.095 a | −0.150 ± 0.064 d | 2.5–4 | −55.682 ± 0.432 a | 0.497 ± 0.133 b | 4–4.5 | −40.558 ± 2.238 a | −3.260 ± 0.526 a | 4.5–23.16 | −55.825 ± 0.097 a | 0.020 ± 0.007 c |
| 14 | N/A | N/A | N/A | 0–3 | −52.764 ± 0.119 a | −0.418 ± 0.067 a | 3–4 | −57.628 ± 0.486 a | 1.206 ± 0.138 a | 4–5.7 | −48.509 ± 0.418 a | −1.182 ± 0.086 a | 5.7–20.2 | −56.184 ± 0.104 a | 0.048 ± 0.008 a |
| 15 | N/A | N/A | N/A | 0–7.5 | −53.667 ± 0.120 a | −0.284 ± 0.028 a | 7.5–13 | −58.697 ± 0.377 a | 0.450 ± 0.036 a | 13–19 | −49.846 ± 0.620 a | −0.229 ± 0.038 a | 19–34 | −54.126 ± 0.250 a | −0.008 ± 0.009 ¶ |
| 16 | N/A | N/A | N/A | 0–8 | −52.209 ± 0.139 a | −0.267 ± 0.030 a | 8–10.5 | −60.157 ± 1.192 a | 0.681 ± 0.128 a | 10.5–32 | −51.052 ± 0.142 a | −0.125 ± 0.006 a | 32–38.5 | −60.612 ± 0.845 a | 0.158 ± 0.024 a |
| 17 | N/A | N/A | N/A | 0–2 | −53.395 ± 0.258 a | −0.647 ± 0.219 c | 2–5 | −55.114 ± 0.371 a | 0.432 ± 0.103 a | 5–9 | −50.252 ± 0.367 a | −0.566 ± 0.052 a | 9–35.5 | −55.198 ± 0.114 a | 0.004 ± 0.005 ¶ |
| 18 | N/A | N/A | N/A | 0–4.8 | −53.432 ± 0.163 a | −0.091 ± 0.058 ¶ | 4.8–6.2 | −57.645 ± 0.822 a | 0.680 ± 0.149 a | 6.2–7.5 | −45.846 ± 2.410 a | −1.204 ± 0.351 c | 7.5–35.7 | −54.795 ± 0.127 a | 0.022 ± 0.006 a |
| Mean | −55.484 | −0.036 | −53.213 | −0.278 | −58.148 | 0.564 | −46.725 | −0.770 | −56.661 | 0.048 | |||||
| SD | 1.651 | 0.078 | 0.692 | 0.182 | 2.221 | 0.306 | 4.481 | 0.902 | 2.449 | 0.064 | |||||
| Q1/4 | −56.378 | −0.063 | −53.723 | −0.318 | −59.062 | 0.422 | −50.049 | −0.898 | −56.273 | 0.015 | |||||
| Med | −55.808 | 9.661 × 10−6 | −53.413 | −0.255 | −57.986 | 0.474 | −48.123 | −0.352 | −55.989 | 0.022 | |||||
| Q3/4 | −54.752 | 0.009 | −52.658 | −0.143 | −57.142 | 0.680 | −44.398 | −0.305 | −55.354 | 0.043 | |||||
| Min | −56.949 | −0.125 | −54.008 | −0.648 | −61.936 | 0.175 | −52.283 | −3.260 | −61.593 | −0.008 | |||||
| Max | −53.696 | 0.018 | −52.209 | −0.091 | −55.115 | 1.206 | −38.327 | −0.125 | −54.126 | 0.172 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miyagi, Y.; Mio, Y.; Yumoto, K.; Hirata, R.; Habara, T.; Hayashi, N. Kinetic Energy and the Free Energy Principle in the Birth of Human Life. Reprod. Med. 2024, 5, 65-80. https://doi.org/10.3390/reprodmed5020008
Miyagi Y, Mio Y, Yumoto K, Hirata R, Habara T, Hayashi N. Kinetic Energy and the Free Energy Principle in the Birth of Human Life. Reproductive Medicine. 2024; 5(2):65-80. https://doi.org/10.3390/reprodmed5020008
Chicago/Turabian StyleMiyagi, Yasunari, Yasuyuki Mio, Keitaro Yumoto, Rei Hirata, Toshihiro Habara, and Nobuyoshi Hayashi. 2024. "Kinetic Energy and the Free Energy Principle in the Birth of Human Life" Reproductive Medicine 5, no. 2: 65-80. https://doi.org/10.3390/reprodmed5020008
APA StyleMiyagi, Y., Mio, Y., Yumoto, K., Hirata, R., Habara, T., & Hayashi, N. (2024). Kinetic Energy and the Free Energy Principle in the Birth of Human Life. Reproductive Medicine, 5(2), 65-80. https://doi.org/10.3390/reprodmed5020008






