Microwave Dynamic Modulation Metasurface Absorber Based on Origami Structure

Abstract

With the rapid advancement of detection technologies, traditional static electromagnetic absorbers increasingly struggle to meet controllable stealth requirements across diverse dynamic environments. To achieve active and controllable modulation of electromagnetic reflection characteristics, this paper proposes a transparent reconfigurable metamaterial absorber based on an origami structure. By adjusting the folding angles of the indium tin oxide (ITO)-polyethylene terephthalate (PET) film, the structure achieves reversible deformation from the vertical state to the horizontal state. This enables continuous modulation of the reflectance from below −10 dB (absorbing state) to nearly 0 dB (reflecting state) within the 4–18.9 GHz frequency range, with a relative bandwidth exceeding 130% and excellent angular stability. The energy loss and current distribution under different states are analyzed, revealing the mechanisms behind broadband absorption and deep modulation. Experimental measurements of the fabricated metamaterial align well with simulation results. Leveraging its flexible structure, reversible modulation capability, and angular stability, this origami-inspired reconfigurable metamaterial demonstrates promising application potential in the fields of adaptive electromagnetic camouflage and stealth protection.

1. Introduction

With the rapid advancement of reconnaissance and detection capabilities, along with the widespread adoption of multi-spectral reconnaissance techniques, traditional static electromagnetic camouflage is increasingly evolving toward higher absorption rates and broader bandwidths. For instance, magnetic absorbing materials represented by ferrites or magnetic metal particles [1,2,3] can achieve strong microwave absorption of up to −50 dB. Metamaterials composed of sub-wavelength unit cells, on the other hand, allow for independent control of permittivity and permeability beyond the ranges achievable with conventional materials [4]. Their design flexibility and rich potential [5,6,7,8,9,10] have also drawn attention to a variety of outstanding properties. Various optimization algorithms, including inverse design [11,12], have been applied to metamaterial design to broaden their operating frequency bands and further enhance absorption performance. However, due to variations in background emissivity across different environments, the aforementioned static electromagnetic camouflage lacks active modulation capabilities [13,14,15], which severely limits its application in diverse settings such as deserts, grasslands, and sea surfaces [16,17]. As a result, adaptive camouflage has gradually become a key research focus [18,19]. Reconfigurable absorbers, through material property modulation and mechanical configuration control, achieve broadband response and real-time tunability, significantly improving concealment performance and environmental adaptability. This positions them with promising potential for dynamic environment camouflage and stealth platform applications [20,21,22].

By applying a bias voltage to materials such as graphene, their electromagnetic parameters can be effectively tuned [23,24,25,26], thereby enabling adjustable absorption performance. Balci et al. [23] developed an adaptive microwave surface with a graphene/electrolyte/graphene “sandwich” configuration, whose core mechanism lies in modulating the surface resistance of the graphene electrodes through applied bias voltage, allowing the absorption rate to vary continuously from approximately 40% to 99%. However, the operating frequency band of this structure is limited to around 10.5 GHz, exhibiting a narrowband absorption characteristic. Moreover, large-area graphene suffers from high energy consumption and excessive heat generation during bias modulation, which can lead to device failure and thus restricts its applicability in complex environments [27].

Tuning the electromagnetic absorption rate through mechanical deformation of the structure [28,29], rather than relying on changes in the intrinsic electromagnetic properties of the material itself, has become a new research focus for reconfigurable absorbers due to its superior stability and environmental adaptability. Song et al. [30] proposed a tunable absorber based on a Miura-origami [31] structure, which achieves dynamic modulation of the absorption rate from approximately 43% to 96% within an ultra-wide frequency range of 4.96–38.8 GHz by switching between the planar and folded states. Although this design demonstrates excellent performance, the large-scale Miura folding structure is difficult to fabricate and suffers from mechanical complexity and limited stability during the deformation process. Therefore, it is urgently necessary to develop simpler and more efficient mechanical regulation strategies for constructing reconfigurable absorbers.

In this work, we employed a simplified origami-inspired structure combined with flexible electronic materials to design a metamaterial capable of broadband tunable absorption. By applying external stimuli, the structure can undergo a reversible transformation from a vertical to a horizontal configuration, thereby enabling dynamic control of its electromagnetic absorption properties. The results demonstrate that within the broad frequency range of 4–18.9 GHz, the reflection can be tuned from below −10 dB (absorption) to around 0 dB (reflection).

2. Design and Analysis

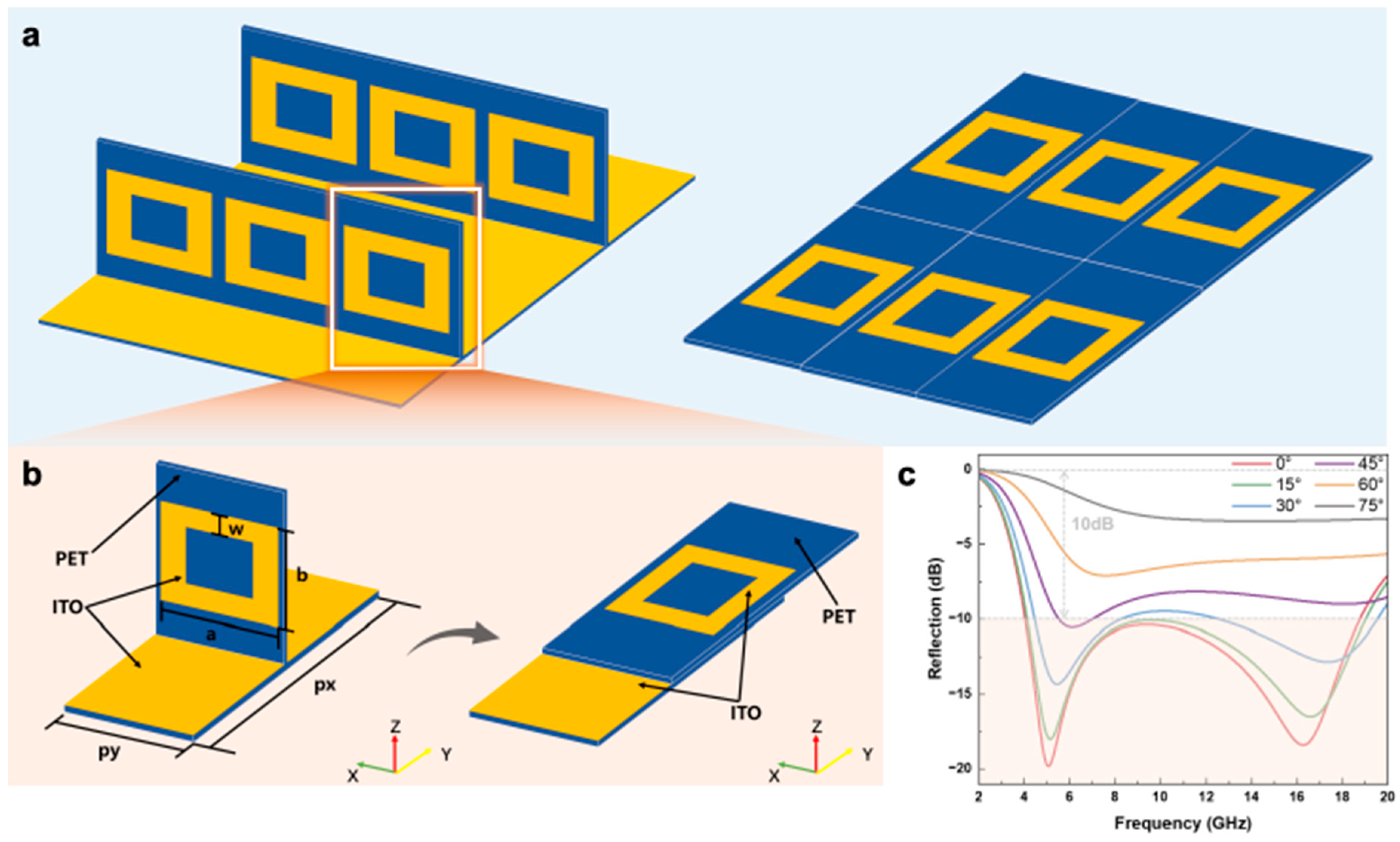
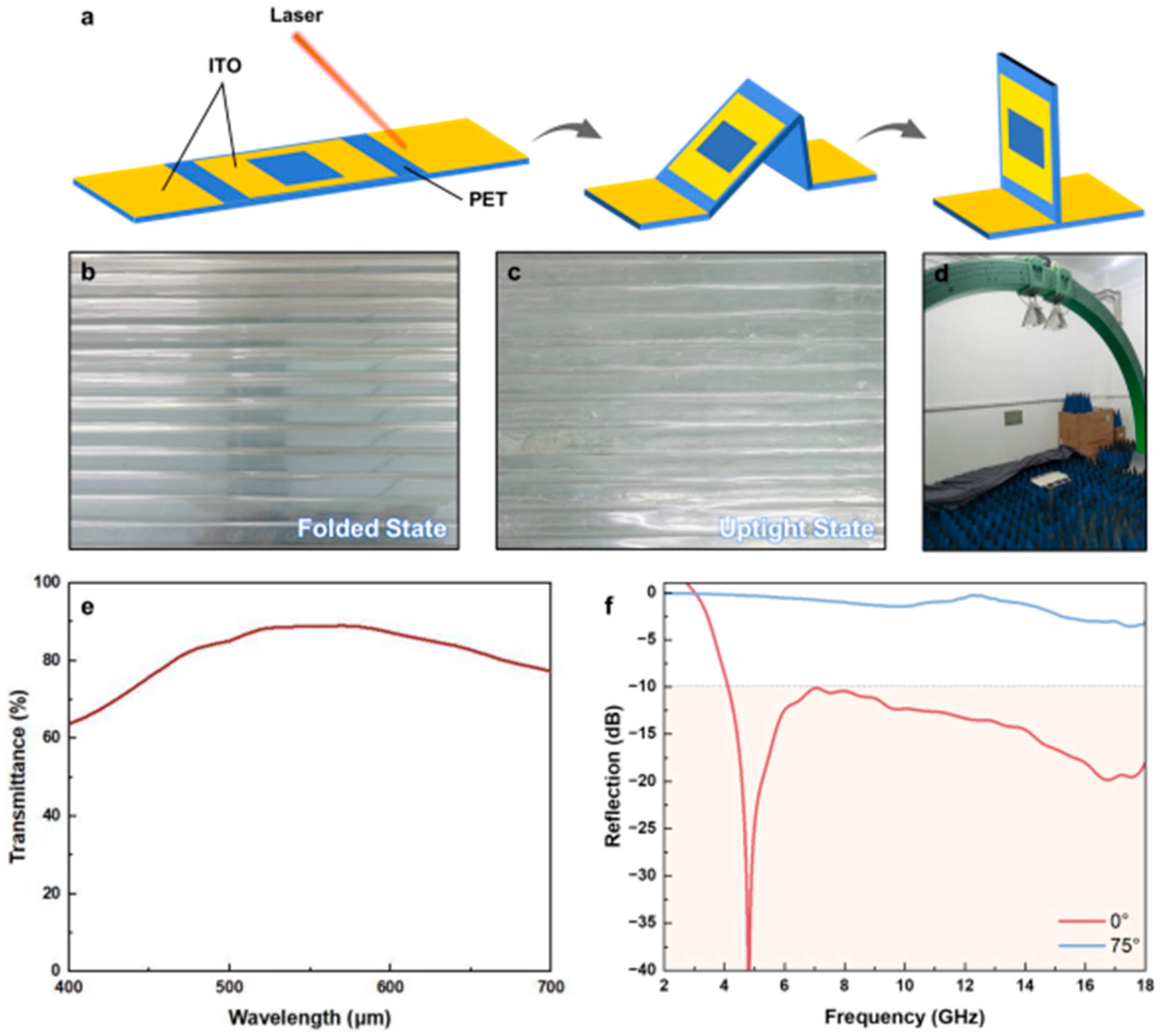
The proposed optically transparent origami metamaterial consists of a rotatable PET layer embedded with periodically arranged ITO square rings and an ITO–PET backing plane, as illustrated in Figure 1a. To achieve optimal microwave absorption performance, the geometric configuration and dimensions of a single unit cell were optimized through numerical simulations. In the simulation, ITO films with a sheet resistance of 50 Ω/sq were used to construct both the backing plane and the upright square rings. The structural parameters were set as follows: px = 12 mm, py = 8.4 mm, a = 8.3 mm, b = 3.4 mm, and w = 1.8 mm. The entire structure was initially fabricated from a single ITO–PET composite film, in which laser etching was employed to predefine folding lines, enabling the central ITO square-ring region to fold under external stimuli and ultimately form a three-dimensional reconfigurable origami structure.

To perform electromagnetic simulations of the designed structure, we utilized the metamaterial simulation module in commercial simulation software to establish a model where TM waves are incident normally onto the origami-inspired metamaterial for accurate solution. During the modeling process, tetrahedral meshes were selected to ensure computational efficiency and precision, and the finite element method (FEM) was employed for solving. The electromagnetic properties of the materials were defined as dielectric characteristics consistent with ITO and PET, ensuring the physical authenticity of the simulation model. To simulate the infinite periodicity of the metamaterial array, periodic boundary conditions were applied in the x and y directions, while an open boundary condition was set in the positive z-direction, and an electric boundary was applied in the negative z-direction. Therefore, the absorptivity of the proposed origami metamaterial can be calculated using Equation (1):

A(ω) = 1 − R(ω) − T(ω) = 1 − |S₁₁|² − |S₂₁|

(1)

where R(ω) and T(ω) represent the reflectivity and transmissivity of the metamaterial, respectively. It is worth noting that in practical applications, an electrical boundary condition can be considered at the bottom of the metamaterial, allowing transmissivity to be neglected. Thus, the sum of reflection and absorption equals the total power. The equation can be simplified as:

A(ω) = 1 − R(ω) = 1 − |S₁₁|²

(2)

Upon completion of the solving process, post-processing was conducted through S-parameter analysis, field distribution plots, and power loss distribution to comprehensively analyze and evaluate the electromagnetic response characteristics of the metamaterial.

As shown in the results, under normal TM incidence, the metamaterial in the upright state exhibits broadband absorption below −10 dB within the 4–18.9 GHz frequency range. As the square-ring structure is gradually folded to a certain angle, the overall absorption decreases and the resonance peak shifts toward higher frequencies. When the folding angle reaches approximately 75°, the metamaterial transitions into a reflection state with reflectivity approaching 0 dB. Therefore, the proposed metamaterial achieves a reflection modulation depth exceeding 10 dB and exhibits ultra-broadband microwave absorption with a relative bandwidth over 130% through mechanical folding of the square-ring structure.

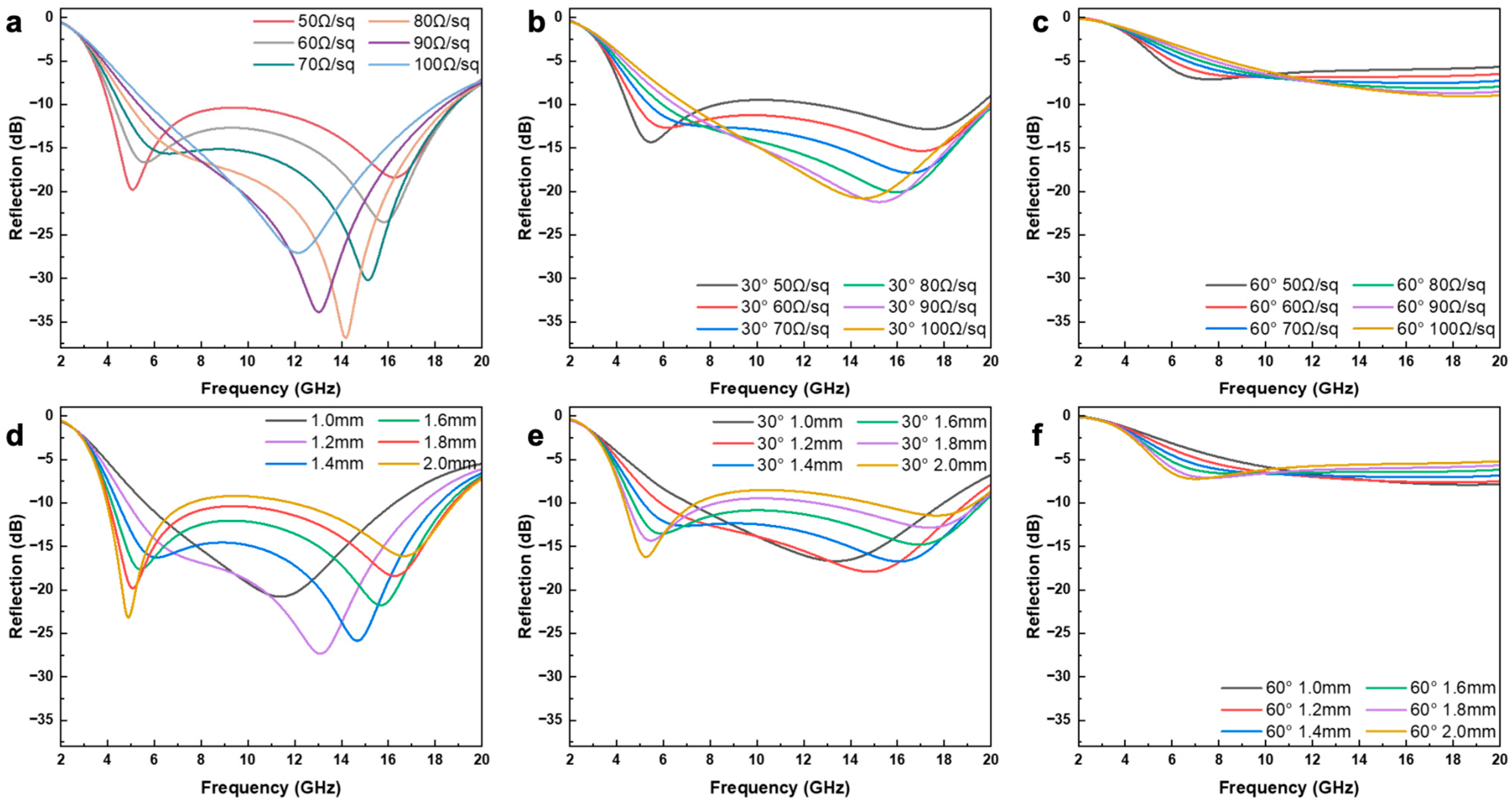
To ensure that the selected structural parameters are grounded in rigorous theoretical justification, a comprehensive set of parametric simulations was performed to quantify the influence of each geometric parameter on the absorption performance. By comparing the variations in reflection coefficients and absorption bandwidths under different parameter conditions, the optimal parameter set was ultimately determined. First, five key parameters—px, py, a, b, and w—were individually swept with the structure in the upright state, as shown in Figure 2. Figure 2a,b indicate that the periodicity parameters px and py exert minimal influence on either the absorption intensity or bandwidth; their variations induce negligible changes in the overall absorption characteristics and can thus be regarded as secondary parameters. As illustrated in Figure 2c, increasing the parameter a significantly enhances the absorption intensity while broadening the absorption bandwidth. Although a peak absorption is achieved at a = 8.2 mm, its corresponding bandwidth is considerably narrower than that of a = 8.3 mm. Therefore, balancing both absorption strength and bandwidth leads to the selection of a = 8.3 mm as the optimal value. Figure 2d shows that variations in b have little effect on the resonance frequency and primarily modulate the absorption amplitude. To maintain stable broadband absorption performance, a value of b = 3.4 mm—which provides a wider effective bandwidth—was selected. Figure 2e demonstrates that increasing w enhances the absorption intensity, while the bandwidth first increases and then narrows. Considering the requirement of maximizing absorption bandwidth, w = 1.8 mm was chosen as the optimal value.

This study focuses on the effects of the surface resistance and width of the ITO square ring. Keeping other geometric parameters constant, numerical simulations of the reflection characteristics were performed under different folding angles (0°, 30°, and 60°), while varying the surface resistance of the square ring from 50 Ω/sq to 100 Ω/sq and the ring width from 1 mm to 2 mm. As shown in Figure 3, Figure 3a–c correspond to the reflection intensity at 0°, 30°, and 60° folding angles under different surface resistances. The results indicate that as the surface resistance increases, the absorption intensity in the low-frequency region decreases, while that in the high-frequency region increases. Simultaneously, the low-frequency absorption peak shifts toward higher frequencies, and the high-frequency peak shifts toward lower frequencies. When the surface resistance reaches approximately 90 Ω/sq, the originally dual absorption peaks gradually merge into a single peak, exhibiting a notable narrowing of the absorption bandwidth. Overall, increasing the surface resistance of the square ring enhances the total absorption strength but leads to a narrower operating bandwidth. At a 30° folding angle, the overall absorption intensity is slightly reduced compared to the upright state, yet the same variation trend with surface resistance remains. When the folding angle further increases to 60°, the absorption peaks become significantly weaker, with the high-frequency peak almost disappearing, while the low-frequency peak still follows the same trend.

Figure 3d–f correspond to the reflection intensity at 0°, 30°, and 60° folding angles under different square-ring widths. The results show that as the ring width decreases from 2 mm to 1 mm, the low-frequency absorption intensity weakens, while the high-frequency absorption becomes stronger. Meanwhile, the low- and high-frequency peaks gradually shift toward the middle and merge into a single absorption peak. Therefore, reducing the ring width enhances the overall absorption strength but results in a narrower absorption bandwidth. At a 30° folding angle, the overall absorption intensity decreases, but the same variation trend remains. When the folding angle increases to 60°, the absorption peaks are significantly attenuated, the high-frequency peak nearly disappears, and the low-frequency peak still follows the aforementioned behavior. In summary, the metamaterial design based on the selected parameters not only achieves absorption performance below −10 dB, but also ensures stable performance across an ultra-wideband frequency range of 4–18.9 GHz. Validation confirms that the chosen parameters maximize the metamaterial’s performance, meeting the practical requirements for ultra-wideband and high-efficiency absorption in critical military applications, thus establishing this as the optimal design solution.

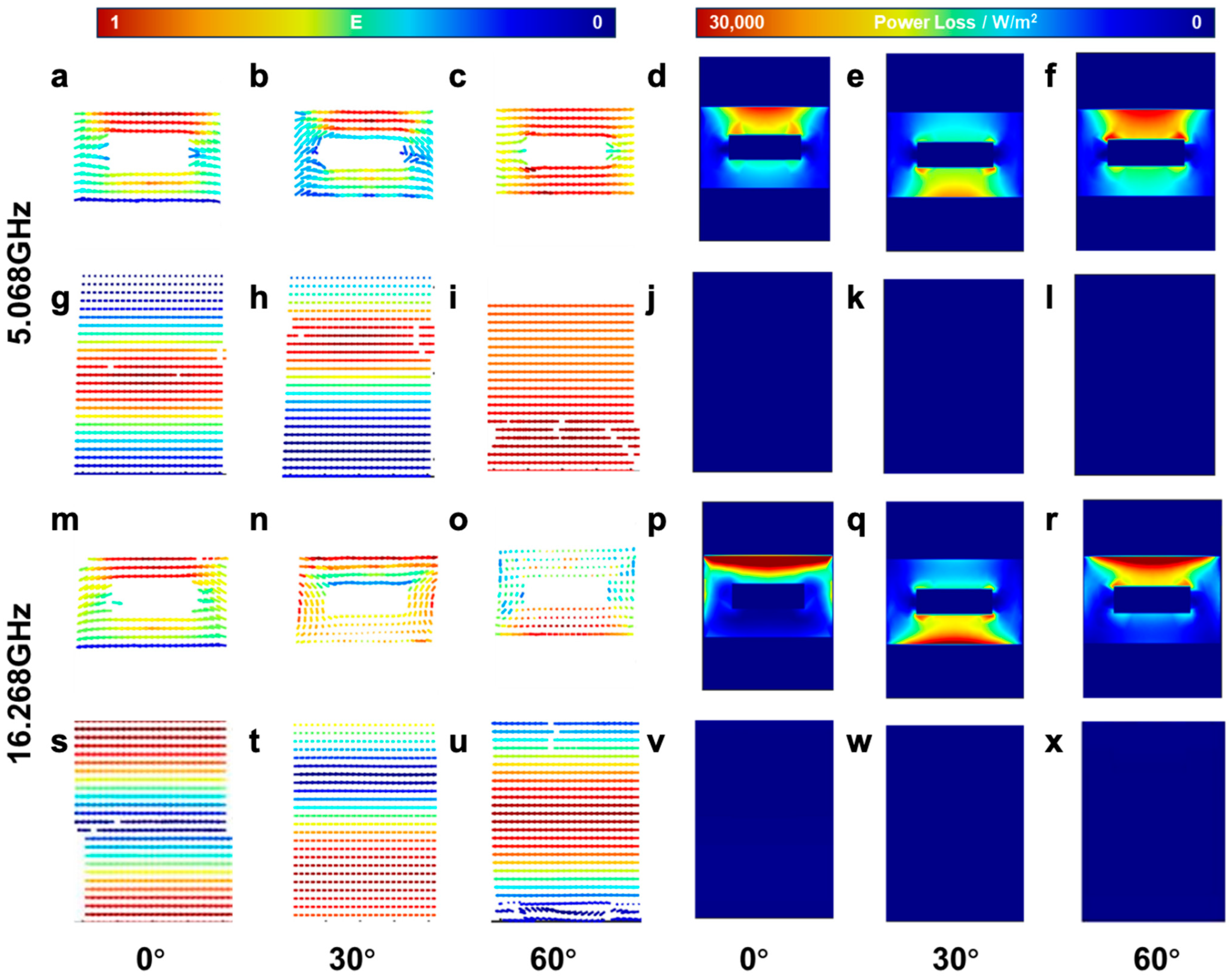
To further elucidate the mechanism underlying the ultra-broadband absorption and deep reflection modulation of the designed metamaterial, electromagnetic field distributions of a single unit cell were analyzed under different folding angles (0°, 30°, and 60°). First, the mechanism of broadband absorption was investigated. Figure 4 illustrates the surface loss and surface current distributions at two reflection-dip frequencies, 5.068 GHz and 16.268 GHz. For the upright configuration (0°), at 5.068 GHz, the currents on the upper and lower arms of the square ring flow in the same direction, while the side arms exhibit much weaker currents. This indicates that the resonance mode at this frequency is not a magnetic resonance induced by a closed-loop current, but rather an electric resonance directly driven by the incident electric field. The incident field is parallel to the upper and lower arms, inducing linear conduction currents and generating opposite charge accumulations at the edges. The upper arm, located on the incident side, experiences a stronger local electric field and stronger capacitive coupling with the backplane, leading to high surface current density and significant Ohmic loss. The lower arm, though carrying current in the same direction, is partially canceled by the reflected field from the backplane, resulting in slightly weaker intensity. In contrast, the side arms, being perpendicular to the incident electric field, have nearly zero field projection and only serve as auxiliary paths for charge redistribution and displacement current closure, thus exhibiting minimal current density. Additionally, the current on the backplane flows in the opposite direction to that on the ring arms and is uniformly distributed, confirming its origin from the mirror current induced by the square ring conductor. The current density on the backplane is highest beneath the ring region and gradually decreases outward, indicating that the absorbed energy is primarily concentrated in this area through Ohmic dissipation. Overall, the coupled interaction between the ring dipole and its mirror current on the backplane constitutes the dominant physical mechanism for absorption at this frequency. At 16.268 GHz, the upper and lower arms of the square ring still carry currents in the same direction, with local phase reversals in certain regions, indicating that electric resonance remains the dominant absorption mechanism. Correspondingly, the backplane current shows a distinct out-of-phase distribution, with strong currents near the edges and weaker ones at the center. This pattern arises because, at high frequencies, the shorter wavelength causes phase differences in the induced currents on the backplane. In the geometric center, induced currents from the upper and lower arms interfere destructively, suppressing current amplitude, while at the edges, the phase difference decreases, leading to constructive interference and enhanced local current density. Therefore, the absorption peak at 16.268 GHz still originates from electric dipole oscillation driven by the incident field, which induces mirror currents on the backplane. The electric field is strongly confined between them, converting electromagnetic energy into Ohmic losses. Consequently, the low- and high-frequency modes provide two separate impedance-matching regions, and when these resonances partially overlap in frequency, the impedance transition between reflection dips becomes smoother, forming a continuous broadband absorption band.

To further reveal the mechanism of deep modulation during the folding process, the current and loss distributions at 5.068 GHz under different folding angles were analyzed, as shown in Figure 4. It can be observed that when the square-ring structure is folded to 30° and 60°, the currents on the upper and lower arms still flow in the same direction, while the current distribution on the side arms becomes noticeably asymmetric, indicating that the dominant absorption mechanism at this frequency remains electric resonance. As the square ring forms an angle θ with the incident electric field, the effective field component along the arm direction decreases to E·cosθ, thereby weakening the induced current intensity on the arms and reducing Ohmic losses on the ring surface. Meanwhile, folding alters the relative spatial position between the upper and lower arms and the backplane, leading to a phase shift in the mirror currents on the backplane. In some regions, the mirror currents transition from in-phase to partially out-of-phase superposition, resulting in a reduction in local energy dissipation areas. Consequently, at 5.068 GHz, both the driving efficiency of electric resonance and the associated energy loss decrease with increasing folding angle. The system’s effective impedance deviates from the free-space impedance, enhancing reflection and leading to a significant decline in absorption performance. In the high-frequency region (16.268 GHz), compared to the stable electric-resonance mode at 0°, the electromagnetic response of the system changes substantially after folding. When the square ring is folded to 30°, the inclined arms reduce the effective projection of the incident electric field along their direction, resulting in an overall decrease in surface current strength. The current distribution becomes more nonuniform with the emergence of local phase-reversal regions, indicating that the resonance mode transitions from a stable electric-dipole-type resonance to a mismatched state. Upon further folding to 60°, the influence of the incident electric field weakens further, the strong-current regions on the ring arms shrink significantly, and only small localized high-field areas remain, preventing the formation of a complete current loop and markedly reducing the efficiency of electric-resonance excitation. Simultaneously, the mirror-current distribution on the backplane is also reconstructed as the folding angle increases. At 30°, the phase delay caused by the shorter wavelength at high frequencies leads to substantial phase variation across different regions; the mirror currents induced by the upper and lower arms cancel each other near the center of the backplane, reducing the local energy dissipation area. When folded to 60°, the backplane exhibits an almost fully out-of-phase mirror-current distribution. Although induced currents still exist on the backplane, they no longer exchange net power with the incident wave; instead, the incident microwave energy is reflected back into free space, and the system transitions into a strong reflection state. In summary, as the folding angle increases, the electric-resonance coupling at high frequencies is progressively destroyed, leading to a continuous decrease in absorption-peak intensity and an enhancement of reflection. This process realizes a tunable transition from an electric-resonance-dominated absorption state to a mirror-type reflection state.

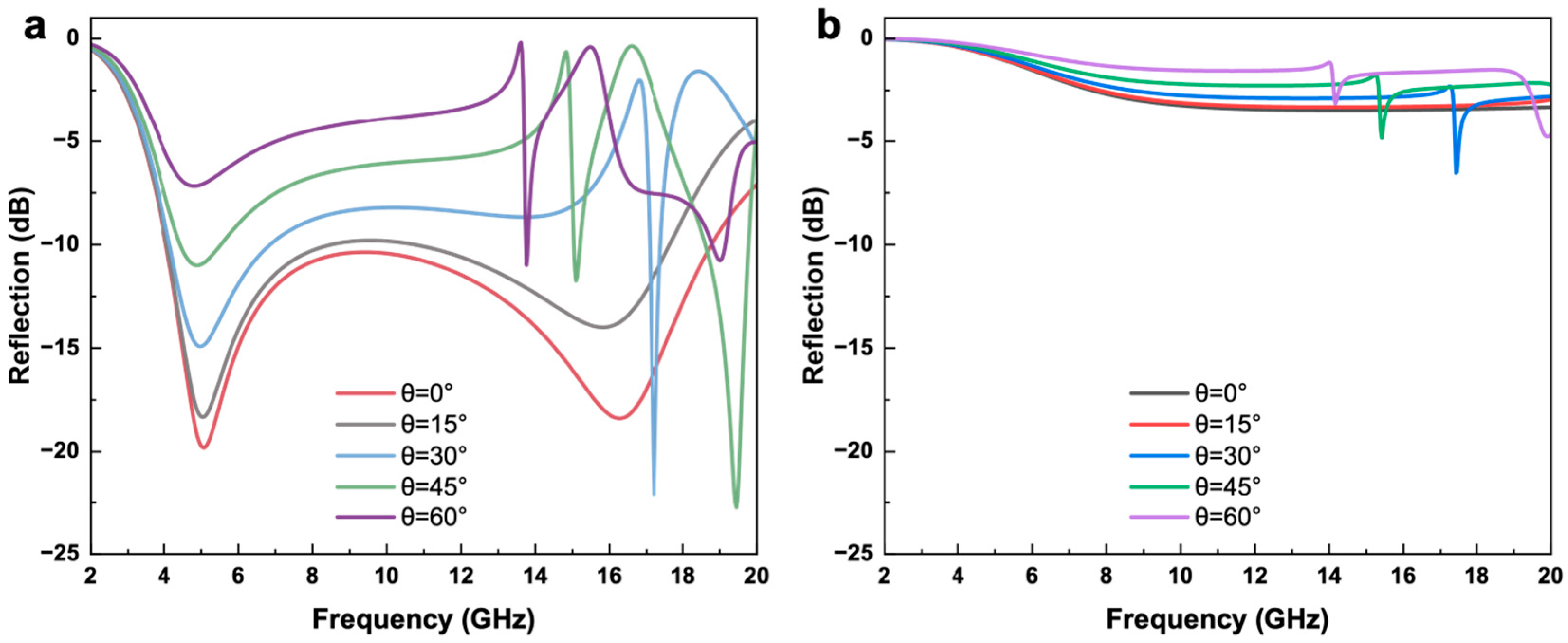
Figure 5 presents the simulated reflection intensity distributions for incident angles ranging from 0° to 60° in both the upright and folded states. The results show that, in the upright state, as the incident angle increases, the overall absorption intensity gradually decreases. The low-frequency absorption peak remains nearly unchanged, while the high-frequency peak slightly shifts toward lower frequencies and gradually diminishes at larger incident angles. It is worth noting that as the incident angle of the electromagnetic wave increases, a distinct sharp peak emerges in the absorption spectrum at higher frequencies. This peak already exists under normal incidence but lies outside the currently observed frequency range (2–20 GHz). Moreover, the increase in the incident angle causes the high-frequency absorption peak to shift toward lower frequencies, resulting in its emergence within the 2–20 GHz observation range. In contrast, in the folded state, the reflection intensity increases progressively with the incident angle, and the high-frequency absorption peak similarly shifts toward lower frequencies. Overall, the structure maintains approximately 80% broadband absorption efficiency across the 4–18.9 GHz range under 30° oblique incidence in the upright configuration, demonstrating excellent angular robustness. Meanwhile, in the folded state, even under large incidence angles, the structure sustains a high-reflection response near 0 dB, indicating that its reflection mode also possesses outstanding angular stability.

3. Fabrication and Validation

We selected ITO-PET with a surface resistance of 50 Ω/sq to fabricate the sample. The processing procedure, as illustrated in Figure 6a, involved laser etching to thin localized areas, enabling the material to be folded into the desired structure, as shown in Figure 6b,c. To validate its optical transparency, the light transmittance was measured using an LS155 color difference haze meter. The test results, presented in Figure 6e, demonstrate an average transmittance of 88.73%, indicating excellent transparency. To verify the design and simulation results of the proposed metamaterial, its reflectivity in the microwave range was tested using the arched reflection method, thereby determining the absorption rate of the structure. Since the sample was placed on a metal plate of equal dimensions, transmittance during testing was considered negligible. A broadband horn antenna operating in the 1–18 GHz range and a vector network analyzer were employed to measure the reflection coefficient of the sample. To approximate normal incidence of plane waves, two horn antennas were positioned on an arched frame at a distance of 2.5 m from the sample with a slight angular separation. The tests were conducted in a microwave anechoic chamber, as depicted in Figure 6d. The results, presented in Figure 6f, demonstrate that the metamaterial exhibits reflection below −10 dB across the 4–18 GHz range in the upright state, while showing significantly enhanced reflection in the folded state. These results are generally consistent with the simulated performance. The minor discrepancies between simulation and experiment mainly arise from mechanical imperfections in the fabricated structure, as the unit cells cannot maintain perfectly rigid planar alignment, leading to slight performance deviations. Nevertheless, the experimental outcomes strongly validate the broadband absorption and deep reflection modulation capabilities of the proposed metamaterial, confirming its potential for practical applications.

4. Discussion

The metamaterial proposed in this study utilizes low-cost ITO-PET thin films as substrate materials, with the aim of replacing traditional precious metal structures, thereby significantly reducing overall fabrication costs. The designed origami structure features a single degree of freedom (unidirectional) crease pattern, which is directly fabricated via laser etching, eliminating the need for additional mechanical or chemical assistance and ensuring uniform and regular distribution of all creases. In contrast, the Miura-ori structure, with its complex crease trajectories and challenging folding characteristics, requires more intricate processing techniques and faces greater challenges in practical applications. Therefore, the origami structure proposed in this study simplifies the manufacturing process and further reduces production costs. Moreover, the design achieves folding deformation only in a specific localized area of the structure, significantly enhancing the device’s structural stability and cyclic durability, thereby ensuring long-term reliability and stability in practical applications.

5. Conclusions

In this work, a reconfigurable transparent absorber based on an ITO–PET composite film is proposed, achieving broadband absorption and deep reflection modulation through reversible structural folding. When the structure is folded from the vertical to the horizontal state, the reflectivity can be continuously tuned from below −10 dB (absorption state) to near 0 dB (reflection state) across the 4–18.9 GHz frequency range, corresponding to a relative bandwidth exceeding 130%, while maintaining excellent stability under various incidence angles. Analysis of surface loss and current distributions under different configurations reveals that the broadband absorption originates from the electric resonance coupling between the square-ring dipole and the mirror current on the backing plane. During the folding process, as this coupling gradually weakens, the system transitions from an electric-resonance-dominated absorption state to a mirror-type reflection state, thereby achieving deep reflection modulation. The established electric resonance model effectively elucidates the physical mechanism underlying the absorption and modulation behaviors. Experimentally, the origami-inspired metamaterial sample was fabricated using a low-cost laser-etching process, and the measured results exhibit excellent agreement with simulations, confirming the feasibility and structural stability of the design. The proposed absorber enables tunable switching between absorption and reflection states within a broadband microwave regime, while featuring lightweight, flexible, and cost-efficient characteristics. This work provides a novel and practical approach for adaptive electromagnetic camouflage, stealth protection, and reconfigurable microwave systems, demonstrating broad application potential.