Rapid Discrimination of Platycodonis radix Geographical Origins Using Hyperspectral Imaging and Deep Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. HSI System
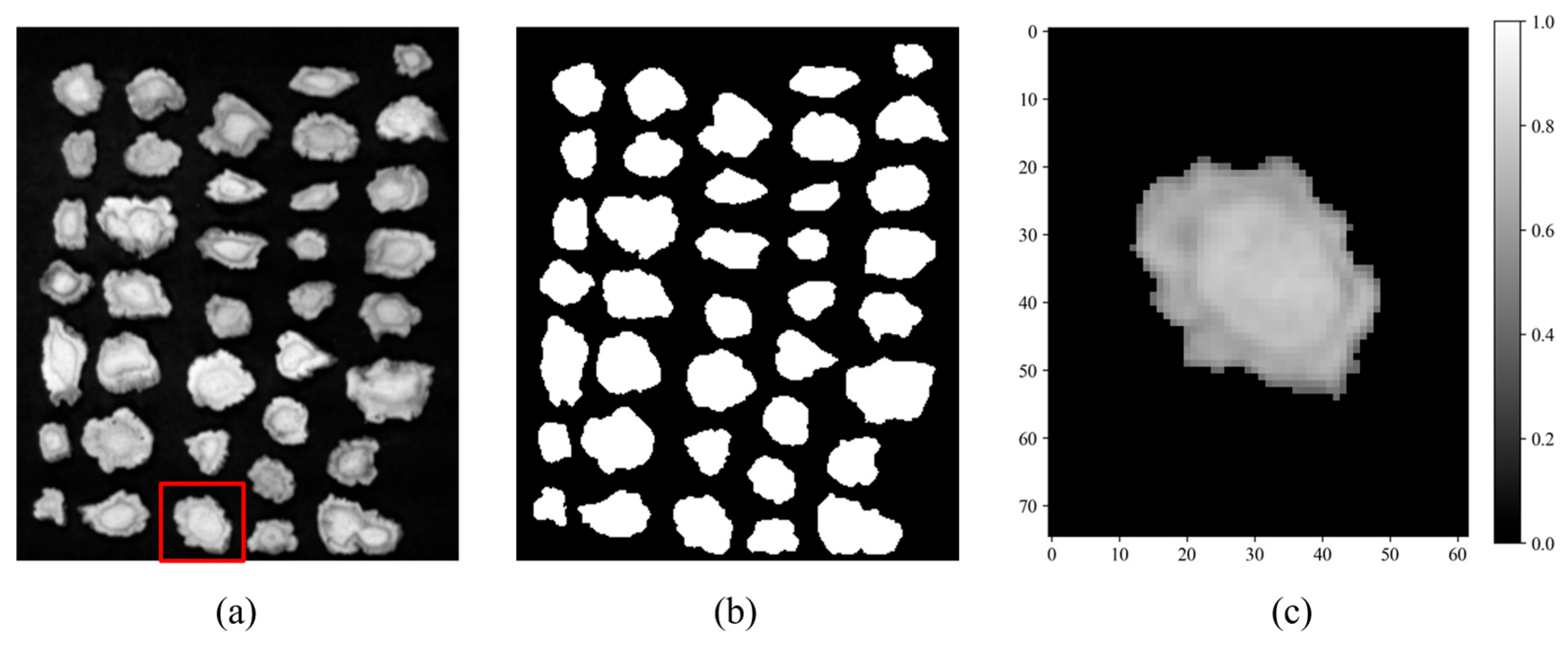
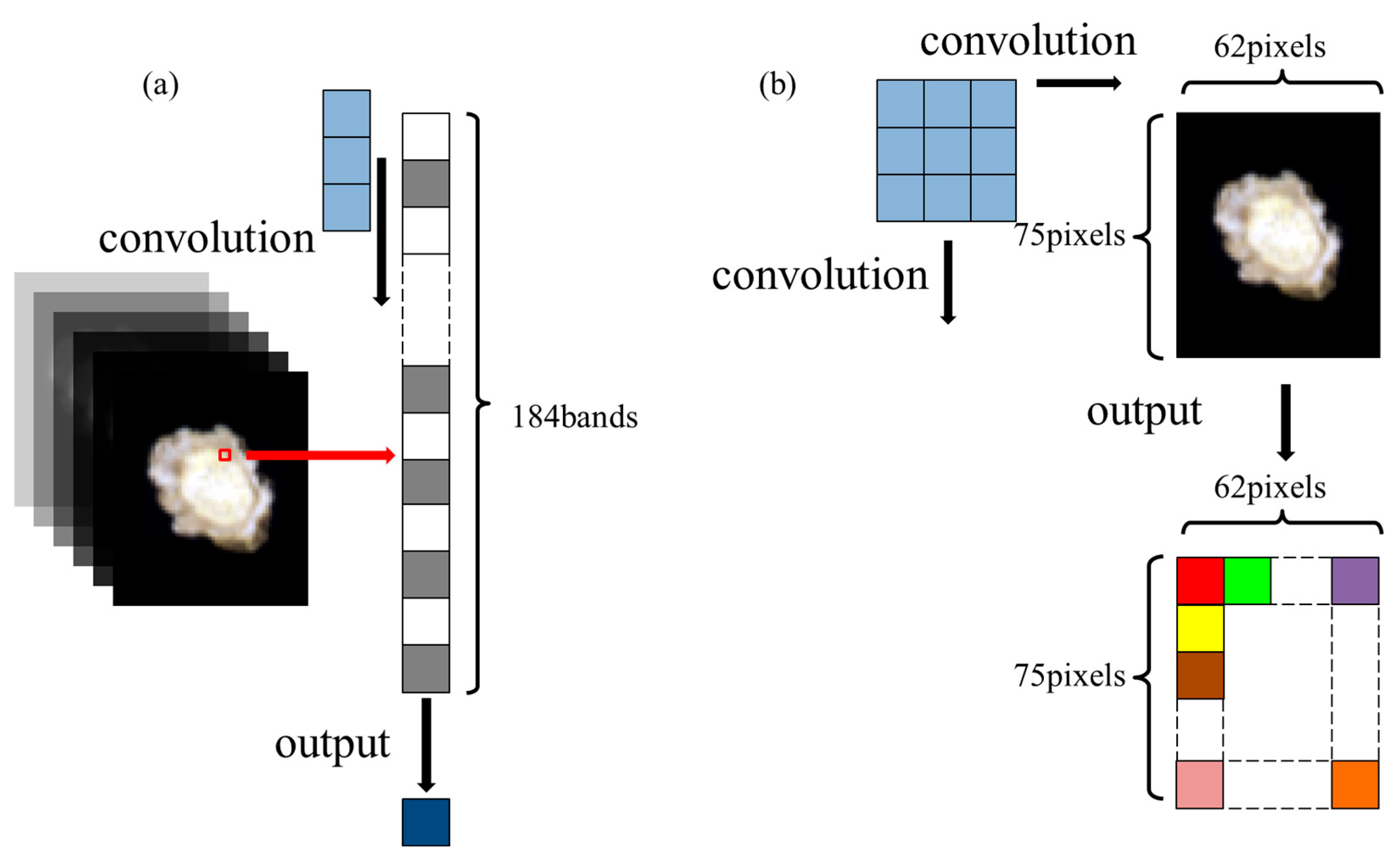
2.3. Dataset Construction
2.4. Preprocessing
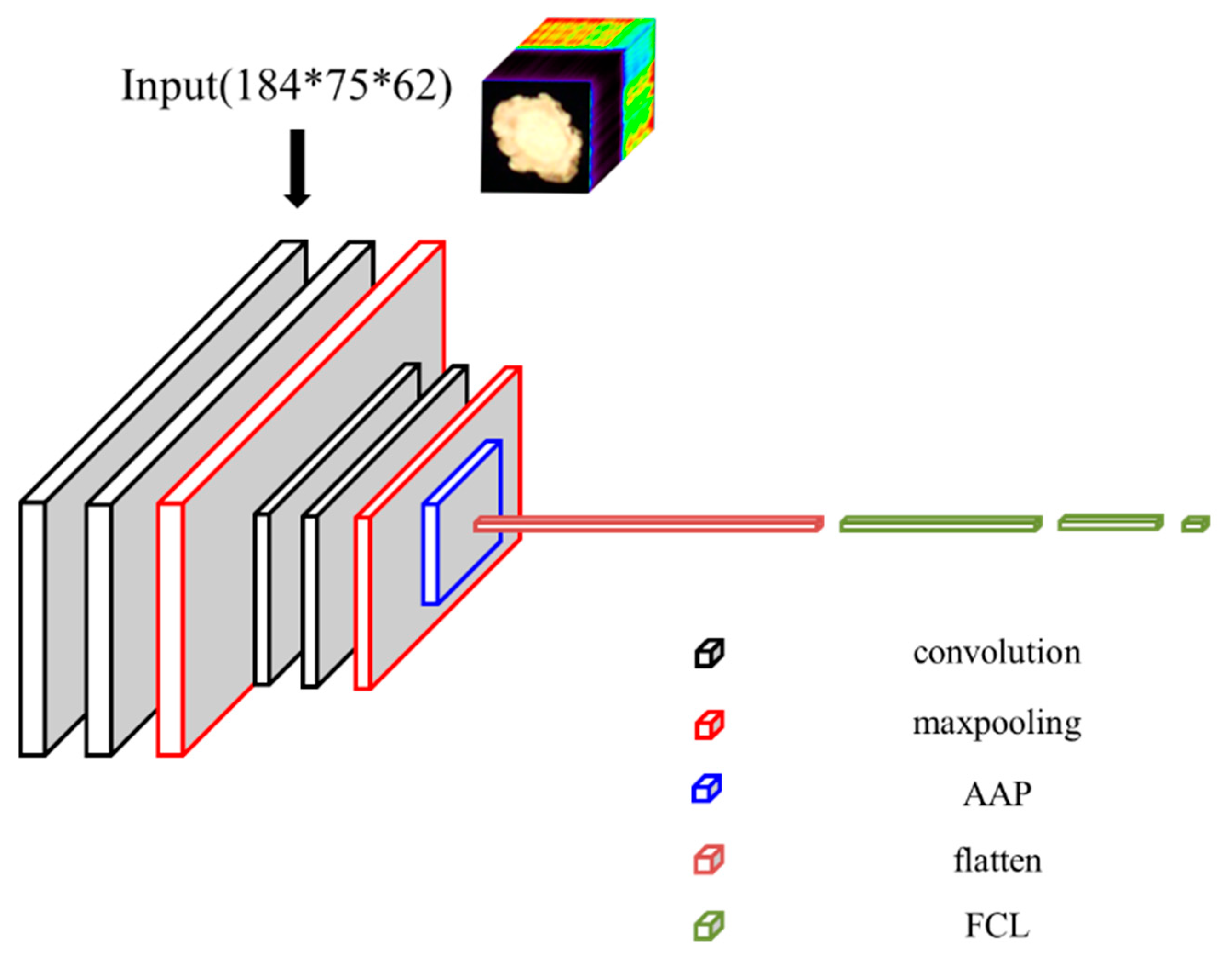
2.5. Origin Classification Network Model
2.6. Training Settings
2.7. Model Performance Evaluation
3. Results and Discussion
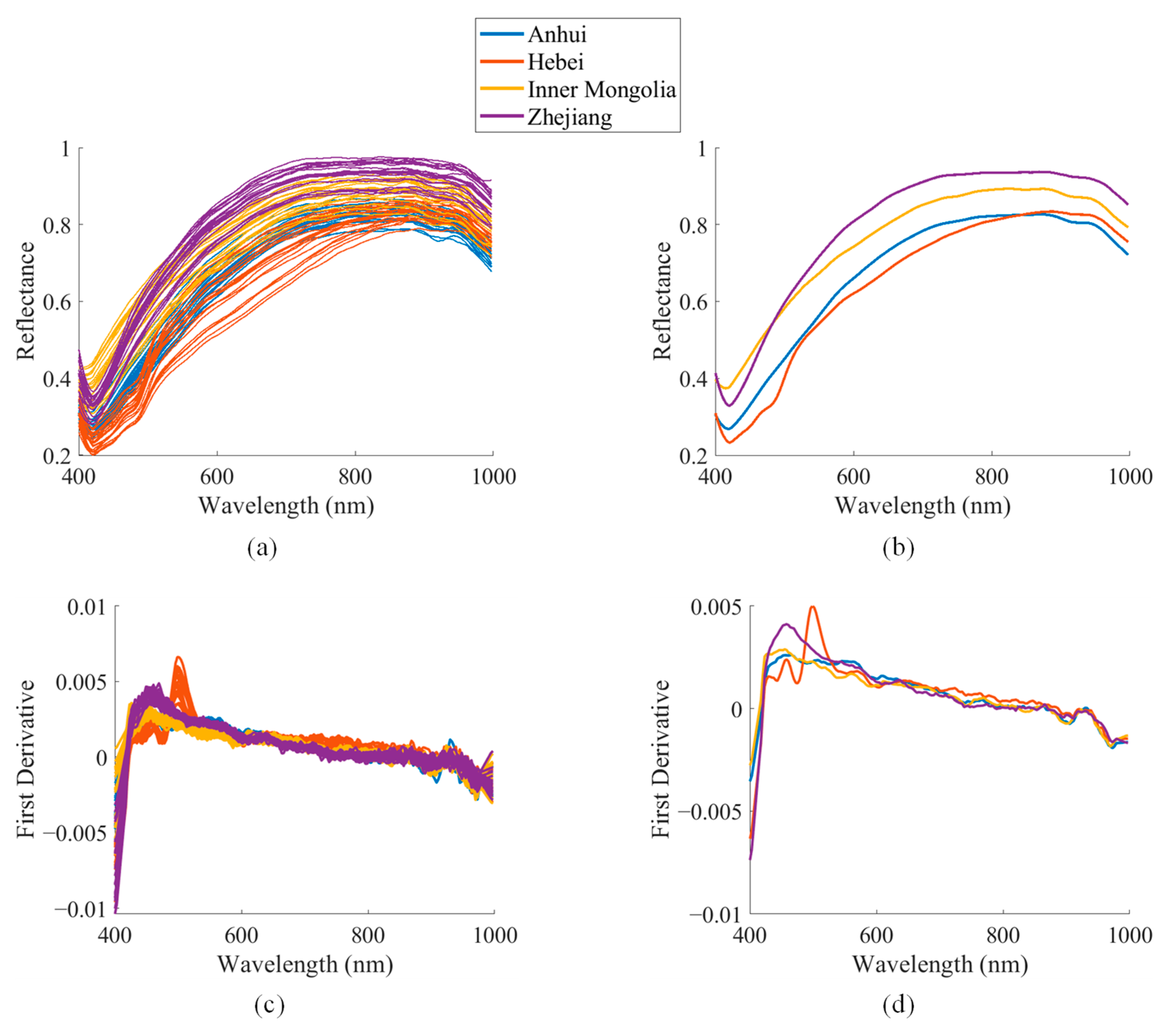
3.1. Spectral Analysis
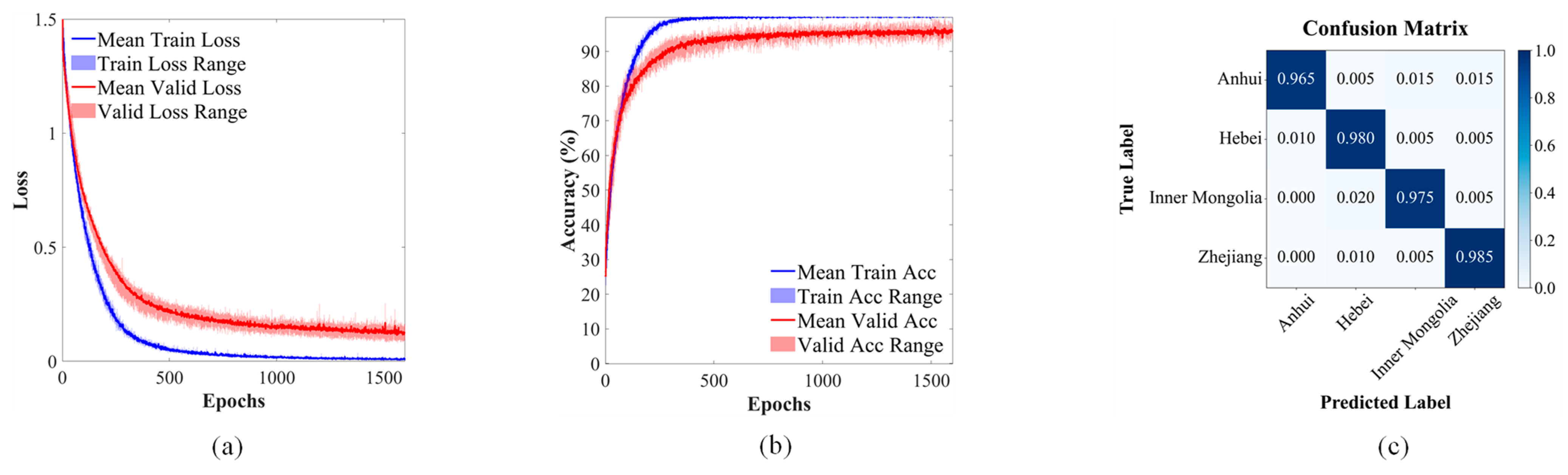
3.2. Model Classification Performance
3.3. Real-World Application Validation
3.4. Ablation Study
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chinese Pharmacopoeia Commission. Pharmacopoeia of the People’s Republic of China, 2020th ed.; China Medical Science Press: Beijing, China, 2020; Volume I. [Google Scholar]
- Zhang, L.; Huang, M.; Yang, Y.; Huang, M.; Shi, J.; Zou, L.; Lu, J. Bioactive platycodins from Platycodonis radix: Phytochemistry, pharmacological activities, toxicology and pharmacokinetics. Food Chem. 2020, 327, 127029. [Google Scholar] [CrossRef]
- Huang, W.; Lan, L.; Zhou, H.; Yuan, J.; Miao, S.; Mao, X.; Hu, Q.; Ji, S. Comprehensive profiling of Platycodonis radix in different growing regions using liquid chromatography coupled with mass spectrometry: From metabolome and lipidome aspects. RSC Adv. 2022, 12, 3897–3908. [Google Scholar] [CrossRef]
- Si, Y.; Gao, Y.; Xie, M.; Li, H.; Cheng, W. Analysis and discrimination of Platycodon grandiflorum from different origins by infrared spectroscopy. Chem. Reagents 2021, 43, 210–215. [Google Scholar]
- Wang, H.; Liu, S.; Wang, H.; Li, W.; Lv, M. Research and application of intelligent hyperspectral analysis technology for Chinese materia medica. China J. Chin. Mater. Med. 2023, 48, 4320–4327. [Google Scholar]
- Zhang, C.; Fei, N.; Li, M.; Li, D.; Huang, X.; Li, C. Traceability study on the origin of Platycodon grandiflorum (Jacq.) A. DC. based on fingerprint analysis of inorganic elements. Chin. J. Inorg. Anal. Chem. 2024, 14, 1006–1014. [Google Scholar]
- Kwon, J.; Lee, H.; Kim, N.; Lee, J.H.; Woo, M.H.; Kim, J.; Kim, Y.S.; Lee, D. Effect of processing method on platycodin d content in Platycodon grandiflorum roots. Arch. Pharm. Res. 2017, 40, 1087–1093. [Google Scholar] [PubMed]
- Park, H.Y.; Shin, J.H.; Boo, H.O.; Gorinstein, S.; Ahn, Y.G. Discrimination of Platycodon grandiflorum and Codonopsis lanceolata using gas chromatography-mass spectrometry-based metabolomics approach. Talanta 2019, 192, 486–491. [Google Scholar] [PubMed]
- Wang, C.; Zhang, N.; Wang, Z.; Qi, Z.; Zheng, B.; Li, P.; Liu, J. Rapid characterization of chemical constituents of Platycodon grandiflorum and its adulterant Adenophora stricta by UPLC-QTOF-MS/MS. J. Mass Spectrom. 2017, 52, 643–656. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Wang, M.; Zhang, L.; Wang, C. Application of molecular methods in the identification of ingredients in Chinese herbal medicines. Molecules 2018, 23, 2728. [Google Scholar] [CrossRef]
- Cui, X.; Song, L.; Sun, J.; Zhou, H. Research on the Application of Intelligent Chinese Herbal Medicine Identification Technology. In Computer Graphics, Artificial Intelligence, and Data Processing; Li, H., Wu, H., Eds.; SPIE: Bellingham, WA, USA, 2024; Volume 13105, pp. 1–7. [Google Scholar]
- Chen, W.; Tong, J.; He, R.; Lin, Y.; Chen, P.; Chen, Z.; Liu, X. An easy method for identifying 315 categories of commonly-used Chinese herbal medicines based on automated image recognition using AutoML platforms. Inform. Med. Unlocked 2021, 25, 100607. [Google Scholar]
- Liu, Y.; Zhang, L.; Zhang, X.; Bian, X.; Tian, W. Modern spectroscopic techniques combined with chemometrics for process quality control of traditional Chinese medicine: A review. Microchem. J. 2025, 213, 113605. [Google Scholar] [CrossRef]
- Addissouky, T.A.; Sayed, I.E.; Ali, M.M.A.; Alubiady, M.H.S. Optical insights into fibrotic livers: Applications of near infrared spectroscopy and machine learning. Arch. Gastroenterol Res. 2024, 5, 1–10. [Google Scholar]
- Guo, Y.; Zhang, L.; Li, Z.; He, Y.; Lv, C.; Chen, Y.; Lv, H.; Du, Z. Online detection of dry matter in potatoes based on visible near-infrared transmission spectroscopy combined with 1D-CNN. Agriculture 2024, 14, 787. [Google Scholar] [CrossRef]
- Ferrari, M.; Mottola, L.; Quaresima, V. Principles, techniques, and limitations of near infrared spectroscopy. Can. J. Appl. Physiol. 2024, 29, 463–487. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J. Hyperspectral imaging for clinical applications. BioChip J. 2022, 16, 1–12. [Google Scholar] [CrossRef]
- Ravikanth, L.; Jayas, D.S.; White, N.D.J.; Fileds, P.G.; Sun, D. Extraction of spectral information from hyperspectral data and application of hyperspectral imaging for food and agricultural products. Food Bioprocess Technol. 2017, 10, 1–33. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar]
- Wu, N.; Zhang, C.; Bai, X.; Du, X.; He, Y. Discrimination of chrysanthemum varieties using hyperspectral imaging combined with a deep convolutional neural network. Molecules 2018, 23, 2831. [Google Scholar] [CrossRef]
- Zhang, L.; Guan, Y.; Wang, N.; Ge, F.; Zhang, Y.; Zhao, Y. Identification of growth years for Puerariae Thomsonii radix based on hyperspectral imaging technology and deep learning algorithm. Sci. Rep. 2023, 13, 14286. [Google Scholar] [CrossRef]
- Behmann, J.; Acebron, K.; Emin, D.; Bennertz, S.; Matsubara, S.; Thomas, S.; Bohnenkamp, D.; Kuska, M.T.; Jussila, J.; Salo, S.; et al. Specim IQ: Evaluation of a new, miniaturized handheld hyperspectral camera and its application for plant phenotyping and disease detection. Sensors 2018, 18, 441. [Google Scholar] [CrossRef]
- Diwu, P.; Bian, X.; Wang, Z.; Liu, Y. Study on the selection of spectral preprocessing methods. Spectrosc. Spect. Anal. 2019, 39, 2800–2806. [Google Scholar]
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Ma, Z.; Di, M.; Hu, T.; Wang, X.; Zhang, J.; He, Z. Visible-NIR hyperspectral imaging based on characteristic spectral distillation used for species identification of similar crickets. Opt. Laser. Technol. 2025, 183, 112420. [Google Scholar] [CrossRef]
- Mao, A.; Mohri, M.; Zhong, Y. Cross-Entropy Loss Functions: Theoretical Analysis and Applications. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; PMLR: Honolulu, HI, USA, 2023; pp. 23803–23828. [Google Scholar]
- Luo, Y.; Zou, J.; Yao, C.; Zhao, X.; Li, T.; Bai, G. HSI-CNN: A Novel Convolution Neural Network for Hyperspectral Image. In Proceedings of the 2018 International Conference on Audio, Language and Image Processing, Shanghai, China, 16–17 July 2018; IEEE: Shanghai, China, 2018; pp. 464–469. [Google Scholar]
- Zhao, R.; Tang, W.; Liu, M.; Wang, N.; Sun, H.; Li, M.; Ma, Y. Spatial-spectral feature extraction for in-field chlorophyll content estimation using hyperspectral imaging. Biosyst. Eng. 2024, 246, 263–276. [Google Scholar] [CrossRef]
- Li, X.; Wu, J.; Bai, T.; Wu, C.; He, Y.; Huang, J.; Li, X.; Shi, Z.; Hou, K. Variety classification and identification of jujube based on near-infrared spectroscopy and 1D-CNN. Comput. Electron. Agric. 2024, 223, 109122. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, W.; Wang, X.; Ma, Z.; Xing, Y.; Dun, X.; Cheng, X. Rapid Discrimination of Platycodonis radix Geographical Origins Using Hyperspectral Imaging and Deep Learning. Optics 2025, 6, 52. https://doi.org/10.3390/opt6040052
Xing W, Wang X, Ma Z, Xing Y, Dun X, Cheng X. Rapid Discrimination of Platycodonis radix Geographical Origins Using Hyperspectral Imaging and Deep Learning. Optics. 2025; 6(4):52. https://doi.org/10.3390/opt6040052
Chicago/Turabian StyleXing, Weihang, Xuquan Wang, Zhiyuan Ma, Yujie Xing, Xiong Dun, and Xinbin Cheng. 2025. "Rapid Discrimination of Platycodonis radix Geographical Origins Using Hyperspectral Imaging and Deep Learning" Optics 6, no. 4: 52. https://doi.org/10.3390/opt6040052
APA StyleXing, W., Wang, X., Ma, Z., Xing, Y., Dun, X., & Cheng, X. (2025). Rapid Discrimination of Platycodonis radix Geographical Origins Using Hyperspectral Imaging and Deep Learning. Optics, 6(4), 52. https://doi.org/10.3390/opt6040052





