Abstract
When interferograms in space heterodyne spectrometers exhibit tilted or distorted fringes, significant errors may occur in the demodulated spectral information. To address this issue, we propose a method for interferogram correction based on automatic spectral analysis. Simulations on erroneous interferograms of monochromatic and polychromatic light demonstrate that this method effectively corrects fringe tilts and significantly improves spectral demodulation accuracy. The standard deviations between the corrected spectra and ideal spectra for monochromatic and polychromatic light are 0.016 and 0.019, respectively, compared to 0.104 and 0.127 for uncorrected spectra. Additionally, the method successfully corrects experimental interferograms of potassium and neon lamps, accurately demodulating characteristic peaks of potassium and neon emission lines. It also enables accurate displacement measurement in a Michelson interferometer experiment. This method, through automatic analysis and one-sided spectral correction, efficiently and accurately corrects erroneous interferograms and enhances spectral demodulation accuracy, showing broad application potential.
1. Introduction
Spatial heterodyne spectroscopy (SHS), an advanced spatially modulated interferometric spectroscopy technique, effectively addresses the limitations of traditional interferometric spectroscopy. Compared to conventional interferometers, SHS eliminates the dependence on moving parts, significantly reducing the risk of mechanical failures and substantially enhancing system stability and reliability. Furthermore, SHS boasts multiple advantages, including high spectral resolution, high throughput, and high stability [1,2,3,4,5,6], demonstrating its crucial role and extensive application potential in various fields such as astronomical observations [7,8], Raman spectroscopy analysis [9,10,11], OH radical detection [12,13,14], and high-precision measurements of atomic emission spectroscopy [15,16].
The SHS captures interference patterns of radiation sources through interferometric methods. However, in practical applications, various factors such as deviations in the grating line direction, defects in optical and electronic components, non-uniformity in response, weak signals, insufficient processing accuracy of optical elements, and errors during instrument packaging can all lead to issues such as dark spots, asymmetry, phase shifts, stripe tilt, or distortion in the interference patterns. These issues result in significant differences between the captured interference patterns and the ideal patterns. Additionally, nonlinear changes in the optical path and limitations of the imaging system itself, such as low resolution or insufficient contrast, can also cause two-dimensional phase distortions, resulting in bending or distortion of the interference fringes [17,18,19]. This fringe distortion not only degrades visual quality but also poses a severe challenge to the accuracy of spectral analysis, potentially leading to deviations in spectral measurements and affecting the reliability of scientific research and applications. Therefore, a deep understanding of the causes of interference fringe distortion and preprocessing of the interference patterns to eliminate errors are crucial for restoring high-quality spectral information for target characteristic analysis [18,19,20,21,22].
To enhance the precision of spectral information reconstruction in spatial heterodyne spectrometers and effectively eliminate interference fringe errors, researchers have developed a series of correction strategies. These strategies encompass phase distortion correction methods [17], radial distortion correction techniques based on interference fringe characteristics [23], baseline correction approaches utilizing wavelet transform principles [24], adaptive baseline correction strategies [25], and precise phase slope fitting methods [26]. These advanced correction methods have been proven to efficiently correct errors in interferograms, thereby ensuring high accuracy in the measurements obtained by spatial heterodyne spectrometers. Schwartz et al. proposed a method to rotate the pattern so that the camera can perceive the stripes in an offset way [27]. Experimental results show that this method can effectively improve the accuracy of spectral measurement and can be widely used in image analysis in the field of physics. Galaktionov et al. improved the reliability and accuracy of interferometric fringe reconstruction and reduced noise impacts through a 4th-order polynomial smoothing algorithm and a fast Fourier transform (FFT) smoothing algorithm [28].
Addressing the issue of error interferogram correction in SHSs, this paper proposes a method based on automatic spectral analysis and correction. The core of this method involves initially performing a Fourier transform on the error interferogram, followed by precisely determining the coordinate indices of each spectral component using a peak-searching function. On this basis, by designing a masking function, the selection of the target unilateral spectrum (i.e., filtering process) and automated correction of spectral components in the y-direction are achieved. Ultimately, precise correction of the interference fringes is accomplished through the application of inverse Fourier transform techniques. This paper first provides an in-depth analysis of the theoretical foundations of the proposed method, elucidating its core principles. Based on this theoretical framework, simulations were conducted to correct the interferograms of monochromatic and polychromatic light with errors, verifying the method’s effectiveness in correcting interferogram errors under different light source conditions. Subsequently, the method was applied to correct the measured erroneous interferograms of potassium and neon lamps and to demodulate their spectra. The demodulated spectral features were found to be in complete agreement with the theoretical values, demonstrating that the method can not only effectively correct the tilt of interference fringes but also enhance the accuracy of spectral demodulation data. Additionally, the paper preliminarily explores the potential application of this method in the field of displacement detection using traditional Michelson interferometers, thereby expanding its scope of application.
2. Method
The design of the SHS incorporates two diffraction gratings, serving as substitutes for the planar mirrors in the traditional Michelson interferometer, as depicted in Figure 1 [29,30,31]. The light beam, collimated by lens L1, is incident on the beam splitter, which divides the incident light into two coherent beams of equal intensity. These two beams are then diffracted by gratings G1 and G2, before returning to the beam splitter. Throughout this procedure, the wavefronts of the two emergent beams intersect at a specific angle, generating a spatially modulated interference pattern that is ultimately captured by a detector. By conducting a Fourier transform analysis on the interference pattern recorded by the detector, the spectral information of the target light source can be accurately reconstructed.
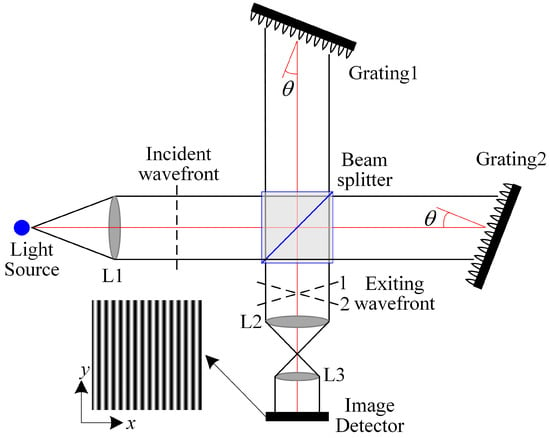
Figure 1.
Illustration of the spatial heterodyne spectroscopy system structure.
As shown in Figure 1, the two gratings are placed at an angle θ to the plane perpendicular to the optical axis. When the incident light with wavenumber σ is diffracted by the two gratings and returns, the angle between the wavefronts of the light emerging from the two gratings is 2γ, and this results in the formation of interference fringes with a specific spatial frequency in space. The spatial frequency of the interference fringes is given by the following equation:
In the above equation, represents the wavenumber of the incident light, is the Littrow wavenumber, and θ is the Littrow angle of the grating.
When the spectral curve of the incident light is denoted as , the resulting interferogram can be expressed as follows:
By performing a Fourier transform on the interferogram derived from Equation (2), the spectral curve of the incident light can be retrieved.
The two-dimensional interferogram acquired by a two-dimensional detector can be described by the following formula:
Under ideal conditions, the two-dimensional interferogram should only contain the frequency signal along the x-direction, with the frequency signal along the y-direction being zero (i.e., ). However, due to systematic errors, such as grating asymmetry or the real y-tilt due to tilt aberrations, frequency signals in the y-direction (i.e., ) will also appear in the two-dimensional interferogram in addition to the frequency signal in the x-direction. This error manifests as a tilt or distortion in the interferogram. In the two-dimensional interferogram, the signal represents the modulation frequency signal of the interference fringes, while the signal represents the noise frequency caused by system asymmetry.
The resulting erroneous interferogram is given by the following equation:
To correct for the error interference fringes in a spatial heterodyne spectrometer, it is necessary to suppress the frequency components in the y-direction. This paper proposes a method based on automatic spectral analysis and correction. The method begins with a Fourier transform (FFT) of the error interference fringe (see Figure 2a). Next, a peak-searching function is used to accurately determine the coordinate indices of each spectral component. Then, a mask function (see Figure 2b) is designed to filter out the target single-sided spectrum. Figure 2c illustrates the filtering process. Figure 2d presents the results of the automated correction of the y-direction spectral components. Finally, inverse Fourier transform (IFFT) technology is employed to accurately correct the interference fringes. The corrected fringes are shown in Figure 2d.
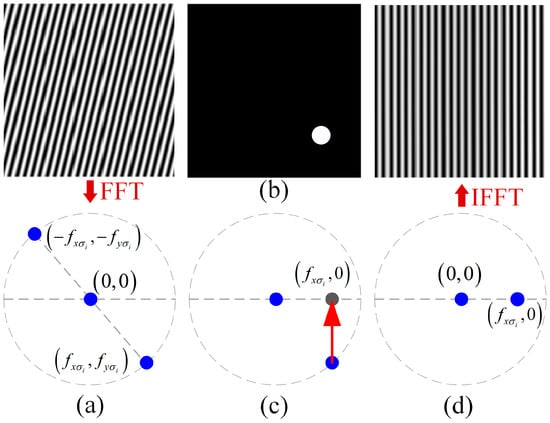
Figure 2.
Schematic diagram of the automatic spectral correction method. (a) Determination of spectral coordinates using the peak search function. (b) Mask pattern. (c) Automatic spectral correction using the masking function. (d) Single-sided spectral filtering and inverse Fourier transform.
Firstly, by performing a Fourier transform on the two-dimensional interferogram represented by Equation (4), we can obtain
Substituting Equation (4) into Equation (5) and further simplifying, we obtain
Equation (6) indicates that the two-dimensional spectral components are distributed at (0, 0), , and , reflecting a certain degree of tilt or distortion in the stripes due to the modulation effect of the noise frequency .
Subsequently, an automatic peak search function is constructed to locate the peaks of specified frequency components in the spectrum and return their index coordinates. Specifically, the peak search is conducted by first sorting all the spectral amplitudes in descending order. In the sorted one-dimensional array, the index of the second largest element (i.e., the element immediately after the maximum value) corresponds to the position of the second largest spectrum in the original amplitude matrix, allowing us to obtain the index coordinates and . Let be the sorted one-dimensional array, and be the index of the second largest spectral amplitude. Then, we have
where is the index of the maximum value element and . It is necessary to convert the index of the second-largest element back to its original two-dimensional index , which can be calculated as follows:
where represents the number of columns in the matrix, which corresponds to the range size of the v-coordinate in the frequency domain. The automatic peak search function acquires the spectral coordinates; this process is clearly depicted in Figure 2a.
Subsequently, set up a mask function with a radius of r, where r is determined by the spectral range. Figure 2b shows the mask pattern. Ensure the mask function fully covers the spectral information to be corrected. Through this mask function, the spectrum at position (u, v) can be extracted to the specified location, and its mathematical expression is as follows:
Using this circular mask function, the zero-order spectrum at location and the spectrum at location are extracted separately, and is placed at . Finally, these two spectral components obtained through masking are combined into a new spectrogram, as shown in Figure 2b. This process can be stated as follows:
Figure 2c displays the spectral information after automatic filtering, where only the spectral components (single-sided spectrum) at specific frequency positions (i.e., and ) are retained. By performing an inverse Fourier transform on these retained spectral components, the correction of the inclined stripes can be achieved. This can be stated as follows:
Finally, the intensity information of the corrected interference fringes can be obtained by performing an element-wise multiplication between the corrected complex function and its complex conjugate.
3. Experiments
3.1. Simulation Analysis of Correction for Error Interferogram in Monochromatic Light
To verify the feasibility of the proposed method, simulations were first conducted on the interferogram of monochromatic light with an incident wavelength of 627 nm. In the system design parameters, the Littrow wavelength of the grating (i.e., in Equation (4)) was set to 630 nm, the Littrow angle ( in Equation (4)) was 10.894°, and the detector pixel count was 512 × 512. The ideal interference pattern and the error-containing interference pattern for the monochromatic light obtained from the simulations are shown in Figure 3a and Figure 3b, respectively. Subsequently, we performed a Fourier transform on the error-containing interference pattern according to Equation (5), and the obtained spectral information is depicted in Figure 3c. The results indicate that the tilt in the interference fringes is due to .
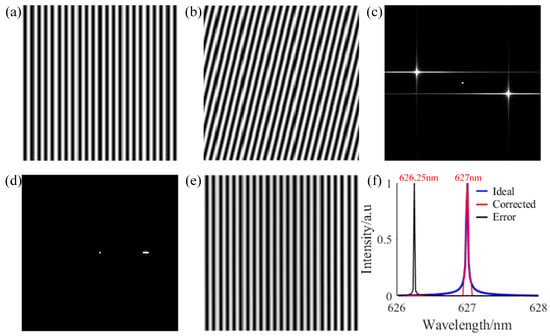
Figure 3.
Results of the monochromatic light stripe correction. (a) Ideal interference pattern. (b) Error-containing interference pattern. (c) The frequency domain of the error-containing interference pattern. (d) The frequency domain after automatic analysis and correction in the frequency domain. (e) Corrected interference pattern. (f) Spectrum.
The proposed method for fringe tilt correction based on automatic spectral analysis, as demonstrated in Equations (7)–(10), centers on the use of an automatic peak-searching function to identify the peak of the specified frequency component in the two-dimensional spectral map. This is followed by the application of a masking function to filter the target spectrum and achieve automated correction of the spectral components in the y-direction. The fringe tilt correction is then realized through the inverse Fourier transform. Based on the automatic spectrum analysis method, we obtained the corrected spectrum, which is illustrated in Figure 3d. Figure 3d further indicates that the proposed method retains only the spectral information at points and . Subsequently, the inverse Fourier transform was performed on the spectral map shown in Figure 3d according to Equations (11) and (12). This process successfully eliminated the influence of the error components in the direction, thereby achieving the correction of the tilted fringes. The corrected interferogram, as shown in Figure 3e, is essentially consistent with the ideal interferogram depicted in Figure 3a.
To further validate the accuracy of the proposed method, the ideal interferogram (Figure 3a), the erroneous interferogram (Figure 3b), and the corrected interferogram (Figure 3e) were processed through a series of steps, including first-order differencing for baseline removal, windowing to reduce sidelobe effects, and Fourier transformation followed by averaging to extract their respective spectral signals. These signals are depicted in Figure 3f with blue, black, and red lines representing the ideal, erroneous, and corrected spectra, respectively. As shown in the figures, the spectral peak of the erroneous interferogram is located at 626.25 nm, exhibiting a noticeable deviation from the characteristic peak position of the incident light source at 627 nm. However, after applying the correction method proposed in this paper, the spectral peak of the corrected spectrum returns to 627 nm, in complete alignment with the peak position of the ideal interferogram. This result fully demonstrates the effectiveness and accuracy of the proposed method in correcting the interference fringes.
To quantitatively assess the effectiveness of the proposed method, the standard deviation between the corrected spectrum and the ideal spectrum was calculated. Assuming the corrected spectrum is and the ideal spectrum is , the formula for the standard deviation can be expressed as follows:
The goal of spectral correction is to minimize the impact of systematic errors and instrument noise on spectral data, bringing the corrected spectrum as close as possible to the ideal spectrum. The standard deviation is an important metric for evaluating the correction effect, reflecting the degree of deviation between the corrected and ideal spectra. The standard deviation between the corrected spectrum and the ideal spectrum was found to be 0.016, indicating an extremely low dispersion between the corrected and ideal spectra, i.e., the corrected spectrum is highly consistent with the ideal state. In contrast, the standard deviation between the uncorrected erroneous spectrum and the ideal spectrum was 0.104, significantly higher than that of the corrected spectrum. This highlights the substantial difference between the uncorrected spectrum and the ideal spectrum. The above results validate the significant improvement in spectral data accuracy achieved by the proposed method.
3.2. Simulation Analysis of Correction for Error Interferogram in Polychromatic Light
Polychromatic light is widely present in daily life, and its complex spectral signal structure poses higher demands for the correction of tilted interference fringes. In this paper, simulations were conducted on the interferograms of polychromatic light with wavelengths of 627 nm, 628 nm, and 629 nm. During this process, only the incident wavelengths were changed, while other parameter values remained constant. The ideal and erroneous interferograms of the polychromatic light obtained from the simulations are shown in Figure 4a and Figure 4b, respectively. In the erroneous interferogram, tilting and distortion of the interference fringes corresponding to the three different wavelengths can be observed. The Fourier transform of Figure 4b yields the corresponding spectral information, as shown in Figure 4c. From the spectral map, it can be seen that the interference fringes corresponding to the three wavelengths exhibit varying degrees of frequency modulation in the y-direction. This modulation is the primary cause of the tilting and distortion of the fringes in the erroneous interferogram.
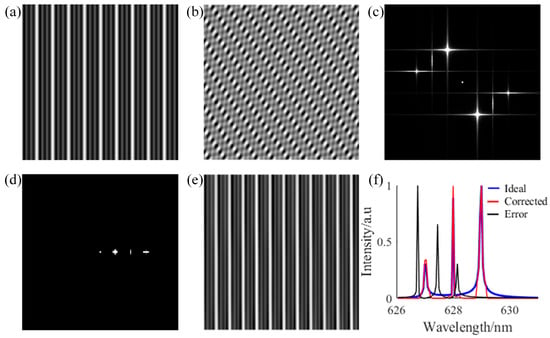
Figure 4.
Results of the polychromatic light stripe correction. (a) Ideal interference pattern. (b) Error-containing interference pattern. (c) The frequency domain of the error-containing interference pattern. (d) The frequency domain after automatic analysis and correction in the frequency domain. (e) Corrected interference pattern. (f) Spectrum.
Based on the automatic spectral analysis method proposed in this paper (as shown in Equations (7)–(10)), we obtained the corrected spectrum, which is illustrated in Figure 4d. Figure 4d demonstrates that the spectral components in the y-direction of the corrected spectrum are zero, i.e., , and only the spectral components at , , , and are retained. The correction method effectively suppresses spectral interference in the y-direction, retaining only the primary frequency components relevant to spectral demodulation. Subsequently, the inverse Fourier transform was applied to the spectral map shown in Figure 4d to restore the spatial domain information. The corrected interferogram is presented in Figure 4e, which successfully achieves the tilt correction of the interference fringes for polychromatic light. The corrected fringes exhibit a more regular and clear structure. The corrected interferogram in Figure 4e is essentially consistent with the ideal interferogram in Figure 4a, thereby validating the effectiveness of the correction algorithm in correcting the tilt of interference fringes in polychromatic light.
To further validate the accuracy of the proposed method in spectral signal demodulation of polychromatic light, the spectral signals were extracted from the ideal interferogram (Figure 4a), the erroneous interferogram (Figure 4b), and the corrected interferogram (Figure 4e), and are presented in Figure 4f as blue, black, and red curves, respectively. As shown in Figure 4f, the spectral signal demodulated from the erroneous interferogram exhibits significant deviations from the ideal spectral signal, reflecting that the distortion of interference fringes severely affects the accuracy of spectral demodulation. However, after applying the correction method proposed in this paper, the spectral peaks of the corrected spectral signal are essentially consistent with those of the ideal spectral signal. This result demonstrates that the proposed algorithm can effectively correct the errors caused by tilted interference fringes in polychromatic light, thereby enhancing the accuracy of spectral demodulation.
To quantitatively evaluate the effectiveness of the proposed method in correcting interferograms of polychromatic light, the standard deviation between the corrected spectrum and the ideal spectrum was further calculated. The results showed that the standard deviation between the corrected spectrum and the ideal spectrum was 0.019, indicating an extremely low degree of dispersion between the corrected spectral data and the ideal spectral data, i.e., the corrected spectrum is essentially consistent with the ideal spectrum. In contrast, the standard deviation between the uncorrected erroneous spectrum and the ideal spectrum was 0.127, which is significantly higher than that of the corrected spectrum. This suggests that, without correction, there is a considerable deviation between the erroneous spectral signal and the ideal spectrum. The above results demonstrate the effectiveness of the proposed correction method in processing spectral data of polychromatic light. It can significantly reduce the dispersion of spectral data, minimize systematic errors and noise interference, and bring the corrected spectral data closer to the ideal state. This not only validates the effectiveness and reliability of the method in improving the accuracy of spectral data for polychromatic light but also provides important support for high-precision processing of polychromatic light spectral data.
3.3. Correction of Potassium Lamp Interference Pattern
In this paper, a correction experiment was conducted for the erroneous interferograms of a potassium lamp. The darkroom conditions were as follows: Complete light blocking was achieved using light-blocking curtains to eliminate external light interference. An optical platform was employed to minimize mechanical vibration interference during data collection. The interferograms of the potassium lamp light source were captured in a darkroom environment. The experimental setup is shown in Figure 5, where Figure 5a illustrates the spatial heterodyne interferometer. The instrument has a wavelength range of 756.8–771.7 nm, a spectral resolution of 0.029 nm, an aperture diameter of less than 30 mm, and a pixel size of 13 µm.

Figure 5.
Experimental setup. (a) Spatial heterodyne spectrometer. (b) Potassium lamp.
Figure 6a shows the captured interferogram of the potassium lamp, while Figure 6b presents a magnified view of a portion of the potassium lamp’s interferogram. From the figures, it can be clearly observed that the interferogram of the potassium lamp exhibits significant fringe tilt and distortion, with indistinct fringe contours. This indicates that the spectral components along the y-axis are non-zero, resulting in spatial distortions of the interference fringes.
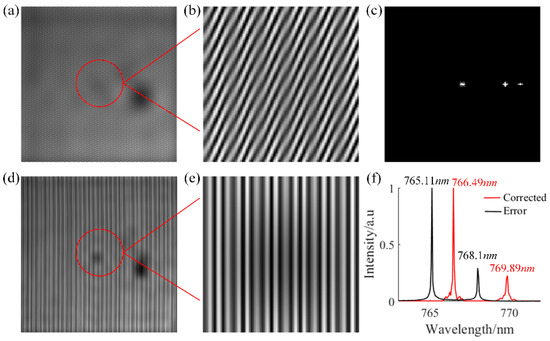
Figure 6.
Correction results of the potassium lamp interference pattern. (a) Error interference pattern of a potassium lamp. (b) Locally enlarged view of the error interference pattern of the potassium lamp. (c) Spectrum corrected by the automatic analysis method in the frequency domain. (d) Corrected interference pattern of potassium lamp in the frequency domain. (e) Locally enlarged view of corrected interference pattern of potassium lamp in the frequency domain. (f) Potassium lamp spectral signal demodulated from the corrected interference pattern.
Based on the proposed automatic spectral analysis and correction algorithm, the interferogram shown in Figure 6a was subjected to spectral correction, with the results presented in Figure 6c. After correction, the spectral components in the y-direction were effectively eliminated from the spectral map, retaining only the spectral components in the x-direction. This indicates that the algorithm successfully separated and removed the error components, thereby optimizing the spectral information of the interferogram. Subsequently, the inverse Fourier transform was applied to the corrected spectrum in Figure 6c, in conjunction with Equation (11), to obtain the corrected potassium lamp interferogram, as shown in Figure 6d. To intuitively demonstrate the correction effect, a magnified view of the corrected interferogram is provided in Figure 6e. The interference fringes, which were originally tilted, have been restored to uniformly distributed vertical structures with clearer fringe contours and significantly reduced noise within the interferogram.
Finally, the corrected potassium lamp interferogram (as shown in Figure 6d) was subjected to a Fourier transform to extract the spectral information, with the results presented in Figure 6f. As shown in the figure, two distinct characteristic peaks are observed at 766.49 nm and 769.89 nm, which are in complete agreement with the characteristic peaks of potassium. Additionally, we used the moving average method for spectral demodulation. The results show that the two characteristic peaks from this method are at 766.471 nm and 769.842 nm, with corresponding spectral deviations of 0.019 nm and 0.048 nm. Comparison indicates that our method significantly enhances the accuracy of spectral demodulation, better meeting the needs of high-precision spectral analysis.
3.4. Correction Experiment of Neon Lamp Interference Pattern
Neon lamps can emit four characteristic spectral lines at wavelengths of 937.3 nm, 942.5 nm, 945.9 nm, and 948.6 nm. Figure 7a shows the interferogram of the neon lamp light source captured in a darkroom environment, with a magnified view presented in Figure 7b. The tilted and distorted interference fringes observed in the figures indicate the presence of non-zero spectral components along the y-axis. The interferogram in Figure 7a was corrected using the automatic spectral analysis and correction algorithm, with the results shown in Figure 7c. After correction, the spectral components in the y-direction were effectively eliminated, retaining only the spectral components in the x-direction. Subsequently, the inverse Fourier transform was applied to the corrected spectrum, yielding the corrected neon lamp interferogram shown in Figure 7d. A magnified view of the corrected interferogram in Figure 7e demonstrates that the method successfully corrected the tilted fringes, restoring them to vertical and parallel structures. This validates the effectiveness of the method in correcting interferograms of polychromatic light and provides a reliable basis for the accurate demodulation of neon lamp spectral signals.
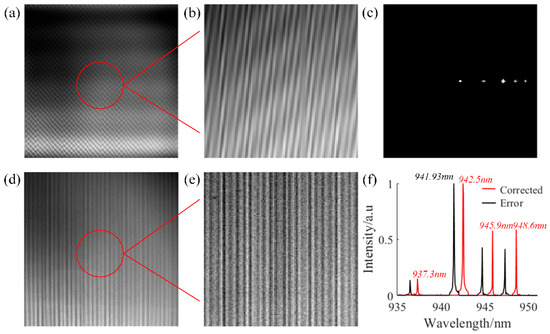
Figure 7.
Correction results of the neon lamp interference pattern. (a) Error interference pattern of the neon lamp. (b) Locally enlarged view of the error interference pattern of the neon lamp. (c) Spectrum corrected by the automatic analysis method in the frequency domain. (d) Corrected interference pattern of neon lamp in the frequency domain. (e) Locally enlarged view of corrected interference pattern of neon lamp in the frequency domain. (f) Neon lamp spectral signal demodulated from the corrected interference pattern.
The spectral information extracted from the corrected interferogram (Figure 7d) through the Fourier transform is shown in Figure 7f. The spectral signal exhibits four distinct peaks at 937.3 nm, 942.5 nm, 945.9 nm, and 948.6 nm, which are in complete agreement with the known characteristic spectral lines of neon. The experimental results confirm that the proposed automatic spectral analysis and correction method can effectively correct erroneous interferograms of polychromatic light and accurately extract the spectral signals of neon lamps.
3.5. Application of Corrected Interference Patterns in Displacement Measurement
To thoroughly examine the feasibility of interference pattern correction in the field of displacement measurement, an experiment on displacement measurement using a Michelson interferometer was conducted. The experimental setup is illustrated in Figure 8. In this setup, a piezoelectric transducer (model P-601.4SL, PI) was employed to drive the reflective mirror to produce minute displacements. Consequently, due to the corresponding changes in the optical path difference, shifts in the interference fringes occur, and the magnitude of these shifts directly reflects the displacement of the measured object.
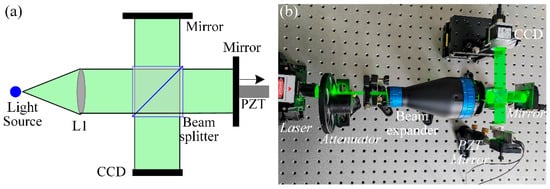
Figure 8.
Michelson interferometer. (a) Schematic diagram of the interferometer. (b) Actual setup of the interferometer.
In the experiment with the Michelson interferometer shown in Figure 8b, we acquired an error interference fringe pattern as illustrated in Figure 9a. Subsequently, in Figure 9d, we present the average profile analysis of this error interference pattern, which indicates that it is difficult to directly solve for the displacement of the measured object from the fringe shifts in this error interference pattern. Therefore, we corrected the frequency spectrum based on the proposed automatic frequency spectrum analysis and correction method (i.e., the method described by Equations (7)–(10)). The corrected frequency spectrum is shown in Figure 9b. Furthermore, in Figure 9c, we display the corrected interference fringe pattern, revealing that the proposed method effectively corrects the interference fringes. To accurately analyze the displacement from the corrected fringes, we provide the profile information of the corrected fringes in Figure 9e. Specifically, the red and black profiles in Figure 9e represent the corrected fringes before and after the movement of the reflective PZT mirror, respectively. By comparing the corresponding fringe orders and combining with calibration calculations, we obtained a fringe shift of 0.133 μm, which is consistent with the actual driving displacement of the piezoelectric ceramic. This result further verifies that our method can efficiently correct error fringes and that the corrected fringes can be used for accurate displacement measurement.
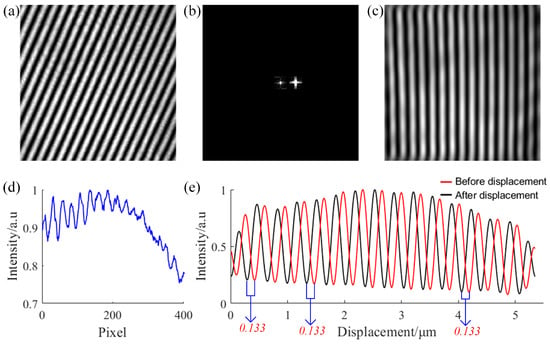
Figure 9.
Experimental results of displacement measurement. (a) Error interference pattern. (b) Frequency spectrum corrected by the automatic frequency domain analysis method. (c) Corrected interference pattern. (d) Average profile of the error interference pattern. (e) Calculation of displacement magnitude.
4. Discussion and Conclusions
In this paper, a correction simulation analysis of error interference patterns for both monochromatic and polychromatic light was first conducted for the proposed automatic spectral analysis and fringe correction method. The results indicate that the method effectively achieves the correction of interference errors, specifically eliminating the influence of error components in the frequency spectrum along the y-direction. Furthermore, a quantitative analysis of the effectiveness of error correction was performed. In the simulation of spatial heterodyne interferometry for monochromatic light, the standard deviation between the corrected spectrum and the ideal spectrum was 0.016, while the standard deviation between the error spectrum and the ideal spectrum was 0.104. This result suggests that the corrected spectral data are closer to the ideal state, with a significant reduction in dispersion. Subsequently, in the simulation of spatial heterodyne interferometry for polychromatic light, the standard deviation between the corrected spectrum and the ideal spectrum was 0.019, while the standard deviation between the error spectrum and the ideal spectrum was 0.127. These results further demonstrate the remarkable effectiveness of the proposed method in improving the accuracy of spectral demodulation data.
Subsequently, interference pattern correction experiments were conducted using potassium and neon lamps. During the experiments, the spectral signal of the potassium lamp was successfully demodulated, with significant characteristic peaks observed at wavelengths of 766.49 nm and 769.89 nm. Additionally, we used the moving average method for spectral demodulation. The results show that the two characteristic peaks from this method are at 766.471 nm and 769.842 nm, with corresponding spectral deviations of 0.019 nm and 0.048 nm. Comparative analysis indicates that our method significantly enhances the accuracy of spectral demodulation, better meeting the needs of high-precision spectral analysis. The spectral signal of the neon lamp was also successfully demodulated, containing four emission lines at 937.3 nm, 942.5 nm, 945.9 nm, and 948.6 nm. The actual experimental results fully prove that the method proposed in this paper can effectively correct error interference patterns and accurately extract the spectral signals of the target object. Finally, to verify the effectiveness of the proposed method in fringe correction, a displacement measurement experiment was conducted based on a Michelson interferometer. The experimental results indicate that after applying the proposed method for fringe correction, accurate measurement of a 133 nm displacement was successfully achieved.
When interference fringes exhibit tilt or distortion in SHSs, the demodulated spectral information may contain significant errors or even be incorrect. To address this challenge, this paper proposes an automatic spectral analysis and fringe correction method. This method utilizes a peak-searching function to index the frequency spectrum positions and employs a masking function to automatically correct the frequency spectrum components along the y-direction. Experimental results show that the method only requires automatic analysis and correction of the unilateral frequency spectrum to effectively correct error interference patterns, thus exhibiting high efficiency. After correcting the interference patterns using this method, the accuracy of spectral information demodulation is significantly improved.
Author Contributions
Conceptualization, S.Y. (Siqian Yang); methodology, S.Y. (Siqian Yang); software, S.Y. (Siqian Yang); validation, T.S., W.X., S.Y. (Siqian Yang) and F.W.; formal analysis, X.W.; investigation, S.Y. (Siqian Yang); data curation, S.Y. (Song Ye); writing—original draft preparation, S.Y. (Siqian Yang); writing—review and editing, T.S., W.X., S.Y. (Song Ye) and F.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Project (2022YFB3901800, 2022YFB3901803), Supported by the National Natural Science Foundation of China (41975033), Key Laboratory of General Optical Calibration and Characterization Technology, Chinese Academy of Sciences, Graduate Education Innovation Program of Guilin University of Electronic Science and Technology (2024YCXS220).
Data Availability Statement
The data presented in this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Q.; Luo, H.; Li, Z.; Ding, Y.; Xiong, W. Analysis of signal-to-noise ratio of spatial heterodyne spectroscopy. Measurement 2024, 237, 115180. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, H.; Li, Z.; Shi, H.; Bai, Y.; Xiong, W. Digital micromirror device and spatial heterodyne spectroscopy combined modulation interference spectroscopy. Opt. Commun. 2022, 507, 127595. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, H.; Bai, Y.; Ding, Y.; Li, Z.; Xiong, W. Optical system design of a DMD–SHS combined modulation interference spectrometer. Appl. Opt. 2023, 62, 2154–2160. [Google Scholar] [CrossRef] [PubMed]
- Long, X.; Huang, Z.; Tian, Y.; Du, J.; Liu, Y. High-resolution on-chip spatial heterodyne Fourier transform spectrometer based on artificial neural network and PCSBL reconstruction algorithm. Opt. Express 2023, 31, 33608–33621. [Google Scholar] [CrossRef]
- Zhang W-l Liu, Z.-Y.; Wang, H.; Chen, Y.; Wang, Y.; Zhao, Z.-Z.; Sun, T. Research status of spatial Heterodyne spectroscopy—A review. Microchem. J. 2021, 166, 106228. [Google Scholar] [CrossRef]
- Lenzner, M.; Diels, J.-C. Concerning the Spatial Heterodyne Spectrometer. Opt. Express 2016, 24, 1829–1839. [Google Scholar] [CrossRef] [PubMed]
- Englert, C.R.; Harlander, J.M.; Brown, C.M.; Marr, K.D. Spatial heterodyne spectroscopy at the Naval Research Laboratory. Appl. Opt. 2015, 54, F158–F163. [Google Scholar] [CrossRef]
- Hosseini, S. Characterization of cyclical spatial heterodyne spectrometers for astrophysical and planetary studies. Appl. Opt. 2019, 58, 2311–2319. [Google Scholar] [CrossRef]
- Zettner, A.; Gojani, A.B.; Schmid, T.; Gornushkin, I.B. Evaluation of a Spatial Heterodyne Spectrometer for Raman Spectroscopy of Minerals. Minerals 2020, 10, 202. [Google Scholar] [CrossRef]
- Hu, G.; Xiong, W.; Luo, H.; Shi, H.; Li, Z.; Shen, J.; Fang, X.; Xu, B.; Zhang, J. Raman Spectroscopic Detection for Simulants of Chemical Warfare Agents Using a Spatial Heterodyne Spectrometer. Appl. Spectrosc. 2017, 72, 151–158. [Google Scholar] [CrossRef]
- Qiu, J.; Qi, X.; Li, X.; Ma, Z.; Jirigalantu; Tang, Y.; Mi, X.; Zheng, X.; Zhang, R. Bayanheshig, Development of a spatial heterodyne Raman spectrometer with echelle-mirror structure. Opt. Express 2018, 26, 11994–12006. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Xiong, W.; Luo, H.; Li, Z. Ground observation result of an OH radical hyper-resolution spectrometer for the middle and upper atmosphere. Appl. Opt. 2019, 58, 5602–5611. [Google Scholar] [CrossRef]
- Luo, H.; Wei, X.; Shi, H.; Chen, D.; Li, Z. Error analysis of field of view registration accuracy of hyper-resolution spatial heterodyne spectrometer for hydroxyl radical OH. Proc. SPIE 2019, 11337, 1133705. [Google Scholar]
- Bartula, R.J.; Ghandhi, J.B.; Sanders, S.T.; Mierkiewicz, E.J.; Roesler, F.L.; Harlander, J.M. OH absorption spectroscopy in a flame using spatial heterodyne spectroscopy. Appl. Opt. 2007, 46, 8635–8640. [Google Scholar] [CrossRef]
- Li, X.; Riedel, J.; You, Y. Practical high-resolution spectroscopy with a spatial heterodyne spectrometer: Determination of instrumental function for lineshape recovery. Spectrochim. Acta Part B At. Spectrosc. 2024, 221, 107053. [Google Scholar] [CrossRef]
- Kumar, V. Analysis of Atomic Structure Using Spectroscopy: An Emission and Absorption Line Spectrum Study. Int. Res. J. Adv. Sci. Hub. 2024, 6, 348–357. [Google Scholar] [CrossRef]
- Englert, C.R.; Harlander, J.M.; Cardon, J.G.; Roesler, F.L. Correction of phase distortion in spatial heterodyne spectroscopy. Appl. Opt. 2004, 43, 6680–6687. [Google Scholar] [CrossRef] [PubMed]
- Burke, M.G.; Fonck, R.J.; McKee, G.R.; Winz, G.R. Spatial heterodyne spectroscopy for fast local magnetic field measurements of magnetized fusion plasmas. Rev. Sci. Instrum. 2023, 94, 033504. [Google Scholar] [CrossRef]
- Pei, H.-y.; Jiang, L.; Wang, J.-j.; Cui, Y.; Fang, Y.-x.; Zhang, J.-m.; Chen, C. Phase distortion correction of fringe patterns in spaceborne Doppler asymmetric spatial heterodyne interferometry. Chin. Opt. 2025, 18, 382–392. [Google Scholar]
- Englert, C.R.; Harlander, J.M. Flatfielding in spatial heterodyne spectroscopy. Appl. Opt. 2006, 45, 4583–4590. [Google Scholar] [CrossRef]
- Soncco, D.C.; Barbanson, C.; Nikolova, M.; Almansa, A.; Ferrec, Y. Fast and Accurate Multiplicative Decomposition for Fringe Removal in Interferometric Images. IEEE Trans. Comput. Imaging 2017, 3, 187–201. [Google Scholar] [CrossRef]
- Ri, S.; Takimoto, T.; Xia, P.; Wang, Q.; Tsuda, H.; Ogihara, S. Accurate phase analysis of interferometric fringes by the spatiotemporal phase-shifting method. J. Opt. 2020, 22, 105703. [Google Scholar] [CrossRef]
- Liu, J.; Wei, D.; Wroblowski, O.; Chen, Q.; Mantel, K.; Olschewski, F.; Kaufmann, M.; Riese, M. Analysis and correction of distortions in a spatial heterodyne spectrometer system. Appl. Opt. 2019, 58, 2190–2197. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Q.; Zhang, L.J.; Xiong, W.; Zhang, W.T.; Ye, S.; Wang, J.J. Study on Inhomogeneous Correction of Interference Pattern of Spatial Heterodyne Spectrometer. Spectrosc. Spectr. Anal. 2017, 37, 1274–1278. [Google Scholar]
- Ye, S.; Gan, Y.; Xiong, W.; Zhang, W.; Wang, J.; Wang, X. Baseline correction of spatial heterodyne spectrometer using wavelet transform. Infrared Laser Eng. 2016, 45, 1117009. [Google Scholar]
- Wang, X.Q.; Ye, S.; Zhang, L.J.; Xiong, W. Study on phase correction method of spatial heterodyne spectrometer. Spectrosc. Spectr. Anal. 2013, 33, 1424–1428. [Google Scholar]
- Schwartz, E.; Ribak, E.N. Enhanced sampling of 2D interference patterns. Appl. Opt. 2017, 56, 1977–1981. [Google Scholar] [CrossRef] [PubMed]
- Ilya, G.; Julia, S.; Vladimir, T.; Alexis, K. Modified Fizeau interferometer with the polynomial and FFT smoothing algorithm. Proc. SPIE 2022, 12223, 122230T. [Google Scholar]
- Németh, G.; Pekker, Á. New design and calibration method for a tunable single-grating spatial heterodyne spectrometer. Opt. Express 2020, 28, 22720–22731. [Google Scholar] [CrossRef]
- Li, S.; Luo, H.; Li, Z.; Ding, Y.; Wang, Q.; Xiong, W. Characteristics of spatial heterodyne spectroscopy for polarization measurement. Appl. Opt. 2023, 62, 2207–2217. [Google Scholar] [CrossRef]
- Ye, S.; Li, Z.; Zhang, Y.; Xiong, W.; Wang, F.; Wang, X.; Zhang, W. Imaging spectrum reconstruction of a spatial heterodyne imaging spectrometer. Appl. Opt. 2022, 61, C13–C19. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).