Sparsity-Guided Phase Retrieval to Handle Concave- and Convex-Shaped Specimens in Inline Holography, Taking the Complexity Parameter into Account
Abstract
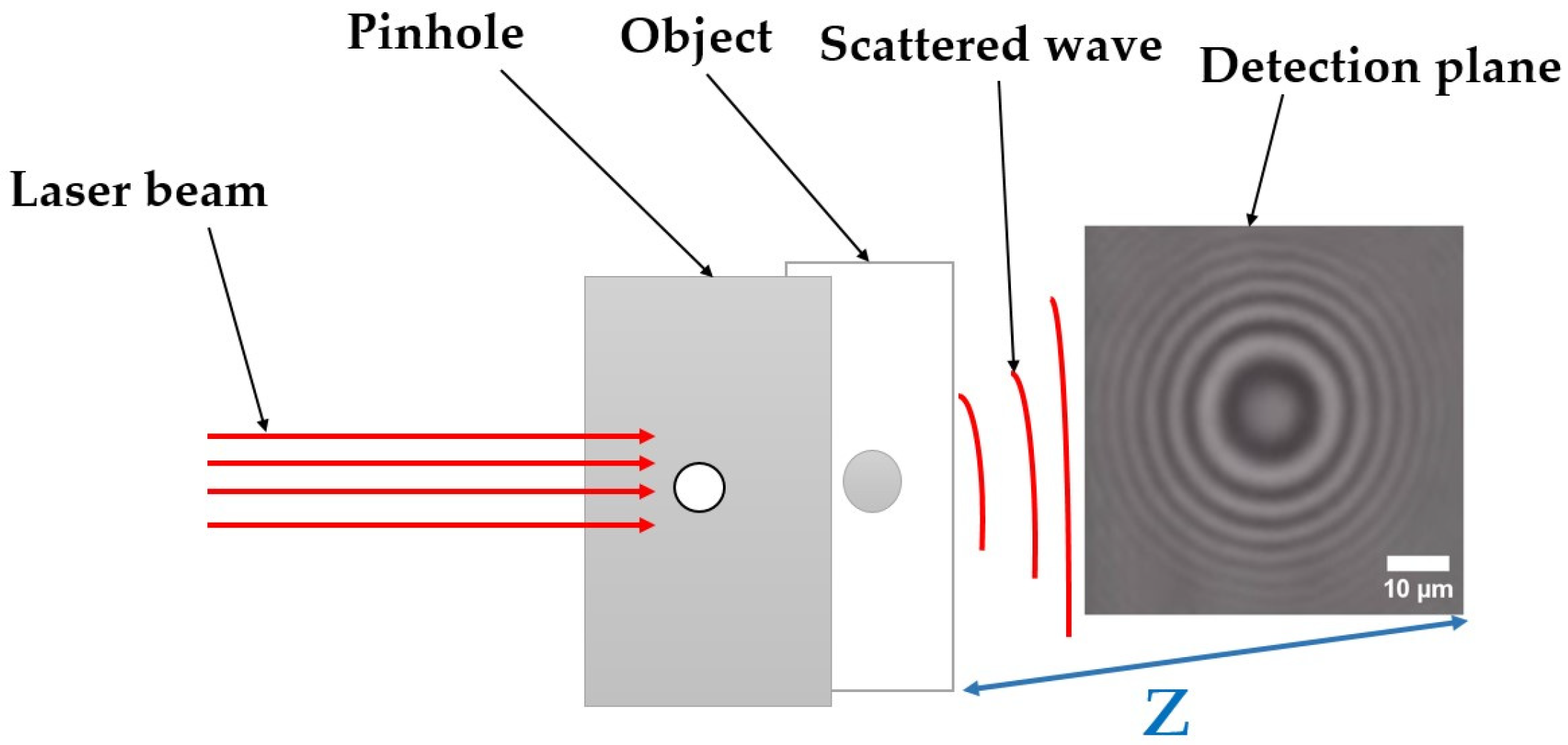
1. Introduction
2. Analysis and Proposed Sparsity-Guided Phase Retrieval
2.1. Total Variation (TV)
2.2. FISTA
2.3. Proposed Sparsity-Guided Phase Retrieval
3. Main Contribution
4. Numerical and Experimental Results
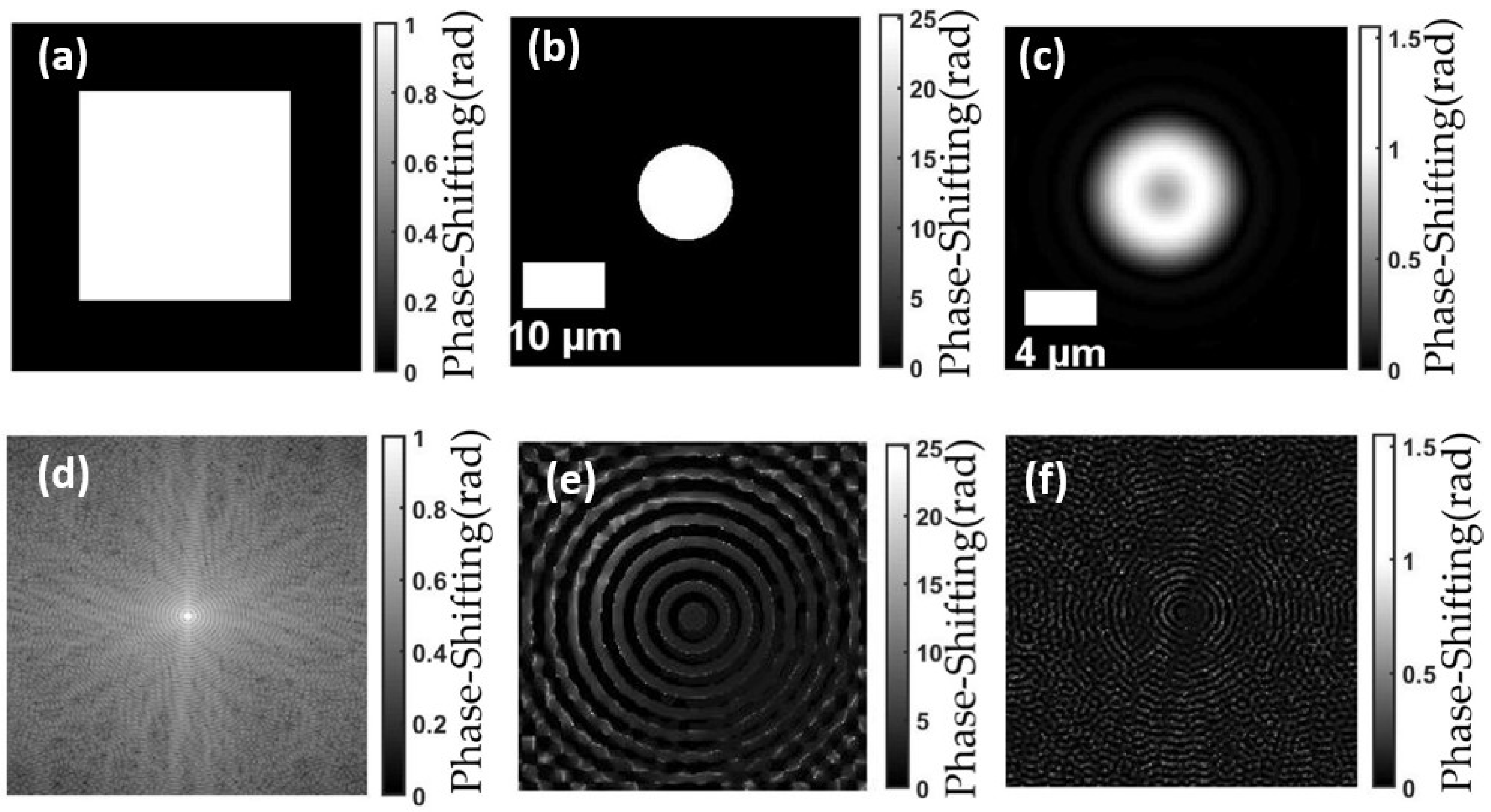
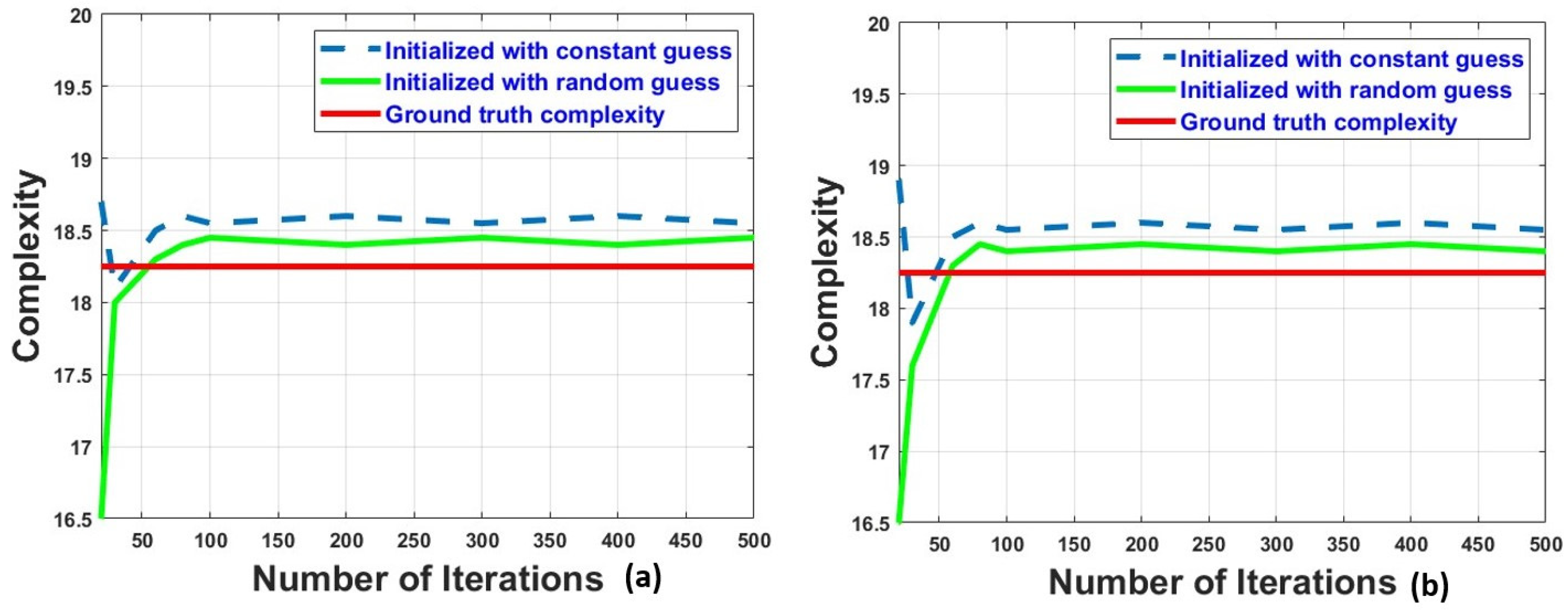
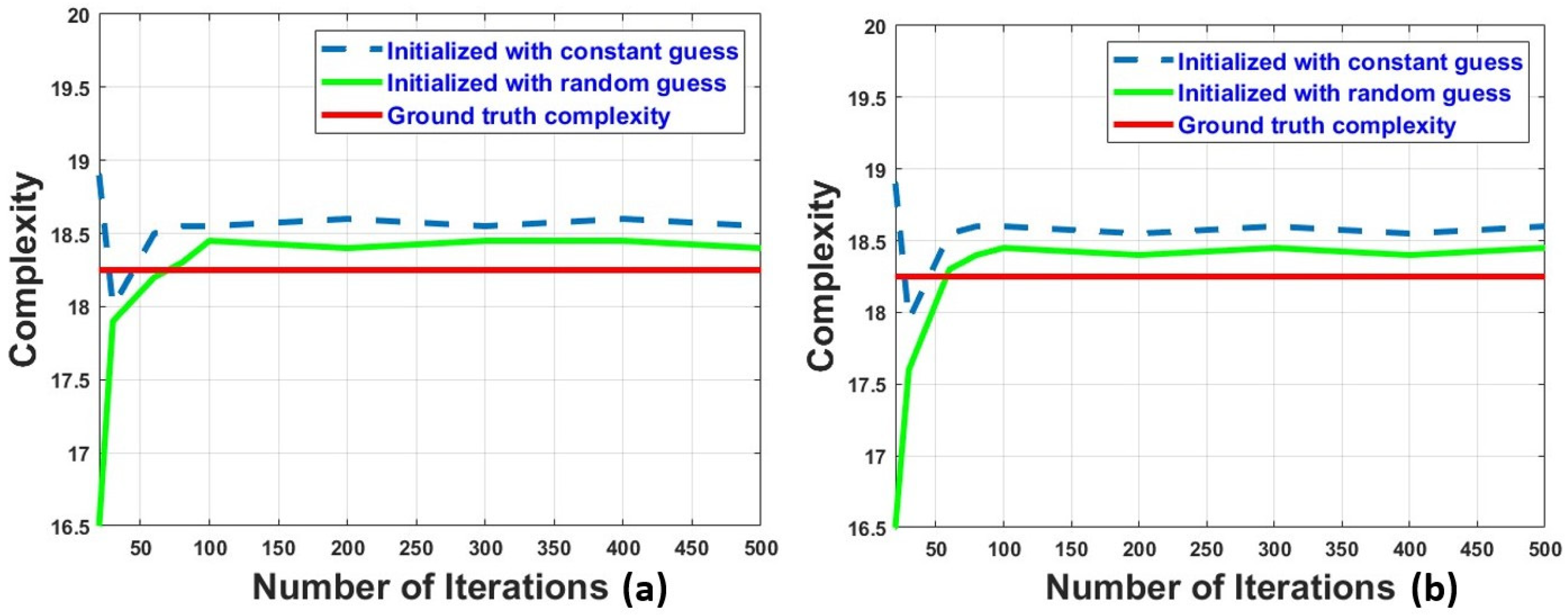
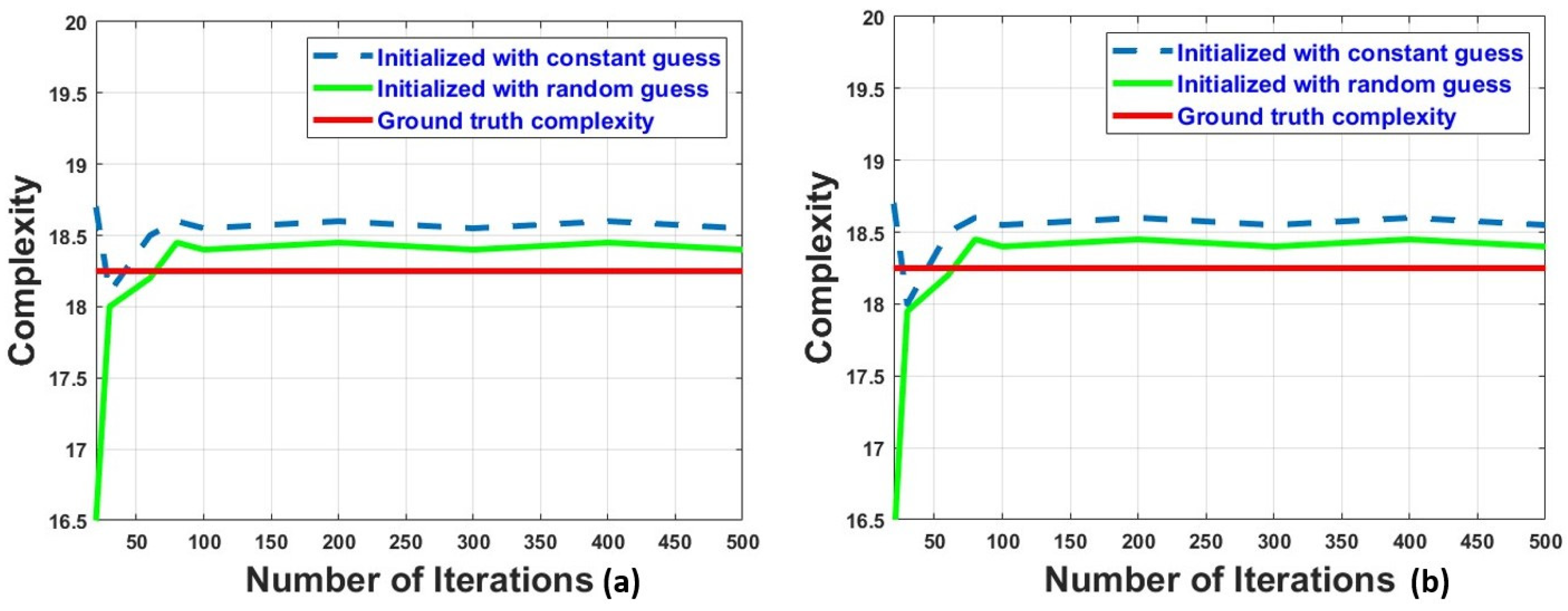
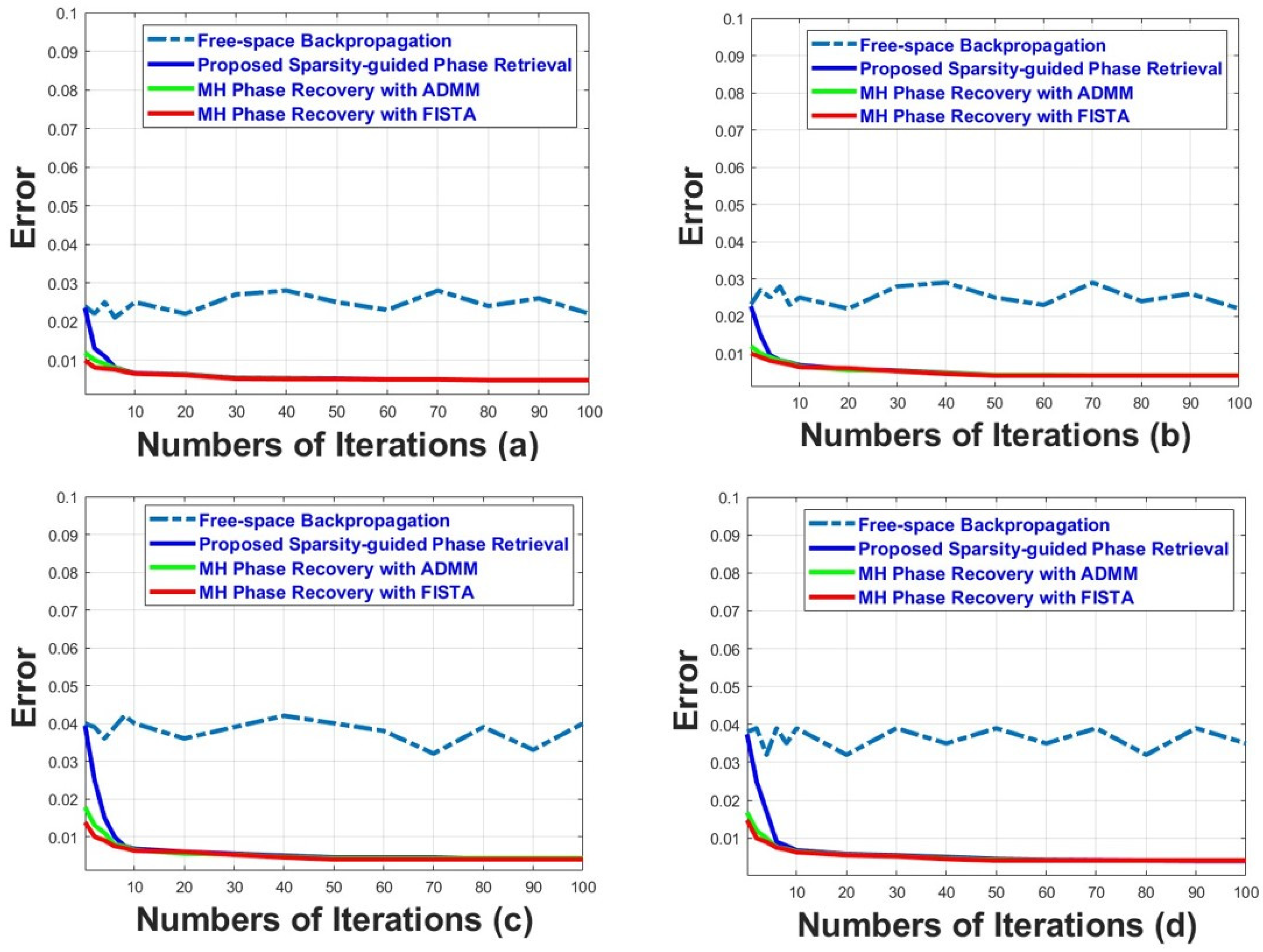
4.1. Numerical Results
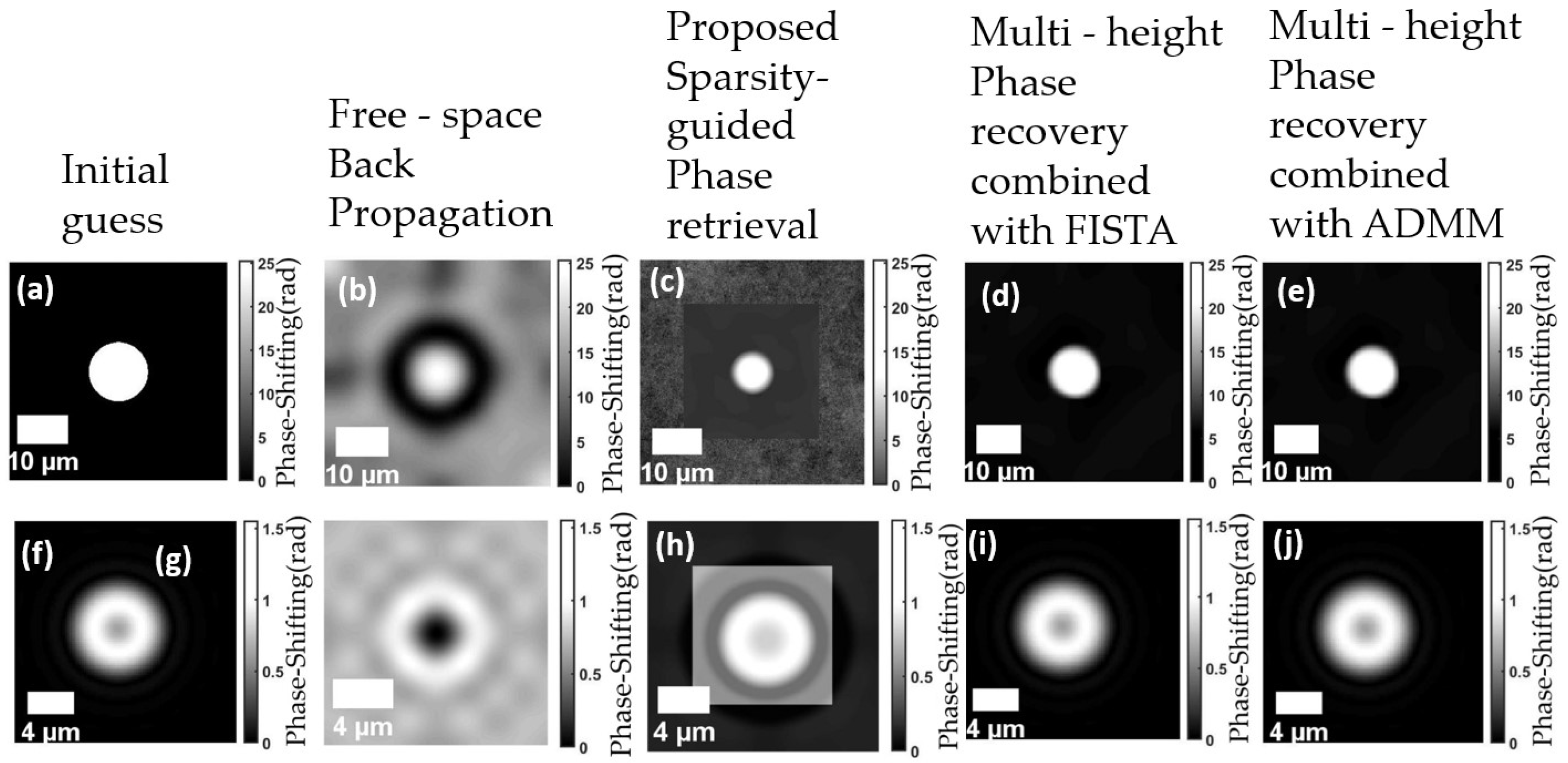
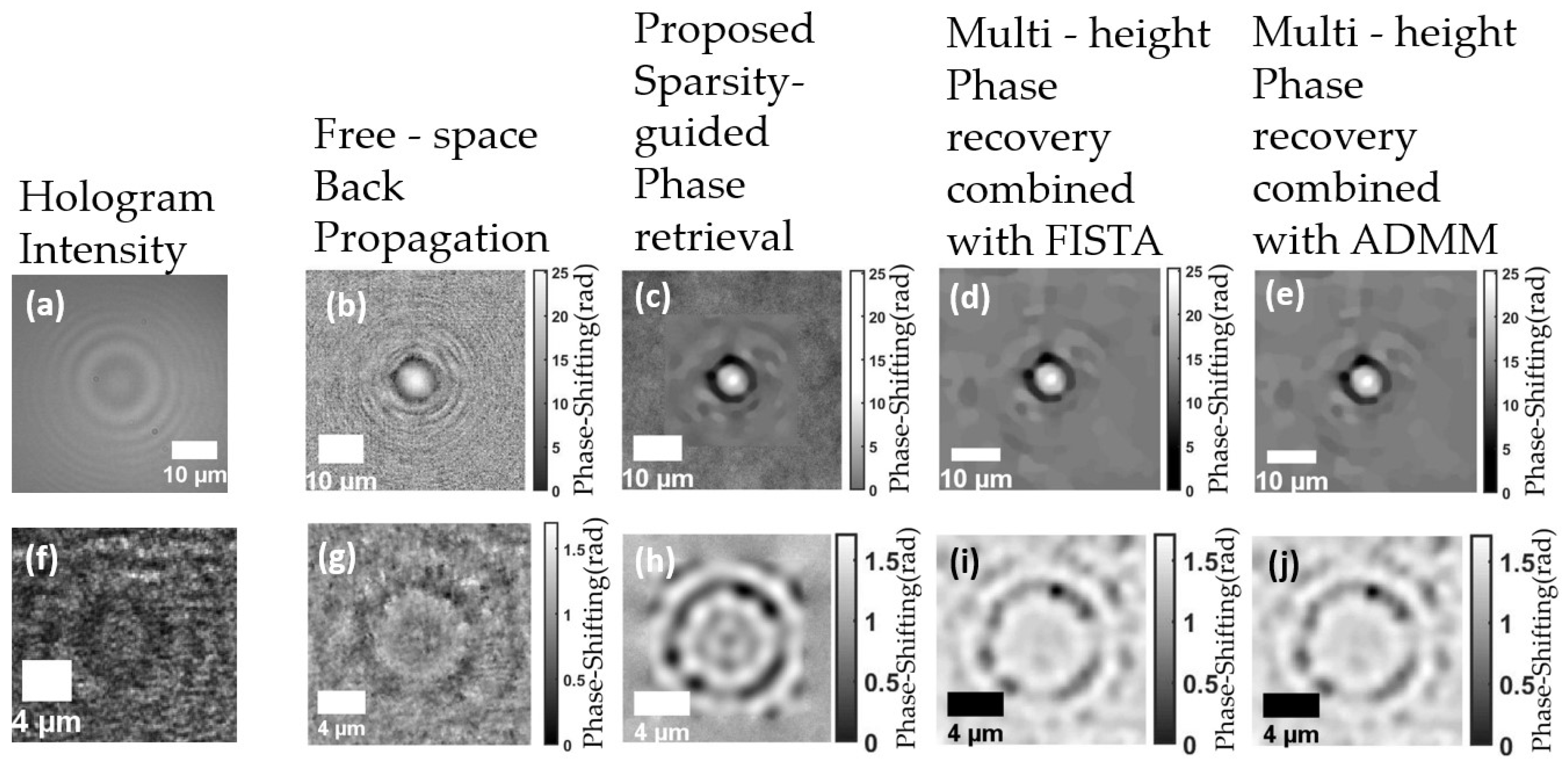
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaganathan, K.; Eldar, Y.C.; Hassibi, B. Phase retrieval: An overview of recent developments. In Optical Compressive Imaging; Routledge: London, UK, 2016; pp. 279–312. [Google Scholar]
- Dong, J.; Valzania, L.; Maillard, A.; Pham, T.-A.; Gigan, S.; Unser, M. Phase retrieval: From computational imaging to machine learning: A tutorial. IEEE Signal Process. Mag. 2023, 40, 45–57. [Google Scholar]
- Gaur, C.; Khare, K. Sparsity-assisted phase retrieval in the Fresnel zone. J. Mod. Opt. 2019, 66, 1296–1304. [Google Scholar]
- Ferraro, P.; Wax, A.; Zalevsky, Z. Coherent Light Microscopy: Imaging and Quantitative Phase; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; p. 46. [Google Scholar]
- Barty, A.; Nugent, K.A.; Paganin, D.; Roberts, A. Quantitative Optical Phase Microscopy. Opt. Lett. 1986, 23, 817–819. [Google Scholar]
- Coene, W.; Janssen, G.; de Beeck, M.O.; Van Dyck, D. Phase Retrieval Through Focus Variation for Ultra-Resolution in Field-Emission Transmission Electron Microscopy. Phys. Rev. Lett. 1992, 69, 3743–3746. [Google Scholar]
- Dainty, J.C.; Fienup, J.R. Phase Retrieval and Image Reconstruction for Astronomy. In Image Recovery: Theory and Application; Stark, H., Ed.; Academic Press: Cambridge, MA, USA, 1987; pp. 231–275. [Google Scholar]
- Nishino, Y.; Miao, J.; Ishikawa, T. Image Reconstruction of Nanostructured Nonperiodic Objects Only from Oversampled Hard x-ray Diffraction Intensities. Phys. Rev. B 2003, 68, 220101. [Google Scholar]
- Momose, A. Recent Advances in X-ray Phase Imaging. Jpn. J. Appl. Phys. 2005, 44, 6355–6367. [Google Scholar]
- Chapman, H.N.; Barty, A.; Bogan, M.J.; Boutet, S.; Frank, M.; Hau-Riege, S.P.; Marchesini, S.; Woods, B.W.; Bajt, S.; Benner, W.H.; et al. Femtosecond Diffractive Imaging with a Soft-X-ray Free-Electron Laser. Nat. Phys. 2006, 2, 839–843. [Google Scholar]
- Gonsalves, R.A.; Devaney, A. Wavefront Sensing by Phase Retrieval. U.S. Patent No. 4,309,602, 5 January 1982. assigned to EIKONIX Corporation; pp. 1–7. [Google Scholar]
- Anand, A.; Pedrini, G.; Osten, W.; Almoro, P. Wavefront Sensing with Random Amplitude Mask and Phase Retrieval. Opt. Lett. 2007, 32, 1584–1586. [Google Scholar]
- Anishchik, S.V.; Optical, M.D. Microscope with nanometer longitudinal resolution based on a Linnik interferometer. J. Opt. 2024, 26, 115602. [Google Scholar] [CrossRef]
- Rostykus, M.; Soulez, F.; Unser, M.; Moser, C. Compact Lens-less Phase Imager. Opt. Exp. 2017, 25, 4438–4445. [Google Scholar]
- Sanz, M.; Picazo-Bueno, J.A.; García, J.; Micó, V. Improved Quantitative Phase Imaging in Lensless Microscopy by Single-Shot Multi-Wavelength Illumination Using a Fast Convergence Algorithm. Opt. Exp. 2015, 23, 21352–21365. [Google Scholar]
- Li, E.; Liu, Y.; Liu, X.; Zhang, K.; Wang, Z.; Hong, Y.; Yuan, Q.; Huang, W.; Marcelli, A.; Zhu, P.; et al. Phase Retrieval from a Single Near-Field Diffraction Pattern with a Large Fresnel Number. J. Opt. Soc. Am. A 2008, 25, 2651–2658. [Google Scholar]
- Gureyev, T.E. Composite Techniques for Phase Retrieval in the Fresnel Region. Opt. Commun. 2003, 220, 49–58. [Google Scholar]
- Gaur, C.; Baranidharan, M.; Khare, K. Sparsity-assisted Solution to the Twin Image Problem in Phase Retrieval. J. Opt. Soc. Am. A 2015, 32, 1922–1927. [Google Scholar]
- Kamilov, U.S.; Papadopoulos, I.N.; Shoreh, M.H.; Psaltis, D.; Unser, M. Isotropic inverse-problem approach for two-dimensional phase unwrapping. J. Opt. Soc. Am. A 2015, 32, 1092–1100. [Google Scholar]
- Koffi, Y.; Bosson, J.M.; Gnetto, M.I.; Mensah, E.F.; Zoueu, J.T. Multi-height phase recovery combined with Fast Iterative Shrinkage-Thresholding Algorithm to handle phase microspheres from complex diffracted field in inline holography. J. Mod. Opt. 2019, 66, 1763–1776. [Google Scholar]
- Rivenson, Y.; Zhang, Y.; Gunaydin, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light Sci. Appl. 2018, 7, 17141. [Google Scholar] [PubMed]
- Rivenson, Y.; Wu, Y.; Wang, H.; Zhang, Y.; Feizi, A.; Ozcan, A. Sparsity-based multi-height phase recovery in holographic microscopy. Sci. Rep. 2016, 6, 37862. [Google Scholar]
- Butola, M.; Sunaina; Khare, K. Phase retrieval with complexity guidance. J. Opt. Soc. Am. A 2019, 36, 202–211. [Google Scholar]
- Kamilov, U.S.; Papadopoulos, I.N.; Shoreh, M.H.; Goy, A.; Vonesch, C.; Unser, M.; Psaltis, D. Optical tomographic image reconstruction based on beam propagation and sparse regularization. IEEE Trans. Comput. Imaging 2016, 2, 59–70. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm with application to wavelet-based image deblurring. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 693–696. [Google Scholar]
- Nemirovsky, A.S.; Yudin, D.B. Problem Complexity and Method Efficiency in Optimization; Wiley-Interscience Series in Discrete Mathematics; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Nesterov, Y.E. A method for solving the convex programming problem with convergence rate O(1/K2). Dokl. Akad. Nauk SSSR 1983, 269, 543–547. [Google Scholar]
- Latychevskaia, T.; Fink, H.W. Practical Algorithms for Simulation and Reconstruction of Digital In-line Holograms. Appl. Opt. 2015, 54, 2424–2434. [Google Scholar] [PubMed]
- Latychevskaia, T.; Fink, H.W. Reconstruction of Purely Absorbing, Absorbing and Phase Shifting, and Strong Phase-shifting Objects from Their Single-shot In-line Holograms. Appl. Opt. 2015, 54, 3925–3932. [Google Scholar]
- Chen, P.-G.; Lo, T.W.; Lei, D. Breaking the mirror symmetry of photonic spin-orbit interaction using a geometrically symmetric chiral resonator. J. Opt. 2024, 26, 07LT01. [Google Scholar]
- Chambolle, A. An Algorithm for Total Variation Minimization and Applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D 1992, 60, 259–268. [Google Scholar]
- Endo, Y.; Shimobaba, T.; Kakue, T.; Ito, T. GPU accelerated compressive holography. Opt. Express 2016, 24, 8437–8445. [Google Scholar]
- Kamilov, U.S. A Parallel Proximal Algorithm for Anisotropic Total Variation Minimization. IEEE Trans. Image Proc. 2016, 26, 539–548. [Google Scholar]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar]
- Kamilov, U.S.; Bostan, E.; Unser, M. Variational justification of cycle spinning for wavelet based solutions of inverse problems. IEEE Signal Process. Lett. 2014, 21, 1326–1330. [Google Scholar]
- Feinup, J.R. Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Phase retrieval algorithms: A personal tour. Appl. Opt. 2013, 52, 45–56. [Google Scholar]
- Veiras, F.E.; Bianchetti, A.; Etchepareborda, P.; Vadnjal, A.L.; Federico, A. A systematic analysis for the quantitative comparison of phase retrieval methods based on alternating projections. Opt. Lasers Eng. 2018, 106, 24–31. [Google Scholar]
- Luo, S.; Tai, X.-C.; Wang, Y. Convex shape representation with binary labels for image segmentation: Models and fast algorithms. arXiv 2020, arXiv:2002.09600. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Ji, Y.; Xu, Y.; Bu, M.; Chen, Y. 3D morphological reconstruction of the red blood cell based on two phase images. Opt. Appl. 2015, 2, 174–182. [Google Scholar]
- Anand, A.; Chhaniwal, V.K.; Patel, N.R.; Javidi, B. Automatic Identification of Malaria-Infected RBC With Digital Holographic Microscopy Using Correlation Algorithms. IEEE Photonics J. 2012, 4, 1456–1464. [Google Scholar] [CrossRef]
- Koren, G.; Polack, F.; Joyeux, D. Iterative Algorithms for Twin-image Elimination in In-line Holography Using Finite-support Constraints. J. Opt. Soc. Am. A 1993, 10, 423–433. [Google Scholar]
- Agnero, M.A.; Konan, K.; Kossonou, A.T.; Bagui, O.K.; Zoueu, J.T. A New Method to Retrieve the Threedimensional Refractive Index and Specimen Size Using the Transport Intensity Equation, Taking Diffraction into Account. Appl. Sci. 2018, 8, 1649. [Google Scholar] [CrossRef]
- Ivan, D.N.; Christ, D.I. Optical Plastic Refractive Measurement in Visible and Near-infared Regions. Appl. Opt. 2000, 39, 2067–2070. [Google Scholar]
- Yichen, W.; Ozcan, A. Lensless digital holographic microscopy and its applications in biomedicine and environmental monitoring. Methods 2018, 136, 4–16. [Google Scholar]
- Memmolo, P.; Miccio, L.; Merola, F.; Gennari, O.; Netti, P.A.; Ferraro, P. 3D Morpholometry of Red Blood Cells by Digital Holography. ISAC 2014, 85, 1030–1036. [Google Scholar]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-nm to 200-μm Wavelength Region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [PubMed]
- Graeme, W.; Johannes, C. Experimental demonstration of holographic three-dimensional light shaping using a Gerchberg–Saxton algorithm. New J. Phys. 2005, 7, 117. [Google Scholar]
- Fienup, J. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koffi, Y.; Bosson, J.M.; Gnetto, M.I.; Zoueu, J.T. Sparsity-Guided Phase Retrieval to Handle Concave- and Convex-Shaped Specimens in Inline Holography, Taking the Complexity Parameter into Account. Optics 2025, 6, 15. https://doi.org/10.3390/opt6020015
Koffi Y, Bosson JM, Gnetto MI, Zoueu JT. Sparsity-Guided Phase Retrieval to Handle Concave- and Convex-Shaped Specimens in Inline Holography, Taking the Complexity Parameter into Account. Optics. 2025; 6(2):15. https://doi.org/10.3390/opt6020015
Chicago/Turabian StyleKoffi, Yao, Jocelyne M. Bosson, Marius Ipo Gnetto, and Jeremie T. Zoueu. 2025. "Sparsity-Guided Phase Retrieval to Handle Concave- and Convex-Shaped Specimens in Inline Holography, Taking the Complexity Parameter into Account" Optics 6, no. 2: 15. https://doi.org/10.3390/opt6020015
APA StyleKoffi, Y., Bosson, J. M., Gnetto, M. I., & Zoueu, J. T. (2025). Sparsity-Guided Phase Retrieval to Handle Concave- and Convex-Shaped Specimens in Inline Holography, Taking the Complexity Parameter into Account. Optics, 6(2), 15. https://doi.org/10.3390/opt6020015





