An Anti-Noise-Designed Residual Phase Unwrapping Neural Network for Digital Speckle Pattern Interferometry

Abstract

DSPI (Digital Speckle Pattern Interferometry) is a non-destructive optical measurement technique that obtains phase information of an object through phase unwrapping. Traditional phase unwrapping algorithms depend on the quality of the images, which demands preprocessing such as filtering and denoising. Moreover, the unwrapping time is highly influenced by the size of the images. In this study, we proposed a new deep learning-based phase unwrapping algorithm combining the residual network and U-Net network. Additionally, we incorporated an improved SSIM function as the loss function based on camera characteristics. The experimental results demonstrated that the proposed method achieved higher quality in highly noisy phase unwrapping maps compared to traditional algorithms, with SSIM values consistently above 0.98. In addition, we applied image stitching to the network to process maps of various sizes and the unwrapping time remained around 1 s even for larger images. In conclusion, our proposed network is able to achieve efficient and accurate phase unwrapping.

1. Introduction

In laser speckle pattern interferometry, continuous-phase information reflecting the topography of the measured object can be obtained through phase unwrapping technology [1]. In addition, the phase unwrapping technology has also been widely used in digital holography [2], grating fringe projection topography measurement [3], synthetic aperture radar [4], and nuclear magnetic resonance imaging [5].

The traditional unwrapping algorithm increases or decreases the phase by an integer multiple of 2π at the position where the phase mutation occurs to eliminate the discontinuity of the phase. Due to the influence of noise, shadows, and defects on the original image, the actual data processing is very complicated. The current phase unwrapping algorithms are mainly divided into two categories according to different principles: path-independent algorithm (based on the minimum norm method) and path tracking method [6].

When the wrapped phase contains noise, down sampling, or local shading, it can affect the processing results of traditional phase unwrapping algorithms. The minimum norm method is a global algorithm, which minimizes the objective function of the whole graph on the premise that the differential of the wrapped phase is consistent with the local differential of the unwrapped phase. It involves finding the minimum difference between the wrapped phase difference and the partial derivative of the true phase. The mathematical model is shown in Equation (1).

$$min\left(J\right)=\sum _{i=0}^{M-2}\sum _{j=0}^{N-1}{\left({\varnothing }_{i+1,j}-{\varnothing }_{i,j}-{∆}_{i,j}^x\right)}^p+\sum _{i=0}^{M-2}\sum _{j=0}^{N-1}{\left({\varnothing }_{i,j+1}-{\varnothing }_{i,j}-{∆}_{i,j}^y\right)}^p$$

(1)

In Equation (1), ${\varphi }_{i,j}$ is the wrapped phase function; ${\mathsf{\Delta }}_{i,j}^x$ and ${\mathsf{\Delta }}_{i,j}^y$ are the phase differences between adjacent phases in the x and y directions, respectively; p represents the p norm; and i, j correspond to the subscripts of the M × N data point matrix, where 0 ≤ i ≤ M − 1 and 0 ≤ j ≤ M − 1.

The global algorithm needs to calculate the whole image directly and takes a long time. On the contrary, the path tracking algorithm is a partial phase diagram wrapping algorithm. That is, under the condition that the integration result is mainly determined by the starting point and the terminal point and is independent of the path, the wrap phase gradient is integrated. The mathematical model is expressed as Equation (2):

$$\phi \left(r\right)={\int }_c\nabla \phi \cdot dr+\phi \left(r_0\right)$$

(2)

where ∇ represents the gradient, ∇φ is the wrap phase gradient, r₀ is the starting point of the integration, dr means the differential of r, and c is any integration path linking r and r₀.

The idea of the path tracking algorithm is to choose the appropriate unwrapping path to avoid errors caused by areas affected by noise, breakpoints, and shadows from being continuously transmitted along the path. The quality of the phase information obtained by unwrapping depends on the selected integration path. The path selection is mainly divided into Goldstein’s branch-cut algorithm [7], Flynn’s minimum discontinuity algorithm [8], the mask-cut algorithm [9], and the quality-guided algorithm [10].

When the wrapped phase map contains noise or aliasing, the minimum norm method cannot limit the propagation of phase errors caused by the unreliable data points in the space, thereby obtaining incorrect wrapped phase maps, while the path tracking method will encounter integration problems and inconsistent paths. In addition to the spatial method, there are some temporal phase unwrapping methods, which cannot be implemented in a single wrapped phase.

The motivation of deep learning is to construct and simulate the neural network of the human brain for analytical learning, which is a new field of machine learning research. Due to the improvement in computer computing power and data volume, neural networks have begun to shine in various fields. Compared with the traditional unwrapping algorithm, the phase unwrapping algorithm based on deep learning has outstanding performance in noise robustness and solution speed.

In 2000, Schwartzkopf first proposed a multilayer perceptron neural network (25 inputs, 5 hidden units, and 3 outputs) to detect phase jumps [11]. For each pixel in the image, the input of the network is the 5 × 5 pixels around the pixel, and the true phase of the pixel is determined according to its wrapped phase value and the surrounding pixel wrapped phase value. For each input, the network has three outputs. The first output represents the probability that the true phase value of the current pixel is equal to its wrapped phase value plus 2π; the second output represents the probability that the true phase value of the current pixel is equal to its wrapped phase value; the third output represents the probability that the true phase value of the current pixel is equal to its wrapped phase value minus 2π. Finally, the trained neural network successfully solves the phase unwrapping problem of the optical Doppler tomography system.

There was no further research in this area until 2018, when Dardikman proposed an algorithm based on the residual neural network to solve the phase unwrapping problem in the field of interferometric phase microscopy [12]. For many thin objects, where the local spatial gradient in the true phase profile does not exceed the absolute value of the element radian, the true phase can be obtained through various path-based phase unwrapping algorithms. However, such algorithms usually do not work for many optically thick objects with steep phase gradients. Deep learning can learn the characteristics of the input data, and with appropriate training, convolutional neural networks can be used to unwrap more accurately. At the same time, the ResNet architecture has been used to recover the phase object from the original intensity image [13] and the single-axis hologram [14], thereby eliminating the spatial artifacts related to dual images and self-interference.

In April 2019, Spoorthi G.E. proposed PhaseNet based on the SegNet network for phase unwrapping [15]. Since the result obtained in this method is still relatively rough, the author used median filtering to obtain the final result.

In 2020, Spoorthi G.E. improved upon PhaseNet and developed “PhaseNet 2.0” [16]. This method does not require post-processing and overcomes the issues of class imbalance, severe noise, and discontinuity, demonstrating strong robustness. Liu Kai treated the computation of edge orders as a classification problem and utilized a lightweight fully connected neural network [17]. This allowed the training process to be completed within one hour, saving a significant amount of time.

In 2021, Zhang Ziwen combined a convolutional neural network with the fast least squares method to overcome the issue of instability in the accuracy of traditional least squares phase unwrapping algorithms. Wu Zhipeng proposed a convolutional neural network for identifying phase discontinuities, which was combined with the traditional cost-flow method to achieve more accurate phase unwrapping [18].

In 2022, Zhou Lifan proposed a deep learning-based branch cutting deployment method called BCNet [19]. The network has fewer layers, high accuracy, and fast execution speed. Chen Xiaomao proposed a lightweight network that combines two attention mechanisms [20]. This method is characterized by its time efficiency. Sica employed interferometric coherence as the input feature of a convolutional neural network model [21]. This method exhibits robustness even in the presence of high-density residues. Ye Xin investigated a generative adversarial network with a mixed loss function to tackle the problem of missing details in textures [22]. By employing a trained GAN, they preserved texture details and significantly reduced the occurrence of speckle noise in valleys.

In 2023, Yang K. designed a deep learning-based MC deployment network called MCNet, which is also referred to as MCNet-PU for phase unwrapping [23]. MCNet can efficiently and accurately deploy MCs automatically without the need for guidance from quality maps. It is simpler and faster than some existing semantic segmentation networks.

Considering these previous works, we proposed a phase unwrapping neural network that combined the residual block and U-Net network, and we designed a loss function adapted from the SSIM function to measure the error of the output unwrapped image. We believe our network could improve the unwrapping quality without the cost of processing speed.

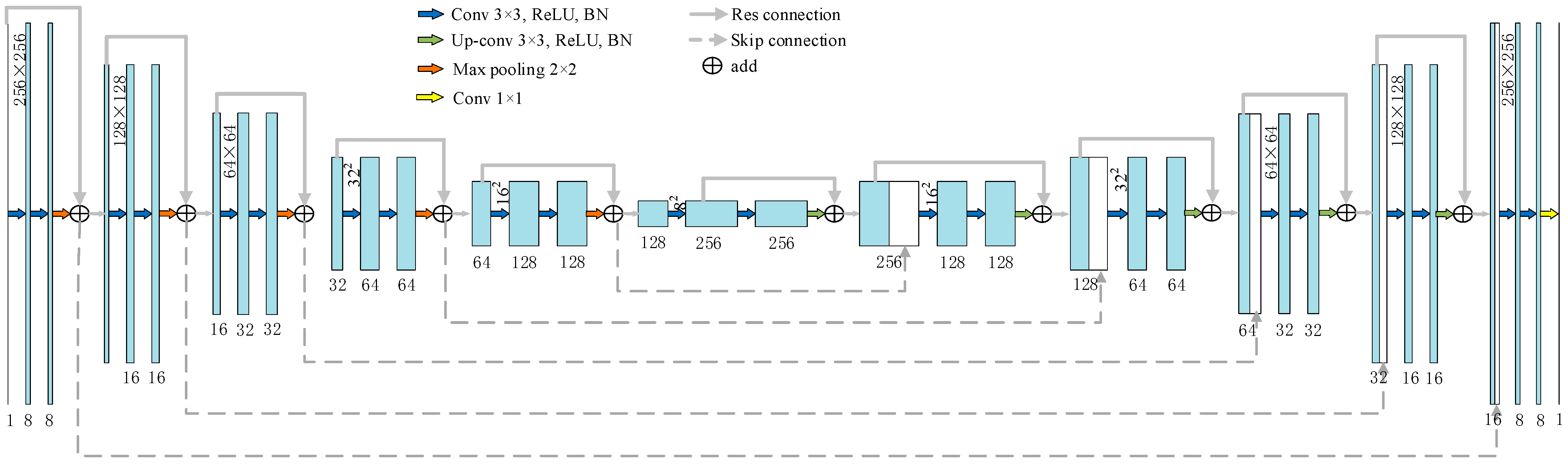
2. Anti-Noise-Designed Residual U-Net Phase Unwrapping Network Design

Phase unwrapping refers to the process of recovering the corresponding phase-unwrapped map from a wrapped phase map. Since the conversion between the wrapped phase map and the phase unwrapping map has a certain regularity, and the convolutional neural network has a strong fitting ability, this paper attempts to apply the method based on the convolutional neural network to solve the phase unwrapping problem. By training the end-to-end network model, the mapping relationship between the wrapped phase map and the phase unwrapping maps can be learned directly.

2.1. Residiual Block

The residual network in the deep network can converge quickly and ensure that the network does not degenerate as the depth increases. Moreover, the difference between the phase unwrapping map and the wrapped phase map has a certain regularity, which is an integer multiple of 2π. The deep residual network is a seemingly simple but extremely effective network structure proposed by Kaiming He in 2015, as shown in the residual block in Figure 1; on the basis of the original ordinary network, there is a shortcut connection between every two layers, H(x) = F(x) + x, constituted by a residual block. Multiple residual blocks are stacked to form a residual network. The practice shows that the deep residual network can improve the performance of the “deep” network effectively.

2.2. U-Net Phase Unwrapping Network

From the network structure of U-net, we could find two main features such as a U-shaped structure and its skip connection. The deeper the network layer, the larger the field of vision of the feature map. The shallow convolution focuses on texture features, and the deep network focuses on the essential features; therefore, the whole network could acquire different level features. In addition, the edges of the larger feature map obtained by deconvolution are lacking in information, as downsampling inevitably loses some edge features and cannot be retrieved from the upsampling. In order to reduce the loss of spatial information caused by the downsampling process, a layer jumping connection is introduced. Through concatenation, the feature map restored by upsampling contains more low-level semantic information, which leads to a better level of detail in the results. Therefore, the edge feature can be retrieved through the splicing of features.

2.3. Neural Network Architecture

It can be seen from U-net that adding jump connections can increase the depth and improve the accuracy of deep CNNs. We add the skip connection to the model, as shown by the gray dashed line in Figure 2 [24]. For each convolution block, the equation for the skip link is y = F(x) + H(x), where F contains two convolution operations and a max pooling or an upsampling operation, and H is either the same mapping or a convolution operation such that the input has the same feature dimension as F.

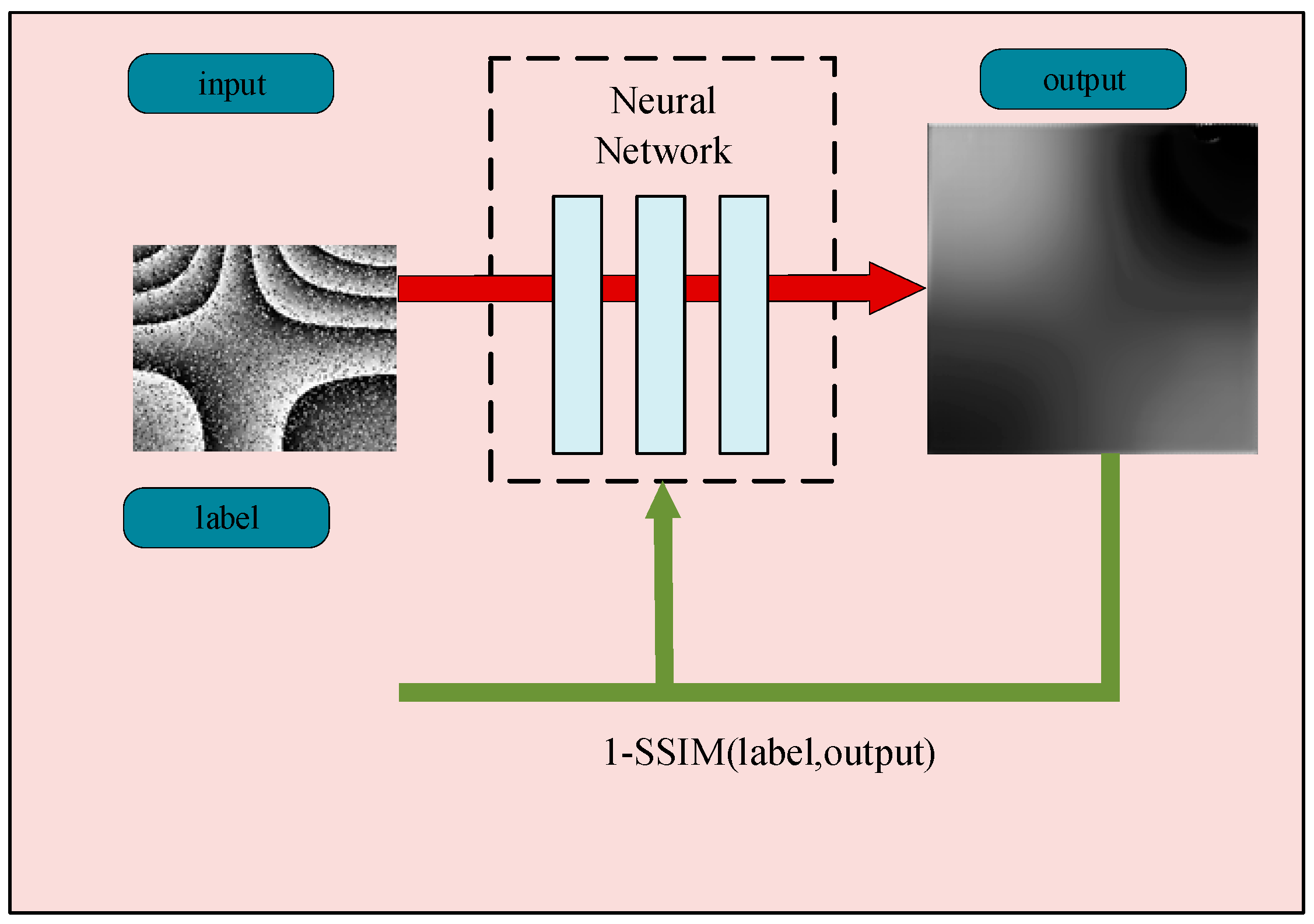
2.4. SSIM Loss Function

Loss functions are used to encourage and discourage certain behaviors. In deep learning, if it is a classification problem, loss functions such as cross-entropy, softmax, and SVM can be used. If it is a regression problem, the cost function generally adopts L2 or L1.

L2 (Euclidean distance between the true value and the predicted value) is non-convex and derivable. L2 is used on the premise of a noisy Gaussian distribution, which is able to suppress large errors but has a relatively poor suppression effect on small errors. For example, using L2 can reproduce the edges well, but it cannot eliminate those small noises well. Most importantly, L2 is different from the human visual system (HVS). HVS is heavily sensitive to local information such as light and color changes, and the light sensitivity of cameras made by humans is based on HVS.

The structural similarity index (SSIM) [25] is used to measure the structural similarity between two images. Just like the HVS, the SSIM is sensitive to local structural changes and is derivable. Even when white noise, contrast enhancement, and mean shifting are applied to the image, SSIM does not change significantly.

The SSIM function consists of three parts: illumination, contrast, and structure.

$$l\left(x,y\right)=\frac{2u_x{u}_y+c_1}{{u_x}^2+{u_y}^2+c_1}$$

(3)

$$c\left(x,y\right)=\frac{2{\sigma }_x{\sigma }_y+c_2}{{{\sigma }_x}^2+{{\sigma }_y}^2+c_2}$$

(4)

$$s\left(x,y\right)=\frac{{\sigma }_{xy}+c_3}{{\sigma }_x{\sigma }_y+c_3}$$

(5)

$$SSIM\left(x,y\right)={\left[l\left(x,y\right)\right]}^{\alpha }{\left[c\left(x,y\right)\right]}^{\beta }{\left[s\left(x,y\right)\right]}^{\gamma }$$

(6)

In Equation (6), α, β, γ > 0 to avoid the systematic error caused by the denominator of 0, and c₁, c₂, c₃ are constants. Generally, α = β = γ = 1 and c₃ = c₂/2. The function F is expressed as

$$SSIM\left(x,y\right)=\frac{\left(2u_x{u}_y+c_1\right)\left(2{\sigma }_x{\sigma }_y+c_2\right)}{\left({u_x}^2+{u_y}^2+c_1\right)\left({{\sigma }_x}^2+{{\sigma }_y}^2+c_2\right)}$$

(7)

where $u_x$, $u_y$, ${\sigma }_x$, ${\sigma }_y$, and ${\sigma }_{xy}$ represent the mean and variance of image x, the mean and variance of y, and the covariance of image x and image y, respectively, and $c_1={\left(k_{1}L\right)}^2$ and $c_2={\left(k_{2}L\right)}^2$ are constants. The default k₁ = 0.01 and k₂ = 0.03. L is the dynamic range of the pixel value; for example, the L value of an 8-bit depth image is 255.

The larger the SSIM value, the more similar the images are. As a loss function, loss = 1 − SSIM is used. Since Pytorch implements the forward calculation part of SSIM-loss, there is no need to consider the derivation mechanism.

3. Dataset Establishment, Network Training, and Enhancement

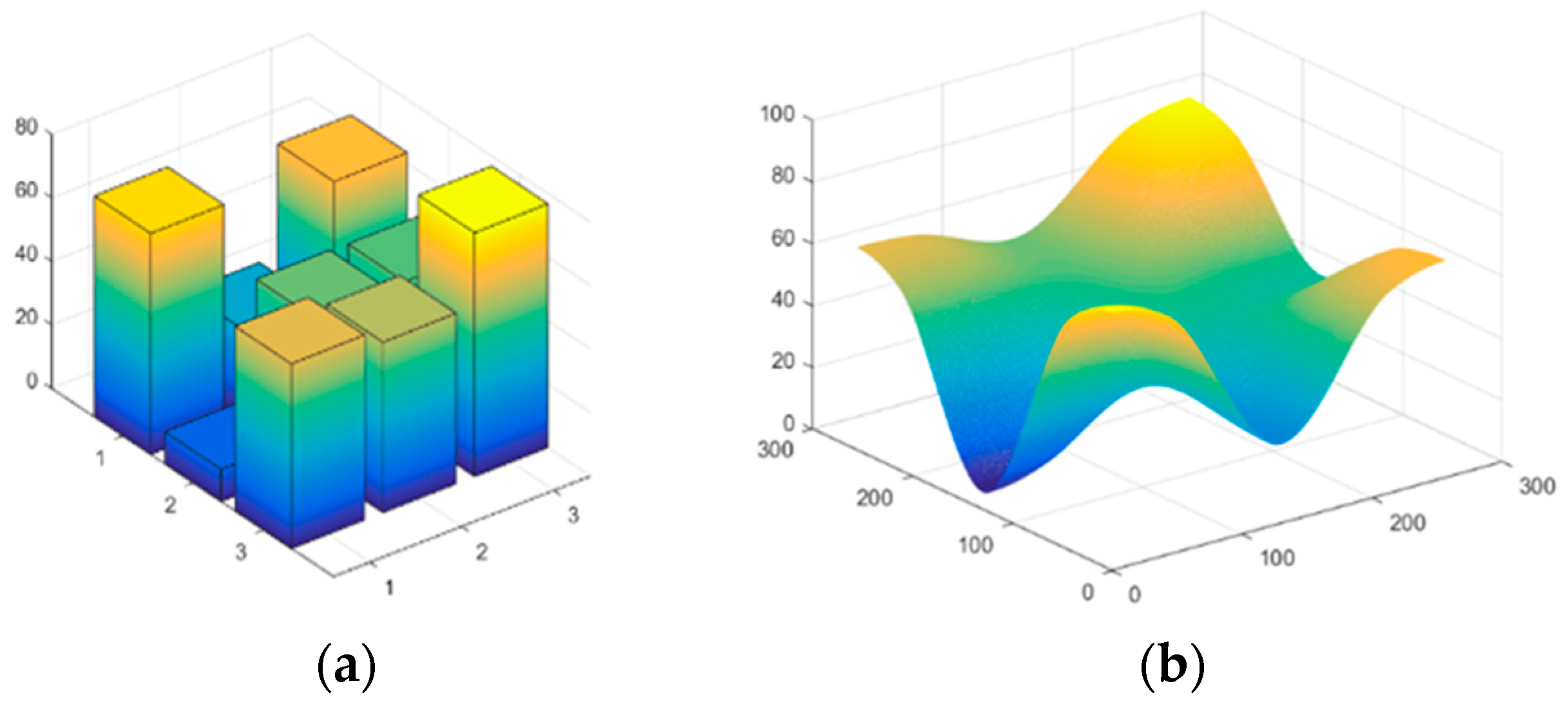
3.1. Dataset Establishment

The phase map can be generated in two steps [26]. The first step is the generation of an initial matrix, with a size ranging from 2 × 2 pixels to 4 × 4 pixels. The size of the initial matrix determines the number and location of the extreme points in the final real phase. The range of values (ranging from 2 to 100) of the initial matrix determines the gradient of the final real phase. And the distribution type of the values is a Gaussian-distributed random matrix. The second step involves transforming the matrix into a 256 × 256 matrix through bicubic interpolation. The distribution type of the initial matrix and the interpolation method determine the distribution of the final real phase. Figure 3 shows an example of a real phase generation process. In this experiment, 40,000 sets of images were generated, which were divided into the training image set and validation image set in a ratio of 9:1. Then, noise with a random magnitude (one of Gaussian noise, salt-and-pepper noise, or multiplicative noise) was added to the wrapped phase map of the training image set.

3.2. Network Implementation Details, Tables, and Schemes

The network architecture is implemented using the Pytorch framework version 1.8.0 based on Python 3.6.6. We performed the network training and testing on a PC with a Core (TM) i9-10850K CPU @ 3.60 GHz and 64 GB of RAM, using an NVIDIA GeForce RTX 3090 GPU.

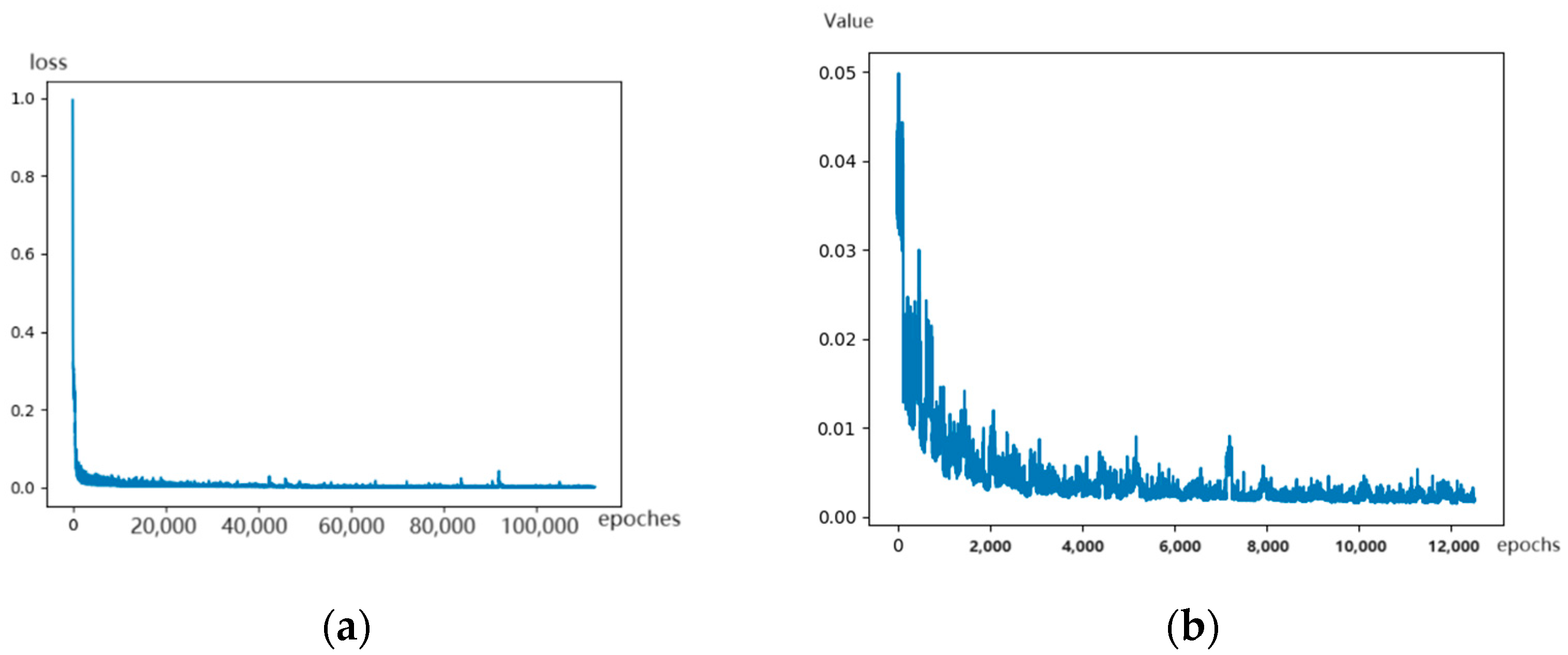
3.3. Network Training Process

As shown in Figure 4, during the training process, the simulated wrapped phase images were fed into the neural network to calculate the outputs. The outputs were then compared with the corresponding ground truth phase images using a loss function, and the parameters and weights of the neural network were updated through backpropagation. The whole process was repeated until the loss function value reached the expected effect and the neural network reached convergence.

This paper used 36,000 noisy wrapped phase maps as the input of the network, and the corresponding real phase maps were used as real values for network training. In the network training process, the Adam optimization strategy was used, the learning rate was 0.001, the batch size was 32, and the 1-SSIM function was used as the loss function. The loss function of the whole training and validation sets is shown in Figure 5 below. It can be seen that the parameters of the network are close to convergence.

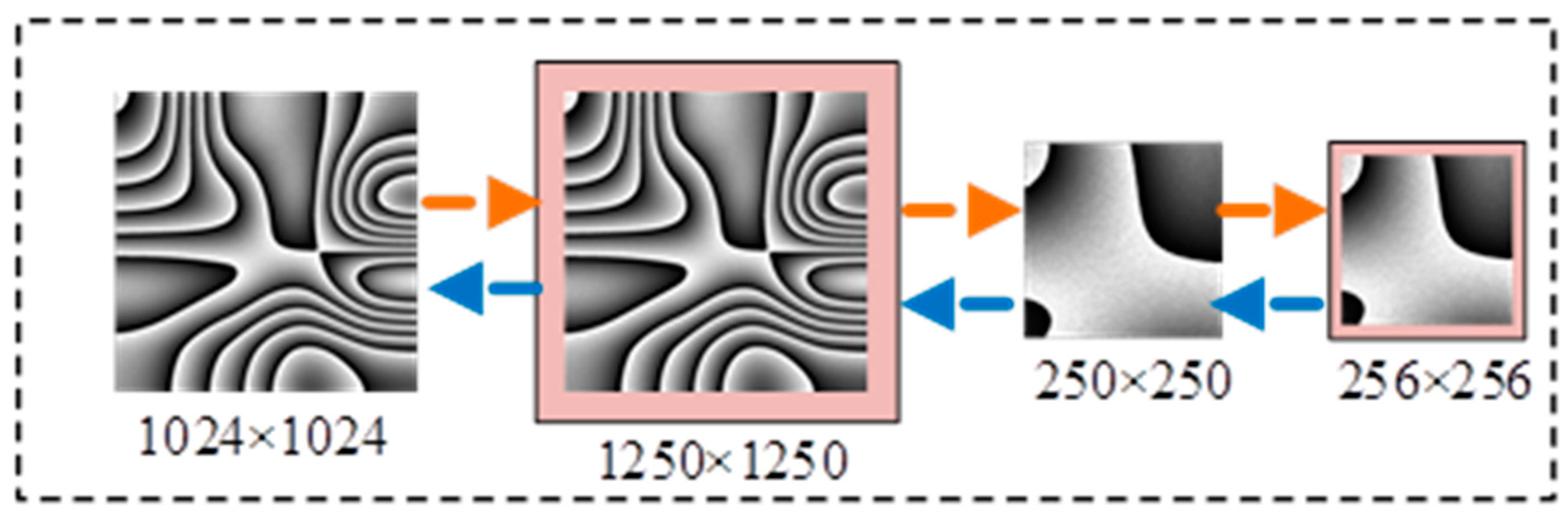
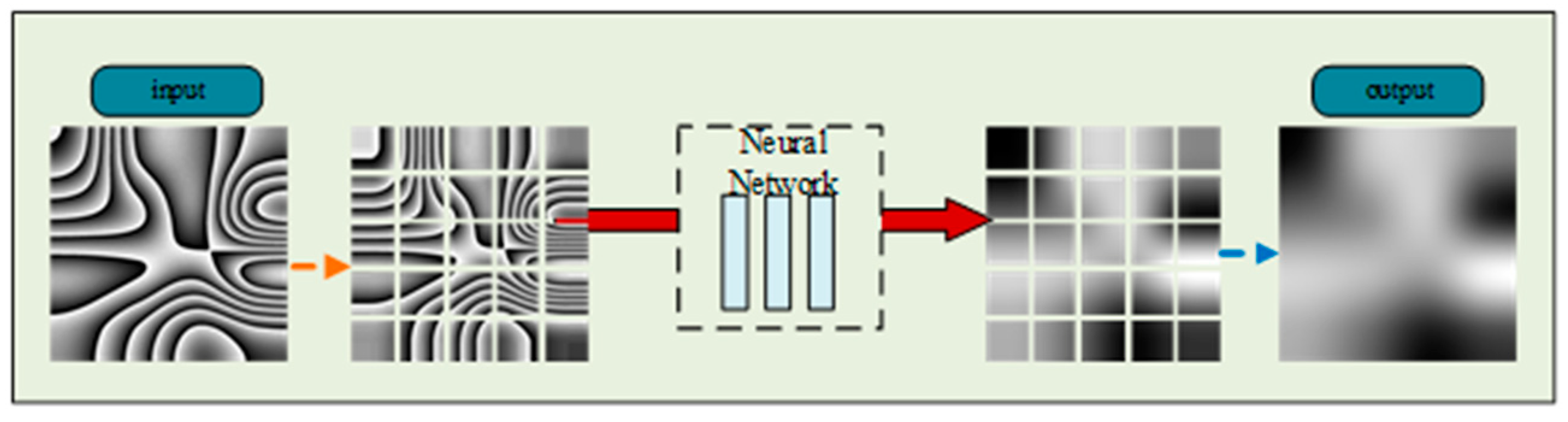
3.4. Image Stitching Function Design

After the training procedure, the network could handle phase maps of arbitrary size, but the unwrapping effect becomes worse as the size of the phase map deviates from 256. Generally, the common methods are downsampling for handling phase maps of larger sizes, as well as interpolation for smaller sizes. But if the fringes of the phase map are dense, downsampling will affect the fringe definition as fringes could disappear. In addition, the network is trained on specific image sizes of 256 × 256, which means that the trained network is the optimal solution under the condition. When the test image size is different from the training size, the network is fixed and may not be the optimal solution for other sizes. This can affect the network’s ability to extract features, and thus it impacts the quality of phase unwrapping.

To make the network have a wider adaptability to the size of the phase map, there are two measures to solve this problem: the image stitching technique or the use of larger-size phase maps to train neural networks. However, considering factors such as the GPU memory and training speed of large-size phase maps, this paper suggests that an algorithm based on phase unwrapping map stitching would be more suitable to deal with this problem.

As shown in Figure 6, this section uses a wrapped phase map with a size of 1024 × 1024 pixels to verify the phase unwrapping based on image stitching. First, the wrapped phase map is expanded by edge replication so that its edge length is t times 250, t = min(250 × t − 1024 ≤ 250); then, it is partitioned into t × t small images of size 250 × 250 pixels. Next, each small image is expanded to 256 × 256 by edge replication and input into the neural network to be unwrapped separately. Finally, each small image is merged by inverse operation and restored to the size of 1024 × 1024 to obtain the final unwrapping result. The schematic diagram of the testing process is shown in Figure 7.

4. Experimental Results and Analysis

To test the network’s effectiveness, simulation data and experimental data of phase maps are adopted to represent the ideal and actual state of phase image acquisition, respectively. The results and related analysis are shown as follows:

4.1. Image Results of Simulation and Experimental Data Testing

As shown in Figure 8a,b, two sets of randomly selected photos from the test dataset are depicted. In set Figure 8a, the top image represents real phase maps with added Gaussian noise, while the bottom image represents the corresponding wrapped phase maps. In set Figure 8b, the top image displays real phase maps with added salt-and-pepper noise, with the bottom images representing the corresponding wrapped phase maps.

The results of direct unwrapping of the wrapped phase map with noise are shown in Figure 9, in which Figure 9a is the wrapped phase map generated by the simulation with noise added. Figure 9b–d report the results of phase unwrapping by the proposed method, the spiral path algorithm, and the reliability-guided algorithm, respectively.

After Gaussian filtering is performed at the top of Figure 10a, and after average filtering is performed at the bottom of Figure 10a, the unwrapping result is shown in Figure 10, where Figure 10a is the wrapped phase map generated by the simulation after denoising; Figure 10b–d, respectively, represent the phase unwrapping results of the algorithm based on the method in this paper, the spiral path algorithm, and the algorithm based on reliability.

Unlike the simulation, the phase map obtained from speckle pattern interferometry often contains a lot of noise, so the anti-noise performance is an important basis for the selection of the unwrapping algorithm. Because the size of the dataset in this paper is 256 × 256, in order to obtain better results, the phase map obtained by the speckle pattern interferometer is downsampled to 256 × 256.

Figure 11a is the wrapped phase map obtained by the speckle pattern interferometer, where Figure 11b–d are the effects after unwrapping by the algorithm based on the spiral path, the algorithm based on reliability, and the Res-unet, respectively.

Figure 12a depicts the wrapped phase map obtained from the speckle interferometer after applying a denoising technique, where Figure 12b–d are the effects after unwrapping by the algorithm based on the spiral path, the algorithm based on reliability, and the Res-unet, respectively.

4.2. Result Analysis and Effectiveness Verification

Apart from the image results presented above, the average unwrapping time and SSIM test were performed to verify the effectiveness of the proposed method. The unwrapping time is shown in

Table 1. Average unwrapping time of different phase unwrapping algorithms (unit: s).

Unwrapping Method	256 × 256	512 × 512	1024 × 1024
Algorithm based on spiral path	0.21	0.24	0.4237
Algorithm based on reliability	0.31	6.5	74.84
Res-unet	1.087	1.085	1.169

.

It can be seen from Table 1 that the algorithm based on reliability guidance has the longest unwrapping time, followed by the algorithm based on the spiral path. The unwrapping time of these two algorithms increases significantly with the increase in image size, and the unwrapping time is proportional to the size of the map to be unwrapped. The unwrapping time of this method for three sizes of images is about 1 s, which is almost not affected by the image size.

From the data in

Table 2. SSIM value between results of different unwrapping algorithms and the unwrapped phase.

Unwrapping Method	Figure 8a	Figure 8a after Denoising	Figure 8b	Figure 8b after Denoising
Algorithm based on spiral path	0.3069	0.8933	0.4237	0.9312
Algorithm based on reliability	0.5947	0.9797	0.8499	0.9828
Res-unet	0.9876	0.9876	0.9932	0.9936

, we can clearly find that, when unwrapping the wrapped phase maps with a lot of noise, the effects of the algorithm based on the spiral path and the algorithm based on reliability are quite unsatisfactory. After denoising the images, the effect is greatly improved. The Res-unet network has maintained this high level of unwrapping.

To summarize, the experimental results indicate that the unwrapping time of the Res-unet network is independent of the size of the phase map, with an average unwrapping time of about 1 s. Moreover, the unwrapping quality is not affected by the quality of the original phase map. Even if the original phase map contains a large amount of noise, this algorithm can still achieve a high level of unwrapping quality. So, the Res-unet network achieved a good time and precision effectiveness.

5. Conclusions and Discussion

Considering the reality that the unwrapping quality of phase images is affected by the original image quality, and also that the unwrapping time is influenced by the size of the original image, we proposed a neural network for phase unwrapping whose architecture combines residual networks and U-Net networks. We also designed a loss function based on the SSIM function and applied it to the network to improve its precision. Additionally, we adopted the image stitching method to improve the adaptability to the size of the phase maps, instead of training the network with larger image datasets or downsampling the image.

After training the network and testing it with simulation and experimental data, the results indicate that our network not only has strong noise suppression capabilities but also better processing performance regardless of the image size compared with the other two traditional unwrapping algorithms based on the spiral path and reliability.

However, there are still improvements that could be made in our study. For example, the dataset for training the network consists of simulated random speckle patterns. Although the network could study the relationship between wrapped and unwrapped images well, the dataset could be improved further by simulating it from an optical propagation perspective, to make it more closely follow the principles of speckle interferometry and experimental conditions. Furthermore, other neural network models such as GANs and GNNs can be adopted to explore the possibility of better phase unwrapping quality or speed.