Temporal Cavity Soliton Interaction in Passively Mode-Locked Semiconductor Lasers
Abstract
1. Introduction
2. Model Equations
3. Temporal Cavity Soliton
4. Interaction Equations
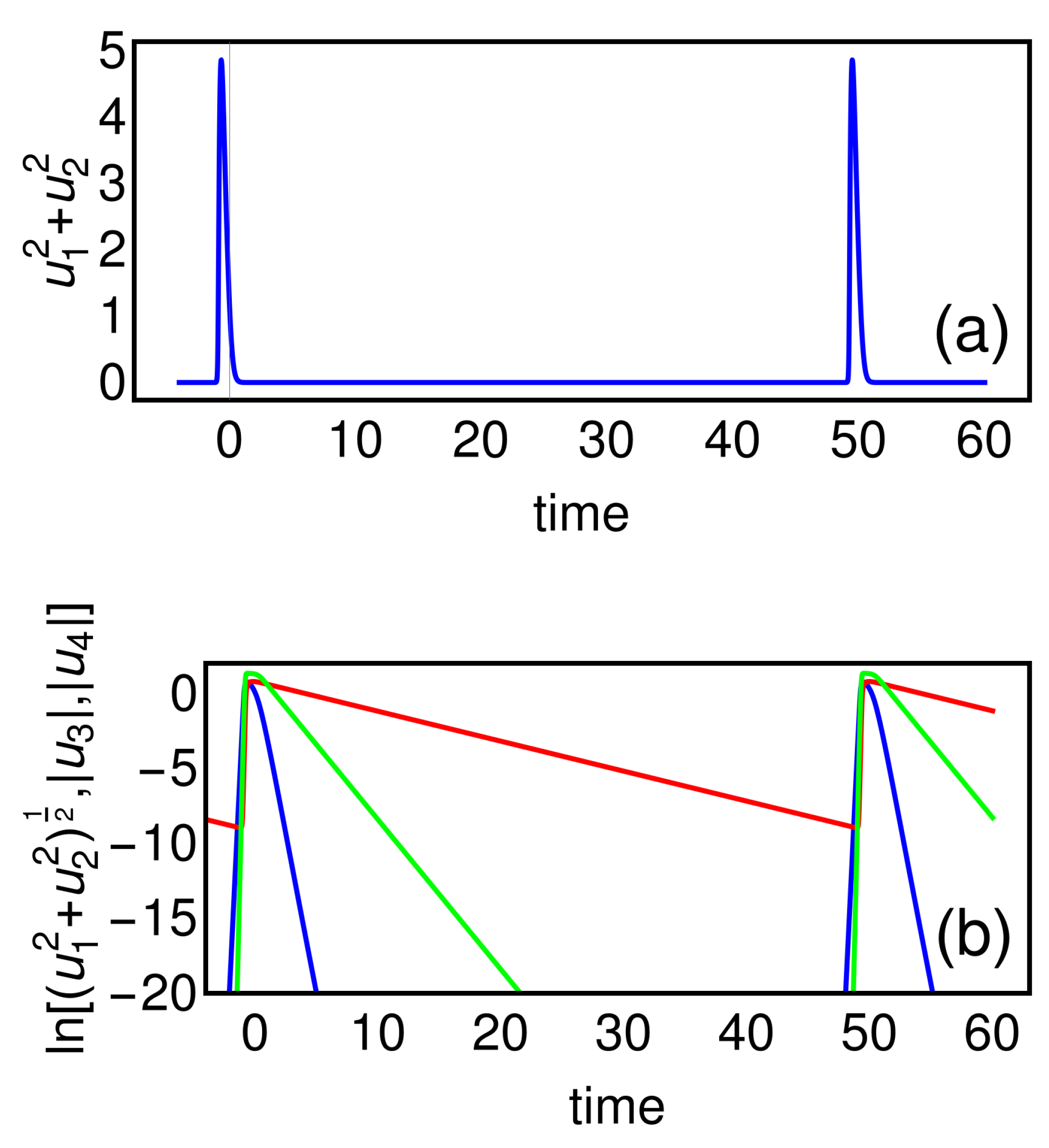
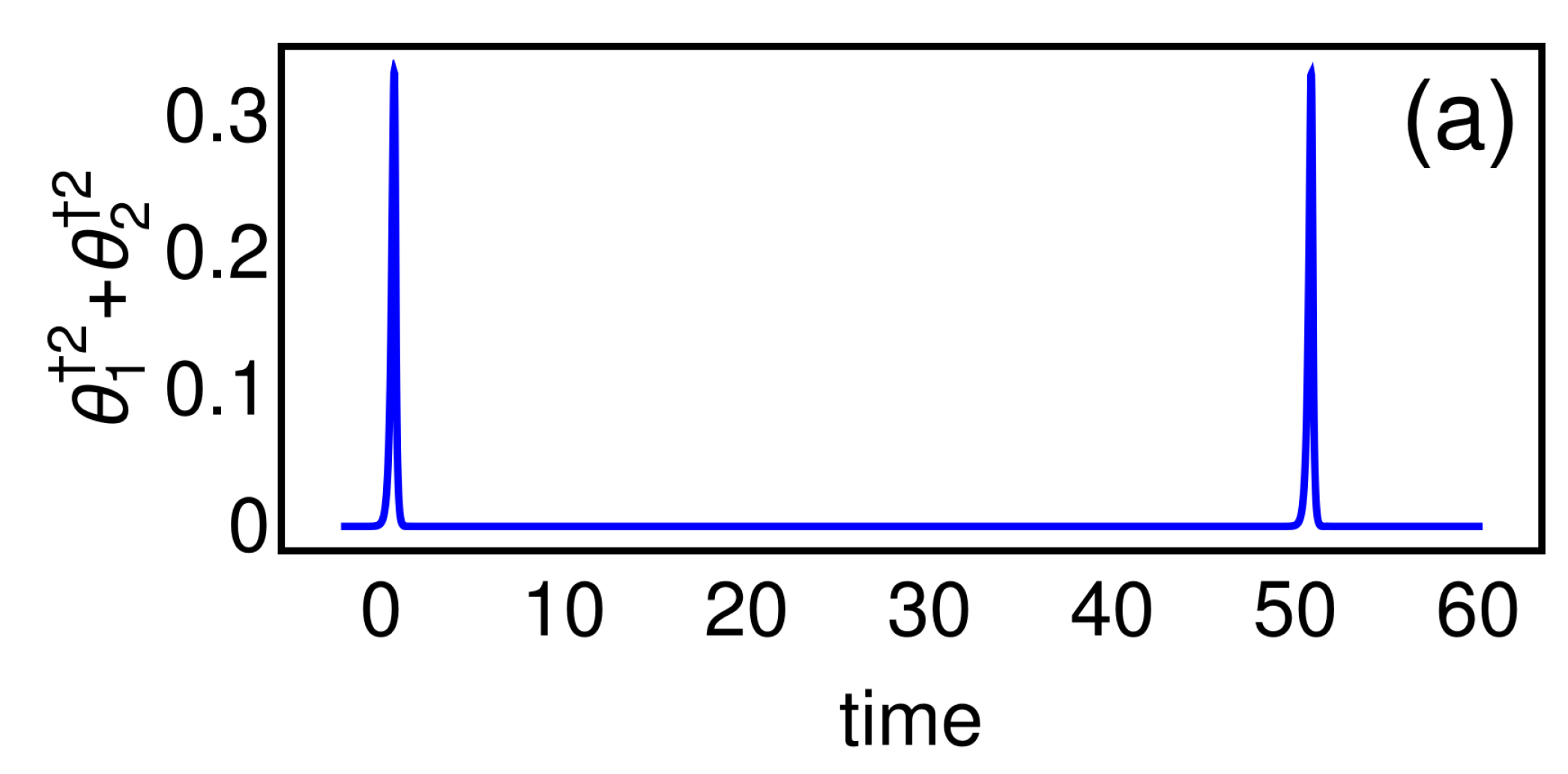
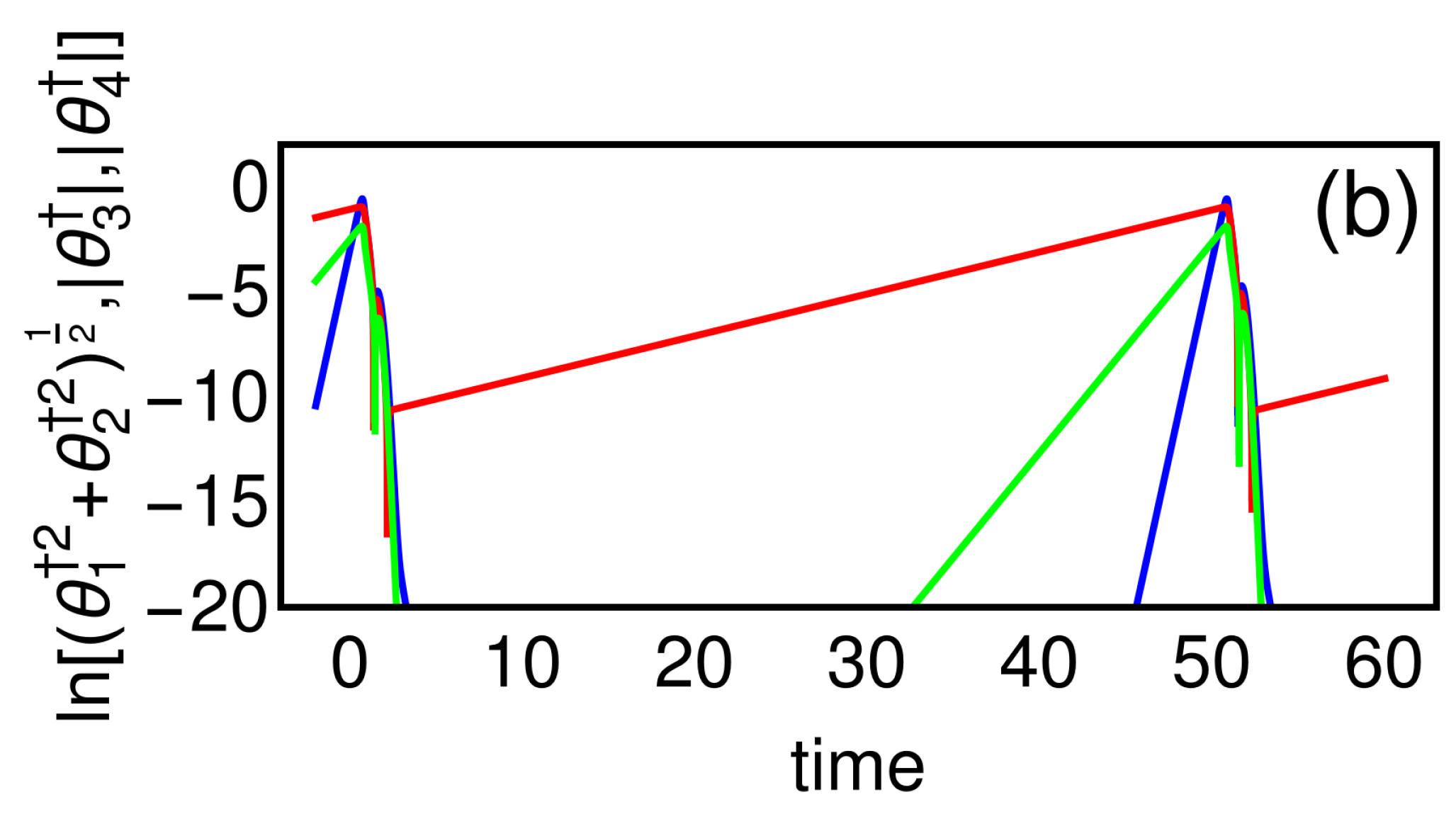
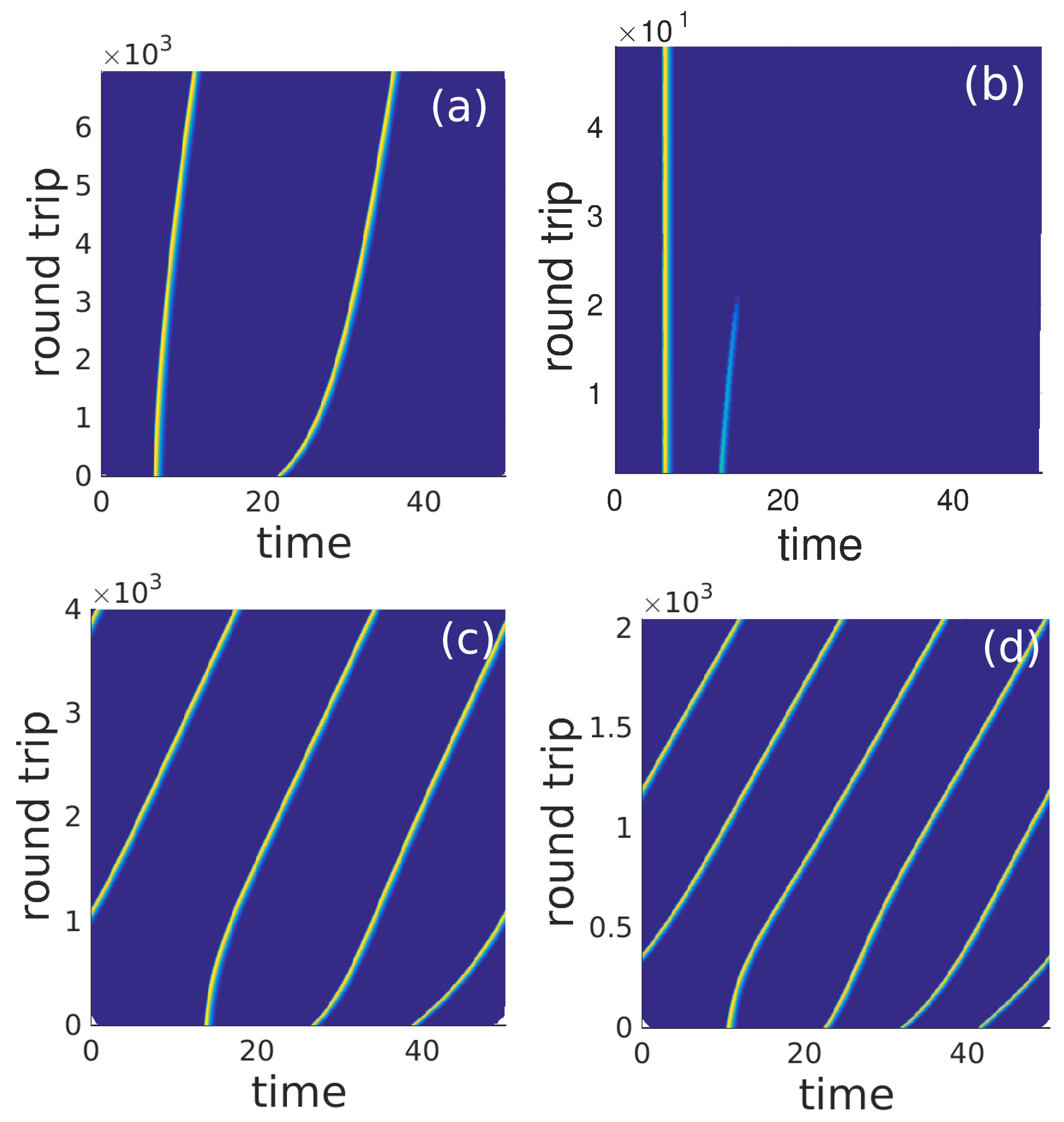
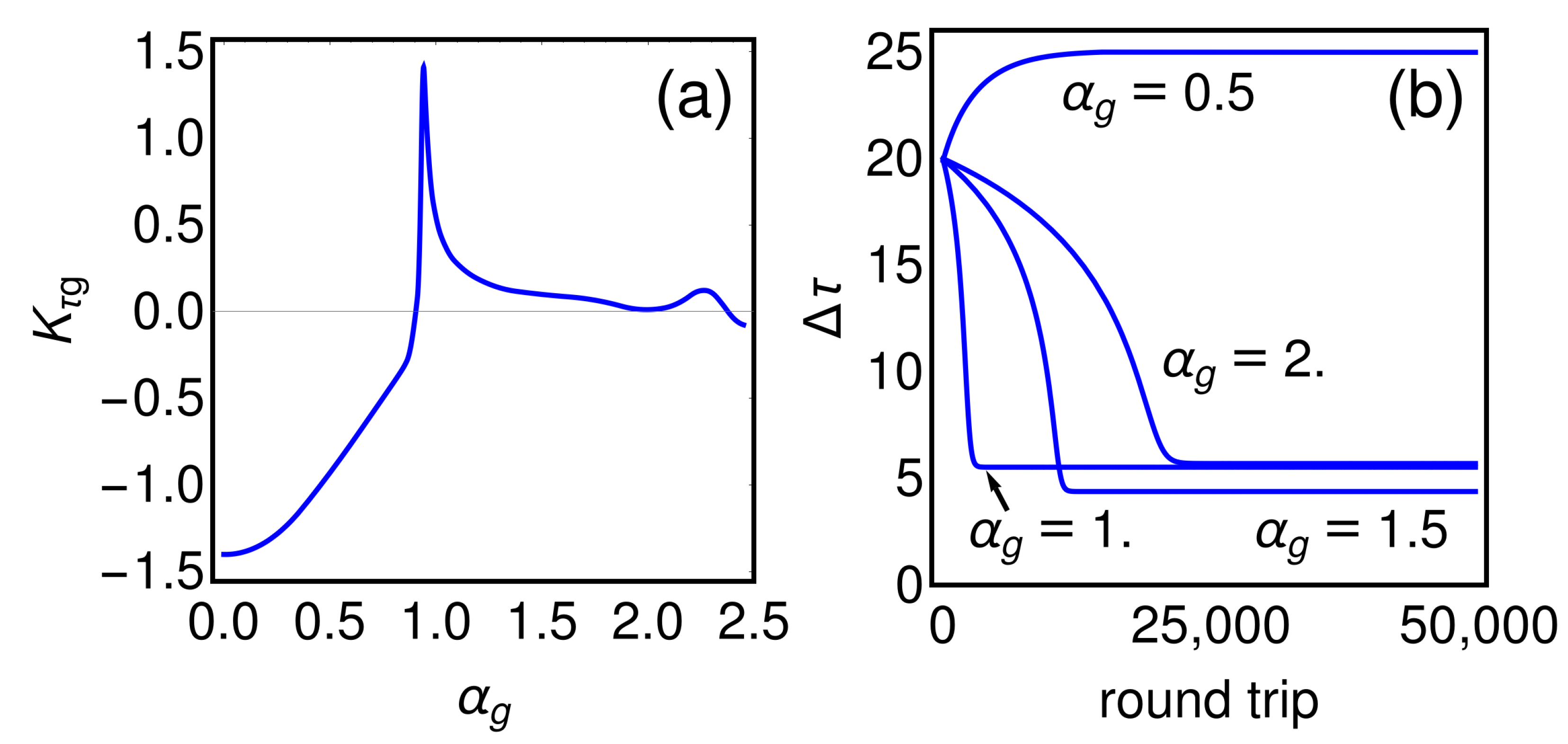
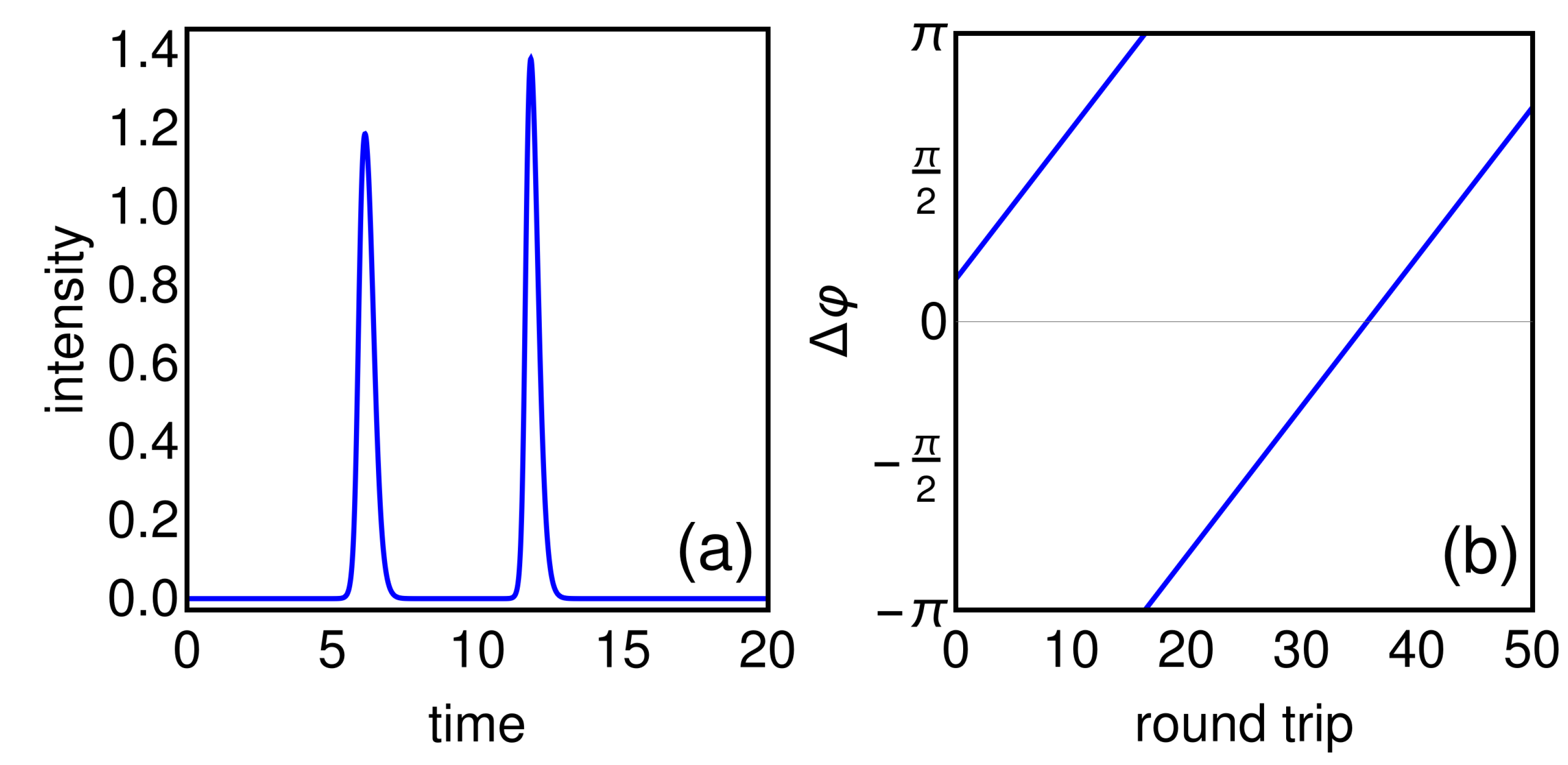
5. Results of Numerical Simulations
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Interaction Equations
References
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, 6402. [Google Scholar] [CrossRef]
- Marconi, M.; Javaloyes, J.; Balle, S.; Giudici, M. How lasing localized structures evolve out of passive mode locking. Phys. Rev. Lett. 2014, 112, 223901. [Google Scholar] [CrossRef]
- Rosanov, N.; Khodova, G. Diffractive autosolitons in nonlinear interferometers. J. Opt. Soc. Am. B 1990, 7, 1057–1065. [Google Scholar] [CrossRef]
- Malomed, B.A. Bound states of envelope solitons. Phys. Rev. E 1993, 47, 2874. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J. Multisoliton solutions of the complex Ginzburg-Landau equation. Phys. Rev. Lett. 1997, 79, 4047. [Google Scholar] [CrossRef]
- Akhmediev, N.; Rodrigues, A.S.; Town, G.E. Interaction of dual-frequency pulses in passively mode-locked lasers. Opt. Commun. 2001, 187, 419–426. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Khodova, G.V.; Rosanov, N.N. Stable bound states of one-dimensional autosolitons in a bistable laser. Phys. Rev. E 2001, 63, 056607. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Horikis, T.P.; Nixon, S.D. Soliton strings and interactions in mode-locked lasers. Opt. Commun. 2009, 282, 4127–4135. [Google Scholar] [CrossRef]
- Kutz, J.N.; Collings, B.; Bergman, K.; Knox, W. Stabilized pulse spacing in soliton lasers due to gain depletion and recovery. IEEE J. Quantum Electron. 1998, 34, 1749–1757. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Akhmediev, N.N. Multisoliton regime of pulse generation by lasers passively mode locked with a slow saturable absorber. J. Opt. Soc. Am. B 1999, 16, 674–677. [Google Scholar] [CrossRef]
- Nizette, M.; Rachinskii, D.; Vladimirov, A.; Wolfrum, M. Pulse interaction via gain and loss dynamics in passive mode locking. Phys. D 2006, 218, 95–104. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Grelu, P.; Lederer, F. Impact of slow gain dynamics on soliton molecules in mode-locked fiber lasers. Opt. Lett. 2012, 37, 175–177. [Google Scholar] [CrossRef]
- Camelin, P.; Javaloyes, J.; Marconi, M.; Giudici, M. Electrical addressing and temporal tweezing of localized pulses in passively-mode-locked semiconductor lasers. Phys. Rev. A 2016, 94, 063854. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Turaev, D. Model for passive mode locking in semiconductor lasers. Phys. Rev. A 2005, 72, 033808. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Turaev, D.; Kozyreff, G. Delay differential equations for mode-locked semiconductor lasers. Opt. Lett. 2004, 29, 1221–1223. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Turaev, D. New model for mode-locking in semiconductor lasers. Radiophys. Quant. Electron. 2004, 47, 857–865. [Google Scholar] [CrossRef]
- Puzyrev, D.; Vladimirov, A.G.; Pimenov, A.; Gurevich, S.V.; Yanchuk, S. Bound pulse trains in arrays of coupled spatially extended dynamical systems. Phys. Rev. Lett. 2017, 119, 163901. [Google Scholar] [CrossRef] [PubMed]
- Munsberg, L.; Javaloyes, J.; Gurevich, S.V. Topological localized states in the time delayed Adler model: Bifurcation analysis and interaction law. Chaos 2020, 30, 063137. [Google Scholar] [CrossRef]
- Vladimirov, A.G. Short-and long-range temporal cavity soliton interaction in delay models of mode-locked lasers. Phys. Rev. E 2022, 105, 044207. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Kovalev, A.V.; Viktorov, E.A.; Rebrova, N.; Huyet, G. Dynamics of a class-A nonlinear mirror mode-locked laser. Phys. Rev. E 2019, 100, 012216. [Google Scholar] [CrossRef] [PubMed]
- Yanchuk, S.; Ruschel, S.; Sieber, J.; Wolfrum, M. Temporal dissipative solitons in time-delay feedback systems. Phys. Rev. Lett. 2019, 123, 053901. [Google Scholar] [CrossRef] [PubMed]
- Stöhr, M.; Wolfrum, M. Temporal dissipative solitons in the Morris–Lecar model with time-delayed feedback. Chaos 2023, 33, 023117. [Google Scholar] [CrossRef]
- Turaev, D.; Vladimirov, A.G.; Zelik, S. Long-range interaction and synchronization of oscillating dissipative solitons. Phys. Rev. Lett. 2012, 108, 263906. [Google Scholar] [CrossRef] [PubMed]
- Vladimirov, A.G.; Gurevich, S.V.; Tlidi, M. Effect of Cherenkov radiation on localized-state interaction. Phys. Rev. A 2018, 97, 013816. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Tlidi, M.; Taki, M. Dissipative soliton interaction in Kerr resonators with high-order dispersion. Phys. Rev. A 2021, 103, 063505. [Google Scholar] [CrossRef]
- Guglielmi, N.; Hairer, E. Implementing Radau IIA methods for stiff delay differential equations. Computing 2001, 67, 1–12. [Google Scholar] [CrossRef]
- Kokhanovskiy, A.; Kuprikov, E.; Kobtsev, S. Single-and multi-soliton generation in figure-eight mode-locked fibre laser with two active media. Opt. Laser Technol. 2020, 131, 106422. [Google Scholar] [CrossRef]
- Halanay, A. Differential Equations: Stability, Oscillations, Time Lags; Academic Press: New York, NY, USA, 1966; Volume 23. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladimirov, A.G. Temporal Cavity Soliton Interaction in Passively Mode-Locked Semiconductor Lasers. Optics 2023, 4, 433-446. https://doi.org/10.3390/opt4030031
Vladimirov AG. Temporal Cavity Soliton Interaction in Passively Mode-Locked Semiconductor Lasers. Optics. 2023; 4(3):433-446. https://doi.org/10.3390/opt4030031
Chicago/Turabian StyleVladimirov, Andrei G. 2023. "Temporal Cavity Soliton Interaction in Passively Mode-Locked Semiconductor Lasers" Optics 4, no. 3: 433-446. https://doi.org/10.3390/opt4030031
APA StyleVladimirov, A. G. (2023). Temporal Cavity Soliton Interaction in Passively Mode-Locked Semiconductor Lasers. Optics, 4(3), 433-446. https://doi.org/10.3390/opt4030031





