Abstract
Visible Light Communication (VLC) has gained popularity in research and business in the last decade. This technology aims to combine lighting and communication into a single device. For now, this technology has been thoroughly studied for an indoor environment, but it is sufficiently mature nowadays to consider its outdoor-environment potentials. The key outdoor challenges are the weather variabilities and smoke particles in cities due to pollution or fires. The aim of this is the study and quantification of the weather and smoke particles’ impact on a short-range optical communication thanks to a simulator. This article’s novelty is the inclusion of the effects of smoke in a short-range outdoor VLC system channel model. This smoke model, which comes from the fire engineering field, states that smoke attenuation is independent of the wavelength, starting from high visibility to 5 m. The visibility represents the distance up to which an object can be distinguished against the background. The effects of fog and smoke are studied in the case of two outdoor VLC scenarios. Smoke and fog models have analogous equations to express the optical attenuation they induce, using the visibility concept. Taking into account the actual light-emitting diode (LED) lamp radiation pattern, the simulator computes the power at the receiver side and the channel attenuation coefficients for a given fog or/and smoke outdoor setting. The main result drawn in this paper is that the channel attenuation levels due to fog and smoke are both in the same order of magnitude, starting from the visibility of about 1 km. The attenuation induced by fog is higher under this threshold of 1 km.
1. Introduction
In an era where everything is going digital, it is crucial to find new ways to exchange data to avoid a possible spectrum crunch [1,2]. In the scope of smart cities, the main concern is outdoor urban connectivity. With 5G on the way, it is necessary to find other telecommunication technologies to complement its offer. As 5G represents a set of technologies, Optical Wireless Communication (OWC), the family of communication technologies that use visible, infrared, and ultraviolet spectrums to transmit data, can be an excellent candidate to complement its offer [2,3]. Ultraviolet communication (UVC) is not studied for smart city applications for safety reasons. When visible light is used to communicate, it is named Visible Light Communication (VLC). This technology offers the advantage of being compliant with light-emitting diode (LED) lighting, which is being increasingly deployed in the streets. VLC upgrades the existing streetlight infrastructure without being too invasive. It combines both roles of communicating and lighting, which reduces the system’s overall power consumption. Furthermore, VLC is progressively gaining interest in research and business [4,5]. As the name suggests, VLC uses the visible range of the electromagnetic spectrum to deliver data through light thanks to light-emitting diodes (LEDs). This technology has been widely studied for indoor use cases because it is believed to be the most promising sector for now. Nevertheless, it is highly relevant to pursue this research in the outdoor VLC scenario as more and more urban lights are becoming LED-based. Indeed, applications such as urban Li-Fi (which stands for Light Fidelity, the high data rate application of VLC), VLC positioning systems, VLC-IoT (Internet of Things), and V2V (Vehicle-to-Vehicle) or V2I (Vehicle-to-Infrastructure) make VLC an interesting candidate for outdoor short-range connectivity [6,7,8]. In those listed application cases, short-range refers to communication links up to a few meters away, as opposed to Free Space Optics (FSO) communication technology which often uses infrared LASER light for long-range communications over a few kilometers [9].
To assess the performances of VLC telecommunication systems, the emitter’s, and receiver’s characteristics as well as propagation conditions of the optical signal must be known. The VLC equipment usually contains an RGB (Red Green Blue) LED emitter with reference peak wavelengths of 630, 530, and 475 nm, respectively, and generally a photodiode receiver. Depending on the environment in which the system is deployed, the optical signal may be more or less impacted. Indeed, whether it is indoors or outdoors, the attenuation and the disturbance on the signal are different. The primary impactors on outdoor VLC equipment, which increase the medium’s total attenuation, are mainly the weather variability and the interactions between the light wave and particles in the atmosphere. These particles include dust, fog, and the possible presence of smoke due to fire or pollutants. These interactions cause phenomena such as scattering and absorption (cf. Section 2). A third effect to consider is the reflection of the optical signal on certain surfaces.
Studying these impacts can be realized in several ways, such as system modeling, making small scale or real scale experiments, and simulations. Modeling is easy once that the emitter, the receiver, and the channel are known. The emitters and receivers are studied through their electronic models [10]. Several elements must be taken into account in the transmission channel, like the setup (the emitter’s location compared to the receiver), the presence of potential obstacles, and meteorological conditions [4]. The downside of modeling is the analytical nature of the study. For experimental studies, the advantage is that the system is the closest to real-life scenarios. On the other hand, all the conditions and equipment are not always available. Performing simulations with access to the communication system’s parameters removes the deterministic part of modeling but controls the environment a little more than real scenarios. This creates good compromise between modeling and experiments. In the case of simulations, as in the present paper, to be closer to field experiments/measurements, it is essential to consider the phenomena and equipment’s natural properties.
The impacts of atmospheric effects on optical communication have already been studied in the scope of FSO communication, which is a long-range LASER-based communication system. The effects studied in the literature are foggy conditions [11,12,13,14]. The main models developed from that field of research have been applied to VLC communication mainly for V2V or V2I scenarios simulations to assess its performance [15,16]. Another paper focusing on performance metrics in the presence of rain and snow in V2V and V2I uses a new set of rain and snow models taken from measurements [17]. These models’ disadvantage is that they were developed for FSO and have never been applied to VLC in practice. Other papers are focusing on outdoor VLC present experimental results on such systems’ feasibility in sunny conditions [18,19]. Fewer papers studied the impact of smoke on optical free-space communication. To the best of our knowledge, only two papers have presented experimental studies in controlled smoke environments [12,20]. The first paper is for FSO applications and the second one for VLC applications. The present paper differentiates itself from them by proposing a simulation tool to assess the isolated or joined effects of fog and smoke. This simulator’s novelty is complemented by a smoke model taken from the fire engineering domain and designed explicitly for LED communication. Table A1 in Appendix A summarizes the main papers found in the literature that studies the impact of atmospheric effects on wireless optical communications and highlights our contribution in bold.
In the present paper, a simulator developed in Python integrates the VLC equipment properties as well as fog and smoke models taken from references in the scientific literature. The models of the emitter, the receiver, and the communication channel are taken from the scientific literature focusing on VLCs. To estimate the impact of outdoor disturbances such as fog and smoke, fog modeling and fire engineering models were studied and integrated into the simulator [21,22].
After the study of each VLC telecommunication component, and the fog and smoke models, a validation process was carried out on each of these elements separately to attest to the conformity of the simulator. The validation process included the generation of figures from the simulator compared to reference figures from the literature.
The present work proposes a methodology that assesses fog and smoke’s impact on a VLC system thanks to a simulator. Two scenarios that could be found in an urban area were defined and studied to narrow the study of their impacts. The first one is a VLC system deployed at a bus shelter, and the second one is a streetlight attached to a wall. The spatial light distribution of the lamp is a key parameter in this simulation. This parameter, also called the radiation pattern, is often assumed to be Lambertian in the literature whatever the LED source is [4,10]. In practice, if a single LED is considered, this approximation is still valid [6,23,24]. However, off-the-shelf LED streetlamps contains several LEDs and complex optical equipment that transform the radiation pattern. So, the approximation does not apply anymore. The radiation pattern of an actual streetlamp was taken from a manufacturer’s database for the second scenario (cf. Section 4) to be as close to reality as possible in this paper [25]. The simulator then computes these systems’ limits thanks to the power margin available when there is fog and or smoke.
2. Theoretical Background
This chapter presents an overview of the theoretical background necessary to understand the models (VLC channel model, weather model, and smoke model) used in the simulations.
2.1. Visible Light Communication Channel Model
This section explains how the path loss (equivalent in a transmission context to the signal loss) is computed considering each element of the telecommunication system’s different characteristics. The optical power received, , in a line-of-sight (LoS) configuration is computed as follows [4,10]:
where is the power transmitted by the source and is the DC channel gain used in this context. Indeed, in pure LoS, the channel is supposed to be flat, so . Therefore, the signal spectrum is not altered by the VLC LoS channel over the entire signal bandwidth [26]. encompasses the characteristics of the medium: an ideal case including only an emitter and a receiver, their respective characteristics, and the distance d between them. In Equation (1), the channel gain is inversely proportional to the square of the distance between the devices. The quantity represents how the optical power emitted by the source is distributed per unit of solid angle. is the elevation angle defined on the negative to positive z-axis, and is the azimuth angle defined in the x–y plane. Most of the time, it is assumed that an LED presents a generalized Lambertian radiation pattern but that approximation is not accurate for all LEDs, especially streetlights [27]. is the surface of the photodiode, and is the inclination between the emitter and the receiver. In Equation (1), the parameter represents the optical gain of the photodetector that has a field-of-view angle, <π/2, and a concentrating lens on top with a refractive index, . The equation linking these three parameters is Equation (2):
In a non-LoS (nLoS) configuration, the contribution of the light reflected by the walls and reaching the receiver must also be considered. Depending on the properties of the reflecting surface, the optical reflection can be diffuse, specular, or both. Several reflection models exist, such as Lambertian and Phong models [28]. Diffuse reflection is considered in the Python simulator.
The resulting power received is the sum of each reflected light ray. Those rays’ phases are not considered because LEDs generate incoherent light, which does not create constructive or destructive interferences.
Equation (3) cumulates the added contributions where k is the number of walls (including ceiling and floor depending on the setup) considered in the room, is the reflection coefficient of the wall. The distances and are defined in Figure 1; is the channel DC gain’s value at the previous computation step. As the first reflection is the predominant power contribution, only the first reflection on any surface (k = 1) is taken into account in the simulator [10].
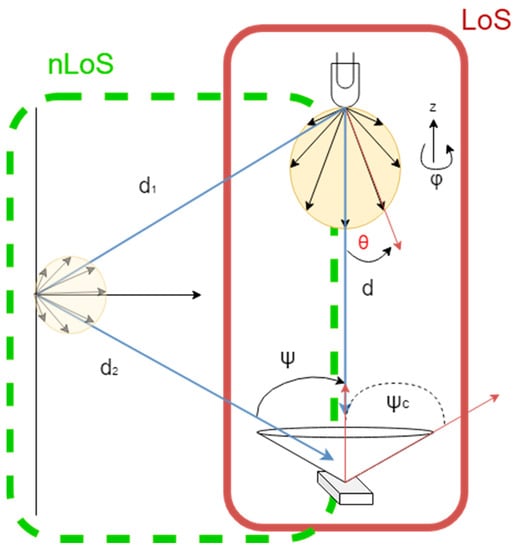
Figure 1.
Line-of-sight (LoS) and non-LoS (nLoS) (case of single reflection) configurations.
2.2. Atmospheric and Smoke Particle Theory
When a light beam travels through air, it undergoes a natural attenuation due to the distance and the power spreading of the light wave due to propagation. Solar irradiance and artificial light induce an increase of noise at the receiver side, but they are not considered in the present paper [29,30]. In outdoor environments, light waves are prone to an additional attenuation by interacting with atmospheric particles found in fog, rain, and smoke. The two main phenomena involved with the atmospheric particles are absorption and scattering by air molecules and solid- or liquid-suspended particles found in the atmosphere. Absorption takes place when the atmospheric particles transform the incident radiant energy into other forms of energy. On the other hand, scattering is the re-radiation in all directions (sometimes with a preferred direction) of the incident light wave by the atmospheric particles [31,32]. Beer–Lambert’s law can express these in Equation (4), where is the total optical attenuation coefficient in km−1, 𝑃r is the received power, 𝑃t the transmitted power, and L is the distance between the emitter and the receiver [9,24].
Equation (5) expresses the different atmospheric loss contributions with and being the absorption and scattering coefficients for both molecular (ml index) and aerosol (al index), respectively.
In this paper, the computation of the attenuation coefficient already considers the absorption and scattering effects. A global attenuation is computed for the atmospheric particles of fog and smoke particles. The total attenuation from Equation (4) becomes the following:
A and K are the attenuation coefficient due to foggy conditions () and the optical attenuation coefficient due to smoke (). Both are presented in the following sections. It is worthwhile noting that the terms ‘optical attenuation coefficient’ and ‘attenuation coefficient’ represent the same variable, with ‘optical attenuation’ being commonly used in the fire engineering domain.
2.2.1. Atmospheric Attenuation
The attenuation coefficient due to atmospheric particles is computed thanks to the visibility parameter. Visibility, , is the distance to an object where the image’s distinction drops to a certain percentage of what the object would be like if it were nearby, typically 2 to 5% [33]. Visibility is typically measured at 550 nm, corresponding to the maximum intensity of the solar spectrum. It is noticeable that, in the case of this paper, the RGB LED light described in Section 1 has to be used. A clear sky has higher visibility than a thick fog. This parameter is used to compute the signal attenuation due to foggy weather, thanks to Kim’s model [34]:
is the attenuation coefficient given in km−1, is the wavelength in nm, and is the particle size-related coefficient, which weights the wavelength contribution depending on the weather condition [10].
Figure 2 illustrates the relationship between the visibility and the attenuation coefficient in dB/km. This is thanks to Kim’s model from Equation (7) for an RGB (red green blue) LED with peak wavelengths of 630, 530, and 475 nm, respectively. It is intuitive to conclude that, the clearer the sky, the smaller the attenuation coefficient is. This model has been widely used in Free Space Optics (FSO) communication links where the distances are in the order of several kilometers. Nevertheless, this model has also been applied in V2V and V2I applications to assess their performance under foggy conditions [15,16]. In the present use-cases, the distances are much shorter as we are in outdoor VLC applications. It can also be observed that the attenuation levels are nearly the same for each wavelength.

Figure 2.
Attenuation coefficient for weather conditions for the three reference wavelengths of an RGB light-emitting diode (LED) light, following Kim’s definition.
2.2.2. Smoke Attenuation
In fire engineering, some laser tools are using the optical properties of smoke to compute the density of smokes produced from a given fuel. Indeed, the relationship between the optical attenuation coefficient, in m−1, and the smoke density, , in g/m³, is established thanks to Bouguer’s law found in Equation (8). The intensity, I, of a single wavelength light beam passing through smoke with a distance, L, is proportional to the light intensity at :
Bouguer’s law also known as Beer–Lambert’s law (cf. Equation (9)), states that there is a link between the optical attenuation coefficient, , the volumetric concentration of a given environment and its optical properties summarised in . The latter parameter is the light extinction coefficient (or, depending on the references, specific extinction coefficient or mass-specific extinction coefficient) in m²/g. In this case, the environment is described by the particles building up the smoke [22]. It is important to note that the optical attenuation coefficient, , considers the smoke’s scattering and absorption effects at once.
The light extinction coefficient is inversely proportional to the wavelength as shown in Equation (10) [35,36,37]. It is believed to be the same for a given type of combustion. In smokes generated by flaming fires, the suggested value for is 8.7 m²/g with an uncertainty of +/−0.2 m²/g for a wavelength of 632.8 nm [38]. In this paper, an RGB LED with peak wavelengths of 630, 530, and 475 nm is used for the transmitter. These wavelengths lead to 8.54, 10.15, and 11.32 m²/g, respectively, for . units assume that light’s attenuation is proportional to the projected area (m²) of particles blocking the beam, which is then normalized by the mass of burned fuel [39].
Studies recommend using the smoke yield or smoke conversion factor, ε, which represents the ratio of smoke produced divided by the amount of fuel burned, to compute the mass concentration or mass density of smoke in fires [22,40]. The computation of the smoke concentration can then be determined by Equation (11), where is the mass of fuel in grams, and is the volume in m³.
The smoke conversion factor is not the same for all fuels. This has been studied and measured for different types of fuel in Reference [22].
Like in the case of fog (cf. Section 2.2.1), there is a relationship between smoke density and the visibility of an object. The theory described here and applied for the first time in this paper to the case of outdoor VLC transmissions was initially developed in emergency indoor evacuation plans to determine if a person inside a building could sufficiently see an exit sign through the smoke. This explains the definition of visibility as the distance a person could see an exit sign through a layer of smoke. Equations (12) and (13) present the relationship between visibility and the attenuation coefficient when the object is powered and emits light () and when it is only a reflecting sign (), respectively. is the visibility computed in meters, and K is the optical attenuation coefficient found in Equation (8) [41,42].
One can note that the visibility, , is inversely proportional to the smoke density, as the thicker the smoke, the lower the visibility. As a reminder, Equation (12) states that the attenuation coefficient is directly proportional to the smoke density. The scale of visibility is not the same as in the previous case of weather conditions. Here, meters are used as opposed to kilometers, as in Equation (7). Visibility of at least 13 m is needed for a safe escape when someone is unfamiliar with the building. When someone is familiar with the place, 2 m are enough, as suggested in Reference [42].
The tricky part about computing the attenuation coefficient due to smoke is the smoke mass concentration knowledge. Indeed, this parameter depends on environmental factors and the fuel burning. The parameter , presented in Equation (11), is the link between the amount of burned fuel, and the amount of produced smoke. A table of the smoke conversion factor of some fuels is available in Reference [22]. Table 1 presents a filtered version of this original reference table where only flaming and smoldering smoke conditions are considered. In the field of combustion, there are several types of flaming conditions. In the reference table, smoldering, flaming, and pyrolysis are considered. smoldering refers to a slow flameless form of combustion that produces smoke. Pyrolysis is the thermal decomposition of a material in an inert medium with very high temperature and flaming is when there is a flame when the fuel is burning [22]. In Table 1, the flaming and smoldering types of combustion are kept as they would be the most encountered in an outdoor environment instead of pyrolysis.

Table 1.
Different fuels and their smoke conversion factor, ε, in flaming and smoldering fire conditions.
The fuel polyoxymethylene has a smoke conversion factor of 0, meaning that it does not produce smoke while burning. So, it will not be considered in further calculations.
For a fixed volume of 3 × 3 × 3 m³, it is interesting to observe the smoke concentration increase effect on the average values of the optical attenuation coefficient due to smoke for each fuel, as shown in Figure 3 and Figure 4. In the case of fuels characterized with a range of values (e.g., Douglas fir with ), a draw from a normal distribution ()) is made every time a figure is generated. The mean of the distribution is the mean value of the smoke conversion factor (), and the standard deviation, , is the standard deviation function in Python.

Figure 3.
Attenuation coefficient for different types of fuel in 1/m.

Figure 4.
Attenuation coefficient for different types of fuel in dB/m.
Figure 3 depicts the attenuation coefficient due to smoke from fuels presented in Table 1 in m−1 by using Equations (9)–(11). The figure was computed for a mass of fuel m ranging from 0.001 to 32 g. This mass represents a concentration of smoke going up to 175 mg/m³, just as in the reference figures from [43]. The graph’s upper limit is roughly between 1.4 and 1.92 m−1, representing visibility of about 2.09 to 1.57 m (by using Equation (13)) if one tries to see a reflective sign through the smoke.
The fuels have the same behavior when the concentration of smoke increases, the optical attenuation values roughly range from 0 to 2 m−1 for a smoke concentration ranging from 0 to 175 mg/m³. It represents an attenuation computed in dB/m ranging from 0 to 8 dB/m. The linear behavior of all the smokes, despite their different smoke conversion factor, enables us to generalize smoke behavior without considering the precise fuel that generated the smoke. The constant nature of can also explain this for different fuels and wavelength burning in well-ventilated mode.
Figure 3 and Figure 4 represent the smoke attenuation coefficient depending on the smoke concentration in m−1 and dB/m, respectively, for the nine fuels studied from Table 1. The representation of the smoke attenuation in m−1 is used in fire engineering instead of dB/m, which is used in telecommunication engineering. It is interesting to note that Equations (12) and (13) state that the attenuation independent of the emitter’s wavelength. Considering that, Figure 3 and Figure 4 show that the discrepancy between the red and blue components is not significant in low smoke concentration and is thus in line with the Equations (12) and (13). Starting from around 100 mg/m³, a gap between each wavelength is noticeable. This gap of 1.3 dB, at 100 mg/m³, corresponds to a visibility gap of 87 cm between the blue and red components. The blue component being the most attenuated one.
The mean visibility at 100 mg/m³ is around 3 m. For higher visibilities, thus lower smoke concentration, the attenuation will be lower and independent from the wavelength. This study focuses on a visibility from 5 to 100 m, which corresponds to attenuation coefficients of 0.6 to 0.03 m−1 (Equation (13)), so the wavelength dependency can be neglected.
2.2.3. Comparison of Attenuation Levels
An analogy can be drawn between the attenuation equations for smoke and fog. Figure 5 highlights this analogy by calculating the optical attenuation as a function of visibility for both phenomena. To assess a telecommunication link, it is conventional to compute the channel attenuation in decibels per unit of length. Equations (7) and (13) are therefore converted to present Figure 5. The attenuation coefficients for fog and smoke are computed for visibility going from 50 m to 50 km for a mean wavelength of 545 nm. Equation (13), which is the visibility for a non-light-emitting sign, is used because it is assumed that the receiver does not emit light.
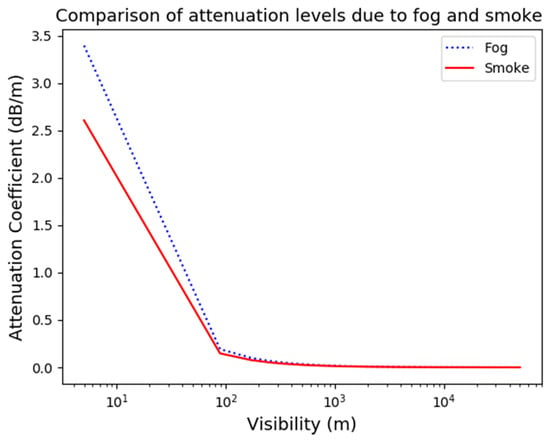
Figure 5.
Attenuation levels for fog and smoke for poor visibility from 50 m to 50 km for a mean wavelength of 545 nm.
When the visibility is low, the attenuation due to fog is more potent than that of smoke. It is understandable given the equations. Indeed, the wavelength dependency of the attenuation stops under 500 m and reduces the fog attenuation (Equation (7)) to 3.91/ (m) compared to 3/ (m) for smoke (cf. Equation (13)). When the visibility increases, starting around 1 km, the graphs tend towards nearly the same value.
In this paper, two outdoor scenarios are studied under fog and/or smoke conditions. In both scenarios, the communication range is small, going from around 2 m to about 6 m. In this frame, Figure 5 shows that for good visibilities, estimated of about 1 to 50 km and more, the attenuation levels can be neglected. Indeed, the graph platoons at around 0.1 to 0.2 dB/m in that visibility range, giving attenuations coefficients of 0.2 to 1.2 dB in the scenarios considered, which is negligible. Nevertheless, in longer-distance communications, such as car-to-car communication, the communication link can be up to around 75 m [44]. This implies attenuation levels of 7.5 to 15 dB, which have much higher impact on the communication link in that visibility range. Smaller attenuation ranges are studied in this work in Section 4.
3. Materials and Methods
The material used in this paper is a communication channel simulator developed in Python. Initially, this simulator was inspired by the MATLAB version that is available in Reference [10]. Our enhanced Python version introduces new parameters of the simulation and graphic representations and flexibility in defining of the parameters of the simulation ‘room’ but takes also into account actual lamp radiation patterns. Several models exist to compute the communication channel, and this chapter gives an overview of these different techniques before laying out the methodology used in the present paper.
3.1. State of the Art of Channel Modeling Techniques
Initially, the first channel model for indoor wireless optical communication systems was defined for infrared systems in 1979 by Reference [45]. Since then, researchers have generalized this concept to visible light. Several techniques exist to evaluate the communication channel of VLC technology and their characteristics are summarized in Table 2. The Barry recursive algorithm is the most famous [46]. It is also the one assumed in the MATLAB reference and used in the present work. The emitter is supposed Lambertian, and the reflection of light rays on a wall is computed geometrically, assuming that the point where the reflection occurred is itself a point source. Barry’s algorithm has the drawback of being deterministic and speculates that the reflection on the walls is specular even though some materials could have a diffuse reflection.

Table 2.
State-of-the-art of existing tools to compute channel impulse response of Visible Light Communication (VLC) systems.
OptiSystem (from Optiwave design system) is a software used to model optical wireless communication systems [47]. This software is based on Barry’s algorithm and models the emitter as a generalized Lambertian emitter and the receiver thanks to its optical characteristics. One of the parameters is the number of reflections considered. It is often used to evaluate a system’s performance in terms of optical power received and SNR. For example, the software enables the computation of the channel impulse response, the channel power distribution, and eye diagram of a Li-Fi communication. The downside is that it is proprietary software.
Another channel modeling technique replaces the geometric reflection (specular assumption) by using ray tracing algorithms. Monte Carlo methods are used to estimate the channel impulse response. Researchers often employ Zemax software to simulate the 3D room and its Ray Tracing algorithm [48].
Afterward, a simulator using 3D CAD (Computer Aided Design) models was developed [49]. They went further by adding reflection phenomena that change the wavelength such as fluorescence (light emission due to the absorption of photons from an incoming electromagnetic wave), phosphorescence (light emission even after being enlightened) or iridescence (property of some surfaces that appear to have different colors depending on the viewing angle). It uses a modified Monte Carlo algorithm to have the most realistic indoor channel modeling algorithm.
To conclude, most of the works for channel modeling focus on indoor environments as these are currently the most promising commercial application for VLC equipment manufacturers [50]. Our current simulator is developed in Python to make it open, flexible, and modular. Its characteristics are inspired by those proposed in MATLAB and OptiSystem from Table 2. The newly added key features are the possibility of using an actual radiation pattern of a real LED streetlight, the possibility to add or remove walls in the space considered, the walls can have different reflection coefficients (not necessarily uniform). On top of that, the computation of the outdoor environment disturbances, such as weather conditions, and smoke influence on the received optical power is done.
3.2. Methodology Used to Develop and Assess the Python Simulation Tool
Figure 6 shows the inputs and outputs of the simulator developed to obtain the results of this paper. The input variables are the emitter and receiver characteristics, the room (number of walls) configuration and the environmental conditions. The assumptions to compute the DC channel and the power received of the signal are the following:

Figure 6.
Structure of the simulator.
- Only the first reflection on the wall (if any) is considered for the non-line-of-sight (nLoS) component. The type of reflection considered is diffuse.
- If there is any fog or smoke, it is assumed to be uniformly distributed in the room, without transitory time.
- The reflection coefficient of materials is uniform on the whole wall and can be adapted to the envisioned use case.
The simulator computes the optical power received on a given receiver plane. The receiver plane is divided into a certain number of cells where Equation (2) is assessed, given the input parameters. Based on this information, other performance metrics could be computed, such as the SNR and the capacity of the system. However, the focus of this paper is the quantification of the attenuation levels of fog and smoke. As a starting point, the Python software simulation results were compared to figures available within the scientific literature, demonstrating their correctness [4,10].
3.3. Radiation Patterns: Lambertian for Scenario 1 and tabulated for Scenario 2
Based on Gfeller’s assumptions, the luminance of a single LED can be considered the same in all directions [45]. Elements with this property are called Lambertian radiators. This gives a uniaxial symmetry to the radiation pattern and makes it independent from, , leading to Equations (14) and (15). For the first scenario (cf. Section 4), a Lambertian emitter is assumed, and its radiation pattern is as follows:
The parameter (cf. Equation (15)) is the mode number, which gives the radiation pattern’s directivity. The half-power angle, , also known as the half-power beamwidth, is the angle between the maximum power axis and the points at half power. Its value is often found in LEDs’ datasheets, and a perfect Lambertian radiator has a half-power angle of 60 degrees. Figure 7 shows the radiation pattern for three half-power angles. Equation (14) was first introduced by Gfeller [45] to model the diffuse radiation of near-infrared LEDs. The exact origin of the parameter is not traceable in any paper to the best of our knowledge. The assumption made in this work is that this parameter’s role is analog to the parameters used in antennas theory, to model the directivity and gain. Further research extended Equation (14) to the case of white LEDs in order to model Li-Fi channel characteristics [10,23].

Figure 7.
Lambertian radiation pattern for three half-power angles.
Considering a Lambertian emitter for a streetlight is not adequate. Indeed, the radiation pattern of the streetlight is designed to enlighten the roads in a preferred direction. Two strategies exist to tackle that problem and integrate a more realistic radiation pattern of the light, using equations from a mathematical model developed in the literature or using a datasheet available for a specific light [27]. In this paper, the second approach is chosen. Radiation measurements from light fixture producers are available either in IES (Illumination Engineering Society) or in EULUMDAT formats. The IES file of a 47 W streetlight NIKKON MURA S with a light temperature of 4000 K was chosen for our scenario 2 (cf. Section 4) and downloaded from the website Lumsearch [25].
The file contains the name of the light, some characteristics, and the radiation pattern. The radiation pattern is provided by a table defined by two angles called C and Gamma. The C angle represents the horizontal plane and goes from 0 degrees to 360 degrees (called azimuth angle, , in Equation (1)). The Gamma angle corresponds to the vertical plane (called elevation angle,, in Equation (1)). The IES file contains 13 azimuth angles (0 to 360 degrees with a step of 30 degrees) and 181 elevation angles (0 to 180 degrees with a step of 1 degree). The luminous flux’s value per solid angle (in cd or lum/sr) is given for each couple of angles to create the radiation pattern. Figure 8 represents the radiation pattern of the NIKKON viewed by using the free software IES Viewer where two “slices” of the radiation pattern of the NIKKON light are represented: the C0°–C180° and the C90°– C270°. It can be noticed that there is no angular symmetry as opposed to the Lambertian radiation pattern in Figure 7.

Figure 8.
Radiation pattern of the NIKKON streetlight viewed in the software Illumination Engineering Society (IES) Viewer.
Two assumptions are made in this work. The first one is that the power reaching the receiver is considered uniform within its area. The second one is that the distance between the emitter and the receiver is far enough apart to make the differential solid angle approximation ( is the surface of the receiver and d, the distance between the emitter and the receiver [51]. The candela value is divided by the luminance efficiency of the light (W/lum), also found in the datasheet, to convert the candelas into W/sr. Considering the differential solid angle approximation the receiver’s total power is then computed thanks to Equation (1).
In scenario 2, this streetlight is designed to hang from 6 m to 8 m above the floor. For further computations, 6 m will be assumed. To compute the photodiode’s power, Equation (1) is evaluated in each cell of the receiver plane matrix. The axes’ origin is located at the center of the transmitter and the position of the receiver is given differentially from this origin in Cartesian coordinates.
The receiver’s spherical coordinates are calculated from the cartesian coordinates to find the receiver’s power thanks to the radiation pattern’s table. The quantity is then taken from the IES file using the elevation and azimuth angles which informs the optical power emitted in the receiver’s direction. If the angle is not existing in the table, a linear interpolation is performed. The total received power is finally calculated by multiplying this value by the receiver’s area and then dividing it by the distance’s square .
4. Results
In this work, defining relevant and realistic outdoor scenarios to assess the weather and smoke impact on a given optical communication is a necessity as no reference scenario is available in the scientific literature. Therefore, a typical Belgian smart bus station equipped with a VLC system (scenario 1) and a VLC streetlight hanging up a wall (scenario 2) were created as depicted in Figure 9 and Figure 10, respectively.

Figure 9.
VLC-enabled bus station.

Figure 10.
VLC-enabled streetlight.
The simulations aimed to compute the additional channel attenuation precisely due to the weather or smoke. This extra attenuation is a crucial element to compute the link budget of a VLC installation and the operating margin of the communication. To put that into practice, parameters from real pieces of equipment were used to compute the limits of the given system (cf. Figure 9 and Figure 10). This methodology can then be used for any VLC system.
Street furniture can either collect or send data to their surroundings, as suggested in Reference [52]. In present scenario 1, a bus stop equipped with an LED emitter could relay information to the end-user waiting for the bus. The wall of the bus shelter is assumed to be made from Plexiglas. The bus shelter dimensions are taken from a deployed actual Belgian bus shelter operated by the TEC (Transport Operator in Wallonia) to simulate this scenario. The LED’s optical power is 2 W, the emitter is located at the center of the ceiling, and the receiver is supposed to be in the 0.75 m plane above the floor inside the bus station, and 0.75 m is the average height of a bus shelter bench. The reflection coefficient of a Plexiglas wall is about 3.1% [53].
The second use case is an emitter located 6 m above the floor, and a lighting area of 6 by 6 m is considered, as shown in Figure 10. A 47 W LED STREET LANTERN (3000K) MURA S NIKKON streetlight is used [25]. The 6-by-6-m receiver plane is located 1.5 m above the floor, corresponding to the average height of an end-user using its end-device. The house is assumed to be built in beige brick, which corresponds to a reflection coefficient of 34.9% [53].
The other key simulation parameters can be found in Table 3. The parameter “Precision of the mesh” refers to the number of cells dividing the receiver plane. The computation time is longer when the number of cells increases. A trade-off should be drawn. This division into cells implies that the optical power computed is, in fact, per unit of surface proportional to the matrix. In the following computations, it is assumed that the surface is unitary.

Table 3.
Simulation parameters for two outdoor use cases.
A given system’s power margin computation, assuming a photodiode (PD) is used as a receiver, is done thanks to its NEP (Noise Equivalent Power) parameter. NEP is defined as follows: Given the photodetector’s noise, the NEP is the power needed to have a signal-to-noise ratio (SNR) of 0 dB in a 1 Hz output bandwidth [54]. This parameter can be found in the datasheets of a photodiode (PD). As a possible example, the PD FDS100 from Thorlabs has a NEP of . A communication bandwidth of 10 kbit/s is assumed, which gives −89.2 dBm for the NEP.
Figure 11 and Figure 12 illustrate the optical power distribution at the bus shelter and on the side of the house, given the two scenarios and the parameters of Table 3. These figures represent the reception level and so allow the coverage of the VLC system to be estimated. Indeed, where the power is higher, the receiver will perform better. For both scenarios, the edges of the considered volume have the weakest powers. This could be countered by putting several emitters close to each other.

Figure 11.
Optical power distribution on the receiver plane at the bus station in dBm, using a Lambertian model

Figure 12.
Optical power distribution on the receiver plane next to the house in dBm, using a real radiation pattern of a NIKKON streetlight.
Essential information such as the maximum, minimum, and mean powers are computed in Table 4 thanks to the value matrices used to graph Figure 11 and Figure 12.

Table 4.
Simulation results in terms of power received.
One can see that given the characteristics in Table 3, the power levels are coincidently roughly the same for both configurations, but this is not always the case. If the same PD is used for both cases, there is a power margin of , which represents for the bus station shelter configuration and for the house’s side configuration.
Given this information, one can compute if the attenuation coefficients of smoke and fog are higher, lower, or equal to this margin in given outdoor conditions. Equation (16) illustrates this computation, and and are the optical attenuation coefficients in dB per unit of length for given visibility for the weather attenuation and a given concentration of smoke for the smoke attenuation.
This result can give first-hand information about the robustness of the outdoor VLC system. The length L in Equation (16) refers to the distance between the transmitter and the receiver. Figure 13 shows both attenuation coefficients for a visibility parameter going from 5 to 100 m, using a logarithmic scale of 15 points. The computation of is done thanks to from Equation (13) because a non-light-emitting receiver is assumed.

Figure 13.
Attenuation levels due to fog and smoke for a visibility range of 5 to 100 m.
The attenuation coefficients per unit of length must be multiplied by the longest distance available in the scenarios at the weakest spot of the use case to assess both scenarios’ total attenuation. Given the short-range nature of the communication, the furthest distances correspond to the volumes’ far-ends in few meters for both cases. The distances computed geometrically thanks to Pythagoras’ theorem, are 2.12 m and 6.3 m for the bus stop and the hanging streetlight respectively.
The total levels of attenuation of smoke and fog are presented in Table 5. For a visibility of 5 m, the level of attenuation is not negligible, keeping in mind that having these conditions at once is, in practice, really rare. The contribution of smoke is slightly higher than that of a thick fog (cf. the values of Figure 13 multiplied by ). Nevertheless, both have the same order of magnitude and must be considered equally.

Table 5.
Attenuation levels for two visibility values.
The attenuation levels are located within the power margin of the scenarios considered. This means that even in poor fog (e.g., ) and smoke conditions, the system would still be running. Nevertheless, it should be noted that the noise of the pieces of equipment are not considered in this simulator. Furthermore, sunlight, which is known to increase the receiver side’s noise level, is not considered either. However, in the case of fog and smoke, this contribution would be lower as the smoke and fog would filter the sun’s irradiance or the illuminance of artificial light. The advantage of this computation methodology is that it can be generalized for any VLC system.
5. Discussion
When building an outdoor Visible Light Communication system, the primary source of attenuation and its impact is the environment. The optical signal can also be reflected in objects between the emitter and the receiver. Nevertheless, it is less prone to happen in an urban area as most VLC systems would be in LoS configuration. The impact of outdoor environments on the optical signal increases the attenuation due to the interaction between the atmospheric particles and the light beam. These particles constitute fog and smoke. Kim’s famous model for fog attenuation and a smoke model from the fire engineering field is used in the simulator. Both use the visibility concept to assess the optical attenuation. In fire engineering, the attenuation coefficient is used to compute the mass concentration of smoke thanks to Bouguer’s law. Two main ways of computing the smoke attenuation exist. The first one focuses on the combustion chemistry to link the smoke concentration to the optical attenuation it induces. The second way of computing the attenuation is by using a simplified model that uses the concept of visibility. The first way of calculating the attenuation states that there is a wavelength dependency for the attenuation for smoke concentration starting from 100 mg/m³, which corresponds to a visibility of 3 m and lower. As the paper focused on visibility going from 5 m to 100 m, the wavelength dependency could be neglected, and use the simplified model to assess smoke attenuation. The latter model is used to make an analogy with Kim’s fog model. This analogy shows that the channel attenuation levels due to fog and smoke are both in the same order of magnitude starting from a 1 km visibility, the attenuation of fog being the highest under this threshold. Furthermore, both phenomena’ attenuation coefficients are proportional to the distance between the emitter and the receiver. Thus, shorter communication links perform best.
It was also concluded that the attenuation levels for good visibilities, estimated of about 1 km to 50 km and more, are negligible. The attenuation coefficients for both phenomena platoon at around 0.1 to 0.2 dB/m in that visibility range, giving attenuations coefficients of 0.2 to 1.2 dB in the scenarios considered.
This paper proposes a new methodology to assess outdoor VLC equipment’s power margin when the emitter’s key characteristics, the receiver, and the medium are known. The power margin represents the difference between the actual power received and the NEP (Noise Equivalent Power) of the receiving photodiode. The NEP is equivalent to the minimum power needed to have an SNR of 0 dB in a 1 Hz output bandwidth.
Two outdoor scenarios, a bus stop and a streetlight equipped with VLC systems, are defined and studied to put this into practice. In order to be as close as possible to reality, the real radiation pattern of a streetlamp was considered. Given the assumptions made in the simulator and the characteristics of the VLC material, the actual power received is computed. Thanks to the fog and smoke models, the attenuation levels due to these phenomena are also computed. The attenuation levels of both phenomena have the same order of magnitude, and thus one should not be neglected compared to the other.
The main conclusion drawn from the results is that the attenuation coefficient values in both scenarios are much smaller than the power margin. This means that VLC communication will always be functional outdoors. These are promising results for the deployment of outdoor VLC use cases such as VLC–IoT systems, urban Li-Fi, and geolocation. However, improvements that still need to be addressed are considering other parasitic noises at the emitter and receiver side, the presence of artificial lighting or sunlight, the real radiation pattern of the LED considered because perfect Lambertian is assumed in this work.
Author Contributions
Conceptualization, S.B. (Sébastien Bette), N.P. and V.M.; Data curation, V.G.; formal analysis, V.G.; funding acquisition, S.B. (Sébastien Bette), N.P. and V.M.; investigation, V.G.; methodology, V.G., R.P.-J. and V.M.; project administration, S.B. (Sébastien Bette), N.P. and V.M.; resources, S.B. (Sébastien Bette), S.B. (Sylvain Brohez) and V.M.; software, V.G.; supervision, S.B. (Sébastien Bette), N.P. and V.M.; validation, V.G.; visualization, V.M.; writing—original draft, V.G. and V.M.; writing—review and editing, V.G., S.B. (Sébastien Bette), Sylvain Brohez, R.P.-J., N.P. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Wal-e-Cities, a research project supported by the European Regional Development Fund (ERDF) of the European Union and by the Wallonia Region, aiming at the development of Smart Cities in Wallonia.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A

Table A1.
State-of-the-art of Free Space Optics (FSO) and VLC systems under various weather conditions.
Table A1.
State-of-the-art of Free Space Optics (FSO) and VLC systems under various weather conditions.
| Aim of the Article | For What | Methodology | Distance | Emitter Used: | Wavelength | Effects | Models Used: |
|---|---|---|---|---|---|---|---|
| Characterize the link margin of an FSO system under different weather conditions [11] | FSO | Simulation: explanation of the effects) | 2.5 km | LASER | 1550 nm | Atmospheric effects (absorption, etc.) | Kim for foggy media |
| Characterization of Fog and Smoke Attenuation in a Laboratory Chamber [12] | FSO | Experiments and proposal of a model | 5.5 m | LASER | 600 to 1600 nm | Fog and smoke in a laboratory chamber | New models developed to match experiments |
| Analysis of a setup put outside measurements [13] | FSO | Experimental and analysis | 80 m–2700m | LASER | 785–850–950 nm | Fog and snow | Analytical model from experiments |
| Performance analysis (power received, SNR, BER) [14] | FSO | Theoretical analysis | Up to 1.5 km | LASER | 650, 850, 950, and 1550 | Fog | Comparison of fog models |
| Channel model of traffic light [18] | VLC (V2I) | Experimental and analytical model drawn | 5–80 m | Traffic light LED | Visible | Sunlight | Analytical model proposed after measurements |
| Demonstration of an outdoor system using a specific type of modulation [19] | VLC (V2V) | Experimental | 100 m | LED | R–G–B: 620–520–470 nm | None | Not applicable |
| Model closed form channel model for V2V [15] | VLC (V2V) | Simulation: ZEMAX | 10 m | Automotive white LED | Visible | scattering | Mie scattering |
| Overview of the VLC technology for outdoor [16] | VLC | Theoretical | Not applicable | LED and laser diodes | Visible | 4 scenarios of outdoor weather | Can be Kim model |
| Signal attenuation measurement in a controlled smoke environment [20] | VLC | Experimental measurement | 30 cm | White LED | Visible | Smoke generated from | Measurements |
| Study of snow and rain effect on a VLC and modulation techniques in terms of SNR, power received and BER, max coverage [17] | VLC (V2I) | Simulation | Up to 300 m | LED | 505 nm | Rain and snow | Marshall, France and Japan rain models |
| Quantify the effects of weather variabilities and smoke on a VLC smart city use case (this paper) | VLC | PYTHON simulator | Up to 8.13 m | LED | 450 nm | Fog and smoke | Kim model (fog) and fire engineering models for smoke |
References
- Kavehrad, M.; Chowdhury, M.I.S. An archipelago of high-bandwidth islands by optical wireless systems—A solution to the USA wireless airwaves spectrum crunch. In Proceedings of the 2012 IEEE Photonics Society Summer Topical Meeting Series, Seattle, WA, USA, 9–11 July 2012; pp. 92–93. [Google Scholar] [CrossRef]
- Kavehrad, M. Optical wireless applications: A solution to ease the wireless airwaves spectrum crunch. In Broadband Access Communication Technologies Vii; International Society for Optics and Photonics: San Francisco, CA, USA, 2013; p. 86450G. [Google Scholar] [CrossRef]
- Ayyash, M.; Elgala, H.; Khreishah, A.; Jungnickel, V.; Little, T.; Shao, S.; Rahaim, M.; Schulz, D.; Hilt, J.; Freund, R. Coexistence of WiFi and LiFi toward 5G: Concepts, opportunities, and challenges. IEEE Commun. Mag. 2016, 54, 64–71. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Alves, L.N.; Zvanovec, S.; Khalighi, M.-A. Visible Light Communications; CRC Press: Boca Raton, FL, USA, 2017; p. 591. [Google Scholar]
- Figueiredo, M.; Alves, L.N.; Ribeiro, C. Lighting the Wireless World: The Promise and Challenges of Visible Light Communication. IEEE Consum. Electron. Mag. 2017, 6, 28–37. [Google Scholar] [CrossRef]
- Haas, H.; Yin, L.; Wang, Y.; Chen, C. What is LiFi? J. Light. Technol. 2016, 34, 1533–1544. [Google Scholar] [CrossRef]
- Riurean, S.; Olar, M.; Ionică, A.; Pellegrini, L. Visible Light Communication and Augmented Reality for Underground Positioning System. MATEC Web Conf. 2020, 305, 89. [Google Scholar] [CrossRef][Green Version]
- Jungnickel, V.; Riege, M.; Wu, X.; Singh, R.; O’Brien, D.C.; Collins, S.; Faulkner, F.; Vazquez, M.M.; Bech, M.; Geilhardt, F.; et al. Enhance Lighting for the Internet of Things. In Proceedings of the 2019 Global LIFI Congress (GLC), Paris, France, 12–13 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Alkholidi, A.G.; Altowij, K.S. Free Space Optical Communications—Theory and Practices. In Contemporary Issues in Wireless Communications; Khatib, M., Ed.; InTech: London, UK, 2014. [Google Scholar]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with MATLAB; Taylor & Francis: Boca Raton, FL, USA, 2013. [Google Scholar]
- Saleem, Z. Free space optical (FSO) link design under diverse weather conditions. WSEAS Trans. Electron. 2006, 3, 225–232. [Google Scholar]
- Ijaz, M.; Ghassemlooy, Z.; Pesek, J.; Fiser, O.; le Minh, H.; Bentley, E. Modeling of Fog and Smoke Attenuation in Free Space Optical Communications Link Under Controlled Laboratory Conditions. J. Light. Technol. 2013, 31, 1720–1726. [Google Scholar] [CrossRef]
- Awan, M.S.; Csurgai-Horváth, L.; Muhammad, S.S.; Leitgeb, E.; Nadeem, F.; Khan, M.S. Characterization of fog and snow attenuations for free-space optical propagation. JCM 2009, 4, 533–545. [Google Scholar] [CrossRef]
- Ali, M.A.A. Performance analysis of fog effect on free space optical communication system. IOSR J. Appl. Phys. 2015, 7, 16–24. [Google Scholar]
- Elamassie, M.; Karbalayghareh, M.; Miramirkhani, F.; Kizilirmak, R.C.; Uysal, M. Effect of fog and rain on the performance of vehicular visible light communications. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–6. [Google Scholar]
- Ndjiongue, A.R.; Ferreira, H.C. An overview of outdoor visible light communications: An overview of outdoor visible light communications. Trans. Emerg. Telecommun. Technol. 2018, 29, e3448. [Google Scholar] [CrossRef]
- Zaki, R.W.; Fayed, H.A.; el Aziz, A.A.; Aly, M.H. Outdoor Visible Light Communication in Intelligent Transportation Systems: Impact of Snow and Rain. Appl. Sci. 2019, 9, 5453. [Google Scholar] [CrossRef]
- Cui, K.; Chen, G.; Xu, Z.; Roberts, R.D. Traffic light to vehicle visible light communication channel characterization. Appl. Opt. 2012, 51, 6594–6605. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Zhang, M.; Liang, S.; Ding, J.; Wang, F.; Lu, X.; Wang, C.; Chi, N. 100-m field trial for 5G wireless backhaul based on circular (7,1) 8-QAM modulated outdoor visible light communication. In Proceedings of the 2017 Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 31 July–4 August 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Xie, R.; Li, Z.; Gu, E.; Huang, Q. Signal attenuation of visible light communication in smoke environment. Opt. Eng. 2019, 58, 1. [Google Scholar] [CrossRef]
- Esmail, M.A.; Fathallah, H.; Alouini, M.-S. Outdoor FSO Communications under Fog: Attenuation Modeling and Performance Evaluation. IEEE Photonics J. 2016, 8, 1–22. [Google Scholar] [CrossRef]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Torero, J.L.; Watts, J.M., Jr.; Wieczorek, C.J. (Eds.) SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016. [Google Scholar]
- Dimitrov, S.; Haas, H. Principles of LED Light Communications: Towards Networked Li-Fi; Cambridge University Press: Cambridge, UK, 2015; p. 228. [Google Scholar]
- Burchardt, H.; Serafimovski, N.; Tsonev, D.; Videv, S.; Haas, H. VLC: Beyond point-to-point communication. IEEE Commun. Mag. 2014, 52, 98–105. [Google Scholar] [CrossRef]
- NIKKON. Datasheet 45W LED STREET LANTERN (3000K) MURA S NIKKON. Available online: https://lumsearch.com/fr/article/Z4uKfIZtRYKEYL-xqyHFNQ (accessed on 15 October 2020).
- Hoeher, A.P. Visible Light Communications: Theoretical and Practical Foundations; Carl Hanser Verlag: Munich, Germany, 2019. [Google Scholar]
- Moreno, I.; Avendaño-Alejo, M.; Saucedo-A, T.; Bugarin, A. Modeling LED street lighting. Appl. Opt. 2014, 53, 4420. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Ke, X. A new indoor VLC channel model based on reflection. Optoelectron. Lett. 2010, 6, 295–298. [Google Scholar] [CrossRef]
- Chung, Y.H.; Oh, S. Efficient optical filtering for outdoor visible light communications in the presence of sunlight or articifical light. In Proceedings of the 2013 International Symposium on Intelligent Signal Processing and Communication Systems, Naha-shi, Japan, 12–15 November 2013; pp. 749–752. [Google Scholar] [CrossRef]
- Islim, M.S.; Videv, S.; Safari, M.; Xie, E.; McKendry, J.J.D.; Gu, E.; Dawson, M.D.; Haas, H. The Impact of Solar Irradiance on Visible Light Communications. J. Light. Technol. 2018, 36, 2376–2386. [Google Scholar] [CrossRef]
- Friedlander, S.K. Smoke, Dust, and Haze Fundamentals of Aerosol Dynamics, 2nd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2000. [Google Scholar]
- Cojan, Y. Propagation du rayonnement dans l’atmosphère. Tech. L’ingénieur Electron. 1995, 6, 35. [Google Scholar]
- Gupta, R.; Aggarwal, A. Fog and Atmospheric Turbulence in FSO: Models to mitigate. Int. J. Contemp. Technol. Res. 2019, 2, 3. [Google Scholar] [CrossRef]
- Kim, I.I.; McArthur, B.; Korevaar, E.J. Comparison of laser beam propagation at 785 nm and 1550 nm in fog and haze for optical wireless communications. In Optical Wireless Communications III; International Society for Optics and Photonics: Boston, MA, USA, 2001; pp. 26–37. [Google Scholar] [CrossRef]
- Mulholland, G.W.; Fernandez, M. The Basis for a Smoke Concentration Measurement Using Light Extinction. In Proceedings of the 2nd International Conference on Fire Research and Engineering, Gaithersburg, ML, USA, 3–8 August 1997. [Google Scholar]
- Putorti, A.D., Jr. Design Parameters for Stack-Mounted Light Extinction Measurement Devices; NASA: Washington, DC, USA, 1999. [Google Scholar]
- Widmann, J.F.; Yang, J.C.; Smith, T.J.; Manzello, S.L.; Mulholland, G.W. Measurement of the optical extinction coefficients of post-flame soot in the infrared. Combust. Flame 2003, 134, 119–129. [Google Scholar] [CrossRef]
- Mulholland, G.W.; Croarkin, C. Specific extinction coefficient of flame generated smoke. Fire Mater. 2000, 24, 227–230. [Google Scholar] [CrossRef]
- Babrauskas, V.; Grayson, S.J. Heat Release in Fires; Taylor & Francis: Abingdon, UK, 1990. [Google Scholar]
- Mulholland, G.W.; Johnsson, E.L.; Fernandez, M.G.; Shear, D.A. Design and testing of a new smoke concentration meter. Fire Mater. 2000, 24, 231–243. [Google Scholar] [CrossRef]
- Jin, T.; Yamada, T. Irritating effects of fire smoke on visibility. Fire Sci. Technol. 1985, 5, 79–90. [Google Scholar] [CrossRef]
- Jin, T. Visibility and human behavior in fire smoke. In SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2, pp. 42–53. [Google Scholar]
- Seader, J.; Einhorn, I. Some physical, chemical, toxicological, and physiological aspects of fire smokes. Symp. Combust. 1977, 16, 1423–1445. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, M.; Ghassemlooy, Z.; Le Minh, H.; Tsai, H.-M.; Tang, X.; Png, L.C.; Han, D. Experimental Demonstration of RGB LED-Based Optical Camera Communications. IEEE Photonics J. 2015, 7, 1–12. [Google Scholar] [CrossRef]
- Gfeller, F.R.; Bapst, U. Wireless in-house data communication via diffuse infrared radiation. Proc. IEEE 1979, 67, 1474–1486. [Google Scholar] [CrossRef]
- Barry, J.R.; Kahn, J.M.; Krause, W.J.; Lee, E.A.; Messerschmitt, D.G. Simulation of multipath impulse response for indoor wireless optical channels. IEEE J. Sel. Areas Commun. 1993, 11, 367–379. [Google Scholar] [CrossRef]
- Khan, M.W.; Mehr-e-Munir, U.F.; Amer, A. Analysis of Key Transmission Issues in Optical Wireless Communication for Indoor and Outdoor Applications. Int. J. Comput. Sci. Inf. Secur. 2018, 16, 3. [Google Scholar]
- Sarbazi, E.; Uysal, M.; Abdallah, M.; Qaraqe, K. Ray tracing based channel modeling for visible light communications. In Proceedings of the 2014 22nd Signal Processing and Communications Applications Conference (SIU), Trabzon, Turkey, 23–25 April 2014; pp. 702–705. [Google Scholar]
- Rodríguez, S.; Mendoza, B.; Miranda, G.; Segura, C.; Jiménez, R.P. Simulation of impulse response for indoor wireless optical channels using 3D CAD models. SPIE Microtechnol. 2011, 8067, 80670A. [Google Scholar]
- Jovicic, A.; Li, J.; Richardson, T. Visible light communication: Opportunities, challenges and the path to market. IEEE Commun. Mag. 2013, 51, 26–32. [Google Scholar] [CrossRef]
- Quimby, R.S. Photonics and Lasers: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Nassar, M.A.; Luxford, L.; Cole, P.; Oatley, G.; Koutsakis, P. The current and future role of smart street furniture in smart cities. IEEE Commun. Mag. 2019, 57, 68–73. [Google Scholar] [CrossRef]
- Bodart, M.; de Peñaranda, R.; Deneyer, A.; Flamant, G. Photometry and colorimetry characterisation of materials in daylighting evaluation tools. Build. Environ. 2008, 43, 2046–2058. [Google Scholar] [CrossRef]
- Mackowiak, V.; Peupelmann, J.; Ma, Y.; Gorges, A. NEP–Noise Equivalent Power; Thorlabs Inc.: Newton, NJ USA, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).