Abstract
The aim of this paper is to comprehensively study how continuous action factors influence the nature of changes in the amplitude and frequency oscillations in one-dimensional nonlinear elastic systems characterized by longitudinal motion. For a wire moving along its axis, the interdependence of amplitude and frequency of oscillation was considered in both resonant and non-resonant cases. The influence of the roller vibrations on the character of the frequency response of oscillatory processes is determined. The influence of the method when fixing the ends on the frequency response is analyzed. Based on the theoretical results of the experimental study, practical recommendations are proposed. A full-scale experiment was carried out to improve the operation of a machine for rewinding wire from non-ferrous and precious materials, and a comparison was made with the theoretical results.
1. Introduction
The modelling, dynamic analysis, and control of systems moving along their axis have attracted considerable interest due to their wide range of applications in industry, including ropeways, magnetic belts, oil and gas pipelines, sheet paper rewinding machines, fiber and filament winders, belt drives and band saws, etc. [1,2,3]. According to their flexibility and geometrical parameters, systems can be classified as strings, beams, and plates. The case of beams is recognized by taking into account the significant bending stiffness of flexible components. There is a lot of work on the stabilization of linear beam systems that can be found in axially moving Euler–Bernoulli beams [4,5], in the dynamic model of two beams [6], and in moving Timoshenko viscoelastic beams [7].
To date, dynamic processes in systems characterized by longitudinal or angular velocity, even for their linear analogues, have rarely been considered due to the lack of an appropriate mathematical apparatus for integrating partial differential equations describing the processes. It is not always possible to construct their solutions using the Fourier method or the D’Alembert method. It is necessary to resort to various approximate asymptotic methods, namely, the harmonic balance method, the small parameter method (Poincaré method), the Galerkin method, and the Krylov–Bogolyubov–Mitropolsky asymptotic method (KBM) for the nonlinear mathematical models that more accurately reflect dynamic processes. In mechanical engineering, processes are modelled as axial moving systems. For these systems, mechanical vibrations of the moving part, especially in the transverse direction, become the main limiting factor that negatively affects the performance and quality of various high-speed precision process equipment.
This group of equipment also includes winding machines used in the production of cables and wire. One of the elements of the technological process is the rewinding of these products from container coils to charging coils. It is extremely difficult or impossible to describe mathematically all the dynamic processes that occur in moving nonlinear elastic systems at this stage. This is primarily due to the problems of integrating differential equations describing the movement of the medium. The complex problem must take into account the influence of kinematic parameters, friction forces, tensions, vibration of tension rollers, nonlinear elastic characteristics of the material, etc. Considering the operating conditions of other elements in the machine’s structure, they become especially relevant when the linear speed of the medium increases and the torques occur during rewinding. Thus, the main requirements for such equipment are the efficient execution of a continuous, high-speed technological process. If all the machine operating conditions are not met, the winding material breaks, leading to a process shutdown and damage to the product. It is also important to ensure that the product is laid uniformly on the appropriate spool. All this must be done at maximum equipment performance. So, to meet all these conditions, it is necessary to correctly calculate the impact of various factors on the operating elements. Reducing transverse vibrations in such moving systems has become an important area of research. It is necessary to take into account the effect of the tension roller vibration and find the law of change in the vibration frequency and amplitude of a one-dimensional nonlinear elastic system under appropriate boundary conditions. The reliability of the obtained calculations directly depends on the accuracy of the mathematical model.
In recent years, many papers have been published on the dynamic analysis [8] and control [9] of oscillating systems moving along their axis. In particular, several control methods have been considered, enabling such systems to be “damped” by stabilizing the oscillations of rollers [10]. However, these approaches primarily pursue the goal of controlling a point(s) rather than having distributed control. The boundary control can be implemented in one of two ways: active control [11] or dynamic process calculations in elastic construction elements [12] that can ensure better control efficiency. The latter algorithm is more difficult to implement because it requires distributed control forces and feedback signals.
The authors of [13] developed an adaptive boundary control scheme for a string moving along its axis. They studied the transverse vibrations of a medium moving with a time-varying velocity. However, the results showed that an infinite number of resonances can occur in the system when the speed fluctuation frequency is equal to (or close to) a least common multiple of an odd number for the natural frequency of a constant speed system.
In an effort to address vibration reduction, many researchers have explored ways to influence the left or right boundary of the system (known as boundary control), where providing control through the support roller is more cost-effective than inserting an additional actuator in the system. Such results have been shown in recent studies of systems moving along an axis [14].
One of the fundamental issues in the study of moving environments concerns the suppression of transverse vibrations that are mainly caused by technical deficiencies and the manufacturing process or from high speed. Many different control approaches have been used to improve performance and suppress vibration, such as adaptive control [15], backstepping control [16] and the Lyapunov method [17], the flatness method [18], and optimal control [19] have been developed in the literature, but none of these studies considered the nonlinear characteristics of the material.
One article [20] considers a nonlinearly elastic string moving between two rollers at a constant transport speed. The authors describe the motion and boundary conditions of the moving system using Hamilton’s generalized principle. Some numerical simulations are presented to illustrate the theoretical results, where the closed system is solved by the finite element method with a quadratic Lagrange basis, followed by a brief conclusion. However, they did not take into account the effect of tension and disturbing external forces.
One paper [21] analyzes the adaptive boundary control of a moving string that demonstrates nonlinear behaviour due to spatial variation in tension. A hydraulic actuator equipped with a damper is used as a control actuator on the right boundary of the string. Numerical simulations were carried out to demonstrate the effectiveness of the proposed adaptive boundary control, but no experimental confirmation was performed.
In the paper [22], simple approximate formulas for the eigenfrequency of such strings are derived based on asymptotic methods in the case of a tensioned beam. Although similar work is known for a beam with variable axial tension, this is believed to be the first time that a single analytical expression has been developed for the full length of a beam. In practice, these oscillating systems have variable tension due to deformation caused by the displacement of the string, the eccentricity of the support roller, external disturbances, and other factors [1,23]. This again leads to a change in the dynamics of the moving string. Therefore, the determination of the interdependencies of the amplitude and frequency of oscillation in time must be established by taking into account changes in tension.
Thus, the analysis of recent fundamental publications has proved that the existing analytical methods for studying the dynamic processes of nonlinear systems with distributed parameters are insufficiently developed. This is especially true for systems characterized by longitudinal motion. Some papers explored the nonlinear oscillations of these media; however, the authors impose a number of restrictions, resulting in certain simplifications of the computational model.
To overcome the above difficulties, this paper presents the asymptotic KBM method. This method is appropriate for weakly nonlinear elastic systems since it allows for the constructing of asymptotic solutions by considering slow changes in amplitude and phase, eliminating secular terms, providing a physically interpretable form of the result, and being relatively simple to implement for this class of oscillatory problems. Considering the importance and relevance of the existing problem for nonlinearly elastic one-dimensional systems characterized by longitudinal or rotational motion, the main objective of this study was to comprehensively explore the influence of not only physical and mechanical parameters but also kinematic parameters on the APC (amplitude phase characteristic) of the system. This approach enables us to predict the resonance zones and establish the most efficient operating modes of the equipment, as well as set less stringent requirements for the system and its elements. The aim of this paper is to comprehensively study how continuous action factors influence the nature of changes in the amplitude and frequency oscillations in one-dimensional nonlinear elastic systems characterized by longitudinal motion. To achieve this goal, the following tasks are defined:
- -
- to obtain analytical and graphical dependences on the oscillation frequency of systems characterized by longitudinal velocity regarding tension, length, material density, elastic modulus, initial amplitude, and other quantities for non-resonant and resonant cases;
- -
- to determine the ability of the method to fix the wire ends on the APC of the system using the example of a rewinding machine;
- -
- to conduct experimental studies and measure the amplitude and the frequency of the oscillation of a wire moving along its axis on a rewinding machine;
- -
- based on the results of the study, to propose technical recommendations for improving the machine operation and to make a comparative characterization between the modes of this type of equipment operation.
2. Materials and Methods
The experimental part of this paper was carried out on a rewinding machine used in production. The transverse oscillations of the wire that occur during rewinding from one coil to another fully reproduce the dynamic processes that are involved in the movement of the studied object. The wire can be made of various steel, precious, and non-ferrous materials with diameters ranging from 0.25 mm to 2 mm. Its kinematic diagram is shown in Figure 1.
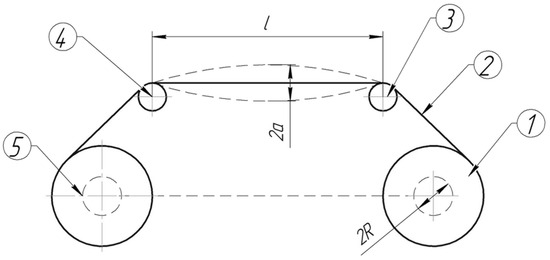
Figure 1.
A kinematic scheme of the rewinding machine. l is the distance between the guide and the compensation rollers (area where measurements were taken); a is the amplitude of the wire oscillation; and R is the initial radius of the receiving coil.
2.1. Description of the Equipment and the Principle of Operation
The main motor 10 RD 09 drives the drive shaft on the receiving coil of (1). The copper wire of (2) between the receiving coil (1) and the driven coils of (5) are two rollers. The compensating roller (4) acts as an oscillation and tension damper. It is located on the rocker arm and dampens external disturbances that occur during the rewinding process. The guide roller (3) is necessary for even wire laying on the receiving coil of (1). During the rewinding process, this roller moves along the axis of the take-up coil (1). This movement is realized due to the fact that the roller (3) is located on the slider, which is in direct contact with the worm. When the worm is rotated by the additional motor, the slider moves along the worm and thus along the drive shaft. The worm is mounted on two supports and two buttons. When the slider reaches the end positions, it presses these buttons. The buttons then switch the rotation direction of the worm, reversing the slider. The wire is rewound from the driven coils (5) and mounted on the bracket.
2.2. Analytical Dependencies for Determining the Oscillation Frequency and Amplitude in a Medium Moving Along Its Axis
To describe the transverse vibrations of the wire, we take the rectilinear x-axis as the coordinate axis. From this axis, the deviations of the wire elements during their transverse vibrations would be counted. The deviations are determined by a single function of two variables y = y(x,t), where x is the coordinate on the axis and t is time.
The transverse oscillations of the wire during rewinding are described by slowly varying parameters in time: longitudinal velocity, inertia moment of the spool, and wire tension. That is why dynamic processes in such a nonlinear elastic medium are represented by a differential equation with slowly varying coefficients [24].
where ; V(τ) is slowly varying longitudinal velocity of the wire; P(τ) is slowly varying wire tension in time; ε is the small positive parameter; νt = ψ; ν is the frequency of the disturbing force; ωt = θ; ω is the frequency of transverse eigen oscillations of the wire; and ρ is the mass per unit length.
Asymptotic methods can be used to find an approximate solution to Equation (1). As already described, some parameters will be slowly changing over time. This also refers to the parameter τ = εt and the eigenfrequency of the wire oscillation. Thus, the general solution of (1) is given by the following form [25]:
where the second term y1(τ,a,ψ,θ,x) is a periodic function. The period is 2π in phase θ. According to the asymptotic Krylov–Bogolyubov–Mitropolsky method, the values of a and θ as functions of time for the non-resonant case are determined in the first approximation by a system of differential equations [26]:
To find unknown functions A1(τ,a), B1(τ,a), and y1(τ,a,ψ,θ,x) to construct asymptotic approximate solutions of (1), it is necessary to integrate the equation system (3).
The solution for Equation (1) for the first asymptotic approximation will be given by
After integrating with respect to ψ, system (4) is next:
To find the asymptotic approximate solution, it was necessary to transform the second-order differential Equation (1) by integrating two equations to yield the first-order Equation (6). Integration of the system into differential Equation (6) by elementary functions is a complex mathematical problem. However, using numerical methods (e.g., the fourth-order Runge-Kutta method), it is possible to solve this system.
2.3. Analytical Dependences of the Oscillation Frequency and Amplitude of Systems for Non-Resonant and Resonant Cases
It should be remembered that the inertia moment and the spool radius, as well as the amount of wire tension during winding, are time varying. The angular speed of the drive is constant. Taking into account all these factors, we consider the transverse oscillations of the wire as a nonlinear oscillatory system with slowly changing coefficients.
So, the differential equation of motion will be in the following form:
for the wire
for the spool
where Mt is the frictional moment between the driven drum and the axis; J(τ) is the inertia moment of the driven drum; P(τ) is wire tension that varies over time; Rt(τ) is the running value of the radius of the wound wire on the spool, varying in time; ωs is the angular speed of rotation of the drive shaft; S is the cross-sectional area of the wire; and E is the elastic modulus.
From Equation (8), it is possible to find the value of the wire tension P(τ). To do this, we will write it down as the following:
Since the angular velocity is constant, the second term in Equation (9) will be equal to 0, and Equation (9) will be in the following form:
where Rt(t) = R + kVt. Thus, from Equation (10), the wire tension force can be determined:
where Ftr is the frictional force between the driven drum and the axis.
Substituting the obtained dependence of the wire tension into (1), one can find the frequency of the wire oscillation:
Due to the obtained dependence of the wire tension force (11), the differential equation to find the APC in the case of a nonlinear elasticity technical law will be as follows:
For the resonant case, when a harmonic force acts on the wire with a frequency close to the frequency of its own transverse oscillations, the system of differential equations (6) takes the following form:
where N is the external disturbing force acting on the wire.
To estimate the effect of longitudinal velocity and time on the change in wire tension, we can use Equation (11) and plot a graph (Figure 2). These dependencies can be constructed on the various parameters, and this enables us to establish the nature of the change in tension.
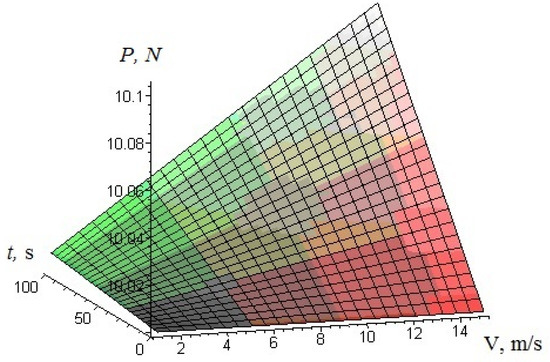
Figure 2.
Dependence of wire tension force on time and its longitudinal velocity.
Attention should be paid to Equation (12) as it contains a root expression. Thus, the oscillation frequency will have a physical meaning if this difference is greater than 0 only. This means that there is a certain critical speed at which the oscillation can break down. We can plot the dependence of the transverse oscillation frequency of the wire using Equation (12), for example, to determine the nature of the oscillation frequency changes over time when the wire winding radius changes (Figure 3) and when there are other dependences (Figure 4, Figure 5 and Figure 6).
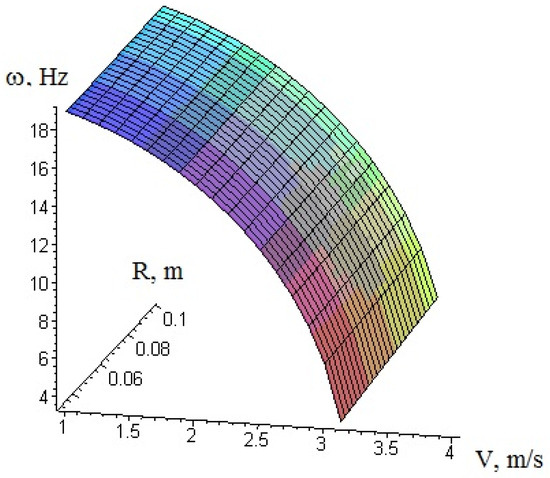
Figure 3.
Dependence of the wire transverse oscillation frequency on the radius of the driven drum and its linear speed.
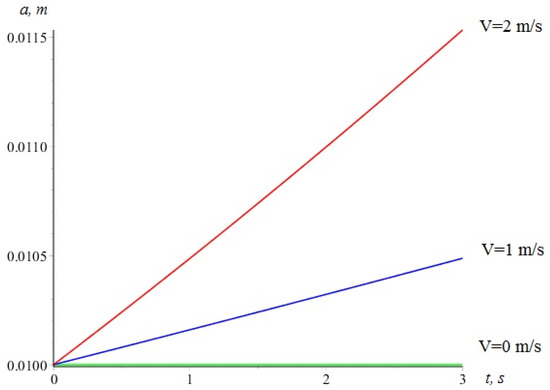
Figure 4.
A plot of amplitude versus time in the non-resonant mode for different longitudinal wire velocities.
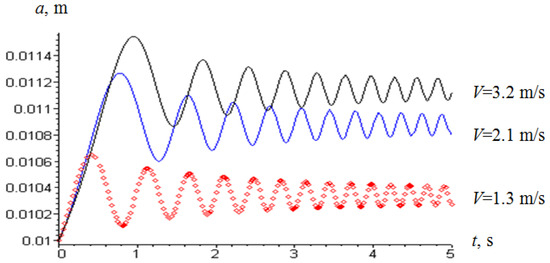
Figure 5.
Dependence of the amplitude of wire transverse oscillations in the resonant mode at different longitudinal velocities (Ftr = 10 N).
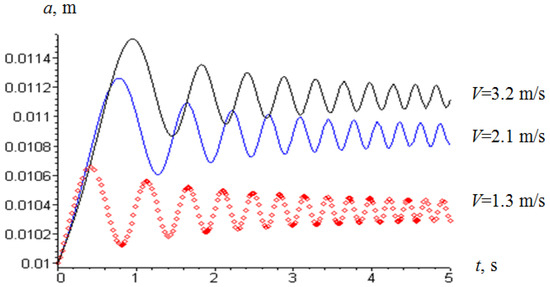
Figure 6.
Dependence of the amplitude of wire transverse oscillations in the resonant mode at different longitudinal velocities (Ftr = 15 N).
2.4. Differential Equations of Transverse Oscillations via the Method of the Fixed Ends
We can consider the case where it is necessary to take into account the oscillations of the compensating roller. If these oscillations follow the harmonic law, then the APC is determined by the differential equations for the resonant case from system (14):
In practice, the compensating roller makes a harmonic oscillation during wire rewinding. For different cases, the amplitude of oscillations depends on the way the roller is fixed. However, for our rewinding machine it is 2 mm. Given that we are considering the resonant case, the frequency of the roller oscillation will be equal to the frequency of the transverse oscillations of the wire moving along its axis (Figure 7 and Figure 8).
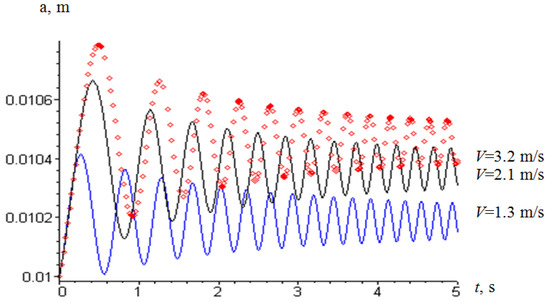
Figure 7.
An amplitude versus velocity plot for the resonant case when one end is vibrating. The amplitude of the force vibrating at the end is equal to F = 5 N.
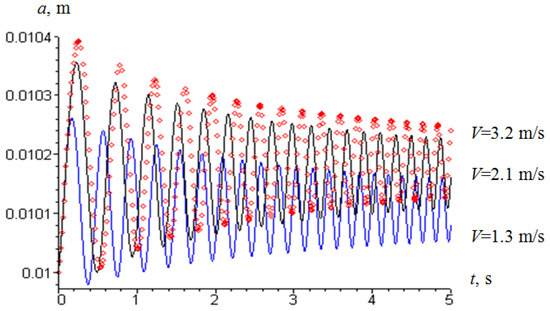
Figure 8.
An amplitude versus velocity plot for the resonant case when one end is vibrating. The amplitude of the force vibrating at the end is equal to F = 2 N.
2.5. Limitations of the KBM Method
The KBM method can be applied if the movement of the system along the axis does not change the conditions of weak nonlinearity and if it does not cause the emergence of additional dynamic factors that violate the asymptoticity of the solution. The overall nonlinearity of the model is expressed through the small parameter ε. It is important for the movement to be uniform, accelerated, or periodic to use the KBM. The application of this method requires that all additional effects (including those arising from the movement) do not cause a sharp increase in the derivatives and do not change the basic type of vibration (i.e., that they can be represented as a slowly modulated harmonic). Therefore, the translational speed of the wire must not exceed the phase speed of the oscillation.
3. Results of Experimental Studies
The frequency and amplitude of the wire oscillation were measured using the MT-565 device. Thanks to the stroboscopic effect, the oscillation frequency of the wire was measured. During the rewinding process, the wire oscillates and periodic illumination makes it possible to record its position at regular intervals. To determine the oscillation frequency, it is necessary to adjust the frequency of flashes on the device so that when it coincides, a stable picture of the position of the test medium is obtained.
The least-squares method was used to plan experimental studies and mathematically process the results. The influence of the longitudinal velocity at a given tension force on the frequency and amplitude of the transverse oscillations of the wire was studied. Based on the design capabilities of the rewinding machine, only the effect of the wire linear velocity on the amplitude and frequency of its transverse oscillations was experimentally determined.
During the practical study, the amplitude and frequency of the wire oscillation were measured for each wire rewinding speed. The measurement results were repeated several times until they coincided with the previously obtained ones (deviations between them were less than 10%). To obtain reliable experimental data, the measurements were performed thirty times. The experimental measurement data are shown in Table 1.

Table 1.
RMS amplitude and maximum deviation.
Experimental studies were carried out for copper and brass wire only. The wire with the following parameters was used for the experiment:
- -
- wire diameter: d = 0.4 mm;
- -
- distance between support points (distance between guide and compensation roller): l = 0.5 m;
- -
- V = 1.3 m/s, V = 2.1 m/s, V = 3.2 m/s;
- -
- kg/m;
- -
- kg/m;
- -
- R = 0.07 m.
By analyzing the results of the experimental studies (Table 1), and considering the influence of the longitudinal speed of the wire when rewinding between the guide and compensation rollers, we can find the RMS value of the oscillation amplitude: , where ai is the measured oscillation amplitude and i is number of measurements. In addition, the maximum deviation from the obtained RMS value can be found using the following equation: . The data obtained are presented in Table 1.
As the longitudinal velocity of the wire increases, the amplitude of its transverse oscillations increases (at a speed of V = 1.3 m/s, the amplitude is 10.7 mm; at a speed of V = 3.2 m/s, it is 25% higher).
As can be seen in Table 2, the deviation of the theoretical data does not exceed 15% of the experimental data. It is obvious that the calculation of the amplitude and the frequency of oscillation did not take into account internal friction, measurement error, and other factors. Thus, these results confirm the reliability of the applied methodology for determining the frequency response of wire oscillations.

Table 2.
Experimental and theoretical results of measurements and calculations.
3.1. Options for Improving the Machine
During the operation of the rewinding machine, the technological process was often disrupted. Further, during the rewinding process, the wire would break. This not only stopped the rewinding process, but also damaged the material itself. Uneven wire tension increased longitudinal wire speed, and defects in the material caused these negative effects. Typically, the efficiency of this equipment was low because, in addition to these shortcomings, the process time increased. To increase the efficiency of the machine, two options for improving the rewinding mechanism are proposed, considering theoretical studies and the optimal choice of system parameters (those that can be changed without disturbing the machine design), as well as the physical properties of the wire material.
3.1.1. A Modified Machine with a Motor That Runs on a Constant Voltage
The angular speed of the motor (1) (Figure 9) that operates at a constant voltage can be adjusted using the supply voltage. When the motor is switched on, it transmits the moment via a belt drive (2) to the drive drum (3) where the wire is wound. There are rollers (5) and (4) between the master and the driven drums (8). During the operation of the machine, the radius of the driving drum will increase as the wire is wound on it. As a result, the longitudinal speed of the wire will also increase through V(t) = ωRt(t), i.e., the longitudinal speed of the wire will be variable (while the motor transmits the torque to the driving shaft at a constant angular speed, the winding radius will increase, and therefore, the longitudinal speed will also increase).
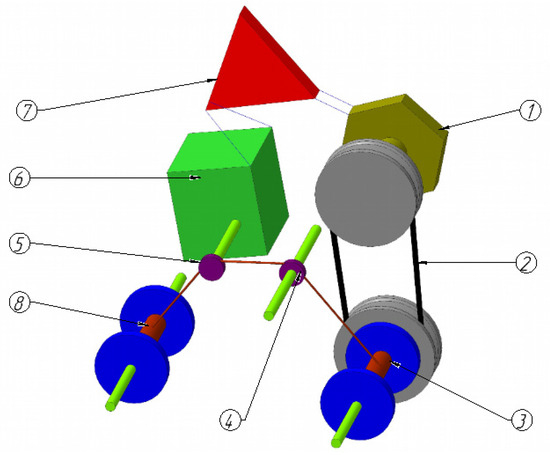
Figure 9.
A scheme for equipment improvement for a motor operating at a constant voltage.
With an increase in speed, the process will become increasingly unstable, i.e., material tears will form. The tachogenerator (6) is used as a tracking device that rotates and corrects the voltage with the help of a compensation roller (4). This voltage is fed to the inverter and then to the amplifier. The electrical block diagram of such an installation is shown in Figure 10. As soon as the compensation roller speed increases, the voltage on the tachogenerator will increase. After the inverter and the amplifier, the voltage is supplied to the motor. This reduces the motor supply voltage by the amount of the generated voltage in the tachometer. The engine speed decreases and the longitudinal velocity of the wire becomes constant.
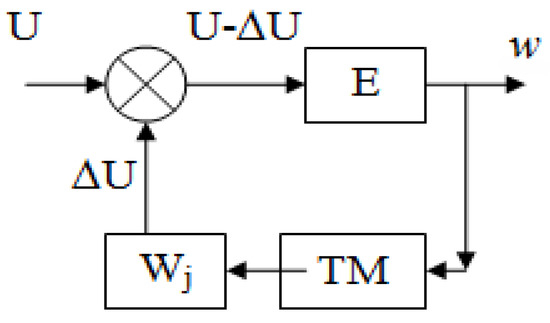
Figure 10.
Electrical block diagram. E is the motor; TM is the tachogenerator; Wj is the transmitting link (amplifier); U is the voltage supplied to the motor; and ∆U is the voltage change.
3.1.2. For a Motor Operating on Alternating Voltage
This option (in Section 3.1.1) is not usually suitable for a variable voltage motor. Given that it is difficult to significantly change the machine design so as to not disrupt the production process or complicate a mechanism with additional monitoring electronics, a simple engineering solution was applied. As a result of the upgrade, the transmission of the moment from the motor (1) (Figure 11) to the drive shaft where the drum is placed (5) was changed. The motor transmitted moment to an additional disc (3) via a belt drive (2). In the improved scheme, an intermediate disc was added between these two components. This disc was spring-loaded (4), touched the wire coil on the driven drum (5), and turned it.
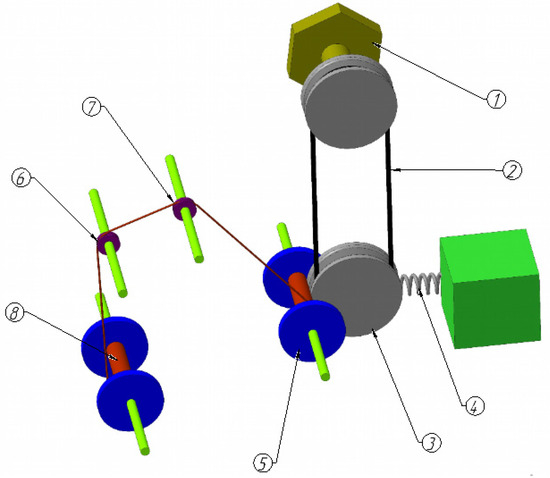
Figure 11.
A scheme for improving equipment for an AC motor.
This element is usually coated with a strong rubber to improve friction during moment transmission and is pressed hard enough against the wire coil to reduce slippage during this transmission. This arrangement transmits the torque from the disc (3) to the drum (5) via a friction transmission. An increasing winding radius will press the drum and disc even harder. However, the winding diameter is significantly changed (doubled). This means that the disc is not fixed rigidly but is instead in a spring-loaded version. Now, the angular velocity of the spool will change (proportionally decreasing with increasing winding radius), but the linear longitudinal velocity of the wire will be constant when moving from the driven drum (8) to the master drum (5), which is required. This improvement scheme can be applied to any motor on rewinding machines.
The above method of improving the AC machine was applied to improve the performance of the equipment. During the operation of the modified machine, the amplitude and frequency of the wire oscillation were also measured. These results are summarized in Table 3.

Table 3.
Experimental and theoretical data after system improvement.
4. Discussion of the Influence of Quantities on Oscillation Characteristics
After analyzing the results presented in Figure 2, it can be said that an increase in speed leads to an increase in tension, and that at a certain value, it can reach a critical value, causing wire breakage. Thus, using Equation (11), it is possible to set the permissible speed value and increase the efficiency of the rewinding machine. This equipment will be able to operate at maximum speed while avoiding possible breaks and stoppages. As can be seen in Figure 3, an increase in the longitudinal velocity leads to a decrease in the oscillation frequency, and a failure occurs at a value of 3.3 m/s. When the wire does not move, i.e., V = 0, the natural frequency of the wire oscillation is 19 Hz. When the longitudinal velocity increases to 2.1 m/s, the frequency decreases by 12.5%.
The analysis of the graphical representation of dependence (12) shows that the radius of the driven drum does not significantly affect the frequency of the transverse vibrations of the wire. This cannot be said about the linear speed of wire rewinding: with its increase, the frequency of transverse vibrations decreases (see Figure 3).
Using Equation (13), using the MAPLE 2015 software environment, it is also possible to obtain a graphical representation of the dependence of the wire oscillation amplitude on the velocity for the non-resonant case (Figure 4). With an increase in the longitudinal velocity, the amplitude increases almost linearly (Figure 4). In particular, at V = 2 m/s, the increase in the amplitude of oscillation is 15% compared with a wire that is not characterized by longitudinal motion (free oscillations of a stationary wire) after 3 s. The results shown in Figure 4 indicate that for low velocities (up to 2 m/s), the amplitude increases according to a linear law. Parameter ε is a small positive parameter that cancels out the significant effect of speed, but at speeds of 3 m/s and higher, there is a significant increase in amplitude according to a polynomial (quadratic) law. When the axial velocity is 0, the amplitude does not change, as was to be expected.
Comparing the results of the oscillatory processes for different velocities presented in Figure 5, it can be stated that an increase in velocity leads to an increase in the amplitude of oscillation and that it can reach a critical value. Thus, it is possible to establish the effective value of the longitudinal velocity of the wire, even for the resonant case. Based on the system of equations (14), a graph of the amplitude change in the resonant mode was constructed for different longitudinal wire velocities at a friction force of 10 N (Figure 5) and 15 N (Figure 6). They are almost identical ones, indicating a very small effect of the friction force between the drive drum and the axle on the oscillation amplitude. However, it should be noted that the change in force is also small, only from 10 N to 15 N. Despite this, there is an influence of speed: at a speed of 3.2 m/s, the oscillation amplitude increases by 8.5% compared with the oscillations of a wire moving along its axis at a speed of 1.3 m/s.
The maximum amplitude value at a wire speed of 3.2 m/s reaches 0.0115 m under homogeneous boundary conditions and 0.0106 m at a linear wire speed of 1.3 m/s. If we take into account the force of 5 N acting on the wire from the oscillation of the roller, then at a longitudinal velocity of 3.2 m/s, the amplitude of oscillation is 0.0108 m (in homogeneous boundary conditions) (Figure 8). Thus, the amplitude will be reduced by 6.7% compared with the stationary rollers. Reducing the force on the rollers to 2 N leads to a 4% decrease in the oscillation amplitude (Figure 8).
It was established that with the introduction of new machine components, wire breaks are reduced by about 13% when the winding speed is increased from 1.3 m/s to 3.2 m/s. This improved the performance of the equipment by 2.5 times.
5. Conclusions
- The mathematical dependencies are obtained, allowing a comprehensive study of how moving medium parameters affect the nature of changes in frequency and amplitude, and to more accurately predict the dynamic phenomena among them.
- For a real physical model, analytical and graphical dependences of the oscillation frequency of systems characterized by longitudinal or angular velocities on different quantities for non-resonant and resonant cases are obtained. The influence of the roller vibrations on the character of the frequency response of oscillatory processes is determined. The influence of the method of fixing the ends on the frequency response is analyzed.
- Based on the results of an analysis of equipment efficiency for different rewinding modes, the optimum speed was found. This improved the equipment’s performance by 13%.
- Practical technical recommendations for improving the operation of the machine have been developed and a comparative characterization between the modes has been realized.
- Based on the theoretical results of this experimental study, practical recommendations are proposed. A full-scale experiment was carried out to improve the operation of a machine for rewinding wire from non-ferrous and precious materials, and a comparison was made with the theoretical results.
- In future studies, we plan to introduce the dependence of the change in the amplitude and the phase of the oscillation on temperature, and to assess the effect of the parameters on the system’s safety margin.
Author Contributions
Conceptualization, A.S. and P.P.; methodology, A.S., M.V., and A.K.; software, A.K.; validation, M.V. and A.K.; investigation, P.P. and M.V.; writing—original draft preparation, M.V. and A.K.; writing—review and editing, A.S. and P.P.; visualization, M.V. and A.K.; project administration, A.S. and P.P.; funding acquisition, P.P. and M.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- He, W.; Meng, T.; He, X.; Ge, S.S. Unified iterative learning control for flexible structures with input constraints. Automatica 2018, 96, 326–336. [Google Scholar] [CrossRef]
- Li, T.C.; Hou, Z.C.; Li, J.F. Stabilization analysis of a generalized nonlinear axially moving string by boundary velocity feedback. Automatica 2008, 44, 498–503. [Google Scholar] [CrossRef]
- Song, M.; Yao, G.; Yu, Y. Dynamic response characteristics of axially moving plates subjected to moving load. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 365. [Google Scholar] [CrossRef]
- Knüfer, S.; Müller, M.A. Nonlinear full information and moving horizon estimation: Robust global asymptotic stability. Automatica 2023, 150, 110603. [Google Scholar] [CrossRef]
- Iqbal, A.; Veer, S.; Gu, Y. Asymptotic stabilization of aperiodic trajectories of a hybrid-linear inverted pendulum walking on a vertically moving surface. In Proceedings of the 2023 American Control Conference (ACC 2023), San Diego, CA, USA, 31 May–2 June 2023; pp. 3030–3035. [Google Scholar] [CrossRef]
- Liu, M.; Yao, G. Nonlinear forced vibration and stability of an axially moving beam with a free internal hinge. Nonlinear Dyn. 2024, 112, 6877–6896. [Google Scholar] [CrossRef]
- Mokhtari, A.; Mirdamadi, H.R. Study on vibration and stability of an axially translating viscoelastic Timoshenko beam: Non-transforming spectral element analysis. Appl. Math. Model. 2018, 56, 342–358. [Google Scholar] [CrossRef]
- Nguyen, Q.C.; Hong, K.S. Simultaneous control of longitudinal and transverse vibrations of an axially moving string with velocity tracking. J. Sound Vib. 2012, 331, 3006–3019. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Boundary control of transverse motion of marine risers with actuator dynamics. J. Sound Vib. 2008, 318, 768–791. [Google Scholar] [CrossRef]
- Lee, S.Y.; Mote Jr, C.D. Vibration control of an axially moving string by boundary control. J. Dyn. Sys. Meas. Control 1996, 118, 66–74. [Google Scholar] [CrossRef]
- Ahn, H.; Ha, S.Y. A mean-field approach for the asymptotic tracking problem of moving continuum target clouds. Stud. Appl. Math. 2024, 152, 568–595. [Google Scholar] [CrossRef]
- Andrukhiv, A.; Sokil, M.; Fedushko, S.; Syerov, Y.; Kalambet, Y.; Peracek, T. Methodology for increasing the efficiency of dynamic process calculations in elastic elements of complex engineering constructions. Electronics 2020, 10, 40. [Google Scholar] [CrossRef]
- Chen, L.Q.; Zhang, N.H.; Zu, J.W. The regular and chaotic vibrations of an axially moving viscoelastic string based on fourth order Galerkin truncaton. J. Sound Vib. 2003, 261, 764–773. [Google Scholar] [CrossRef]
- Pham, P.T.; Hong, K.S. Dynamic models of axially moving systems: A review. Nonlinear Dyn. 2020, 100, 315–349. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, J. Using nanoparticles to enable simultaneous radiation and photodynamic therapies for cancer treatment. J. Nanosci. Nanotechnol. 2006, 6, 1159–1166. [Google Scholar] [CrossRef] [PubMed]
- Krstic, M.; Smyshlyaev, A. Adaptive boundary control for unstable parabolic PDEs—Part I: Lyapunov design. IEEE Trans. Autom. Control. 2008, 53, 1575–1591. [Google Scholar] [CrossRef]
- Nagarkatti, S.P.; Zhang, F.; Costic, B.T.; Dawson, D.M.; Rahn, C.D. Speed tracking and transverse vibration control of an axially accelerating web. Mech. Syst. Signal Process. 2002, 16, 337–356. [Google Scholar] [CrossRef]
- Meurer, T. Control of Higher–Dimensional PDEs: Flatness and Backstepping Designs; Springer Science Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Fung, T.C. Stability and accuracy of differential quadrature method in solving dynamic problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 1311–1331. [Google Scholar] [CrossRef]
- Cheng, Y.; Wu, Y.; Guo, B.Z. Absolute boundary stabilization for an axially moving Kirchhoff beam. Automatica 2021, 129, 109667. [Google Scholar] [CrossRef]
- Nguyen, Q.C.; Hong, K.S. Asymptotic stabilization of a nonlinear axially moving string by adaptive boundary control. J. Sound Vib. 2010, 329, 4588–4603. [Google Scholar] [CrossRef]
- Lubbad, R.; Moe, G. Closed-Form Solutions for Vibrations of Nearly Vertical Strings and Beams by Means of Asymptotic Methods. J. Eng. Mech. 2008, 134, 1064–1070. [Google Scholar] [CrossRef]
- Cai, X.; Krstic, M. Nonlinear stabilization through wave PDE dynamics with a moving uncontrolled boundary. Automatica 2016, 68, 27–38. [Google Scholar] [CrossRef]
- Mitropolsky, Y.A.; Van Dao, N. Applied Asymptotic Methods in Nonlinear Oscillations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 55, p. 342. [Google Scholar] [CrossRef]
- Slipchuk, A.; Pukach, P.; Vovk, M.; Slyusarchuk, O. Advancing asymptotic approaches to studying the longitudinal and torsional oscillations of a moving beam. East. Eur. J. Enterp. Technol. 2022, 3, 31–39. [Google Scholar] [CrossRef]
- Slipchuk, A.; Pukach, P.; Vovk, M. Asymptotic Study of Longitudinal Velocity Influence and Nonlinear Elastic Characteristics of the Oscillating Moving Beam. Mathematics 2023, 11, 322. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).