Numerical and Experimental Analysis of Impact Force and Impact Duration with Regard to Radiosondes: Is a PUR Foam Shell an Effective Solution?
Abstract
1. Introduction
2. Methods and Materials
2.1. Methods of FEM Drop Tests
2.2. Method of Experimental Drop Tests
3. Results and Discussion
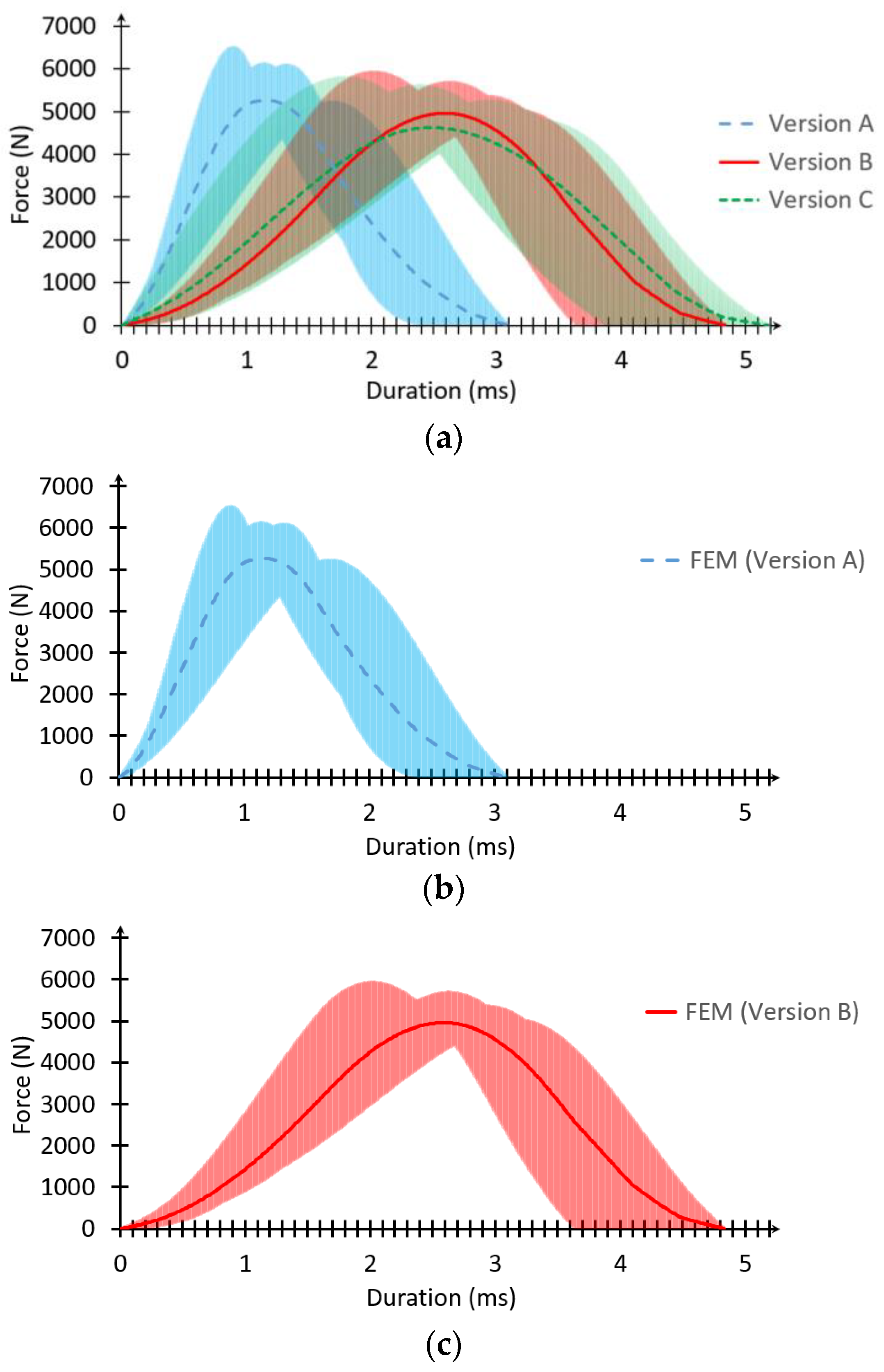
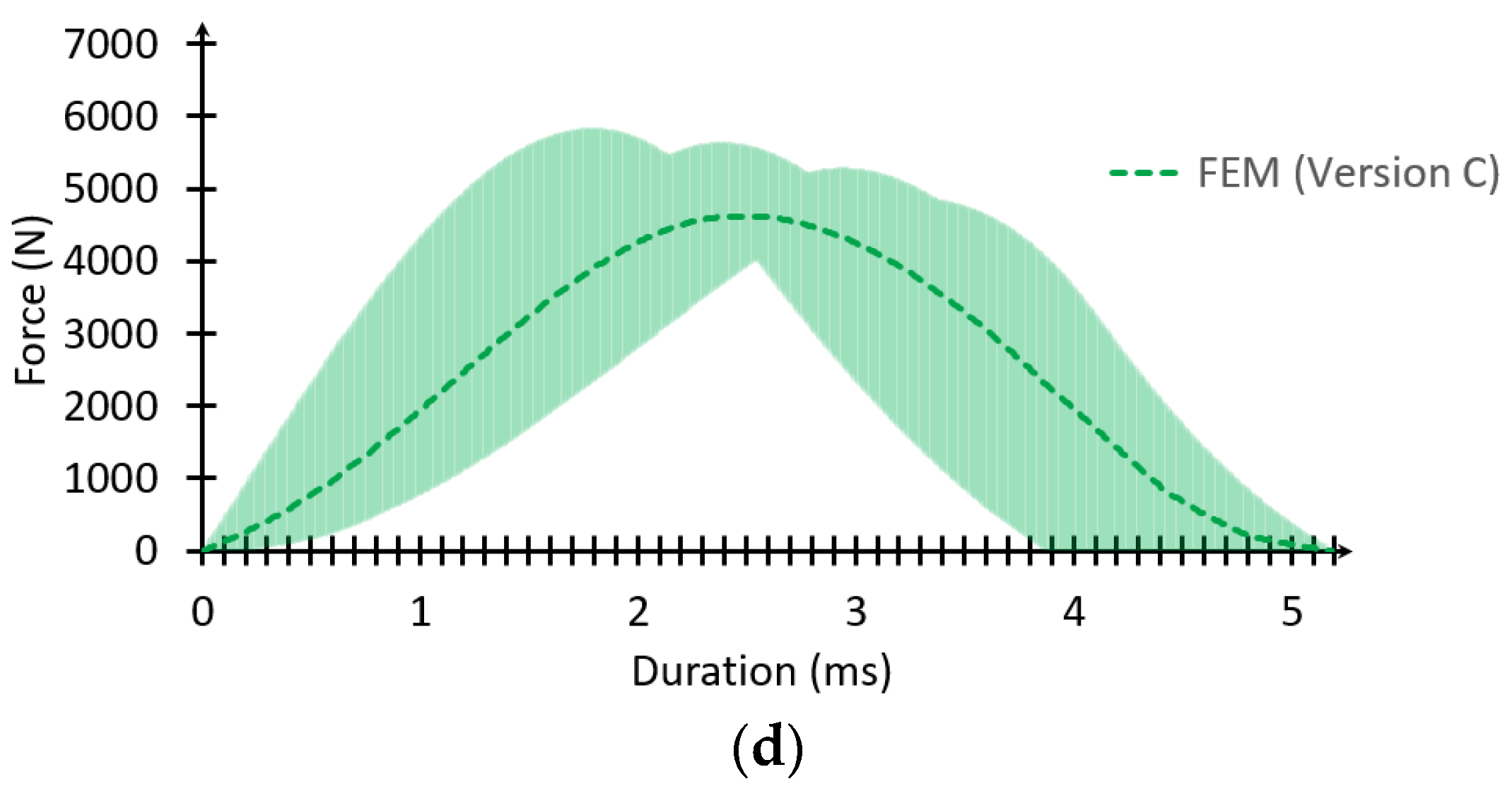
3.1. Results of FEM Drop Tests
3.2. Results of the Experimental Drop Tests
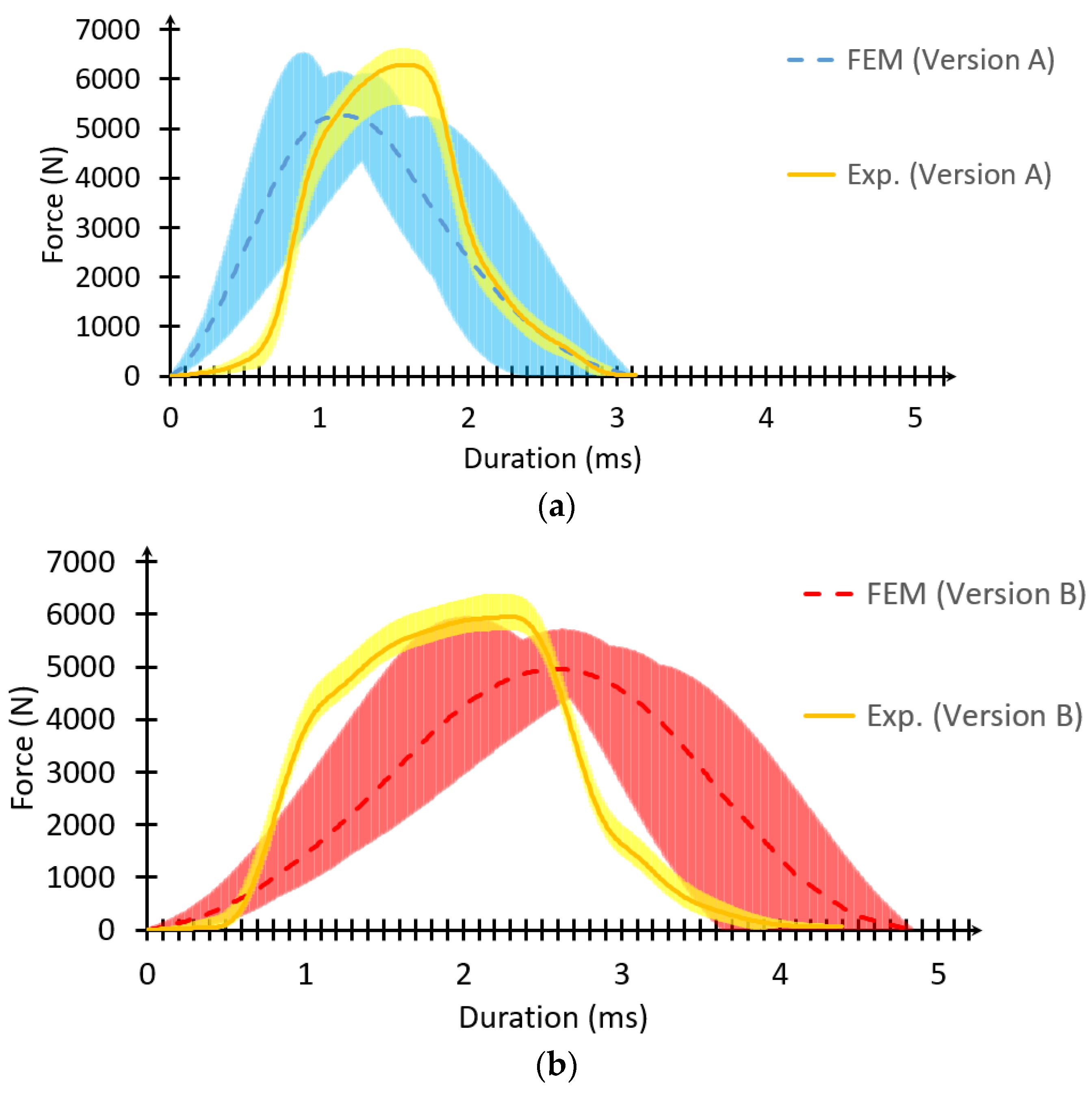
3.3. Comparison of FEM Results to Experimental Drop Tests
3.4. Limitations of This Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Commission. Commission Implementing Regulation (EU) No 923/2012; European Union: Brussels, Belgium, 2012. [Google Scholar]
- Dabberdt, W.F.; Turtiainen, H. OBSERVATIONS PLATFORMS|Radiosondes. In Encyclopedia of Atmospheric Sciences, 2nd ed.; North, G.R., Pyle, J., Zhang, F., Eds.; Academic Press: Oxford, UK, 2015; pp. 273–284. ISBN 978-0-12-382225-3. [Google Scholar] [CrossRef]
- Mills, N.J. Chapter 12—Product Packaging Case Study. In Polymer Foams Handbook; Mills, N.J., Ed.; Butterworth-Heinemann: Oxford, UK, 2007; pp. 281–306. ISBN 978-0-7506-8069-1. [Google Scholar] [CrossRef]
- Bhagavathula, K.B.; Meredith, C.S.; Ouellet, S.; Romanyk, D.L.; Hogan, J.D. Density, Strain Rate and Strain Effects on Mechanical Property Evolution in Polymeric Foams. Int. J. Impact Eng. 2022, 161, 104100. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Modeling Structures of Open Cell Foams. Comput. Mater. Sci. 2017, 131, 160–169. [Google Scholar] [CrossRef]
- Do, S.; Huynh, N.U.; Reed, N.; Mohammad Shaik, A.; Nacy, S.; Youssef, G. Partially-Perforated Self-Reinforced Polyurea Foams. Appl. Sci. 2020, 10, 5869. [Google Scholar] [CrossRef]
- Raut, N.P.; Kolekar, A.B.; Gombi, S.L. Methods of Damage Detection on Composites under Low Velocity Impact: Review. Mater. Today Proc. 2020, 27, 2823–2827. [Google Scholar] [CrossRef]
- Gara, N.; Ramachandran, V.; Rengaswamy, J. Analytical and FEM Analyses of High-Speed Impact Behaviour of Al 2024 Alloy. Aerospace 2021, 8, 281. [Google Scholar] [CrossRef]
- Zochowski, P.; Bajkowski, M.; Grygoruk, R.; Magier, M.; Burian, W.; Pyka, D.; Bocian, M.; Jamroziak, K. Comparison of Numerical Simulation Techniques of Ballistic Ceramics under Projectile Impact Conditions. Materials 2022, 15, 18. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Liu, C.; Zhu, X.; Zhou, D.; Lv, X.; Kuang, X. Translational Medical Bioengineering Research of Traumatic Brain Injury among Chinese and American Pedestrians Caused by Vehicle Collision Based on Human Body Finite Element Modeling. Front. Neurol. 2024, 14, 1296902. [Google Scholar] [CrossRef] [PubMed]
- Wdowicz, D.; Ptak, M. Numerical Approaches to Pedestrian Impact Simulation with Human Body Models: A Review. Arch. Comput. Methods Eng. 2023, 30, 4687–4709. [Google Scholar] [CrossRef]
- Aleksandrowicz, P. Modeling Head-On Collisions: The Problem of Identifying Collision Parameters. Appl. Sci. 2020, 10, 6212. [Google Scholar] [CrossRef]
- Porkolab, L.; Lakatos, I. Possibilities for Further Development of the Driver’s Seat in the Case of a Non-Conventional Seating Positions. Heliyon 2024, 10, e28909. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, S.; Farsi, H.; Kheiralipour, K. Drop Test of Pear Fruit: Experimental Measurement and Finite Element Modelling. Biosyst. Eng. 2016, 147, 17–25. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, L.; Guo, W.; Han, Z.; Wang, R.; Zhang, W.; Yuan, Y.; Gao, J.; Liu, S. Multiscale Static Compressive Damage Characteristics of Kiwifruit Based on the Finite Element Method. Foods 2024, 13, 785. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; He, Z.; Hao, W.; Li, K.; Ding, X.; Cui, Y. Kiwifruit Harvesting Damage Analysis and Verification. Processes 2023, 11, 598. [Google Scholar] [CrossRef]
- An, X.; Zhu, P.; Li, Z.; Fadiji, T.; Wani, A.A. Effect of Expanded Polyethylene (EPE) Foam Packing Net Design on the Mechanical Damage Resistance of Strawberry Fruit during Transportation. Food Packag. Shelf Life 2023, 40, 101193. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y. Investigation of Bird-Strike Resistance of Composite Sandwich Curved Plates with Lattice/Foam Cores. Thin-Walled Struct. 2023, 182, 110203. [Google Scholar] [CrossRef]
- Wang, F.; Lv, C.; Pan, Y.; Zhou, L.; Zhao, B. Efficient Non-Destructive Detection for External Defects of Kiwifruit. Appl. Sci. 2023, 13, 11971. [Google Scholar] [CrossRef]
- Hegyi, N.; Jósvai, J. Material Analysis For Light Unmanned Free Balloon Payload’s Outer Shell. In Proceedings of the 12th IEEE International Conference on Cognitive Infocommunications (2021), Online, 23–25 September 2021; Nikodem, J., Klempous, R., Eds.; IEEE: Piscataway, NJ, USA, 2021; pp. 903–908. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
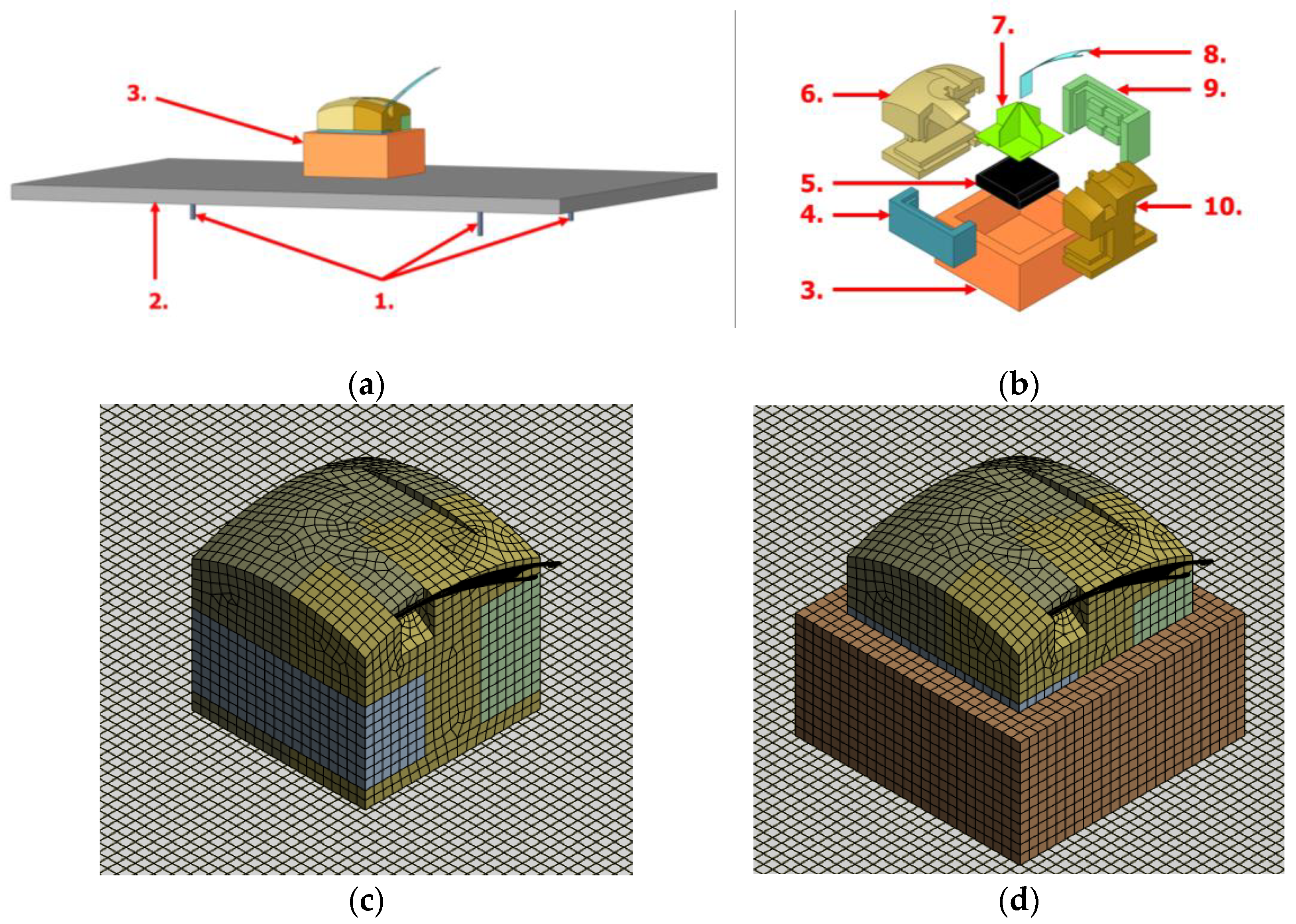





| Material | ρ (kg/m3) | E (Pa) | ν (-) | K (Pa) | G (Pa) | Constitutive Equation |
|---|---|---|---|---|---|---|
| EPS | 48 | 1.3767 × 107 | 0.0621 | 5.2400 × 106 | 6.481 × 106 | Crushable Foam |
| PUR foam 1 | 48 | 3.4500 × 105 | 0.0400 | 1.2500 × 105 | 1.659 × 105 | Mooney–Rivlin two-parameter model |
| PUR foam 2 | 96 | 3.3465 × 105 | 0.0400 | 1.2125 × 105 | 1.6089 × 105 | Mooney–Rivlin two-parameter model |
| C45 | 7800 | 2.1000 × 1011 | 0.3125 | 1.8670 × 1011 | 8.0000 × 1010 | Linear Elastic Model |
| PCB laminate, Epoxy/Glass fiber, FR-5.0 | 1045 | 3.5500 × 108 | 0.4144 | 6.9120 × 108 | 1.2549 × 108 | Linear Elastic Model |
| Test | Peak Force (N) | Average ±SD (N) | Duration (ms) | Average ±SD (ms) |
|---|---|---|---|---|
| Radiosonde 0° tilted (Version A) | 6121.47 | 5988.61 ± 540.03 | 2.45 | 2.68 ± 0.32 |
| Radiosonde 2.5° tilted (Version A) | 6508.56 | 2.41 | ||
| Radiosonde 5° tilted (Version A) | 6094.54 | 2.77 | ||
| Radiosonde 7.5° tilted (Version A) | 5229.87 | 3.10 | ||
| Radiosonde 0° tilted (Version B) | 5928.16 | 5501.68 ± 392.43 | 3.65 | 4.28 ± 0.52 |
| Radiosonde 2.5° tilted (Version B) | 5687.11 | 4.11 | ||
| Radiosonde 5° tilted (Version B) | 5366.80 | 4.49 | ||
| Radiosonde 7.5° tilted (Version B) | 5024.66 | 4.86 | ||
| Radiosonde 0° tilted (Version C) | 5803.69 | 5378.03 ± 421.94 | 3.89 | 4.58 ± 0.55 |
| Radiosonde 2.5° tilted (Version C) | 5608.85 | 4.43 | ||
| Radiosonde 5° tilted (Version C) | 5254.92 | 4.82 | ||
| Radiosonde 7.5° tilted (Version C) | 4844.67 | 5.18 |
| Test | Maximal Size at Deformation (mm) | Average ±SD (mm) |
|---|---|---|
| Radiosonde (Version B) | 134.21 | 140.77 ± 5.93 |
| Radiosonde 2.5° tilted (Version B) | 137.91 | |
| Radiosonde 5° tilted (Version B) | 143.23 | |
| Radiosonde 7.5° tilted (Version B) | 147.71 | |
| Radiosonde (Version C) | 133.84 | 140.86 ± 6.13 |
| Radiosonde 2.5° tilted (Version C) | 138.31 | |
| Radiosonde 5° tilted (Version C) | 143.27 | |
| Radiosonde 7.5° tilted (Version C) | 148.02 |
| Test | Peak Force (N) | Average ±SD (N) | Duration (ms) | Average ±SD (ms) |
|---|---|---|---|---|
| Radiosonde (Version A)–Exp. 1 | 5976.5 | 6244.58 ± 484.53 | 3.1 | 3.02 ± 0.13 |
| Radiosonde (Version A)–Exp. 2 | 6628.6 | 2.9 | ||
| Radiosonde (Version A)–Exp. 3 | 6492.1 | 2.9 | ||
| Radiosonde (Version A)–Exp. 4 | 6607.1 | 3.0 | ||
| Radiosonde (Version A)–Exp. 5 | 5518.6 | 3.2 | ||
| Radiosonde (Version B)–Exp. 1 | 6390.5 | 5928.2 ± 332.84 | 3.7 | 4.13 ± 0.26 |
| Radiosonde (Version B)–Exp. 2 | 5981.4 | 4.2 | ||
| Radiosonde (Version B)–Exp. 3 | 5685.5 | 4.4 | ||
| Radiosonde (Version B)–Exp. 4 | 6047.2 | 4.2 | ||
| Radiosonde (Version B)–Exp. 5 | 5536.4 | 4.2 |
| Test | Maximal Size at Deformation (mm) | Average ±SD (mm) |
|---|---|---|
| Radiosonde (Version B)–Exp. 1 | 135 | 138 ± 3.61 |
| Radiosonde (Version B)–Exp. 2 | 142 | |
| Radiosonde (Version B)–Exp. 3 | 137 | |
| FEM (Version B) | - | 140.77 ± 5.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hegyi, N.; Jósvai, J.; Fekete, G. Numerical and Experimental Analysis of Impact Force and Impact Duration with Regard to Radiosondes: Is a PUR Foam Shell an Effective Solution? Appl. Mech. 2025, 6, 19. https://doi.org/10.3390/applmech6010019
Hegyi N, Jósvai J, Fekete G. Numerical and Experimental Analysis of Impact Force and Impact Duration with Regard to Radiosondes: Is a PUR Foam Shell an Effective Solution? Applied Mechanics. 2025; 6(1):19. https://doi.org/10.3390/applmech6010019
Chicago/Turabian StyleHegyi, Norbert, János Jósvai, and Gusztáv Fekete. 2025. "Numerical and Experimental Analysis of Impact Force and Impact Duration with Regard to Radiosondes: Is a PUR Foam Shell an Effective Solution?" Applied Mechanics 6, no. 1: 19. https://doi.org/10.3390/applmech6010019
APA StyleHegyi, N., Jósvai, J., & Fekete, G. (2025). Numerical and Experimental Analysis of Impact Force and Impact Duration with Regard to Radiosondes: Is a PUR Foam Shell an Effective Solution? Applied Mechanics, 6(1), 19. https://doi.org/10.3390/applmech6010019






