Inverse Uncertainty Quantification in Material Parameter Calibration Using Probabilistic and Interval Approaches
Abstract
1. Introduction
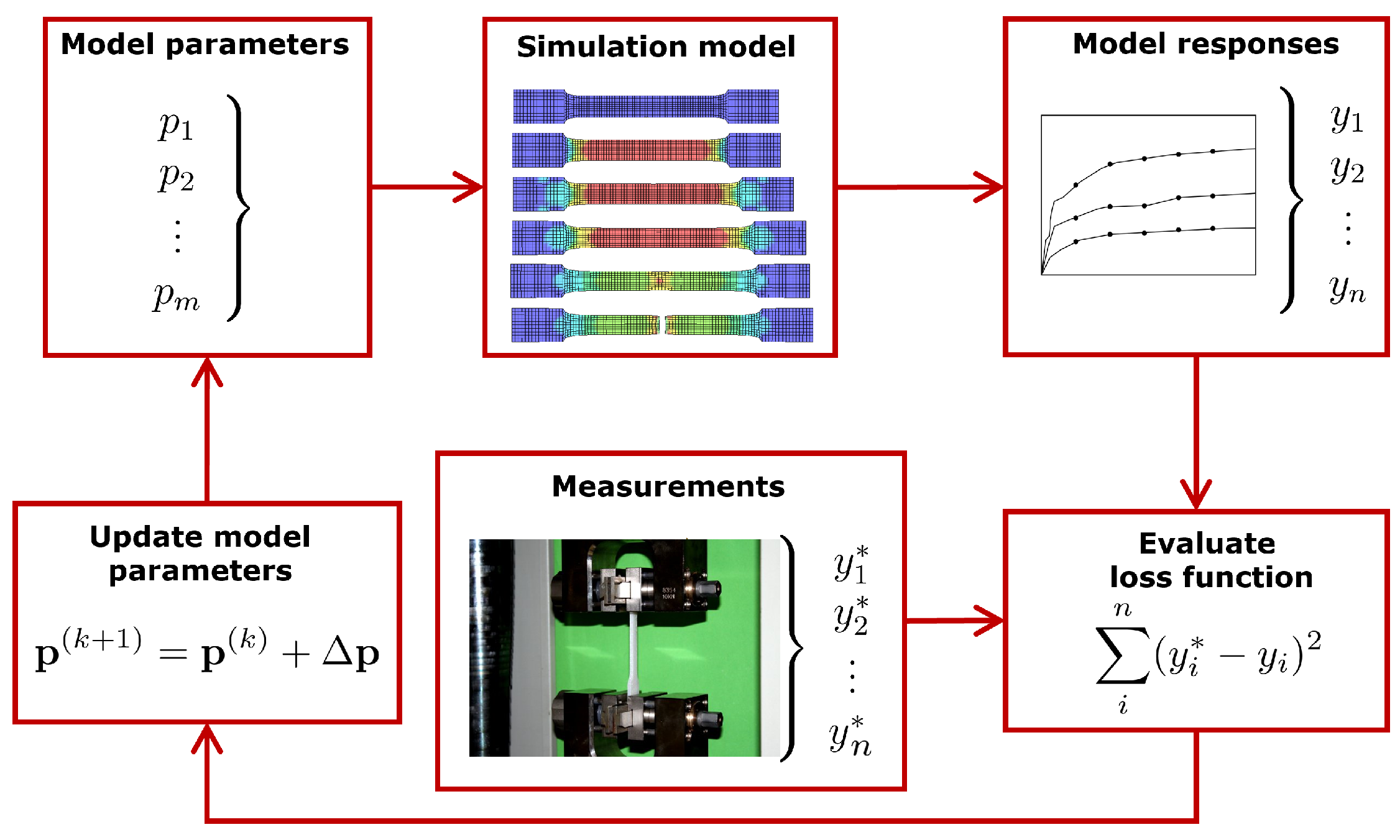
2. Materials and Methods
2.1. Sensitivity Analysis of the Forward Problem
2.2. Maximum Likelihood Approach
2.3. Bayesian Updating
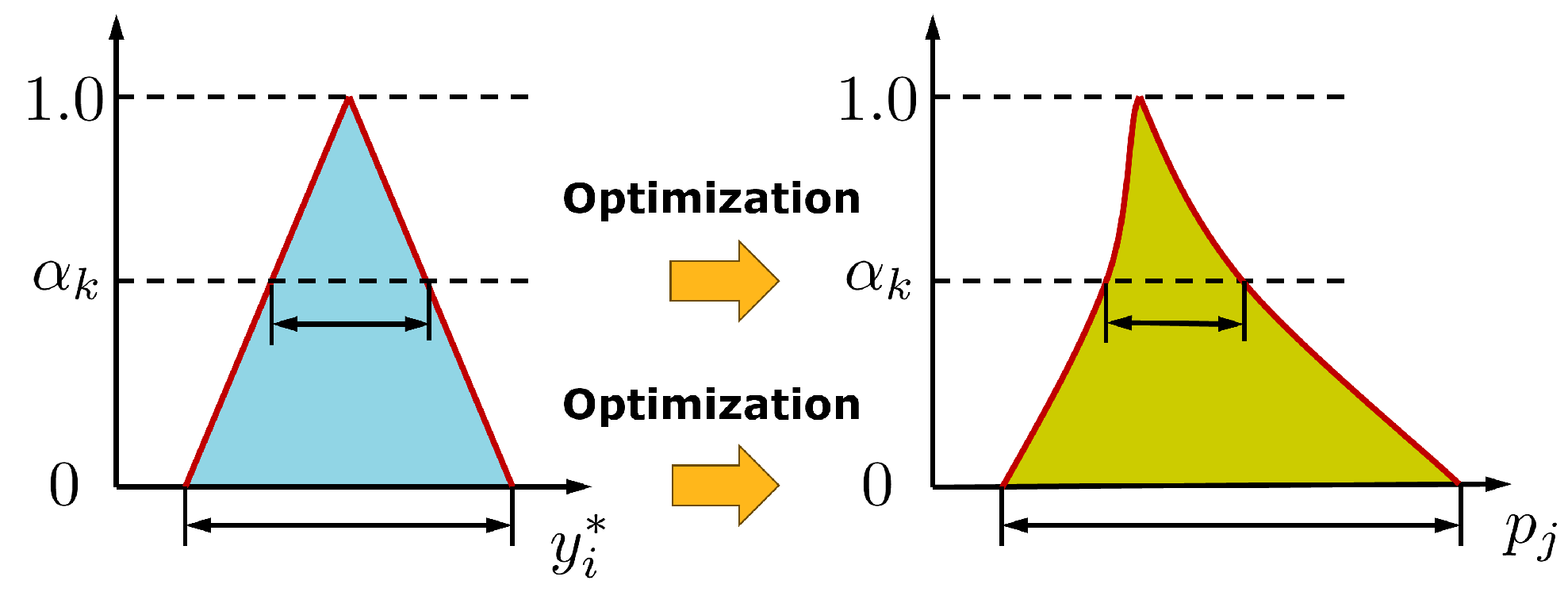
2.4. Interval Optimization
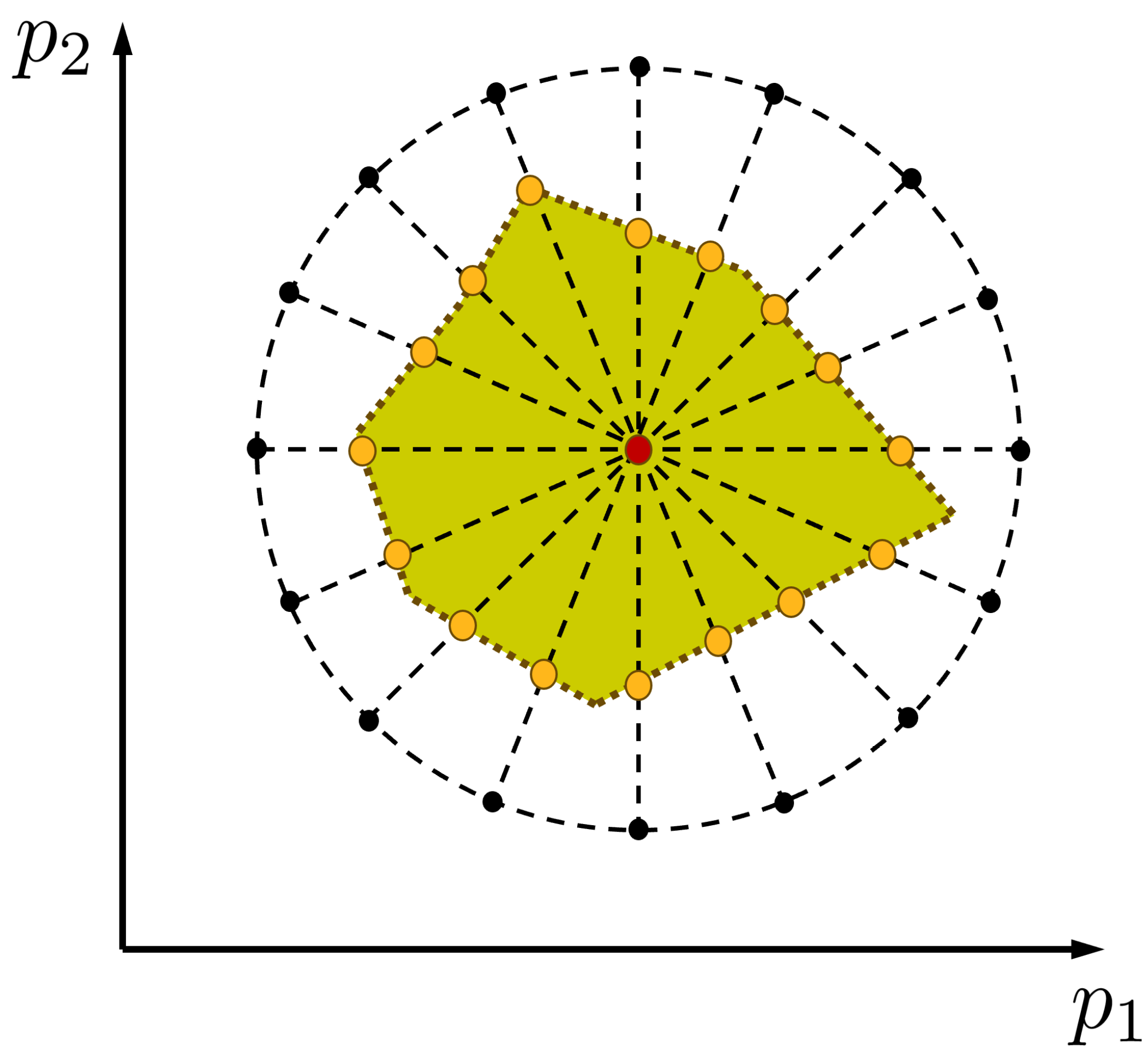
2.5. Radial Line-Search Approach
3. Results
3.1. Bilinear Elasto-Plasticity Model
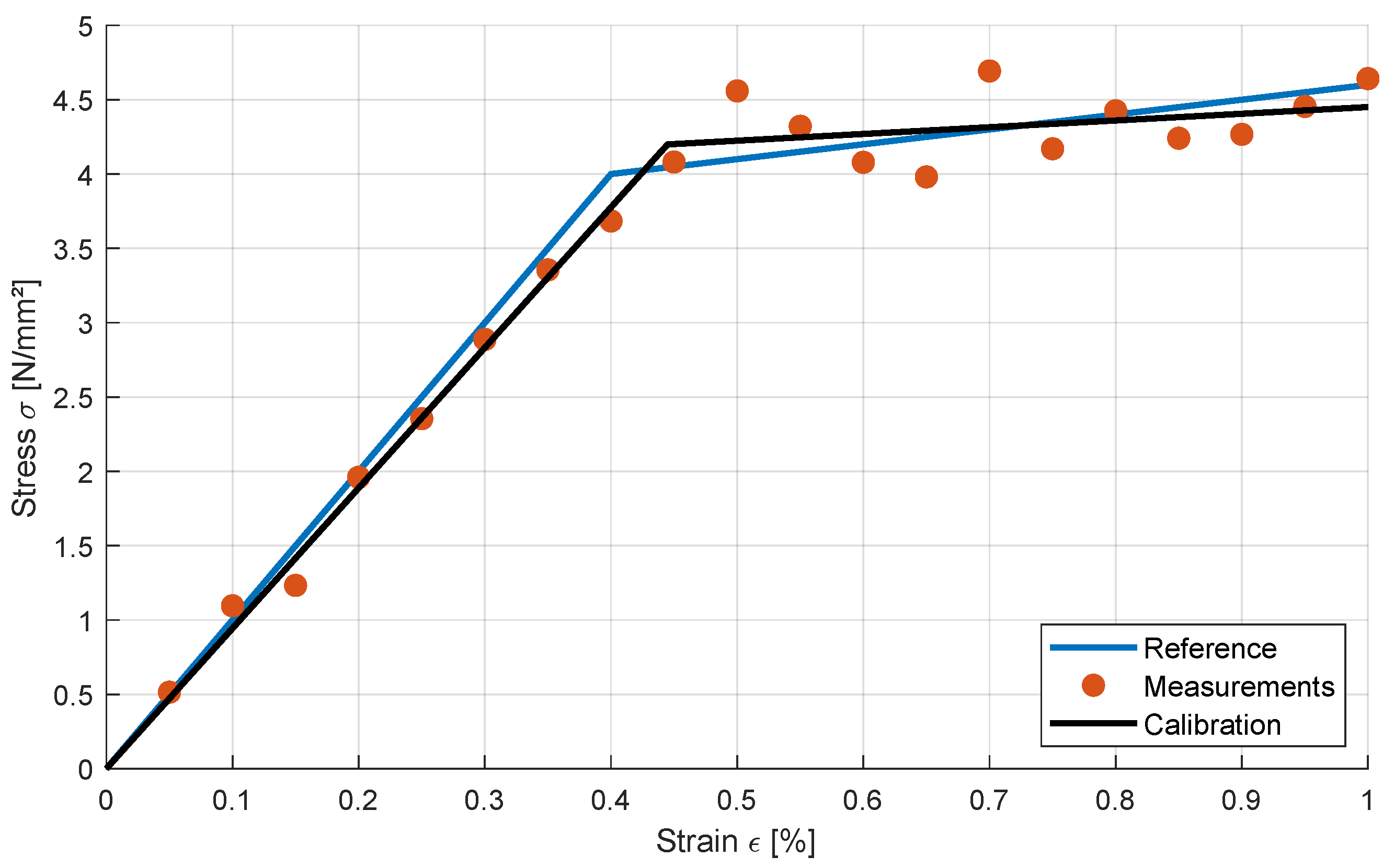
3.1.1. Deterministic Calibration with Noisy Measurements
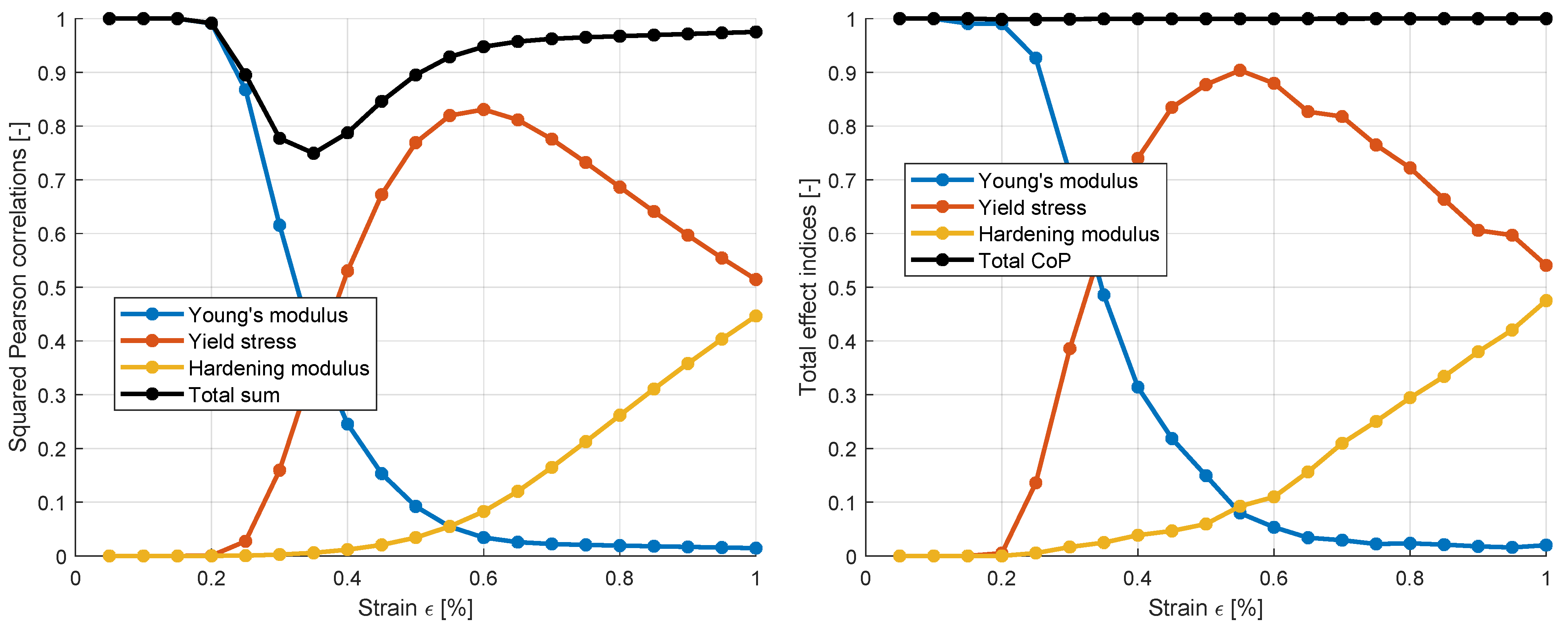
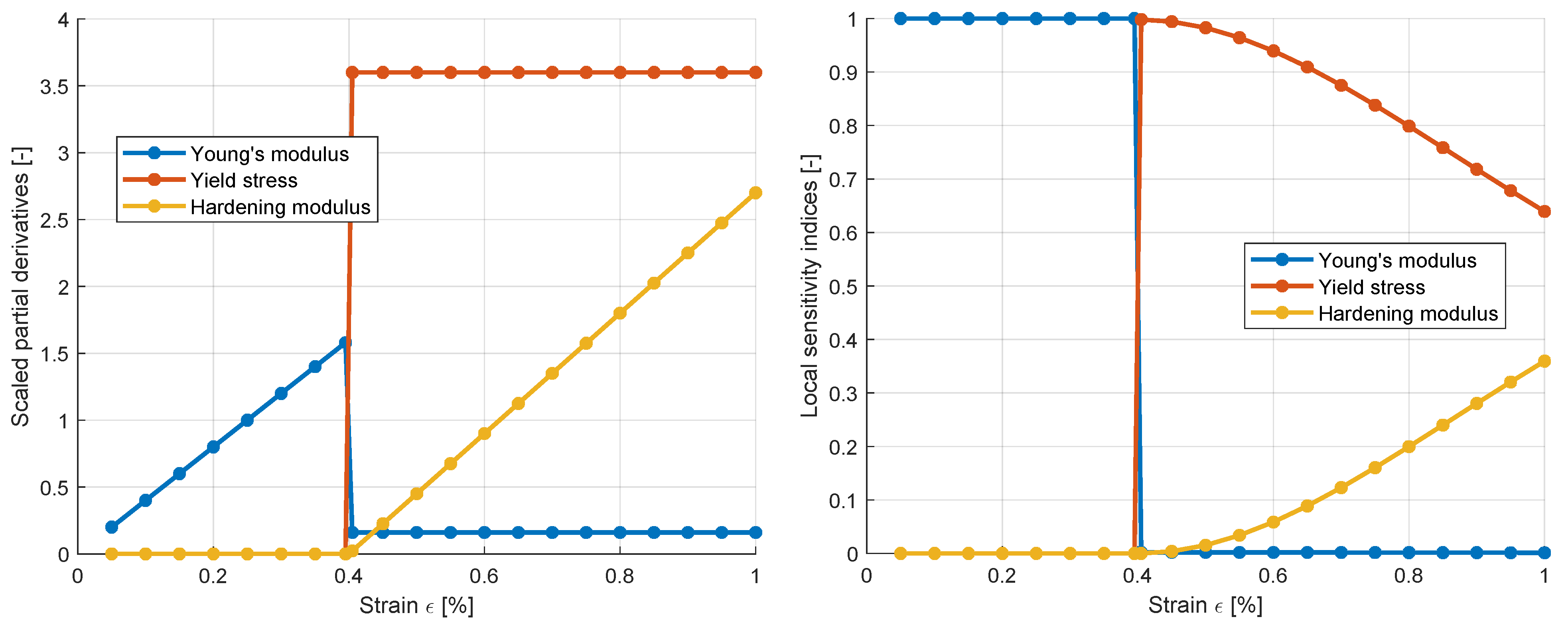
3.1.2. Sensitivity Analysis
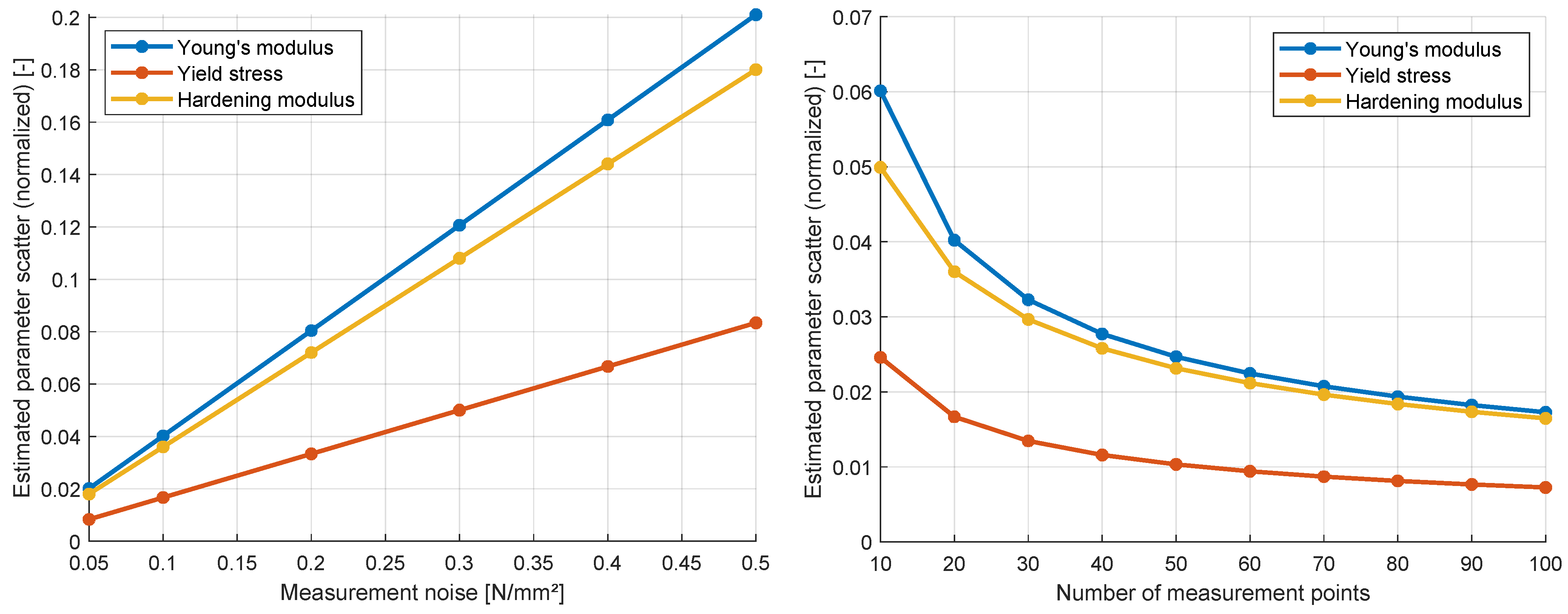
3.1.3. Maximum Likelihood Approach
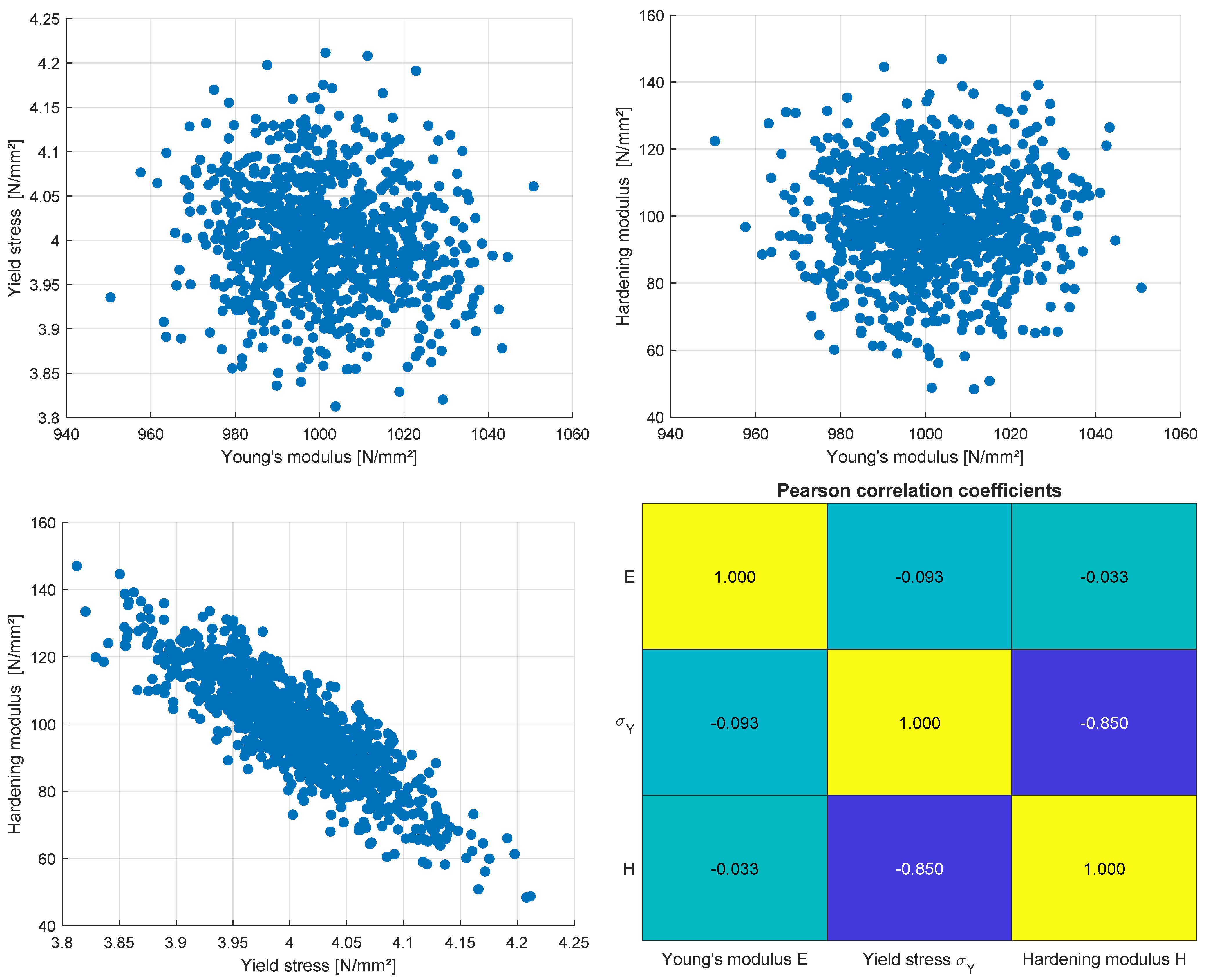
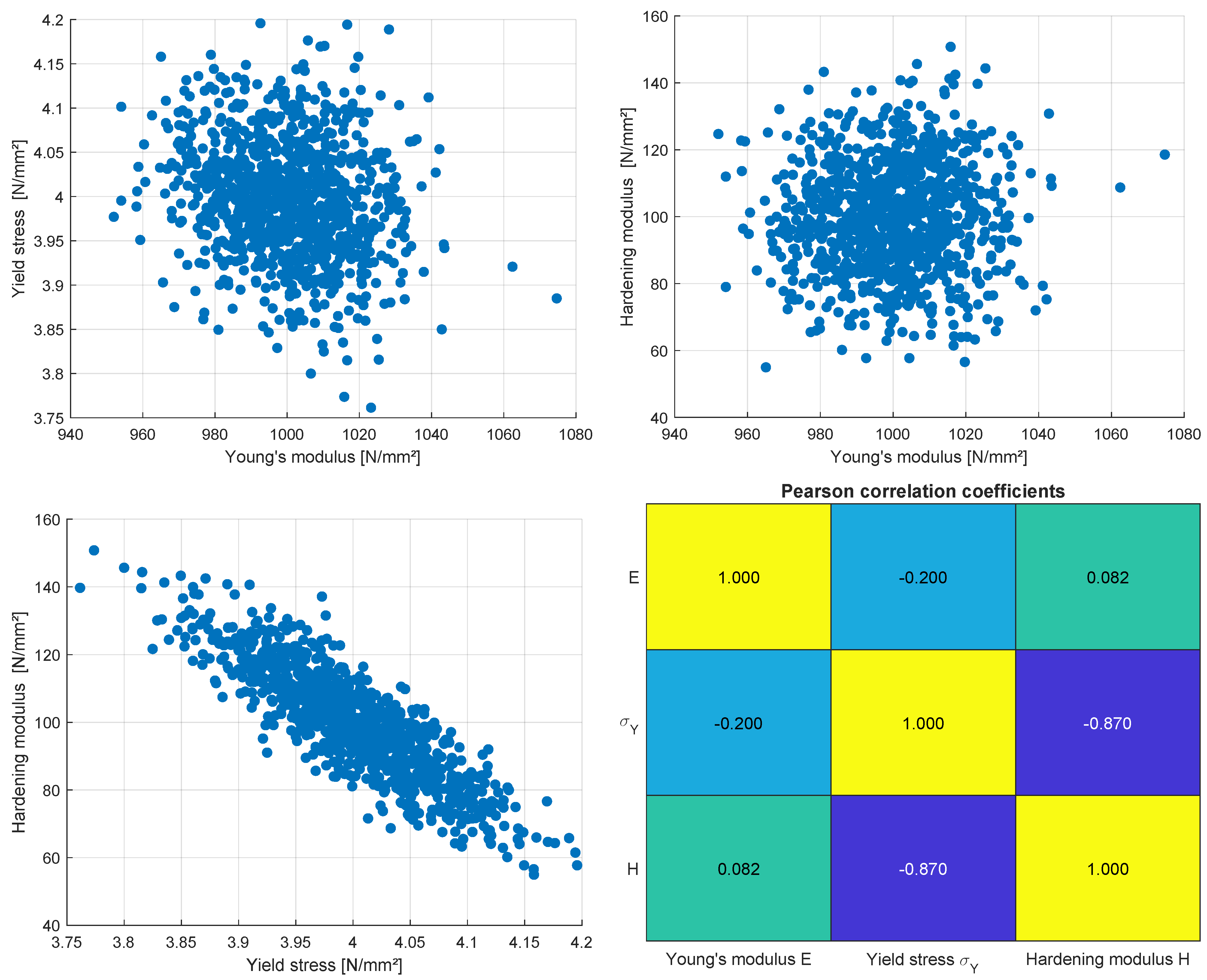
3.1.4. Bayesian Updating
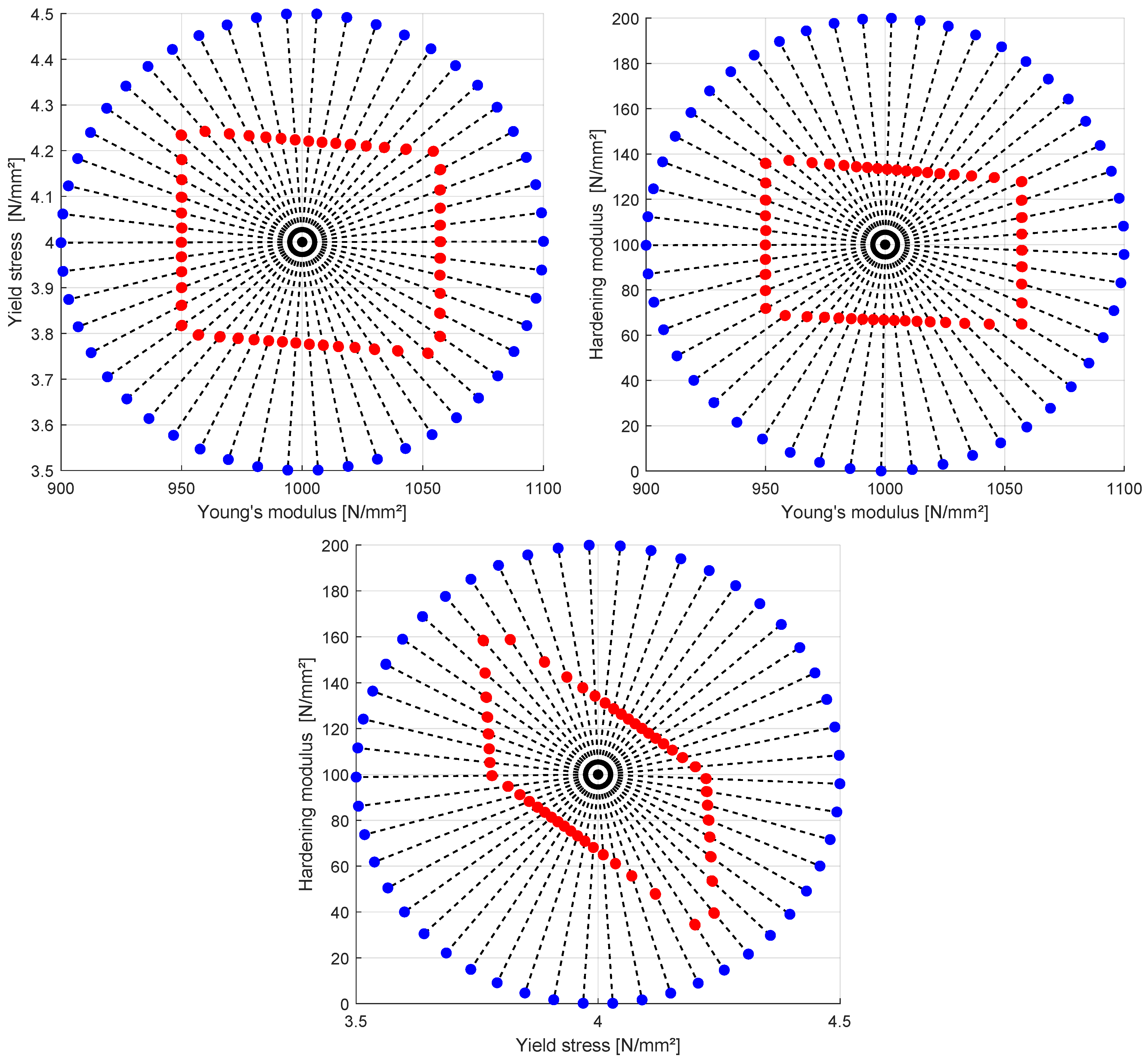
3.1.5. Interval Optimization and Radial Line-Search

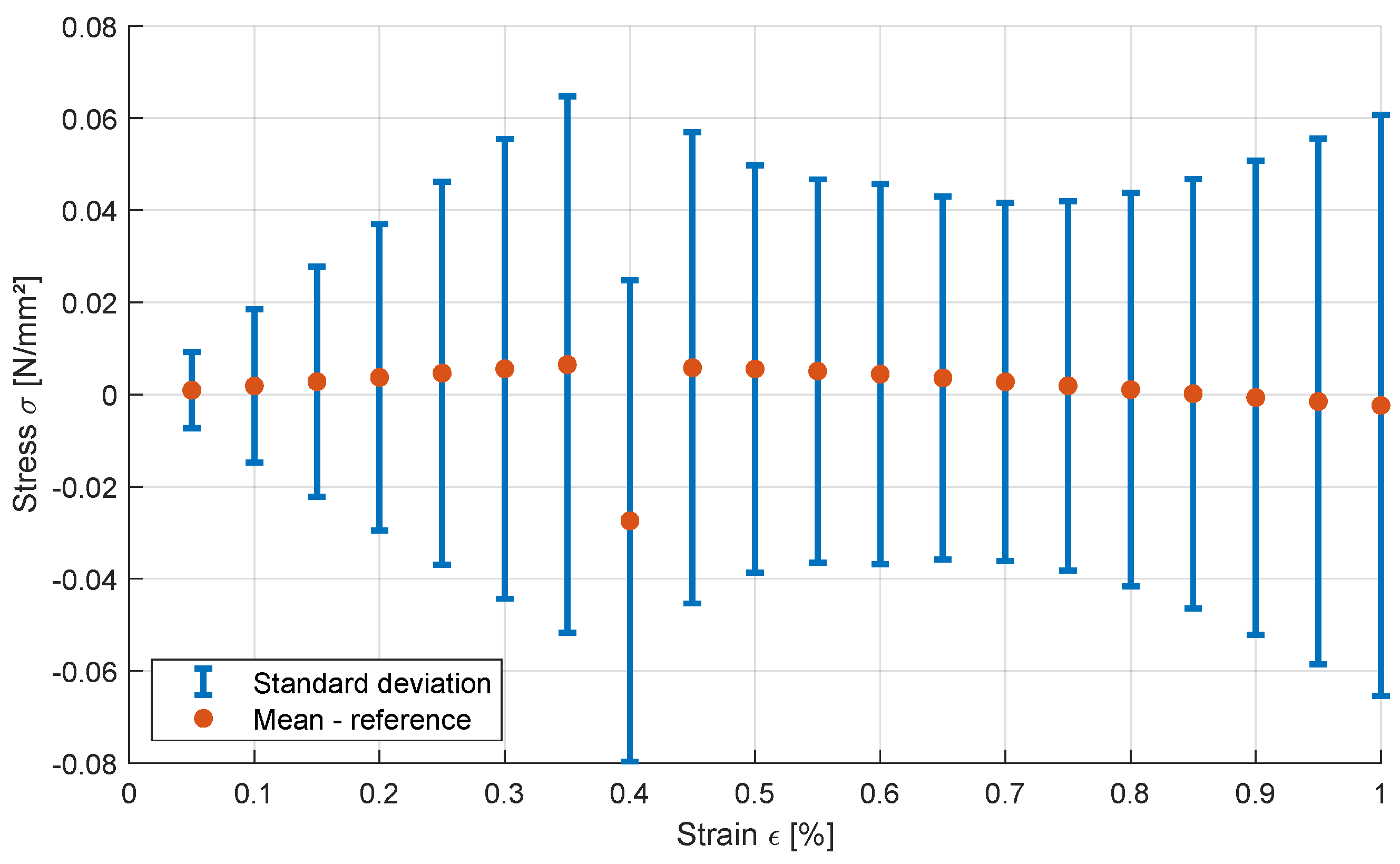
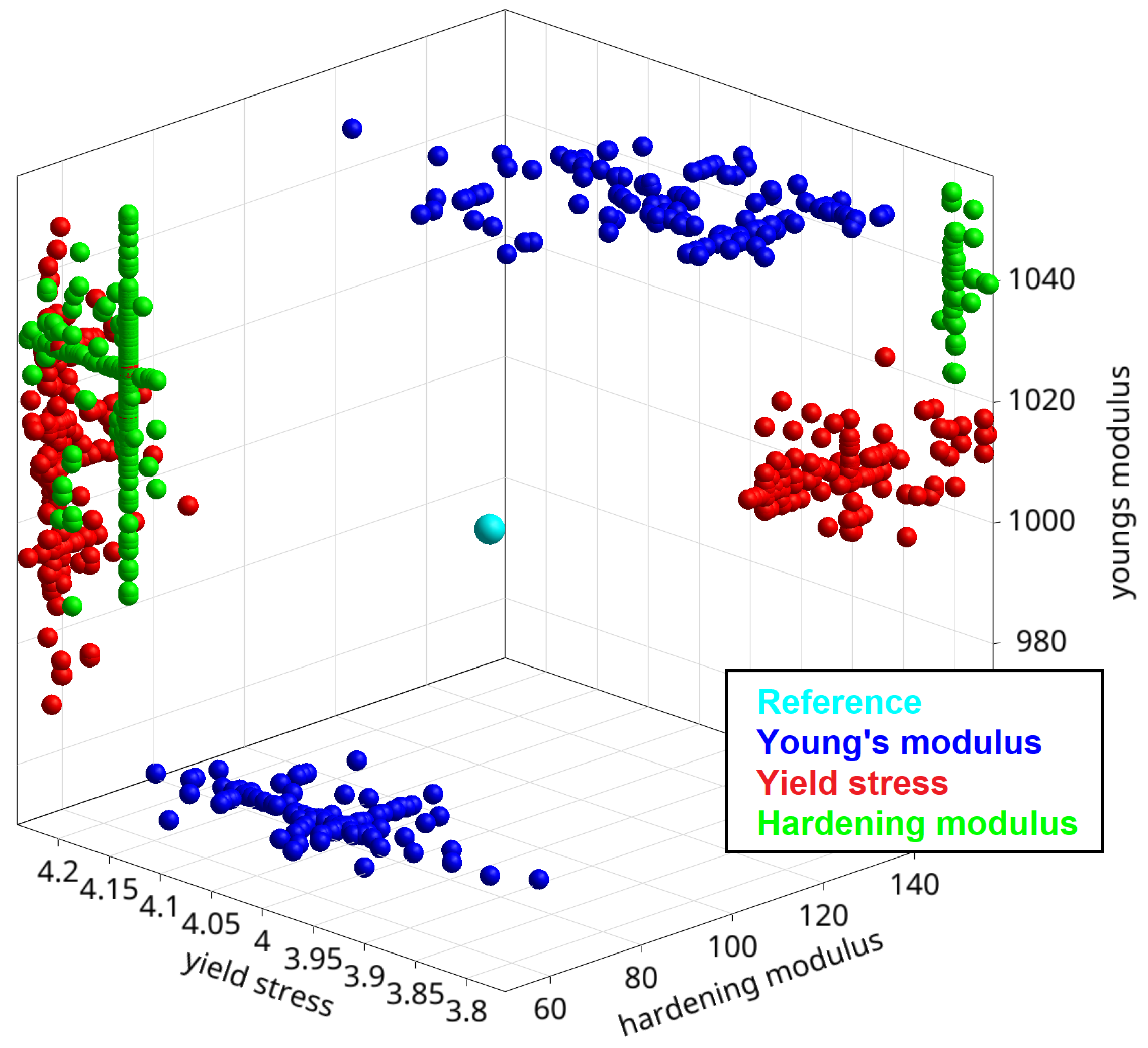
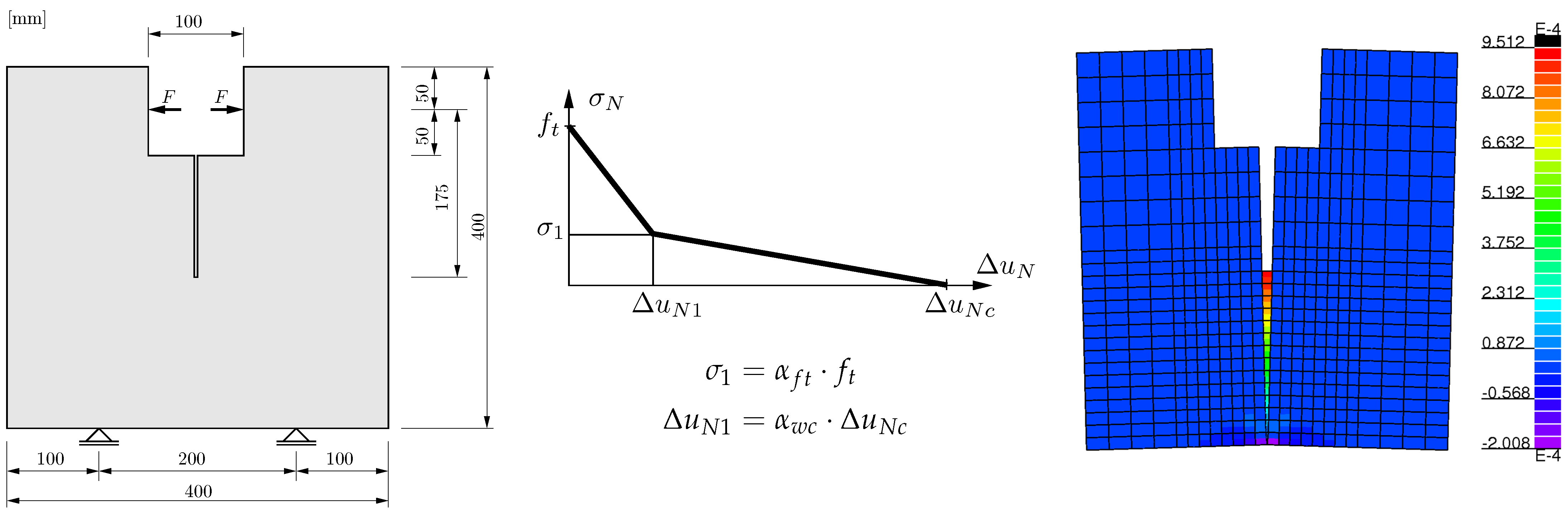
3.2. Tension-Softening Model for Concrete Cracking
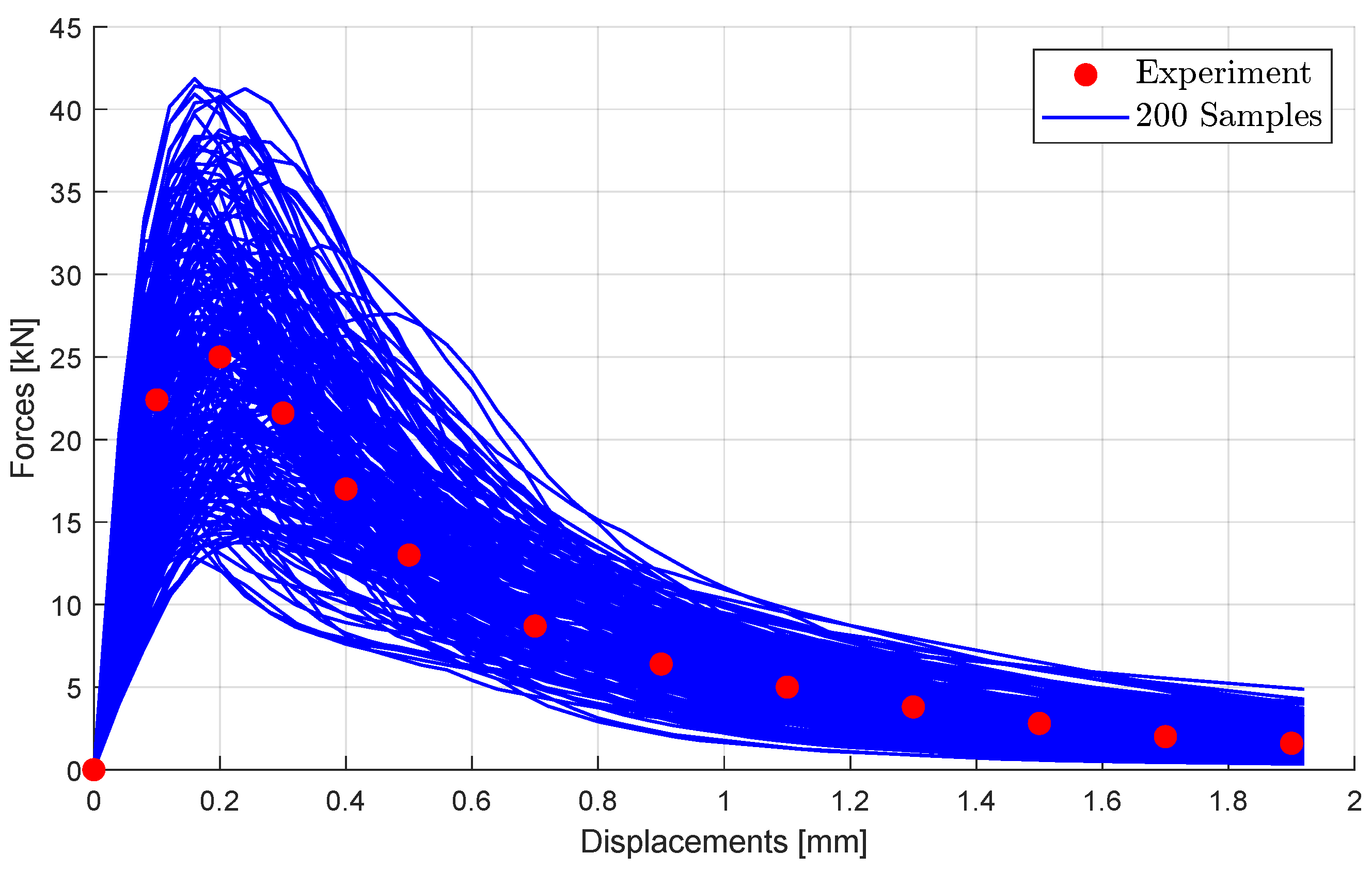
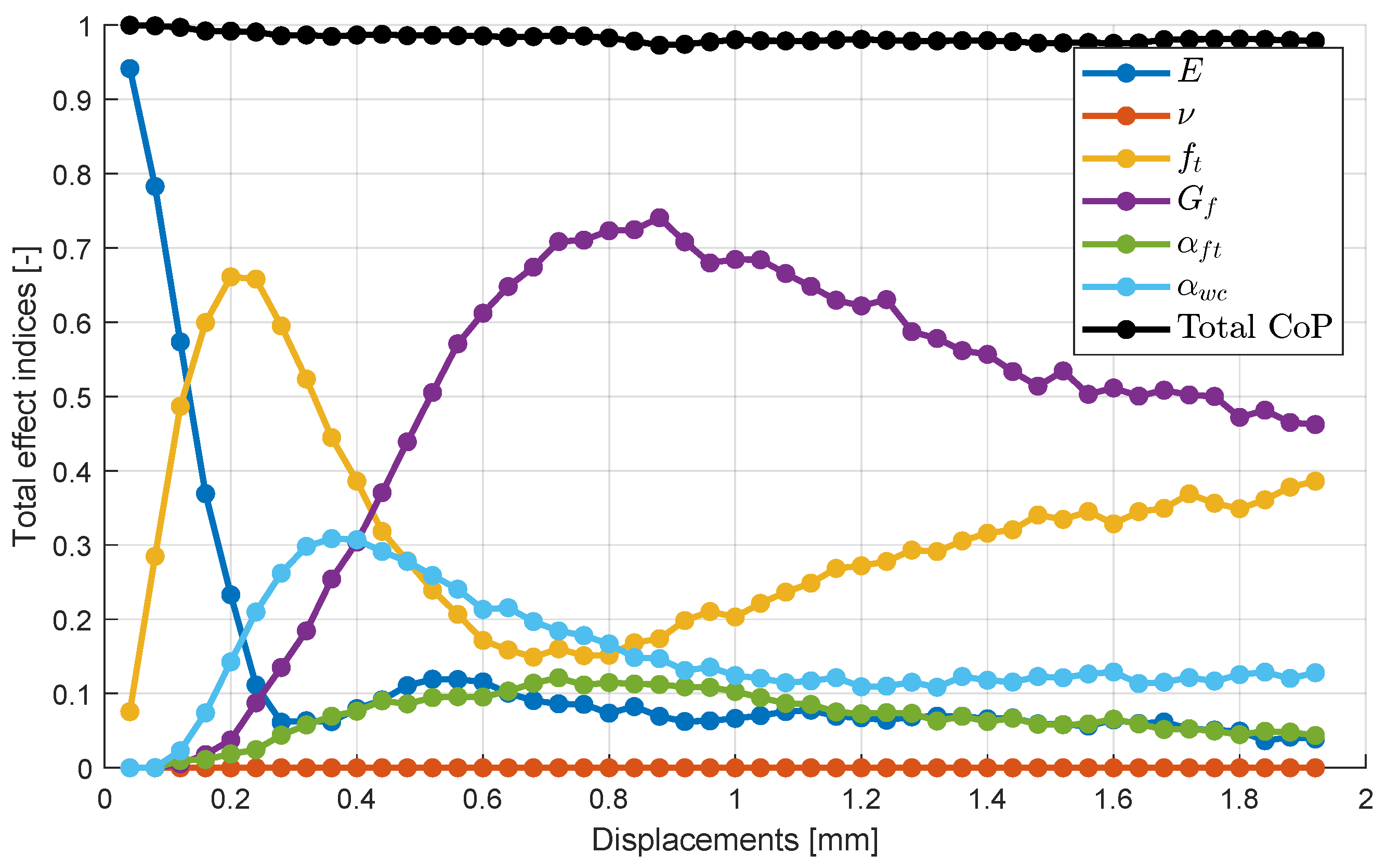
3.2.1. Sensitivity Analysis and Deterministic Parameter Optimization
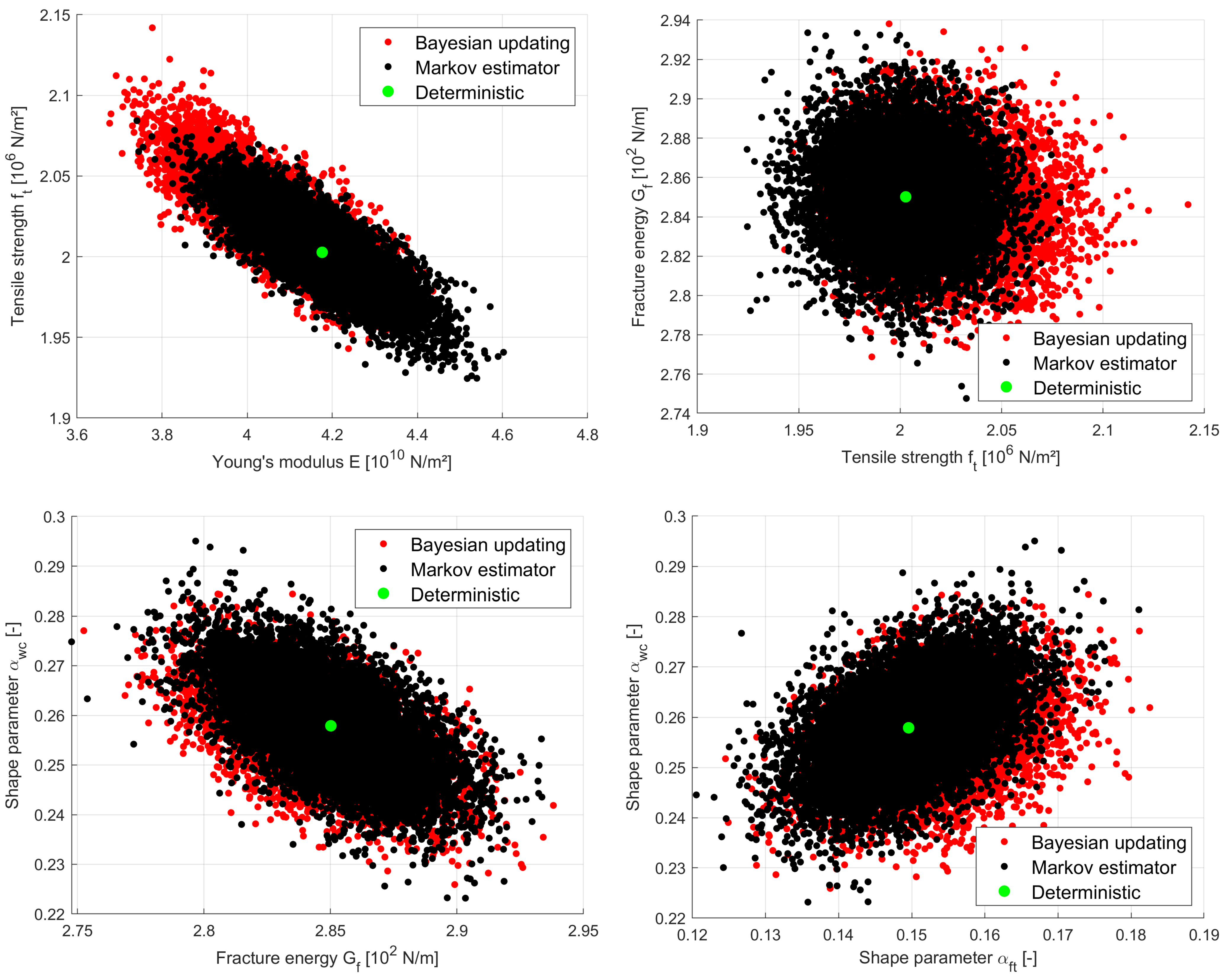
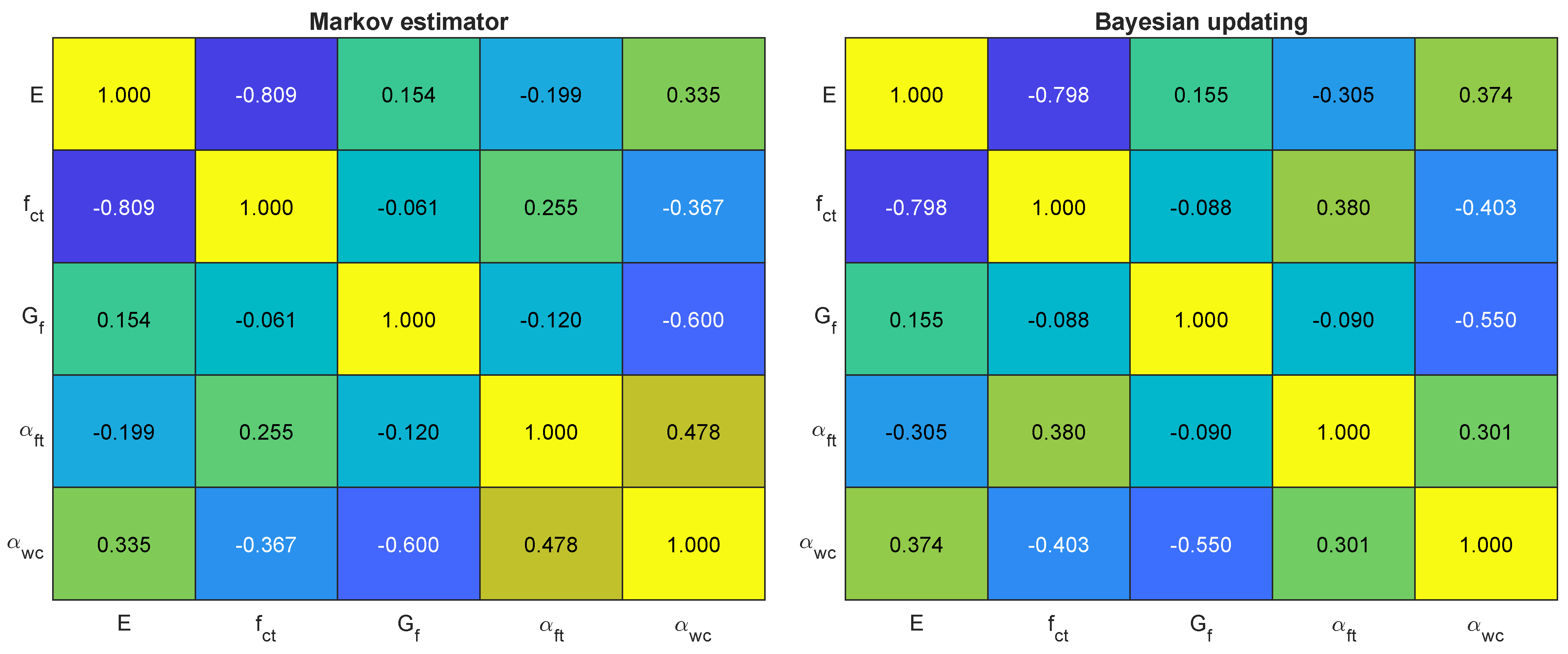
3.2.2. Probabilistic Uncertainty Estimation
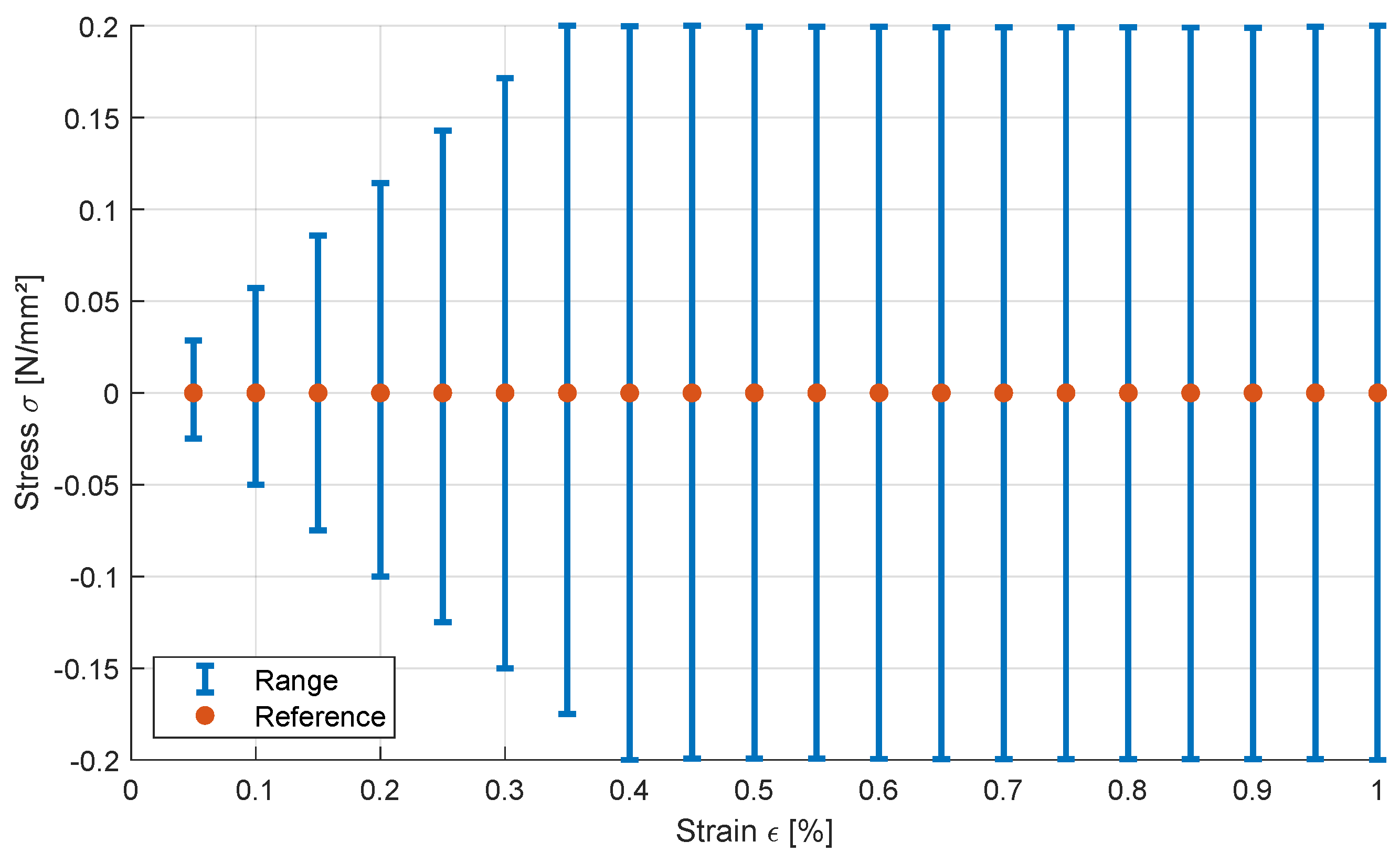
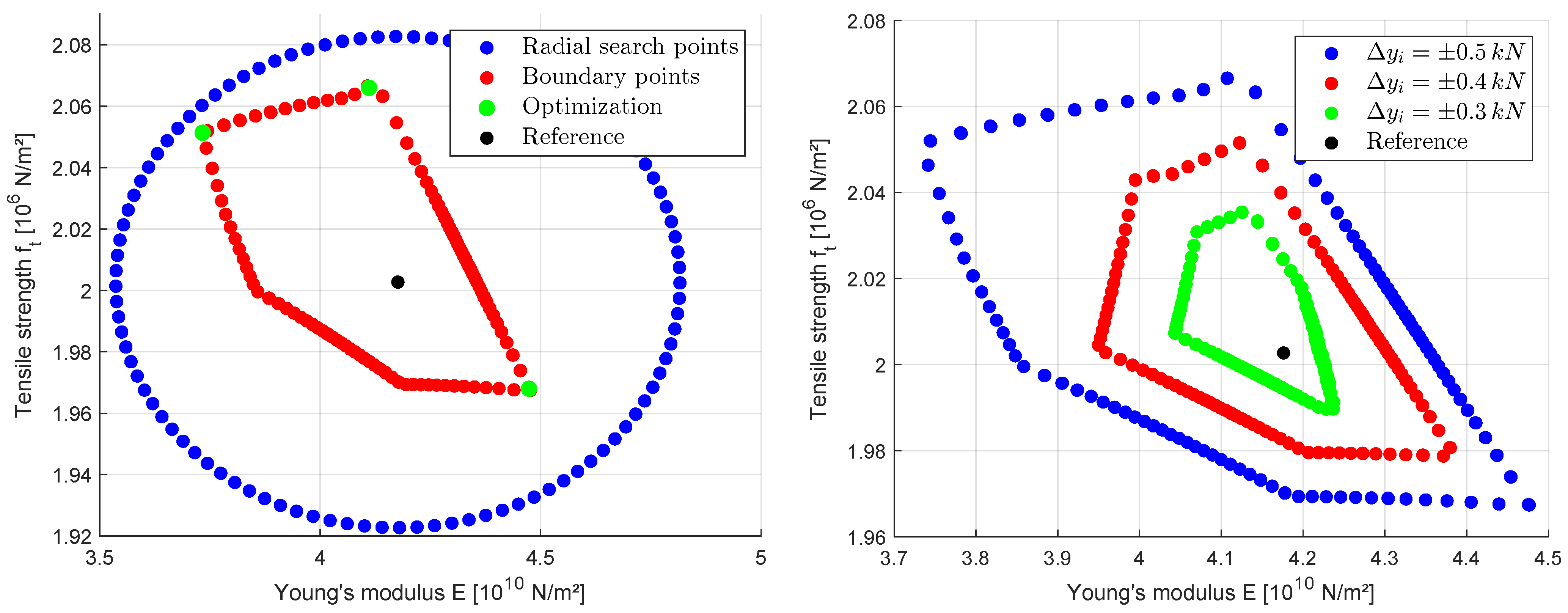
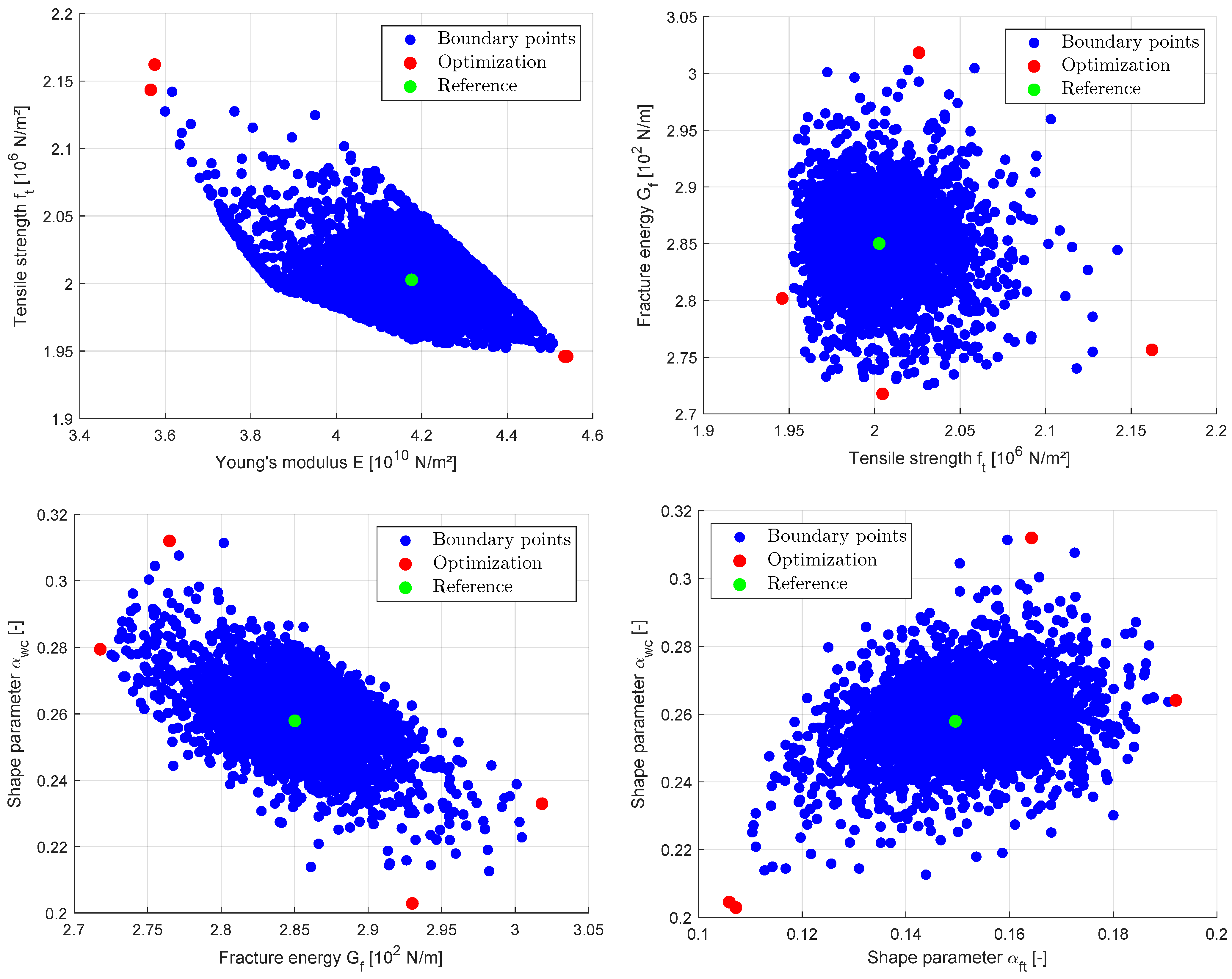
3.2.3. Interval Approaches
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCMC | Markov Chain Monte Carlo; |
| CoP | Coefficient of Prognosis; |
| CoV | Coefficient of Variation; |
| LHS | Latin Hypercube Sampling; |
| MOP | Metamodel of Optimal Prognosis. |
References
- Beck, J.V.; Arnold, K.J. Parameter Estimation in Engineering and Science; Wiley Interscience: New York, NY, USA, 1977. [Google Scholar]
- Most, T. Identification of the parameters of complex constitutive models: Least squares minimization vs. Bayesian updating. In Proceedings of the 15th Working Conference IFIP Working Group 7.5 on Reliability and Optimization of Structural Systems, Munich, Germany, 7–10 April 2010. [Google Scholar]
- Ereiz, S.; Duvnjak, I.; Fernando Jiménez-Alonso, J. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Machaček, J.; Staubach, P.; Tavera, C.E.G.; Wichtmann, T.; Zachert, H. On the automatic parameter calibration of a hypoplastic soil model. Acta Geotech. 2022, 17, 5253–5273. [Google Scholar] [CrossRef]
- Scholz, B. Application of a Micropolar Model to the Localization Phenomena in Granular Materials: General Model, Sensitivity Analysis and Parameter Optimization. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal Process. 2015, 56, 123–149. [Google Scholar] [CrossRef]
- Ledesma, A.; Gens, A.; Alonso, E. Estimation of parameters in geotechnical backanalysis—I. Maximum likelihood approach. Comput. Geotech. 1996, 18, 1–27. [Google Scholar] [CrossRef]
- Rappel, H.; Beex, L.A.; Noels, L.; Bordas, S. Identifying elastoplastic parameters with Bayes’ theorem considering output error, input error and model uncertainty. Probabilistic Eng. Mech. 2019, 55, 28–41. [Google Scholar] [CrossRef]
- Rappel, H.; Beex, L.A.; Hale, J.S.; Noels, L.; Bordas, S. A tutorial on Bayesian inference to identify material parameters in solid mechanics. Arch. Comput. Methods Eng. 2020, 27, 361–385. [Google Scholar] [CrossRef]
- Bi, S.; Beer, M.; Cogan, S.; Mottershead, J. Stochastic model updating with uncertainty quantification: An overview and tutorial. Mech. Syst. Signal Process. 2023, 204, 110784. [Google Scholar] [CrossRef]
- Tang, X.S.; Huang, H.B.; Liu, X.F.; Li, D.Q.; Liu, Y. Efficient Bayesian method for characterizing multiple soil parameters using parametric bootstrap. Comput. Geotech. 2023, 156, 105296. [Google Scholar] [CrossRef]
- Lye, A.; Cicirello, A.; Patelli, E. Sampling methods for solving Bayesian model updating problems: A tutorial. Mech. Syst. Signal Process. 2021, 159, 107760. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- de Pablos, J.L.; Menga, E.; Romero, I. A methodology for the statistical calibration of complex constitutive material models: Application to temperature-dependent elasto-visco-plastic materials. Materials 2020, 13, 4402. [Google Scholar] [CrossRef] [PubMed]
- Unger, J.F.; Könke, C. An inverse parameter identification procedure assessing the quality of the estimates using Bayesian neural networks. Appl. Soft Comput. 2011, 11, 3357–3367. [Google Scholar] [CrossRef]
- Lucas, A.; Iliadis, M.; Molina, R.; Katsaggelos, A.K. Using deep neural networks for inverse problems in imaging: Beyond analytical methods. IEEE Signal Process. Mag. 2018, 35, 20–36. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. Regularization, Bayesian inference, and machine learning methods for inverse problems. Entropy 2021, 23, 1673. [Google Scholar] [CrossRef] [PubMed]
- Cividini, A.; Maier, G.; Nappi, A. Parameter estimation of a static geotechnical model using a Bayes’ approach. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 215–226. [Google Scholar] [CrossRef]
- Bolzon, G.; Fedele, R.; Maier, G. Parameter identification of a cohesive crack model by Kalman filter. Comput. Methods Appl. Mech. Eng. 2002, 191, 2847–2871. [Google Scholar] [CrossRef]
- Furukawa, T.; Pan, J.W. Stochastic identification of elastic constants for anisotropic materials. Int. J. Numer. Methods Eng. 2010, 81, 429–452. [Google Scholar] [CrossRef]
- Beer, M.; Ferson, S.; Kreinovich, V. Imprecise probabilities in engineering analyses. Mech. Syst. Signal Process. 2013, 37, 4–29. [Google Scholar] [CrossRef]
- Faes, M.; Moens, D. Recent trends in the modeling and quantification of non-probabilistic uncertainty. Arch. Comput. Methods Eng. 2020, 27, 633–671. [Google Scholar] [CrossRef]
- Kolumban, S.; Vajk, I.; Schoukens, J. Approximation of confidence sets for output error systems using interval analysis. J. Control Eng. Appl. Inform. 2012, 14, 73–79. [Google Scholar]
- Crespo, L.G.; Kenny, S.P.; Colbert, B.K.; Slagel, T. Interval predictor models for robust system identification. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 872–879. [Google Scholar]
- van Kampen, E.; Chu, Q.; Mulder, J. Interval analysis as a system identification tool. In Proceedings of the Advances in Aerospace Guidance, Navigation and Control: Selected Papers of the 1st CEAS Specialist Conference on Guidance, Navigation and Control, Munich, Germany, 13–15 April 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 333–343. [Google Scholar]
- Fang, S.E.; Zhang, Q.H.; Ren, W.X. An interval model updating strategy using interval response surface models. Mech. Syst. Signal Process. 2015, 60, 909–927. [Google Scholar] [CrossRef]
- Möller, B.; Graf, W.; Beer, M. Fuzzy structural analysis using α-level optimization. Comput. Mech. 2000, 26, 547–565. [Google Scholar] [CrossRef]
- Gabriele, S.; Valente, C. An interval-based technique for FE model updating. Int. J. Reliab. Saf. 2009, 3, 79–103. [Google Scholar] [CrossRef]
- Khodaparast, H.H.; Mottershead, J.; Badcock, K. Interval model updating: Method and application. In Proceedings of the ISMA, University of, Leuven, Leuven, Belgium, 20–22 September 2010. [Google Scholar]
- Liao, B.; Zhao, R.; Yu, K.; Liu, C. A novel interval model updating framework based on correlation propagation and matrix-similarity method. Mech. Syst. Signal Process. 2022, 162, 108039. [Google Scholar] [CrossRef]
- Mo, J.; Yan, W.J.; Yuen, K.V.; Beer, M. Efficient non-probabilistic parallel model updating based on analytical correlation propagation formula and derivative-aware deep neural network metamodel. Comput. Methods Appl. Mech. Eng. 2025, 433, 117490. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar]
- Most, T.; Will, J. Sensitivity analysis using the Metamodel of Optimal Prognosis. In Proceedings of the 8th Optimization and Stochastic Days, Weimar, Germany, 24–25 November 2011. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Krige, D. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. Chem. Metall. Min. Soc. S. Afr. 1951, 52, 119–139. [Google Scholar]
- Lancaster, P.; Salkauskas, K. Surface generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; PWS Publishing Company: Boston, MA, USA, 1996. [Google Scholar]
- Ansys Germany GmbH. Ansys OptiSLang User Documentation; Weimar, Germany, 2023R1 ed.; 2023. Available online: https://www.ansys.com/products/connect/ansys-optislang (accessed on 18 April 2024).
- Most, T.; Gräning, L.; Wolff, S. Robustness investigation of cross-validation based quality measures for model assessment. Eng. Model. Anal. Simul. 2025, 2. [Google Scholar] [CrossRef]
- Huntington, D.; Lyrintzis, C. Improvements to and limitations of Latin hypercube sampling. Probabilistic Eng. Mech. 1998, 13, 245–253. [Google Scholar] [CrossRef]
- Bucher, C. Computational Analysis of Randomness in Structural Mechanics; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: London, UK, 2009. [Google Scholar]
- Nie, J.; Ellingwood, B.R. Directional methods for structural reliability analysis. Struct. Saf. 2000, 22, 233–249. [Google Scholar] [CrossRef]
- Nie, J.; Ellingwood, B.R. A new directional simulation method for system reliability. Part I: Application of deterministic point sets. Probabilistic Eng. Mech. 2004, 19, 425–436. [Google Scholar] [CrossRef]
- Estep, D. Practical Analysis in One Variable; Springer: New York, NY, USA, 2002. [Google Scholar]
- Most, T. Assessment of structural simulation models by estimating uncertainties due to model selection and model simplification. Comput. Struct. 2011, 89, 1664–1672. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB User Documentation; Natick, MA, USA, R2022b ed. 2022. Available online: https://www.mathworks.com (accessed on 23 December 2024).
- Trunk, B.G. Einfluss der Bauteilgrösse auf die Bruchenergie von Beton. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 1999. [Google Scholar]
- Most, T. Stochastic Crack Growth Simulation in Reinforced Concrete Structures by Means of Coupled Finite Element and Meshless Methods. Ph.D. Thesis, Bauhaus-Universität Weimar, Weimar, Germany, 2005. [Google Scholar]

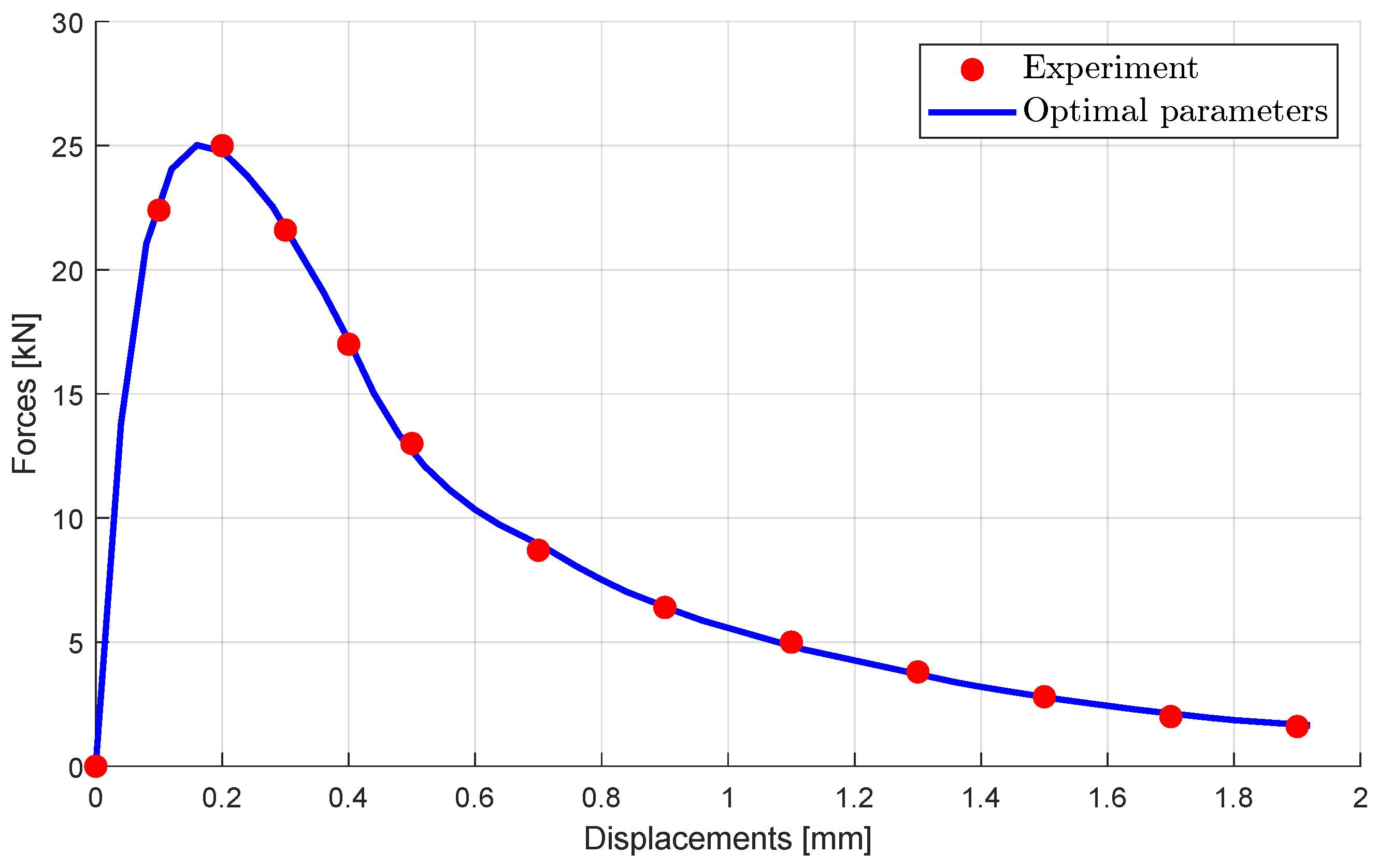

| Parameter | Unit | Reference Value | Bounds | Deterministic Optimization |
|---|---|---|---|---|
| Young’s modulus E | N/m2 | 2.830 | 1.00–6.00 | 4.176 |
| Poisson’s ratio | − | 0.180 | 0.10–0.40 | - |
| Tensile strength | N/m2 | 2.270 | 1.00–4.00 | 2.003 |
| Fracture energy | N/m2 | 2.850 | 2.00–4.00 | 2.850 |
| Shape parameter | − | 0.163 | 0.05–0.50 | 0.150 |
| Shape parameter | − | 0.242 | 0.05–0.50 | 0.258 |
| Parameter | Unit | Markov Estimator | Bayesian Updating | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Stddev | CoV | Mean | Stddev | CoV | |||
| Young’s modulus E | N/m2 | 4.176 | 0.116 | 0.028 | 4.065 | 0.136 | 0.033 | |
| Tensile strength | N/m2 | 2.003 | 0.023 | 0.011 | 2.025 | 0.030 | 0.015 | |
| Fracture energy | N/m | 2.850 | 0.024 | 0.008 | 2.847 | 0.026 | 0.009 | |
| Shape parameter | − | 0.150 | 0.008 | 0.051 | 0.153 | 0.008 | 0.055 | |
| Shape parameter | − | 0.258 | 0.009 | 0.034 | 0.256 | 0.009 | 0.035 | |
| Parameter | Unit | Reference | Optimization | Line-Search Ranges | |||
|---|---|---|---|---|---|---|---|
| Min | Max | ||||||
| Young’s modulus E | N/m2 | 4.176 | 3.566 | 4.540 | ±1.200 | ||
| Tensile strength | N/m2 | 2.003 | 1.946 | 2.162 | ±0.176 | ||
| Fracture energy | N/m2 | 2.850 | 2.718 | 3.018 | ±0.240 | ||
| Shape parameter | − | 0.150 | 0.106 | 0.192 | ±0.080 | ||
| Shape parameter | − | 0.258 | 0.203 | 0.312 | ±0.080 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Most, T. Inverse Uncertainty Quantification in Material Parameter Calibration Using Probabilistic and Interval Approaches. Appl. Mech. 2025, 6, 14. https://doi.org/10.3390/applmech6010014
Most T. Inverse Uncertainty Quantification in Material Parameter Calibration Using Probabilistic and Interval Approaches. Applied Mechanics. 2025; 6(1):14. https://doi.org/10.3390/applmech6010014
Chicago/Turabian StyleMost, Thomas. 2025. "Inverse Uncertainty Quantification in Material Parameter Calibration Using Probabilistic and Interval Approaches" Applied Mechanics 6, no. 1: 14. https://doi.org/10.3390/applmech6010014
APA StyleMost, T. (2025). Inverse Uncertainty Quantification in Material Parameter Calibration Using Probabilistic and Interval Approaches. Applied Mechanics, 6(1), 14. https://doi.org/10.3390/applmech6010014





