Strengthening Transformer Tank Structural Integrity through Economic Stiffener Design Configurations Using Computational Analysis

Abstract

Power transformers play a vital role in adjusting voltage levels during transmission. This study focuses on optimizing the structural design of power transformer tanks, particularly high-voltage (HV) tank walls, to enhance their mechanical robustness, performance, and operational reliability. This research investigates various stiffener designs and their impact on stress distribution and deformation through finite element analysis (FEA). Ten different configurations of stiffeners, including thickness, width, type, and position variations, were evaluated to identify the optimal design that minimizes stress and deflection while considering weight constraints. The results indicate that specific configurations, particularly those incorporating 16 mm thick H beams, significantly enhance structural integrity. Experimental validation through pressure testing corroborated the simulation findings, ensuring the practical applicability of the optimized designs. This study’s findings have implications for enhancing the longevity and reliability of power transformers, ultimately contributing to more efficient and resilient power transmission systems.

1. Introduction

Electricity is not merely a commodity; it is the lifeblood of our economy and quality of life. To make generated electricity accessible to different consumers based on power rating, transformers act as silent workhorses responsible for voltage transformation [1]. Different types of transformers are available for this voltage transformation; power transformers are particularly crucial due to their role in adjusting voltage levels between generators and distribution circuits [2]. Nevertheless, power transformers are also essential for reducing power losses during transmission. This reduction is especially important when a continuous full-capacity load operation is required [3]. Ensuring the transformer’s structural integrity is crucial for achieving highly efficient conversion. Power transformer design, types, and accessories depend on their size, application, and location. A power transformer comprises several distinct parts, each of which adds to the transformer’s overall performance differently. The main parts include the core, windings, tap changer, insulators, transformer oil, transformer tank, conservator, breather, Buchholz relay, cooling tubes, and explosion vent [4]. The transformer tank holds the oil, which grounds the magnetic circuit and different metal pieces while providing the transformer’s numerous components with physical support and protection. A power transformer tank’s material composition is determined by several criteria, including cost-effectiveness, corrosion resistance, and required strength [5]. Considering the mechanical robustness characteristics, stainless steel and different carbon steels, such as low-, medium- and high-graded steel, are commonly used to fabricate tank bodies. While stainless steel transformers offer excellent performance in moisture-rich environments due to their exceptional corrosion resistance, their higher fabrication costs make them an impractical choice for this application. As an alternative, carbon steel, particularly mild steel, is commonly used in transformer tank fabrication in light of its cost-effectiveness and equivalent performance [6].

Along with material selection, effective transformer tank design is critical due to several mounted components, including butterfly valves for the radiator and the inspection cover. Additionally, the electrical design complexity further underscores the tank’s critical role [7]. To ensure the transformer tank design is optimized, it must be validated to ensure compliance with industry standards. Both International Electrotechnical Commission (IEC) standards and Bangladesh’s industry standards indicate that the tank should be type-tested. As per Bangladesh’s national standards, transformer tanks must undergo testing under both positive and negative pressure conditions, with no permanent or significant deflection permitted. Such deformation could result in oil leakage or explosions due to the high pressures involved [8]. To address this issue, adding stiffeners in areas exposed to high voltages (HVs) is crucial for reinforcing these tanks against deformation, stress, and mechanical failures [9]. The bottom plate of the transformer tank is reinforced with base plates and lifting arrangements, effectively distributing forces against the ground to enhance stability and support. The top covers are thickened to accommodate high-voltage bushings [10]. Furthermore, the widths of the left and right sides are smaller than those of the other sides.

Among the existing techniques, stiffeners have proven to be the most economical and efficient method for reinforcing the walls of power transformer tanks made from mild steel plates. When welded onto important stress locations, stiffeners significantly improve the tank body’s structural integrity without requiring a complete redesign of the plate thickness or complex forming methods [11]. This technique makes sure that the tank can effectively endure operational loads by strategically adding reinforcement where it is most needed. Various studies have explored the impact of stiffeners on reducing stress and deformation. Research has focused on the placement of stiffeners, their shapes, and the thickness of the HV tank wall. For instance, Smith et al. conducted research on stiffeners through finite element analysis (FEA) of different loading conditions and revealed that optimal placement strategies minimize the localized stress concentrations and enhance stability [12]. After that, Zhang et al. investigated the effect of stiffener shape on stress distribution and deformation control. They investigated different-sized stiffeners of L, T, and I shapes to evaluate the best-possible stiffeners with significant bending and buckling resistance [13]. Following this, Kumar et al. reported that along with stiffener design optimization, the thickness of the HV tank wall is also a critical aspect when it comes to mitigating stress and enhancing resilience [14].

Researchers have shown significant interest in the design variations of stiffeners and their direct effects on the stress and deformation of HV tank walls. Previous studies have provided a detailed comparison of different stiffener designs using advanced simulation techniques, revealing that curved or corrugated stiffeners offer enhanced flexibility and strength, eventually reducing the overall stress and deformation compared to traditional straight stiffeners [15]. This focus on design variations fills a gap in the literature, where the emphasis has often been on placement, shape, and wall thickness rather than the intrinsic design characteristics of stiffeners.

This article first demonstrates the design of high-voltage (HV) tank wall structures using a commercial computer aided design (CAD) software. It also investigates HV tank wall structures through finite element analysis (FEA) using commercial computational software, ANSYS 2023R2, to enhance their robustness and strength, as shown in Figure 1. This study explores various stiffener shapes and configurations to reinforce transformer tank bodies, aiming to meet stringent strength standards. Initial analysis of a conventional HV tank wall design identified critical stress and deflection points, leading to the introduction of various stiffeners with modifications in thickness, width, and shape. The results demonstrated that a 16 mm thick HV beam achieved the best balance between strength and robustness, effectively reducing the maximum stress and deflection. In addition to structural improvements, a cost–benefit analysis was conducted to evaluate material usage, manufacturing complexity, and maintenance requirements to ensure that the designs are economically viable. This study also aligns its findings with existing standards and proposes updates based on recent research. Experimental validation using scale models further supports the practical applicability of the results, offering reassurance and confidence in the proposed enhancements for transformer tank designs.

2. Materials

Material Selection

Material selection for power transformer tanks is critical due to cost-effectiveness, corrosion resistance, and mechanical strength requirements. Low-carbon steel, particularly ASTM A36, stands out as the primary material choice for transformer tank bodies, ensuring compatibility with fabrication processes and operational durability [16]. Table 1 depicts the typical properties of ASTM A36, sourced from Shanghai Metal Corporation HK Ltd. (Mongkok Kowloon, Hong Kong).

Stainless steel exhibits outstanding performance in severe environments or locations prone to moisture exposure due to its exceptional corrosion resistance [17]. This material significantly reduces the risk of rust and deterioration over time, extending the transformer’s operational lifespan. However, the cost of stainless steel is higher than carbon steel, making it less economical for general-purpose transformer tanks [18]. Consequently, medium-carbon steel offers higher strength compared to low-carbon steel, making it suitable for applications where increased mechanical strength is necessary [19]. However, medium-carbon steels may pose challenges in formability and welding compared to low-carbon steels. They are typically considered for larger transformers or situations where mechanical robustness is prioritized over ease of fabrication [20]. On the contrary, low-carbon steel, specifically ASTM A36, is widely used in transformer tank fabrication due to its favorable properties, including formability, weldability, and cost-effectiveness [21]. ASTM A36 steel is known for its excellent welding characteristics, allowing for various machining processes such as grinding, punching, tapping, drilling, and machining without significant difficulties. Its lower yield strength compared to higher-carbon steels like medium- or high-carbon steel facilitates easier bending and shaping during manufacturing, which is advantageous for forming intricate tank geometries. High-carbon steels offer superior strength but are less ductile and more brittle than low- and medium-carbon steels. This characteristic makes them less suitable for transformer tank applications where toughness and weldability are crucial considerations [22]. Additionally, high-carbon steel presents challenges in shaping and welding processes, limiting its usage in transformer tank construction [23].

Table 1. Typical properties of mild steel plate (ASTM A36) [24].

Property	Metric
Tensile strength, ultimate	400–550 MPa
Tensile strength, yield	250 MPa
Elongation at break (in 200 mm)	20.0%
Elongation at break (in 50 mm)	23.0%
Modulus of elasticity	200 GPa
Bulk modulus (typical for steel)	140 GPa
Poisson’s ratio	0.260
Shear modulus	79.3 GPa
Density	7.85 g/cm3

Table 1. Typical properties of mild steel plate (ASTM A36) [24].

Property	Metric
Tensile strength, ultimate	400–550 MPa
Tensile strength, yield	250 MPa
Elongation at break (in 200 mm)	20.0%
Elongation at break (in 50 mm)	23.0%
Modulus of elasticity	200 GPa
Bulk modulus (typical for steel)	140 GPa
Poisson’s ratio	0.260
Shear modulus	79.3 GPa
Density	7.85 g/cm3

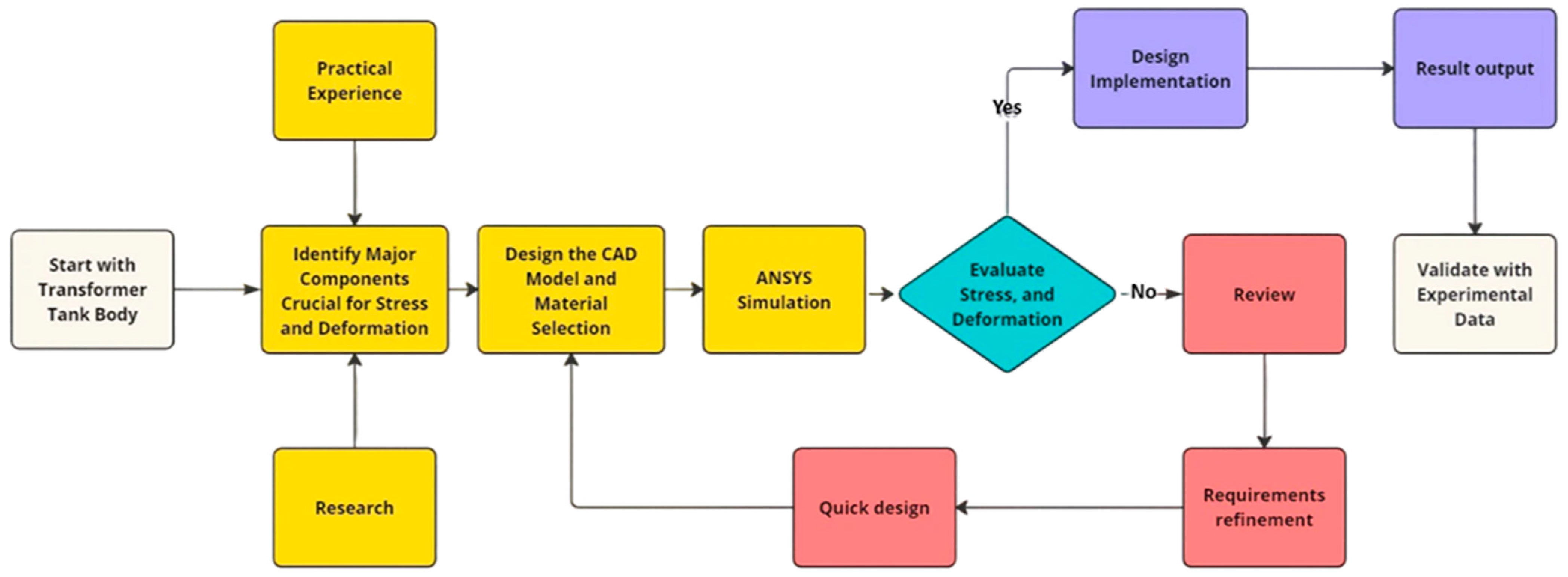
3. Methodology

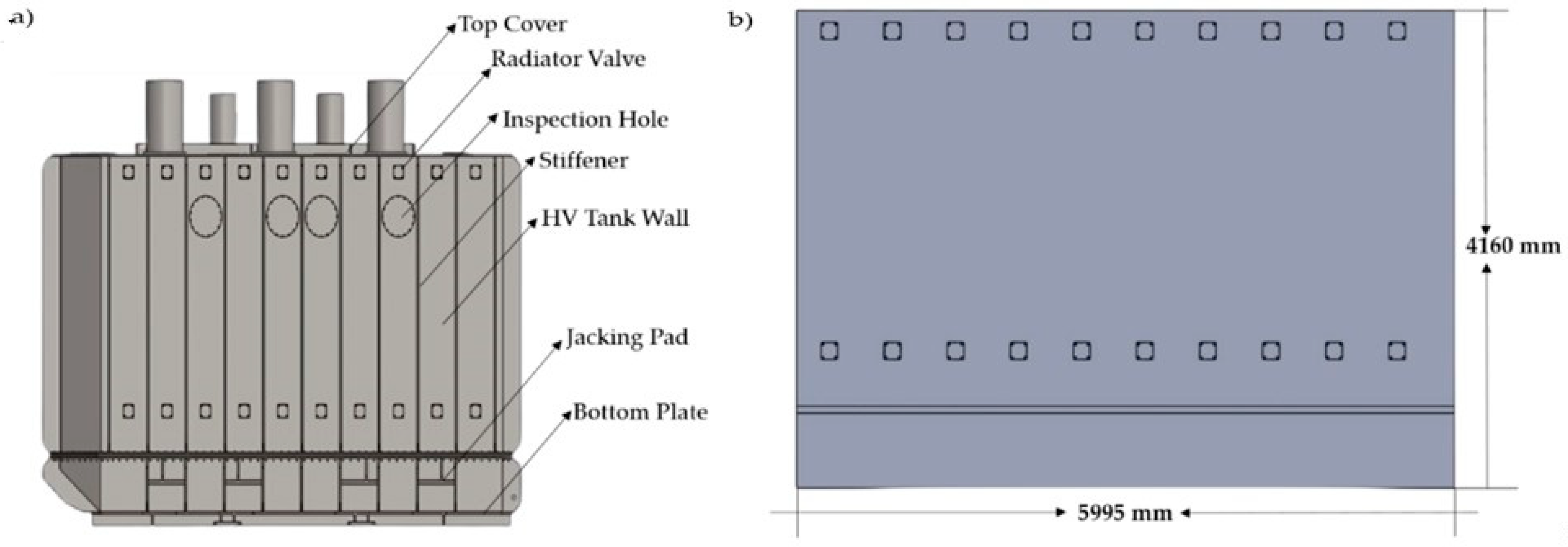
3.1. Proposed Design

This study aimed to optimize the design of transformer tank walls through a comprehensive approach integrating CAD modelling using Autodesk Fusion (Autodesk, San Francisco, CA, USA), FEA, and practical validation. The structural integrity analysis of the HV tank wall shown in Figure 2 illustrates the structural integrity analysis of HV tank walls following consecutive steps. A 132 kV power transformer (Energypac Engineering Ltd., Dhaka, Bangladesh) was modelled in Autodesk Fusion 360 software (student licence) with dimensions of 5995 mm (length) × 2370 mm (width) × 4160 mm (height), as shown in Figure 2b.

Different approaches were taken into account, such as the stiffener width, thickness, support addition, and HV wall thickness modifications. A comparative analysis was conducted between 10 different types of designs in order to evaluate the best compatible design with robust characteristics. In the design optimization process shown in Figure 3, it is acknowledged that traditional optimization algorithms provide a feasible approach; however, insights from industry experts indicated that the design parameters proposed—such as the thickness and shape—are frequently either unavailable in the market or misaligned with established industrial standards. Consequently, the focus shifted toward heuristic methods and practical techniques. This approach emphasizes iterative design adjustments shown in Figure 4 that are rooted in industry practices and supported by empirical data, ensuring that optimization efforts yield results that are both practical and applicable in real-world settings.

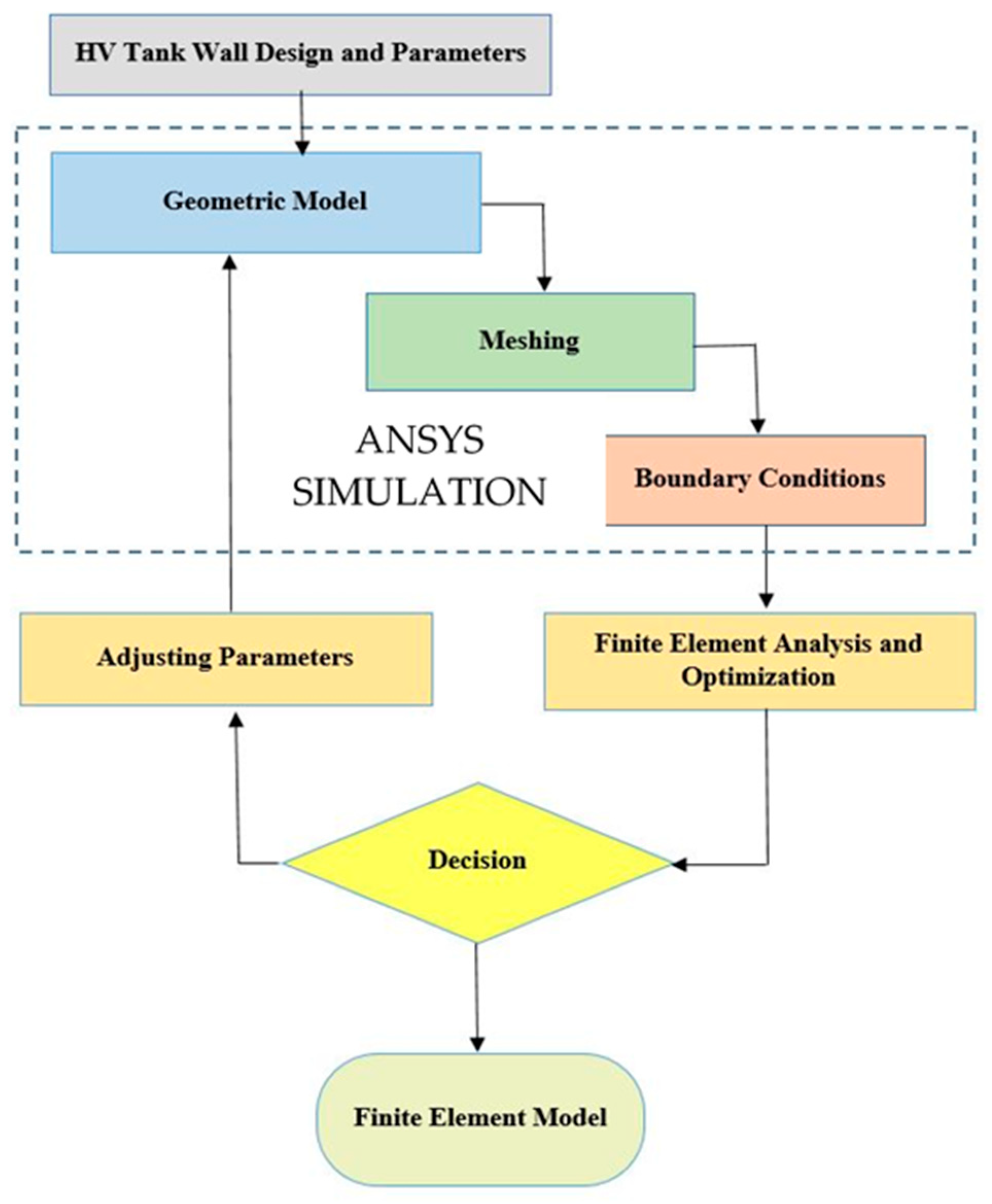
3.2. Numerical Method

The stress and deformation characteristics of the flat stiffened steel plates were analyzed using specialized equations derived from plate theory and structural mechanics. The bending stress in a flat stiffened steel plate is determined using classical plate bending theory [25]:

$${\sigma }_b={\displaystyle \frac{My}{I}}$$

(1)

where $I=I_{Plate}+\sum I_{stiffeners}$

$I_{Plate}$ is the moment of inertia of the plate.

$\sum I_{stiffeners}$ is the sum of the moments of inertia of the stiffeners about the neutral axis.

Now, the maximum deflection $w_{max}$ of a flat stiffened plate under a uniform load q is calculated as:

$$w_{max}={\displaystyle \frac{q{L}^4}{KD}}$$

(2)

where

The flexural rigidity D for a stiffened plate is computed as $D={\displaystyle \frac{E{t}^3}{12\left(1-{\nu }^2\right)}}$

After that, the shear stress τ in a flat stiffened steel plate subjected to a shear force V is given by:

$$\tau ={\displaystyle \frac{VQ}{It}}$$

(3)

The static behavior of a simply supported flat steel plate with vertical and horizontal stiffeners subjected to transverse loads can be described using the following governing partial differential equation for the deflection w (x, y):

$$D{\nabla }^{4}w\left(x,y\right)=q\left(x,y\right)$$

(4)

${\nabla }^{4}w$ is the Biharmonic operator, which is defined as:

$${\nabla }^{4}w={\displaystyle \frac{{\partial }^{4}w}{\partial x^4}}+2{\displaystyle \frac{{\partial }^{4}w}{\partial x^2\partial y^2}}+{\displaystyle \frac{{\partial }^{4}w}{\partial y^4}}$$

(5)

Boundary Conditions: At the edges where the plate is simply supported:

Deflection is zero: w = 0 at y = 0 and y = h

The bending moment is zero (which translates to the second derivative of the deflection being zero):

$${\displaystyle \frac{{\partial }^{2}w}{\partial y^2}}=0 at y=0 and y=h$$

(6)

Similarly, for the x-direction: w = 0 at x = 0 and x = l and

$${\displaystyle \frac{{\partial }^{2}w}{\partial x^2}}=0 at x=0 and x=l$$

(7)

Incorporating vertical and horizontal stiffeners into plate designs significantly increases the complexity of the analysis. While the governing equations remain consistent, adequate flexural rigidity (D) may require adjustment to reflect the contributions of the stiffeners. This can be achieved by employing a proper thickness or modifying the material properties based on the stiffener configuration. Given this complexity, numerical methods—particularly, the finite element method (FEM)—are frequently utilized to analyze stiffened plates. FEM enables a comprehensive evaluation of the deflection and stress distributions, thereby enhancing practical design and assessment processes.

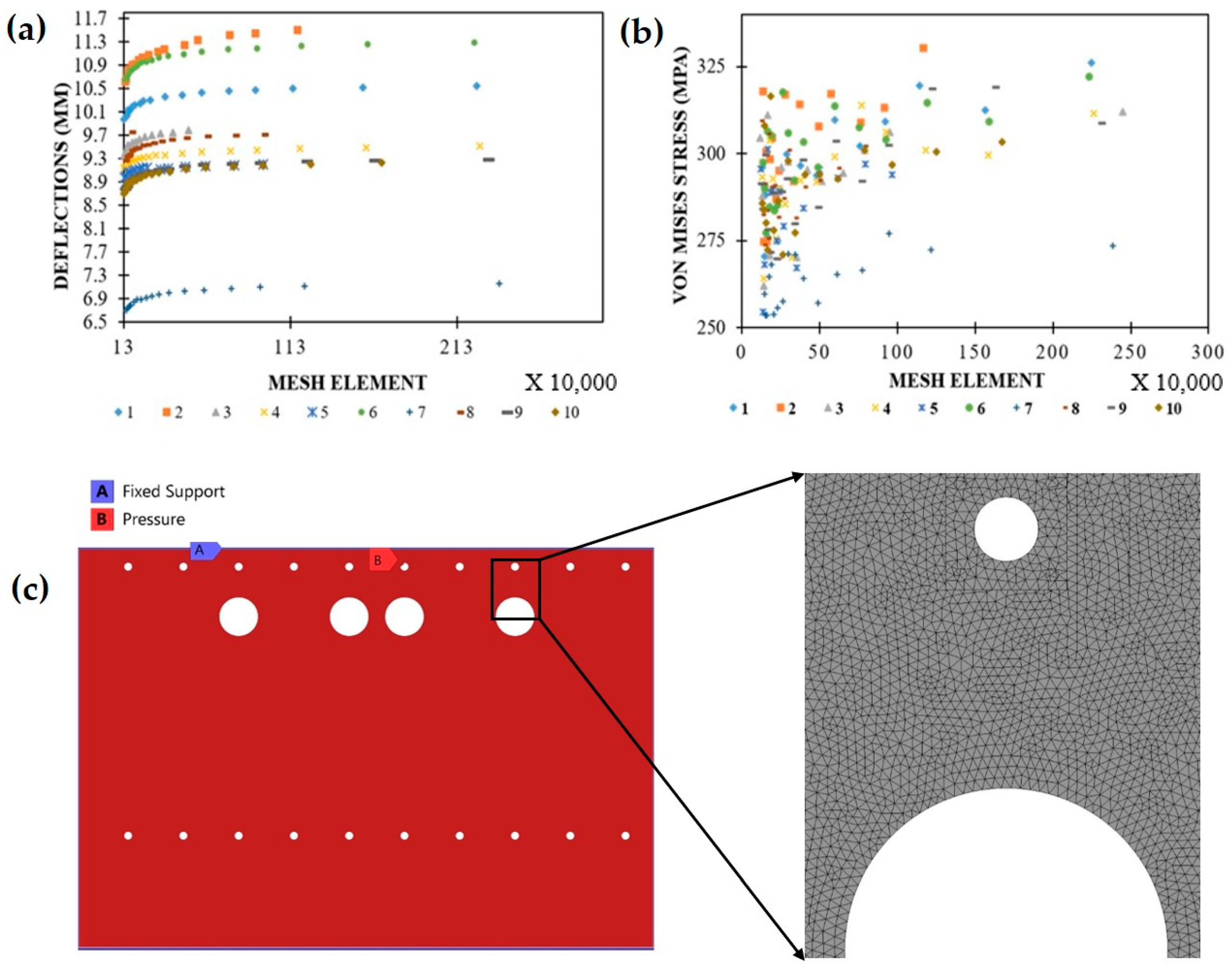
3.3. Finite Element Analysis

The structural integrity and resistance against failure were prioritized through static nonlinear finite element analysis conducted in the ANSYS static structural module (ANSYS, Inc., Canonsburg, PA, USA). This involved strengthening critical weld joints at the wall corners, bottom, cover, stiffeners, and H beams to enhance the tank’s flexibility and load-bearing capacity [26]. This analysis was crucial for evaluating the maximum stress and deformation under standard pressure conditions of 0.1 MPa, in accordance with the IEC 60076-1 standard [27]. A refined finite element mesh was generated to represent geometric complexities and stiffness variations accurately. A mesh dependency test was carried out for all types of HV tank walls, confirming consistent results, as shown in Figure 5a,b. Boundary conditions were applied to simulate internal pressures and fixed supports were defined on all sides of the HV tank walls (Figure 5c). The positions of the fixed supports and the applied pressure on the HV tank wall model are depicted in Supplementary Figures S1 and S2, illustrating the outer and inner sides, respectively. In addition, the mesh configuration for static analysis of the High-Voltage (HV) Tank Wall is illustrated in Supplementary Figure S3. Simulations were conducted to assess the maximum deformation and stress. In this context, the typical locations of maximum deformation and maximum Von-Mises stress are shown in Supplementary Figures S4 and S5, respectively. Various configurations of stiffeners, including variations in thickness, width, and types (flat bar and H beam), underwent systematic evaluation through multiple simulations to identify an optimal design that minimized stress concentrations while meeting deflection limits and weight constraints.

3.4. Experimental Testing

Power transformers’ efficient functioning relies heavily on their oil tanks’ structural integrity. To ensure optimal performance and longevity, rigorous testing methodologies are essential. One such method is the experimental setup for power transformer tank pressure testing shown in Figure 6, designed to assess a tank’s ability to withstand operational conditions and identify potential leaks or deformations. This comprehensive procedure involves meticulous material preparation, precise welding techniques, thorough post-welding inspections, leakage testing, deformation measurements, and stringent safety considerations. Steel plate materials are gathered in this regard, meeting the specifications outlined in the design drawing. These plates are then grouped according to pattern requirements, distinguishing between side walls, top covers, and bottom plate sections. The assembly process begins with the precise fixation of steel plates using spot welding techniques, ensuring a robust and uniform structure. Following the welding process, post-welding steps are undertaken to ensure the tank’s integrity. The tank undergoes a thorough inspection to detect any incomplete welds or defects. Subsequently, all radiator valves, inspection covers, bushing holes, and tap changer holes are sealed to prevent potential leaks. Nut bolts securing the tank and tray parts are tightened to reinforce the assembly’s structural integrity.

A critical phase of the experimental setup involves conducting a leakage test to ascertain the tank’s airtightness. The tank is connected to a controlled air pressure source, and the air pressure is gradually increased up to the standard limit. Continuous monitoring for any pressure drop is performed, as this could indicate the presence of leaks. Pressure readings are meticulously recorded at regular intervals, ensuring comprehensive data collection.

In addition to leakage testing, deformation measurements play a vital role in assessing the tank’s structural integrity. Measuring scales are strategically positioned at various locations on the tank, allowing for accurate deformation measurements. A pressure gauge is attached to the tank wall to monitor changes in pressure as deformation occurs. Any alterations in the tank’s shape or bulging are carefully documented, providing valuable insights into its performance under pressure.

4. Results and Discussion

This study aimed to optimize the structural design of the high-voltage (HV) tank wall for a 120 MVA 33 kV power transformer by focusing on minimizing the maximum stress and deflection while prioritizing weight reduction. The analysis included an original baseline design featuring a 10 mm thick HV tank wall and 25 mm thick stiffeners, with experimental validation against simulation predictions.

4.1. Performance Assessment

The original design demonstrated a maximum elastic deflection of 13 mm under standard pressure conditions, while the numerical simulations predicted a maximum deflection of 10.562 mm (see

Table 2. Experimental data on 120 MVA power transformer tank under pressure testing deformation.

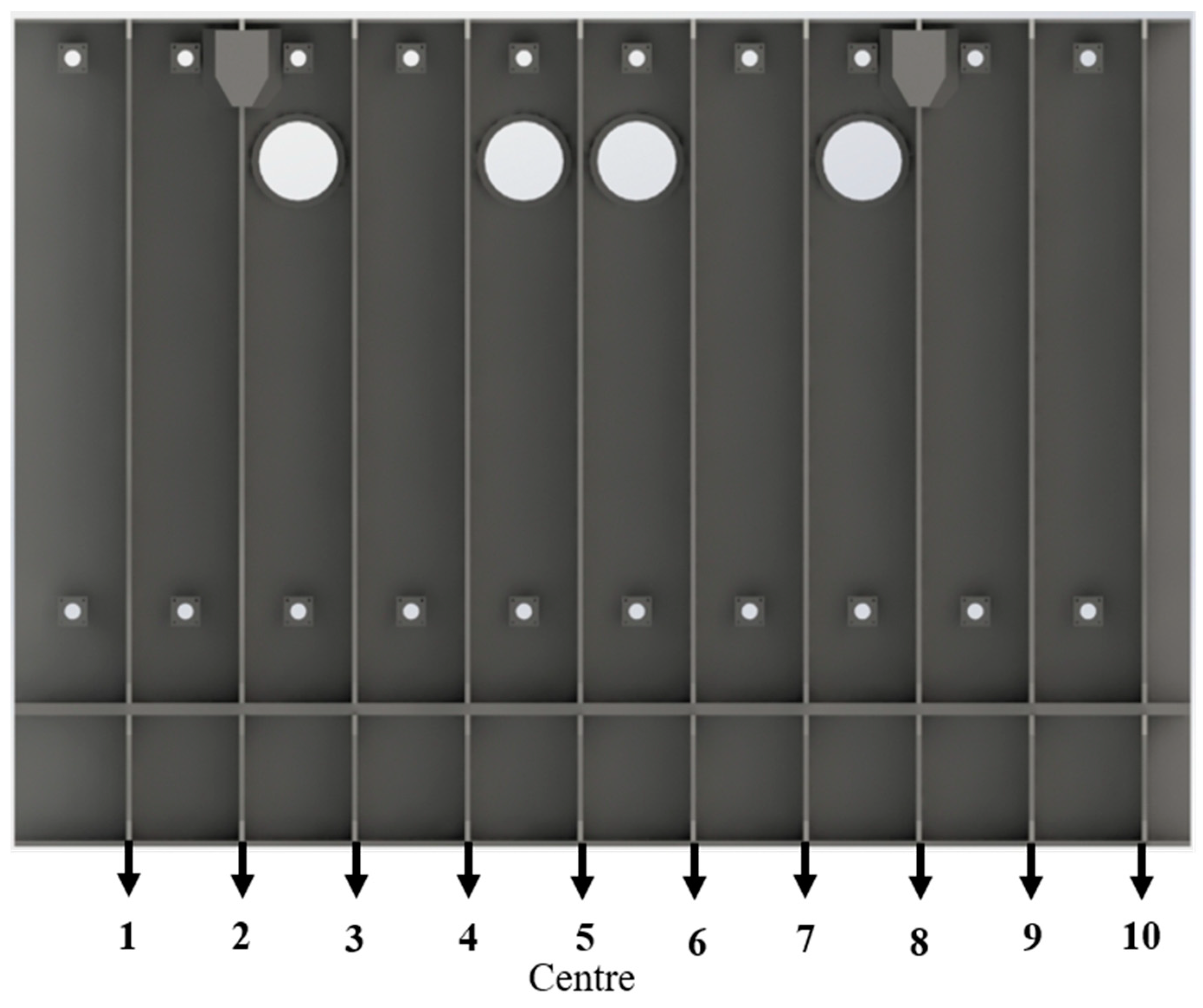
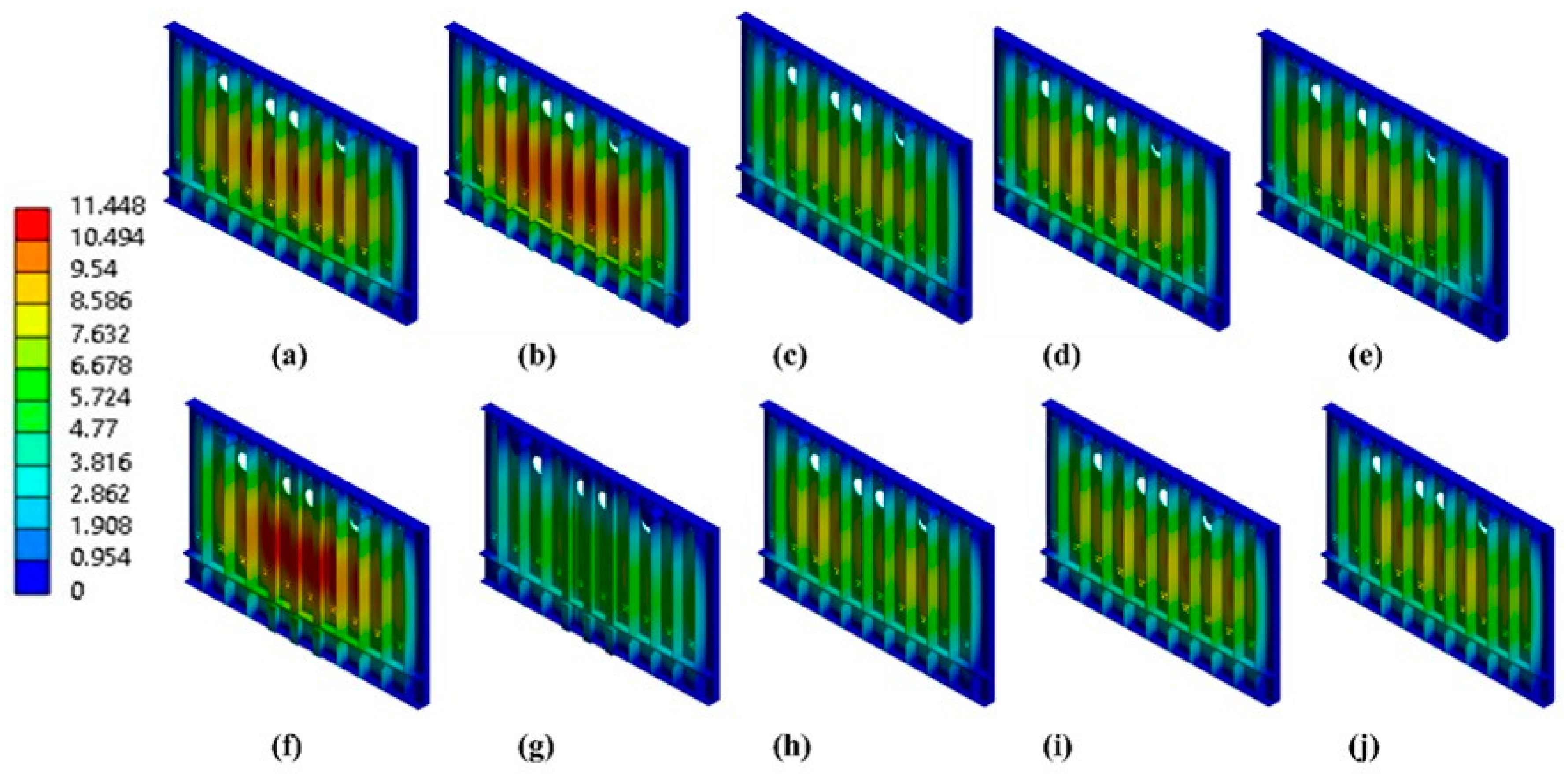
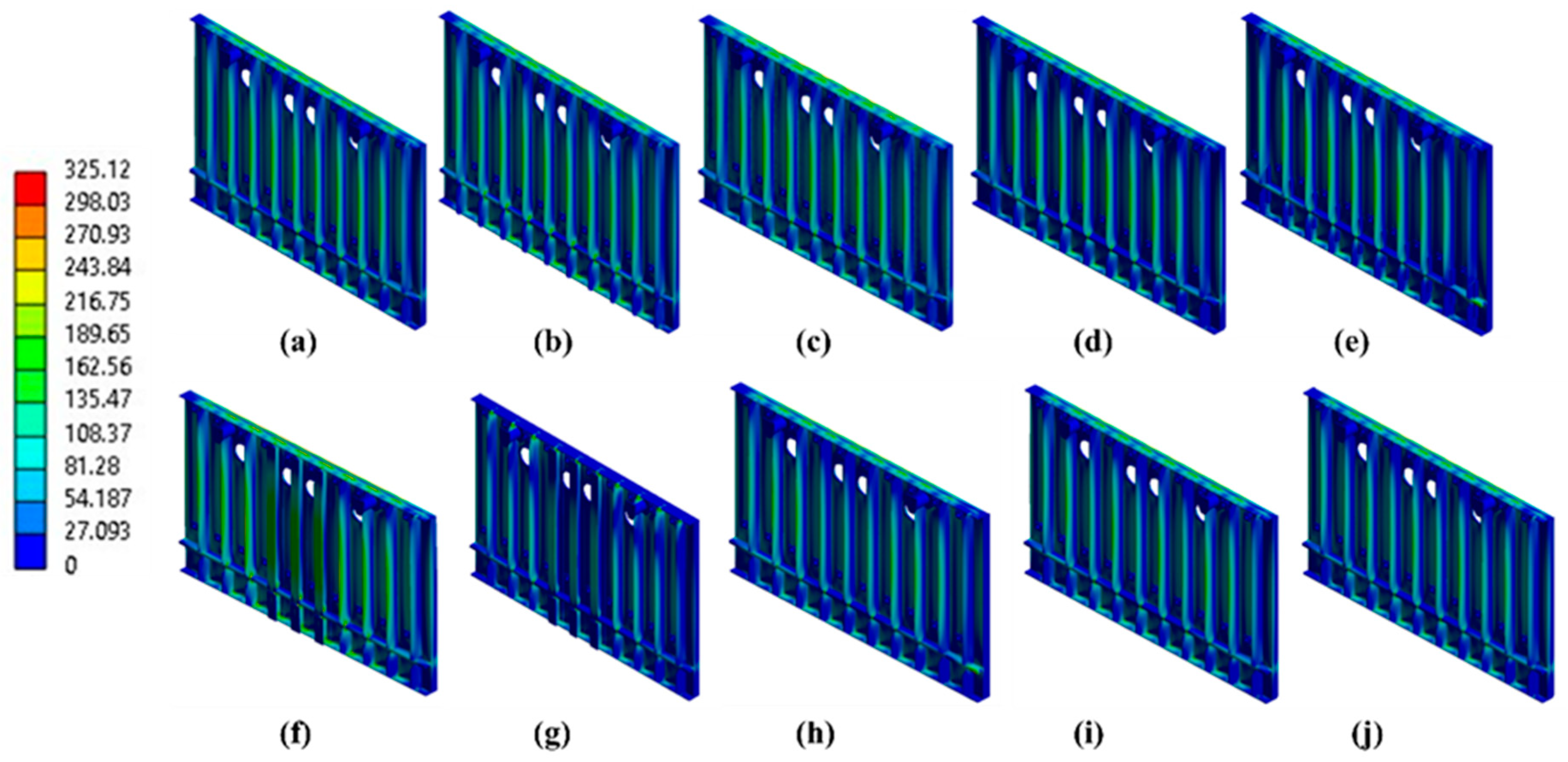
Time	Pressure (kg/cm2)	Left Side (mm)	Center (mm)	Right Side (mm)
8.30 AM	0	31	30	30
9.15 AM	0.4	26	25	24
9.35 AM	0.7	24	20	21
9.50 AM	0.9	20	18	18
10.00 AM	1	20	17	18
11.00 AM	0	28	27	27
Elastic Deformation (mm)		11	13	12
Plastic Deformation (mm)		3	3	3

). This close alignment validates the simulation’s accuracy and its ability to reflect real-world behavior effectively. Notably, the maximum von Mises stress recorded in the simulations was 316.11 MPa (see

Table 3. Maximum stress and maximum deformation analysis data from ANSYS static simulations for ten design modifications.

Model	Maximum Stress (MPa)	Maximum Deflection (mm)	Weight (kg)	Stiffeners		Wall Thickness (mm)	Add-ons
				Thickness (mm)	Width (mm)
a	316.11	10.562	5442.45	25	260	10	No
b	313.21	11.448	5354.62	25	300	10	No
c	304.59	9.3764	5848.98	30	260	10	No
d	299.63	9.4941	5842.14	25	260	12	No
e	297.02	9.1918	5744.55	25	260	10	Support added on both sides of each stiffener
f	325.12	11.321	5488.74	25	260	10	03 Nos 12 mm thickness H beam at center
g	273.57	7.1607	5708.92	25	260	10	03 Nos 16 mm thickness H beam at center
h	305.68	9.7617	5811.10	40	260	10	03 Nos at center
i	319.09	9.2778	5767.61	40	260	10	04 Nos at positions 3, 5, 6, and 8
j	300.61	9.2043	5851.81	40	260	10	04 Nos at positions 2, 4, 6, and 8

), which is well within the allowable range for ASTM A36 steel [28], indicating a robust design with minimal risk of crack initiation. On the other hand, according to the finite element analysis (FEA), the highest von Mises stress of 325.12 MPa was observed in Model f, specifically at stiffener number 8 in the top position. While the magnitude of the maximum stress varied among the different models analyzed, the vertical position of this maximum stress remained consistent. However, the horizontal position varied across the different design models. Notably, this stress level is also within the acceptable limits for the material.

Modifications to the design led to various performance outcomes. Increasing the width of the stiffener from 260 mm to 300 mm (Model b) resulted in an increased deflection of 11.448 mm. Meanwhile, it reduced the stress to 313.21 MPa, suggesting a favorable trade-off between stress reduction and weight savings, and, in contrast, increasing the thickness of the stiffeners (Model c) marginally reduced the deflection but significantly increased the stress and weight, making this design less advantageous.

Model d involved increasing the HV tank wall thickness from 10 mm to 12 mm, which successfully reduced deflection and stress with only a minimal increase in weight, indicating strong potential for structural performance enhancement. Additional supports (Model e) shown in Figure 7, further improved the deflection to 9.1918 mm (Figure 8) and stress to 297.02 MPa (Figure 9), while maintaining a weight close to the original design.

When evaluating the H beam configurations (Models f and g), it was found that using thicker H beams (Model g with 16 mm beams) significantly reduced deflection to 7.1607 mm and stress to 273.57 MPa despite a moderate increase in weight. This suggests that targeted reinforcements can substantially improve structural performance.

Overall, the investigation highlighted that the designs involving significantly thicker stiffeners or additional components often resulted in higher weights without proportional benefits in stress and deflection reduction. For instance, Model h with 40 mm thick stiffeners achieved a deflection of 9.7617 mm, but at the cost of increased weight, making it less desirable for weight-sensitive applications.

4.2. Compliance with Standards

The findings confirm that the HV tank wall’s maximum recorded permanent deflection of 3 mm is well below the IEC standard limit of 19 mm for flat plates exceeding 3000 mm in length [29]. This reinforces the tank’s capability of withstanding substantial loading without permanent deformation, ensuring structural integrity. Continuous monitoring of stress levels during operation is essential to prevent them from approaching critical thresholds, particularly at welded joints and other vulnerable areas. Regular inspections are recommended to mitigate risks associated with potential mechanical failure.

5. Conclusions

This study successfully identified optimal design configurations for the robust HV tank wall of a 120 MVA power transformer, balancing the requirements of stress reduction, deflection minimization, and weight constraints. Model g, with three 16mm thick H-beams, emerged as the most promising option among the evaluated designs. It effectively reduced deflection and stress while managing the increase in weight.

A robust power transformer tank is essential for ensuring the reliability and efficiency of power transmission systems. Its structural integrity helps to withstand mechanical and thermal stresses, reducing failure risks and downtime. Improved thermal management enhances cooling and extending the transformer’s lifespan while minimizing oil leaks, thus protecting the environment and ensuring safety compliance. This robustness contributes to grid stability, justifies the initial investment through long-term maintenance savings, and fosters innovations in resilient infrastructure.

This research underscores the critical role of stiffeners in enhancing the structural integrity and reliability of transformer tanks. It also establishes a systematic methodology that integrates advanced CAD modeling, finite element analysis (FEA), and experimental validation for future optimization studies.

Further research is recommended to explore these designs’ fatigue and vibration behavior to refine the transformer tank wall configurations. These advancements are crucial for meeting the evolving needs of modern electrical infrastructure, ultimately ensuring safer and more efficient power transmission systems.