Intelligent Decision-Making Analytics Model Based on MAML and Actor–Critic Algorithms
Abstract
1. Introduction
- Balanced Weight Quantification: A standardized AHP-CRITIC fusion method that systematically combines subjective expert knowledge (AHP) and objective data characteristics (CRITIC) for strategy evaluation.
- Meta-Learning Enhanced RL: Integration of the MAML framework with the Actor–Critic algorithm featuring inner-outer loop parameter optimization for rapid adaptation to new tasks.
- Practical Validation: Comprehensive evaluation on enterprise indicator anomaly detection with a novel Balanced Performance Index (BPI) demonstrating superior efficiency and adaptability.
2. Related Work
2.1. Reinforcement Learning for Decision Making
2.2. Meta-Learning Approaches
2.3. Multi-Criteria Decision Analysis
3. Background
3.1. Reinforcement Learning Fundamentals
3.2. Actor–Critic Architecture
3.3. Meta-Learning Framework
3.4. Evaluation Metrics
4. Algorithm
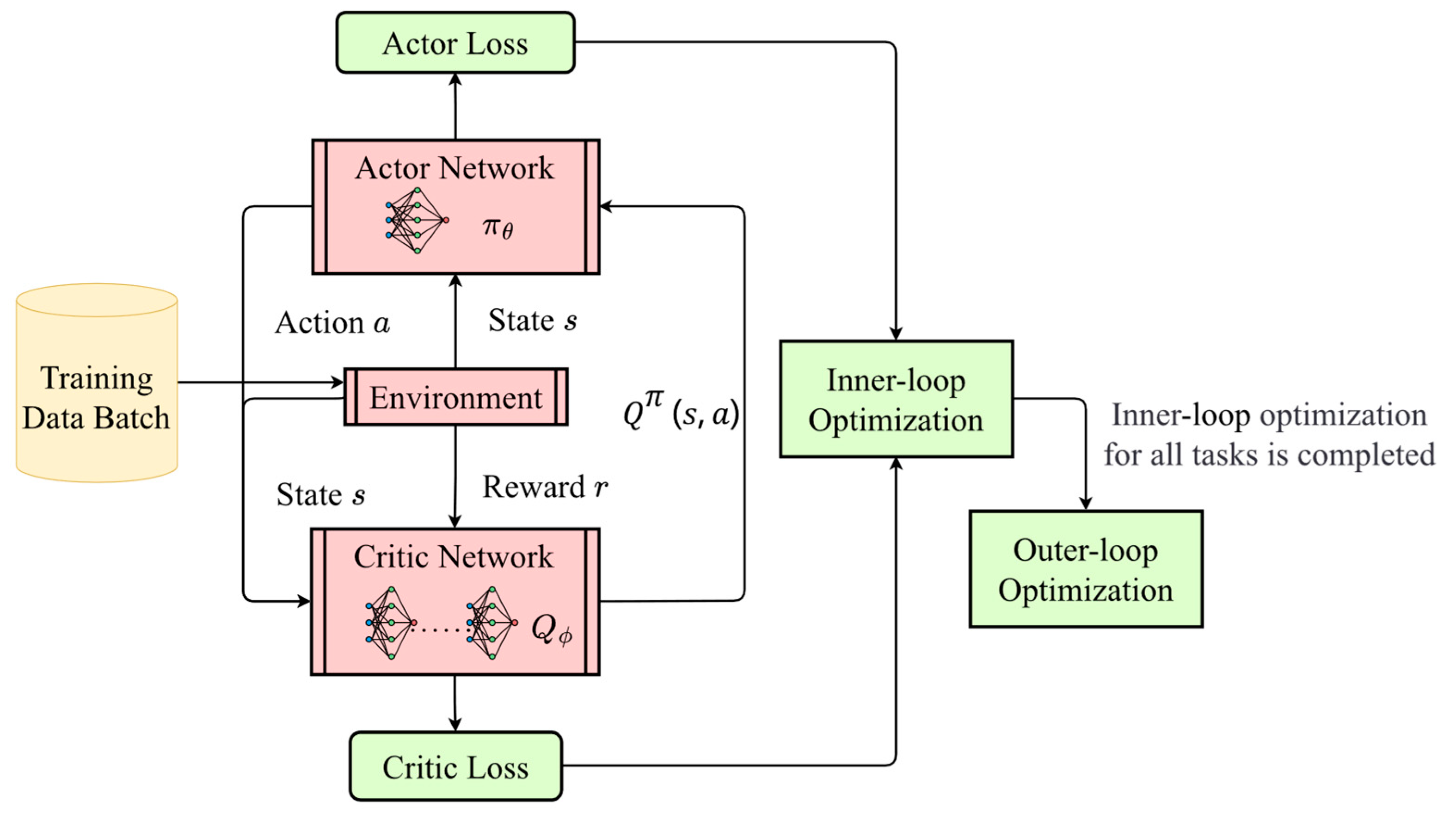
4.1. Actor–Critic Algorithm Based on MAML Framework
- (1)
- Inner-loop Optimization (Task-specific updates): For each specific task, a small-step gradient update is applied using a gradient descent algorithm to optimize the model’s parameters. This process involves performing a few gradient descent steps on each task to learn model parameters that adapt to the task.
- (2)
- Outer-loop Optimization (Meta-update): After completing the inner-loop update, the task-adapted model parameters are fed back. Based on the performance feedback from these tasks, the global initial model parameters are updated to improve generalization for future tasks.
| Algorithm 1: Actor–Critic algorithm based on the MAML framework | |
| Input: List of tasks val, inner learning rate inner_lr, discount factor , batch size batch. Output: The optimal strategy taken. | |
| 1 | Initialize the parameters and for and , and initialize the state |
| 2 | while not converged do |
| 3 | Select action based on the current policy ; |
| 4 | Execute action and observe reward and the next state |
| 5 | Calculate the error , where |
| 6 | Update the network by minimizing the loss to update parameter |
| 7 | Update the network using the policy gradient method to update parameter : |
| 8 | Update the state |
| 9 | Update the outer layer parameters: |
| 10 | end |
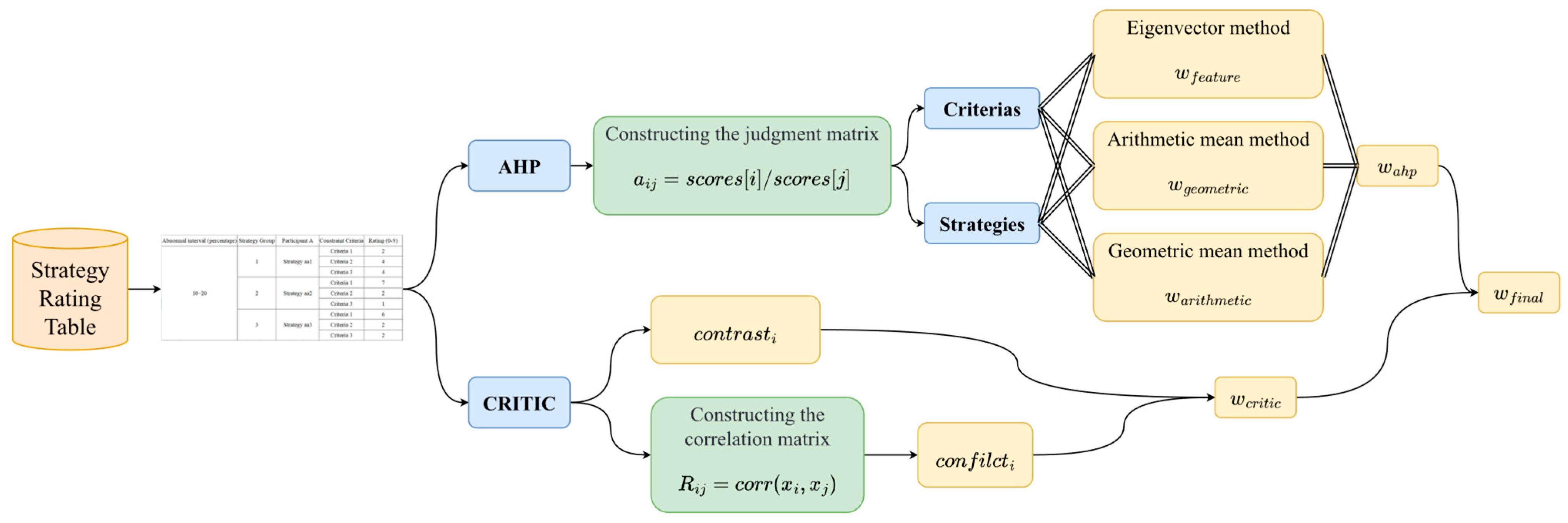
4.2. AHP-CRITIC Weight Quantification Method
- (1)
- The AHP method is used for multi-criterion decision analysis, which determines the weight of each criterion and scheme by constructing a judgment matrix, and converts the action plan into the form of a judgment matrix, which is a systematic data processing method, which can improve the transparency and interpretability of decision-making [15]. In this paper, AHP is used to calculate subjective strategy weights. The principle of constructing the judgment matrix is as follows:
- (2)
- The CRITIC (Criteria Importance Through Intercriteria Correlation) method is used for feature evaluation and to calculate the importance of each feature [16]. In this paper, it is used to calculate the amount of information carried by each strategy, i.e., the objective strategy weight.
5. Experiment
5.1. Experiment Setup
- (1)
- Calculation of Strategy Group Benefit Value
- (2)
- Strategy Group Setup
- (3)
- Space Settings
- (4)
- Reward Function Settings
- (5)
- Termination Condition
- (6)
- Training and Testing Data
- (7)
- Network Parameter Settings
5.2. Comparative Experiments
- (1)
- Algorithm Validity
- (2)
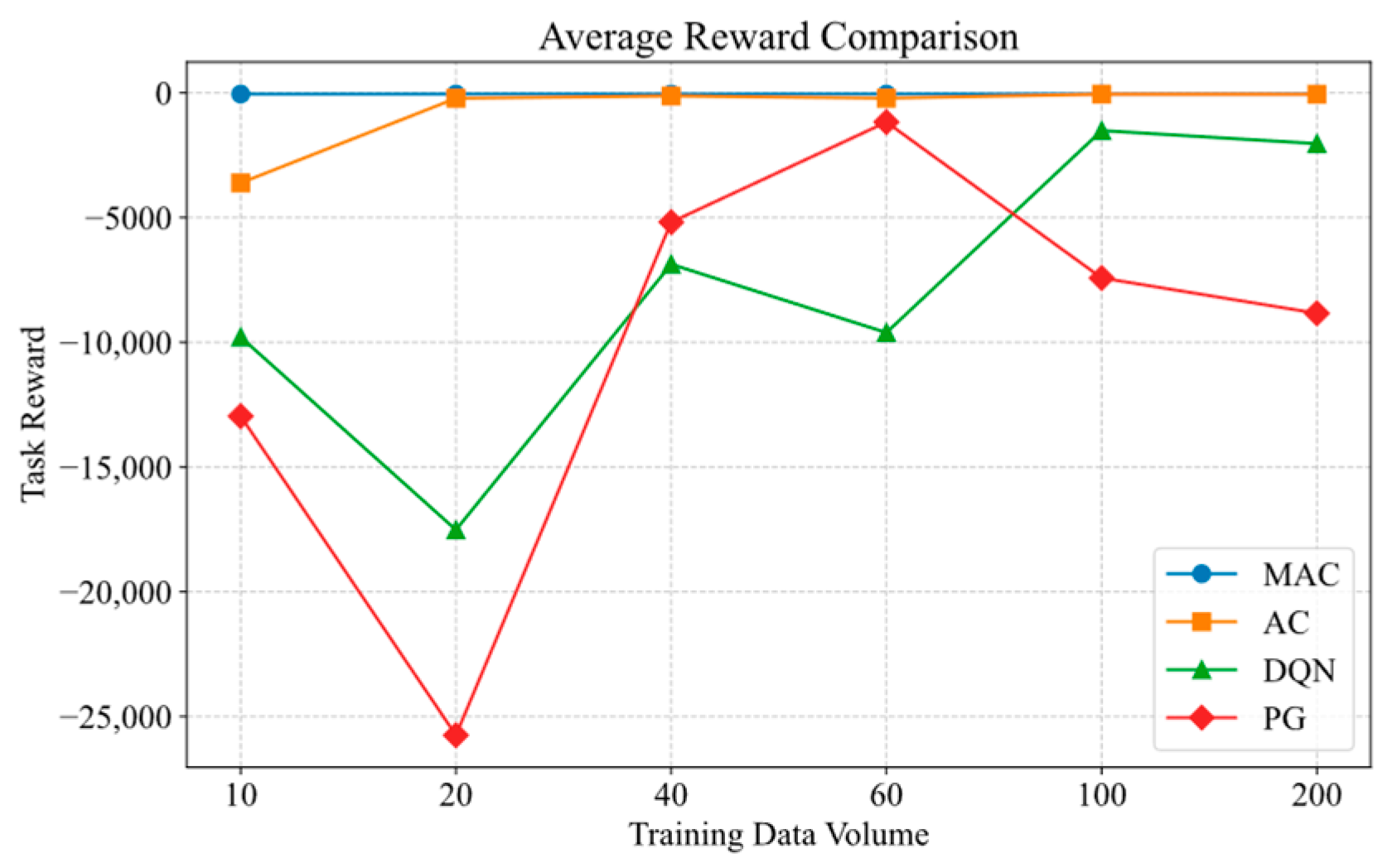
- Comparison of Reward Values
- (3)
- Comparison of Time Consumption
- (4)
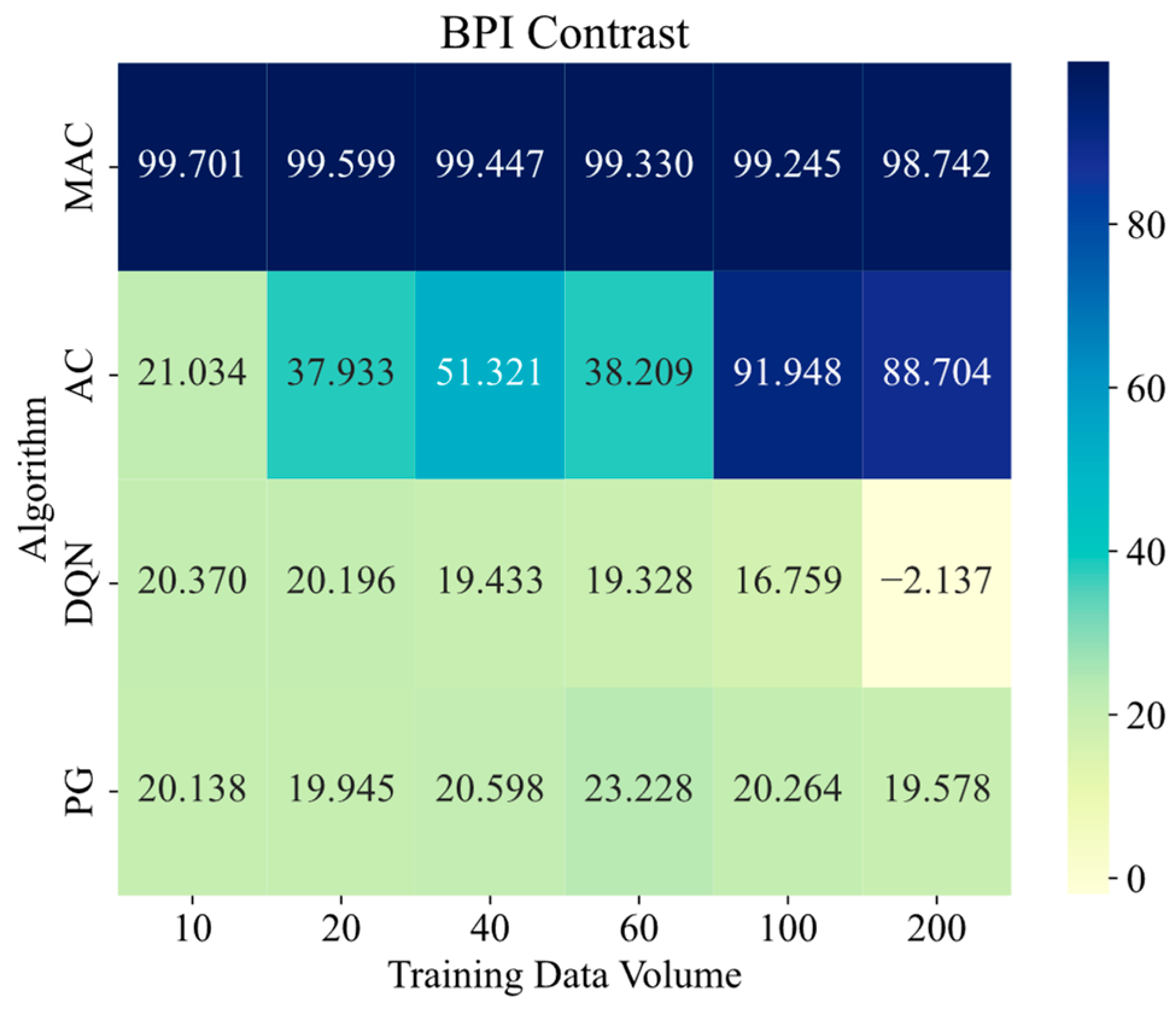
- Comparison of Balanced Performance Index
- (5)
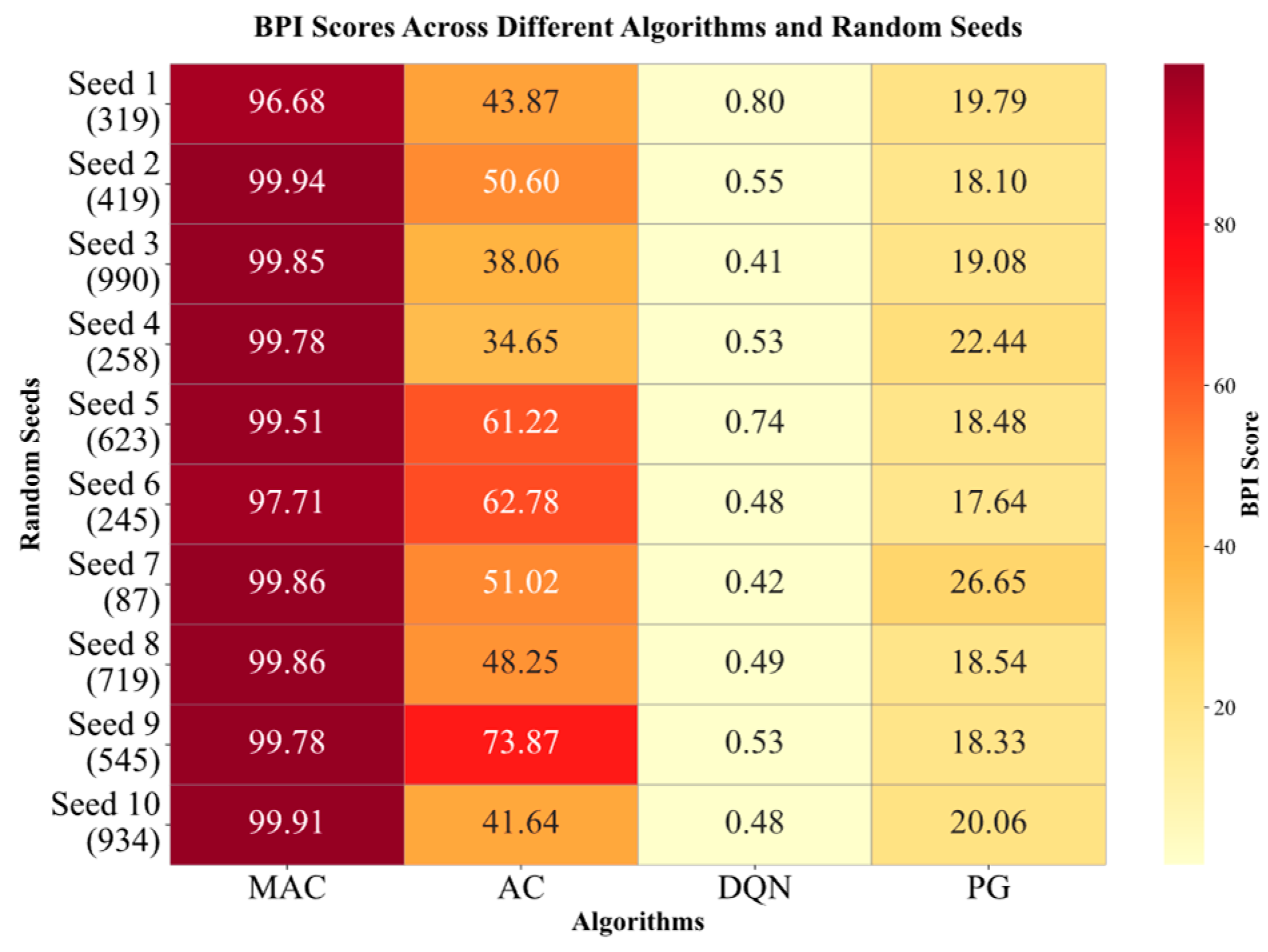
- Comparison of Algorithm BPI under Different Random Seed Conditions
- (6)
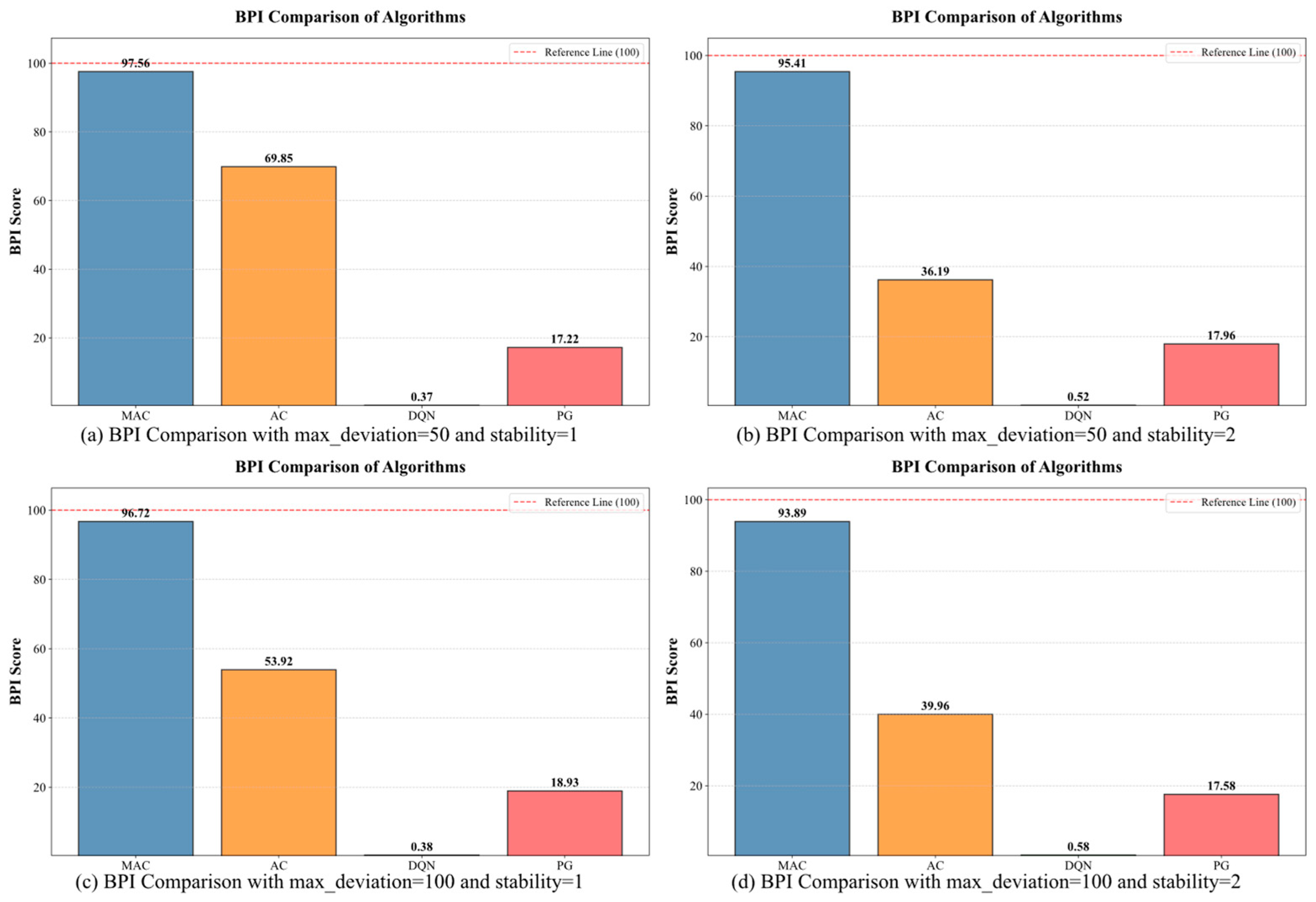
- Generalization experiments under different environmental conditions.
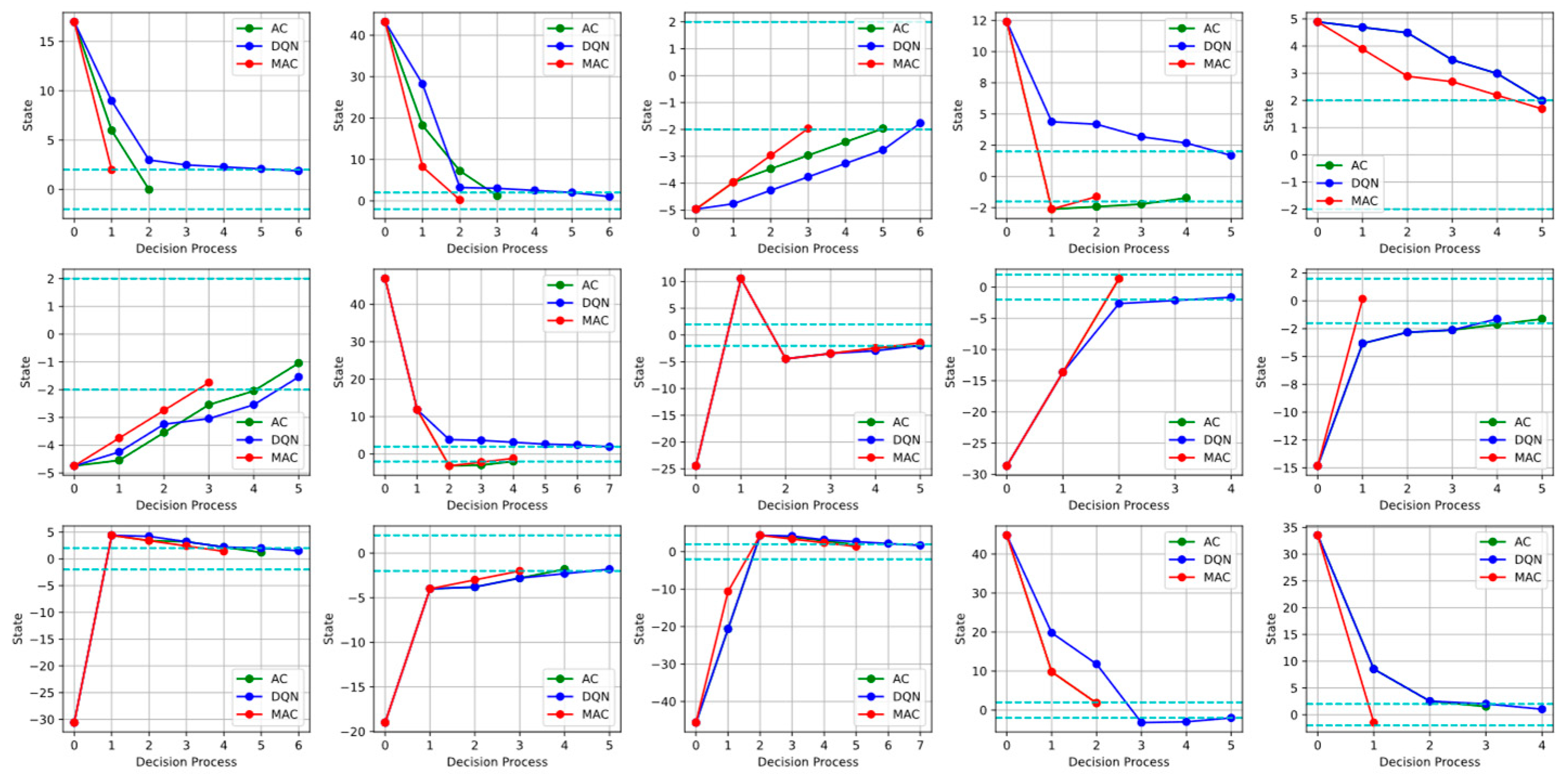
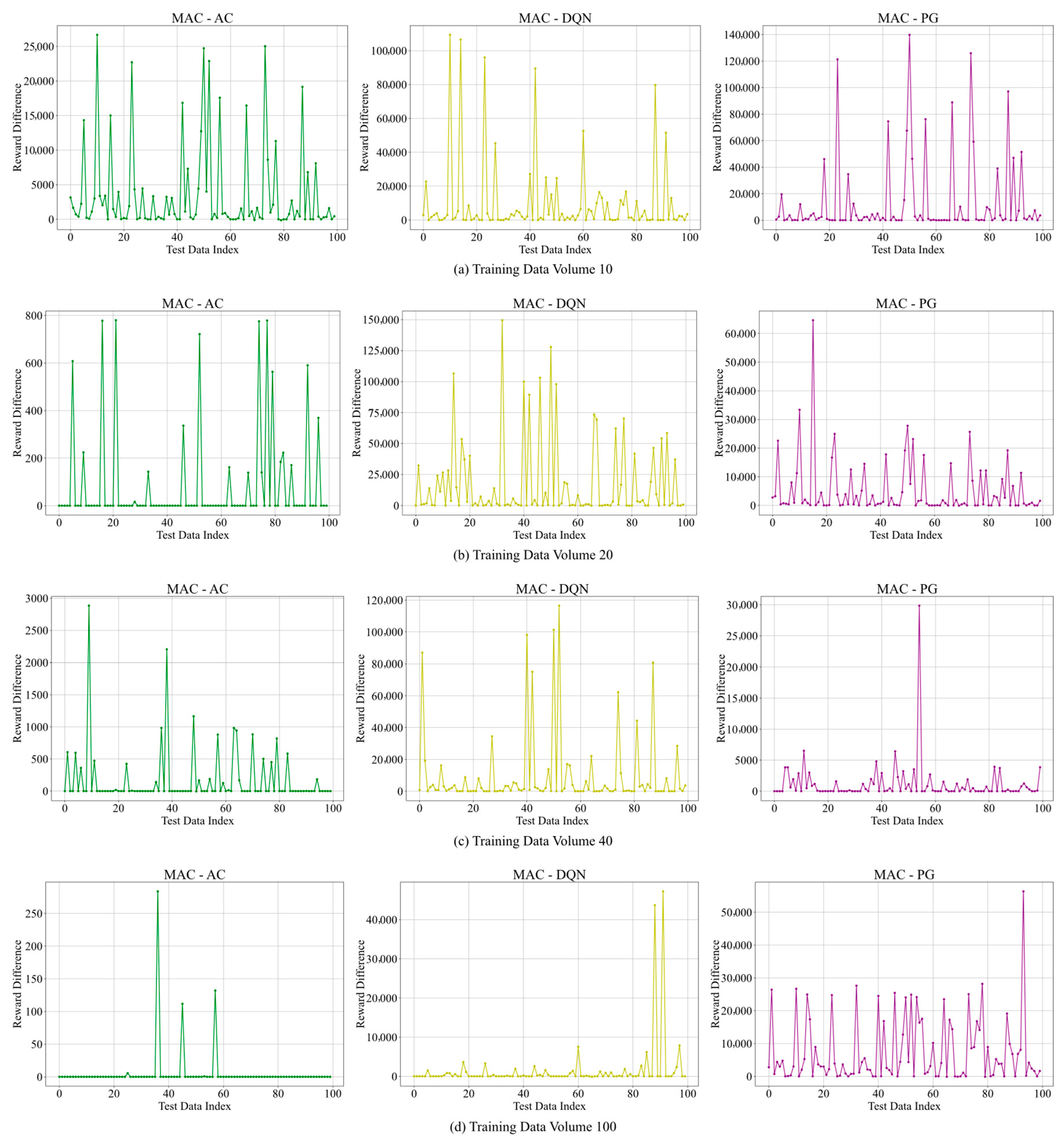
6. Experimental Results Analysis
6.1. Performance Superiority Under Data Scarcity
6.2. Robustness Validation
6.3. Environmental Adaptability
6.4. Decision Quality Assessment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Konda, V.R.; Tsitsiklis, J.N. On Actor-Critic Algorithms. In Proceedings of the International Conference on Machine Learning, Los Angeles, CA, USA, 23–24 June 2003; Society for Industrial and Applied Mathematics: Washington, DC, USA, 2003; pp. 1008–1014. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML 2016), New York, NY, USA, 19–24 June 2016; ICML Press: New York, NY, USA, 2016; pp. 1928–1937. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. Available online: https://arxiv.org/abs/1707.06347 (accessed on 16 July 2025). [CrossRef]
- Fujimoto, S.; Van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. Available online: https://arxiv.org/abs/1802.09477 (accessed on 16 July 2025). [CrossRef]
- Jiang, S.; Zeng, Y.; Zhu, Y.; Pou, J.; Konstantinou, G. Stability-Oriented Multiobjective Control Design for Power Converters Assisted by Deep Reinforcement Learning. IEEE Trans. Power Electron. 2023, 38, 12394–12400. [Google Scholar] [CrossRef]
- Zeng, Y.; Jiang, S.; Konstantinou, G.; Pou, J.; Zou, G.; Zhang, X. Multi-Objective Controller Design for Grid-Following Converters with Easy Transfer Reinforcement Learning. IEEE Trans. Power Electron. 2025, 40, 6566–6577. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017; ICML Press: Sydney, Australia, 2017; Volume 3, pp. 1126–1135. [Google Scholar]
- Chen, Y.Y.; Huo, J.; Ding, T.Y.; Gao, Y. A Survey of Meta Reinforcement Learning. Ruan Jian Xue Bao (J. Softw.) 2024, 35, 1618–1650. [Google Scholar] [CrossRef]
- Munikoti, S.; Natarajan, B.; Halappanavar, M. GraMeR: Graph Meta Reinforcement Learning for Multi-Objective Influence Maximization. J. Parallel Distrib. Comput. 2024, 192, 109–123. [Google Scholar] [CrossRef]
- Shi, Y.G.; Cao, Y.; Chen, Y.; Zhang, L. Meta Learning Based Residual Network for Industrial Production Quality Prediction with Limited Data. Sci. Rep. 2024, 14, 8122. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, D.; Xi, Y.; Jia, S. Reinforcement Learning with Actor-Critic for Knowledge Graph Reasoning. Sci. China Inf. Sci. 2020, 63, 223–225. [Google Scholar] [CrossRef]
- Mazouchi, M.; Nageshrao, S.; Modares, H. Conflict-Aware Safe Reinforcement Learning: A Meta-Cognitive Learning Framework. IEEE/CAA J. Autom. Sin. 2022, 9, 466–481. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The CRITIC Method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zhang, H.G.; Liu, C.; Wang, J.; Ma, L.; Koniusz, P.; Torr, P.H.; Yang, L. Saliency-Guided Meta-Hallucinator for Few-Shot Learning. Sci. China Inf. Sci. 2024, 67, 132101. [Google Scholar] [CrossRef]
- Zhou, S.; Cheng, Y.; Lei, X.; Duan, H. Multi-Agent Few-Shot Meta Reinforcement Learning for Trajectory Design and Channel Selection in UAV-Assisted Networks. In Proceedings of the IEEE International Conference on Communications (ICC 2022), Seoul, Republic of Korea, 16–20 May 2022; IEEE Press: Shanghai, China, 2022; pp. 166–176. [Google Scholar]
- Guo, S.; Du, Y.; Liu, L. A Meta Reinforcement Learning Approach for SFC Placement in Dynamic IoT-MEC Networks. Appl. Sci. 2023, 13, 9960. [Google Scholar] [CrossRef]
- Zhao, T.T.; Li, G.; Song, Y.; Wang, Y.; Chen, Y.; Yang, J. A Multi-Scenario Text Generation Method Based on Meta Reinforcement Learning. Pattern Recognit. Lett. 2023, 165, 47–54. [Google Scholar] [CrossRef]
- Wei, Z.C.; Zhao, Y.; Lyu, Z.; Yuan, X.; Zhang, Y.; Feng, L. Cooperative Caching Algorithm for Mobile Edge Networks Based on Multi-Agent Meta Reinforcement Learning. Comput. Netw. 2024, 242, 110247. [Google Scholar] [CrossRef]
- Xi, X.; Li, J.; Long, Y.; Wu, W. MRLCC: An Adaptive Cloud Task Scheduling Method Based on Meta Reinforcement Learning. J. Cloud Comput. 2023, 12, 75. [Google Scholar] [CrossRef]

| Abnormal Interval (Percentage) | Strategy Group | Participant A | Constraint Criteria | Rating (0–9) |
|---|---|---|---|---|
| 10~20 | 1 | Strategy aa1 | Criteria 1 | 2 |
| Criteria 2 | 4 | |||
| Criteria 3 | 4 | |||
| 2 | Strategy aa2 | Criteria 1 | 7 | |
| Criteria 2 | 2 | |||
| Criteria 3 | 1 | |||
| 3 | Strategy aa3 | Criteria 1 | 6 | |
| Criteria 2 | 2 | |||
| Criteria 3 | 2 |
| Abnormal Interval | Strategy Group 1 (Strategy Name, Benefit Value) | Strategy Group 2 (Strategy Name, Benefit Value) | Strategy Group 3 (Strategy Name, Benefit Value) |
|---|---|---|---|
| [−50%, 20%) | “A1”, 35 | “A2”, 25 | “A3”, 15 |
| [−20%, 10%) | “B1”, 15 | “B2”, 11 | “B3”, 8 |
| [−10%, −5%) | “C1”, 8 | “C2”, 6 | “C3”, 4 |
| [−5%, 0%) | “D1”, 1 | “D2”, 0.5 | “D3”, 0.2 |
| [0%, 5%) | “E1”, −1 | “E2”, −0.5 | “E3”, −0.2 |
| [5%, 10%) | “F1”, −8 | “F2”, −6 | “F3”, −4 |
| [10%, 20%) | “G1”, −15 | “G2”, −11 | “G3”, −8 |
| [20%, 50%) | “H1”, −35 | “H2”, −25 | “H3”, −15 |
| Parameter | Value |
|---|---|
| MAML inner learning rate | 0.01 |
| MAML outer learning rate | 0.01 |
| Meta-task batch size | 5 |
| the learning rate of the Actor and Critic networks | 0.001 |
| Discount factor | 0.98 |
| Number of hidden layers in the Actor network | 3 |
| Number of hidden layers in the Critic network | 3 |
| Number of neurons in each hidden layer of the Actor network and Critic network | 128, 256, 128 |
| Activation function of the Actor network | Softmax, ReLU |
| Activation function of the Critic network | ReLU |
| Optimizer | Adam |
| Learning rate scheduler | StepLR |
| Learning rate decay step size | 200 |
| Learning rate decay factor | 0.5 |
| AHP-CRITIC weight coefficient | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, B.; Li, H.; Wang, H.; Huang, Y. Intelligent Decision-Making Analytics Model Based on MAML and Actor–Critic Algorithms. AI 2025, 6, 231. https://doi.org/10.3390/ai6090231
Zhang X, Zhang B, Li H, Wang H, Huang Y. Intelligent Decision-Making Analytics Model Based on MAML and Actor–Critic Algorithms. AI. 2025; 6(9):231. https://doi.org/10.3390/ai6090231
Chicago/Turabian StyleZhang, Xintong, Beibei Zhang, Haoru Li, Helin Wang, and Yunqiao Huang. 2025. "Intelligent Decision-Making Analytics Model Based on MAML and Actor–Critic Algorithms" AI 6, no. 9: 231. https://doi.org/10.3390/ai6090231
APA StyleZhang, X., Zhang, B., Li, H., Wang, H., & Huang, Y. (2025). Intelligent Decision-Making Analytics Model Based on MAML and Actor–Critic Algorithms. AI, 6(9), 231. https://doi.org/10.3390/ai6090231






