Optimizing NFL Draft Selections with Machine Learning Classification

Abstract

The National Football League draft is one of the most important events in the creation of a successful franchise in professional American football. Selecting players as part of the draft process, however, is difficult, as a multitude of factors affect decisions to opt for one player over another; a few of these include collegiate statistics, team need and fit, and physical potential. In this paper, we utilize a machine learning approach, with various types of models, to optimize the NFL draft and, in turn, enhance team performances. We compare the selections made by the system to the real athletes selected, and assess which of the picks would have been more impactful for the respective franchise. The specific investigation allows for further research by altering the weighting of specific factors and their significance in this decision-making process to land on the ideal player based on what a specific team desires. Using artificial intelligence in this process can produce more consistent results than high-risk traditional methods. Our approach extends beyond a basic Random Forest classifier by simulating complete draft scenarios with player attributes and team needs weighted. This allows comparison of different draft strategies (best-player-available vs. need-based) and demonstrates improved prediction accuracy over conventional methods.

1. Introduction

In the 2017 NFL draft, the Chicago Bears traded up the draft to the second overall selection in the draft, where they selected UNC quarterback Mitchell Trubisky. Within just 5 years, Trubisky had turned into a backup quarterback in the NFL and is now struggling for a starting job in Pittsburgh. An article on Bleacher Report describes this draft selection as the worst draft mistake of the past decade [1]. Just eight selections later in that draft, the Kansas City Chiefs selected Texas Tech’s quarterback, Patrick Mahomes II. Since 2017, Mahomes has won two Super Bowl Championships and two Most Valuable Player Awards, and is on track to potentially become the greatest quarterback to ever play the sport. This difference in performance between two candidates in the major league is franchise-altering, as the Chiefs are now commended as one of the best teams in the league, while the Bears are onto a new quarterback and near the bottom of the league. It should be noted that each player’s draft context likely influenced the trajectory of his career. As one analyst notes, the Chiefs were better suited to Mahomes’ ‘boom-or-bust’ potential, whereas the Bears at the time preferred a more certain prospect in Trubisky. Nevertheless, the Bears made one of the worst mistakes in draft history that night in 2017, and artificial intelligence can play a significant role in avoiding such mistakes. Previous research employing data-driven approaches and machine learning has underscored the potential effectiveness of such methods for player evaluation and draft optimization [2,3].

In the past, NFL scouting and draft methods have relied heavily on human intuition (the subjective “eye test”), which introduces considerable risk [4]. Human expertise is a necessity as it allows for qualitative insights to be considered, but reliance on subjective judgment introduces error at times. Empirical evidence supports this, with studies indicating a high “bust rate” among early-round picks; for example, only 30% of first-round players drafted between 2010 and 2017 signed a second contract with their original team, suggesting many teams were dissatisfied with their initial selections [5]. This systemic inefficiency reveals a critical need for more reliable, data-driven methodologies. The NFL draft is not just a sporting event but also a significant business decision with multi-million-dollar implications, and improved draft selections mean enhanced team performance, which goes a long way to increasing the profitability of a franchise through ticket sales, merchandise revenue, and general brand value. Artificial intelligence (AI) and machine learning (ML) are one route for addressing these decision-making challenges, introducing a greater sense of objectivity, consistency, and data-driven insights to a largely subjective process. Research into AI in draft selections can contribute to growth in the field of sports management and economics, demonstrating how AI can minimize financial risk and improve asset acquisition in a highly competitive market. The integration of AI for player evaluation is also increasingly prevalent across the NFL, underscoring the timeliness and relevance of AI-driven draft strategies.

1.1. Key Terms

NFL Draft: The NFL draft is the annual event that is the subject of this investigation. The 32 teams in the NFL are assigned the same slots in each of the seven rounds of the draft (team performance from the previous season is inversely related to the draft slot). For example, the worst-performing team selects with the first pick in each of the seven rounds. These selections may be traded throughout the year for other selections or even current players, resulting in teams having fewer than or more than seven selections in a single draft. At each selection, the team that is selecting may choose from a pool of hundreds of college football players who declared for that draft that year. The draft system is the premier method to find young, talented, and relatively inexpensive players in the National Football League.

Machine Learning Classification: Machine learning classification is a subfield of machine learning that focuses on categorizing data into predefined classes. In the context of the NFL draft, a classification model could be trained on historical player data (e.g., college statistics, combine results, position) and their corresponding NFL success (e.g., Pro Bowl selections, career length, performance metrics). The model would then learn to predict which class a new, undrafted player belongs to, such as “successful NFL player” or “unsuccessful NFL player”, based on their pre-draft attributes. This allows for an automated and data-driven approach to identifying prospects with a higher likelihood of NFL success.

Player Evaluation: Player evaluation is the comprehensive process by which NFL teams assess the skills, potential, and character of college football players eligible for the draft. This process involves extensive scouting, including attending college games, reviewing game film, interviewing players and coaches, and analyzing Combine and pro day results. The goal is to determine a player’s fit within the team’s scheme, culture, and roster needs, as well as to project their future performance at the professional level. While traditionally a human-driven process, the integration of data analytics and artificial intelligence aims to enhance the objectivity and accuracy of these evaluations.

Random Forest: Random Forest is an ensemble machine learning algorithm used for both classification and regression tasks. It operates by constructing a multitude of decision trees during training and outputting the class that is the mode of the classes (for classification) or the mean prediction (for regression) of the individual trees. In the context of draft optimization, a Random Forest model could be used to predict a player’s future NFL performance or categorize them into different success tiers. Each decision tree in the forest would consider various player attributes, and, by combining the predictions of many trees, the Random Forest can provide a more robust and accurate prediction than a single decision tree, reducing overfitting and improving generalization.

Draft Optimization: Draft optimization refers to the research process attempting to improve the selections these NFL teams make during the draft. While some teams consistently make draft selections that turn out well for them, other teams may not do the same, and, at times, even the best-drafting teams do not draft well. Most of the scouting, which is the process NFL teams use to judge draft prospects and determine if they are fit for their respective NFL team, is carried out by humans with little technological involvement. This investigation aims to broaden that field of research by exploring making draft selections solely with artificial intelligence. While it is important to point out that AI making selections may never be able to think like humans or analyze non-tangible factors, it can make up for some of the human error involved in this selection process.

1.2. Outlining the Problem

In this investigation, the main scientific problems being addressed are the subjectivity and sub-optimality of the traditional NFL draft selection processes. Despite extensive scouting efforts from every franchise, there are still plenty of missed opportunities for every franchise, and this research aims to study whether machine learning models can quantifiably improve conventional draft selection methods. The specific research objectives are to develop, evaluate, and compare various AI models for optimizing NFL draft selections. This involves two classification tasks: first, predicting individual player draft positions, and, second, simulating an entire draft by assigning these players to teams based on two different draft strategies (best-player-available, or BPA, and need-based drafting).

Machine learning is well-suited for this investigation because of its efficient analysis and processing of large, multi-variable datasets [6]. The various metrics used to evaluate players are complex, ranging from statistics to physical attributes to qualitative assessments. Machine learning can efficiently find patterns in these datasets that are harder for humans to catch, offering a comprehensive decision-making process. To prevent the artificial intelligence models from learning using inapplicable data, the scope of this problem will be narrowed to post-2011 data only, and the model will only predict using drafts for 2019 or later. As the four years since 2019 have given enough time for player career evaluations to be appropriately made, 2019 is the most recent usable year. This study into the capabilities of AI in NFL draft prospect evaluation helps to set a precedent for rigorous application of machine learning in applied fields, emphasizing the potential contribution AI has in sports analytics. We also incorporate both quantitative player metrics and qualitative scouting reports into our model, and we explicitly include team positional needs in the draft decision process. This end-to-end draft simulation framework provides new insights beyond prior player-centric models.

1.3. Data

The data obtained to complete the research task are from Kaggle, an online data science platform with millions of datasets to be used for machine learning projects or data science purposes. This investigation utilized a dataset by creator Jack Lichtenstein, posted publicly (at no cost) on Kaggle. Lichtenstein’s dataset was curated with data from ESPN, a broadcasting network that releases information on NFL draft prospects on their website for each annual draft. Among the five different datasets in the folder, there are two (“nfl_draft_profiles.csv” and “nfl_draft_prospects.csv”) that are of use to this investigation.

Both datasets consist of around 13,000 prospects, including all prospects since the year 1967 (the first year in the common NFL draft era) [7]. For each prospect, both datasets are linked through a unique player ID and additionally through their names, allowing for the merging of both files to create a master dataset as a Python 3.13.0 pandas dataframe. This merging resulted in a singular dataset retaining all important columns of the two original ones, with 16 columns total, as shown below in

Table 1. Columns of master dataset.

Number	Column	Non-Null Count	Dtype
0	“draft_year”	3807 non-null	int64
1	“player_id”	3807 non-null	int64
2	“player_name_x”	3807 non-null	object
3	“pos_abbr”	3807 non-null	object
4	“school”	3779 non-null	object
5	“pick”	2677 non-null	float64
6	“overall”	2677 non-null	float64
7	“round”	2677 non-null	float64
8	“pos_rk”	3721 non-null	float64
9	“ovr_rk”	3472 non-null	float64
10	“grade”	3706 non-null	float64
11	“player_name_y”	3807 non-null	object
12	text1	1914 non-null	object
13	text2	2933 non-null	object
14	text3	533 non-null	object
15	text4	2 non-null	object

. Additionally, after merging the two datasets, data from 1967 to 2010 were removed from the dataset. Regarding the scope of this prediction method: data from 2010 or earlier should not be used to predict the drafts of 4 years ago as the NFL landscape is rapidly changing and there is little similarity between how teams make selections in modern drafts and how they made selections in pre-2010 drafts.

1.4. Literature Review

In this section, an overview of the current state of artificial intelligence (AI) and machine learning (ML) applications in sports is provided, specifically within American football. This context will help establish the greater significance of the current research in sports analytics.

Artificial intelligence is reshaping professional sports by shifting evaluation and operational strategies from subjective analysis to objective, data-driven methodologies. These AI applications extend across several domains, including player performance evaluation, game strategy development, injury prediction and management, talent identification, audience engagement, and even sports betting systems [8]. The growing reliance on AI in these areas reflects its growing role in enhancing decision-making efficiency, generating competitive advantages, and improving overall stakeholder outcomes. As such, insights from focused investigations, such as AI-driven NFL draft optimization, are increasingly applicable across the broader landscape of sports management.

A major part of this transformation is the use of AI and machine learning in evaluating players and identifying talent, especially with regards to optimizing draft strategy. These models assess player potential by integrating data from both pre-draft physical testing and in-game performance metrics. Despite some progress in the research in these fields, there are limitations in handling external context that show the need for human oversight in AI-generated outputs.

Past research has identified several indicators of rookie NFL success, centering on both college performance and physical traits. While NFL Combine results often influence draft order, their predictive value for career performance remains limited and very position-dependent. The 40-yard dash, for instance, is strongly correlated with higher draft selection and long-term success for running backs, yet it offers less reliable insight when applied to wide receivers [9]. In contrast, quarterback evaluation relies less on traditional drills and more on alternative physical metrics, such as jump measurements, hand size, and arm length, along with cognitive assessments like the Wonderlic. Mirabile’s findings suggest that Wonderlic scores do not significantly predict rookie success, while Welter’s study points to their continued relevance in organizational evaluations [10,11]. Moreover, quarterbacks as a group are particularly difficult to evaluate, and Berri and Simmons found that pre-draft assessments do not usually align with professional outcomes [12]. Height and weight, though commonly considered, are also role-specific, with greater relevance for offensive linemen and wide receivers than for other positions.

Collegiate production remains an important factor in predictive modeling, with the “college dominator” metric being a strong indicator for wide receivers and tight ends [2,3]. For quarterbacks, passing statistics are important, but additional rushing ability shows a stronger connection with long-term NFL success. Another consistent predictor is age at entry; younger prospects tend to have longer and more productive careers, as shown in Kim’s analysis [13]. These findings show that a singular player evaluation approach cannot be used for all positions, and that various different systems accounting for positional differences would be a better measure for evaluating players.

2. Materials and Methods

2.1. Predictive Modeling Approach

The investigation followed a multi-step modeling approach beginning with simple regression models and progressing to more complex classification-based draft simulations. This stepwise development ensured that we first established a clear baseline before introducing additional complexity, with the ultimate aim of developing a system capable of optimizing NFL draft selections.

Initially, a baseline model was created to simply predict a player’s appropriate draft position (the selection number), independent of the team making the pick. This initial phase was a regression model, taking in player data and outputting a number representing the approximate selection number the player would be expected to take. The methodology for this stage was aligned with established predictive modeling principles and microeconometric analysis.

After this baseline model was created, the research turned to a classification problem. This meant shifting from predicting a numerical pick for each player to simulating an entire draft, where each player is assigned to a specific team based on their predicted value and other strategic considerations. Via this shift, a few different draft strategies and their implications were explored.

Lastly, this model was extended once more to incorporate team-specific positional needs, developing a fully functional draft simulator. The simulator goes through the teams in order of their draft selections, outputting the most optimal player for each team at each selection. This progression from simple player evaluation to comprehensive draft simulation allowed for an overarching assessment of how AI can be used in this decision-making process.

2.2. Model Building Process

The primary machine learning algorithm used for the initial predictive tasks is the Random Forest (RF) regressor. The RF regressor has established robustness and very high accuracy when handling complex relationships, and can manage various types of data, including player statistics.

2.2.1. Inputs and Features

For the initial iteration of the simulator, the Random Forest regressor was configured to predict the numerical draft pick value. This first iteration of the model was trained using four input variables, namely, the player’s position (encoded as a numerical value), the player’s draft grade, their ranking among players at the same position, and overall ranking. It is ideal to include over four input variables, and this is an idea explored further in the investigation; however, to establish a high-performing baseline, those four variables proved to be enough.

Feature engineering efforts exploring physical attributes were included as additional dimensions to the model in an attempt to increase predictive power. The two attributes present were player height and weight, but they proved to be insignificant in improving model performance. This finding is unsurprising in some senses, as there is no ideal set of physical attributes for succeeding in the NFL, and, if there was one, it would alter for every position present in the league. For example, height benefits wide receivers, who need a taller frame to catch higher-thrown footballs, but it is less relevant for offensive linemen, whose main priority is strength. This does suggest that future models could benefit from position-specific feature engineering or even separate models for different player roles.

Another feature of testing involved using text-based data to train the model, rather than just numerical data. More specifically, the original dataset includes sets of comments on each player, serving as a textual evaluation of the skills and abilities of the player, provided by experts working with ESPN. The natural language processing aspect comes in when these strings of text are converted to single-number grades out of 10. This process uses tf-idf (term frequency-inverse document frequency, a method that evaluates word relevance based on a collection of documents) to numericize the string, and then gives weights to unique words in the description, such as “polarizing”, “covet”, and “boom-or-bust”, as samples from one of the evaluations. Each player is given a numbered grade out of 10 to represent the overall sentiment of the comments.

2.2.2. Determining Hyperparameters

The RF regressor was initialized with a random_state of 42, for reproducibility. The performance of an RF model is heavily influenced by its hyperparameters, which control the learning process and model complexity. Key hyperparameters include n_estimators (the number of decision trees in the forest), max_depth (the maximum depth of each decision tree), max_features (the number of features to consider when looking for the best split), and min_samples_split (the minimum number of samples required to split an internal node).

The initial models used a fixed n_estimators value (e.g., 100, 200, 300), but other techniques such as GridSearchCV or RandomizedSearchCV can be used to systematically determine optimal hyperparameters, by evaluating the model’s performance against hundreds of combinations of hyperparameters to identify the optimal set. Altering hyperparameters comes with both benefits and drawbacks (for example, increasing n_estimators may improve performance but increases runtime), so it is important to carefully optimize the parameters to ensure the model being used is optimal.

2.2.3. Simulation Target: Optimization Strategy

Initially, with the RF regressor, the simulation target was the prediction of a player’s overall draft pick number. This is a regression problem, where the model outputs a number representing the predicted draft slot given a player’s attributes. The model was optimized by reducing the root mean squared percentage error (RMSPE) and maximizing the Pearson’s correlation coefficient (PCC) between predicted and actual pick values in an attempt to model realistic predictions.

When the research transitioned into a classification problem, the target changed from predicting a pick number to assigning players to specific teams within a simulated draft environment. The selection of the optimal player at their respective draft slot, based on strategic considerations (best-player-available or need-based drafting), was the target of the optimization. This target was validated by comparing simulated draft outcomes against real-world selections, evaluating how closely the AI-driven choices mirrored and improved upon actual draft results. This shift from simple prediction to strategic simulation represents a more complex and realistic application of AI in decision support. For example, a team could use a similar AI simulator to predict other teams’ selections before their own selection, to inform themselves of their realistically available options for their pick.

2.3. Accounting for Player Types and Positions

Player position was included as one of the four core input variables in the RF regressor (encoded as a numerical value), which allowed for it to be considered when the model made predictions. However, a uniform model across all player types/positions has limitations; the relevance of specific attributes varies across positions, and it cannot be overlooked that, in the draft selection process, different teams need different positions. Therefore, a single model with position as an input would struggle to be realistic, creating a need for the need-based drafting approach explored later in the paper. This model implicitly considers player positions by considering what position groups each team needs most at that time when they are being assigned a player. While player talent is still considered, there is now room for positional needs to be considered, creating the most realistic simulator of the draft in this investigation.

2.4. Evaluation Metrics

For the earliest regression tasks, predictive power was defined as the conjunction of both the RMSPE (root mean squared percentage error) and the PCC (Pearson’s correlation coefficient). The RMSPE is shown in the first formula below, and uses a percentage or ratio between 0 and 1 to represent the combined distance of predicted y-values from actual y-values, where a lower RMSPE correlates to the predicted and actual values being closer, or more realistic predictions. Similarly, the Pearson’s correlation coefficient formula is also shown below, also a ratio between 0 and 1. However, when the PCC is maximized (closer to 1), this implies that the predicted and actual values are closer to each other, making the predictions more realistic. All RMSPE and PCC values were computed as averages of five distinct trials to ensure the precision and reliability of the performance statistics.

$$RMSPE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left({\displaystyle \frac{y_i-\widehat{y_i}}{y_i}}\right)}^2}$$

(1)

Formula (1): Root mean squared percentage error (RMSPE).

$$r={\displaystyle \frac{\sum (x_i-\widehat{x_i})(y_i-\widehat{y_i})}{\sqrt{\sum {(x_i-\widehat{x_i})}^2\sum {(y_i-\widehat{y_i})}^2}}}$$

(2)

Formula (2): Pearson’s correlation coefficient (PCC).

Residuals (the numerical difference between the predicted value and the actual value for each player) were also briefly used to provide a visual of model performance in specific predictions.

For the classification tasks, a few other metrics were computed to evaluate the performance of this model, including the mean absolute error (MAE) and top-K accuracy. The metrics are computed via Formula (3) (MAE) and Formula (4) (Top-K). The MAE serves as a method of comparing a set of numerical predictions to the true numerical values (creating the difference term $x_i-x$), and sums the absolute value of these differences over n, the number of predictions made. To the other end, a variant of the Top-K method was introduced, where successful predictions (classified as within $k=3$ picks of the true selection) were considered accurate, and the score of any other pick was proportional to how close it was to being accurate. This concept is defined by a piecewise function, as shown below in Formula (4).

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mid x_i-x\mid$$

(3)

Formula (3): Mean absolute error (MAE).

$$s_k={\displaystyle \frac{{\sum }_{i=1}^{n}f\left(i\right)}{n}};f\left(i\right)=\left\{\begin{array}{cc}1\hfill & |x_i-x|\le 5\hfill \\ max(0,1-{\displaystyle \frac{|x_i-x|}{x}})\hfill & \mathrm{else}\hfill \end{array}\right.$$

(4)

Formula (4): Top-K score.

2.5. Integration of AI in the Simulation Model

The simulation model developed in this resear ch is an environment for testing AI-driven draft strategy. The AI models are not just external predictors, but rather integral elements that drive the simulations by making player evaluations and strategic decisions in this simulated draft environment. The simulation follows the structure of the NFL draft, sequentially processing draft picks in the same order of teams as the real NFL draft, with each pick being a selection from the pool of available players based on the strategy being used (BPA or need-based). The AI’s role is to provide the intelligence for these decisions. Figure 1 is a diagram showing the simulation framework with its AI components integrated.

3. Results

3.1. Initial Team-Free Predictions

The initial phase of the research developed a Random Forest regressor to predict the overall draft pick number of a player, given their position, draft grade, position rank, and overall rank. We used draft data from 2016–2019 as the training set and reserved the 2020 draft class as an independent test set. This hold-out approach ensured that the performance metrics reflected the model’s ability to generalize to new data. An 80:20 ratio between training and testing data (with 2016–2019 as training and 2020 as testing data) consistently yielded more efficient results compared to a 75:25 split, as shown in

Table 2. Predictive performance of the first simulator iteration (75:25 train:test split).

RF: Trained with “pos_abbr”, “grade”, “pos_rk”, “ovr_rk”
Train Data Shape	Test Data Shape	RMSPE (5 trials)	PCC (5 trials)
(1121, 4)	(335, 4)	0.42737	0.93892

.

The 80:20 split, shown in

Table 3. Predictive performance of the first simulator iteration (80:20 train:test split).

RF: Trained with “pos_abbr”, “grade”, “pos_rk”, “ovr_rk”
Train Data Shape	Test Data Shape	RMSPE (5 trials)	PCC (5 trials)
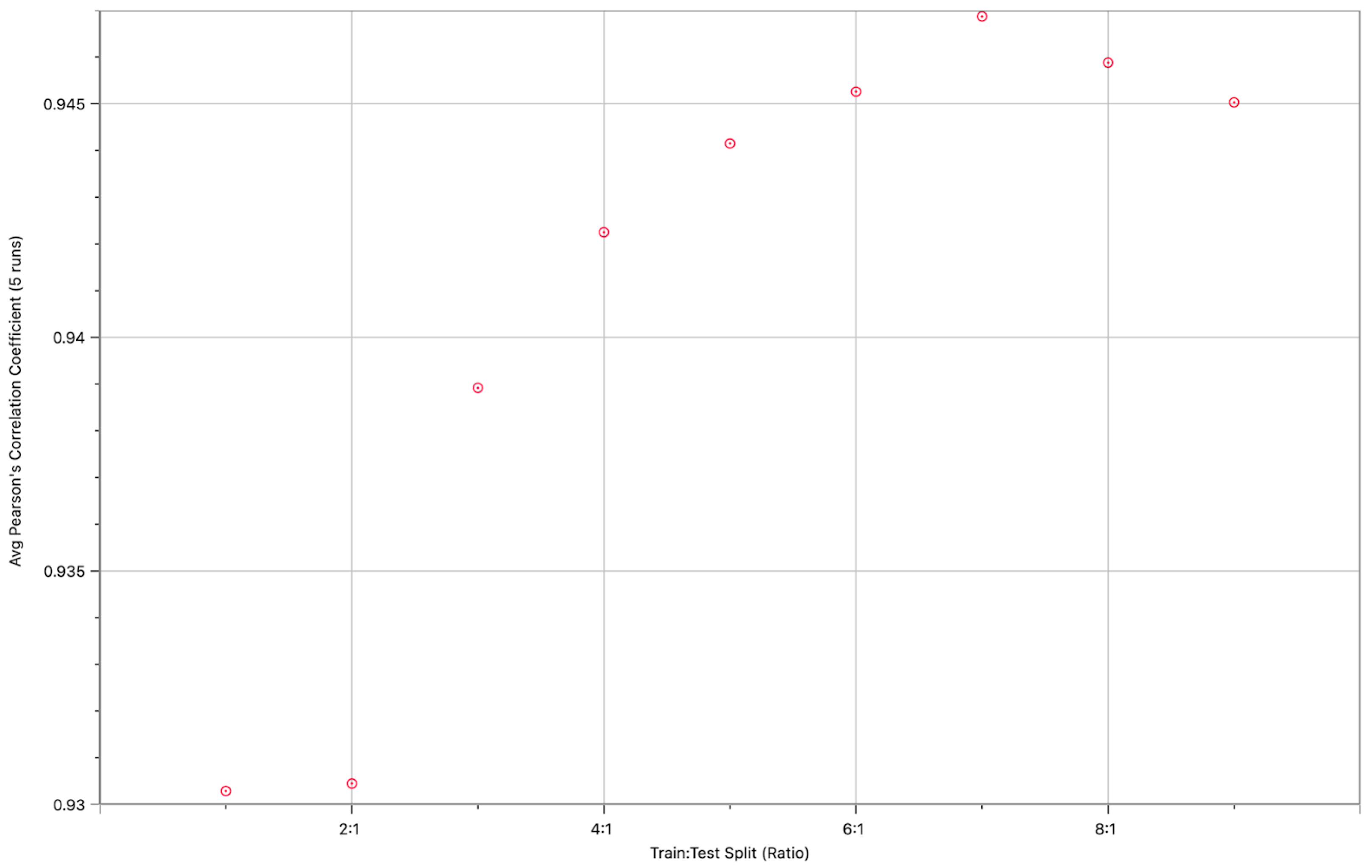
(1492, 4)	(335, 4)	0.41215	0.94225

, with a training data shape of (1492, 4) and testing data shape of (335, 4), produced a lower average RMSPE of 0.41215 and a higher average PCC of 0.94225 over five trials, indicating improved predictive accuracy. Further exploration of the train:test split ratio revealed diminishing returns in predictive power gained beyond a certain point, despite an apparent peak at a 7:1 ratio for the Pearson’s correlation coefficient. This suggests that simply increasing training data indefinitely can lead to issues such as overfitting, where the model becomes too specialized to the training data and performs poorly on unseen data. Additionally, runtime increases significantly with larger training datasets, making a balanced split more practical. The next mini-investigation was to determine how the train:test split affected the predictive power of this model beyond just 4:1. The graph below shows a scatter plot, with the train:test split ratio as the independent variable and Pearson’s correlation coefficient, the same measure of linearity used above, as the dependent variable.

While it may appear that a 7:1 train:test split ratio produces the best results, it is important to note that the correlation coefficient does not increase by as much from 6:1 to 7:1 as it does from 3:1 to 4:1, signifying a drop-off in predictive power gained. The statistics shown in

Table 4. Predictive power: Random Forest.

Training Data: 2014–2019/Testing Data: 2020
	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	2200, 4	335, 4	0.38887	0.94629

detail the 7:1 train:test split ratio and the associated error and correlation values.

Simply using more training data for more accurate results is susceptible to common artificial intelligence pitfalls such as overfitting, where the model is too familiarized with the excessive training data and cannot test on newer data as well, as can be seen in Figure 2. In addition, one other downside of potential overfitting with the dataset could mean that the more-trained model does not perform as well on other testing datasets and is not as consistent. Additionally, runtime increases at a greater rate as more training data are added, meaning it is ideal to use this 4:1 train:test split ratio.

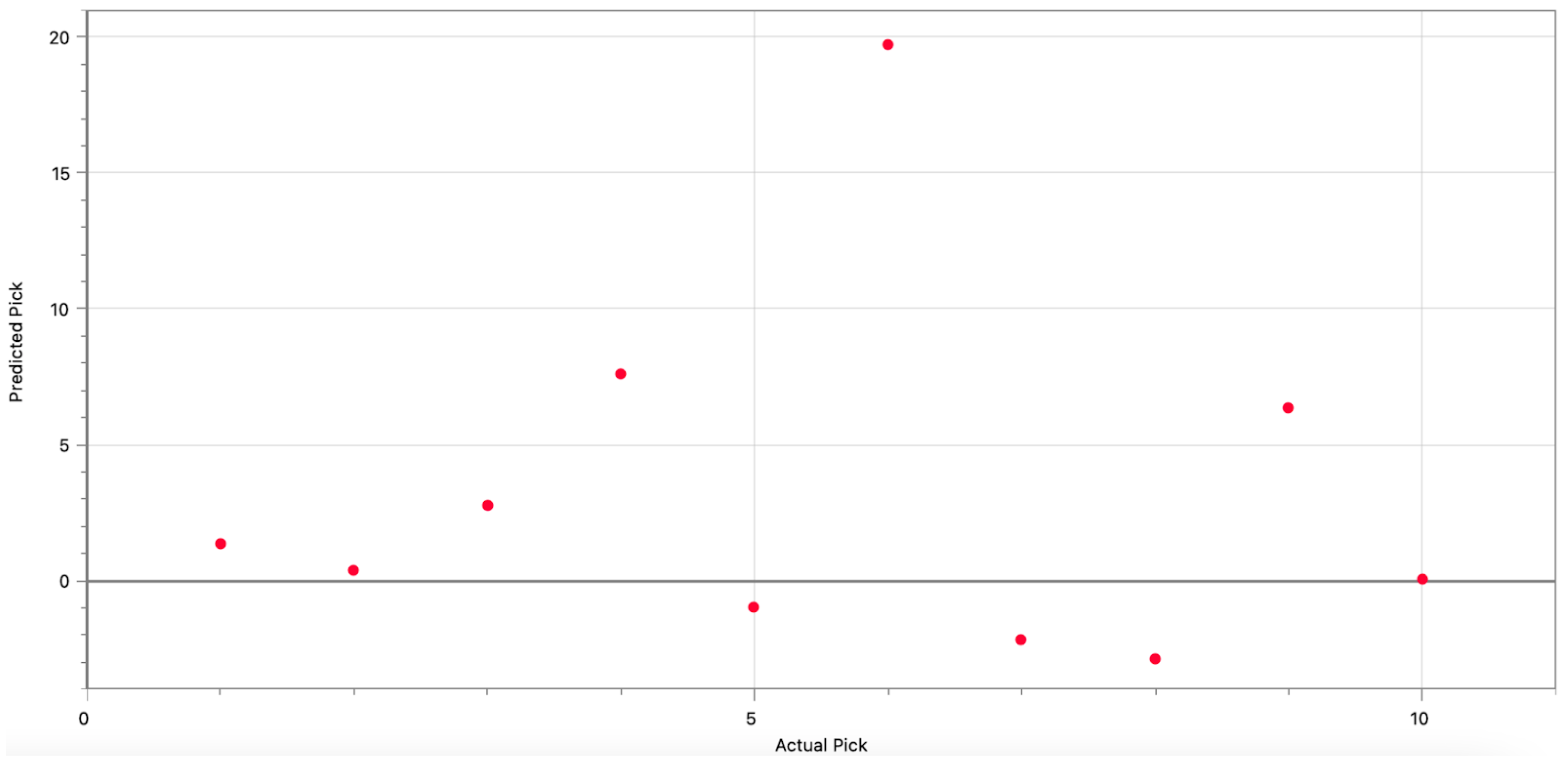
The model was also evaluated on residuals, and Figure 3 shows how the model performed on each of the top 10 selections in the 2020 NFL draft. The model was generally accurate, predicting to within five slots for 7 of the 10 draftees. However, for pick 6 (current LA Chargers quarterback Justin Herbert), the model predicted him to be taken 20 slots lower than he actually was. This aligns with the popular opinion at the time of the draft, as many experts felt the Chargers “reached” by taking Herbert and should have waited longer.

Comparison with other model types (Decision Tree Regressor, DTR, and Support Vector Machine, SVM, with a linear kernel) consistently demonstrated that the Random Forest regressor was the most efficient model for this prediction problem, as can be seen in

Table 5. Predictive power (tested 2016–2019): various models.

Training Data: 2016–2019/Testing Data: 2020
	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	1492, 4	335, 4	0.41318	0.94068
RF	n = 200	1492, 4	335, 4	0.41031	0.94196
RF	n = 300	1492, 4	335, 4	0.41215	0.94225
DTR		1492, 4	335, 4	0.53062	0.89107
SVM	‘linear’	1492, 4	335, 4	0.49095	0.89657

and

Table 6. Predictive power (tested 2017–2019): various models.

Training Data: 2017–2019/Testing Data: 2020
	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	1121, 4	335, 4	0.42737	0.93892
RF	n = 200	1121, 4	335, 4	0.42586	0.93841
RF	n = 300	1121, 4	335, 4	0.42701	0.93806
DTR		1121, 4	335, 4	0.59055	0.89339
SVM	‘linear’	1121, 4	335, 4	0.49096	0.89655

, yielding superior RMSPE and PCC values across different training data spans.

3.2. Continued Feature Engineering

The next attempts to increase the predictive power of the regression model incorporated physical attributes, including height and weight, and the results are shown in

Table 7. Predictive power: Random Forest with height.

Training Data: 2017–2019/Testing Data: 2020
Model	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	1121, 5	335, 5	0.41966	0.92931

.

It is visible that the inclusion of height statistics into the model training did not play a significant role in improving model performance, as the correlation coefficient calculated was lower than that of the Random Forest trained with the original four dimensions. A lower error value was received, but the change proved to be unimportant to the success of the model. The correlation between weight and draft position was weaker than that of height, producing lower correlation and higher error.

Table 8. Predictive power: Random Forest.

Training Data: 2014–2019/Testing Data: 2020
Model	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	2200, 6	335, 6	0.42655	0.92003

and

Table 9. Predictive power: Random Forest.

Training Data: 2017–2019/Testing Data: 2020
Model	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	1121, 6	335, 6	0.44287	0.91340

show the inclusion of both weight and height, totaling six dimensions for each player the model trained on, with each being on a different training dataset size.

The data strongly imply weight and height are irrelevant statistics for predicting a player’s draft position, as the combination of both statistics simply adds more dimensions while decreasing correlation between actual and predicted datasets and also increasing the model’s error. This conclusion is not surprising; in the NFL, each position demands a varied set of physical attributes based on their position’s responsibilities. For example, teams generally opt for taller and sleeker wide receivers (players tasked with catching the ball), as the height puts that player at an advantage against shorter players, while a sleeker build increases player acceleration and speed. However, other positions, such as positions in the offensive line, demand stronger and heavier players to better protect the quarterback, and height is typically irrelevant in the selection of offensive linemen. Therefore, the idea of utilizing physical attributes in prediction was temporarily abandoned.

The investigation also explored the use of text-based data, specifically, expert comments on each player converted into numerical grades using tf-idf, with the results displayed in

Table 10. Predictive power: NLP-developed model.

Training Data: 2017–2019/Testing Data: 2020
Model	Size	Train Shape	Test Shape	RMSPE	PCC
RF	n = 100	1121, 5	335, 5	0.41966	0.92931

.

Adding this text-derived dimension proved less effective, resulting in both a higher error and lower correlation than previously tested models without this dimension. A potential explanation for this outcome is the bimodal distribution of the sentiment scores; the comments often gravitated towards extreme positive or negative sentiments, leading to a lack of nuanced intermediate values that could effectively differentiate player skill levels.

3.3. Classification Attempts: Best-Player-Available

The following table exhibits the results of the AI utilizing a BPA draft strategy, to simulate the first round of the league’s 2017 draft. One unaccounted for difference in the order of teams between the simulation and the actual draft is that teams may trade selections between themselves in the real draft, resulting in a different draft order than originally expected. Such trades are near impossible to predict, as they are based upon changes of heart within the draft period and are supplied by intuition significantly more than planning. Therefore, the simulator developed did not account for these trades between teams. For the BPA strategy, this abandonment of in-draft trading does not matter, as the ranking of players does not change depending on what team selects them.

In the below table, the ‘Round, Pick’ column gives the specific slot in which a selection was made (for example, 1.03 implies the third pick of the first round). Positive numbers in the pick difference column imply a player was selected higher in the simulation than the real draft, and vice versa. For example, Jamal Adams was selected four spots higher in the simulation (slot 2) than in the real draft (slot 6). If a player is not assigned a number, that means the simulation predicted him to be drafted in the first round, but, in reality, he was not drafted in the first round. The simulation of the first round of the 2017 NFL draft using the BPA strategy yielded the results in

Table 11. First round predictions: BPA.

Round, Pick	Team	Player	Pick Difference
1.01	CLE	M. Garrett	0
1.02	SF	J. Adams	+4
1.03	CHI	L. Fournette	+1
1.04	JAX	S. Thomas	−1
1.05	TEN	M. Lattimore	+6
1.06	NYJ	J. Allen	+11
1.07	LAC	O. Howard	+12
1.08	CAR	C. McCaffrey	0
1.09	CIN	H. Reddick	+4
1.10	BUF	M. Hooker	+5
1.11	NO	D. Barnett	+3
1.12	CLE	R. Foster	+19
1.13	ARI	J. Davis	N/A
1.14	PHI	F. Lamp	N/A
1.15	IND	D. Cook	N/A
1.16	BAL	M. Humphrey	0
1.17	WSH	C. Davis	−12
1.18	TEN	M. Williams	−11
1.19	TB	D. Njoku	+10
1.20	DEN	T. McKinley	+6
1.21	DET	R. Ramczyk	+11
1.22	MIA	C. Robinson	N/A
1.23	NYG	M. Trubisky	−21
1.24	OAK	E. Engram	−1
1.25	HOU	G. Bolles	−5
1.26	SEA	J. Ross	−17
1.27	KC	P. Mahomes	−17
1.28	DAL	T. Bowser	N/A
1.29	GB	C. Harris	−7
1.30	PIT	T. Watt	0
1.31	ATL	T. Charlton	−3
1.32	NO	T. White	−5

.

Exactly four of the players held a pick difference of 0, meaning their real and simulated draft slots were the same, and the team that drafted the player was also the same. These four players were Myles Garrett (Cleveland Browns), Christian McCaffrey (Carolina Panthers), Marlon Humphrey (Baltimore Ravens), and T. J. Watt (Pittsburgh Steelers). Surprisingly, these four players are among the best at their respective positions in the league, meaning that the model may be more accurate with predicting landing spots for the league’s successful players. Overall, 12.5% of the first round simulations were true matches (same draft slot and same team), with half of the other 28 selections being correctly predicted to within 10 slots. Overall, this position-blind approach provided a reasonable baseline: 12.5% of the first-round picks were predicted exactly (same slot and team), and many others were within 10 slots of the actual pick. However, the results indicated room for improvement, motivating the next step of incorporating team needs into the model.

3.4. Classification Attempts: Need-Based Selections

The algorithm works by initially assigning the best player available when a team makes its selection. It then iterates through the rest of the players available, and, if the combination of a player’s need score and the predicted pick (where they would be predicted to be drafted on a neutral board, without the factor of teams) is better than the current best player available, they replace that player as the “optimal” player. This need score is derived from those five position groups each team most needs; if a player’s position is higher on that list for a specific position, they have a much better chance of being drafted to that team than if their position is not in the top five positions needed for a team. The overall score for a player–team combination is calculated as $n\ast (5-i)-p$, where n is a constant value (higher values of n correlate to more importance in terms of team need, rather than player talent, on a general level ), i represents the importance of the player’s position to the team drafting at the moment ($0-5$), and p is the neutral “predicted pick” value.

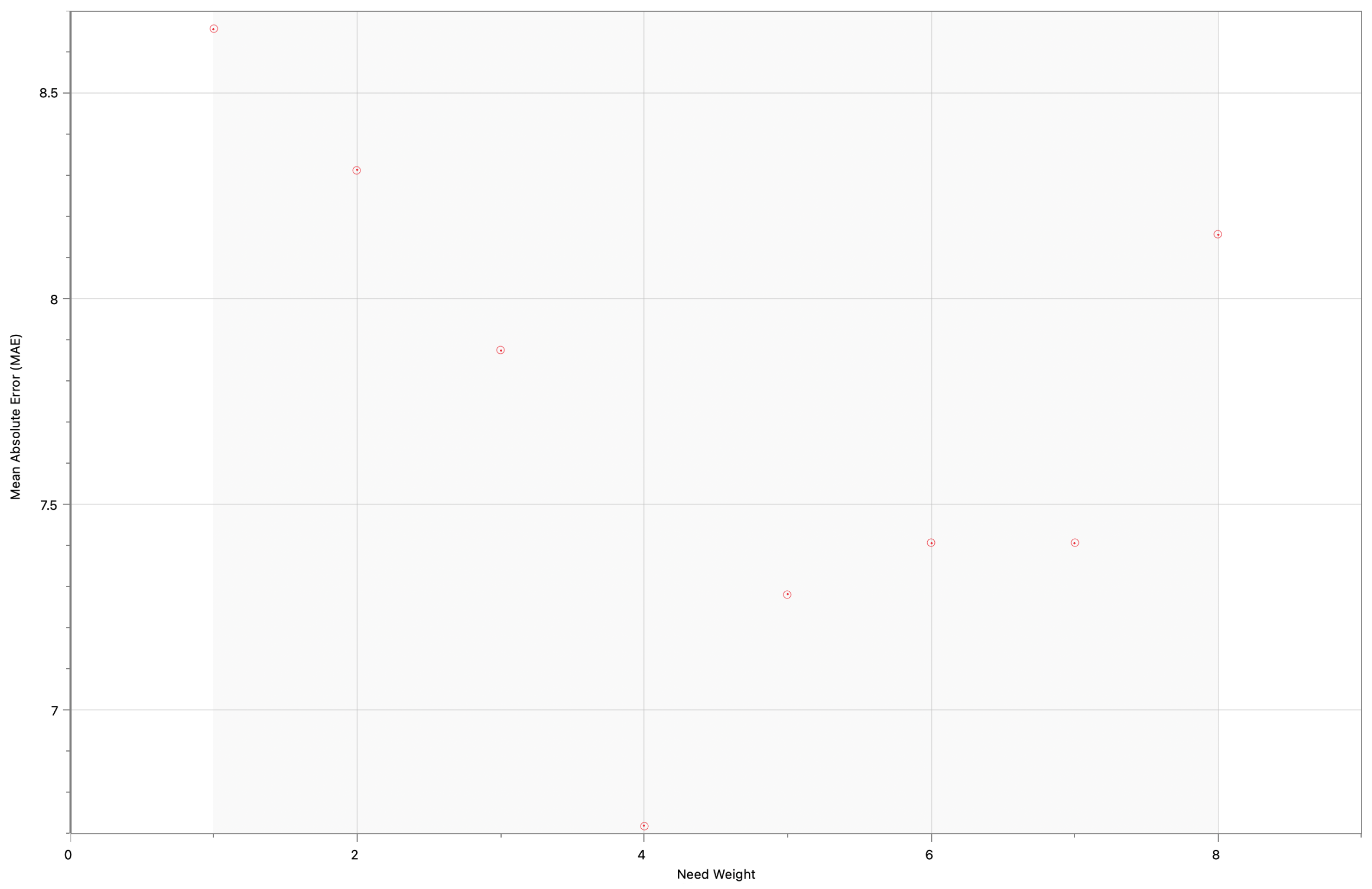
Various weightings for n in the formula were utilized, with $n=4$ being the most optimal (and the one used to generate the predictions table below). The range was constricted to $n\in (1,8)$ to exclude unnecessarily high values of n, which forced the simulator to operate a strategy where player skill is essentially insignificant. Via calculating the MAE and Top-K score for each integer value of n in the range $(1,8)$, it was found that $n=4$ had the lowest MAE, at around $6.7$ (on average, each selection differs from the actual by $6.7$ picks), and the highest Top-K accuracy score, at $77.4$, was at least three points better than any other value of n. As an example, Figure 4 below shows how the MAE varies with the values of n in the given range.

Table 12. First round predictions: need-based drafting.

Round, Pick	Team	Player	Pick Difference
1.01	CLE	M. Garrett	0
1.02	SF	S. Thomas	+1
1.03	CHI	M. Lattimore	+8
1.04	JAX	J. Adams	+2
1.05	TEN	L. Fournette	−1
1.06	NYJ	M. Hooker	+9
1.07	LAC	C. Davis	−2
1.08	CAR	C. McCaffrey	0
1.09	CIN	H. Reddick	+4
1.10	BUF	M. Williams	−3
1.11	NO	R. Foster	+20
1.12	CLE	D. Barnett	+2
1.13	ARI	M. Trubisky	−11
1.14	PHI	M. Humphrey	+2
1.15	IND	J. Allen	+2
1.16	BAL	J. Ross	−7
1.17	WSH	J. Davis	+4
1.18	TEN	O. Howard	+1
1.19	TB	D. Cook	+22
1.20	DEN	R. Ramczyk	+12
1.21	DET	T. McKinley	+5
1.22	MIA	F. Lamp	+16
1.23	NYG	C. Robinson	+11
1.24	OAK	T. White	+3
1.25	HOU	P. Mahomes	−15
1.26	SEA	G. Bolles	−6
1.27	KC	D. Watson	−15
1.28	DAL	D. Njoku	+1
1.29	GB	T. Bowser	+18
1.30	PIT	C. Harris	−8
1.31	ATL	T. Charlton	−3
1.32	NO	K. King	+1

, constructed in the same way as that in Section 4.1, shows the predictions of the need-based drafting simulator, along with the differences between the simulator and the actual outcomes.

3.5. Evaluation of Predictions

Comparing the best-player-available (BPA) and need-based drafting strategies reveals both similarities and distinct advantages. Both simulations exhibited a degree of alignment, with several players predicted within one pick of each other in both scenarios. This suggests that team need serves to complement, rather than completely override, the influence of player skill in the AI model’s decision-making process.

It is most important to consider not only the models’ performance compared to each other, but also how the models compare to the true NFL draft in 2017. Comparing the need-based simulator and the BPA simulator via the Top-K score and the MAE metric, the need-based simulator has both a lower MAE ($6.7$ to $8.8$) and a higher Top-K score ($77.5$ to $71.9$) than the BPA simulator. This means that need-based drafting deviated from the real draft by two whole picks less than the BPA simulator, on average, and was $6\%$ better at predicting the players’ draft positions to within three picks of their true draft positions. However, the true NFL draft outcome is not necessarily the most “accurate”; NFL teams often make mistakes while drafting, and end up regretting passing on some players. Via a study by the 33rd team, only $30\%$ of players drafted in the first round between 2010 and 2017 ended up signing a second contract with that team, showing that most teams were generally dissatisfied with who they selected. With that, it can be said that need-based drafting is definitely better at emulating realistic drafting than BPA drafting, but only further investigation can reveal the true success of both methods compared to real drafting.

4. Conclusions

This research investigated an application of machine learning (in particular, Random Forest models) in optimizing NFL draft selections. We moved beyond a basic RF application by developing and comparing two distinct drafting strategies (BPA vs. need-based). Specifically, the need-based simulator achieved a lower mean absolute error (MAE = 6.7) and higher Top-3 accuracy (77.5%) than the BPA model (MAE = 8.8, Top-3 = 71.9%), indicating closer alignment with actual draft outcomes. These findings demonstrate that explicitly accounting for team needs improves prediction accuracy, directly linking our results to the study’s objectives. In combination with our feature engineering, this approach contributes to our understanding of AI’s potential in sports analytics [14]. Moreover, similar data-driven approaches have been effective in other leagues, such as in relating college metrics to pro basketball success [15].

Furthermore, the study offers general managers and front office personnel a powerful tool for data-informed decision-making. By simulating various draft scenarios, teams can anticipate potential selections by opposing franchises, and thereby understand the realistic availability of prospects for their own picks. This foresight allows teams to refine their strategy, identify optimal choices, and navigate the complexities of the draft with a clearer understanding of the board, enhancing their ability to build a competitive roster. The computational efficiency of the simulation, terminating within 10 s on every iteration, highlights the practical feasibility of integrating such AI-driven tools into real-world draft operations.

The findings of the investigation are valuable to NFL teams, or analysts, attempting to model the outcome of the draft and offer valuable insights into more effective draft strategies. Realistically, teams drafting via need-based approaches is more realistic than simply selecting the best player available, and is a strategy that should be adopted more across the board. With additional metrics, more year-by-year analysis, and integrated trade simulation, AI insights can be used by general managers to ensure franchises make the optimal selections for their draft, potentially setting them up for decades of success.

4.1. Research Strengths and Weaknesses

The investigation evaluated the accuracy and realism of several different strategies, including both best-player-available (BPA) drafting and need-based drafting. Comparing both strategies is increasingly important in drafts, where a bubble of uncertainty surrounds every prospect, and the investigation clearly identified one strategy as more realistic and productive than the other. Using both numerical and text-based data, the model struck a balance between pure quantitative and qualitative assessments to efficiently grade players and predict their landing spots, using several different metrics to grade its performance. From a computational standpoint, the program has a significantly short runtime, terminating within 10 s on every iteration, opening the gate for more variables, data, and models to be incorporated in the simulation process.

A couple of drawbacks of the research center on its inability to be generalized across different seasons and conditions. It serves as more of a case study of a single draft year, 2017, but it can be predicted that other seasons would reveal similar insights into the draft. However, analyzing the way the draft changes over time and the way strategies evolve (with new general managers, for example) is a different avenue of potential research that this investigation could lead to. Another potential weakness is that the strategy deemed optimal is uniform across all teams in the draft, which is highly unrealistic; most teams will opt for some combination of both strategies, which is impossible to know, but can be potentially predicted.

4.2. Areas of Further Investigation

There are a couple areas of potential further investigation based on the evaluations. In the earlier stages of the research, various values of n_estimators were fixed for the Random Forest model, and the value with the most optimal statistics was utilized in the later research. However, a possible further investigation may involve plotting the number of estimators against model performance, to select the optimal number of trees in the model.

Additionally, other individual collegiate athlete statistics, such as stat lines in college, performances at the NFL Combine, and more, could improve the predictive model. Some of these characteristics include age at NFL entry, collegiate stat lines, and cognitive assessments. One issue, though, is that these stat lines sometimes cannot be generalized to players of all positions; for example, touchdowns and receiving yards are the most important statistics to wide receivers, but, for offensive linemen, sacks allowed and missed blocks are far more significant, with the other statistics being essentially irrelevant.

Customizing the drafting process for each team would serve as another similar investigation. It would be difficult to replicate how teams draft in real life with AI, as the general public has little idea what factors influence a team’s coaching staff’s decision to draft a player or not; however, several simulations could be ran with varying strategies for each team to test hypotheses on how specific teams draft.

The same predictive approach could add another dimension if trading between teams was factored into extended research. For example, teams could trade up to a higher pick in the middle of the simulation based on how the simulation has been going. However, this usually requires roster considerations outside the scope of the draft, making it difficult to accomplish.