Exploring Artificial Personality Grouping Through Decision Making in Feature Spaces
Abstract
1. Introduction
2. Related Works
3. Methodology
3.1. Application Example and Data Notation
3.2. The Group’S Decision Map
3.2.1. Normalization
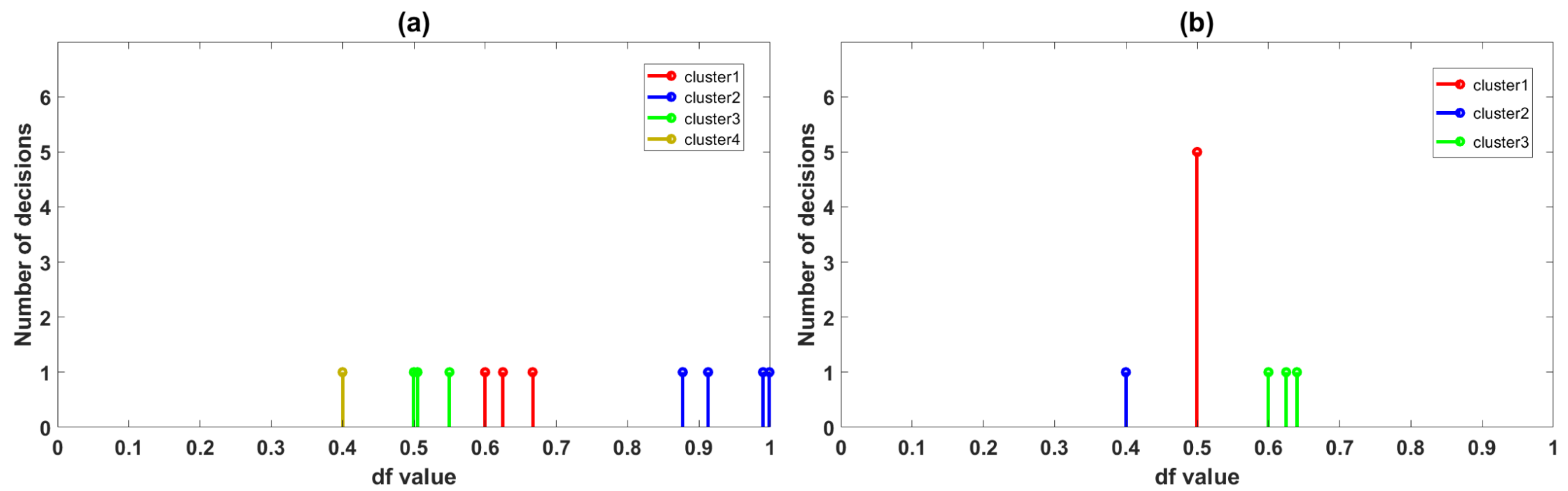
3.2.2. Clusters of Decisions
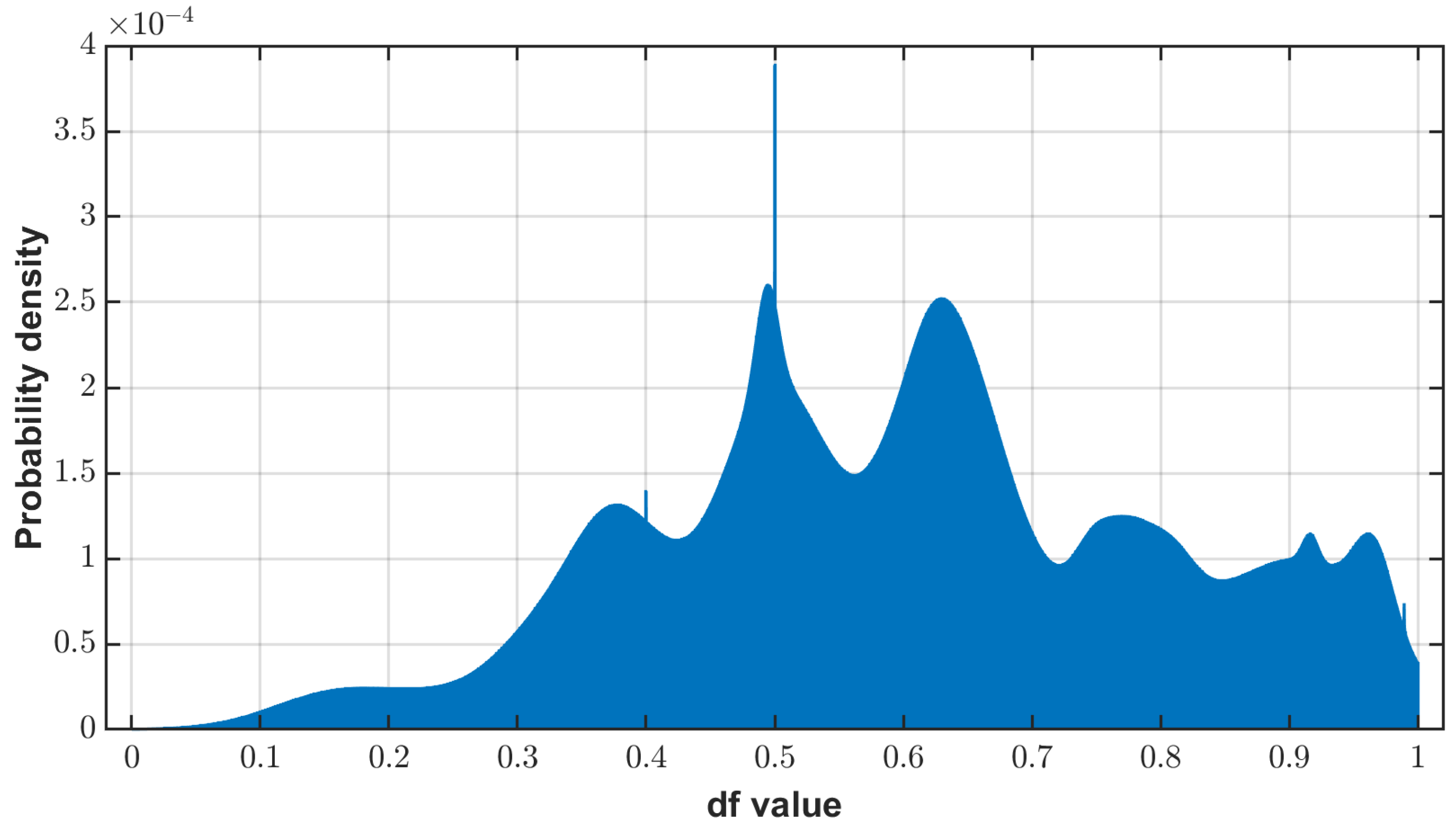
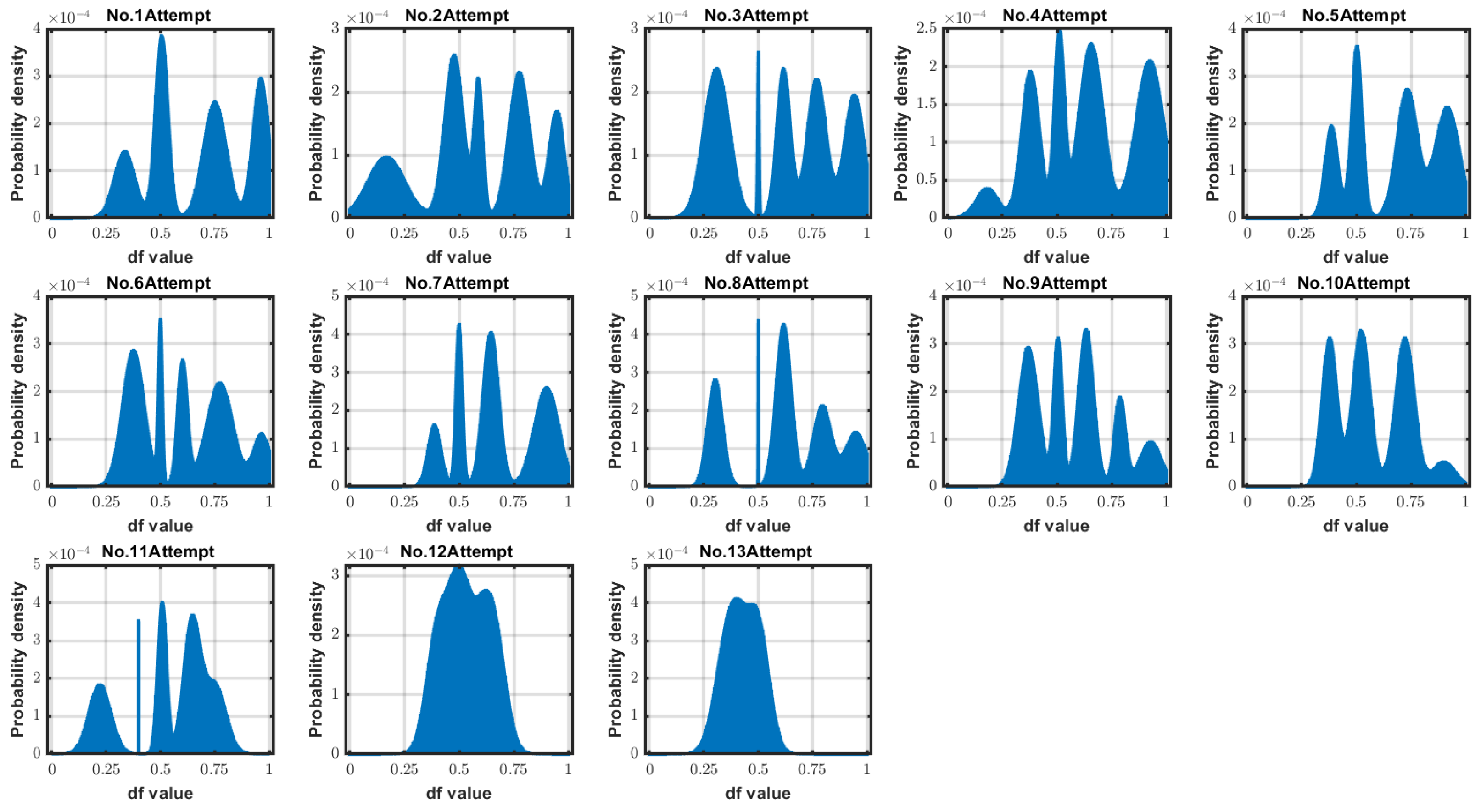
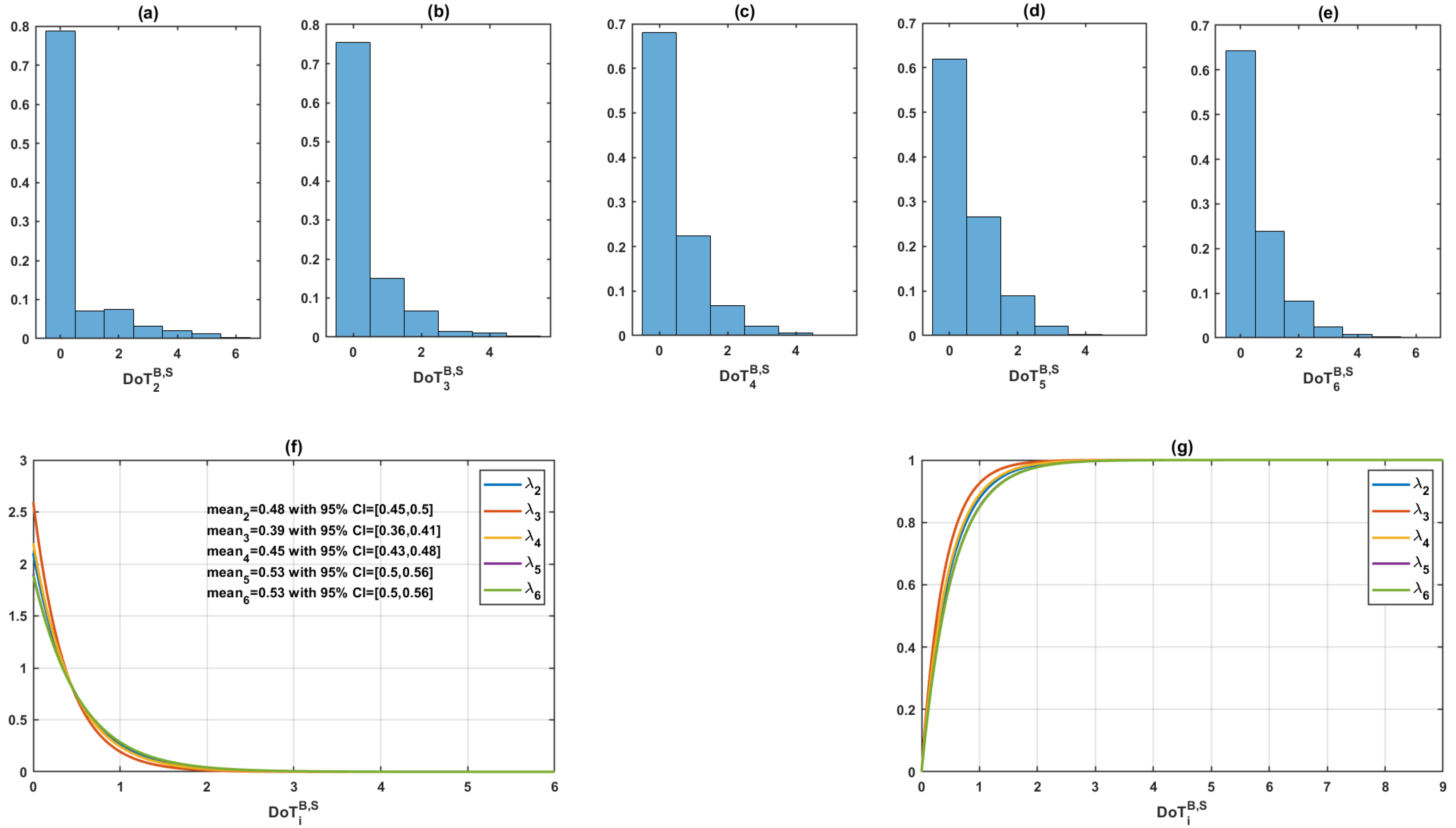
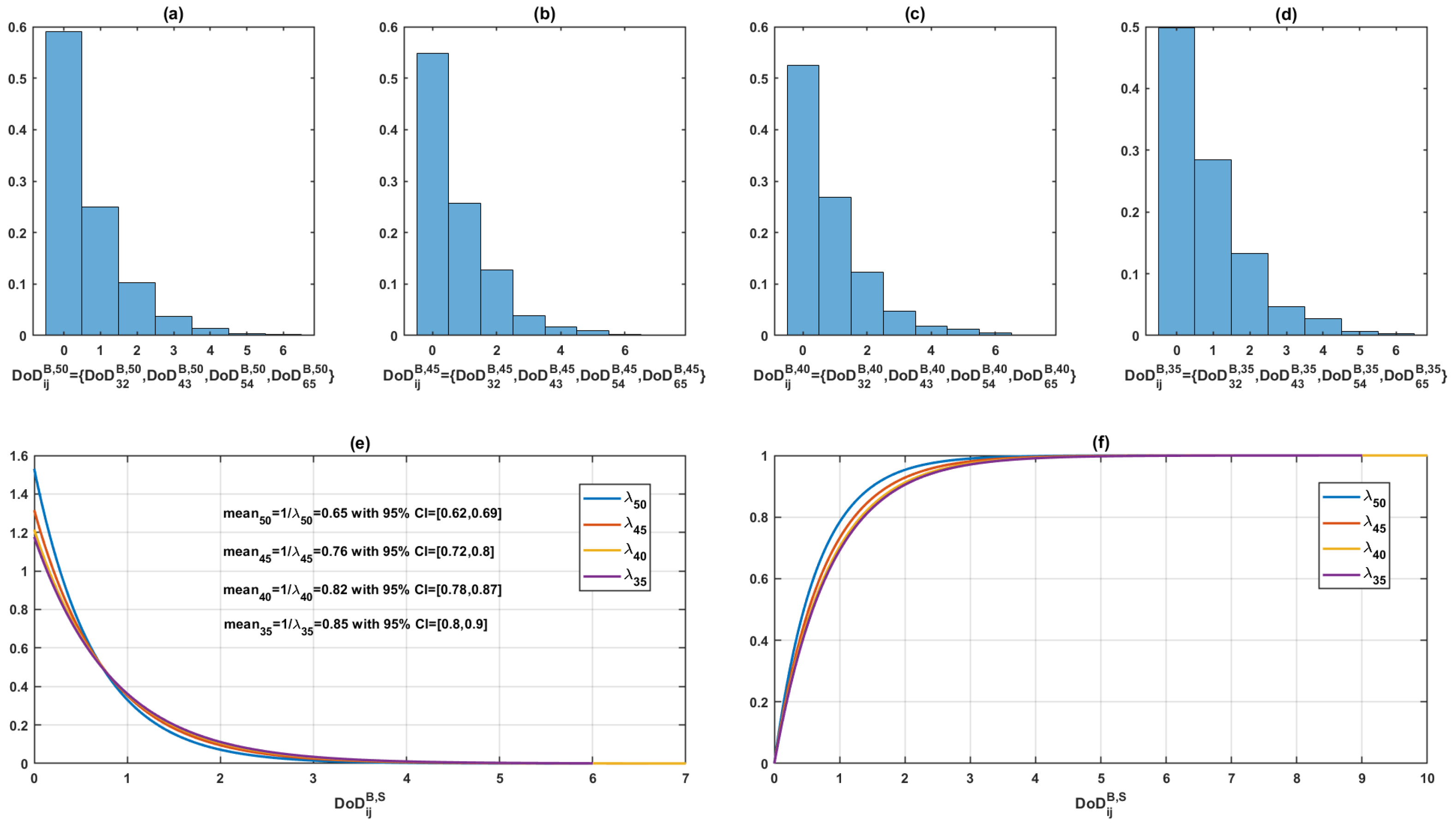
3.2.3. Estimating the Commonality of Decisions
3.2.4. Association and Accumulation
3.3. From HP to AP
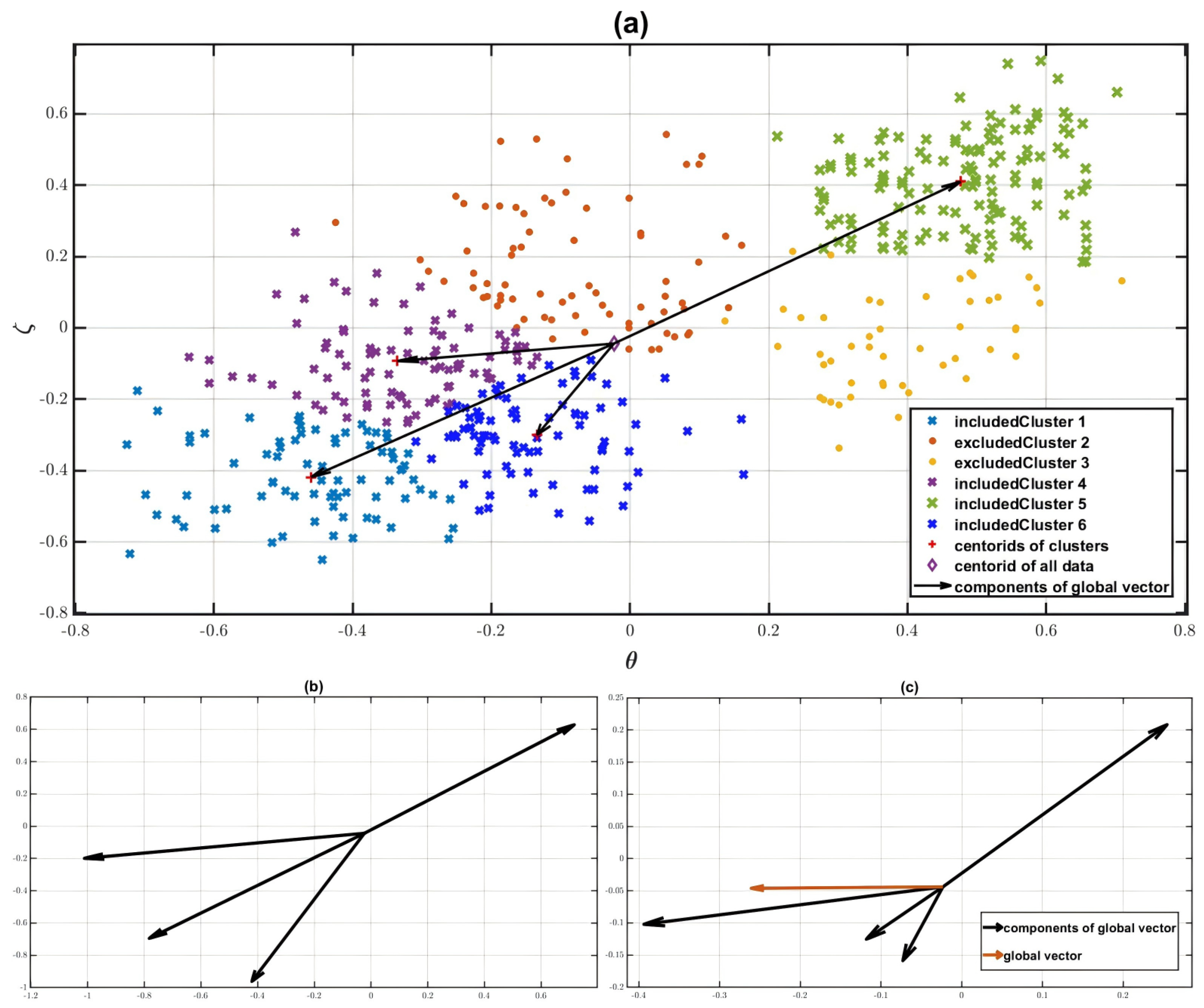
3.3.1. Two-Dimensional Commonality Interpretation
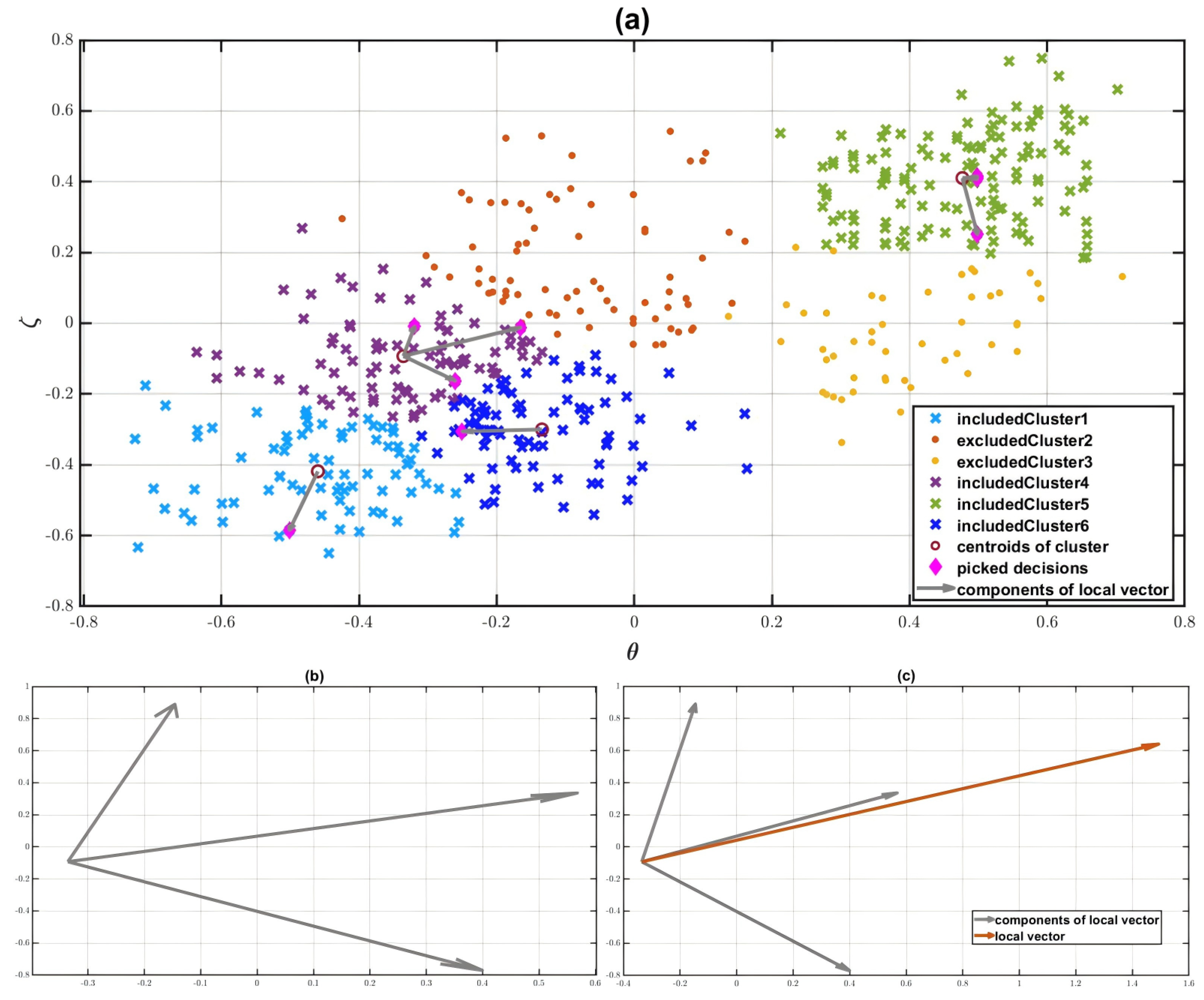
3.3.2. Decision Sequence in Multi-Dimensional Feature Space
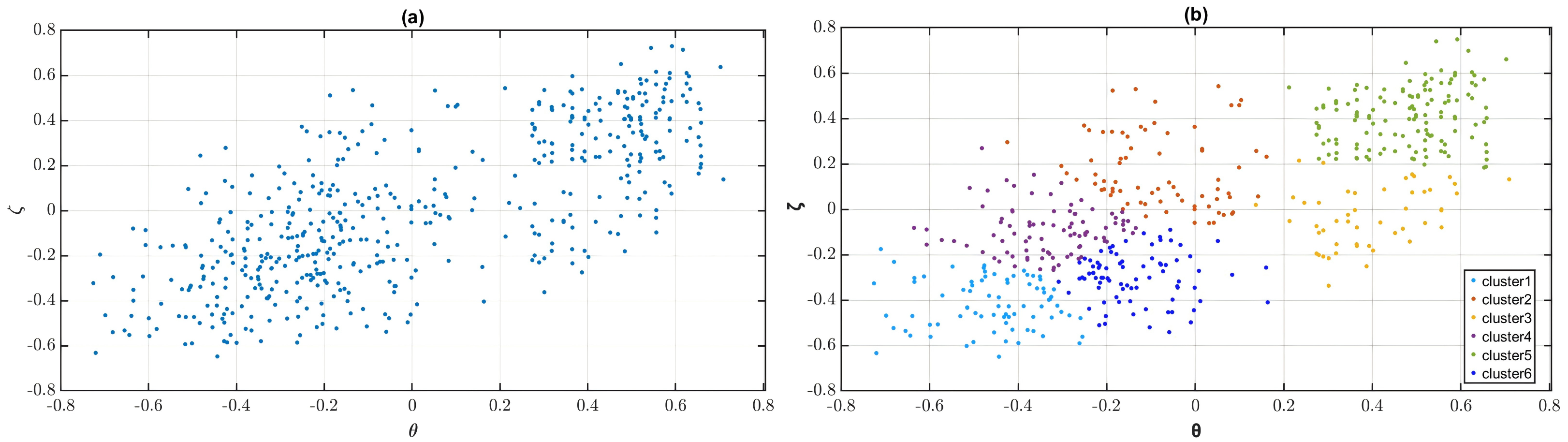
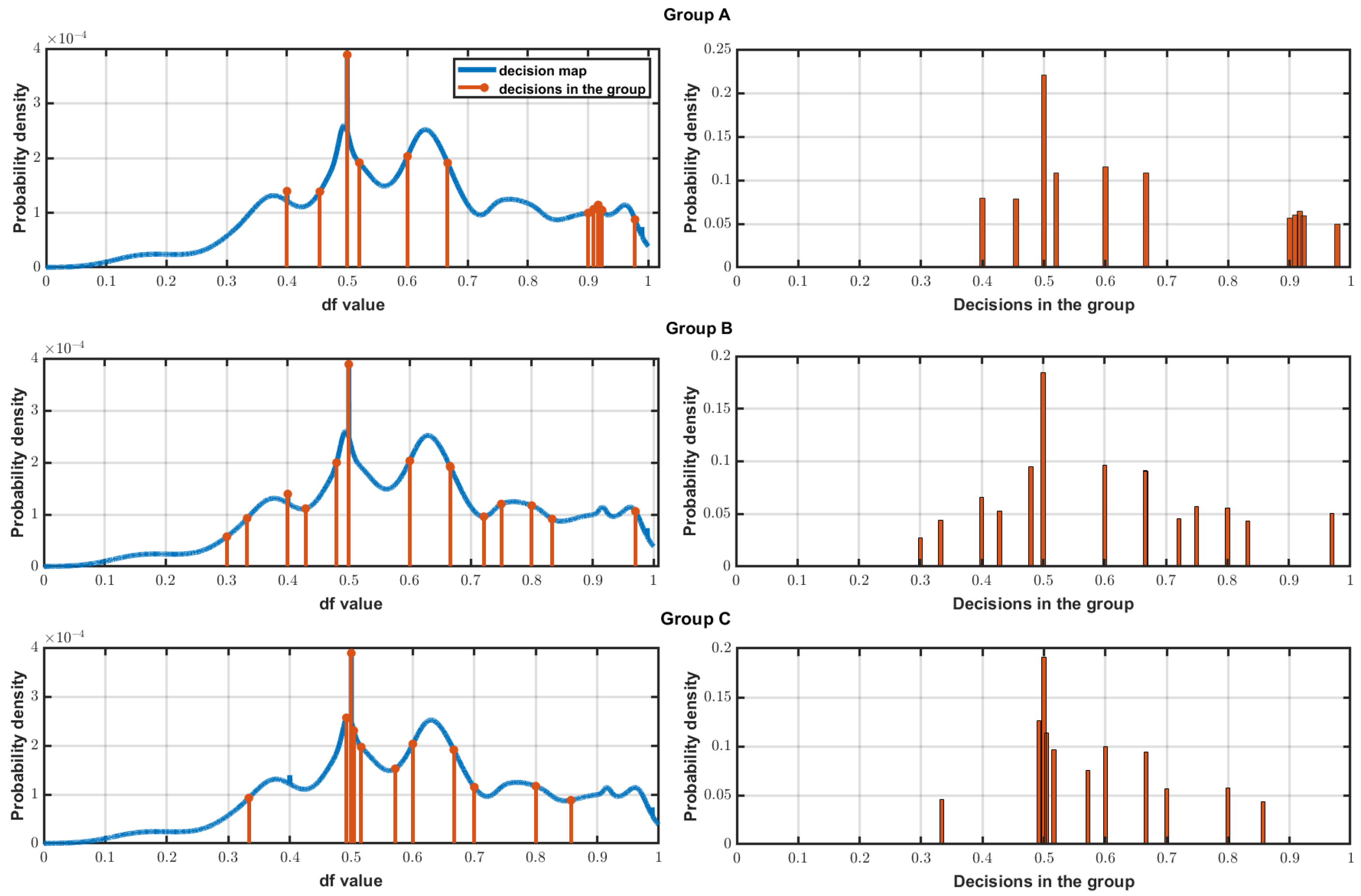
3.3.3. Grouping Process
4. Results and Discussion
4.1. Orthogonal Features
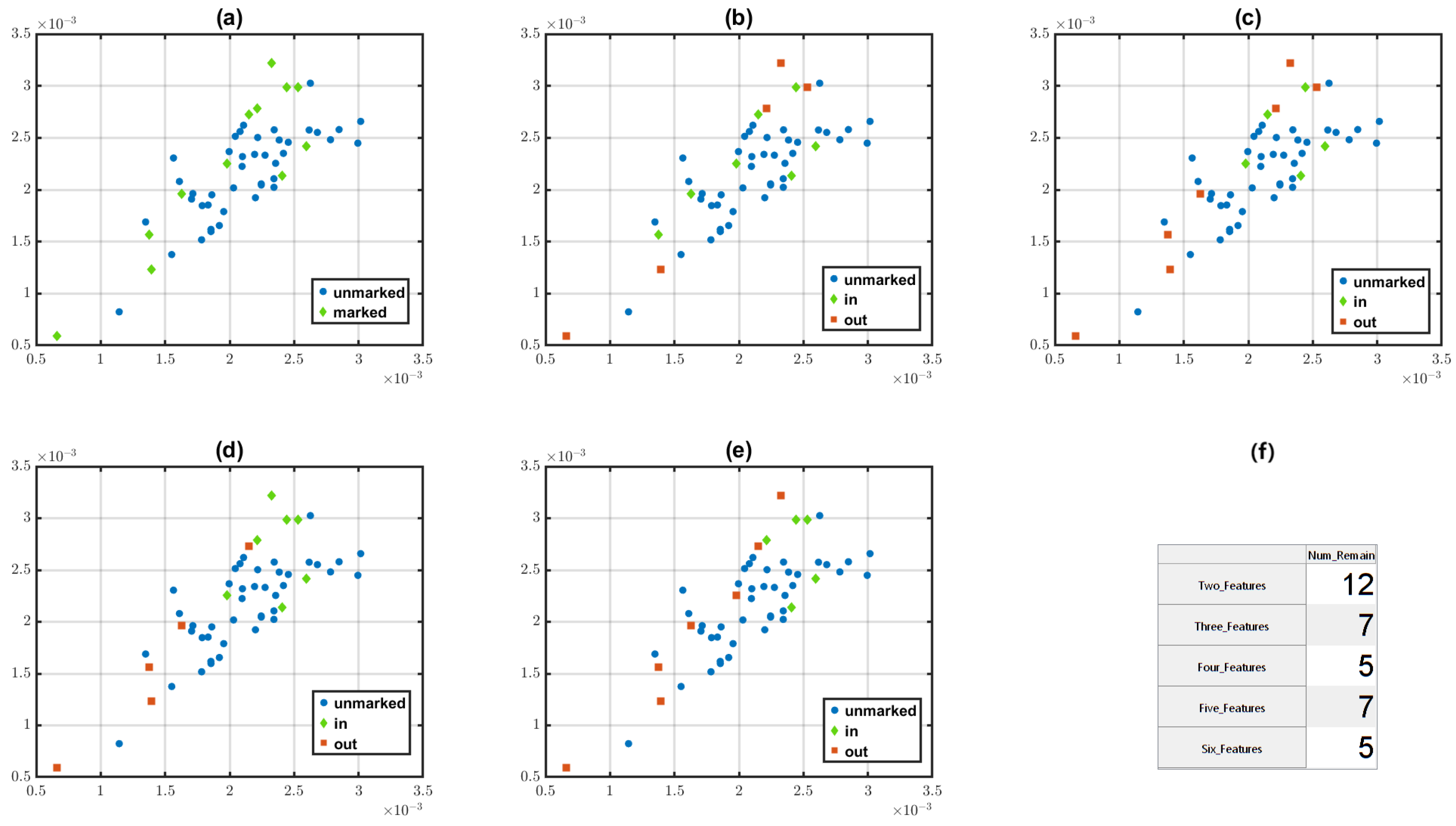
4.2. Variation of Grouping
4.3. Grouping Stability
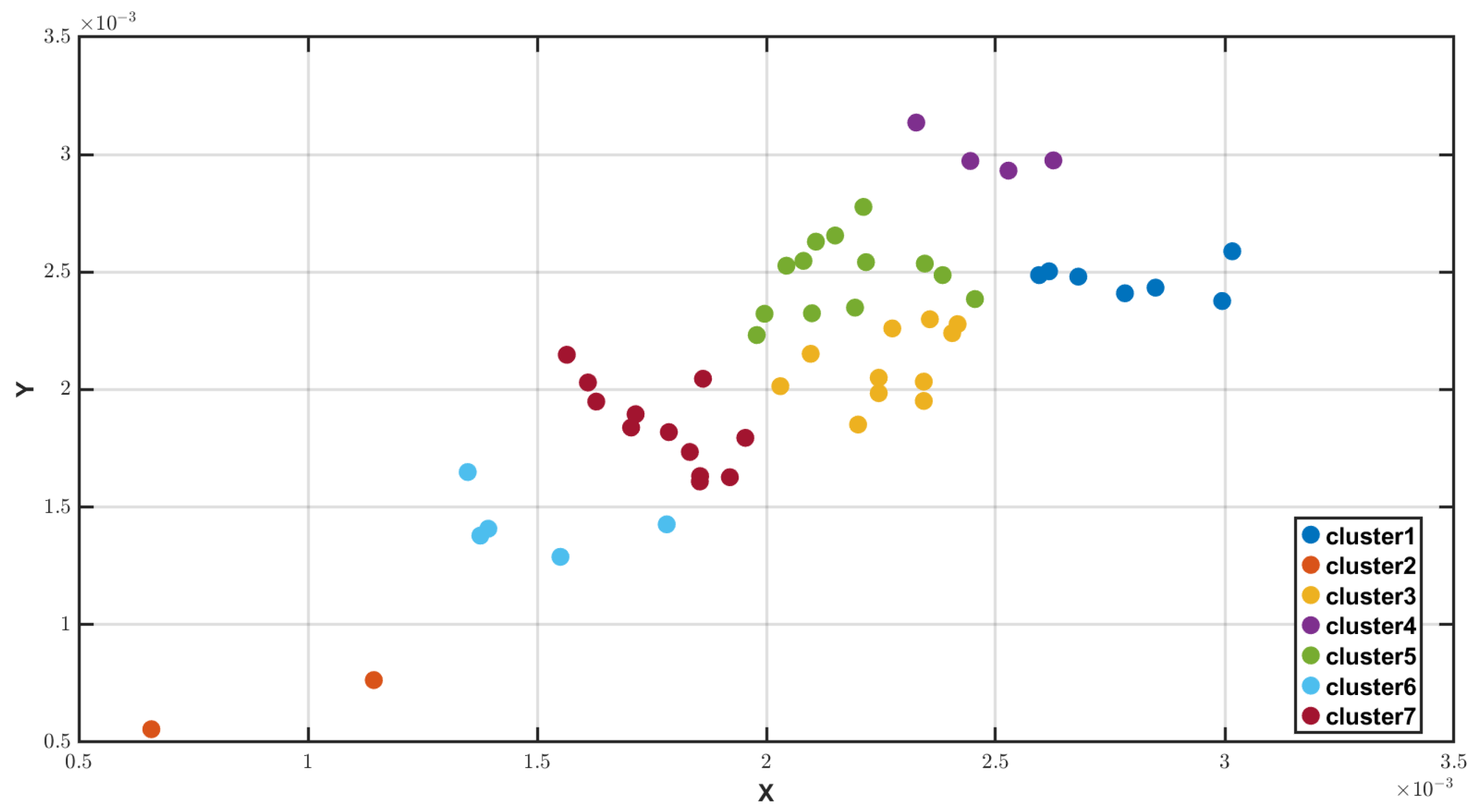
4.4. Grouping Result
4.5. Limitations and Future Plans
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matthews, G.; Deary, I.J.; Whiteman, M.C. Personality Traits; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Roberts, B.W.; Yoon, H.J. Personality psychology. Annu. Rev. Psychol. 2022, 73, 489–516. [Google Scholar] [CrossRef]
- Dhelim, S.; Aung, N.; Bouras, M.A.; Ning, H.; Cambria, E. A survey on personality-aware recommendation systems. Artif. Intell. Rev. 2022, 55, 2409–2454. [Google Scholar]
- Tkalčič, M.; Chen, L. Personality and recommender systems. In Recommender Systems Handbook; Springer: New York, NY, USA, 2012; pp. 757–787. [Google Scholar]
- Völkel, S.T.; Schödel, R.; Buschek, D.; Stachl, C.; Winterhalter, V.; Bühner, M.; Hussmann, H. Developing a personality model for speech-based conversational agents using the psycholexical approach. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020; pp. 1–14. [Google Scholar]
- Bouchet, F.; Sansonnet, J.P. Intelligent agents with personality: From adjectives to behavioral schemes. In Cognitively Informed Intelligent Interfaces: Systems Design and Development; IGI Global: Hershey, PA, USA, 2012; pp. 177–200. [Google Scholar]
- Mou, Y.; Shi, C.; Shen, T.; Xu, K. A systematic review of the personality of robot: Mapping its conceptualization, operationalization, contextualization and effects. Int. J.-Hum.-Comput. Interact. 2020, 36, 591–605. [Google Scholar]
- You, S.; Robert, L.P., Jr. Human-robot similarity and willingness to work with a robotic co-worker. In Proceedings of the 2018 ACM/IEEE International Conference on Human-Robot Interaction, Chicago, IL, USA, 5–8 March 2018; pp. 251–260. [Google Scholar]
- Luo, L.; Ogawa, K.; Peebles, G.; Ishiguro, H. Towards a personality ai for robots: Potential colony capacity of a goal-shaped generative personality model when used for expressing personalities via non-verbal behaviour of humanoid robots. Front. Robot. AI 2022, 9, 728776. [Google Scholar]
- Vinciarelli, A.; Mohammadi, G. A survey of personality computing. IEEE Trans. Affect. Comput. 2014, 5, 273–291. [Google Scholar] [CrossRef]
- Chamorro-Premuzic, T. Personality and Individual Differences; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Poulton, E.C. Behavioral Decision Theory: A New Approach; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Zhou, Y.; Khatibi, S. A New AI Approach by Acquisition of Characteristics in Human Decision-Making Process. Appl. Sci. 2024, 14, 5469. [Google Scholar] [CrossRef]
- Mendelson, M.J.; Azabou, M.; Jacob, S.; Grissom, N.; Darrow, D.; Ebitz, B.; Herman, A.; Dyer, E.L. Learning signatures of decision making from many individuals playing the same game. In Proceedings of the 2023 11th International IEEE/EMBS Conference on Neural Engineering (NER), Baltimore, MD, USA, 24–27 April 2023; pp. 1–5. [Google Scholar]
- Appelt, K.C.; Milch, K.F.; Handgraaf, M.J.; Weber, E.U. The Decision Making Individual Differences Inventory and guidelines for the study of individual differences in judgment and decision-making research. Judgm. Decis. Mak. 2011, 6, 252–262. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Davrazos, G.; Kotsiantis, S. Explainable Artificial Intelligence-Based Decision Support Systems: A Recent Review. Electronics 2024, 13, 2842. [Google Scholar] [CrossRef]
- Ullah, A.; Mohmand, M.I.; Hussain, H.; Johar, S.; Khan, I.; Ahmad, S.; Mahmoud, H.A.; Huda, S. Customer analysis using machine learning-based classification algorithms for effective segmentation using recency, frequency, monetary, and time. Sensors 2023, 23, 3180. [Google Scholar] [CrossRef] [PubMed]
- Alba, J.W.; Marmorstein, H. The effects of frequency knowledge on consumer decision making. J. Consum. Res. 1987, 14, 14–25. [Google Scholar] [CrossRef]
- Ng, A.Y.; Russell, S. Algorithms for inverse reinforcement learning. In Proceedings of the Icml, Standord, CA, USA, 29 June–2 July 2000; Volume 1, p. 2. [Google Scholar]
- Camerer, C.F.; Ho, T.H. Violations of the betweenness axiom and nonlinearity in probability. J. Risk Uncertain. 1994, 8, 167–196. [Google Scholar] [CrossRef]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, CA, USA, 13 June 2003; pp. 2–11. [Google Scholar]
- Cho, J.; Hyun, D.; Kang, S.; Yu, H. Learning heterogeneous temporal patterns of user preference for timely recommendation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 1274–1283. [Google Scholar]
- Pant, S.; Kumar, A.; Ram, M.; Klochkov, Y.; Sharma, H.K. Consistency indices in analytic hierarchy process: A review. Mathematics 2022, 10, 1206. [Google Scholar] [CrossRef]
- Broekhuizen, H.; Groothuis-Oudshoorn, C.G.; van Til, J.A.; Hummel, J.M.; IJzerman, M.J. A review and classification of approaches for dealing with uncertainty in multi-criteria decision analysis for healthcare decisions. Pharmacoeconomics 2015, 33, 445–455. [Google Scholar] [PubMed]
- Sahoo, S.K.; Goswami, S.S. A comprehensive review of multiple criteria decision-making (MCDM) Methods: Advancements, applications, and future directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Elbanna, S.; Thanos, I.C.; Jansen, R.J. A literature review of the strategic decision-making context: A synthesis of previous mixed findings and an agenda for the way forward. M@n@gement 2020, 23, 42–60. [Google Scholar]
- Hartley, C.A.; Phelps, E.A. Anxiety and decision-making. Biol. Psychiatry 2012, 72, 113–118. [Google Scholar] [CrossRef]
- Deck, C.; Jahedi, S. The effect of cognitive load on economic decision making: A survey and new experiments. Eur. Econ. Rev. 2015, 78, 97–119. [Google Scholar] [CrossRef]
- Chatzimparmpas, A.; Martins, R.M.; Kucher, K.; Kerren, A. Featureenvi: Visual analytics for feature engineering using stepwise selection and semi-automatic extraction approaches. IEEE Trans. Vis. Comput. Graph. 2022, 28, 1773–1791. [Google Scholar] [CrossRef] [PubMed]
- Dunn, J.; Mingardi, L.; Zhuo, Y.D. Comparing interpretability and explainability for feature selection. arXiv 2021, arXiv:2105.05328. [Google Scholar]
- Pyle, D. Data Preparation for Data Mining; Morgan Kaufmann: Burlington, MA, USA, 1999. [Google Scholar]
- Cerda, P.; Varoquaux, G.; Kégl, B. Similarity encoding for learning with dirty categorical variables. Mach. Learn. 2018, 107, 1477–1494. [Google Scholar] [CrossRef]
- Ravuri, A.; Vargas, F.; Lalchand, V.; Lawrence, N.D. Dimensionality Reduction as Probabilistic Inference. arXiv 2023, arXiv:2304.07658. [Google Scholar]
- Younis, H.; Trust, P.; Minghim, R. Understanding High Dimensional Spaces through Visual Means Employing Multidimensional Projections. arXiv 2022, arXiv:2207.10800. [Google Scholar] [CrossRef]
- Xiao, Z.; Xu, X.; Xing, H.; Luo, S.; Dai, P.; Zhan, D. RTFN: A robust temporal feature network for time series classification. Inf. Sci. 2021, 571, 65–86. [Google Scholar] [CrossRef]
- Zhang, R.; Hao, Y. Time Series Prediction Based on Multi-Scale Feature Extraction. Mathematics 2024, 12, 973. [Google Scholar] [CrossRef]
- Leão, C.P.; Carneiro, M.; Silva, P.; Loureiro, I.; Costa, N. Decoding the Effect of Descriptive Statistics on Informed Decision-Making. In Proceedings of the International Conference Innovation in Engineering, Nagoya, Japan, 16–18 August 2024; Springer: Cham, Switzerland, 2024; pp. 135–145. [Google Scholar]
- Devore, J.L.; Berk, K.N.; Carlton, M.A. Overview and descriptive statistics. In Modern Mathematical Statistics with Applications; Springer: Cham, Switzerland, 2021; pp. 1–48. [Google Scholar]
- Mazumdar, N.; Sarma, P.K.D. Sequential pattern mining algorithms and their applications: A technical review. Int. J. Data Sci. Anal. 2024. [Google Scholar] [CrossRef]
- Hosseininasab, A.; van Hoeve, W.J.; Cire, A.A. Constraint-based sequential pattern mining with decision diagrams. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1495–1502. [Google Scholar]
- Nguyen, T.N.; Jamale, K.; Gonzalez, C. Predicting and Understanding Human Action Decisions: Insights from Large Language Models and Cognitive Instance-Based Learning. In Proceedings of the AAAI Conference on Human Computation and Crowdsourcing, Pittsburgh, PA, USA, 16–19 October 2024; Volume 12, pp. 126–136. [Google Scholar]
- Sun, X.; Li, X.; Zhang, S.; Wang, S.; Wu, F.; Li, J.; Zhang, T.; Wang, G. Sentiment analysis through llm negotiations. arXiv 2023, arXiv:2311.01876. [Google Scholar]
- Liu, T.; Yu, H.; Blair, R.H. Stability estimation for unsupervised clustering: A review. Wiley Interdiscip. Rev. Comput. Stat. 2022, 14, e1575. [Google Scholar] [CrossRef] [PubMed]
- Beran, R. An introduction to the bootstrap. In The Science of Bradley Efron; Springer: Berlin/Heidelberg, Germany, 2008; pp. 288–294. [Google Scholar]
- Hussein, A.; Gaber, M.M.; Elyan, E.; Jayne, C. Imitation learning: A survey of learning methods. ACM Comput. Surv. (CSUR) 2017, 50, 1–35. [Google Scholar]
- Pei, G.; Li, H.; Lu, Y.; Wang, Y.; Hua, S.; Li, T. Affective computing: Recent advances, challenges, and future trends. Intell. Comput. 2024, 3, 0076. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep reinforcement learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5064–5078. [Google Scholar] [CrossRef]
- Zhong, Y.; Kuba, J.G.; Feng, X.; Hu, S.; Ji, J.; Yang, Y. Heterogeneous-agent reinforcement learning. J. Mach. Learn. Res. 2024, 25, 1–67. [Google Scholar]



| Feature Type | Example |
|---|---|
| Decision frequency [17,18] | Decision Types: Count the frequency of different types of decisions made (e.g., risk-averse decisions, exploratory decisions, impulsive decisions). Contextual Features: Analyze the decision frequency across different contexts or domains (e.g., work-related decisions, personal decisions). |
| Decision Outcome [19,20] | Success Rate: Calculate the proportion of successful decisions over a series of decisions. Risk-Taking Behavior: Assess the tendency to take risks based on decision outcomes. |
| Temporal [21,22] | Decision Patterns Over Time: Analyze changes in decision-making behavior over time (e.g., adaptation, learning from past decisions). Decision Patterns Over Time: Analyze changes in decision-making behavior over time (e.g., adaptation, learning from past decisions). |
| Consistency and Variability [23,24] | Consistency of Decisions: Measure how consistent decision making is across similar contexts or scenarios. Decision Context: Capture the depth of understanding or analysis applied to different decision contexts. |
| Complexity and Depth of Decisions [25,26] | Decision Depth: Determine the complexity of decisions made (e.g., simple vs. complex decisions). Decision Context: Capture the depth of understanding or analysis applied to different decision contexts. |
| Emotional and Cognitive Factors [27,28] | Emotional Response: Infer emotional states associated with decisions (e.g., confidence level, anxiety). Cognitive Load: Estimate cognitive effort or load during decision making. |
| Technique Type | Example |
|---|---|
| Data Pre-processing [31,32] | Cleaning and normalizing raw decision data (e.g., handling missing values, standardizing formats). Encoding categorical variables (e.g., decision types, contexts) into numerical representations suitable for analysis. |
| Dimensionality Reduction [33,34] | Apply techniques like Principal Component Analysis (PCA) or t-Distributed Stochastic Neighbor Embedding (t-SNE) to reduce the dimensionality of feature space while preserving essential decision patterns. |
| Time-Series Analysis [35,36] | Extract temporal features such as trends, seasonality, and periodicity in decision sequences using time-series analysis methods. |
| Statistical Metrics [37,38] | Calculate descriptive statistics (e.g., mean, median, variance) for decision attributes (e.g., decision time, outcome) to capture decision-making patterns. |
| Sequence Analysis [39,40] | Utilize sequence-mining algorithms (e.g., frequent pattern mining, sequential pattern mining) to identify common decision sequences or motifs. |
| Text Analysis [41,42] | Use natural language processing (NLP) techniques to analyze textual descriptions or justifications accompanying decisions for sentiment or cognitive cues. |
| Notation | Description |
|---|---|
| A | Action space, a set of all possible actions could be made in the given state. |
| S | State space, a set of all possible states. |
| a | The action (i.e the chosen number) decided by each participate in each attempt. |
| s | The current state of the task (i.e., the range of the target number) in each attempt. |
| i | The subscription representing the index of attempt. |
| j | The superscription representing the index of participant. |
| D | The demonstration dataset of each participant performed in the task is represented by state-action pairs, e.g., . |
| The set of ratios used to divide the range of target number. | |
| F | The function mapping the action (i.e., the chosen number) to a decision (i.e., the ratio) to divide the range of target number. |
| C | The group of decisions with similar strategy. |
| The ambiguous decision clusters estimated based on Gaussian distribution. | |
| The Decision Map representing a group of people’s characteristics in decision-making. |
| Global Feature | Local Feature 1 | Local Feature 2 | Local Feature 3 | Local Feature 4 | Local Feature 5 | Local Feature 6 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 197.97 | 0.13 | 36.76 | 0.11 | 312.39 | 0.19 | 139.32 | 0.04 | 139.64 | 0.20 | 347.22 | 0.13 | 102.49 | 0.20 |
| 156.18 | 0.15 | 27 | 0.29 | 330.22 | 0.62 | 249.15 | 0.28 | 327.02 | 0.27 | 0 | 0 | 81.88 | 0.56 |
| 123.73 | 0.21 | 273.86 | 0.23 | 305.98 | 0.14 | 98.06 | 0.14 | 95.93 | 0.15 | 357.21 | 0.33 | 148 | 0.17 |
| 198.66 | 0.14 | 7.68 | 0.13 | 19.14 | 0.35 | 238.95 | 0.05 | 259.69 | 0.28 | 0 | 0 | 90.52 | 0.08 |
| 67.09 | 0.13 | 343.93 | 0.18 | 0 | 0 | 269.83 | 0.13 | 186.18 | 0.55 | 226.09 | 0.48 | 0 | 0 |
| Estimate | SE | tStat | pValue | |
|---|---|---|---|---|
| 3.00 | 6.08 | 49.78 | 6.56 | |
| −6.87 | 4.46 | −1.54 | 0.13 | |
| −1.21 | 3.7 | −3.29 | 2.14 | |
| 6.29 | 2.40 | 0.26 | 0.80 | |
| 3.05 | 3.59 | 0.85 | 0.40 | |
| 1.67 | 2.34 | 0.71 | 0.48 | |
| 4.09 | 3.59 | 1.14 | 0.26 | |
| 4.65 | 2.65 | 1.76 | 0.09 | |
| 2.77 | 3.59 | 0.08 | 0.94 | |
| −9.29 | 2.20 | −0.42 | 0.68 | |
| 9.25 | 3.27 | 2.82 | 7.40 | |
| 4.36 | 2.80 | 1.56 | 0.13 | |
| 5.76 | 3.53 | 1.63 | 0.11 | |
| 5.08 | 3.25 | 0.02 | 0.99 | |
| 5.41 | 3.81 | 1.42 | 0.16 |
| Feature Space | Total Number of Features | Number of Orthogonal Features | Orthogonal Features |
|---|---|---|---|
| 14 | 4 | [] | |
| 14 | 6 | [] | |
| 21 | 7 | [] | |
| 6 | 6 | [] |
| Aspect | Imitation Learning [45] | Affective Computing [46] | Reinforcement Learning [47] | Agent Differentiation [48] | Our Proposed Method |
|---|---|---|---|---|---|
| Definition | Learning by mimicking human behavior from demonstrations | Computing systems that detect and respond to human emotions | Learning through trial and error to maximize long-term rewards | Categorizing agents based on their complexity, autonomy, and cognitive abilities | Learning strategical decision making from a group of people as a generative source for making differentiable APs |
| Core Focus | Replicating observed actions | Recognizing and responding to emotional states | Balancing exploration and exploitation for optimal decision making | Defining agent types based on goals, memory, learning and rationality | Generating differentiable APs |
| Learning Approach | Supervised, labeled expert demonstrations | Data-driven, often multimodal (facial expressions, voice, physiology) | Reward-based, often using deep learning | Varies from reflexive to cognitive agents | Unsupervised learning, non-Markovian as generative resource |
| Data Requirements | High-quality, context-rich demonstrations | Multimodal emotional data (speech, facial expressions, physiological signals) | Reward signals and state transitions | Varies, from simple rules to complex cognitive models | Decisions made in given context |
| Key Algorithms | Behavioral cloning, inverse reinforcement learning, GAIL | Emotion recognition models, sentiment analysis, speech emotion detection | Q-Learning, Deep Q-Networks, Actor-Critic Methods | Finite State Machines, Goal-based Agents, Utility-based Agents | Generative modelling in orthogonal space |
| Real-World Applications | Autonomous driving, humanoid robots, game AI | Emotional support systems, social robots, virtual assistants | Robotics, gaming, financial trading | Chatbots, industrial robots, personal assistants | Strategical navigation and steering in autonomous driving, strategical exploration and exploitation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Khatibi, S. Exploring Artificial Personality Grouping Through Decision Making in Feature Spaces. AI 2025, 6, 184. https://doi.org/10.3390/ai6080184
Zhou Y, Khatibi S. Exploring Artificial Personality Grouping Through Decision Making in Feature Spaces. AI. 2025; 6(8):184. https://doi.org/10.3390/ai6080184
Chicago/Turabian StyleZhou, Yuan, and Siamak Khatibi. 2025. "Exploring Artificial Personality Grouping Through Decision Making in Feature Spaces" AI 6, no. 8: 184. https://doi.org/10.3390/ai6080184
APA StyleZhou, Y., & Khatibi, S. (2025). Exploring Artificial Personality Grouping Through Decision Making in Feature Spaces. AI, 6(8), 184. https://doi.org/10.3390/ai6080184







