Optimized Interdisciplinary Research Team Formation Using a Genetic Algorithm and Publication Metadata Records

Abstract

Forming interdisciplinary research teams is challenging, especially when the pool of candidates is large and/or the addressed research projects require multi-disciplinary expertise. Based on their previous research outputs, like published work, a data-driven team formation procedure selects the researchers that are likely to work well together while covering all areas and offering all skills required by the multi-disciplinary topic. The description of the research team formation problem proposed in this paper uses novel quantitative metrics about the team candidates computed from bibliographic metadata records. The proposed methodology first analyzes the metadata fields that provide useful information and then computes four synthetic indicators regarding candidates’ skills and their interpersonal traits. Interdisciplinary teams are formed by solving a complex combinatorial multi-objective weighted set cover optimization problem, defined as equations involving the synthetic indicators. Problem solving uses the NSGA-II genetic algorithm. The proposed methodology is validated and compared with other similar approaches using a dataset on researchers from Politehnica University of Timisoara extracted from the IEEE Xplore database. Experimental results show that the method can identify potential research teams in situations for which other related algorithms fail.

1. Introduction

Bibliometric databases offer helpful information to support a range of research-related activities, like the identification of hot topics, framing research problems, and finding suitable journals to disseminate the obtained results, as they include concise summarizing information about scientific publications. Moreover, forming suitable teams of experts to define and work on a research project may particularly benefit from bibliometric data analysis by using the extracted data about the authors’ areas, accomplishments, levels of visibility within their community, and their previous interactions with other researchers to evaluate their teamwork skills. Research teams are often established based on an ad-hoc basis or using limited information, like affiliations, reputation, and similar approaches, but with an arguably limited, systematic analysis of the data contained in bibliometric databases. Opportunities can be missed to group teams that could frame original research needs and offer creative solutions to these needs.

Lappas et al. [1] were among the first to use bibliometric data in research team formation. They considered both individual technical skills to accomplish the task requirements and the members’ ability to effectively work together as a team based on four paper metadata information, i.e., authors, title, publication name and publication year, extracted from the DBLP bibliometric database. Since the work of Lappas et al., the DBLP database has been intensively used as an information source about Computer Science researchers, despite its narrow domain coverage and reduced publication metadata structure (e.g., it does not contain information, like a publication’s keywords, abstract, citation count, or the views/downloads count) to evaluate various research team formation methods [2,3]. Even though some work proposed data acquisition from more comprehensive databases, such as Google Scholar [4], Scopus [5], or PubMed [6], they are still based on the same reduced set of metadata fields, arguably offering an incomplete and inaccurate description of the candidates. Hence, using bibliometric data for effective team formation has still not achieve its full potential.

This paper attempts to address some of the above limitations by proposing a novel theoretical model on collaborative research work in teams and a set of metrics expressing the features of the model and which can be computed from bibliometric data to boost the effectiveness of team formation through a novel, carefully-tailored multi-objective optimization model for team formation. The main contributions of the paper are as follows:

• The number of bibliometric metadata considered by the data-driven team formation methodology is increased by utilizing the number of citations and downloads, authors’ affiliations, and publication abstract in deriving the candidates’ personal and interpersonal skills.
• A theoretical model is proposed that describes the collaborative work of research teams that participate in interdisciplinary research. Teams are formed out of the representatives of the groups with diverse expertise. Then, the research work is carried out in collaborative environments to frame and analyze interdisciplinary needs, and in individual environments, when groups work quasi-independently on problems in their areas of expertise. The collaborative behavior is expressed by the cognitive contributions and social interactions that emerge during team and group work.
• Four novel synthetic indicators are provided to effectively describe experts’ knowledge and their collaborative prospects. The indicators reflect the features of the above theoretical model, and are computed from the bibliometric metadata.
• A novel multi-objective team formation optimization method is suggested that includes the candidate-related indicators calculated using bibliometric data.
• The proposed methodology is validated for a specified case study on forming an interdisciplinary research team.

The remainder of this paper is organized as follows: Section 2 presents the related work on using bibliometric data in different research-related activities, with an emphasis on team formation for research projects. Section 3 focuses on the description of the research team optimization problem, including the theoretical model for collaborative team work, and four candidate-related indexes grounded in the model and which are extracted from bibliometric data. Section 4 discusses the methods used in solving the team formation problem, while Section 5 provides an experimental case study on deriving effective teams utilizing bibliometric information extracted from the IEEE Xplore database and using NSGA-II evolutionary multi-objective algorithm to solve the team formation problem. The last section concludes the paper by summarizing key findings and offering potential future directions.

2. Related Work

The objectivization of team formation has been a long-term desideratum for professionals and scholars in the field, crucially depending on the significance, completeness, and accuracy of available data about candidates. In the particular case of research teams, an important resource that may be effectively employed is represented by bibliometric databases. Besides their primary goal to collect, organize, and store publication-related concise information, bibliometric databases are valuable sources of insights for aiding and legitimizing decision making in research activities. Knowledge extracted from bibliometric data now has a large spectrum of applications in identifying research directions, hot topics, and trends; discovering the scientific gaps and formulating related research themes; and so on. Undoubtedly building expert teams to accomplish a research task may also greatly benefit from extracting personal and interpersonal candidates-related traits from bibliometric information, even though this realm is not mature yet.

2.1. Team Formation Approaches Using Bibliometric Data

In an attempt to build competent teams of experts, two categories of approaches have been explored. The first approach considers teams as sub-graphs to be extracted from larger social networks with vertices representing the candidates and edges representing their previous collaborations. The second approach models team formation as a combinatorial multi-objective optimization problem.

The graph-based team formation approach is rooted in the work by Lappas et al. [1], in which teams are constructed based on the skill requirements and minimum communication cost by analyzing a weighted and undirected social graph using diameter-related or minimum spanning trees algorithms. Their approach was also pursued by other work too. Li et al. [7] modified the enhanced Steiner algorithm introduced by [1] by providing a density-based mechanism to select the seed node and a node grouping-based method to boost the effectiveness of the team formation procedure. Kargar and An suggested two procedures to derive top-k teams of experts: one that minimizes the sum of distances function considering communication costs between pairs of skill holders in the case of an egalitarian team, and the other minimizes the leader distance function considering the costs between the leader and each of skill holder when the team has a leader [8]. Rangapuram et al. formulate the problem as a generalized version of the classical densest subgraph problem with cardinality constraints that allow modeling the inclusion of a given team leader or a group of designated experts, enforcing geographical location or restricting the team size [9].

For the second category, which bases the team formation on solving combinatorial optimization problems, we mention two seminal papers: Berktaș and Yaman modeled team formation as a quadratic set covering problem (i.e., diameter-constrained team formation with sum-of-distances objective) and then solved it with an adapted branch-and-bound algorithm [10]; and, Neveditha et al. [11] proposed a three-objective optimization model that encompasses the minimization of team size, personnel costs and communication costs, the optimal team being extracted using the NSGA-II genetic algorithm.

2.2. Evaluating Scholars’ Characteristics

Until now, the use of bibliometric data has been generally limited to generating simplified datasets meant to evaluate and compare expert team formation methods, rather than constructing a fully bibliometric data-driven team formation method. From this perspective, DBLP is the standard database employed [2,10,12], even though there are a few notable exceptions using [4], Scopus [5] or PubMed [6], but otherwise without significant procedural differences. Please note that DBLP only collects publications in the field of computer science and the records include only ‘author’, ‘title’, ‘journal’, ‘volume’, and ‘year’, but without capturing fields like ‘author affiliation’, ‘keywords’, ‘abstract’, ‘citation count’, or ‘downloads count’. Due to its record simplicity, any evaluation of the candidate’s skills and collaboration traits may be affected by errors. From another point of view, by neglecting publications’ keywords or abstract fields, existing works have limitations in assessing the candidate’s areas of expertise [13], this being aggravated by the simplistic way that the candidate’s expertise in a given area is evaluated (i.e., extracting the key terms from only ‘title’ fields using bag-of-word approaches and then applying a threshold to filter out candidates with a reduced number of publications in the area characterized by the given key term [10,12]).

To improve the accuracy of the research team formation process, this paper argues that bibliometric databases with more complex publication metadata records should be considered (e.g., Web of Science, Scopus or IEEE Xplore) [14], and also to include new and relevant metadata fields in the evaluation of candidates. Moreover, a comprehensive team formation optimization model, encompassing the insights extracted from bibliometric data, is needed to support such an endeavor.

3. Research Team Formation Based on Bibliometric Data

Formalizing the team formation optimization problem depends not only on the project the team must work on and the pool of team candidates, but also on the type, size, and trustworthiness of the available data about the candidates. Hence, bibliometric data can provide valuable insights regarding researchers’ expertise and their collaboration profiles.

Using bibliometric data for research team formation goes back to about 2009, when Lappas et al. [1] inquired the DBLP database for obtaining raw data about candidates. They used metadata on paper titles and authorship to infer the researchers’ areas of expertise, and the paper authorship to derive the co-authorship graph. Later, the number of citation [15,16] was suggested to evaluate the reputation of a paper or author, and the keywords were utilized to supplement the title when identifying the researchers’ areas of expertise [17]. Based on the careful analysis of the structure of the paper metadata records, we argue that the list of currently used bibliometric metadata fields to evaluate researchers can be expanded by including the paper abstracts alongside the title and keywords to identify the candidates’ areas of expertise, and the publication download counts in correlation with citation counts to reveal the popularity of a paper or author. Moreover, we considered that interpersonal collaborations may be better characterized by considering not only the already-existing dyadic collaborations between candidates, but also candidates’ cooperation inside groups larger than pairs (e.g., already-existing triadic and tetradic inter-member collaborations). Based on these arguments, we propose in this section a model for research team formation.

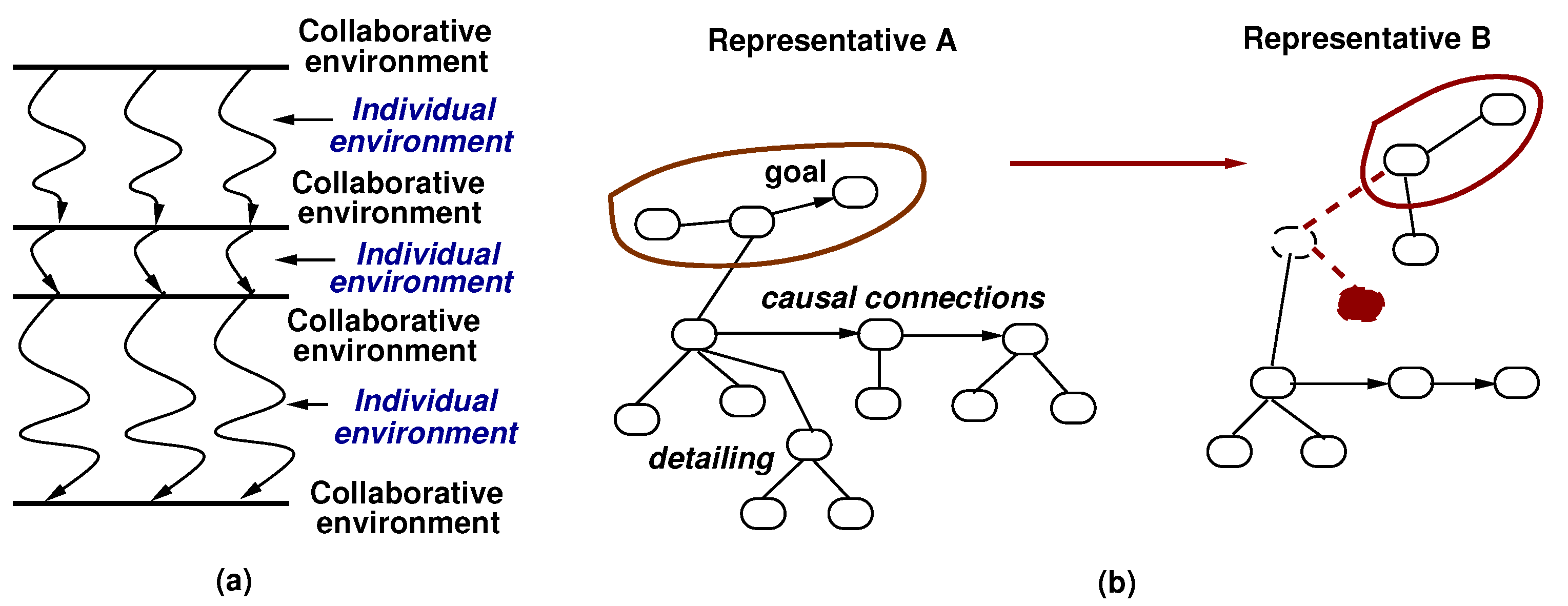
3.1. A Theoretical Model for Collaborative Work on Interdisciplinary Research Problems

The suggested theoretical model is a qualitative model that represents the features of interdisciplinary collaborations involving multiple research groups. It serves to support the quantitative metrics defined in Section 3.2 and then used by the optimization algorithm for team formation. The qualitative model proposes a two-layer representation of the collaborative interactions between groups, in which the top layer corresponds to the collaborations among the representatives of the groups, and the bottom layer refers to the individual work. Team collaboration is characterized by the dynamics of the two layers, including parameters that describe the cognitive contributions of collaborations for the interdisciplinary problems as well as the individual domains, and the social characteristics of the collaborative environments, e.g., team structuring and roles, consensus reaching, and conflict management.

More specifically, the assumed interaction model for a collaborative research team considers that a team spans a number of research groups with distinct expertise but which collaborate on interdisciplinary projects and problems. Each research group has a leader. Hence, this produces a two-layer structuring, with the top layer represented by the collaborative team including the leaders of the groups, and the second layer formed by the participating groups. For example, it is common that collaborative research on interdisciplinary problems is the joint collaboration between groups or laboratories with different types of expertise. The research work is then conducted in two distinct situations: (1) the collaborative environmentin which the representatives, e.g., the leaders of the groups, jointly work on framing research objectives and questions about the interdisciplinary research needs, and integrating the obtained results and insights, and (2) the individual environment, in which the participating groups work individually or with minimal inter-group interaction on the research problems pertaining to the specific expertise of the group. The performance of a collaborative research team can be characterized with respect to the dynamics between the behavior of the collaborative and individual environments.

Figure 1a summarizes the proposed model to characterize team collaborations based on the dynamics of the behavior of the collaborative and individual environments. The sequences of work in collaborative environments are spaced out by quasi-separate work in the individual environments of the groups. Each step is characterized by three parameters:

$$<U_G,U_I,S>$$

(1)

where parameter $U_G$ is the utility of the cognitive contributions produced by the entire team, such as the novelty and usefulness of the broad solutions for the interdisciplinary problems, parameter $U_I$ is the cognitive contribution with respect to the individual domains of the groups in the team, and parameter S describes the social characteristics of the groups, like the amount of interactions, thrust, and confidence in the group. Research in social psychology shows that social aspects are critical in a team’s behavior [18,19,20]. The next paragraph summarizes the modeling of parameters $U_G$, $U_I$, and S.

The description of parameters $U_G$ and $U_I$ is based on the interaction process illustrated in Figure 1b.

With respect to the definition of parameter $U_G$, the figure shows the interaction between two participants, i.e., two team leaders, in a collaborative environment. Each participant communicates referring to concepts, their features, and the relations between concepts to express ideas about the collaborative work. These ideas refer to the associative components of the knowledge graph [21,22], and represent broader, higher-level statements, like goals, problem decomposition, sub-problem summarizing, idea restatement from a different perspective, questions, concerns, negations, and alternatives of ideas, clarification of unknowns and uncertainties, and conclusions, and are less statements about details and causal features of the work [23]. The latter are mainly addressed as part of the work in the individual environment of each group. Hence, every participant to a collaborative environment attempts to understand and utilize the ideas communicated by their collaborators to generate new ideas towards framing a new problem or research question [22].

Parameter $U_G$ describes the capacity of the participants (i) to connect at a higher-level with the other participants’ ideas without having to know all the details, (ii) to correctly reason under unknowns and uncertainties, (iii) to flexibly relate to the ideas of others and incorporate the received input into their own knowledge structure, and (iv) to effectively reason at various levels of abstraction, such as to understand how details of their own area of expertise connect to the broader requirements of the interdisciplinary project. The interaction process should converge to new goals and problem descriptions that reflect everyone’s experience, are accepted by everyone, and further serve to guide the work of the groups in the individual environments. Problems should be solvable within the groups expertise, and be relevant to the involved communities.

With respect to the description of the parameter $U_I$, the cognitive contribution reflects the novelty and usefulness of the ideas that study and produce solutions to the sub-problems assigned to each group participating to the interdisciplinary work. The ideas express reasoning about the detailed components and the causal elements of a solution, decision making about options, as well as an analysis of the advantages and disadvantages of the causal elements, options, and solutions [23,24,25]. Parameter $U_I$ might also reflect limited contributions across domains, like constraints originated in a domain are used during the sub-problem solving and solution building in another domain. Hence, parameter $U_I$ reflects aspects, like (i) the degree to which the sub-problem requirements and constraints are detailed by the solution, (ii) the degree to which the solutions created in the individual environments overlap and differ with each other, e.g., they represent a gradual evolution of the studied sub-problem, and (iii) the flexibility of the solution to be used together with the solutions separately created by other groups of the team.

Finally, parameter S describes the social characteristics of a group collaboration, like (i) the implicit structuring of the team and the implicit role played by each group within the collaborative team, (ii) the perceived need to get collective agreements about the group decisions on goals and sub-problem definition (i.e., degree of group synchronization), (iii) the importance assigned to ideas of others, and (iv) the management of conflictual situations. These factors relate to social elements, like confidence, trust and social safety, and characterize team behavior [18,19,20]. Social factors are important in deciding a participant’s behavior in a team.

Each of the three parameters $U_G$, $U_I$, and S indicates an increase (+) or a decrease (−) of their values for the activities in the two environments, e.g., collaborative (CE) and individual environments (IE). This gives rise to sixteen different configurations:

• (1) <CE, $U_G^{+}$, $U_I^{+}$, $S^{+}$>, (2) <CE, $U_G^{+}$, $U_I^{+}$, $S^{-}$>,
• (3) <CE, $U_G^{+}$, $U_I^{-}$, $S^{+}$>, (4) <CE, $U_G^{+}$, $U_I^{-}$, $S^{-}$>,
• (5) <CE, $U_G^{-}$, $U_I^{+}$, $S^{+}$>, (6) <CE, $U_G^{-}$, $U_I^{+}$, $S^{-}$>,
• (7) <CE, $U_G^{-}$, $U_I^{-}$, $S^{+}$>, (8) <CE, $U_G^{-}$, $U_I^{-}$, $S^{-}$>,
• (9) <IE, $U_G^{+}$, $U_I^{+}$, $S^{+}$>, (10) <IE, $U_G^{+}$, $U_I^{+}$, $S^{-}$>,
• (11) <IE, $U_G^{+}$, $U_I^{-}$, $S^{+}$>, (12) <IE, $U_G^{+}$, $U_I^{-}$, $S^{-}$>,
• (13) <IE, $U_G^{-}$, $U_I^{+}$, $S^{+}$>, (14) <IE, $U_G^{-}$, $U_I^{+}$, $S^{-}$>,
• (15) <IE, $U_G^{-}$, $U_I^{-}$, $S^{+}$>, (16) <IE, $U_G^{-}$, $U_I^{-}$, $S^{-}$>.

The characterization of the parameter variations is as follows:

• $U_G^{+}$, $U_G^{-}$: The improvement or reduction in the values of parameters $U_G$ are reflected by the nature, number, and impact of team outputs, like team publications. The nature of the team publications refers to (i) the degree to which publications include all the participants to a team (i.e., all the groups in a collaborative project), (ii) the expertise of the participants (i.e., the expertise of the groups), (iii) the evolution (e.g., gradient) with respect to the previous publications by the same team, including the similarity and novelty of the new work with respect to previous work, (iv) the flexibility of incorporating new ideas that were initially not part of any participant’s expertise, like identifying new research needs, and (v) the capacity to interact at different levels of abstraction. The impact is characterized by the degree to which the ideas of a team publication, such as that expressed by its keywords, overlaps with the ideas of subsequent papers, as well as the number of citations received by the paper.
• $U_I^{+}$, $U_I^{-}$: The increase and reduction in the values of parameters $U_I$ are described by the nature, number, and impact of the groups participating in a team project, like the publications of each of the groups. The nature of a group’s publications include (i) the amount of connections with the team publications, e.g., the overlapping of keywords, (ii) the degree to which the group’s papers explored the ideas expressed in team publications, (iii) the evolution of new papers by the group as compared to its previous papers, like the similarity and differences between papers, (iv) the nature of the publications, like analysis or new in-depth solutions, and (v) the links with the papers of other groups of the same team, including any ideas that were adopted by a group from another group and the flexibility to use the constraints expressed by collaborating groups. The impact of a group’s publication refer to the degree to which any insight and conclusion impact the work of the entire team, including any new goals and needs expressed in the team publications, and the number of citations received from the other groups of the team as well as from outside the team.
• $S^{+}$, $S^{-}$: The changes in the values of the parameters S describe the convergence and divergence of the ideas (i.e., topics) discussed in the team publications and group publications, like keywords that occurred in both group and team papers and keywords in group papers but not in the joint publications of the team. The role played by a group in a team is characterized by its participation to the team work as expressed by the way its expertise, i.e., shown by the keywords of its publications, impacts the work of other groups and the entire team. The need of a group to get the team’s assessment of its new ideas is reflected by situations in which new ideas of the group are continued or discontinued by the group, if the team did not adopt them. The management of conflicts is captured by the way that a group behaves after a situation, in which the group’s ideas are not embraced by the team. The group can remain involved with the team’s joint work, or can start to diverge by focusing only on its own group publications.

The next subsections present the use of the model components to define the metrics and equations used in optimizing team formation in interdisciplinary research projects.

3.2. Employing Bibliometric Data in Candidates’ Assessment

We argue that bibliometric data can be employed to characterize the next elements:

• Identify a Researcher’s Areas of Expertise (RAE) based on the information in three paper metadata fields, namely title, keywords, and abstract, each of them being meant to effectively summarize the publication. For this, we extract the relevant key terms that best encapsulate the researcher’s scientific output using adequate NLP techniques and associate these key terms with scientific areas to establish thier areas of expertise. Parameter RAE is used to express the requirements of parameters $U_G$ and $U_I$ in the theoretical model.
• Compute four candidate-related indexes to reflect a researcher’s technical and teamwork skills. The four indexes are as follows:

  ⋄

  Researcher’s General Expertise (RGE) can be evaluated from the total number of publications, the total number of citations, and the total number of downloads. While the total number of publications of a given author may be obtained by counting the number of thier paper metadata records, the total number of citations or downloads may be computed by summing up the citation counts or download counts paper metadata fields. It is important to mention that the general level of expertise is a measure of a researcher’s reputation and represents an overall indicator that considers the entire scientific contribution of a researcher. Alternatively, if other indexes (e.g., h-index in WoS or Scopus databases) are available, they may also be employed. Parameter RGE is utilized to mainly describe the features of parameter $U_G$ of the theoretical model.

  ⋄

  Researcher’s Level of Expertise within a Given Area (RLEGA) can be evaluated based on the number of scientific publications in that area and their corresponding number of citations and number of downloads. The mechanism to obtain these three values is similar to that used for assessing RGE but considers only the publications, which have the scientific area’s characteristic key term or key terms between their relevant key terms. Parameter RLEGA serves to formulate the facets of parameter $U_I$ of the theoretical model.

  ⋄

  Researcher’s Collaboration Ability (RCA) can be evaluated by considering the total number of their co-authors and also the number of co-authors having other affiliations. While the former offers a general perspective on the researcher’s collaboration prospects, the latter may be increasingly important for research projects that presume multilingual, multicultural, or multinational teams. Parameter RCA helps to specify the elements of parameters $U_G$ and S of the theoretical model.

  ⋄

  Interpersonal Collaborations Inside Specified Groups (ICISG) of researchers can be evaluated using the total number of previous collaborations of that particular group. Here, a group of researchers may have two, three, or even more members, and their fruitful collaboration is characterized/specified by a higher total number of proven collaborations (i.e., all the group members are co-authors of the same publications). Parameter ICISG captures the elements of parameter S in the theoretical model.

The use of bibliometric metadata in identifying and evaluating the abilities of individuals or groups of individuals are presented in

Table 1. Paper Metadata Using in Team Formation.

Paper Metadata Field	Identify RAE	Evaluate RGE	Evaluate RLEGA	Evaluate RCA	Evaluate ICISG
title	✓	–	–	–	–
abstract	✓	–	–	–	–
keywords	✓	–	–	–	–
author name	–	✓	✓	✓	✓
author affiliation	–	–	–	✓	–
citing paper count	–	✓	✓	–	–
citing patent count	–	✓	✓	–	–
downloads count	–	✓	✓	–	–
paper ID	–	✓	✓	✓	✓

.

The four indexes derived from a corpus of publication metadata (i.e., RGE, RLEGA, RCA, and ICISG) are the main pillars of the proposed methodology. They can take other mathematical formulations, like in the examples given in the case study presented at the end of this subsection.

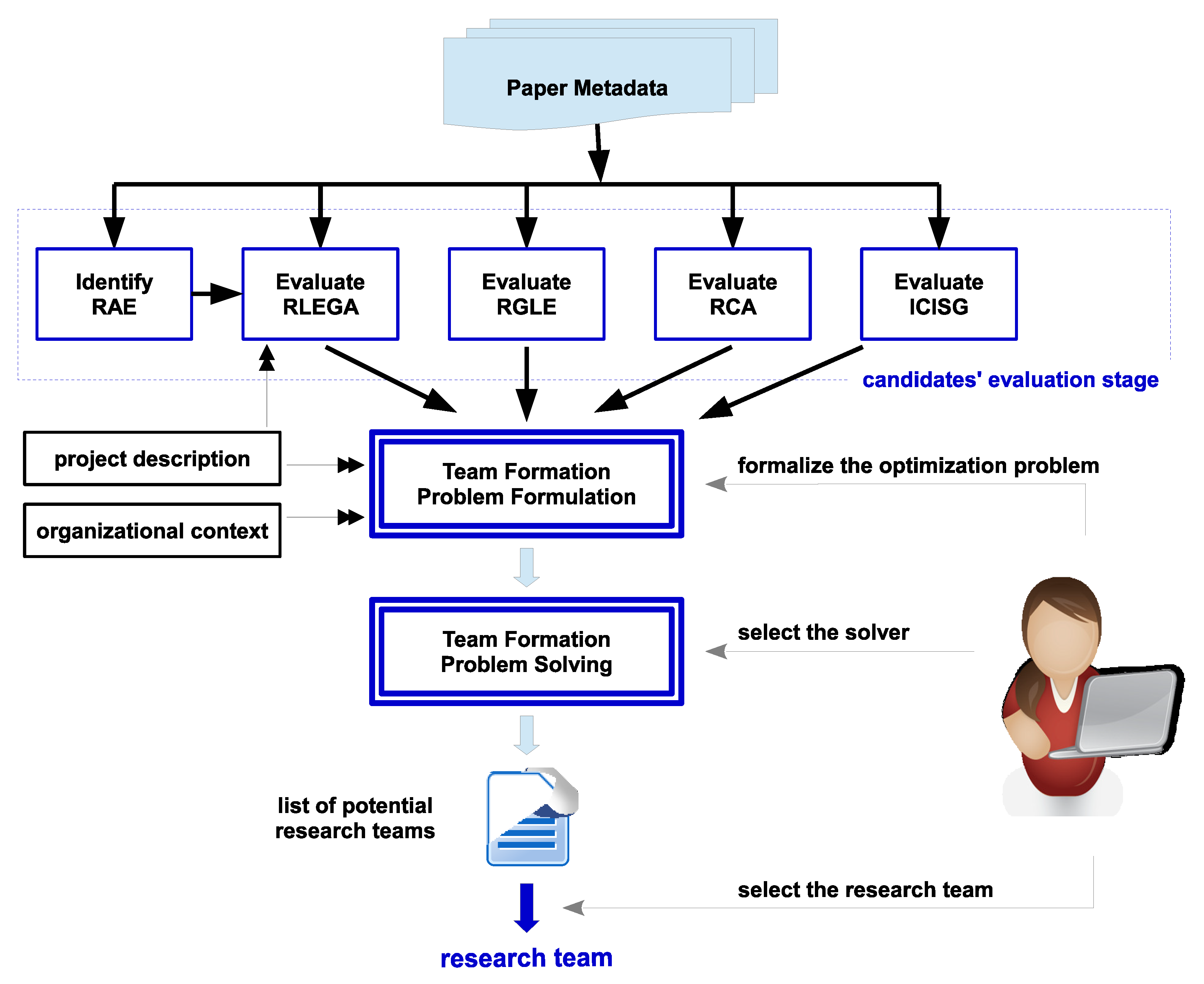
3.3. Proposed Bibliometric Data-Driven Egalitarian Team Formation Methodology

Driven by the theoretical model in Section 3.1 and the insight extracted from bibliometric data about the possible participants to a research team, we propose a methodology for egalitarian research team formation. By egalitarian team we define a team without predefined team structure and roles of the participants, even though a structure and roles can implicitly result during collaboration depending on everyone’s participation to the collaborative work. The flowchart of the methodology is presented in Figure 2 and implements a human-in-the-loop recommender system that takes as inputs a carefully crafted set of publication metadata, the specifications of the project to be carried out, and information about the organizational context in which the selected research team will operate.

The first phase of the methodology is devoted to paper metadata pre-processing and candidates’ assessment, and provides a core set of indicators of the candidates’ technical and non-technical skills. While indexes RGE, RCA, and ICISG do not depend on the project itself, characterizing the overall scientific activity of the candidates, e.g., for obtaining RLEGA, we need to focus only on the group of key terms that specifically describe the areas of expertise required by the project. For this, we need to identify all the project’s relevant key terms inside the overall list of key terms provided by the block ‘identify RCA’. If one or more key terms are not included in the overall list, the paper metadata corpus must be reprocessed by forcing the term/terms to be searched within the papers’ title, keywords, and abstract metadata fields.

In the next step of the methodology, the team formation problem formalization is performed using the available information about the research project, organizational context (i.e., budget, location, interaction with other research projects, etc.), and the required candidates’ features. As a result, a multi-objective combinatorial optimization problem is set-up, which can later be reshaped or simplified to meet the needs of the selected problem solver method.

The recommended teams are presented to the initiator who may choose their favorite team composition. If the process provides no adequate results (i.e., an acceptable research team), the initiator may restart its endeavor by making changes in the previous phases (e.g., trying to acquire new information, modifying the problem formulation, or selecting another solver.

As observed in Figure 2, the proposed methodology is human-assisted, with the team initiator playing a main role in formalizing the optimization problem, in selecting the solving method, and in selecting the most suitable team for fulfill the research project.

3.3.1. Team Formation Based on Bibliometric Data Inputs

Based on the theoretical model in Section 3.1 and driven by the previous four indicators (i.e., RGE, RCA, ICISG, and RLEGA) extracted from bibliometric data, we propose a multi-objective weighted set-cover formalization of the team formation optimization problem, as follows:

$${\displaystyle \begin{array}{ll}\left(\mathrm{F}1\right):\hfill & \mathrm{minimize}{\displaystyle \sum _{S_i\in S}}{x}_{S_i}\hfill \end{array}}$$

(2)

$$\begin{array}{cc}\hfill \left(\mathrm{F}2\right):& \mathrm{maximize}{\displaystyle \frac{1}{\left(\genfrac{}{}{0pt}{}{{\sum }_{\begin{array}{l}{S}_i\in S\hfill \end{array}}{x}_{S_i}}{1}\right)}}·\sum _{S_i\in S}RG{E}_{S_i}·x_{S_i}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \left(\mathrm{F}3\right):& \mathrm{maximize}{\displaystyle \frac{1}{\left(\genfrac{}{}{0pt}{}{{\sum }_{\begin{array}{l}{S}_i\in S\hfill \end{array}}{x}_{S_i}}{1}\right)}}·\sum _{S_i\in S}RC{A}_{S_i}·x_{S_i}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \left(\mathrm{F}4\right):& \mathrm{maximize}{\displaystyle \frac{1}{\left(\genfrac{}{}{0pt}{}{{\sum }_{\begin{array}{l}{S}_i\in S\hfill \end{array}}{x}_{S_i}}{2}\right)}}·\sum _{\begin{array}{l}j=1\dots \left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)\hfill \\ S_i\in S\hfill \end{array}}ICIS{G}_j^{\left(2\right)}·{\sqcap }_j^{\left(2\right)}\hfill \end{array}$$

(5)

$$\begin{array}{ll}\hfill & \mathrm{subject\; to}{\displaystyle \sum _{S_i\in S}}{RLEGA}_{S_i,e}·x_{S_i}>\tau for\; alle\in P\hfill \end{array}$$

(6)

where Equation (2) minimizes the number of team members, Equation (3) maximizes the average team member’s general expertise, Equation (4) maximizes the average team member collaboration potential, Equation (5) maximizes the average collaboration between groups of two team members (i.e., dyadic collaborations), and the constraint assures that any scientific area, described by the key term e, of the research project, is covered with the expertise with a redundancy $\tau$. The rest of the notations are briefly presented in the following list:

Equation (2) wants to maintain a workable team size by avoiding situations in which excessively large teams are formed. Equation (3) captures the elements of the parameters $U_G$ of the theoretical model. Equation (4) relates to the features of the parameters $U_I$ and S of the model. Equation (5) refers to the characteristics of the parameter S of the model in Section 3.1.

Notations:
P	research project composed of a given set of tasks
e	element from P (task) $e\in P$
m	number of candidates
$S_i$	set of tasks from P that can be solved by candidate i, $i=1,\dots ,m$, $S_i\subseteq P$
$x_{S_i}$	binary flag corresponding to candidate i ($x_{S_i}=1$, if candidate i is
	included in the team)
S	collection of all individual abilities $S=\left\{S_i\right|i=1,\dots ,m\}$ — a set of sets
${\sqcap }_j^{\left(k\right)}$	jth product of k different flags $x_{S_i}$, $j=1\dots \left({\displaystyle \genfrac{}{}{0pt}{}{m}{k}}\right)$
$\left({\displaystyle \genfrac{}{}{0pt}{}{{\sum }_{\begin{array}{l}{S}_i\in S\hfill \end{array}}{x}_{S_i}}{1}}\right)$	number of team members
$\left({\displaystyle \genfrac{}{}{0pt}{}{{\sum }_{\begin{array}{l}{S}_i\in S\hfill \end{array}}{x}_{S_i}}{2}}\right)$	number of pairs of team members

Equations (2)–(6) of the multi-objective combinatorial optimization problem may be augmented by including criteria or constraints that are specific to project specifications or organizational context, including cost- or performance-related requirements. Moreover, information about collaborations within groups that are larger than two team members (e.g., triadic or tetradic inter-member collaborations) may constitute additional optimization objectives, as described by the following equation:

$$\left(\mathrm{F}5\right):\mathrm{maximize}{\displaystyle \frac{1}{\left(\genfrac{}{}{0pt}{}{{\sum }_{\begin{array}{l}{S}_i\in S\hfill \end{array}}{x}_{S_i}}{k}\right)}}·\sum _{\begin{array}{l}j=1\dots \left({\displaystyle \genfrac{}{}{0pt}{}{m}{k}}\right)\hfill \\ S_i\in S\hfill \end{array}}ICIS{G}_j^{\left(k\right)}·{\sqcap }_j^{\left(k\right)}$$

(7)

where k is the group size. Equation (7) relates to the specifics of the parameters $U_I$ and S of the theoretical model.

3.3.2. Description of the Candidates-Related Indexes

This paragraph describes the way that the four RGE, RCA, ICISG, and RLEGA indexes, previously described in Section 3.2, may be computed using information extracted from the corpus of publication metadata.

A.

Description of parameter RGE

Each candidate’s expertise has, in our model, two facets that must be considered: (i) scientific production, described by the total number of publications $pn$, and (ii) popularity within the scientific community, described by two components, namely the total number of citations $cn$, and, the total number of downloads $dn$ received by the candidate (i.e., considering all candidate’s publications).

$${\mathfrak{E}}_i={\mu }_1·p{n}_i+{\mu }_2·c{n}_i+{\mu }_3·d{n}_i$$

(8)

where ${\mathfrak{E}}_i$ is the candidate’s expertise and ${\mu }_1,{\mu }_2,{\mu }_3\in {\mathbb{R}}_{+}$ are weights that control the balance between the three expertise components. If ${\mu }_1+{\mu }_2+{\mu }_3=1$, the three weights represent the percentages in which the three components form the overall expertise value.

We may now obtain the RGE for candidate i by normalizing (e.g., using min–max or z-score normalization methods) the value of ${\mathfrak{E}}_i$ for the entire pool of m candidates:

$$RG{E}_i=\underset{i=1,\dots ,m}{normalize}\left({\mathfrak{E}}_i\right)$$

(9)

or, in the case where we replace Equation (3) with a minimization objective, $RG{E}_i$ is replaced by parameter $inv\_RG{E}_i$ expressed as follows:

$$inv\_RG{E}_i=1-\underset{i=1,\dots ,m}{normalize}\left({\mathfrak{E}}_i\right)$$

(10)

Parameter RGE relates to the elements of parameter $U_I$ of the model, and its evolution over time can be used to assess the parameter variations $U_I^{+}$ and $U_I^{-}$.

B.

Description of parameter RCA

We suggest the expression of a researcher’s collaboration ability ${\mathfrak{C}}_i$ based on two values extracted from the authors’ affiliation data, namely: (i) the total number of the candidate’s co-authors from their institution ($ci$), and, (ii) the total number of the candidate’s co-authors from outside his/her institution ($co$). While the former reflects the collaborations in thier organization, the latter reveals the candidate’s ability to work in more heterogeneous teams that are sometimes multilingual, multicultural, and even multinational.

$${\mathfrak{C}}_i={\delta }_1·c{i}_i+{\delta }_2·c{o}_i$$

(11)

where weights ${\delta }_1,{\delta }_2\in {\mathbb{R}}_{+}$ control the balance between the two collaboration-related components. If the selection of these weights satisfies ${\delta }_1+{\delta }_2=1$, they represent the percentages of taking the two components into account.

The RCA for candidate i is found by normalizing (e.g., using min-max or z-score normalization methods) the value of parameter ${\mathfrak{C}}_i$ for the entire pool of m candidates:

$$RC{A}_i=\underset{i=1,\dots ,m}{normalize}\left({\mathfrak{C}}_i\right)$$

(12)

or, if we want to transform Equation (F3) into a minimization objective, parameter $RC{A}_i$ is replaced by parameter $inv\_RC{A}_i$:

$$inv\_RC{A}_i=1-\underset{i=1,\dots ,m}{normalize}\left({\mathfrak{C}}_i\right)$$

(13)

Parameter RCA refers to the elements of parameters $U_G$, $U_I$, and S of the model. Its evolution over time can be used to find facets of the parameter variations $U_G^{+}$, $U_G^{-}$, $U_I^{+}$, $U_I^{-}$, $S^{+}$, and $S^{-}$.

C.

Description of parameter ICISG

Interpersonal collaborations inside a team of size k quantifies the current cooperation history of the specified k members. This value is based on the number of previous collaborations of that particular team obtained by examining the publication authorship. For example, for a team composed of three members A, B, and C, this value is derived from the total number of publications where all three members are co-authors.

Since the importance of even a single such collaboration is high (e.g., a number of previous collaborations higher than one highlights an existing relationship), for calculating the parameter ICISG value, we suggest a nonlinear function, namely the hyperbolic tangent function $tanh\left(x\right)$, which diminishes its slope when increasing parameter $x\in \mathbb{N}$:

$$ICIS{G}_j^{\left(k\right)}=tanh\left(\eta ·i{g}_j^{\left(k\right)}\right)$$

(14)

where parameter $i{g}_j^{\left(k\right)}$ is the total number of previous collaborations between all k members of the jth team, and $\eta$ is a scaling factor. It is noteworthy mentioning that, by using the hyperbolic tangent function, the values of parameter $ICIS{G}_j^{\left(k\right)}$ are already normalized.

In team formation, parameter ICISG is naturally used inside maximization objective functions. If we want to switch to minimization objectives, we may use $inv\_ICIS{G}_j^{\left(k\right)}$ instead of $ICIS{G}_j^{\left(k\right)}$, where

$$inv\_ICIS{G}_j^{\left(k\right)}=1-tanh\left(\eta ·i{g}_j^{\left(k\right)}\right)$$

(15)

While existing one-to-one relationships between candidates ($k=2$) are often used to evaluate collaboration abilities [1,26,27] for the team formation process, we consider that past collaborations inside larger teams ($k>2$) offer new and valuable insights too.

Parameter ICISG pertains to the characteristics of parameters S of the model. Its evolution over time illustrate the parameter variations $S^{+}$ and $S^{-}$.

D.

Description of parameter RLEGA

A researcher’s level of expertise on a given scientific area may be evaluated based on the number of scientific publications in that area ($pna$), their corresponding number of citations ($cna$), and number of downloads ($dna$). The procedure to obtain the three values is similar to the one used for parameter RGE, but only considers the publications, which have the scientific area’s key terms or the key terms between their relevant key terms.

$${\mathfrak{A}}_{i,e}={\gamma }_1·pn{a}_{i,e}+{\gamma }_2·cn{a}_{i,e}+{\gamma }_3·dn{a}_{i,e}$$

(16)

where parameter ${\mathfrak{A}}_{i,e}$ is the candidate’s expertise in a specified area e and weights ${\gamma }_1,{\gamma }_2,{\gamma }_3\in {\mathbb{R}}_{+}$ control the balance between the three expertise components. If ${\gamma }_1+{\gamma }_2+{\gamma }_3=1$, the three weights represent the percentages in which the three components are considered in the overall expertise value.

The expertise level of candidate i in the scientific area e is characterized by the following equation:

$$RLEG{A}_{i,e}=tanh(\rho ·{\mathfrak{A}}_{i,e})$$

(17)

where weight $\rho$ is a scaling factor.

Since the values of parameter $RLEG{A}_{i,e}$ are used to evaluate the potential contribution of each candidate i to the coverage with expertise of a specified area e (Equation (6) is a typical constraint in multi-cover optimization problems to assure the needed redundancy ${\tau }_e$), their values cannot exceed the sum of the parameters $RLEGA$ for all candidates in field e:

$${\tau }_e\le {\tau }_{e,max}=\sum _{S_i\in S}RLEG{A}_{S_i,e}$$

(18)

Parameter RLEGA relates to the elements of parameter $U_I$ of the model, and its changes over time reflect the parameter variations $U_I^{+}$ and $U_I^{-}$.

3.3.3. Weights Selection

Our proposed procedure implements a human-in-the-loop team recommendation system, which is sensitive to the choice of weights from (8) to (17). This was one of the primary reasons for including a human in the process depicted in Figure 2. Since a team formation process is generally carried out or supervised by a team initiator, they will be the one to select the needed weights based on their experience and by exactly knowing: (i) what the elements—like the number of publications, number of citations, or number of already existing collaborations—represent when evaluating candidates’ expertise; and, (ii) which are the goals and constraints that the research team has to face. In this context, the team initiator may employ a try-and-error strategy to pick the right model parameters.

4. Problem-Solving

Multi-objective optimization problems are not easy to solve, as the objective functions generally conflict with each other. The problems described by Equations (2)–(7) is no exception. To address the difficulty in solving this problem, we suggest pre-filtering the original pool of candidates to obtain a shortlist. For example, we may only retain candidates with at least three published papers [1], exclude candidates with no relevant activity in the field for more than five years, or drop candidates with less than two hundred citations. Then, we can rely on the following three approaches to solve the problem:

-

Solving the research team formation problem is not time-critical and, if the shortlist of candidates is no longer than two hundred, we can use a brute-force approach by computing all possible solutions and then deciding which one is the best.

-

If the objective functions can be ranked by their importance, which is often the case in team formation problems, a lexicographic method [28] can be used.

-

If the number of candidates is huge and approaches to reduce the initial number of objective functions (e.g., linear scalarization or $ϵ$-constraint method [29]) are ineffective, an evolutionary algorithm (e.g., NSGA-II or NSGA-III) can be utilized.

The following case study used the NSGA-II evolutionary multi-objective algorithm [30] to solve the team formation problem.

5. Case Study

This section illustrates the proposed methodology on a case study, and compares it against similar approaches.

5.1. Problem Description

The research team formation optimization problem described by Equations (2)–(6) is used to identify potential teams of researchers from Politehnica University of Timisoara, Romania to fulfill a scientific project P, described by the following key terms: ‘hard_real_time’, ‘machine_learning’, ‘computer_vision’, ‘gesture_recognition’, and ‘image_processing’. Each of the scientific areas modeled by the key terms needs to be covered by researchers’ expertise with redundancy $\tau$.

5.2. Dataset

The related metadata corpus, containing the fields ‘authors’, ‘content type’, ‘citing paper count’, ‘citing patent count’, ‘download count’, ‘title’, ‘abstract’, ‘index terms’, ‘publication year’, and, ‘doi’, was extracted on 4 July 2023 from IEEEXplore for the years 2010–2022. The downloaded records correspond to papers having at least one author from Politehnica University of Timisoara. The metadata corpus contains 1992 records and 1179 authors that were anonymized to fulfill the requirements regarding data protection.

We used TagMe [31] to extract a total of 2651 key terms from the metadata fields ($lp=0.1$) containing the publication ‘title’, ‘keywords’, and ‘abstract’. It is important that the $lp$ value chosen to calibrate TagMe processing is less than the $lp$ values for each of the key terms that model the research theme, otherwise, one or more key terms will be automatically dropped from the extracted key term list. In this case, considering the values in

Table 2. Link probabilities for key terms describing the theme.

Key Term	$\mathbf{lp}$ Value
hard_real_time	0.423076
machine_learning	0.751253
computer_vision	0.776346
gesture_recognition	0.764705
image_processing	0.332503

, the considered value ($lp=0.1$) must fulfill the condition $lp<0.332503$, which is true.

The dataset is described in more detail in our data article [32] and is freely available in Mendeley Data [33].

5.3. Parameters and Implementation

The parameters used in the case study are presented below:

[P1].

Parameters used to derive the coefficients in the optimization problem:

• RGE-related parameters: ${\mu }_1=0.9$, ${\mu }_2=0.0999$, ${\mu }_3=0.0001$
• RCA-related parameters: ${\delta }_1=0.3$, ${\delta }_2=0.7$
• ICISG-related parameters: $\eta =1$
• RLEGA-related parameters: ${\gamma }_1=0.9$, ${\gamma }_2=0.0999$, ${\gamma }_3=0.0001$, $\rho =1$

[P2].

Parameters for candidates filtering

• Minimal number of papers relevant for the project: 1
• Minimal number of citations received for papers relevant for the project: 1

[P3].

Parameters of the NSGA-II solver

• Number of objectives: 4
• Number of constraints: 5
• Coverage redundancy: $\tau =[4,4,4,4,4]$
• Optimization problem type: ElementwiseProblem—evaluates a single solution at a time
• Population size: 100
• Number of generations: 100
• Sampling type: binary random sampling
• Mutation type: bit flip mutation
• Crossover type: two-point crossover
• Python function used: NSGA2() from pymoo package
• Number of independent runs: 30.

The first group of parameters, denoted by [P1], is related to the computation of the four candidate-related indices (i.e., RGE, RCA, ICISG, and RLEGA) from information extracted from publication metadata, using the Equations (8)–(17). The [P2] category describes the parameters used for candidates’ prefiltering and the [P3] set presents details about the Python implementation of the NSGA-II solver, $\tau$ being the redundancy in expertise for covering the five key terms, while choosing a sufficiently large population size and number of generations assures that all possible non-dominated solutions are found.

It is noteworthy to mention that the most time-consuming and computationally intensive part of our methodology is represented by the bibliographic data processing to identify researchers’ areas of expertise and to evaluate the four candidate-related indicators, namely RGE, RLEGA, RCA, and, ICISG. In our specific case study, it took approximately six hours using a laptop based on an Intel Core i7-8550U processor and 8 GB of RAM.

After candidate filtering, only 84 relevant candidates were retained. This candidate shortlist offers the following set of maximal coverage redundancy values, corresponding to the five key terms included in the project theme, e.g., derived using Equation (18):

$${\tau }_{max}=[6.51057, 29.837, 30.1965, 12.3179, 27.5543]$$

(19)

which assures at least one optimal solution of the problem, since each component of vector $\tau$ is less than the corresponding component of ${\tau }_{max}$.

The method was implemented in Python using the pymoo multi-objective optimization library [34], employing the standard NSGA-II method without any alterations to its original formulation.

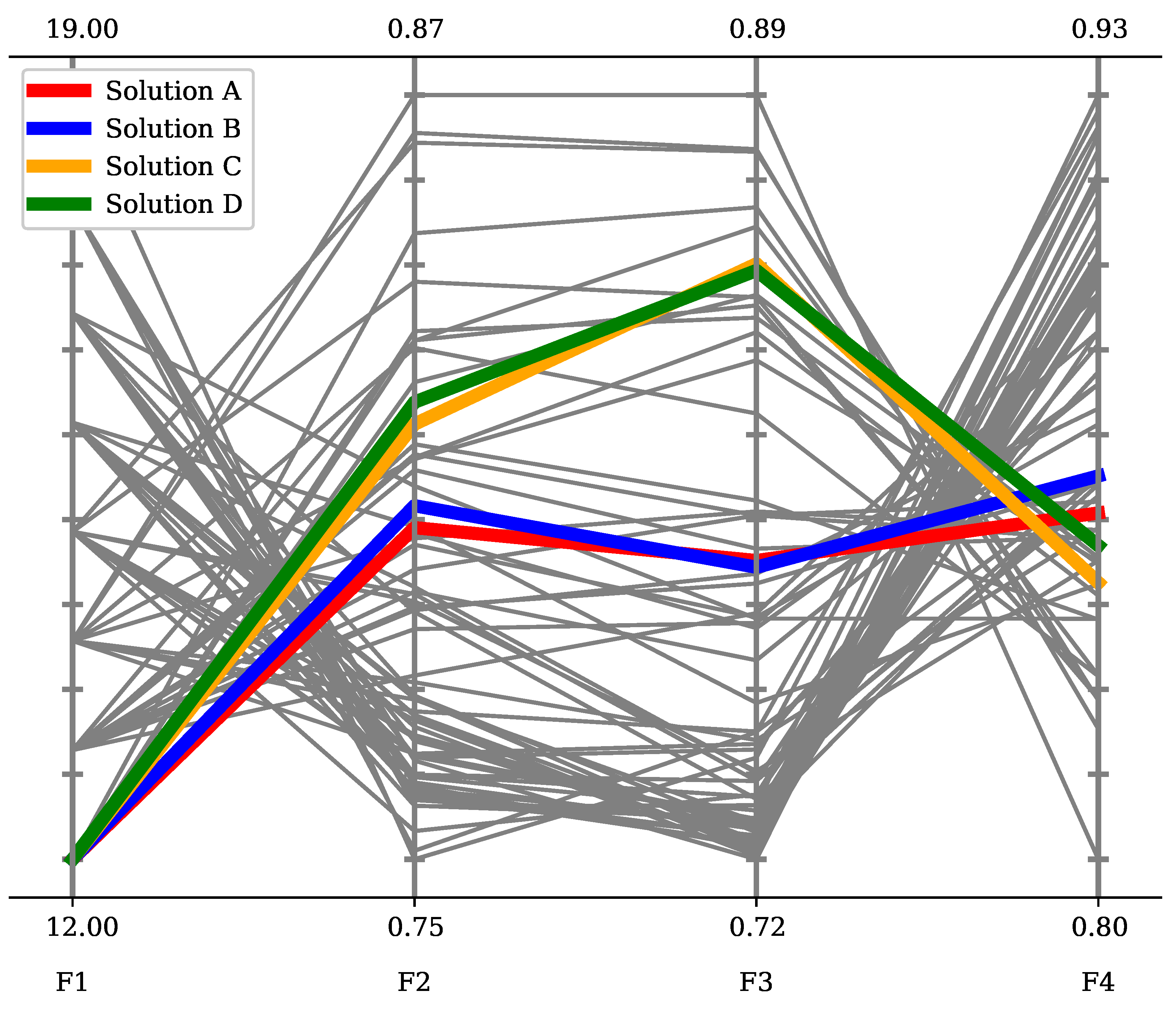
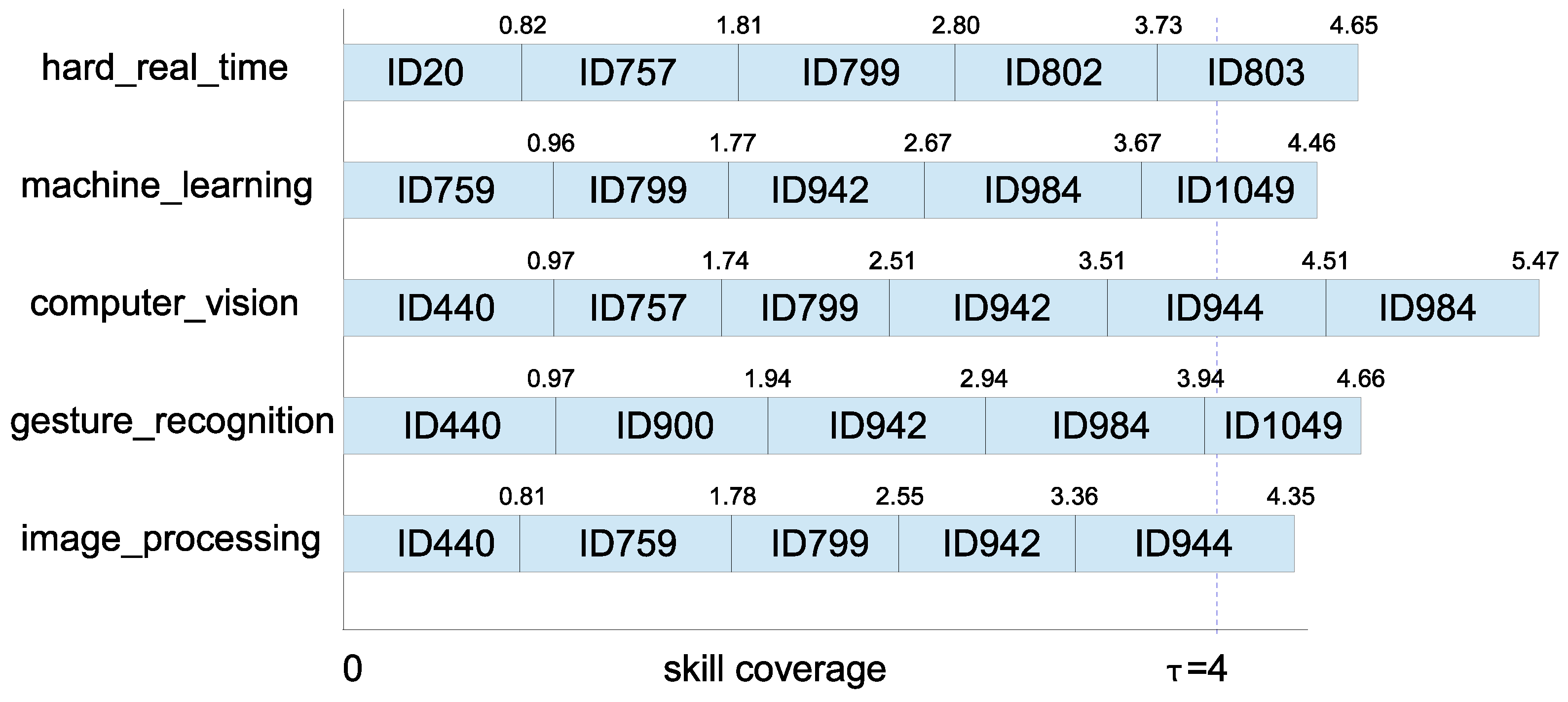
5.4. Experimental Results

A total of 68 solutions were obtained. They are all presented in a parallel coordinate plot in Figure 3, while the best nine solutions, ranked in a lexicographic order of their objective function values, are presented in

Table 3. Optimal teams with fewer team members.

Solution	F1	F2	F3	F4	Team Members
A	12	0.799417	0.787422	0.857966	ID20, ID440, ID757, ID759, ID799, ID802, ID803, ID900, ID942, ID944, ID984, ID1049
B	12	0.803007	0.785988	0.864100	ID20, ID440, ID757, ID759, ID799, ID803, ID804, ID900, ID942, ID944, ID984, ID1049
C	12	0.81634	0.851387	0.846426	ID20, ID440, ID757, ID759, ID793, ID799, ID802, ID803, ID900, ID942, ID984, ID1049
D	12	0.81993	0.849952	0.852561	ID20, ID440, ID757, ID759, ID793, ID799, ID803, ID804, ID900, ID942, ID984, ID1049
E	12	0.823195	0.844692	0.850582	ID440, ID732, ID757, ID759, ID773, ID799, ID802, ID803, ID900, ID942, ID984, ID1049
F	12	0.830031	0.84242	0.827504	ID440, ID757, ID759, ID773, ID799, ID802, ID803, ID804, ID900, ID942, ID984, ID1049
G	12	0.83153	0.83979	0.849494	ID20, ID440, ID757, ID759, ID773, ID799, ID803, ID804, ID900, ID942, ID984, ID1049
H	12	0.847529	0.863582	0.826959	ID440, ID757, ID759, ID799, ID802, ID803, ID804, ID888, ID900, ID942, ID984, ID1049
I	13	0.77525	0.776073	0.894248	ID20, ID138, ID732, ID757, ID759, ID793, ID799, ID803, ID848, ID942, ID944, ID984, ID1127

.

We observe that the considered research project may be solved using a minimal team composed of twelve members (Solutions A–H), but the rest of the objectives, namely F2–F4, have higher values than the ones of other proposed teams.

To evaluate the adequacy of the best team for the given research project, we analyzed the skill coverage of the team. Figure 4 presents how the skill requirements are covered by the members of the best team (Solution A). The solution has a good balance between the number of members with the necessary expertise to tackle each of the five key terms (i.e., each key term is covered by 5 or 6 team members). Also, a significant number of members have expertise in more than three areas (e.g., ID799 and ID942 cover 4 key terms, while ID440 and ID984 cover 3 key terms), being able to create functional bridges inside the team and by this to assure a good starting point for the team to function.

Comparison with Similar Methods

The existing work on using bibliometric information in expert team formation mostly uses the DBLP database [1,2,3,8,10,11]. The DBLP database not only provides paper metadata for a narrow scientific area (like Computer Science) but also has a simple record structure that doesn’t allow a deeper investigation of candidates personal and interpersonal skills. Even though few methods use other bibliometric databases, they also employ the same reduced number of metadata fields (i.e., ‘authors’ and ‘title’) without taking advantage of a more complex record structure [4,5,6]. By incorporating new key insights that bibliometric data provides, the proposed methodology offers more accurate and more relevant teams as a result of the following two aspects:

• A more complex multi-objective optimization approach that supports the presented description of the research team formation problem (i.e, the approach has four optimization objectives, while the state-of-the-art methods contain at most three objectives [11]);
• The described method employs more paper metadata fields in attaining the candidates’ personal and interpersonal traits, which allows capturing some new insight. For example, considering ‘title’, ‘keywords’, and ‘abstract’ to obtain the key terms instead of only ‘title’ as in the existing work, provides a higher level of key term granularity, hence giving a greater control over the data-driven team formation process. Furthermore, using fields ‘citation count’ and ‘downloads count’ can offer a better evaluation of the researcher’s expertise in a given domain than using only the number of publications, while utilizing the ‘affiliation’ field by categorizing the co-authors as either from the same organization or from different organizations may better model candidates’ interpersonal prospects.

To evaluate how implying information from the ‘title’, ‘keywords’, and ‘abstract’ fields impacts the entire research team formation process, we experimented with the proposed method in four different scenarios. The results are presented in

Table 4. Comparison between approaches considering diverse metadata fields in deriving the key terms.

Metadata Fields	Key Terms	${\mathit{\tau }}_{\mathbf{maxHRT}}$	${\mathit{\tau }}_{\mathbf{maxML}}$	${\mathit{\tau }}_{\mathbf{maxCV}}$	${\mathit{\tau }}_{\mathbf{maxGR}}$	${\mathit{\tau }}_{\mathbf{maxIP}}$	Shortlisted Candidates	Team Members
’title’	1844	6.5105	0.7678	3.8345	4.4193	3.6055	11	no team
’keywords’	1254	0	18.0555	21.9328	7.6421	15.8878	56	no team
’title’ + ’keywords’	2651	6.5105	18.0555	21.9328	7.6851	17.5061	61	15
’title’ + ’keywords’ + ’abstract’	6493	6.5105	29.8370	30.1965	12.3179	27.5543	84	12

. Considering the three mentioned fields offers a more comprehensive image of each of the extracted publications than using, for example, only two or even one of the fields (please note that state-of-art methods use the datasets extracted from DBLP, which has only the ‘title’ field but misses the ‘keywords’ and ‘abstract’ fields). For example, if we consider only the ‘title’ field, we extract a total of only 1844 key terms, and if we only use the ‘keyword’ field to characterize each paper, we extract a total of only 1254 key terms for the entire publication corpus, instead of 2651 key terms when employing ‘title’ and ‘keywords’ and 6493 key terms when using all the three mentioned metadata fields.

We can also notice that when using only the ‘title’ or only ‘keywords’ field, no team is formed. This is reflected by the ${\tau }_{max}$ components, corresponding to each of the five key terms that model the research project, that need to be higher than 4 (i.e., the considered needed redundancy for each of the key terms). Moreover, in the case of employing only the ‘keywords’ metadata field, ‘hard_real_time’ key term was even not identified as a key term. This happens because some key terms are not identified in the candidate’s portfolio, since such terms may only appear in the other two metadata fields (i.e., ‘abstract’ and ‘keyword’; and, ‘abstract’ and ‘title, respectively).

5.5. Limitations

The proposed research team formation methodology has the following limitations:

• The methodology uses only insights from publication metadata, without considering other categories of research outputs, like products, video and audio materials, internal research reports, essays, policy papers or presentations;
• The methodology’s reliance on detailed bibliometric metadata that are generally extracted from subscription-based bibliographic databases, limits its accessibility for researchers with limited resources;
• Since the bibliographic records do not share a standard format accross all databases, the methodology needs slight adaptations when different databases are employed.
• The accuracy of our research team formation procedure is affected by bibliographic records that are corrupted or belong to fake or manipulated publications.
• Some qualitative aspects of teamwork, such as critical thinking, leadership, time management, accountability, responsibility, or conflict resolution, cannot be revealed by bibliometric records and, because of this, are not considered in our methodology.

6. Conclusions

This paper presents a novel methodology for interdisciplinary team formation based on an extended set of bibliographic record fields. The paper proposes a theoretical model for team behavior expressed as cognitive contributions and social interactions, four candidate-related indices that express the features of the model and are calculated using paper metadata, and a combinatorial multi-objective optimization method to form teams by solving a set of equations expressed using the indices. The proposed methodology is validated and compared with other similar approaches using a dataset extracted from the IEEE Xplore database. The experimental results show that the proposed methodology could build research teams to tackle challenging situations, especially when aiming for productivity, innovation, and collaboration.

Future work will validate the proposed methodology on other relevant databases, including Web of Science and Scopus, and analyze how combining information from diverse bibliometric sources can enhance the accuracy of the proposed approach. Moreover, we intend to evaluate the performance of such data-driven research team formation procedures when using additional data regarding candidates coming from other sources, including social networks.