ODEI: Object Detector Efficiency Index
Abstract
1. Introduction
2. Metric Calculation Breakdown
2.1. Acronym List
- A: bounding box annotation;
- B: inference batch size;
- C: training dataset object class number;
- DTest: test dataset;
- DTrain: training dataset;
- N: test dataset image number;
- OD: object detector;
- P: bounding box prediction;
- R: object detector input image resolution;
- TC: prediction confidence threshold;
- TNMS: IoU threshold for non-maximum suppression (NMS);
- TTFP: IoU threshold for TP and FP prediction identification.
2.2. Problem Formulation
2.3. OD Raw Output
2.4. Prediction Class Determination
2.5. Confidence Filtering
2.6. Non-Maximum Suppression
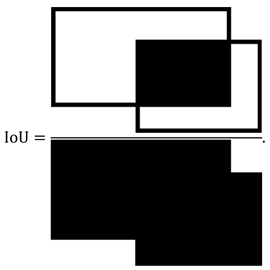
2.7. TP and FP Identification
2.8. PR Curve Construction
2.9. AP Calculation
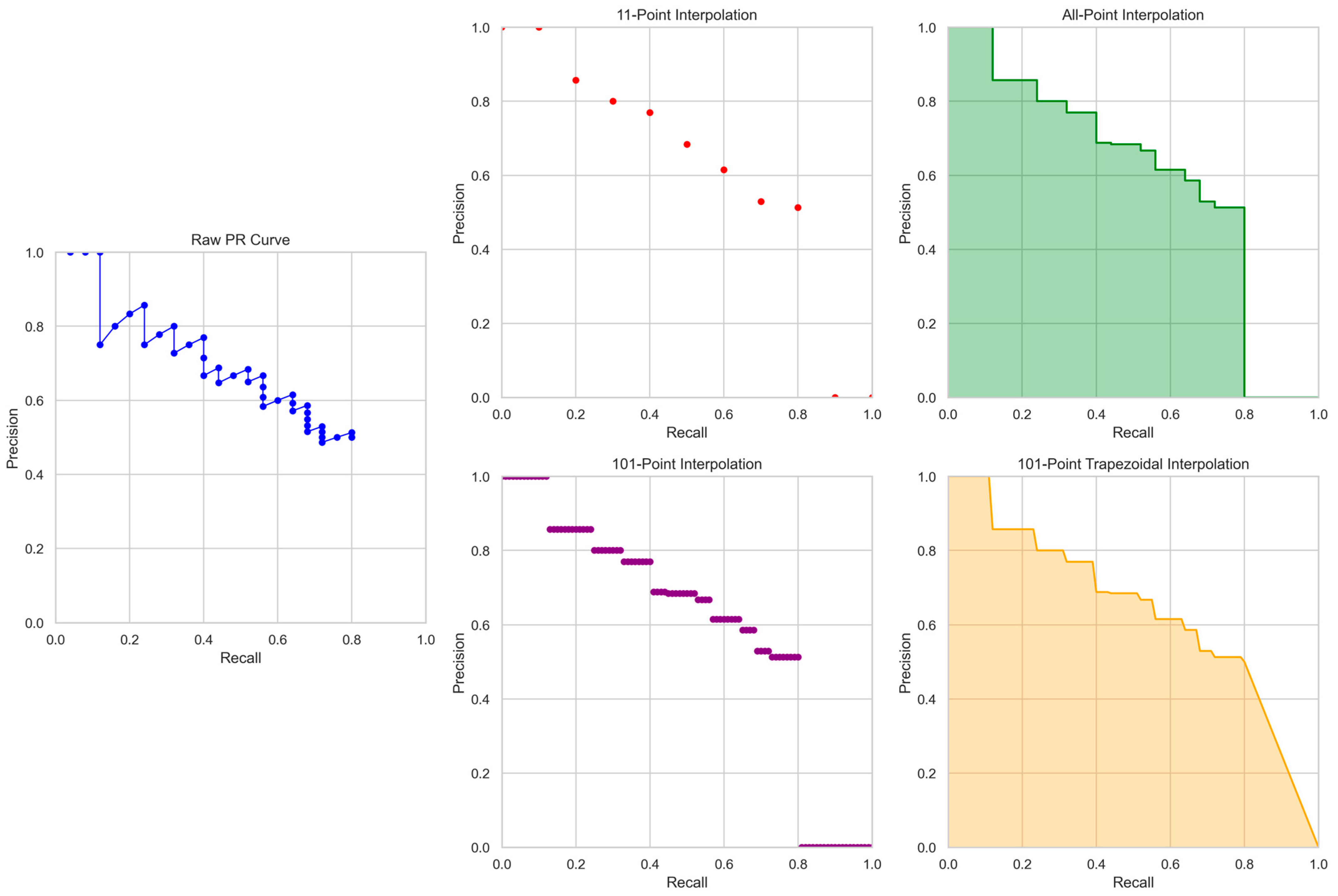
2.9.1. 11-Point Interpolation
2.9.2. All-Point Interpolation
2.9.3. 101-Point Interpolation
2.9.4. 101-Point Trapezoidal Interpolation
2.10. mAP Calculation
2.11. GFLOPs Counting
- torch.nn.AdaptiveAvgPool1d;
- torch.nn.AdaptiveAvgPool2d;
- torch.nn.AdaptiveAvgPool3d;
- torch.nn.AvgPool1d;
- torch.nn.AvgPool2d;
- torch.nn.AvgPool3d;
- torch.nn.BatchNorm1d;
- torch.nn.BatchNorm2d;
- torch.nn.BatchNorm3d;
- torch.nn.Conv1d;
- torch.nn.Conv2d;
- torch.nn.Conv3d;
- torch.nn.ConvTranspose1d;
- torch.nn.ConvTranspose2d;
- torch.nn.ConvTranspose3d;
- torch.nn.GRU;
- torch.nn.GRUCell;
- torch.nn.InstanceNorm1d;
- torch.nn.InstanceNorm2d;
- torch.nn.InstanceNorm3d;
- torch.nn.LayerNorm;
- torch.nn.LeakyReLU;
- torch.nn.Linear;
- torch.nn.LSTM;
- torch.nn.LSTMCell;
- torch.nn.PReLU;
- torch.nn.RNN;
- torch.nn.RNNCell;
- torch.nn.Softmax;
- torch.nn.SyncBatchNorm;
- torch.nn.Upsample;
- torch.nn.UpsamplingBilinear2d;
- torch.nn.UpsamplingNearest2d.
- torch.nn.AdaptiveMaxPool1d;
- torch.nn.AdaptiveMaxPool2d;
- torch.nn.AdaptiveMaxPool3d;
- torch.nn.Dropout;
- torch.nn.MaxPool1d;
- torch.nn.MaxPool2d;
- torch.nn.MaxPool3d;
- torch.nn.PixelShuffle;
- torch.nn.ReLU;
- torch.nn.ReLU6;
- torch.nn.Sequential;
- torch.nn.ZeroPad2d.
2.12. ODEI Calculation
2.13. Mandatory Parameter Declaration
- Dataset name: name of the benchmarking dataset, which must be open-source and publicly accessible. Examples from the FiftyOne Dataset Zoo [21] include VOC-2007, VOC-2012, COCO-2014, COCO-2017, etc.
- Dataset split: portion of the dataset used for benchmarking. Common options include Train, Validation, Test, and Full, where Full means the entire dataset is used.
- Weight format: model weight file format. Examples include PyTorch, TensorFlow, TensorFlow Lite, TensorRT, ONNX, etc.
- Image size: model input image resolution. Examples include 320 representing 320 × 320, 480 representing 480 × 480, 640 representing 640 × 640, etc.
- Confidence threshold: minimum confidence score used to filter low-confidence predictions during postprocessing. Values range from 0 to 1.
- IoU threshold: maximum IoU allowed during NMS to filter overlapping predictions. Values range from 0 to 1. Use NA when NMS is not applicable to a model.
- Interpolation method: PR curve interpolation method for AP calculation as described in Section 2.9. Examples include 11-point, All-point, 101-point, 101-point trapezoidal, etc.
3. Example Metric Usage
3.1. YOLOv12
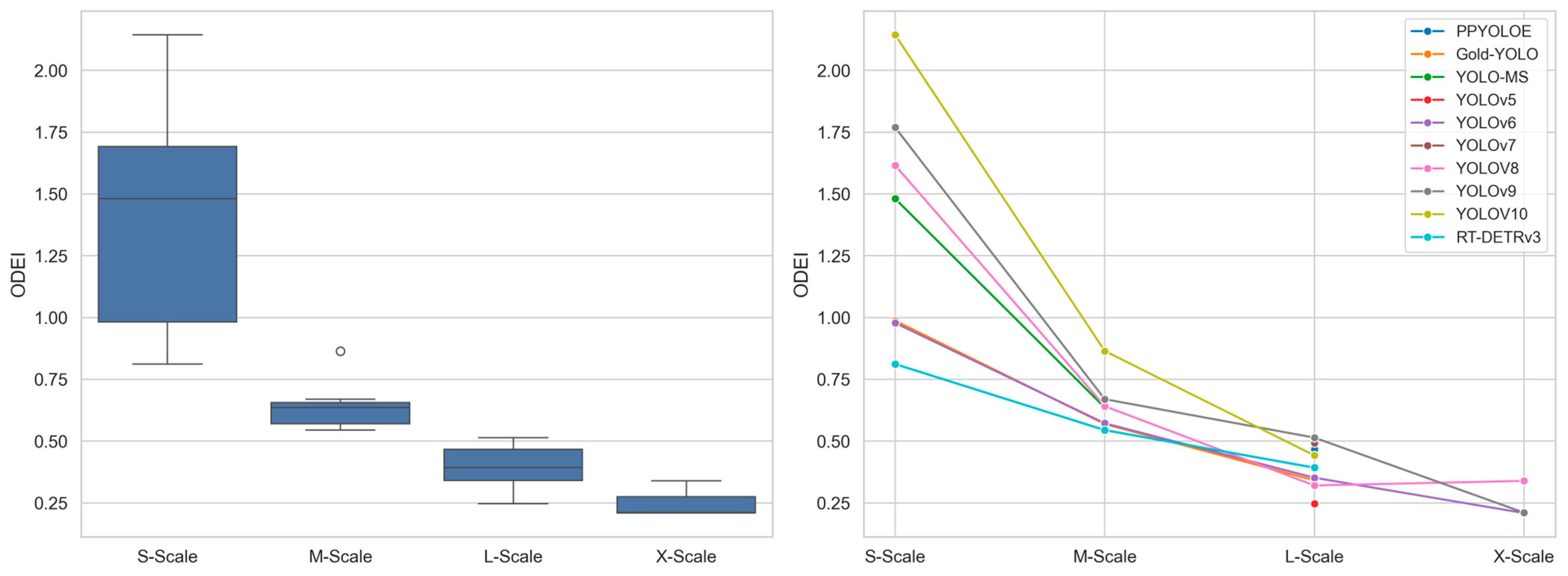
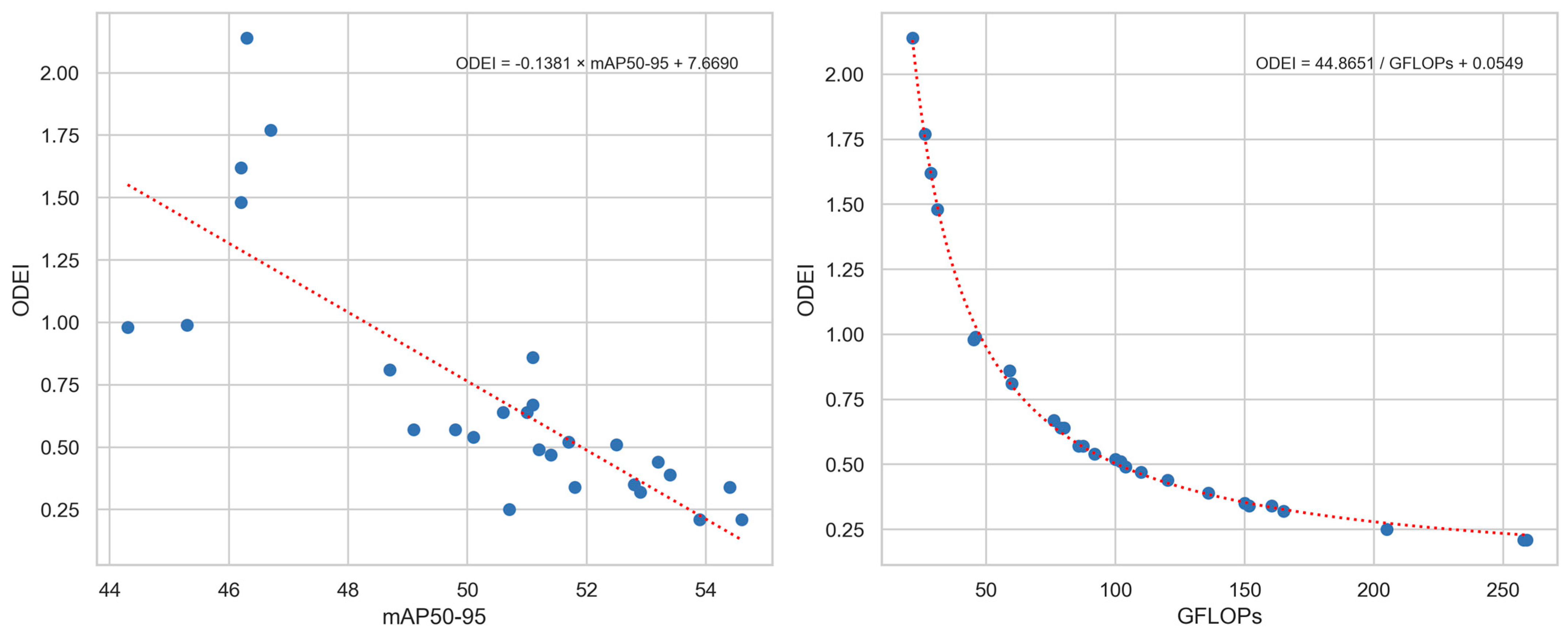
3.2. RT-DETRv3
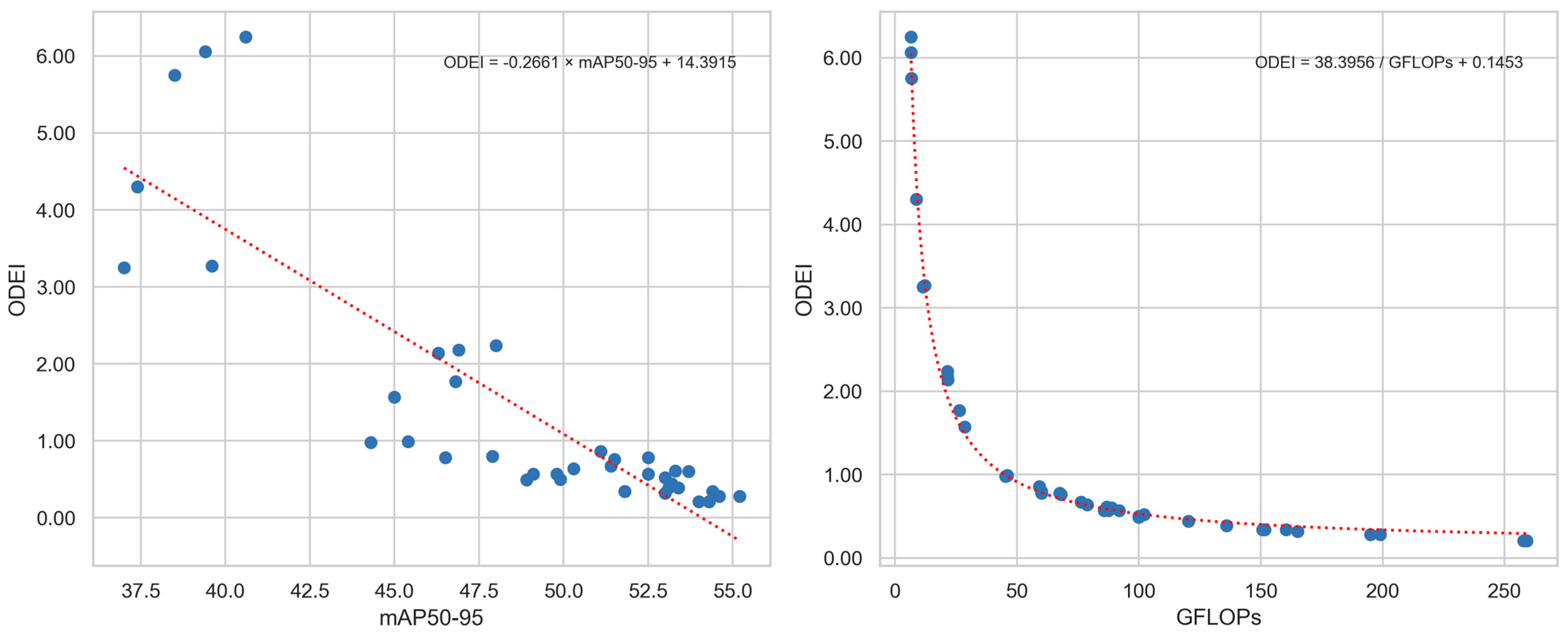
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and f-Score. In Advances in Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Ríos, J.O. Dynamically Adapting Floating-Point Precision to Accelerate Deep Neural Network Training. 2023. Available online: https://upcommons.upc.edu/bitstream/handle/2117/404063/TJHOR1de1.pdf?sequence=1&isAllowed=y (accessed on 24 June 2025).
- Suhaimi, N.S.; Othman, Z.; Yaakub, M.R. Comparative Analysis Between Macro and Micro-Accuracy in Imbalance Dataset for Movie Review Classification. In Proceedings of the Seventh International Congress on Information and Communication Technology, London, UK, 21–24 February 2022; pp. 83–93. [Google Scholar]
- Takahashi, K.; Yamamoto, K.; Kuchiba, A.; Koyama, T. Confidence Interval for Micro-Averaged F 1 and Macro-Averaged F 1 Scores. Appl. Intell. 2022, 52, 4961–4972. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Kwon, Y.; Lee, J. Optimizing Real-Time Object Detection in a Multi-Neural Processing Unit System. Sensors 2025, 25, 1376. [Google Scholar] [CrossRef] [PubMed]
- Ryu, J.; Kim, H. Adaptive Object Detection: Balancing Accuracy and Inference Time. In Proceedings of the 2023 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Busan, Republic of Korea, 23–25 October 2023. [Google Scholar]
- Ultralytics/Ultralytics/Nn/Modules/Head.Py. Available online: https://github.com/ultralytics/ultralytics/blob/main/ultralytics/nn/modules/head.py (accessed on 24 June 2025).
- Ultralytics/Ultralytics/Utils/Ops.Py. Available online: https://github.com/ultralytics/ultralytics/blob/main/ultralytics/utils/ops.py (accessed on 24 June 2025).
- Ultralytics/Ultralytics/Engine/Validator.Py. Available online: https://github.com/ultralytics/ultralytics/blob/main/ultralytics/engine/validator.py (accessed on 24 June 2025).
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The PASCAL Visual Object Classes Challenge 2007. Available online: http://host.robots.ox.ac.uk/pascal/VOC/voc2007/index.html (accessed on 24 June 2025).
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. VOCdevkit_08-Jun-2007.Tar. Available online: http://host.robots.ox.ac.uk/pascal/VOC/voc2007/VOCdevkit_08-Jun-2007.tar (accessed on 24 June 2025).
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. Visual Object Classes Challenge 2010 (VOC2010). Available online: http://host.robots.ox.ac.uk/pascal/VOC/voc2010/index.html (accessed on 24 June 2025).
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. VOCdevkit_08-May-2010.Tar. Available online: http://host.robots.ox.ac.uk/pascal/VOC/voc2010/VOCdevkit_08-May-2010.tar (accessed on 24 June 2025).
- Lin, T.-Y.; Maire, M.; Belongie, S.; Bourdev, L.; Girshick, R.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L.; Dollár, P. Microsoft COCO: Common Objects in Context. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Cocoapi/PythonAPI/Pycocotools/Cocoeval.Py. Available online: https://github.com/cocodataset/cocoapi/blob/master/PythonAPI/pycocotools/cocoeval.py (accessed on 24 June 2025).
- Ultralytics/Ultralytics/Utils/Metrics.Py. Available online: https://github.com/ultralytics/ultralytics/blob/main/ultralytics/utils/metrics.py (accessed on 24 June 2025).
- Detection Evaluation. Available online: https://cocodataset.org/#detection-eval (accessed on 24 June 2025).
- THOP: PyTorch-OpCounter. Available online: https://github.com/ultralytics/thop/tree/main (accessed on 24 June 2025).
- Thop/Thop/Profile.Py. Available online: https://github.com/ultralytics/thop/blob/main/thop/profile.py (accessed on 24 June 2025).
- FiftyOne Dataset Zoo. Available online: https://docs.voxel51.com/dataset_zoo/index.html (accessed on 24 June 2025).
- Tian, Y.; Ye, Q.; Doermann, D. YOLOv12: Attention-Centric Real-Time Object Detectors. arXiv 2025, arXiv:2502.12524. [Google Scholar]
- Wang, S.; Xia, C.; Lv, F.; Shi, Y. RT-DETRv3: Real-Time End-to-End Object Detection with Hierarchical Dense Positive Supervision. arXiv 2024, arXiv:2409.08475. [Google Scholar]
- Zhao, Y.; Lv, W.; Xu, S.; Wei, J.; Wang, G.; Dang, Q.; Liu, Y.; Chen, J. DETRs Beat YOLOs on Real-Time Object Detection. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024. [Google Scholar] [CrossRef]
- Yuan, W.; Choi, D. UAV-Based Heating Requirement Determination for Frost Management in Apple Orchard. Remote Sens. 2021, 13, 273. [Google Scholar] [CrossRef]
- Yuan, W. Accuracy Comparison of YOLOv7 and YOLOv4 Regarding Image Annotation Quality for Apple Flower Bud Classification. AgriEngineering 2023, 5, 413–424. [Google Scholar] [CrossRef]
- Yuan, W.; Choi, D.; Bolkas, D.; Heinemann, P.H.; He, L. Sensitivity Examination of YOLOv4 Regarding Test Image Distortion and Training Dataset Attribute for Apple Flower Bud Classification. Int. J. Remote Sens. 2022, 43, 3106–3130. [Google Scholar] [CrossRef]
- Yuan, W. AriAplBud: An Aerial Multi-Growth Stage Apple Flower Bud Dataset for Agricultural Object Detection Benchmarking. Data 2024, 9, 36. [Google Scholar] [CrossRef]
- Yuan, W.; Li, P. Lightweight GAN-Assisted Class Imbalance Mitigation for Apple Flower Bud Detection. Big Data Cogn. Comput. 2025, 9, 28. [Google Scholar] [CrossRef]
- Darknet/Cfg/Yolov4.Cfg. Available online: https://github.com/AlexeyAB/darknet/blob/master/cfg/yolov4.cfg (accessed on 24 June 2025).
- Darknet/Src/Detector.C. Available online: https://github.com/AlexeyAB/darknet/blob/master/src/detector.c (accessed on 24 June 2025).
- Yolov7/Test.Py. Available online: https://github.com/WongKinYiu/yolov7/blob/main/test.py (accessed on 24 June 2025).
- Yolov7/Utils/Metrics.Py. Available online: https://github.com/WongKinYiu/yolov7/blob/main/utils/metrics.py (accessed on 24 June 2025).
- Ultralytics/Ultralytics/Cfg/Default.Yaml. Available online: https://github.com/ultralytics/ultralytics/blob/main/ultralytics/cfg/default.yaml (accessed on 24 June 2025).
- Object Detection. Available online: https://paperswithcode.com/task/object-detection (accessed on 24 June 2025).
- Object Detection Leaderboard. Available online: https://huggingface.co/spaces/hf-vision/object_detection_leaderboard (accessed on 24 June 2025).
- Computer Vision Model Leaderboard. Available online: https://leaderboard.roboflow.com/ (accessed on 24 June 2025).
- Detection Leaderboard. Available online: https://cocodataset.org/#detection-leaderboard (accessed on 24 June 2025).
| Prediction Rank | Confidence | TP/FP | Cumulative TP | Precision | Recall |
|---|---|---|---|---|---|
| 1 | 0.99 | TP | 1 | 1/1 | 1/Aj |
| 2 | 0.98 | FP | 1 | 1/2 | 1/Aj |
| 3 | 0.92 | TP | 2 | 2/3 | 2/Aj |
| 4 | 0.91 | FP | 2 | 2/4 | 2/Aj |
| 5 | 0.85 | FP | 2 | 2/5 | 2/Aj |
| 6 | 0.83 | TP | 3 | 3/6 | 3/Aj |
| … | |||||
| Pj | 0.69 | TP | TPj | TPj/Pj | TPj/Aj |
| Parameter | Description | Example |
|---|---|---|
| DN | Dataset name | VOC-2007, VOC-2012, COCO-2014, COCO-2017, NR |
| DS | Dataset split | Train, Validation, Test, Full, NR |
| WF | Model weight format | PyTorch, TensorFlow, TensorFlow Lite, TensorRT, ONNX, NR |
| IS | Image input size | 320, 480, 640, NR |
| CT | Confidence threshold | 0.001, 0.25, 0.5, NR |
| IT | NMS IoU threshold | 0.45, 0.65, 0.7, NA, NR |
| IM | PR curve interpolation method | 11-point, All-point, 101-point, 101-point trapezoidal, NR |
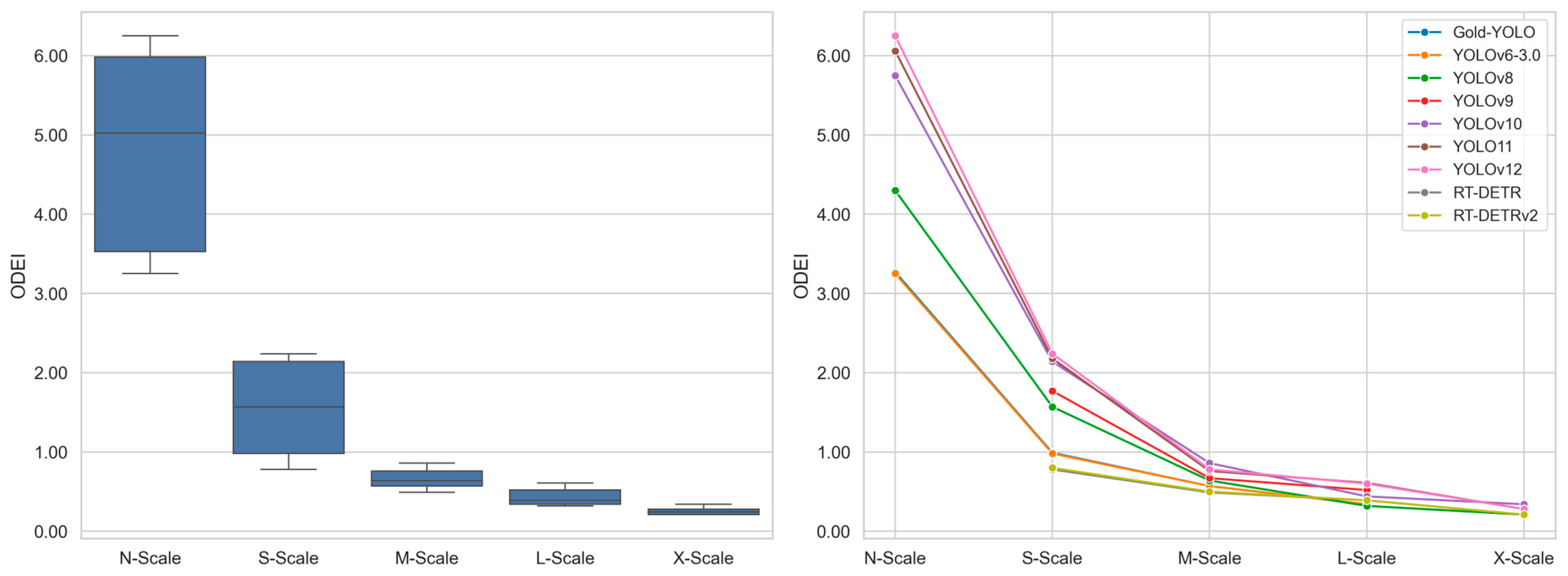
| Model | mAP50–95 | GFLOPs | ODEI |
|---|---|---|---|
| YOLOv6-3.0-N | 37.0 | 11.4 | 3.25 |
| Gold-YOLO-N | 39.6 | 12.1 | 3.27 |
| YOLOv8-N | 37.4 | 8.7 | 4.30 |
| YOLOv10-N | 38.5 | 6.7 | 5.75 |
| YOLO11-N | 39.4 | 6.5 | 6.06 |
| YOLOv12-N | 40.6 | 6.5 | 6.25 |
| YOLOv6-3.0-S | 44.3 | 45.3 | 0.98 |
| Gold-YOLO-S | 45.4 | 46.0 | 0.99 |
| YOLOv8-S | 45.0 | 28.6 | 1.57 |
| RT-DETR-R18 | 46.5 | 60.0 | 0.78 |
| RT-DETRv2-R18 | 47.9 | 60.0 | 0.80 |
| YOLOv9-S | 46.8 | 26.4 | 1.77 |
| YOLOv10-S | 46.3 | 21.6 | 2.14 |
| YOLO11-S | 46.9 | 21.5 | 2.18 |
| YOLOv12-S | 48.0 | 21.4 | 2.24 |
| YOLOv6-3.0-M | 49.1 | 85.8 | 0.57 |
| Gold-YOLO-M | 49.8 | 87.5 | 0.57 |
| YOLOv8-M | 50.3 | 78.9 | 0.64 |
| RT-DETR-R34 | 48.9 | 100.0 | 0.49 |
| RT-DETRv2-R34 | 49.9 | 100.0 | 0.50 |
| YOLOv9-M | 51.4 | 76.3 | 0.67 |
| YOLOv10-M | 51.1 | 59.1 | 0.86 |
| YOLO11-M | 51.5 | 68.0 | 0.76 |
| YOLOv12-M | 52.5 | 67.5 | 0.78 |
| YOLOv6-3.0-L | 51.8 | 150.7 | 0.34 |
| Gold-YOLO-L | 51.8 | 151.7 | 0.34 |
| YOLOv8-L | 53.0 | 165.2 | 0.32 |
| RT-DETR-R50 | 53.1 | 136.0 | 0.39 |
| RT-DETRv2-R50 | 53.4 | 136.0 | 0.39 |
| YOLOv9-C | 53.0 | 102.1 | 0.52 |
| YOLOv10-B | 52.5 | 92.0 | 0.57 |
| YOLOv10-L | 53.2 | 120.3 | 0.44 |
| YOLO11-L | 53.3 | 86.9 | 0.61 |
| YOLOv12-L | 53.7 | 88.9 | 0.60 |
| YOLOv8-X | 54.0 | 257.8 | 0.21 |
| RT-DETR-R101 | 54.3 | 259.0 | 0.21 |
| RT-DETRv2-R101 | 54.3 | 259.0 | 0.21 |
| YOLOv10-X | 54.4 | 160.4 | 0.34 |
| YOLO11-X | 54.6 | 194.9 | 0.28 |
| YOLOv12-X | 55.2 | 199.0 | 0.28 |
| Model | mAP50–95 | GFLOPs | ODEI |
|---|---|---|---|
| YOLOv6-3.0-S | 44.3 | 45.3 | 0.98 |
| Gold-YOLO-S | 45.4 | 46.0 | 0.99 |
| YOLO-MS-S | 46.2 | 31.2 | 1.48 |
| YOLOv8-S | 46.2 | 28.6 | 1.62 |
| YOLOv9-S | 46.7 | 26.4 | 1.77 |
| YOLOV10-S | 46.3 | 21.6 | 2.14 |
| RT-DETRv3-R18 | 48.7 | 60.0 | 0.81 |
| YOLOv6-3.0-M | 49.1 | 85.8 | 0.57 |
| Gold-YOLO-M | 49.8 | 87.5 | 0.57 |
| YOLO-MS | 51.0 | 80.2 | 0.64 |
| YOLOv8-M | 50.6 | 78.9 | 0.64 |
| YOLOv9-M | 51.1 | 76.3 | 0.67 |
| YOLOV10-M | 51.1 | 59.1 | 0.86 |
| RT-DETRv3-R34 | 50.1 | 92.0 | 0.54 |
| RT-DETRv3-R50m | 51.7 | 100.0 | 0.52 |
| Gold-YOLO-L | 51.8 | 151.7 | 0.34 |
| YOLOv5-X | 50.7 | 205.0 | 0.25 |
| PPYOLOE-L | 51.4 | 110.0 | 0.47 |
| YOLOv6-L | 52.8 | 150.0 | 0.35 |
| YOLOv7-L | 51.2 | 104.0 | 0.49 |
| YOLOV8-L | 52.9 | 165.0 | 0.32 |
| YOLOv9-C | 52.5 | 102.1 | 0.51 |
| YOLOV10-L | 53.2 | 120.3 | 0.44 |
| RT-DETRv3-R50 | 53.4 | 136.0 | 0.39 |
| YOLOv8-X | 53.9 | 257.8 | 0.21 |
| YOLOv10-X | 54.4 | 160.4 | 0.34 |
| RT-DETRv3-R101 | 54.6 | 259.0 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, W. ODEI: Object Detector Efficiency Index. AI 2025, 6, 141. https://doi.org/10.3390/ai6070141
Yuan W. ODEI: Object Detector Efficiency Index. AI. 2025; 6(7):141. https://doi.org/10.3390/ai6070141
Chicago/Turabian StyleYuan, Wenan. 2025. "ODEI: Object Detector Efficiency Index" AI 6, no. 7: 141. https://doi.org/10.3390/ai6070141
APA StyleYuan, W. (2025). ODEI: Object Detector Efficiency Index. AI, 6(7), 141. https://doi.org/10.3390/ai6070141






