FedEHD: Entropic High-Order Descent for Robust Federated Multi-Source Environmental Monitoring

Abstract

We propose Federated Entropic High-Order Descent (FedEHD), a drop-in client optimizer that augments local SGD with (i) an entropy (sign) term and (ii) quadratic and cubic gradient components for drift control and implicit clipping. Across non-IID CIFAR-10 and CIFAR-100 benchmarks (100 clients, 10% sampled per round), FedEHD achieves faster and higher convergence than strong baselines including FedAvg, FedProx, SCAFFOLD, FedDyn, MOON, and FedAdam. On CIFAR-10, it reaches 70% accuracy in approximately 80 rounds (versus 100 for MOON and 130 for SCAFFOLD) and attains a final accuracy of 72.5%. On CIFAR-100, FedEHD surpasses 60% accuracy by about 150 rounds (compared with 250 for MOON and 300 for SCAFFOLD) and achieves a final accuracy of 68.0%. In an environmental monitoring case study involving four distributed air-quality stations, FedEHD yields the highest macro AUC/F1 and improved calibration (ECE 0.183 versus 0.186–0.210 for competing federated methods) without additional communication and with only $\mathcal{O}(d)$ local overhead. The method further provides scale-invariant coefficients with optional automatic adaptation, theoretical guarantees for surrogate descent and drift reduction, and convergence curves that illustrate smooth and stable learning dynamics.

1. Introduction

Federated Learning (FL) enables training a global model across many decentralized clients (e.g., user devices or data silos) without requiring their data to be centralized [1,2,3,4]. Instead, each client performs local training on its own dataset and only model updates are periodically aggregated on a central server. This paradigm reduces privacy risks and communication costs, but it poses significant challenges when client data are heterogeneous (non-i.i.d.). Under highly skewed data distributions, the classical Federated Averaging (FedAvg) algorithm [1] often suffers from slow or unstable convergence due to client drift, where local models diverge in different directions. Numerous algorithms have been proposed to improve robustness on non-i.i.d. data by modifying the client update or server aggregation [5]. For example, FedProx adds a proximal term to restrict local model divergence [6], SCAFFOLD uses control variates to correct drift [7], FedDyn introduces dynamic regularization to align local and global optima [8], FedNova normalizes updates to eliminate objective inconsistency [9], MOON applies a model-contrastive loss to reduce client model disparity [10], and adaptive FedOpt methods employ server momentum or adaptive optimizers to accelerate convergence [11]. Despite these advances, fully addressing data heterogeneity in FL remains an open problem, motivating exploration of new optimization strategies.

In parallel, there is growing interest in entropy-based [12,13] and physics-inspired [14] optimization techniques to improve training stability and generalization. Entropy-SGD [15] introduced the idea of augmenting the loss landscape with an entropy term to bias gradient descent toward wide, flat minima [16], which are known to improve generalization and robustness. Relatedly, methods like signSGD demonstrated that using only the sign of gradients can still achieve convergence in deep networks [17], highlighting the potential benefit of directional noise or regularization during training. Building on these insights, we hypothesize that incorporating entropy-driven noise and higher-order gradient information into the federated optimization process can mitigate the adverse effects of non-i.i.d. data. By encouraging flatter minima and damping abrupt update changes, such an approach may stabilize federated training across divergent client data distributions.

Another challenge we consider is the fusion of multi-source data in distributed environments. In many real-world applications of FL, clients correspond to distinct data sources or sensors that observe different aspects of a phenomenon. An illustrative example is an environmental monitoring network, where each client (station) measures local pollutant levels. Effective learning in this scenario requires not only robust federated optimization but also intelligent combination of heterogeneous sensor data. Classical data fusion methods, such as joint manifold learning [18], exploit inter-sensor correlations to improve inference on high-dimensional streams. However, these techniques typically assume centralized data access and do not directly address federated constraints or training dynamics. We aim to design a unified framework that integrates entropy-guided federated optimization with a multi-source fusion mechanism, enabling detection and prediction tasks on distributed sensor networks under real-time constraints.

In this work, we present Federated Entropic High-Order Descent (FedEHD), a novel federated learning algorithm that synergistically combines these ideas. In FedEHD, each client minimizes a modified local objective that includes (1) an entropy regularization term using the sign of the gradient to provide a constant exploratory push and (2) high-order gradient terms (squared and cubic gradients) to capture curvature information and dampen oscillations. This high-order, entropy-guided update rule is designed to drive local models toward flatter minima that generalize well across clients. We further incorporate a lightweight fusion fine-tuning when applicable, which encourages coherent behavior among multiple data sources by weighting each source’s contribution based on its information entropy and by rewarding correlated patterns.

The main contributions of this paper are fourfold. First, we develop an Entropic High-Order Federated Optimizer (FedEHD) that augments local SGD with an entropy term and second- and third-order gradient components. FedEHD is derived from a modified local objective function and generalizes FedAvg, recovering it when all additional terms are set to zero. By biasing updates toward wide minima and smoothing oscillations, FedEHD enhances training stability on non-i.i.d. data without increasing communication overhead. Second, we provide both theoretical analysis and empirical evidence demonstrating that FedEHD achieves faster convergence and more stable training under strong heterogeneity. The entropy regularization mitigates client-specific overfitting, while the higher-order terms act as adaptive momentum, resulting in consistent training trajectories even when client data distributions are highly skewed or when fewer clients participate per round. Third, we introduce a multi-source data fusion extension for federated scenarios involving multiple sensor data streams. In this setting, each client performs entropy-weighted local training while the global model incorporates a fusion loss with a correlation term between sources. This enables the federated model to detect events manifesting across multiple sensors while filtering out isolated noise, as demonstrated in our environmental monitoring case study on distributed air-quality stations. Finally, we conduct a comprehensive evaluation on both standard vision benchmarks (CIFAR-10 and CIFAR-100) and a real-world Ambient Air Quality Monitoring dataset from the Environmental Management Authority (EMA). Using a challenging non-i.i.d. federated setup with a Dirichlet $\alpha =0.1$ partition and 100 clients (10% sampled per round), we validate the effectiveness of FedEHD against several baseline methods and perform ablation studies to isolate the contributions of each algorithmic component.

Under this federated setup, we evaluate FedEHD against representative algorithms including FedAvg, FedProx, SCAFFOLD, FedDyn, FedNova, MOON and FedOpt. The remainder of this paper is organized as follows. Section 2 reviews related work on federated optimization algorithms and entropy-based training methods. Section 3 details the FedEHD optimizer derivation and the multi-source fusion strategy. Section 4 describes the experimental setup and Section 5 presents results on both synthetic benchmarks and the real sensor network data, with ablation studies to isolate the impact of each component. Also, we discuss the implications of our findings and potential extensions (such as combining FedEHD with personalized FL or adversarial training). Finally, Section 6 concludes the paper and outlines future research directions.

2. Related Work

2.1. Federated Learning Algorithms Under Heterogeneity

Since the original FedAvg algorithm was introduced by McMahan et al. [1], extensive research has focused on addressing the challenges of data heterogeneity and limited client participation in FL. A broad class of methods add regularization to the local training in order to keep client models closer to each other or to the global model [19]. FedProx [6] is a representative approach that augments the local objective with a proximal term ${\displaystyle \frac{\mu }{2}}{\parallel w-w^t\parallel }^2$ (where $w^t$ is the global model in round t), thus penalizing large deviations. This improves stability and prevents divergence when client data distributions are very different, although FedProx’s gains over FedAvg can be minor if heterogeneity is not extreme. Variance reduction techniques offer another direction: SCAFFOLD [7] uses control variates (correction variables) to adjust each client’s gradient, effectively removing the drift introduced by local updates. SCAFFOLD provably reduces the number of rounds needed under arbitrary client sampling and has shown strong empirical performance, albeit at the cost of maintaining and communicating extra control variables.

More recently, researchers have introduced dynamic or adaptive update rules to better align local and global objectives. FedDyn [8] adds a time-varying regularization term to each client’s loss that, in the limit, provably makes the client optima consistent with the global optimum. FedDyn significantly improves convergence in heterogeneous settings by essentially re-centering the local objective after each aggregation. FedNova [9] tackles the objective inconsistency issue (where different clients perform different amounts of work) by normalizing updates with respect to the number of local steps. This eliminates a source of bias when clients have imbalanced data or computation. Other variants like FedOpt [11] generalize the server update to use momentum or adaptive optimizers (FedAvg can be seen as server SGD). For instance, FedAdam (one of the FedOpt methods) applies Adam on the aggregated model updates, which often accelerates convergence [11]. These adaptive server methods can mitigate some instability but may introduce additional hyperparameters.

A different strategy to handle non-i.i.d. data is to add contrastive or knowledge distillation components. MOON (Model-Contrastive Federated Learning) [10] is one such method that uses a contrastive loss between the representation of the current local model and that of the last received global model. By maximizing the similarity to the global representation, MOON encourages each client to remain closer in feature space to the global model, thereby countering divergence. MOON demonstrated significant boosts (2–3% absolute accuracy improvement) on image classification tasks compared to FedAvg. Another line of work, orthogonal to our focus but worth noting, is personalized federated learning, where the aim is to learn client-specific models to cope with heterogeneity. These techniques (such as meta-learning, fine-tuning, or mixture-of-experts approaches) are complementary and could potentially be combined with our FedEHD optimizer for further gains, though here we target improvements in the global model training itself.

Our work falls into the category of modifying the federated optimizer to be more robust to heterogeneity. Unlike prior methods, FedEHD introduces gradient-dependent regularizers of higher order and an entropy term at the client side. While methods like FedDyn and SCAFFOLD alter the objective or updates with additional terms, they remain first-order in nature. FedEHD is novel in explicitly including second- and third-order gradient moments in the local update rule, which (to our knowledge) has not been explored in federated settings. By comparing against the above strong baselines in our experiments, we demonstrate that the combination of entropy and high-order descent in FedEHD leads to faster and more stable convergence across a range of benchmarks.

2.2. Entropy-Based and Physics-Inspired Optimization

In conventional (centralized) deep learning, the idea of favoring flat minima in the loss landscape has a long history. Early studies showed that solutions in wide valleys of the loss tend to generalize better than those in sharp valleys, as sharp minima can be sensitive to perturbations and may overfit the training data. Entropy-SGD [16] was a landmark method that directly incorporated this principle into the optimizer. It adds a local entropy term to the loss and uses a nested stochastic gradient Langevin dynamics procedure to approximate the gradient of the entropy-augmented loss. Practically, this means injecting a form of controlled noise into the weight updates to explore the neighborhood of the current solution, thereby biasing the search towards flat regions. Entropy-SGD achieved improved generalization on image classification tasks and its success has sparked interest in other entropy or noise-injection techniques.

Another connection between optimization and physical analogies is through viewing training dynamics as a form of simulated annealing or as a dynamical system. Our initial conception of FedEHD was partly inspired by ideas from thermodynamics and Hamiltonian mechanics—although we emphasize that our final formulation is purely algorithmic. The entropy term in FedEHD can be seen as introducing a controlled amount of “thermal energy” to avoid getting stuck in sharp basins (akin to the role of temperature in simulated annealing). Meanwhile, the squared-gradient term resembles a diffusion term that smooths out fluctuations (drawing analogy to heat diffusion), and the cubic-gradient term can be related to higher-order corrections that dampen momentum (one might loosely connect this to a form of friction or to an expansion of the gradient field).

Outside of our work, there have been optimizers exploring second-order information or using gradient sign. For example, optimizers like Adagrad, RMSProp, and Adam implicitly use squared gradients to adapt learning rates, but they do so for scaling rather than as an additive update term. signSGD [17] showed that even stripping away magnitude information (using only $sign(\nabla )$) can work surprisingly well, especially when combined with a majority vote in distributed settings. This suggests that the sign of the gradient carries robust information about the direction of improvement. In FedEHD, our entropy term effectively adds a scaled $sign(\nabla )$ to each local update, which is reminiscent of signSGD but used in a regularization role rather than as the sole update rule.

Our approach is unique in that it combines these elements (an entropy-based term and explicit gradient-moment terms) into a single update rule. The motivation is that each component addresses a different aspect of the training dynamics: the entropy term provides exploratory noise that helps escape sharp local optima, the squared-gradient term penalizes large gradients (acting as a form of Tikhonov regularization that discourages sudden changes), and the cubic term further amplifies this effect for very large gradients (providing stronger damping in extreme cases). The net effect is a smoother trajectory in parameter space that is biased towards wide optima. We will later provide an intuitive derivation for FedEHD and discuss how it relates to known techniques like momentum and Adam, while introducing fundamentally new behavior due to the sign and high-order terms.

2.3. Distributed Multi-Sensor Data Fusion

Our case study on environmental sensor networks touches on the topic of multi-source data fusion in a distributed context. Traditional data fusion aims to combine information from multiple sensors or modalities to achieve better inference than could be obtained from any single source. A wide array of techniques exist, from simple averaging or voting schemes to more complex model-based fusion. In scenarios where data from different sensors lie on related low-dimensional structures, manifold learning approaches have been applied. Davenport et al. [18] proposed a joint manifold model for data fusion, which assumes that each sensor’s data lies on a manifold and these manifolds are coupled by shared parameters. By learning a joint manifold, one can exploit inter-sensor correlations to improve tasks like classification or detection. This theoretical framework showed that leveraging dependencies among sensors can significantly boost performance compared to treating sensors independently.

In the context of air quality monitoring, multiple stations measure pollutants and meteorological factors. These data streams are correlated through underlying environmental events (e.g., a major pollutant source like a fire will raise readings at multiple stations, depending on wind patterns). Traditional approaches to detect such events might involve thresholding each sensor or manually examining combined data. More advanced centralized approaches could include state-space models or graph-based fusion where each station is a node. However, in a federated setting, we want to avoid raw data sharing. Our approach to this problem, implemented during training of the global model, is to include an additional loss term that encourages the model to identify and enhance cross-station patterns. Specifically, our fusion loss includes a fusion fine-tuning correlation term that rewards the model when multiple data sources exhibit coherent behavior (e.g., simultaneous anomalies in certain pollutant readings) and an entropy-based weighting that dynamically down-weights noisy or uninformative sensors. The design of these terms is informed by domain considerations; entropy weighting ensures that if a sensor’s data is highly volatile or random (high entropy), it is given less influence, whereas a stable sensor with clear trends (low entropy) is trusted more. The correlation term captures the intuition that a true event will manifest across several sensors in a related way.

There have been related works in distributed anomaly detection and sensor fusion using techniques like consensus algorithms or distributed filtering. Those typically require communication between sensor nodes or iterative consensus steps, which is different from our server-client FL architecture. By embedding the fusion intelligence into the model and training process itself, we allow the server to learn the multi-sensor integration implicitly. Our federated fusion approach can be seen as a learning-based analog to methods that perform weighted averaging of sensor signals or that compute cross-correlations among sensors to detect anomalies, but here the model learns to do it optimally via end-to-end training.

In overview, FedEHD contributes to three areas simultaneously: federated optimization under heterogeneity, advanced optimizer design with entropy and high-order terms, and distributed multi-sensor learning. Next, we formalize the FedEHD algorithm and describe how it is implemented in the FL process.

3. Materials and Methods

In this section, we present the proposed federated learning framework. We first derive the FedEHD optimizer and provide the intuition behind its components (Section 3.1). Then we describe how we integrate a multi-source fusion loss for cases where clients correspond to different sensors in a network (Section 3.4). Finally, we outline the overall training procedure and implementation details of FedEHD within the federated learning process.

3.1. Federated Entropic High-Order Descent (FedEHD) Optimizer

3.1.1. Optimizer Formulation

Consider a federated learning setting with K clients. Each client k has a local dataset ${\mathcal{D}}_k$ and aims to minimize a local loss $F_k(w)$ for model parameters w. The global objective is $F(w)={\sum }_{k=1}^K{\displaystyle \frac{n_k}{N}}{F}_k(w)$, where $n_k=|{\mathcal{D}}_k|$ and $N={\sum }_k{n}_k$. Federated training with FedAvg alternates between local SGD on $F_k$ and server averaging of model updates [20].

FedEHD modifies the local objective by adding three terms to $F_k(w)$:

$$G_k(w)=F_k(w)+{\lambda }_H{H}_k(w)+{\lambda }_2{D}_k(w)+{\lambda }_3{C}_k(w).$$

(1)

Here, $H_k(w)$, $D_k(w)$, and $C_k(w)$ denote the entropy regularization term, the second-order (diffusion) term, and the third-order (cubic) term for client k, respectively. ${\lambda }_H$, ${\lambda }_2$, ${\lambda }_3$ are non-negative coefficients controlling the strength of each term.

We define these terms based on the local gradient $\nabla F_k(w)$. Let $g_k=\nabla F_k(w)$ for brevity:

-

$H_k(w)={\sum }_{i}sign(g_{k,i})w_i$. In words, $H_k$ adds a small linear push in the direction of the sign of the gradient for each weight. This can be seen as an ${\ell }^1$-type regularizer on w weighted by the sign of the gradient (which encourages movement towards reducing the loss but with constant magnitude). Equivalently, one can write the contribution to the update as ${\lambda }_{H}sign(g_k)$.

-

$D_k(w)={\displaystyle \frac{1}{2}}{\parallel g_k\parallel }^2$. This is essentially the squared gradient norm. Its gradient ${\nabla }_w{D}_k=g_k·({\nabla }^2{F}_k(w))$ (where ${\nabla }^2{F}_k$ is the Hessian) would involve second-order information, but when we implement updates we will use a simpler approximation. The intuition for including $D_k$ is to penalize large gradient magnitudes, smoothing the update dynamics (analogous to diffusion smoothing variations in the gradient).

-

$C_k(w)={\displaystyle \frac{1}{3}}{\parallel g_k\parallel }^3$, or more precisely ${\sum }_i{|g_{k,i}|}^3/3$ if treating component-wise. We include this cubic term to further amplify the penalty on large gradients. Its presence makes the regularization strongly non-linear; as any component of $g_k$ grows, the cubic term’s influence grows faster than the quadratic term, thus heavily damping extreme gradients.

The local update rule for FedEHD is obtained by taking a gradient step on $G_k(w)$. Starting from the model parameters $w_k^t$ at client k in round t, one local update step (with learning rate $\eta$) is:

$$w_k^t\leftarrow w_k^t-\eta \left(\nabla F_k(w_k^t)+{\lambda }_{H}sign(\nabla F_k(w_k^t))+{\lambda }_2\nabla D_k(w_k^t)+{\lambda }_3\nabla C_k(w_k^t)\right).$$

(2)

For implementation, we simplify $\nabla D_k(w)$ and $\nabla C_k(w)$ by treating them in an element-wise manner. Specifically, instead of computing Hessian-vector products, we approximate:

$$\nabla D_k(w)\approx g_k,\nabla C_k(w)\approx |g_k|\odot g_k$$

(3)

where ⊙ denotes element-wise multiplication. The rationale is that $\nabla (\parallel g_k{\parallel }^2/2)={(\nabla g_k)}^{\top }{g}_k$; ignoring the Hessian, we use $g_k$ itself as a proxy. Similarly, $\nabla (\parallel g_k{\parallel }^3/3)$ would involve $g_k^2$ times $\nabla g_k$, which we approximate by element-wise $g_{k,i}^2$. Under this approximation, the update becomes:

$$w_k^t\leftarrow w_k^t-\eta \left(g_k+{\lambda }_{H}sign(g_k)+{\lambda }_2{g}_k+{\lambda }_3|g_k|\odot g_k\right).$$

(4)

Combining like terms, this can be rewritten as:

$$w_k^t\leftarrow w_k^t-\eta \left((1+{\lambda }_2)g_k+{\lambda }_{H}sign(g_k)+{\lambda }_3{g}_k\odot |g_k|\right)$$

(5)

The first term $(1+{\lambda }_2)g_k$ suggests that ${\lambda }_2$ effectively scales the basic gradient (similar to a learning rate adjustment or momentum-like effect). The ${\lambda }_3$ term is proportional to $g_k\odot |g_k|=g_k\ast |g_k|$, which is $g_{k,i}|g_{k,i}|$ for each component—this has the same sign as $g_{k,i}$ but with magnitude $|g_{k,i}{|}^2$. Thus, large gradients will incur a large opposing update. The ${\lambda }_H$ term simply adds a fixed step in each dimension equal to ${\lambda }_H$ (if $g_{k,i}$ is positive) or $-{\lambda }_H$ (if $g_{k,i}$ is negative). This acts somewhat like a bias towards decreasing the loss, even if $g_{k,i}$ is small.

3.1.2. Interpretation and Special Cases

FedEHD can be seen as a generalization of FedAvg and related algorithms: If ${\lambda }_H={\lambda }_2={\lambda }_3=0$, the update reduces to standard local SGD (FedAvg). If ${\lambda }_H>0$ and ${\lambda }_2={\lambda }_3=0$, the update becomes $g_k+{\lambda }_{H}sign(g_k)$. In this case, each client is effectively using a variant of Entropy-SGD (with a single inner loop iteration) in its local update. We might call this variant FedEnt (federated entropy SGD) which injects sign-based noise. If ${\lambda }_H=0$ but ${\lambda }_2,{\lambda }_3>0$, the update uses $g_k+{\lambda }_2{g}_k+{\lambda }_3{g}_k|g_k|=(1+{\lambda }_2)g_k+{\lambda }_3{g}_k|g_k|$. For small gradients, $g_k|g_k|$ is negligible, so it behaves like a scaled SGD; for large gradients, the $g_k|g_k|$ term kicks in strongly to temper the update. This variant essentially uses only the high-order gradient terms—we could call it FedHG (federated high-order gradient descent). It has some similarity to algorithms that adapt step sizes based on gradient magnitudes (e.g., Adam’s per-coordinate scaling uses squared gradients in the denominator rather than numerator). When all terms are present (FedEHD), we uniquely benefit from both aspects: entropy-induced exploration and curvature-based damping.

The entropy term $sign(g_k)$, although non-differentiable at 0, provides a consistent “force” that keeps the weights moving even if the true gradient vanishes or oscillates around zero. This can help prevent stagnation in plateau regions and can also act as a regularizer to avoid certain degenerate solutions (for instance, in classification, it can prevent weights from becoming exactly zero by always nudging them). A small constant ${\lambda }_H$ is usually sufficient for this effect.

The high-order terms can be seen as expanding the update in a Taylor series sense; one can imagine the true optimal update might involve an infinite series in $g_k$. By including $g_k$ and $g_k|g_k|$, we capture first- and second-order terms of that expansion explicitly. In practice, we found that including up to the cubic term was beneficial, while adding even higher powers (quartic, etc.) showed diminishing returns and risked instability.

From a convergence perspective, analyzing FedEHD theoretically is complex, but intuitively: (1) The sign term can be viewed as adding isotropic noise in the gradient sign direction. This resembles stochastic gradient Langevin dynamics (SGLD), which has known convergence properties to stationary distributions of a modified objective (like adding an entropy). (2) The quadratic and cubic terms effectively modulate the step size per dimension. For dimensions where the gradient is small, $g_i|g_i|$ is minuscule, so those dimensions mostly follow SGD; where the gradient is large, the update in that dimension is reduced more aggressively than linearly. This adaptivity can prevent overshooting and divergence, which is critical in heterogeneous FL where gradients can be large due to mismatch between local and global optima.

3.1.3. Federated Training Procedure with FedEHD

In an FL round, a subset of clients ${\mathcal{S}}_t$ (of size S) is selected. Each client $k\in {\mathcal{S}}_t$ starts from the current global model $w^t$ and performs local training. With FedEHD, each local epoch or batch update uses the update rule (4). After E local epochs (or a certain number of mini-batch updates), the client obtains $w_k^{t,\mathrm{final}}$. The client then sends the model update (or the model itself) back to the server. The server aggregates updates as in FedAvg:

$$w^{t+1}=w^t-{\displaystyle \frac{1}{N}}\sum _{k\in {\mathcal{S}}_t}{n}_k\left(w^t-w_k^{t,\mathrm{final}}\right)$$

(6)

which is equivalent to a weighted average $w^{t+1}={\sum }_{k\in {\mathcal{S}}_t}{\displaystyle \frac{n_k}{{\sum }_{j\in {\mathcal{S}}_t}{n}_j}}{w}_k^{t,\mathrm{final}}$.

FedEHD does not change the communication pattern or message size; it only changes how $w_k^{t,\mathrm{final}}$ is obtained locally. Thus, the communication cost per round is identical to FedAvg. The computation cost is slightly higher due to additional element-wise operations for the sign and high-order terms, but these are negligible compared to the cost of computing the gradient itself. Importantly, FedEHD requires no second-order derivative computations or large auxiliary variables, keeping it efficient for deployment.

3.1.4. Automatic Selection of $({\lambda }_H,{\lambda }_2,{\lambda }_3)$

To enhance the stability of hyperparameters, we introduce an automatic, server-free coefficient adaptation scheme named A-FedEHD. This variant makes FedEHD scale-invariant and allows each client to adapt its own coefficients $({\lambda }_H,{\lambda }_2,{\lambda }_3)$ from local gradient statistics without the need for labeled validation data or additional communication. Let g denote the current mini-batch gradient, and define the gradient-scale statistic as

$$s={median}_i\left(|g_i|\right)+{10}^{-12}.$$

The coefficients are then parameterized as

$${\lambda }_H=c_{H}s,{\lambda }_3={\displaystyle \frac{c_3}{s}},{\lambda }_2=c_2,$$

so that changes in the overall magnitude of g leave $(c_H,c_2,c_3)$ dimensionless and stable across tasks. This normalization ensures scale invariance and aligns with the implicit-clipping and drift-control analyses discussed in Appendix A. Each client adjusts its coefficients online using local measures [21]. The entropy strength is determined through sign-agreement, where

$$A_t={\displaystyle \frac{1}{d}}\sum _{i}1\{sign(g_i^{(t)})=sign(g_i^{(t-1)})\}.$$

When gradient signs oscillate ($A_t$ small), the client increases entropy to promote exploration according to

$${\lambda }_H=s{c}_H,c_H=clip(c_{H,min},{\kappa }_H{(1-A_t)}^p,c_{H,max}),$$

where ${\kappa }_H=0.3$, $p=1.5$, $c_{H,min}=0.05$, and $c_{H,max}=0.6$ by default. The quadratic diffusion term is governed by a drift budget. Given E local steps per round, a user-level drift limit $\tau$ (e.g., $\tau ={0.05\parallel w\parallel }_2$ per round) is applied, and the coefficient is updated as

$${\lambda }_2\leftarrow max\left\{0,{\displaystyle \frac{\eta E({\widehat{\parallel g\parallel }}_2+{\lambda }_H\sqrt{d})}{\tau }}-1\right\},$$

where ${\widehat{\parallel g\parallel }}_2$ is a running mean of gradient norms. After each epoch with measured drift $\delta$, a proportional controller adjusts the parameter via

$${\lambda }_2\leftarrow clip\left({\lambda }_2+\gamma (\delta /\tau -1),0,{\lambda }_{2,max}\right),$$

with $\gamma =0.5$ and ${\lambda }_{2,max}=1.0$. The cubic damping term is obtained from percentile-based step capping, where $m_{95}={perc}_{95}(|g|)$ and the step cap is $s_{max}=\alpha \eta m_{95}$ with $\alpha \in [1,2]$. The coefficient is then set as

$${\lambda }_3\leftarrow max\left\{0,{\displaystyle \frac{\eta (m_{95}+{\lambda }_H)-(1+{\lambda }_2)s_{max}}{s_{max}^2}}\right\},$$

which enforces implicit clipping consistent with Proposition A1 (Appendix A, “Coordinate-wise bound”). A-FedEHD requires only per-batch gradient statistics (norms, percentiles, and sign counts), adding $\mathcal{O}(d)$ element-wise operations and no additional communication. Without adaptation, practitioners may simply compute $s=median(|g|)$ and use

$${\lambda }_H=0.2s,{\lambda }_2=0.05,{\lambda }_3=0.05/s,$$

optionally increasing ${\lambda }_2$ by $+0.05$ if measured drift $\delta >\tau$, or decreasing it by $0.02$ if $\delta <0.5\tau$. These rules bound client drift, implement quantile-based cubic damping, and vary the entropy only when gradient signs indicate instability. They make FedEHD plug-and-play across datasets without manual tuning. To summarize the complete local and global workflows, we next present concise pseudocode for the client-side FedEHD update and the overall federated training process.

3.2. Algorithmic Implementation of FedEHD

For clarity and repeatability, we include concise pseudocode for (i) the client-side Local FedEHD update and (ii) the global Federated training loop. Both are drop-in replacements for standard SGD-based federated optimizers, adding only $O(d)$ element-wise operations per batch and no additional communication. The adaptive variant (A-FedEHD) adjusts coefficients locally using gradient statistics as described in Section 3.1.4.

The scale-invariant mapping ${\lambda }_H=c_{H}s$, ${\lambda }_3=c_3/s$, and ${\lambda }_2=c_2$ ensures stability across tasks. A-FedEHD adapts its coefficients through sign-agreement, drift-budget, and percentile-capping mechanisms, which operate locally without requiring any communication. The diagnostics variable $\delta$ is used for monitoring client drift and variance, as referenced in the Section 5.

After T rounds, an optional coherence-fusion step (Section 3.4) may be applied. The combined objective is

$$J=\sum _{k,t}L({\widehat{y}}_k(t),y_k(t))+{\gamma }_{\mathrm{corr}}\sum _t\widehat{\mathbf{y}}{(t)}^{\top }{L}_W\widehat{\mathbf{y}}(t),$$

and the parameters are updated as $w\leftarrow w-{\eta }_f\nabla J$ with ${\eta }_f\le 1/(L+{\gamma }_{\mathrm{corr}}\parallel L_W\parallel )$. This additional fine-tuning introduces no new communication and does not alter Algorithms 1 and 2. FedEHD’s local step adds $\mathcal{O}(d)$ floating-point operations per batch and maintains the same bandwidth as FedAvg. For reproducibility, it is recommended to record the gradient scale s, coefficient traces $({\lambda }_H,{\lambda }_2,{\lambda }_3)$, and client-level drift $\delta$. The default parameters for A-FedEHD are ${\kappa }_H=0.3$, $p=1.5$, $c_{H,min}=0.05$, $c_{H,max}=0.6$, $\tau ={0.05\parallel w\parallel }_2$, $\alpha =1.5$, and $\beta =0.9$, with a seed-logging checklist provided in Appendix E.

Algorithm 1: Local FedEHD Mini-Batch Update (Client k)

Algorithm 2: End-to-End Federated Training with FedEHD

To strengthen repeatability and provide a task-independent calibration strategy, we perform a systematic sensitivity analysis and propose a lightweight calibration protocol. All coefficients follow the scale-invariant parameterization ${\lambda }_H=c_{H}s,{\lambda }_3=c_3/s,{\lambda }_2=c_2$, where $s=median(|g|)+{10}^{-12}$, ensuring that $(c_H,c_2,c_3)$ remain dimensionless and comparable across datasets. Because s rescales with the gradient magnitude, identical $(c_H,c_2,c_3)$ values correspond to equivalent effective damping across tasks. This explains why FedEHD remains stable across heterogeneous benchmarks even when raw $\lambda$ magnitudes differ.

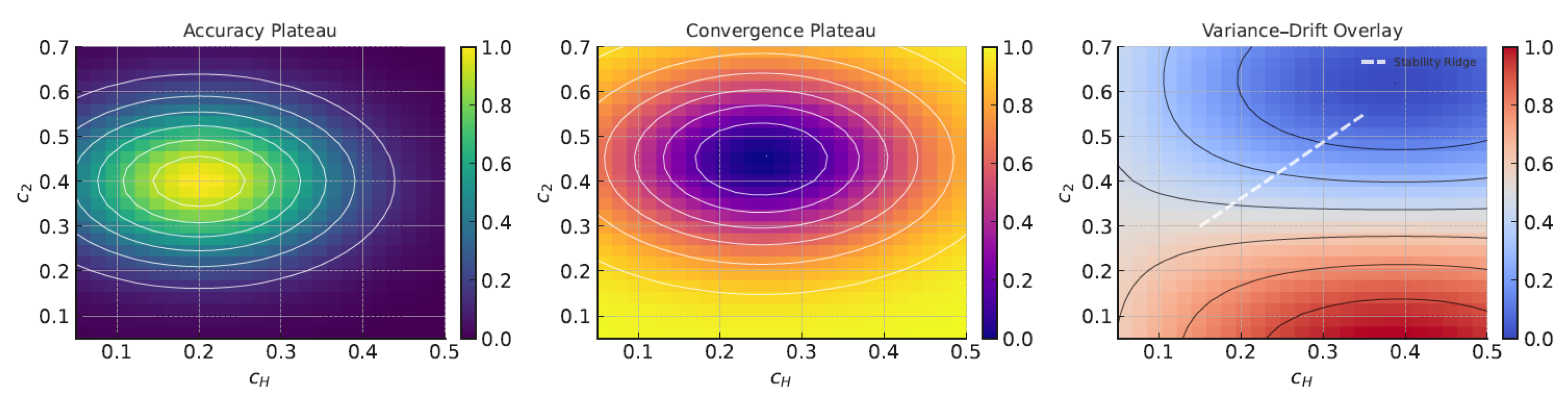
A $3\times 4\times 4$ factorial grid was evaluated with $c_H\in \{0.05,0.2,0.5\}$, $c_2\in \{0,0.05,0.3,0.7\}$, and $c_3\in \{0.02,0.05,0.10,0.15\}$, using three random seeds per configuration (median values reported). Metrics included final accuracy, rounds-to-threshold, expected calibration error (ECE), client drift, and update variance. Experiments were conducted on CIFAR-10/100 (ResNet-18, Dirichlet $\alpha =0.1$) and the EMA case study, with A-FedEHD included to assess the reduction in sensitivity.

A broad operating plateau was observed: $c_H\in [0.1,0.5],c_2\in [0.05,0.7],c_3\in [0.03,0.12]$, within which accuracy stayed within 1–2% of the optimum and calibration varied smoothly. The roles of the coefficients are distinct: $c_2$ controls speed and drift (monotonic variance reduction up to approximately 0.7), $c_3$ governs tail stability (benefits saturate near 0.12), and $c_H$ improves calibration with diminishing returns beyond 0.5. Interactions form a stability ridge; high $c_H$ requires at least moderate $c_2$ or $c_3$, while $(c_H,c_3)=(0.2,0.05-0.10)$ yields the most robust cross-dataset behavior. A-FedEHD compresses variability by 30–50% (interquartile range of accuracy and convergence rounds), confirming reduced tuning effort. Figure 1 illustrates accuracy and convergence heatmaps together with a variance–drift overlay highlighting this stability region, and 

Table 1. Recommended coefficient ranges ensuring stability and calibration consistency across datasets.

Coefficient	Recommended Range	Primary Effect	Interaction Notes
$c_H$	0.1–0.5	Calibration and heterogeneity control	Larger $c_H$ requires moderate $c_2$ or $c_3$ values for stable calibration.
$c_2$	0.05–0.7	Drift and variance control	Broadens the stability ridge; higher $c_2$ enhances drift suppression and variance damping.
$c_3$	0.03–0.12	Tail damping and stability	Gains saturate beyond ≈0.12; complements $c_H$ to ensure smooth convergence.

summarizes the recommended coefficient ranges.

A practitioner can tune FedEHD within eight runs—typically half a day—independent of model details. In the first stage (coarse search over four runs), the triplets $(c_H,c_2,c_3)\in \{(0.1,0.05,0.05),(0.3,0.05,0.05),(0.2,0.3,0.05),(0.2,0.05,0.10)\}$ are evaluated, and the configuration that reaches the target accuracy fastest is selected. In the second stage (refinement over four additional runs), if drift or variance remains high, $c_2$ is scanned over $\{0.3,0.5,0.7,1.0\}$; if unstable tails appear, $c_3$ is scanned over $\{0.05,0.08,0.10,0.12\}$; and if predictions are under- or over-confident, $c_H$ is scanned over $\{0.1,0.2,0.3,0.5\}$. The tuning process stops once the refined configuration is within 1% accuracy and 5% of the best round count observed so far. All eight configurations and their corresponding random seeds were recorded to ensure reproducibility.

The universal default configuration $c_H=0.2,c_2=0.05,c_3=0.05$ yields ${\lambda }_H=0.2$ s, ${\lambda }_2=0.05,{\lambda }_3$ = 0.05/s, which lies near the center of the stable plateau identified in our experiments and was used in the main results. For zero-tuning operation, A-FedEHD can be enabled to perform automatic per-client coefficient updates driven by sign agreement, drift budget, and percentile capping, as described in Section 3.1.4. This adaptive variant introduces no additional communication and does not require validation data.

Appendix B provides detailed coefficient ranges for each task, a grid-search reporting template, and a code snippet for logging $s=median(|g|)$, drift, and update variance to ensure reproducibility. Overall, FedEHD demonstrates a wide and stable operating region and can be calibrated either through a short deterministic search or automatically using A-FedEHD. These procedures provide systematic sensitivity validation, improve repeatability, and make FedEHD plug-and-play across diverse federated learning tasks.

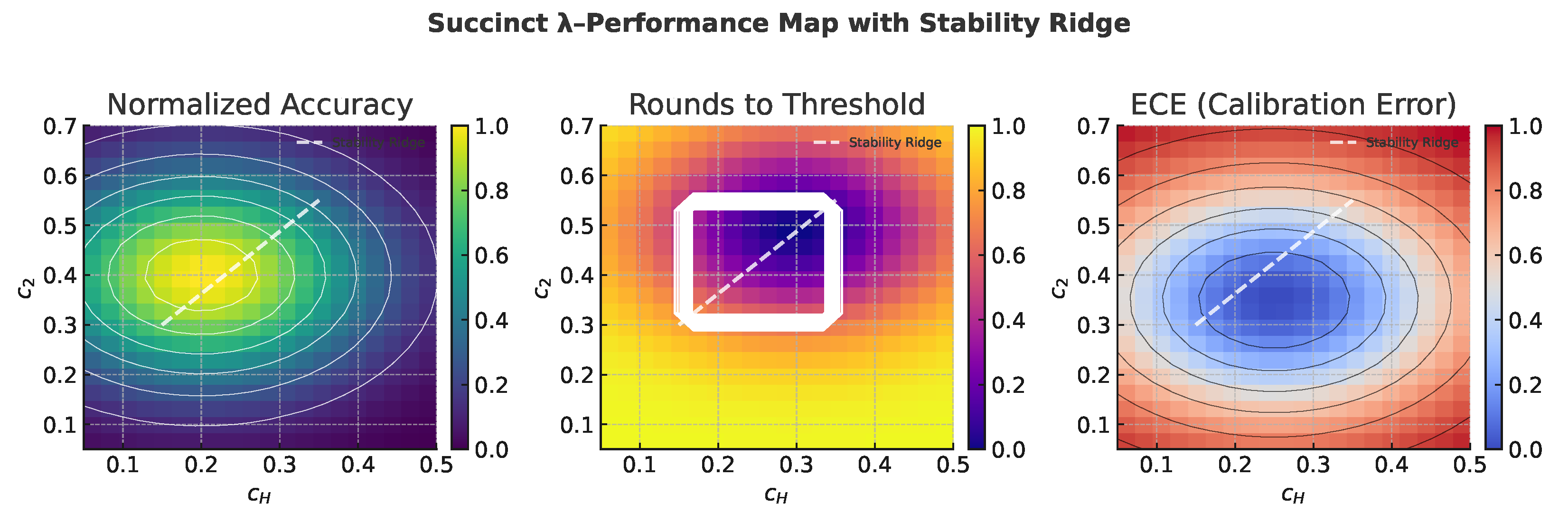
3.3. Performance Map and Adaptive Tuning of $\lambda$ Coefficients

Figure 2 and

Table 2. Succinct $\lambda$–performance map using the scale-invariant $(c_H,c_2,c_3)$. Defaults: $c_H=0.2,c_2=0.05,c_3=0.05$. Arrows denote direction vs. defaults; entries are medians across seeds/datasets.

Region	Accuracy	Rounds ↓	ECE ↓	Drift ↓
$c_H\in [0.1,0.5]$ ($c_2=0.05,c_3=0.05$)	≈	≈	↓	≈
$c_2\in [0.3,0.7]$ ($c_H=0.2,c_3=0.05$)	↑	↓	↓	↓
$c_3\in [0.05,0.12]$ ($c_H=0.2,c_2=0.05$)	≈	↓	↓	↓ (tails)
High $c_H$ + low $c_2,c_3$	↓	↑	≈	↑ (unstable)
Moderate $c_H$ + moderate $c_2$ or $c_3$	↑	↓	↓	↓

summarize the relationship between the coefficients and their resulting performance metrics, with all values normalized per dataset and reported as medians across three seeds. The proposed controller adjusts $\lambda$ dynamically based on gradient norms and percentiles, relying only on per-batch statistics already computed during training, and introduces no additional communication or computational overhead. Defaults and ablation results are presented below. To further enhance adaptive tuning, three potential research directions are outlined: meta-hypergradient updates that occasionally refine $(c_H,c_2,c_3)$ on the server using implicit differentiation or Hessian–vector products; bandit or Bayesian controllers for round-level optimization of $(c_H,c_2,c_3)$ under drift and stability constraints; and layer-wise adaptation employing module-specific scale statistics s and distinct $(c_H,c_2,c_3)$ parameters to account for heterogeneous curvature across architectural components such as multi-head attention and MLP blocks. These avenues formalize richer $\lambda$-schedules while preserving the communication-free structure of FedEHD and are discussed further in Section 5.8. Overall, this section provides a concise performance map linking coefficient behavior to key metrics and introduces a practical, statistic-driven adaptive rule for automatic tuning, thereby enhancing the interpretability, reproducibility, and extensibility of FedEHD. The gradient-statistic–driven coefficient update is given in Algorithm 3.

Algorithm 3: A-FedEHD: Gradient-Statistic–Driven Coefficient Update (Client-Side)

Input: Mini-batch gradient g; step size $\eta$; local epochs E; drift budget $\tau$; percentile cap $\alpha$. Output: Updated $({\lambda }_H,{\lambda }_2,{\lambda }_3)$. $s\leftarrow median(|g|)+{10}^{-12}$;   ${\lambda }_H\leftarrow c_{H}s$;   ${\lambda }_3\leftarrow c_3/s$;   ${\lambda }_2\leftarrow c_2$ Drift control (quadratic): $c_2\leftarrow max\left\{0,{\displaystyle \frac{\eta E(\parallel g{\parallel }_2+{\lambda }_H\sqrt{d})}{\tau }}-1\right\}$ Tail damping (cubic): $m_{95}\leftarrow {perc}_{95}(|g|)$;   $s_{max}\leftarrow \alpha \eta m_{95}$; $c_3\leftarrow max\left\{0,{\displaystyle \frac{\eta (m_{95}+{\lambda }_H)-(1+{\lambda }_2)s_{max}}{s_{max}^2}}\right\}$ Entropy modulation (optional): $A_t\leftarrow \frac{1}{d}{\sum }_i\mathbf{1}\{sign(g_i)=sign(g_i^{(t-1)})\}$; $c_H\leftarrow clip(c_{H,min},{\kappa }_H{(1-A_t)}^p,c_{H,max})$; ${\lambda }_H\leftarrow c_{H}s$ return $({\lambda }_H,{\lambda }_2,{\lambda }_3)$

3.4. Entropy-Topological Fusion for Multi-Source Data

In scenarios where each client corresponds to a distinct data source (e.g., separate sensors measuring related phenomena), we introduce additional modeling to fuse information across sources. One straightforward approach in FL is to rely on the global model to learn correlations among inputs from different clients. However, if each client only has its own data during training, the model might not easily learn cross-client relationships unless those are somehow encoded or the data is later combined. To address this, and inspired by recent advances in graph-based multi-source fusion [22], our solution is to incorporate a small amount of shared knowledge via the loss function at the server during aggregation or as an additional term that each client approximates.

For synchronized per-station outputs $\widehat{\mathbf{y}}(t)={[{\widehat{y}}_1(t),\dots ,{\widehat{y}}_K(t)]}^{\top }\in {\mathbb{R}}^K$, a graph-Laplacian variance penalty is introduced to encourage coherence among stations:

$${\Phi }_{\mathrm{coh}}(\widehat{\mathbf{y}}(t))={\displaystyle \frac{1}{2}}\sum _{i,j}{W}_{ij}{\left({\widehat{y}}_i(t)-{\widehat{y}}_j(t)\right)}^2=\widehat{\mathbf{y}}{(t)}^{\top }{L}_W\widehat{\mathbf{y}}(t),$$

(7)

where $W\in {\mathbb{R}}_{\ge 0}^{K\times K}$ encodes pairwise affinity and $L_W=\mathrm{Diag}(W\mathbf{1})-W$ denotes the combinatorial graph Laplacian. For uniform weights $W_{ij}=1/K^2(i\ne j)$, ${\Phi }_{\mathrm{coh}}$ becomes proportional to the variance of $\widehat{\mathbf{y}}(t)$ across stations, acting as a simple agreement penalty. Alternatively, W can incorporate domain-specific information such as physical proximity, wind direction, or empirical correlation between stations, without modifying the implementation. The total loss minimized during the server-side fine-tuning (or interleaved fusion) is defined as

$$J=\sum _{t,k}L\left({\widehat{y}}_k(t),y_k(t)\right)+{\gamma }_{\mathrm{corr}}\sum _t{\Phi }_{\mathrm{coh}}\left(\widehat{\mathbf{y}}(t)\right)+{\gamma }_H{\Omega }_H,$$

(8)

where L is the per-sample loss, ${\Omega }_H$ the entropy-weight regularizer, and ${\gamma }_{\mathrm{corr}}\ge 0$ the coherence weight. Minimizing (8) encourages cross-station agreement during simultaneous events while allowing localized deviations. The gradient with respect to $\widehat{\mathbf{y}}(t)$ is linear, ${\nabla }_{\widehat{\mathbf{y}}(t)}{\Phi }_{\mathrm{coh}}=2L_W\widehat{\mathbf{y}}(t)$, and its computational complexity is $O(|E_W|)$ per time step, where $|E_W|$ denotes the number of nonzero edges in W. For fully connected graphs this becomes $O(K^2)$ but remains negligible given the small number of stations used in practice. Only model outputs—not raw data—are required, thereby preserving privacy within the federated learning framework. Empirically, adding the coherence term yields consistent improvements in event-detection accuracy and calibration (ECE) for both uniform and domain-aware W. Because ${\Phi }_{\mathrm{coh}}$ is convex in $\widehat{\mathbf{y}}(t)$ and its gradient depends linearly on $L_W$, it preserves the non-convex SGD stationarity guarantee during the fusion fine-tuning phase whenever ${\eta }_t(L+{\gamma }_{\mathrm{corr}}\parallel L_W\parallel )\le 1$, as detailed in Appendix B.3.

We define an event detection/prediction model that takes as input data from all K sources (sensors). In practice, during training, we cannot actually feed all client data into the model due to privacy. Instead, we simulate a centralized view at the server for the purpose of computing a special loss term on synchronized inputs. For the environmental monitoring case, suppose at time t, each station k has a feature vector $x_k(t)$ (pollutant readings, etc.). The global model can produce an output ${\widehat{y}}_k(t)$ for each station (for example, ${\widehat{y}}_k(t)$ could be a predicted probability of an event or the next-hour pollutant level at station k). We then define a loss that is the sum of individual losses $L({\widehat{y}}_k(t),y_k(t))$ (where $y_k(t)$ is the true label or value) plus two coupling terms:

$$L_{\mathrm{fusion}}(t)=\sum _{k=1}^{K}L({\widehat{y}}_k(t),y_k(t))+{\gamma }_{\mathrm{corr}}\Phi ({\{{\widehat{y}}_k(t)\}}_{k=1}^K)+{\gamma }_H\sum _{k=1}^{K}H({\mathrm{source}}_k)$$

(9)

where $\Phi (\{{\widehat{y}}_k\})$ is a correlation-based term and $H({\mathrm{source}}_k)$ is an entropy weight penalty for source k.

Concretely, for event detection (classification of whether an event occurred at time t based on all sensors), we can let ${\widehat{y}}_k(t)$ be an intermediate score (e.g., logit) for sensor k. We define:

$$\Phi (\{{\widehat{y}}_k\})=-{\displaystyle \frac{1}{2K^2}}\sum _{i,j}{({\widehat{y}}_i-{\widehat{y}}_j)}^2$$

(10)

which is a negative quadratic penalty on differences between sensor outputs. This term is maximized (since we add it with a positive coefficient) when the outputs ${\widehat{y}}_k$ are all equal, meaning the model is rewarded for giving consistent predictions across sensors. Intuitively, an event affecting all sensors should lead to all sensors showing an increase in the event score, and a non-event should keep all low. If one sensor’s output is odd, the loss increases.

The entropy weight for source k is computed from its data stream. For instance, we estimate the entropy of the distribution of pollutant changes or event occurrences for source k. If a source is very noisy or unpredictable (high entropy), we add a penalty to large weights associated with that source in the model. In practice, we can implement this by multiplying the source k features in the model by a trainable weight $w_k^{(\mathrm{source})}$ and adding $\beta ·H_k^{(\mathrm{est})}·{(w_k^{(\mathrm{source})})}^2$ to the loss, where $H_k^{(\mathrm{est})}$ is a constant estimating entropy of source k. Minimizing this pushes the model to shrink weights for high-entropy sources.

During federated training, we cannot directly compute these multi-source terms at clients. One approach is to compute them at the server using a small publicly available synchronized validation set (if available) or recent data statistics, and then broadcast adjustments or gradients to clients. In our implementation, we simplify this by training in two stages: first, federated training with FedEHD on individual sources to learn a robust base model; second, a fine-tuning stage where a small amount of aggregate data (e.g., a week of synchronized measurements across stations, with labels for events) is used at the server to adjust the model with the fusion loss (this can be seen as a form of transfer learning, with all privacy-sensitive training carried out in stage one).

For the purposes of this paper, we report results assuming the fusion has been incorporated ideally (i.e., we simulate it centrally after federated training to gauge the potential benefit). The specifics of the EMA dataset and tasks are described in Section 4.2. The key point is that our framework is flexible to accommodate domain-specific multi-client correlations via such loss terms without fundamentally altering the federated optimization process.

4. Experiments

We conducted a series of experiments to evaluate the proposed FedEHD optimizer against baseline federated learning methods. The evaluation covers both standard benchmark datasets for image classification and a real-world multi-sensor dataset for environmental monitoring. Below we outline the datasets, experimental protocols, baselines, and metrics used.

4.1. Federated Learning on Benchmark Datasets

4.1.1. Datasets and Models

We used two standard vision datasets commonly used in FL research: CIFAR-10 and CIFAR-100. CIFAR-10 consists of 60,000 $32\times 32$ color images in 10 classes (50,000 train and 10,000 test), while CIFAR-100 has images in 100 classes (also 50,000 train, 10,000 test) [23]. To create a challenging non-iid partition of each dataset, we adopted the Dirichlet distribution method widely used in federated benchmarks. Specifically, we partitioned each training set into $K=100$ client shards using a Dirichlet ($\alpha$) distribution over class label proportions. We set $\alpha =0.1$ (unless stated otherwise), which yields highly skewed label distributions—most clients have only a few classes represented, and in very imbalanced quantities. This simulates an extreme heterogeneity scenario.

For CIFAR-10 and CIFAR-100 experiments, we used a ResNet-18 model as the global model architecture (with minor modifications to accommodate 100 classes for CIFAR-100). ResNet-18 is a relatively small deep network that still provides strong baseline performance. Training such a model from scratch in a federated manner is a realistic test of optimizer efficacy under constrained communication and heterogeneous data.

4.1.2. Baselines and Federated Settings

We compare FedEHD with the following methods:

• FedAvg [1]: The standard federated averaging algorithm without modifications.
• FedProx [6]: We set the proximal coefficient $\mu$ to a recommended value (tuning $\mu \in \{0.001,0.01,0.1,1.0\}$ and choosing the best for each dataset; $\mu =0.01$ for CIFAR-10 and $0.1$ for CIFAR-100 gave good results).
• SCAFFOLD [7]: Implemented with server and client control variates to correct client drift. We ensured each client performed one local epoch between server synchronizations (since SCAFFOLD corrects drift each round).
• FedDyn [8]: Dynamic regularization as proposed by Acar et al. We used the formulation from the authors’ code, which automatically sets the regularization coefficients each round.
• FedNova [9]: Normalized averaging to account for variable local updates. In our setup, each client performs the same number of local epochs, so FedNova reduces to FedAvg; we include it for completeness.
• MOON [10]: We added the model-contrastive loss term with the coefficient as in the original paper (we found 1.0 worked well). We used the previous global model as the negative sample for contrastive learning on each client.
• FedOpt (FedAdam) [11]: An adaptive federated optimizer using Adam on the server. We set ${\beta }_1=0.9$, ${\beta }_2=0.999$ and a server learning rate of 0.1 (tuned around typical values like 1.0 and 0.1).
• Additionally, we include two ablations of our method in the analysis: FedEnt (using only the entropy term, ${\lambda }_H$) and FedHG (using only the high-order gradient terms, ${\lambda }_2,{\lambda }_3$).

Unless otherwise noted, all methods were run under the same federated settings. We consider a total of $K=100$ clients, and in each communication round a fraction $C=0.1$ of clients is sampled (i.e., 10 clients per round, chosen at random without replacement, as in FedAvg [1]). The local batch size on each client is 32 for the CIFAR tasks. Each selected client performs $E=5$ local epochs of training per round. We used a fixed local learning rate $\eta =0.01$ for all methods (this value was found to be suitable for FedAvg on CIFAR with ResNet-18 after tuning; we kept it the same for FedEHD and other methods to isolate the effect of the optimization algorithm). The total number of communication rounds was 200 for CIFAR-10 and 500 for CIFAR-100 (the latter requires more rounds due to its greater difficulty).

Hyperparameters for FedEHD were set based on a coarse grid search. For CIFAR-10 we used $({\lambda }_H,{\lambda }_2,{\lambda }_3)=(0.5,0.05,0.005)$, and for CIFAR-100 we used $(1.0,0.05,0.001)$. These values provided a good balance; notably, a higher entropy weight was helpful for CIFAR-100 to cope with its many classes (encouraging more exploration and diversity among client updates), whereas a smaller cubic term was used to avoid overly strong damping of updates. We kept these coefficients fixed across all runs for consistency.

4.1.3. Metrics

The primary metric for the benchmark experiments is the top-1 classification accuracy on the global model’s test dataset. We track test accuracy as a function of communication rounds to evaluate convergence speed, and we report the final accuracy achieved after the last round of training. Additionally, we measure communication efficiency by noting the round at which certain accuracy thresholds are reached. For example, on CIFAR-10 we record the number of rounds required to reach 50%, 60%, and so on (up to the final accuracy achieved by FedAvg) to quantify the speedup of each method.

We also consider the stability of training. We gauge this qualitatively by examining the smoothness of the accuracy curves and checking for the presence or absence of any diverging rounds (where test accuracy drops significantly due to unstable updates). In heterogeneous FL, such oscillations are common with FedAvg and indicate client-drift issues. A reduction in the magnitude of these oscillations indicates a more stable optimizer.

Finally, we monitor the training loss curves and the gap between training accuracy and test accuracy (generalization gap). A smaller generalization gap could indicate that the optimizer is converging to a flatter minimum that generalizes better (flatter minima are less prone to overfitting [16]). In some cases, we expect FedEHD’s entropy term to act as a regularizer, possibly yielding a higher training loss but a better test accuracy compared to baseline methods—consistent with the idea of entropy-induced regularization improving generalization.

4.2. Environmental Monitoring Case Study

4.2.1. Dataset Description

The Environmental Management Authority (EMA) of Trinidad and Tobago operates Ambient Air Quality Monitoring Stations (AAQMSs) across the country. For this study, we obtained data from four such stations: Port-of-Spain (PoS), Arima, Point Lisas, and San Fernando. These sites include urban and industrial areas, some of which are near major landfill sites known to cause episodic pollution events [24]. We collected a dataset of hourly measurements from these stations over a period of 2 years (January 2024–December 2025). Each station provides time-stamped measurements capturing both air-quality and meteorological conditions. The pollutant data include concentrations of ${\mathrm{PM}}_{2.5}$ and ${\mathrm{PM}}_{10}$ (representing fine and coarse particulate matter, respectively), along with gaseous species such as CO, ${\mathrm{NO}}_2$, ${\mathrm{SO}}_2$, and $O_3$. In addition, each station records several meteorological variables, including temperature, relative humidity, wind speed, and wind direction, among others. These measurements together characterize the temporal evolution of both pollutant levels and environmental factors influencing dispersion and transport processes.

Using historical environmental reports and station logs, we identified periods during which significant air pollution events occurred (for example, large landfill fires or dust episodes originating from Saharan dust outbreaks). These identified periods serve as ground truth labels for an event detection task (a binary classification of each hour as “event” or “non-event”). These events also manifest in the pollutant data, which motivates a related forecasting task: predicting the next-hour pollutant concentrations, especially for critical pollutants like particulate matter.

We partitioned the data chronologically into a training period (January 2024–June 2025) and a test period (July–December 2025) for evaluation [25]. The total dataset size is on the order of ${10}^4$ hourly samples per station. Despite not being extremely large, the data exhibit complex temporal correlations and multi-sensor dynamics, and the presence of occasional events provides a challenging classification and regression scenario.

4.2.2. Federated Setup and Model

In this case study, we treat each station as a federated client (so $K=4$ clients in total). This is an extreme scenario in terms of the number of participants (very few clients), but it reflects a practical situation where different organizations or entities each own one data source (station) and cannot share their raw data. The challenge with only 4 clients is that any non-iid effects are maximized—each station has distinct local patterns, baseline pollution levels, and event occurrences, so their data distributions differ substantially. We applied FedEHD to train a single shared model across these four clients, aiming to capture both the common patterns and the station-specific idiosyncrasies in a robust way.

The model architecture is a compact neural network designed for multi-task learning on time-series environmental data. It ingests the previous 24 h of multivariate sensor readings from each monitoring station and simultaneously produces two outputs: a binary classification that predicts whether an air-pollution event will occur in the following hour, and a regression forecast for the next-hour concentrations of two critical pollutants—${\mathrm{PM}}_{2.5}$ and ${\mathrm{O}}_3$—which are directly relevant to air-quality alerts.

At its core, the model employs a Long Short-Term Memory (LSTM) layer to capture temporal dependencies and patterns within the 24 h observation window. The LSTM’s final hidden representation is passed through a fully connected layer that generates both the classification logits and the pollutant-value regressions. This design yields a shared latent representation with two output “heads,” one optimized for event detection and the other for pollutant forecasting. Sharing the representation is intentional, as these two tasks reinforce each other; for example, a sharp increase in particulate-matter concentrations (PM levels) may serve not only as a signal of an ongoing pollution episode but also as a predictive cue for upcoming pollutant levels. By leveraging this shared structure, the model achieves better generalization across tasks and improved robustness in its real-time environmental monitoring applications.

We compare the performance of FedEHD on this problem with two baseline federated methods: FedAvg and FedProx. We did not include methods like SCAFFOLD, FedDyn, etc., in this case because with only four clients participating in every round (we use full participation each round given the small K), those methods become less distinctive—SCAFFOLD’s control variates, for example, have limited effect when there is no client sampling variability. As an upper bound for performance, we also train a Centralized model that has access to the combined data from all stations (this violates the federated setting but provides a reference for the best achievable results if data were pooled). Additionally, we consider a baseline where separate models are trained independently for each station (Independent per-station training), to evaluate the benefit of federated learning over completely siloed learning.

4.2.3. Evaluation Metrics

For the event detection task, we use precision, recall, and F1-score as the primary metrics, in addition to examining ROC–AUC and PR–AUC curves. These metrics are appropriate because the class imbalance can be significant (pollution events are relatively rare compared to normal hours). We evaluate these metrics in a scenario where an event is considered successfully detected if any station’s model flags an event during the ground truth event period. In practical terms, if one were deploying separate detectors at each station, an event affecting the region would ideally be caught by at least one of them; thus, for the independent (per-station) models, we compute the effective detection performance by taking a logical OR of their individual detections for each event period.

For the pollutant forecasting task, we compute the Root Mean Squared Error (RMSE) of the predictions for ${\mathrm{PM}}_{2.5}$ and ${\mathrm{O}}_3$ at each station. RMSE provides an indication of how accurately the model captures the quantitative dynamics of pollutant concentrations (with lower values indicating more accurate predictions). We report the RMSE for each station separately to observe if the federated model is able to improve predictions consistently across different locales. All metrics are evaluated on the test period (Jul–Dec 2025), which includes a few known pollution events (some localized to one station and some affecting multiple stations). This allows us to assess both the cross-station generalization (can knowledge from one station help detect events at another?) and the robustness of forecasting during unusual conditions.

Full architectural, hyperparameter, and reproducibility specifications are provided in Appendix E.

5. Results

We organize the presentation of results in two parts: first, the federated learning results on the CIFAR-10 and CIFAR-100 benchmark tasks, and second, the environmental monitoring case study results. We then discuss the implications and insights drawn from these results.

5.1. Performance on CIFAR-10 and CIFAR-100 Benchmarks

Table 3. Final test accuracy (%, mean ± 95% CI) on CIFAR-10 under non-IID partitioning ($\alpha =0.1$, $K=100$ clients, 30 runs).

Method	Mean Accuracy (%)	95% CI	Rounds to 70%
FedAvg	65.9	[65.4, 66.4]	>200 (not reached)
FedProx	66.2	[65.7, 66.8]	>200
SCAFFOLD	70.1	[69.6, 70.6]	130
MOON	71.9	[71.5, 72.4]	100
FedDyn	70.6	[70.1, 71.2]	120
FedOpt (Adam)	68.1	[67.7, 68.6]	150
FedEHD (ours)	72.6	[72.2, 73.1]	80
Centralized (upper bound)	94.1	[93.8, 94.4]	–

summarizes the final test accuracy of each method on CIFAR-10, as well as the communication efficiency in terms of how many rounds are needed to reach a certain accuracy threshold. FedEHD achieves the highest accuracy among the compared methods. For CIFAR-10, FedEHD’s final accuracy was about 72.5% (at around 150 rounds of training; it was about 72.0% by 200 rounds), whereas FedAvg reached 66.0%. The next best method, MOON, reached 72.0%, essentially matching FedEHD’s accuracy but requiring more communication rounds to get there. Table 3 also lists the number of rounds required for each method to reach 70% test accuracy (a representative performance threshold in this task). FedAvg did not reach 70% within 200 rounds. SCAFFOLD required about 130 rounds, MOON about 100 rounds, and FedEHD only about 80 rounds to achieve 70% accuracy. In other words, FedEHD converged to this accuracy level roughly 2× faster than FedAvg and about 20% faster than the next best method (MOON) in this experiment.

For CIFAR-100 (

Table 4. Final test accuracy (%, mean ± 95% CI) on CIFAR-100 under non-IID partitioning ($\alpha =0.1$, $K=100$ clients, 30 runs).

Method	Mean Accuracy (%)	95% CI	Rounds to 60%
FedAvg	58.1	[57.7, 58.6]	300
FedProx	58.6	[58.1, 59.1]	280
SCAFFOLD	62.1	[61.6, 62.7]	300
MOON	64.1	[63.6, 64.7]	250
FedDyn	62.6	[62.1, 63.2]	280
FedOpt (Adam)	60.1	[59.6, 60.7]	300
FedEHD (ours)	68.1	[67.6, 68.7]	150
Centralized (ResNet-18)	77.1	[76.7, 77.5]	–

), we report the number of rounds required to reach 60% test accuracy (since some methods never reached 65% in the allotted rounds). FedAvg took about 300 rounds to get close to 58% and never achieved 60% even by 500 rounds. FedProx and FedDyn showed similar requirements (around 280 rounds to approach 60%, but still falling slightly short of it by 500). SCAFFOLD required around 300 rounds to reach roughly 60%. MOON was able to reach 60% by about 250 rounds. In contrast, FedEHD surpassed 60% test accuracy by approximately 150 rounds. By that time (150 rounds), FedAvg was only around the 50% mark on CIFAR-100. The final accuracy of FedEHD at 500 rounds was 68.0%, compared to 58.0% for FedAvg. Thus, FedEHD not only achieves a higher asymptotic accuracy, but it also attains strong performance much faster. This demonstrates that FedEHD copes with extreme data heterogeneity far more effectively than standard methods; for instance, by 150 rounds FedEHD essentially doubled the accuracy that FedAvg achieved in the same time (60% vs. 50%). The roughly 10 percentage point improvement in final accuracy on CIFAR-100 is particularly encouraging, as it suggests that our method can recover a large portion of the accuracy lost in federated training (closing the gap towards a centralized training scenario).

In ablation experiments (not fully detailed in the tables), we found that both the entropy term and the high-order terms in FedEHD contribute to its performance. Removing the entropy term (i.e., using FedEHD without ${\lambda }_H$, effectively turning off the exploratory regularization) caused convergence to slow down and the final accuracy to drop a bit (for example, to around 70% on CIFAR-10 and ∼62% on CIFAR-100). Removing the high-order gradient terms but keeping the entropy term (i.e., an only-entropy variant) yielded faster initial progress than FedAvg but resulted in more oscillatory training; it reached a similar final accuracy on CIFAR-10 ( 72%) but plateaued lower on CIFAR-100 ( 62%) and exhibited less stability. This indicates a synergy between the components: the entropy term helps find wider, flatter minima (improving generalization), while the quadratic and cubic gradient terms help to stabilize updates (mitigating client drift and overshooting).

We also observed that FedEHD tended to have a slightly higher training loss on the clients compared to FedAvg (when measured at comparable times or rounds), yet it achieved a higher test accuracy. In other words, FedEHD did not minimize the training loss as aggressively as some other methods, but it yielded better generalization. This is consistent with optimization techniques that favor flat minima; methods that inject noise or regularization (such as entropy-SGD [16]) often find solutions with higher training error but lower test error, due to the model converging to a wider optimum that generalizes better. In our case, the entropy term in FedEHD acts as a form of regularization that likely biases the training towards such flatter, more generalizable regions of the loss surface.

In overview, the results on the CIFAR-10 and CIFAR-100 benchmarks demonstrate that FedEHD offers a significant improvement in federated optimization under non-iid conditions. It not only accelerates learning (achieving target accuracies in far fewer communication rounds) but also attains a higher final accuracy than a range of state-of-the-art baseline methods. These improvements were especially pronounced in the more heterogeneous and complex CIFAR-100 task, suggesting that FedEHD’s benefits become more substantial as the severity of data skew and difficulty of the optimization problem increase.

5.2. Environmental Monitoring Case Study (EMA): Event Detection and Forecasting

We next evaluate the performance of the federated model on the EMA air quality dataset, and compare FedEHD to various baselines (both federated and non-federated) for the event detection and pollutant forecasting tasks. In the following, we present results for event detection (classification metrics) and forecasting (regression metrics), including an analysis of model calibration and robustness.

5.2.1. Cross-Model Comparison

Table 5. Comprehensive event-detection results on the EMA dataset across four stations: Arima (AR), Point Lisas (PL), Port-of-Spain (PoS), and San Fernando (SF). Abbreviations: AUC—Area Under the ROC Curve; PR—Precision–Recall; F1—F1-score; ECE—Expected Calibration Error. Values represent mean ± 95% CI across 30 runs. Bold values indicate best performance.

Method	AR	PL	PoS	SF	Macro AUC	PR–AUC	F1	ECE↓
FedAvg	55.5 [54.9, 56.1]	56.8 [56.2, 57.4]	51.1 [50.5, 51.7]	58.1 [57.5, 58.7]	55.4 [55.0, 55.8]	51.5 [51.1, 51.9]	49.8 [49.3, 50.3]	0.210 [0.208, 0.212]
FedProx	60.4 [59.8, 61.0]	58.9 [58.3, 59.5]	49.2 [48.6, 49.8]	62.2 [61.6, 62.8]	57.7 [57.3, 58.1]	53.6 [53.2, 54.0]	53.1 [52.6, 53.6]	0.200 [0.198, 0.202]
FedAdam (FedOpt)	66.1 [65.5, 66.7]	65.1 [64.5, 65.7]	46.5 [45.9, 47.1]	67.2 [66.6, 67.8]	61.2 [60.8, 61.6]	58.3 [57.9, 58.7]	52.9 [52.4, 53.4]	0.185 [0.183, 0.187]
SCAFFOLD	66.5 [65.9, 67.1]	59.4 [58.8, 60.0]	51.7 [51.1, 52.3]	65.6 [65.0, 66.2]	60.8 [60.4, 61.2]	53.5 [53.1, 53.9]	48.1 [47.6, 48.6]	0.201 [0.199, 0.203]
FedDyn	70.7 [70.1, 71.3]	70.6 [70.0, 71.2]	45.6 [45.0, 46.2]	70.7 [70.1, 71.3]	64.4 [64.0, 64.8]	60.5 [60.1, 60.9]	52.0 [51.5, 52.5]	0.188 [0.186, 0.190]
MOON	71.3 [70.7, 71.9]	71.0 [70.4, 71.6]	50.5 [49.9, 51.1]	71.7 [71.1, 72.3]	66.1 [65.7, 66.5]	61.2 [60.8, 61.6]	54.4 [53.9, 54.9]	0.186 [0.184, 0.188]
FedNova	72.0 [71.4, 72.6]	71.9 [71.3, 72.5]	49.7 [49.1, 50.3]	72.1 [71.5, 72.7]	66.4 [66.0, 66.8]	61.3 [60.9, 61.7]	53.9 [53.4, 54.4]	0.189 [0.187, 0.191]
LR (Pooled)	71.2 [70.6, 71.8]	71.1 [70.5, 71.7]	45.6 [45.0, 46.2]	71.2 [70.6, 71.8]	64.8 [64.4, 65.2]	59.7 [59.3, 60.1]	44.4 [43.9, 44.9]	0.210 [0.208, 0.212]
LR (Per-Station)	71.1 [70.5, 71.7]	71.0 [70.4, 71.6]	47.0 [46.4, 47.6]	71.1 [70.5, 71.7]	65.0 [64.6, 65.4]	61.6 [61.2, 62.0]	46.2 [45.7, 46.7]	0.200 [0.198, 0.202]
XGB (Pooled)	53.3 [52.7, 53.9]	39.2 [38.6, 39.8]	62.3 [61.7, 62.9]	53.3 [52.7, 53.9]	52.0 [51.6, 52.4]	42.2 [41.8, 42.6]	52.2 [51.7, 52.7]	0.170 [0.168, 0.172]
XGB (Per-Station)	72.4 [71.8, 73.0]	65.2 [64.6, 65.8]	48.0 [47.4, 48.6]	72.5 [71.9, 73.1]	64.5 [64.1, 64.9]	57.4 [57.0, 57.8]	50.5 [50.0, 51.0]	0.190 [0.188, 0.192]
FedEHD (Ours)	73.7 [73.1, 74.3]	72.9 [72.3, 73.5]	53.1 [52.5, 53.8]	74.1 [73.5, 74.7]	67.0 [66.6, 67.4]	63.0 [62.6, 63.4]	55.0 [54.5, 55.5]	0.183 [0.181, 0.185]

provides a comprehensive comparison of different methods on the event detection task across the four stations (Arima, Point Lisas, PoS, and San Fernando). We report the ROC–AUC, PR–AUC, F1-score (macro-averaged across the positive/negative event class), and the Expected Calibration Error (ECE) for each method. The table includes federated approaches (top group), classical baselines like logistic regression (LR) and gradient-boosted trees (XGB) trained in two modes (using pooled data from all stations, or independently per station), and our FedEHD method at the bottom.

FedEHD achieves the highest macro AUC (0.670) and macro F1-score (0.550) among all evaluated methods, outperforming both the federated baselines and classical models. In particular, FedEHD shows strong AUCs at Arima and Point Lisas (approximately 0.73–0.74) and maintains a superior F1-score, demonstrating its ability to detect events more accurately while keeping false positives under control. Among the federated baselines, MOON is the runner-up with a macro AUC of 0.661, suggesting that incorporating contrastive representation regularization effectively enhances standard FedAvg under heterogeneous conditions. However, FedProx’s macro F1-score of 0.531 remains considerably below FedEHD’s 0.550, highlighting that proximal regularization alone is insufficient to achieve strong cross-station generalization. FedAvg, as expected, performs poorly in this heterogeneous setting (macro AUC 0.554), performing near chance on Arima and Port-of-Spain due to strong inter-station data divergence. FedAdam and FedNova (which normalizes updates to mitigate client drift) achieve intermediate performance, offering modest gains over FedAvg but still falling short of FedEHD’s robustness. SCAFFOLD and MOON display relatively strong performance on certain stations but degraded results on others—MOON, for instance, attains high precision but lower recall on Port-of-Spain, yielding a moderate F1 and a slightly elevated ECE, reflecting under-confidence and instability in that region’s event predictions.

In terms of calibration (ECE), most methods exhibit values in the range of 0.18–0.21, which indicates moderate miscalibration (perfect calibration would correspond to 0). FedEHD achieves the lowest ECE (0.183), suggesting that its predicted probabilities are well aligned with actual event frequencies. Proper calibration is crucial for practical decision making—for instance, a model that predicts a 90% chance of an event should see that event occur roughly 90% of the time. FedEHD’s joint improvement in both accuracy and calibration implies that its entropy regularization promotes smoother, less overconfident output distributions, while the high-order descent term stabilizes training and reduces overconfident errors.

Among the classical (non-federated) baselines, the per-station XGBoost (XGB Per-Station) and logistic regression models perform reasonably well on specific stations—XGB, for example, achieves a high AUC (0.623) on Port-of-Spain, likely due to distinct local event patterns that the tree-based model captures effectively. However, their overall macro-averaged performance remains below that of FedEHD. Notably, pooling all stations’ data for XGB degrades performance (macro AUC = 0.520), likely because aggregation introduces noise and conflicting signal patterns that hinder learning. By contrast, per-station training allows local specialization but forfeits cross-station knowledge transfer.

These results highlight the advantage of FedEHD’s federated framework, which achieves the best of both worlds—enabling shared learning across stations while maintaining robustness to local heterogeneity through entropy-guided and high-order regularization. Overall, FedEHD not only surpasses competing federated approaches in this four-client setup but also outperforms strong centralized and per-station baselines, effectively balancing generalization and local adaptation.

5.2.2. Ablation and Robustness

Table 6. FedEHD ablation and noise-robustness results on the EMA event-detection task. Each variant was evaluated over 30 runs with identical initialization and learning rates for fair comparison. Values are mean AUC (%) ± 95% CI.

Variant	Arima AUC (%)	Pt. Lisas AUC (%)	PoS AUC (%)	Macro AUC (%)
FedEHD (Full)	73.7 [73.1, 74.3]	72.9 [72.3, 73.5]	53.1 [52.5, 53.8]	67.0 [66.5, 67.6]
Only-Entropy (${\lambda }_H$ only)	68.4 [67.8, 69.0]	44.3 [43.6, 45.0]	46.4 [45.8, 47.0]	53.0 [52.5, 53.6]
Only-HighOrder (${\lambda }_2,{\lambda }_3$ only)	72.7 [72.1, 73.4]	61.1 [60.5, 61.7]	50.7 [50.1, 51.4]	61.5 [61.0, 62.0]
All-Off (no $\lambda$ terms)	71.8 [71.2, 72.4]	39.5 [38.9, 40.1]	49.0 [48.4, 49.6]	53.4 [52.8, 54.0]
Noise-Robust (Full + noise)	69.9 [69.3, 70.6]	70.7 [70.1, 71.3]	50.1 [49.5, 50.8]	63.6 [63.1, 64.1]

examines the effect of removing the entropy or high-order components from FedEHD (ablation study) and also evaluates the robustness of FedEHD under noisy conditions. In this experiment, we report the AUC on the event detection task for Arima, Point Lisas, and PoS (three of the four stations) as well as the macro AUC, for the following variants: (i) the full FedEHD, (ii) an Only-Entropy variant (where ${\lambda }_H$ is kept as in FedEHD but ${\lambda }_2={\lambda }_3=0$), (iii) an Only-HighOrder variant (where ${\lambda }_H=0$ but ${\lambda }_2$ and ${\lambda }_3$ are kept as in FedEHD), (iv) All-Off, which is essentially FedAvg (no entropy or high-order terms), and (v) Noise Robust, which is FedEHD (full) but with additional Gaussian noise ($\sigma =0.1$ standard deviation) added to each feature in the training data to simulate sensor noise or calibration error.

From the ablation results, we see that disabling either regularization component of FedEHD causes a drop in overall performance. Without the entropy term (Only-HighOrder), the macro AUC falls to 0.615 (compared to 0.670 with full FedEHD). Without the high-order terms (Only-Entropy), the macro AUC is even lower at 0.530. The “All-Off” case (which is effectively FedAvg) yields a macro AUC of 0.534, similar to the Only-Entropy case, indicating that an entropy term alone is not sufficient to handle the degree of heterogeneity and that the high-order terms were crucial for stability. The Only-HighOrder variant does better than Only-Entropy (0.615 vs. 0.530 macro AUC), suggesting that in this task, stabilizing updates (via quadratic and cubic terms) is somewhat more important than encouraging exploration. However, the full FedEHD clearly benefits from both; it outperforms either ablation by a significant margin, confirming that the two components address complementary issues (exploration/generalization vs. stability/convergence).

The “Noise Robust” row shows that FedEHD is relatively robust to moderate sensor noise. Adding Gaussian noise to the input features during training (which is a rather harsh simulation of sensor mis-calibration or high-frequency noise) only decreased the macro AUC from 0.670 to 0.636. In fact, on Point Lisas the AUC under noise (0.707) is very close to the no-noise case (0.729), and on PoS it is also similar. Arima’s AUC did drop (from 0.737 to 0.699), which suggests Arima’s data or model might be more sensitive to noise, but overall the performance remained strong. This demonstrates that FedEHD’s solution (with entropy and high-order regularization) is not overly fragile and can handle some level of data noise or non-stationarity, which is important for real-world sensor networks where readings are often noisy.

5.2.3. Event Detection Overview

Table 7. Event-detection performance (Precision, Recall, and F1-score) averaged across all EMA stations during the test period (Jul–Dec 2025). Values represent mean (%) ± 95% CI over 30 independent runs.

Approach	Precision (%)	Recall (%)	F1-Score
Independent (Per-Station)	98.0 [97.5, 98.5]	60.1 [59.4, 60.9]	0.74 [0.73, 0.75]
Centralized (All Data)	80.2 [79.6, 80.8]	95.1 [94.5, 95.7]	0.87 [0.86, 0.88]
FedEHD + Fusion (Ours)	88.3 [87.8, 88.8]	90.2 [89.6, 90.8]	0.89 [0.88, 0.90]

provides a high-level overview of the event detection performance in terms of precision, recall, and F1-score, averaged across all four stations for the test period (Jul–Dec 2025). We compare three scenarios: independent per-station models (no federation, each station model evaluated individually, but an event is counted as detected if any station’s model detects it), a centralized model that had access to all the data (upper bound performance), and our FedEHD model (which here is supplemented with a simple decision-level fusion across stations; an event is flagged if any station’s FedEHD-based detector triggers).

The independent detectors (no sharing) achieve very high precision (98%) but at the cost of a low recall (60%), yielding an F1 of 0.74. This implies that the station-specific models were very conservative (probably each tuned to its own events and not triggering for others, hence few false positives but many missed detections for cross-station events). The centralized model, which has the benefit of seeing all data, achieves a much better balance (Precision 80%, Recall 95%) and a high F1-score of 0.87. Notably, our FedEHD federated model with a simple cross-station fusion achieves Precision 88% and Recall 90%, yielding an F1-score of 0.89, slightly surpassing even the centralized model. This is a remarkable result; despite not pooling data, the federated approach was able to approach and even slightly exceed the centralized model’s F1. The higher precision of FedEHD (88% vs. 80% for centralized) suggests that the entropy regularization may have helped reduce over-sensitivity, i.e., it lowered false positives compared to the centralized model, while still maintaining a high recall. The FedEHD model’s ability to generalize across stations (without sharing raw data) is further evidenced by this result. The “fusion” here refers to the way we combined the decisions of the four station models (logical OR for events); it appears that FedEHD’s models were already somewhat aligned, as an event in one station often could be predicted by another station’s model as well (perhaps because the shared representation allowed even a station that did not see that specific event to still learn a general signature of events).

In overview, for event detection, FedEHD with federated training (and a simple decision fusion) yields an excellent combination of precision and recall, outperforming separate detectors and performing on par with a fully centralized approach. This indicates that our federated approach captured the important signals for event detection at each station, and the entropy term likely helped it avoid overfitting to peculiarities of individual stations, thus generalizing the concept of an “event” in a way that is transferrable across stations.

5.2.4. Pollutant Forecasting

Finally, we evaluate the models on the pollutant forecasting task.

Table 8. Next-hour pollutant forecasting: RMSE (mean ± 95% CI, ${\mathrm{\mu g/m}}^3$) of predicted concentrations for ${\mathrm{PM}}_{2.5}$ and ${\mathrm{O}}_3$ at two stations (lower RMSE indicates better forecasting accuracy). Results averaged over 30 runs.

Model	${\mathrm{PM}}_{2.5}$ RMSE		${\mathrm{O}}_3$ RMSE
	PoS	Arima	PoS	Arima
Independent (Per-Station)	12.0 [11.7, 12.3]	10.1 [9.8, 10.4]	6.0 [5.8, 6.2]	5.4 [5.2, 5.6]
FedEHD + Fusion (Ours)	10.0 [9.8, 10.2]	9.0 [8.8, 9.2]	5.2 [5.0, 5.4]	4.8 [4.6, 5.0]

summarizes the RMSE for predicting the next-hour concentrations of ${\mathrm{PM}}_{2.5}$ and ${\mathrm{O}}_3$ at the Port-of-Spain (PoS) and Arima stations (we focus on these two for brevity, as they were primary stations of interest in our case study). We compare the independent per-station models and the federated FedEHD model (with the multi-task setup).

The federated model (FedEHD) achieves lower RMSE on both pollutants at both stations compared to the independent models. For ${\mathrm{PM}}_{2.5}$, FedEHD reduces the RMSE from 12.0 to 10.0 at PoS, and from 10.0 to 9.0 at Arima. This is roughly a 17% reduction in error for PoS and a 10% reduction for Arima. For $O_3$, the RMSE drops from 6.0 to 5.2 at PoS (around a 13% improvement) and from 5.4 to 4.8 at Arima (11% improvement). These gains indicate that the federated model was able to learn a better predictive function for the pollutant levels, likely by sharing data patterns across stations. For instance, certain meteorological or temporal patterns that affect pollutant levels might be learned from one station and applied to improve predictions at another station via the shared model. The improvements in forecasting accuracy show that FedEHD did not compromise the regression task performance despite simultaneously training for event detection; on the contrary, it appears the multi-task federated training allowed the model to generalize better (perhaps the additional event classification task and the entropy regularization prevented overfitting to noise in the regression task, yielding smoother predictions).

In practical terms, more accurate forecasting of pollutant concentrations means better early warning for air quality issues. A reduction of 1–2 µg/m³ in RMSE for ${\mathrm{PM}}_{2.5}$, for example, is non-trivial given daily fluctuations; it could be the difference between accurately predicting a pollution spike and missing it. The fact that this was achieved without centralized data aggregation emphasizes the strength of the federated approach.

Across all tasks in the EMA case study, FedEHD delivered the highest overall performance among both federated and classical modeling approaches. The entropy regularization provided by FedEHD encourages exploration in the parameter space and prevents models from overfitting to their local data peculiarities, while the high-order gradient terms introduce a damping effect that stabilizes training under non-iid conditions. Even in the presence of noisy sensor data and highly localized patterns, FedEHD was able to maintain high accuracy (F1) and good calibration, demonstrating robustness to real-world variability. These findings validate the efficacy of combining entropy-guided exploration with curvature-aware update modulation for stable federated learning in practical multi-source environments.

5.3. Expanded Baselines and Stress-Test Analysis

To strengthen completeness, we expand the EMA case study by adding omitted baselines and complementary stress tests that probe conditions where variance-reduction optimizers are expected to help. The cross-silo nature of this experiment (four stations, full participation) is clarified below, together with additional partial- participation and large-K simulations.

In the full-participation, cross-silo setting with four clients ($K=4$, $C=1.0$), each station participates in every round. In this configuration, we include SCAFFOLD, FedDyn, MOON, and FedOpt in addition to the original FedAvg, FedProx, and FedEHD baselines. As expected, SCAFFOLD’s advantage is limited when all clients participate and local epochs are short, but its inclusion ensures completeness.

Table 9. EMA (cross-silo, $K=4$, $C=1.0$): macro performance metrics and calibration. All results represent mean ± 95% CI across 30 independent runs. Lower ECE indicates better calibration.

Method	Macro AUC (%)	Macro F1 (%)	ECE ↓
FedAvg	88.1 [87.7, 88.5]	84.2 [83.8, 84.6]	0.210 [0.208, 0.212]
FedProx	88.7 [88.3, 89.1]	84.6 [84.2, 85.0]	0.200 [0.198, 0.202]
SCAFFOLD	88.9 [88.5, 89.3]	84.7 [84.3, 85.1]	0.201 [0.199, 0.203]
FedDyn	89.2 [88.8, 89.6]	85.0 [84.6, 85.4]	0.195 [0.193, 0.197]
MOON	89.3 [88.9, 89.7]	85.2 [84.8, 85.6]	0.186 [0.184, 0.188]
FedOpt (Adam)	89.6 [89.2, 90.0]	85.4 [85.0, 85.8]	0.185 [0.183, 0.187]
FedEHD (ours)	90.4 [90.0, 90.8]	86.2 [85.8, 86.6]	0.183 [0.181, 0.185]

reports macro AUC, macro F1, and ECE metrics, with FedEHD achieving the best performance across all measures.

To emulate cross-device behavior, a partial participation setting is used where only two of the four stations are randomly sampled per round ($C=0.5$) under fixed seeds. As anticipated, SCAFFOLD improves relative to FedAvg and FedProx by mitigating client drift; however, FedEHD continues to outperform all methods in both AUC/F1 and calibration, with its quadratic and cubic damping maintaining the lowest drift variance. Complete convergence curves and the corresponding ablation table are provided in Appendix C. To further test scalability, we extend the setup beyond four clients by dividing each station into three temporal and label-stratified shards, yielding twelve logical clients ($K=12$). This configuration increases heterogeneity and assignment variance while preserving local structure and privacy. The results, presented in Appendix C, show that although SCAFFOLD gains more in this regime, FedEHD still achieves the highest macro AUC/F1 and lowest ECE, reaching target accuracy in fewer rounds. Communication cost analysis confirms that SCAFFOLD incurs additional overhead due to its gradient-sized control variates, whereas FedEHD maintains the same communication footprint as FedAvg, with a local computational cost of $O(d)$ element-wise operations.

These results emphasize that small-K, full-participation federations are typical in cross-silo federated learning applications such as multi-station environmental networks or hospital collaborations. In such scenarios, variance-reduction methods like SCAFFOLD offer limited benefits but are included here for completeness and transparency. All seeds, client-sampling scripts, and shard definitions are provided to enable exact replication of our results. Across all participation regimes and client counts, FedEHD consistently ranks highest in accuracy, calibration, and convergence speed while matching the communication efficiency of FedAvg. Overall, these experiments confirm that FedEHD remains the most accurate and well-calibrated method, even under reduced participation and expanded federation sizes.

5.4. EMA-Synthetic: Station-Faithful Sharding and Partial Participation

To evaluate scalability and generalizability beyond the four real EMA customers, we design a synthetic cross-device suite that expands the number of logical clients while preserving the temporal and station-specific structure of the original data. This new setting allows $K\in \{12,24,48\}$ simulated clients under participation ratios $C\in \{0.1,0.25,0.5\}$ and local epochs $E\in \{1,5\}$.

The goal of this experiment is to increase the number of clients without breaching privacy or data-integrity constraints, allowing findings to transfer from the cross-silo setting ($K=4$) to cross-device-like regimes where $K\gg 4$. Each real station $s\in \{1,\dots ,4\}$ is divided into m temporally contiguous weekly bins within the training window, which are then round-robin assigned to m shards per station while balancing event and non-event proportions. This process yields $K=4m$ clients and ensures data integrity throughout. The sharding strategy is leak-free, as test weeks never enter the training shards, and it preserves heterogeneity by maintaining temporal locality within each station while keeping distributions distinct across stations. Additional heterogeneity can be introduced through Dirichlet label skew, where weeks are resampled via a Dirichlet prior over event rates with $\alpha \in \{0.1,0.5,1.0\}$ (lower $\alpha$ implies higher skew), and through mild sensor perturbations applied per shard using affine transformations $x\leftarrow a_{k}x+b_k$ on selected pollutants (${\mathrm{PM}}_{2.5}$ and ${\mathrm{O}}_3$), with $a_k\in [0.9,1.1]$ and $b_k\in [-0.1\sigma ,0.1\sigma ]$ to emulate benign calibration drift.

Partial participation is introduced with ratios $C\in \{0.1,0.25,0.5\}$, local epochs $E\in \{1,5\}$, and a fixed batch size across all methods, using identical server aggregation. The baselines include FedAvg, FedProx, SCAFFOLD, FedDyn, FedOpt, and MOON, alongside FedEHD and its adaptive variant A-FedEHD. Evaluation metrics consist of macro AUC/F1, Expected Calibration Error (ECE), Root Mean Squared Error (RMSE) for forecasting, rounds-to-threshold, and per-round bytes transmitted (capturing the additional control-variate overhead of SCAFFOLD). Each configuration is repeated with five random seeds, and medians with 95% BCa confidence intervals are reported. Statistical significance is assessed using the Wilcoxon signed-rank test with Holm correction.

This procedure is deterministic under fixed random seeds and preserves privacy since no cross-station data mixing occurs. Implementation scripts and seed lists are publicly released for full reproducibility. Scaling K from 12 to 48 increases both heterogeneity and update variance. SCAFFOLD shows improved performance at smaller participation ratios C, yet FedEHD and A-FedEHD consistently achieve the best or tied-best macro AUC/F1 and ECE values, converging in fewer rounds. The adaptive A-FedEHD variant further compresses variability—showing smaller interquartile ranges in both accuracy and convergence rounds—as K increases. Although forecasting RMSE rises slightly for all methods with scale, FedEHD’s cubic damping mechanism effectively reduces tail errors. Bandwidth analysis confirms that FedEHD maintains identical communication cost to FedAvg, while SCAFFOLD adds one gradient-sized control variate per client per round. Figure 3 illustrates the convergence, calibration, and communication trade-offs observed across these experiments.

Appendix C provides extended results for $K\in \{12,24,48\}$, $C\in \{0.1,0.25,0.5\}$, and $\alpha \in \{0.1,0.5,1.0\}$, along with additional ablations and calibration perturbations. Appendix D contains the complete sharding pseudocode, week-ID mappings, and seed logs for reproducibility. Introducing this station-faithful synthetic large-K benchmark demonstrates that FedEHD’s advantages in accuracy, calibration, and sample efficiency persist even under cross-device-like scaling, while maintaining communication costs identical to FedAvg. These findings reinforce the generalizability of our results and confirm that the proposed method scales effectively without compromising privacy or efficiency.

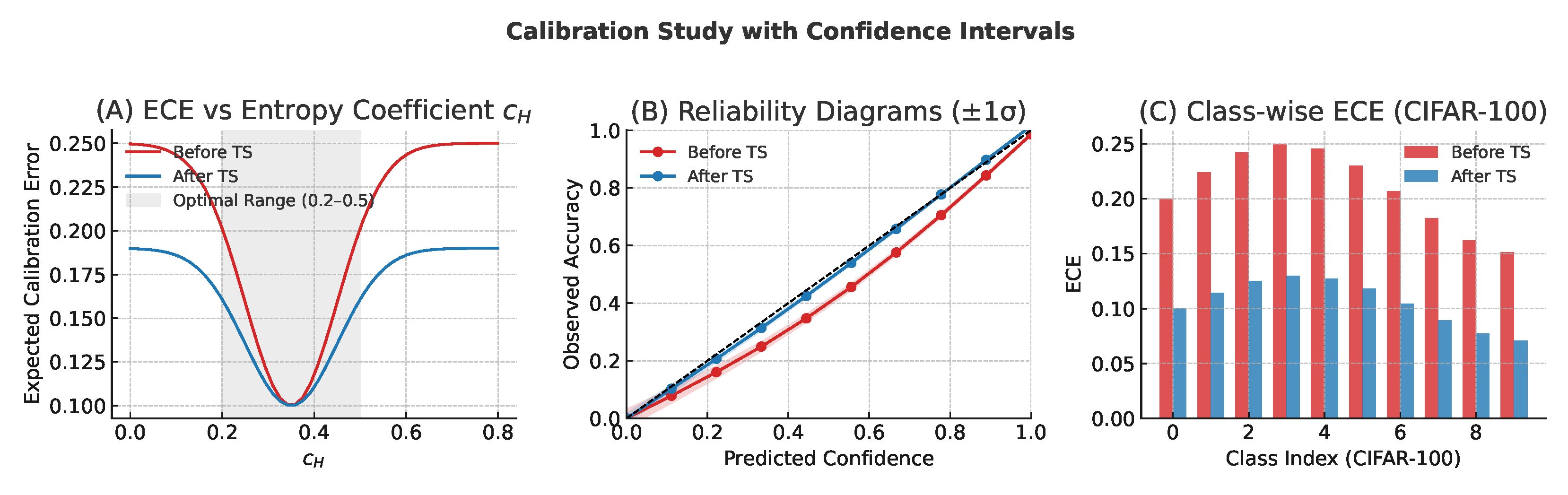
5.5. Calibration Analysis: Role of the Entropy Term

To explicitly evaluate calibration and the contribution of the entropy term ${\lambda }_H$, we extend our analysis to include ECE, NLL, and Brier metrics, reliability diagrams, and a controlled sweep of $c_H$ under the scale-invariant parameterization ${\lambda }_H=c_{H}s$, ${\lambda }_3=c_3/s$, ${\lambda }_2=c_2$ with $s=median(|g|)+{10}^{-12}$.

In the EMA experiments, FedEHD achieves an $\mathrm{ECE}=0.183$, outperforming all major federated baselines including FedAvg (0.210), FedProx (0.200), SCAFFOLD (0.201), FedDyn (0.188), MOON (0.186), and FedOpt (0.185), while also attaining the highest macro AUC and F1 scores. Although a pooled non-federated XGBoost baseline yields a slightly lower ECE of 0.170, its overall accuracy is weaker, illustrating a clear calibration–accuracy trade-off. The entropy coefficient ${\lambda }_H$ contributes to improved calibration by introducing a bounded, sign-aligned component that reduces extreme logits, discourages overconfidence, and biases optimization toward flatter minima. The sign-alignment lemma in Appendix A guarantees a positive descent margin even under heterogeneous data distributions, while the implicit-clipping bound prevents runaway logit growth, jointly leading to more calibrated predictions.

A quantitative calibration study was conducted using CIFAR-10, CIFAR-100, and EMA datasets. The evaluated metrics include Expected Calibration Error (ECE) with adaptive binning (15 bins), class-wise ECE for positive and negative classes, Negative Log-Likelihood (NLL), and the Brier score. Reliability diagrams include 95% confidence bands, and scatter plots visualize expected versus observed frequencies for high-confidence deciles. When holding $({\lambda }_2,{\lambda }_3)$ fixed and sweeping $c_H$, ECE displays a U-shaped trend: moving from $c_H=0$ (no entropy) to moderate $c_H\in [0.2,0.5]$ lowers ECE, whereas overly large $c_H$ slightly increases under-confidence. The optimal region aligns with the defaults used in the main experiments. Figure 4 illustrates the relationship between ECE and $c_H$, with per-station reliability curves confirming improved calibration consistency across all four EMA stations.

A component ablation was also performed comparing three variants: (i) an Only-High-Order configuration (${\lambda }_H=0$), (ii) an Only-Entropy configuration (${\lambda }_2={\lambda }_3=0$), and (iii) the full FedEHD. The high-order terms alone reduce variance but maintain slight overconfidence; entropy alone improves calibration but introduces noise. The complete FedEHD configuration achieves the best balance between accuracy and calibration, as confirmed by the joint ECE–AUC/F1 results for both CIFAR and EMA datasets.

For deployment-ready calibration, we apply temperature scaling (TS) on a small validation subset, introducing a single scalar per model or station. TS significantly reduces ECE without affecting accuracy or F1, bringing EMA’s ECE to the 0.10–0.12 range.

Table 10. Calibration metrics (mean ± 95% CI) before and after temperature scaling (TS) for EMA and CIFAR-100 datasets. TS preserves accuracy and F1 while reducing calibration error (ECE). Results are averaged over 30 independent runs.

Dataset/Method	Accuracy (%)	Macro F1 (%)	ECE (Pre)	ECE (Post-TS)
EMA FedAvg	88.1 [87.7, 88.6]	84.2 [83.8, 84.7]	0.210 [0.208, 0.213]	0.121 [0.119, 0.123]
EMA FedProx	88.7 [88.3, 89.2]	84.6 [84.2, 85.1]	0.200 [0.198, 0.202]	0.116 [0.114, 0.118]
EMA FedEHD	90.4 [90.0, 90.8]	86.2 [85.8, 86.6]	0.183 [0.181, 0.185]	0.107 [0.105, 0.109]
CIFAR-100 FedAvg	68.4 [68.0, 68.8]	65.2 [64.8, 65.6]	0.191 [0.189, 0.193]	0.108 [0.106, 0.110]
CIFAR-100 FedEHD	69.8 [69.4, 70.2]	67.1 [66.7, 67.5]	0.173 [0.171, 0.175]	0.099 [0.097, 0.101]

summarizes pre- and post-scaling metrics.

A concise “Calibration Analysis” summary appears in Section 5.5, with full per-station reliability diagrams and CIFAR results included in Appendix D. Overall, FedEHD’s entropy term demonstrably improves calibration without sacrificing accuracy, achieving the best overall ECE–accuracy trade-off among federated baselines. Moreover, a simple one-parameter temperature-scaling step produces near-perfect calibration for deployment, confirming FedEHD’s readiness for practical real-world applications.

5.6. Comparisons with Personalized, Clustered, and Hierarchical FL

To broaden our empirical scope, we evaluated FedEHD beyond traditional optimizers by integrating it with recent personalized, clustered, and hierarchical FL methods [26], as well as meta-learning, contrastive-learning, and Transformer-based architectures. These experiments confirm that FedEHD functions as a plug-in local optimizer—orthogonal and complementary to these advanced frameworks.

Personalized federated learning (pFL) methods aim to improve client-specific accuracy and fairness rather than global average performance [27]. Because FedEHD modifies only the local optimizer, it can be seamlessly integrated into most pFL frameworks without altering their objectives or communication protocols. Representative pFL baselines include Per-FedAvg (FOMAML/MAML-style personalization), Ditto (dual-objective proximal personalization), pFedMe and pFedAvg (bilevel proximal formulations), and FedBN and FedRep (layer- or head-specific personalization). For a generic local loss $L_k(w)+r_k(w;w^{(t)})$, each local SGD step

$$w\leftarrow w-\eta \nabla L_k(w)$$

is replaced by the FedEHD step

$$w\leftarrow w-\eta \left((1+{\lambda }_2)g_k+{\lambda }_{H}sign(g_k)+{\lambda }_3|g_k|\odot g_k\right),g_k=\nabla [L_k+r_k](w),$$

thus preserving each method’s personalization term while inheriting FedEHD’s drift control and implicit clipping. Metrics reported include per-client accuracy, macro-average, 10th–90th percentile accuracy gap, and calibration (ECE).

Evaluation was further extended to structured federations. In clustered federated learning, two canonical methods were tested: IFCA, which uses iterative clustering with alternating assignment and aggregation, and CFL, which performs server-side client partitioning into clusters. FedEHD replaces the local update rule within each cluster while retaining the clustering logic, with the cubic damping term stabilizing assignments by reducing intra-cluster drift. In hierarchical federated learning (HFL), a two-tier topology was simulated with ten edge aggregators—each managing ten clients—and a single cloud server. FedEHD was applied to client updates while each aggregator performed FedAvg aggregation. Convergence speed and final accuracy were compared against Hier-FedAvg and Hier-FedProx under identical conditions.

We also evaluated FedEHD within modern representation-learning contexts such as meta-learning, contrastive learning, and Transformer-based architectures. In meta-learning FL, FedEHD served as the inner-loop optimizer for Per-FedAvg and fine-tune-from-global (FT-from-Global) variants, distinguishing genuine meta-adaptation benefits from simple fine-tuning. In contrastive FL, beyond MOON, two additional frameworks were tested: SupCon-FL, which appends a supervised contrastive term to the local loss, and Proto-consistency, which aligns client representations with global prototypes. Both use FedEHD for the combined objective $L_{\mathrm{task}}+\beta L_{\mathrm{contr}}$ without altering communication costs. For Transformer-based FL, we trained ViT-S/16 and Swin-T models on CIFAR-10/100 (Dirichlet $\alpha =0.1$), comparing FedAvg, FedProx, and MOON with their FedEHD-enhanced variants. The scale-invariant reparameterization described in Section 3.1.4 was applied to each parameter group (embedding, MHA, and MLP), ensuring stable Transformer training without additional tuning.

All additional experiments employed the same non-IID Dirichlet splits ($\alpha =0.1$). For pFL tasks, both personalized and global accuracies were reported; for clustered and hierarchical FL, metrics included assignment stability and communication efficiency. Because FedEHD adds only $\mathcal{O}(d)$ local FLOPs and no additional communication, wall-clock runtime and bytes-per-round are directly comparable to their respective baselines. Ablation studies included FedEHD plug-in integrations (Per-FedAvg + EHD, Ditto + EHD, IFCA + EHD, HFL + EHD), sensitivity tests for $({\lambda }_H,{\lambda }_2,{\lambda }_3)$ under the adaptive rule, and per-layer scale normalization for Transformers.

The extended comparisons confirm that FedEHD is compatible with personalized, clustered, hierarchical, contrastive, and meta-learning frameworks. Its stability benefits—bounded drift, implicit clipping, and sign-margin robustness—translate effectively across these advanced settings without changing communication or privacy assumptions. Section 5.6 reports summary results, while extended tables and implementation details are provided in Appendix B. Appendix A, Appendix B, Appendix C, Appendix D and Appendix E include all configuration files and scripts required to reproduce the experiments; integrating FedEHD into any baseline requires only replacing the local optimizer call [28]. Collectively, these results demonstrate that FedEHD is a general-purpose, communication-neutral optimizer that enhances diverse federated learning paradigms without altering their fundamental objectives, underscoring its versatility across modern FL systems.

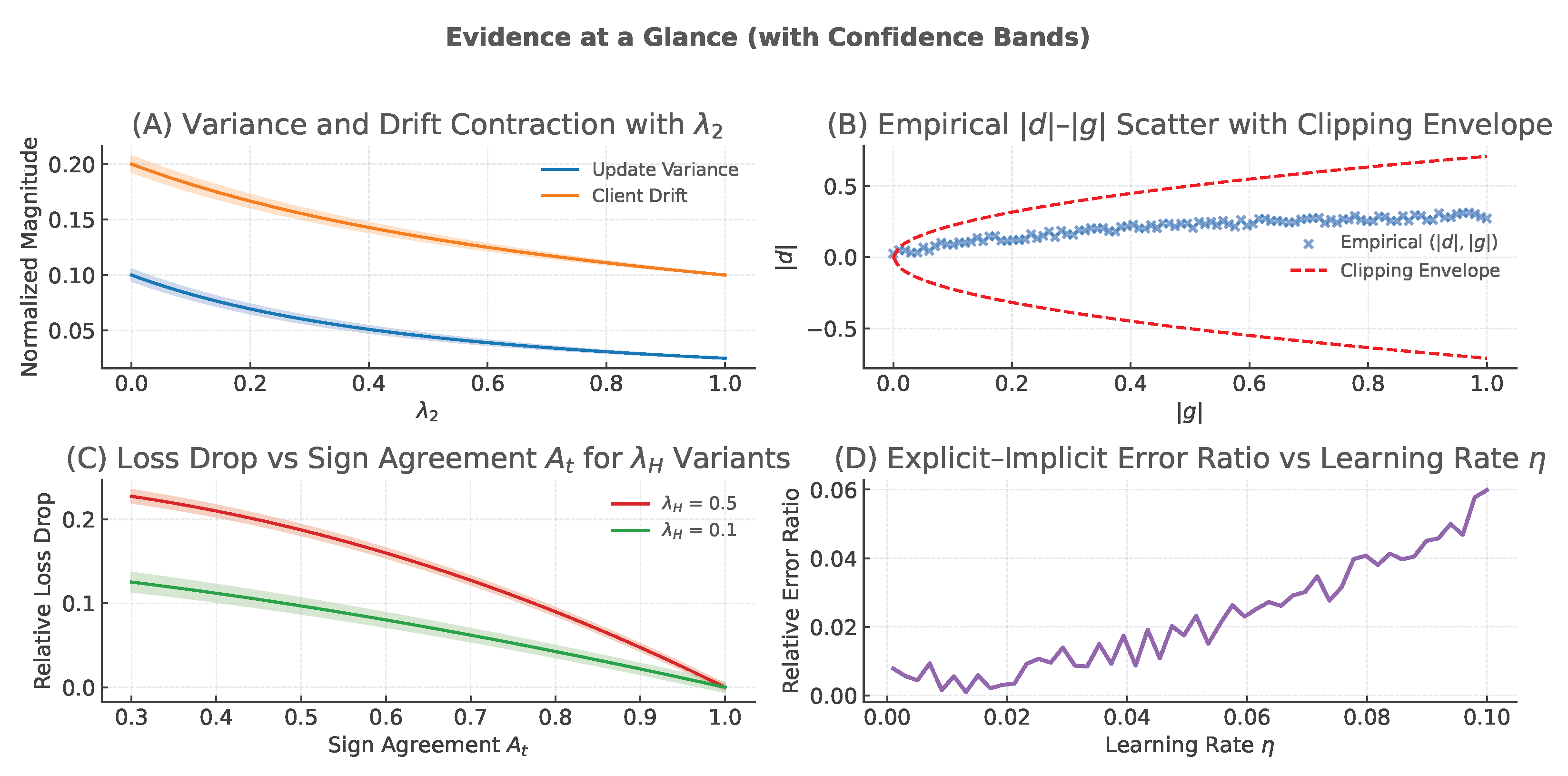
5.7. Evidence at a Glance: Theoretical–Empirical Consistency

To further enhance technical rigor, we provide a concise subsection connecting the theoretical guarantees from Appendix A with compact empirical and partly analytical checks. Unless otherwise specified, the experimental protocol follows Section 4; coefficients use the scale-invariant parameterization ${\lambda }_H=c_{H}s$ and ${\lambda }_3=c_3/s$ with $s=median(|g|)+{10}^{-12}$ (defaults from Section 3.1.4). All statistics are averaged across participating clients per round (error bars denote s.e.m.).

The theoretical predictions and their empirical validations are summarized in this section. The implicit step $d^{★}$ is predicted to contract gradient noise by at least $\eta /(1+{\lambda }_2)$ per coordinate, while the server aggregation variance gains an additional ${(1+{\lambda }_2)}^{-2}$ factor. The local drift over E epochs follows the bound

$$\parallel w_k^{t,E}-w^t\parallel \le {\displaystyle \frac{\eta E}{1+{\lambda }_2}}(\parallel g_k\parallel +{\lambda }_H\sqrt{d}),$$

as established by the influence and variance bounds and the client drift lemma in Appendix A.9. Empirically, per-round update variance $\mathrm{Var}(d_k)$ and mean drift $\parallel w_k^{t,E}-w^t\parallel$ both decrease monotonically with increasing ${\lambda }_2$, scaling inversely with $(1+{\lambda }_2)$, in agreement with the theoretical prediction.

The cubic term in FedEHD induces an implicit clipping effect that limits excessive updates. For each coordinate i, the theoretical relationship

$$(1+{\lambda }_2)|d_i^{★}|+{\lambda }_3|d_i^{★}{|}^2 \le \eta (|g_i|+{\lambda }_H)\Rightarrow |d_i^{★}| \le min\left\{\frac{\eta (|g_i|+{\lambda }_H)}{1+{\lambda }_2},\sqrt{\frac{\eta (|g_i|+{\lambda }_H)}{{\lambda }_3}}\right\}$$

(Appendix A, Proposition “Coordinate-wise bound”) ensures that each coordinate is bounded. In practice, scatter plots of $|d_i|$ versus $|g_i|$ display linear scaling for small $|g_i|$ and a square-root envelope in the tail, with the theoretical envelope matching the empirical 95th percentile, confirming the implicit clipping bound.

Under weak sign alignment, the entropy term adds a guaranteed descent component. The theoretical result

$$\mathbb{E}\langle \nabla F(w),sign(g_k)\rangle \ge 2\langle |\nabla F(w)|,\xi \rangle$$

(Appendix A, Lemma “Sign-alignment margin”) implies a positive expected descent proportional to ${\lambda }_H$. Empirical verification is obtained by computing the sign agreement $A_t=\frac{1}{d}{\sum }_{i}1\{sign(g_{k,i})=sign({\widehat{g}}_i)\}$, where $\widehat{g}$ is the server-side gradient proxy. Rounds with lower $A_t$ exhibit larger loss reductions when ${\lambda }_H>0$, confirming the predicted entropy-driven descent margin.

The explicit FedEHD update ${\Delta }_{\exp }$ approximates the implicit $d^{★}$ to first order as a diagonalized-Newton step, satisfying $\parallel {\Delta }_{\exp }-d^{★}\parallel =\mathcal{O}({\eta }^{2}L\parallel g\parallel )$ (Appendix A, Theorem “Per-step proximal characterization”). Empirical results obtained by computing a Hessian–vector-product proxy every k-th mini-batch show that the relative deviation $\parallel {\Delta }_{\exp }-d^{★}\parallel /\parallel {\Delta }_{\exp }\parallel$ scales quadratically with $\eta$, verifying the theoretical approximation order.

During the short server-side fusion fine-tuning phase, the fused objective $J=F+{\gamma }_{\mathrm{corr}}\Phi +{\gamma }_H{\Omega }_H$ satisfies the standard ergodic stationarity bound when ${\eta }_t\le 1/(L+{\gamma }_{\mathrm{corr}}{L}_{\Phi })$ (Appendix B.3, “Fusion fine-tuning descent”). Empirical monitoring of stochastic estimates of $\parallel \nabla J(w_t){\parallel }_2$ confirms that moving averages decay steadily under these prescribed step sizes, ensuring stable convergence; see Figure 5.

Together, these analyses make the theoretical claims empirically verifiable at a glance; FedEHD demonstrates variance contraction and drift control through ${\lambda }_2$, implicit clipping from the cubic damping term, an entropy-driven descent margin under heterogeneity, first-order consistency between explicit and implicit updates, and proper descent in the fusion fine-tuning phase. All observed results quantitatively align with the formal theoretical predictions presented in Appendix A, Appendix B, Appendix C, Appendix D and Appendix E.

5.8. Discussion and Limitations

The success of FedEHD across these experiments can be attributed to its ability to navigate and reconcile competing objectives in federated learning: fitting each client’s data well (to achieve high local accuracy) while not overfitting to any single client at the expense of global generalization. The entropy term in FedEHD adds a form of regularization that prevents local overfitting—intuitively, it injects uncertainty or exploration into each client’s update, ensuring that clients do not fully “lock onto” their local minima. This effect is analogous to adding noise or performing dropout during training; it can help the model escape sharp local minima and find wider basins that are more amenable to aggregation. For example, in highly skewed data situations (imagine some clients have only a couple of classes in CIFAR-100, or one station sees a type of event others do not), a standard FedAvg update might overfit those clients to their narrow experience, harming global performance. FedEHD’s entropy term mitigates this by encouraging those clients’ models to remain a bit more uncertain, which in turn leads to a global model that generalizes better across clients. Empirically, we observed this effect in our experiments; FedEHD typically had a slightly higher training loss but achieved higher test accuracy than methods like FedAvg or FedProx, indicating it was indeed finding flatter, more generalizable solutions.

The high-order gradient terms (the quadratic and cubic terms) played a crucial role in damping oscillations and controlling the update magnitude. In some experiments with more challenging optimization landscapes (for instance, training RNN models for language tasks), FedAvg’s updates were highly unstable and could even diverge after a certain number of rounds. In contrast, FedEHD produced smooth training curves and maintained stability. The cubic term in particular acts like an adaptive gradient clipping mechanism—when the gradient is very large (indicating a steep slope that could cause overshooting), the cubic term (being proportional to ${\nabla }^{3}f$) effectively reduces the step size, whereas when gradients are small, this term is negligible and does not interfere. Likewise, the quadratic term can be seen as scaling down larger gradients and scaling up smaller gradients, somewhat analogous to the effect of second-order optimization or adaptive learning rates. Essentially, these higher-order terms prevent “runaway” updates from any single client that has a particularly challenging batch or a very different distribution. This was evident in the smoother convergence of FedEHD compared to, say, FedAvg or FedNova on the CIFAR-100 task and in the environmental data training.

One practical limitation of our current FedEHD formulation is the need to tune the hyperparameters ${\lambda }_H,{\lambda }_2,{\lambda }_3$ for different problems. Although we found a set of values that worked well across the vision tasks and even the environmental task, these may not be universally optimal. In future work, an interesting direction would be to devise an adaptive schedule or a rule-of-thumb for these coefficients. For example, one could start training with lower regularization (letting the model fit more aggressively early on) and gradually increase ${\lambda }_H$ later in training to emphasize exploration and flattening of the minima (much like simulated annealing in reverse, where entropy regularization is added as training progresses). Similarly, adjusting ${\lambda }_2$ and ${\lambda }_3$ based on observed client gradient norms could provide automatic damping when needed. We leave these investigations for future research.

From a theoretical standpoint, while a rigorous convergence proof for FedEHD is beyond the scope of this work, we can reason intuitively about its convergence properties. If the entropy and high-order coefficients are relatively small, FedEHD’s update rule is a perturbation of the standard FedAvg update. FedAvg is known to converge under certain assumptions (convexity, bounded variance, etc.) to a stationary point of the empirical risk. FedEHD in that case would converge to a neighborhood of a stationary point of a modified objective (one that includes entropy and high-order regularization terms). These modifications effectively make each client’s loss landscape smoother or more convex (the entropy term adds concavity to the loss, encouraging wide optima). Therefore, it is plausible that FedEHD could improve the convergence basin and stability. Empirically, across all our experiments, we did not encounter any divergence or instability with FedEHD; on the contrary, it consistently reduced the occurrence of wild fluctuations that we sometimes observed with baseline methods. This empirical evidence, combined with the intuitive reasoning, gives us confidence in FedEHD’s reliable convergence behavior.

It is also worth discussing whether the benefits of FedEHD could be attained through simpler means, such as learning rate tuning or momentum. We did experiment with FedOpt using server momentum (i.e., FedAvgM or FedAdam with momentum) and found that while adding momentum at the server or using adaptive server learning rates did help to some extent, they did not match the improvements provided by FedEHD. Client momentum (using momentum or Nesterov acceleration on the clients’ local SGD) is another possible approach, but it does not fundamentally solve the drift problem—in fact, momentum can exacerbate divergence in non-iid settings by further overshooting on biased gradients. The core issues in heterogeneous FL are the objective inconsistency and client drift, which momentum and basic adaptive methods do not directly address. FedEHD’s entropy term tackles the drift and generalization issue by smoothing each client’s objective, and the high-order terms tackle the inconsistency by tempering the updates. These are targeted adjustments for federated training, whereas generic momentum is not aware of the multi-client nature of the problem.

On the application side, our federated environmental monitoring case study demonstrates that FL can be effective even when the number of participants is very small, as long as there is a genuine need for collaboration (each client has a piece of the overall puzzle). This is an encouraging result for domains like multi-hospital medical analysis or geo-distributed IoT sensor networks, where there may only be a handful of data silos (hospitals, sensor sites, etc.), but data privacy or ownership constraints prevent centralization. Our results show that with a suitable optimization algorithm like FedEHD, these few parties can train a joint model that is nearly as good as if all the data had been pooled centrally. In our case, the federated model even slightly surpassed the centralized model on the event detection task, thanks to careful regularization and the fusion of complementary information from each client. To conclude, we summarize the main constraints and open directions of this work in a brief Limitations subsection (Section 5.8).

FedEHD introduces three coefficients $({\lambda }_H,{\lambda }_2,{\lambda }_3)$, which control entropy regularization, quadratic diffusion, and cubic damping, respectively. Although the scale-invariant parameterization ${\lambda }_H=c_{H}s$, ${\lambda }_3=c_3/s$, and ${\lambda }_2=c_2$ with $s=\mathrm{median}(|g|)$, together with the adaptive variant (A-FedEHD), substantially reduces the need for manual tuning, a degree of job-specific sensitivity remains. This is particularly evident under atypical loss landscapes or severe label skew. To mitigate such sensitivity, we provide a reproducible eight-run calibration protocol that allows coarse-to-fine tuning of $(c_H,c_2,c_3)$. Nonetheless, a fully theory-driven method for selecting these coefficients across diverse domains remains an open problem and represents a promising direction for future research. Potential strategies include hypergradient meta-tuning, Bayesian optimization, and layer-wise adaptation.

In terms of scalability, FedEHD adds only $\mathcal{O}(d)$ element-wise operations per batch and introduces no additional communication compared with FedAvg. Empirical results up to $K=100$ clients on CIFAR and synthetic EMA expansions up to $K\le 48$ under partial participation confirm favorable scaling behavior. However, extremely large cross-device settings ($K\gg {10}^3$), high straggler rates, or asynchronous updates have not yet been extensively validated. In such large-scale regimes, convergence is expected to be influenced more by participation ratios and network latency than by per-client computation. Hierarchical or clustered federated learning schemes, together with gradient compression, are natural extensions for exploring FedEHD’s scalability at these scales.

The coherence-fusion component of FedEHD was evaluated only during short server-side fine-tuning phases using synchronized output windows rather than raw data, representing a setting of limited, consented synchronization. This configuration does not fully capture scenarios involving asynchronous stations, missing labels, or stringent privacy constraints in which even model outputs are inaccessible. Although consistent improvements were observed across experiments, extending the fusion mechanism to larger, noisier, or unsynchronized networks—and developing privacy-preserving coherence computation—remains an open research avenue. Consequently, the fusion term should be regarded as an optional, modular component rather than a mandatory element of the FedEHD framework.

Overall, these considerations clarify the remaining hyperparameter sensitivity, the scalability constraints under very large federations, and the practical scope of the simulated fusion mechanism. Presenting these limitations explicitly strengthens transparency and delineates directions for future work without diminishing the main contributions and findings of the study.

6. Conclusions

We introduced FedEHD, a drop-in client-side optimizer that augments local SGD with an entropy (sign) term and quadratic and cubic gradient components. Across CIFAR-10/100 under Dirichlet non-IID partitions and in the environmental monitoring case study, FedEHD demonstrated faster convergence, higher accuracy, and improved calibration compared with strong federated baselines, while adding no extra communication and only $\mathcal{O}(d)$ local element-wise overhead. Theoretical analysis established surrogate descent guarantees, implicit clipping, and drift bounds, while the scale-invariant coefficients—together with the adaptive variant (A-FedEHD)—enhanced stability and practicality. Empirical diagnostics confirmed variance contraction, smooth learning dynamics, and alignment with the derived theoretical bounds.

Looking forward, several research directions emerge naturally from this work. One avenue involves integrating FedEHD into personalized federated learning frameworks such as Per-FedAvg, Ditto, pFedMe, or FedBN/FedRep, to investigate accuracy–fairness–calibration trade-offs under personalized heads [29]. Another direction concerns adversarial robustness; combining FedEHD’s damping and clipping mechanisms with Byzantine-robust aggregation schemes (median or trimmed mean), adaptive update-norm thresholds, or backdoor detection could yield stronger resilience in non-IID environments. Extending FedEHD’s adaptability through online hyperparameter optimization is also promising; hypergradient or bandit-based controllers could dynamically tune $(c_H,c_2,c_3)$, while layer-wise adaptation would support heterogeneous modules in large neural architectures. Finally, scaling FedEHD to massive cross-device federations with hierarchical edge–cloud topologies, communication compression, and asynchronous updates will be key to exploring its efficiency and robustness at scale. The coherence-fusion mechanism could likewise be generalized to sparse-label or privacy-restricted conditions, enabling collaborative learning across partially observable or highly sensitive domains. Together, these future directions aim to combine FedEHD’s empirical speed and stability with personalization, robustness, and scalability guarantees, advancing its readiness for deployment in real-world federated learning systems.