Scaling Swarm Coordination with GNNs—How Far Can We Go?
Abstract
1. Introduction
- Algorithmic contribution: We formalize DGQL, integrating GNN architectures into Q-learning to process dynamic agent-neighbor interaction graphs while maintaining permutation invariance and variable neighborhood handling capabilities.
- Empirical evaluation: We demonstrate DGQL’s effectiveness on two cooperative benchmark tasks—goal reaching and obstacle avoidance—establishing successful learning of decentralized coordination policies under the CTDE paradigm.
- Scalability analysis: We provide the first systematic quantification of zero-shot scalability for GNN-based swarm policies, evaluating models trained on ten-agent swarms when deployed with populations up to three times larger, thereby revealing task-dependent efficiency degradation patterns.
2. Related Work
2.1. Scalability in the Number of Agents
2.2. Scalability in State and Action Spaces
2.3. Decentralized Execution and Communication
2.4. Positioning of Our Work
3. Background
3.1. Swarming Model Formalization
- represents the set of environment states, which are not directly observable by the agents.
- denotes the set of observations available to the agents.
- is the set of actions that an agent can perform to interact with the environment.
- defines the reward function, mapping observations/actions pairs to rewards.
- is the agent’s local policy—the collective interaction of these individual policies results in the emergent swarm behavior.
- is the number of agents in the swarm.
- denotes a swarming agent, as defined earlier.
- is the global state transition function, mapping the current global state (an element of ) and a joint action (an element of ) to the next global state.
- defines the observation model that provides each agent with its local observations derived from the global state.
3.2. Multi-Agent Reinforcement Learning
3.3. Graph Neural Networks
- Message Computation: For each edge , a message is computed. This message typically depends on the embeddings of the source node u and the target node v from the previous layer, and , potentially incorporating edge features if available. This step is governed by a learnable message function as the following:
- Message Aggregation: Each node v aggregates the incoming messages from its neighbors. Let denote the set of neighbors of node v in graph . The aggregation function (e.g., sum, mean, and max) combines the messages into a single vector as the following:Note that some formulations aggregate messages based on (messages to neighbors) or use slightly different definitions. The core idea remains aggregating neighborhood information.
- Embedding Update: The embedding of node v for the current layer, , is computed by combining its previous embedding with the aggregated message . This update is performed using a learnable update function (often a neural network layer like an MLP, potentially combined with activation functions like ReLU) as the following:
4. Deep Graph Q-Learning
- Graph-based State Representation: Instead of treating agents independently based solely on local observations, DGQL represents the swarm’s state at time t as a graph , where nodes correspond to agents and edges represent neighbor relationships (e.g., based on communication range or proximity, determined by ). The initial node features are derived from the agents’ local observations .
- Graph Q-Network (GQN): The standard Deep Q-Network is replaced by a GQN. This network takes the graph and node features as input and computes Q-values for each agent and each possible action . The GQN architecture first employs GNN layers (as described in Section 2) that perform message passing to compute node embeddings for each agent i. These embeddings encode information about the agent’s state and its K-hop neighborhood within the graph . Then, a final output layer maps each agent’s final embedding to its action-value estimates: for each , where represents the learnable parameters of the entire GQN. Critically, the GQN parameters are shared across all agents, promoting homogeneous behavior and facilitating learning from collective experience.
- Centralized Training with Graph Experience Replay: DGQL operates within a CTDE paradigm. During training, experiences are stored in a replay buffer . Each experience tuple contains the full graph representation and collective information from a transition: , where is the joint action and is the vector of individual rewards. Storing the graph structure allows the GQN to learn from the system’s interaction topology during optimization.
4.1. Centralized Training
- The current swarm state is represented as a graph .
- The GQN computes Q-values for all agents.
- A joint action is selected (e.g., using an -greedy strategy independently for each agent based on its Q-values).
- The transition, including the graph structures, is stored in the replay buffer .
- A batch is sampled from .
- The GQN parameters are updated via a gradient descent step on the loss .
4.2. Decentralized Execution
| Algorithm 1 Deep graph Q-learning (DGQL) |
|
Notation in Table 1, the circles  – – refer to the steps described in the text. refer to the steps described in the text.
|
| Algorithm 2 Decentralized DGQL execution (per environment step) |
|
Notation in Table 1 |
| Notation Summary | |
|---|---|
| General | |
| Environment | |
| Episode and time step indices | |
| Maximum number of training episodes | |
| Exploration rate and discount factor | |
| Replay buffer | |
| Action space | |
| C | Target network update frequency |
| Networks and Learning | |
| Graph Q-network and target network | |
| TD target for agent i | |
| Q-values for all agents | |
| Q-values for agent i | |
| Output layer mapping embeddings to Q-values | |
| Observations and Graphs | |
| Joint observations at time t | |
| Local observation of agent i at time t | |
| Interaction graph at time t | |
| Set of neighbors of agent i at time t | |
| Agents and Messages | |
| Agent and neighbor indices | |
| Embedding of agent i at layer k | |
| Feature extraction function | |
| Message and update functions at layer k | |
| ⨁ | Aggregation operator (e.g., sum, mean, max) |
| Aggregated message for agent i at layer k | |
| Edge features between agents j and i | |
| K | Number of GNN layers (message passing rounds) |
| k | Current layer index |
| Actions and Rewards | |
| Joint action | |
| Rewards at time | |
4.3. Complexity and Communication Cost
5. Evaluation
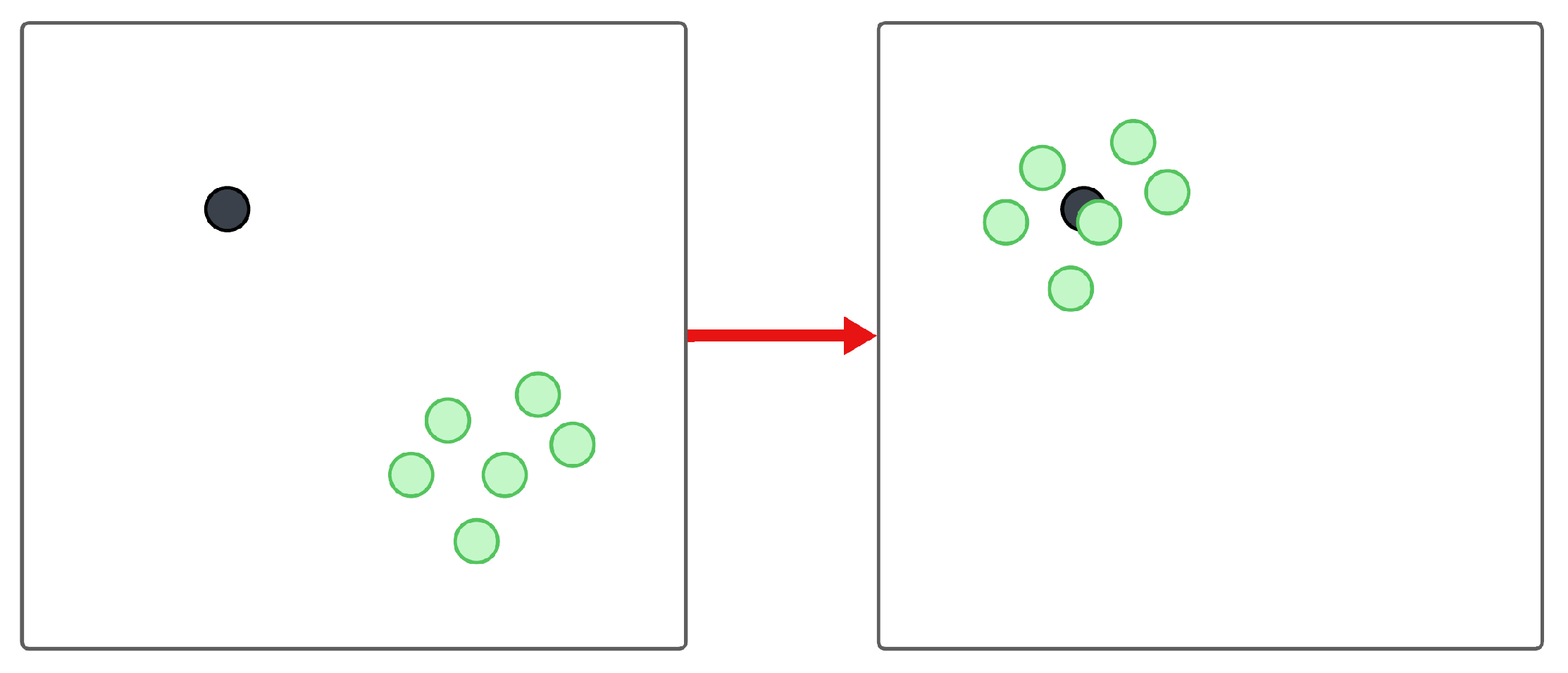
5.1. Tasks
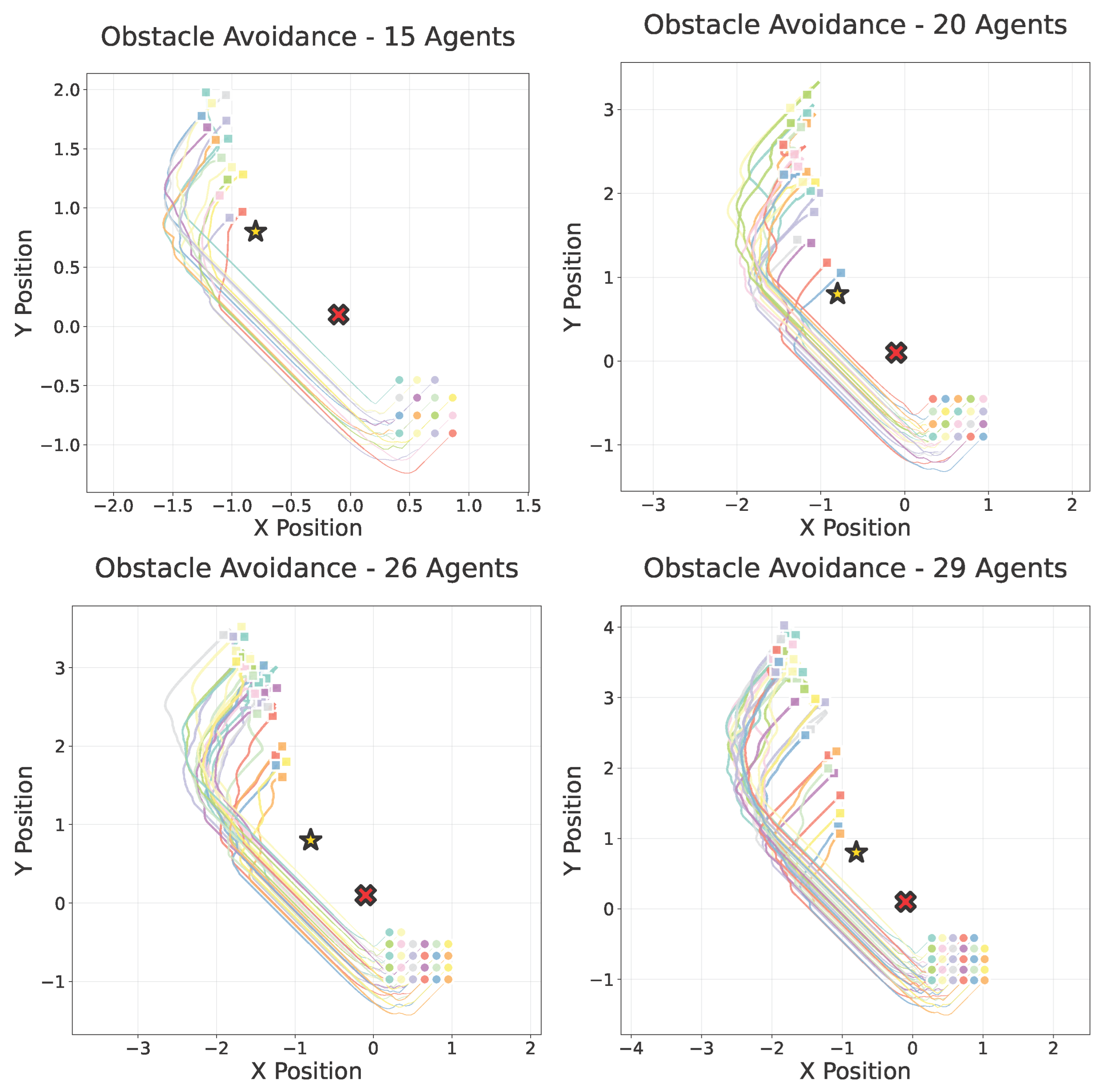
Obstacle Avoidance (Figure 3)
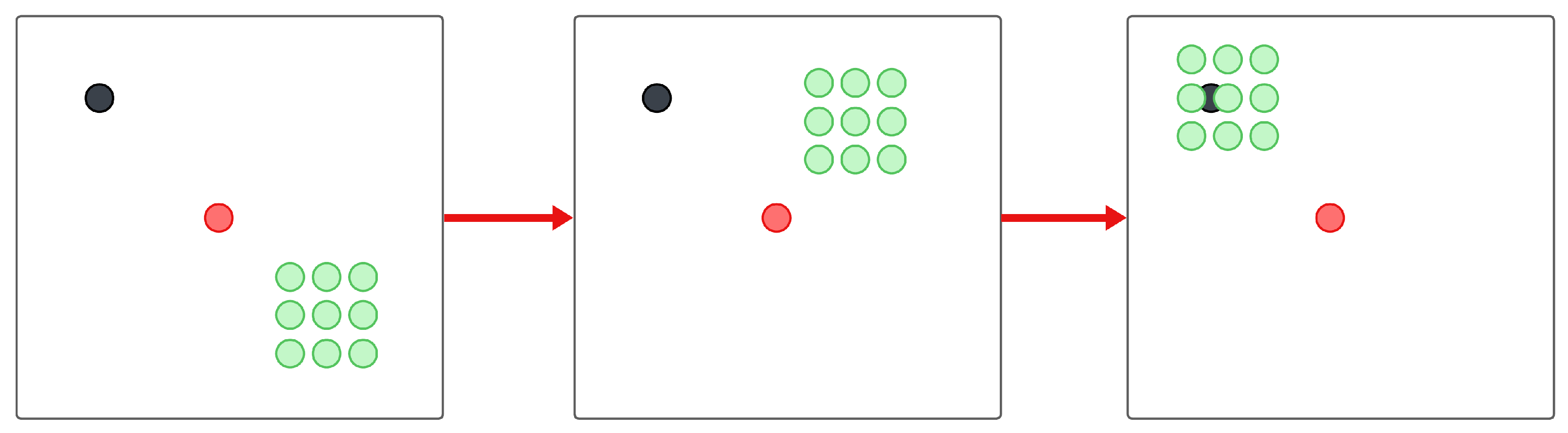
5.2. Experimental Setup
Reproducibility
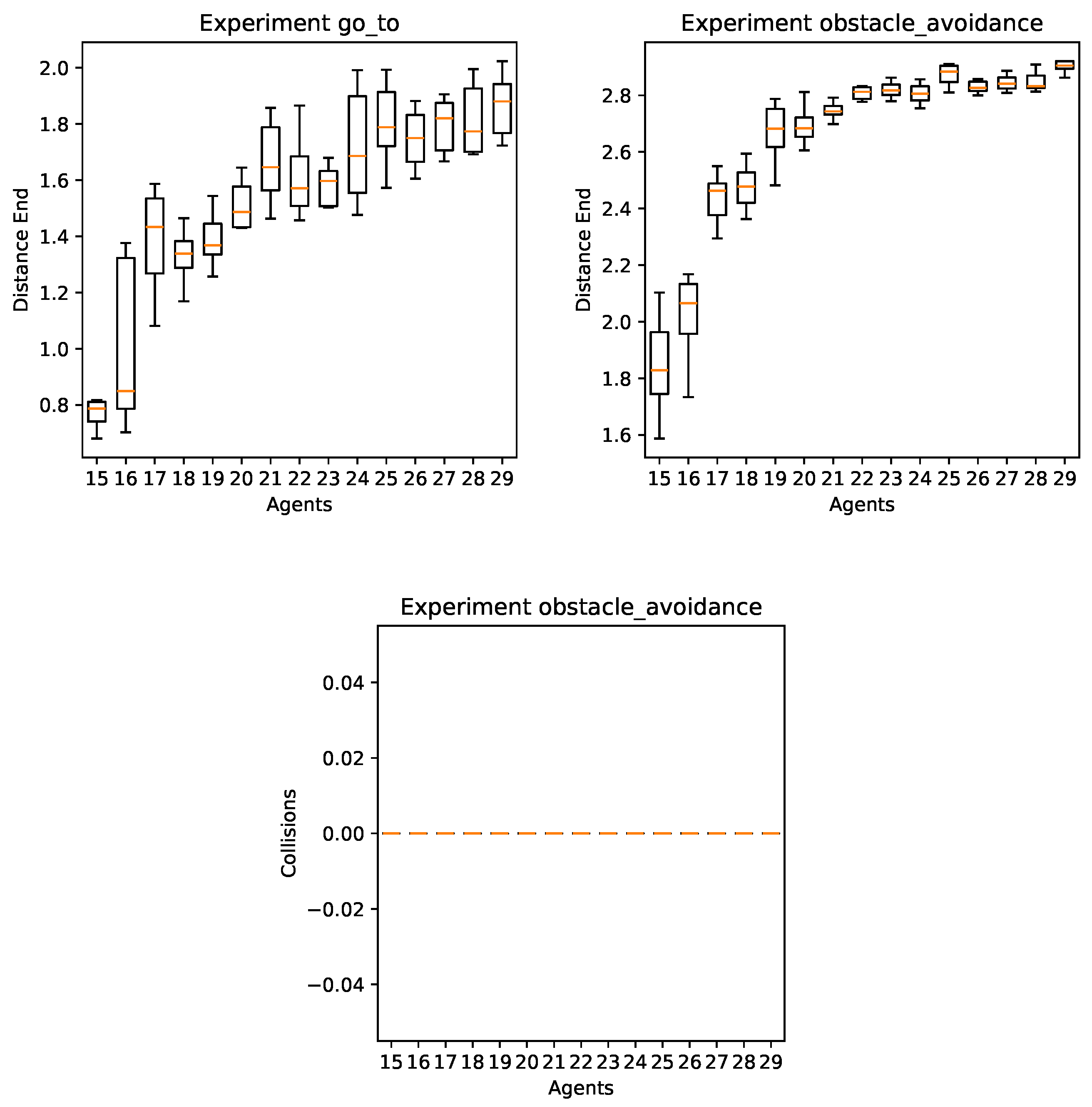
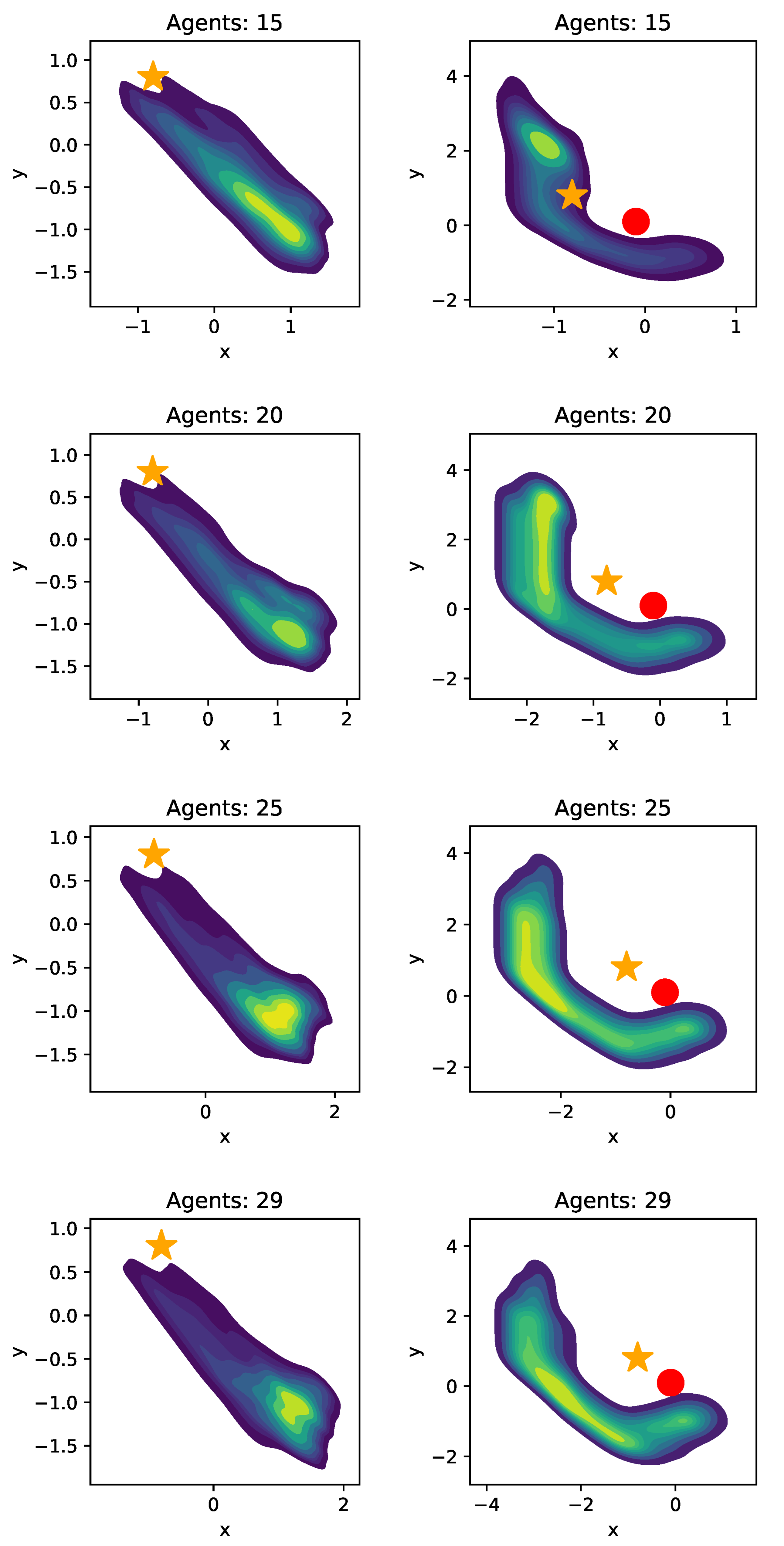
5.3. Results
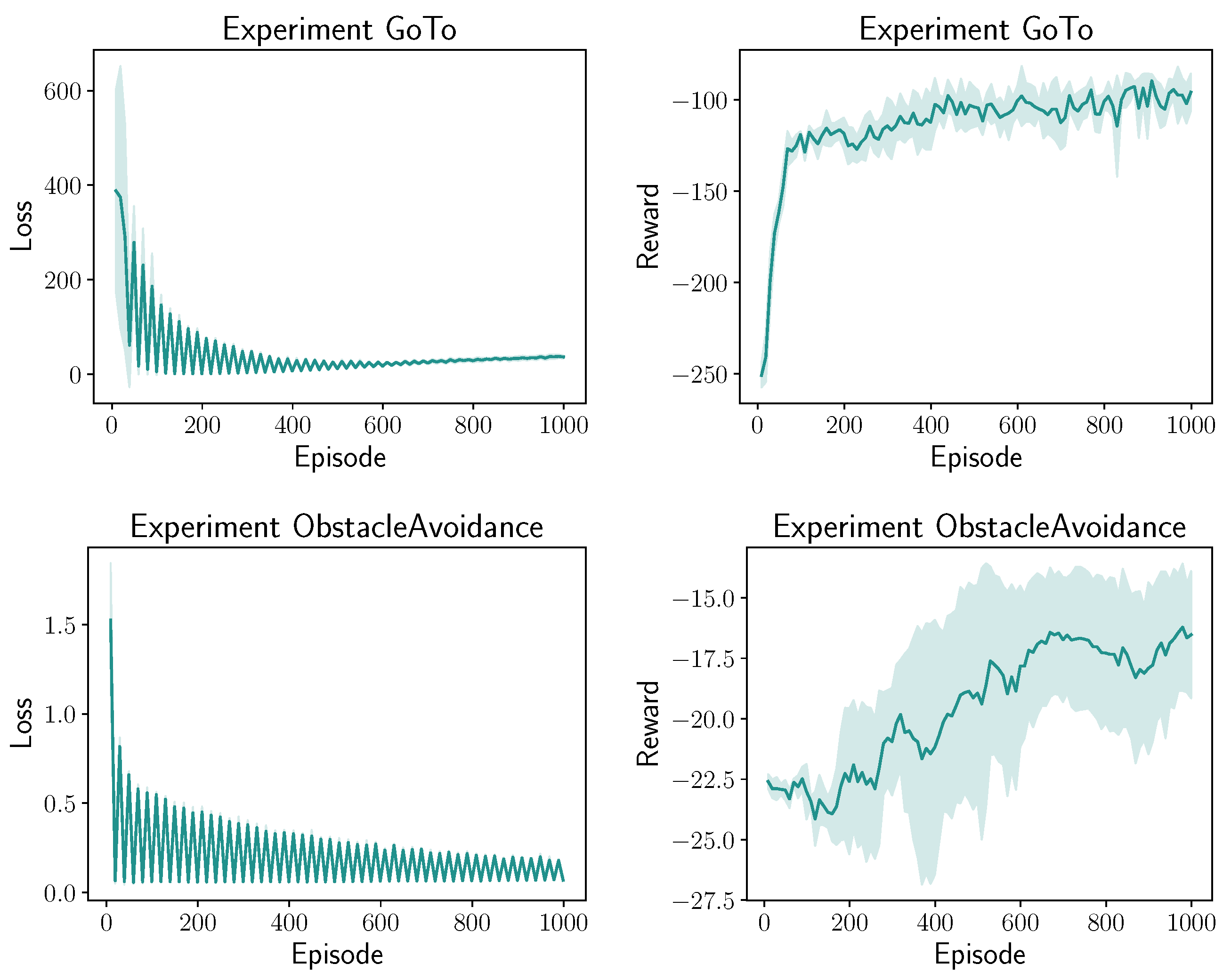
5.3.1. Training Results
5.3.2. Testing Results
6. Discussion
6.1. Final Remarks
6.2. Limitations and Threats to Validity
- Limited training diversity: We train on a single swarm size (ten agents), which may bias the learned coordination patterns toward this specific scale and limit generalization to significantly different sizes. However, this choice enables a controlled investigation of zero-shot scalability—training on diverse swarm sizes would conflate learning scalable representations with learning to handle size variation directly.
- Shallow GNN architecture: Our use of single-layer message passing () constrains the receptive field to immediate neighbors, potentially missing longer-range coordination dependencies critical for larger swarms. This limitation is deliberate and aligns with minimal local-rule models (e.g., Reynolds’ Boids [61]). The agents react only to 1-hop neighbors via a sparse kNN neighborhood in our case), letting coordination emerge as information propagates over time through motion rather than explicit multi-hop messaging. This choice reduces communication and computation, avoids oversmoothing, and supports real-time deployment.
- Simplified communication model: The k-nearest neighbor topology may not accurately reflect real-world communication constraints, such as limited bandwidth, interference, or range limitations in physical robot platforms. Nevertheless, the kNN model provides a reasonable approximation of proximity-based communication common in robotic swarms, and the parameter choice represents realistic communication fanout for resource-constrained devices.
- Task complexity: Our evaluation focuses on relatively simple 2D navigation tasks with basic dynamics. More complex scenarios involving heterogeneous objectives, dynamic environments, or 3D coordination may reveal different scalability patterns. We deliberately chose these canonical swarm coordination problems to establish baseline scalability behavior in well-understood scenarios before tackling more complex domains. The tasks capture fundamental swarm coordination challenges (collision avoidance, goal convergence, formation maintenance) that form building blocks for more sophisticated behaviors.
- Limited evaluation metrics: We primarily assess terminal distance to goal and collision counts, omitting other important factors such as energy consumption, communication overhead, convergence time, and trajectory efficiency that may be critical for real deployments. Our metric selection focuses on task completion quality—the most direct measure of coordination effectiveness—while additional metrics would be valuable for comprehensive deployment evaluation.
- Hyperparameter sensitivity: We did not perform an explicit sensitivity analysis on the hyperparameters of the proposed method. While this choice keeps the focus on scalability behavior, exploring how parameter variations affect performance represents an important direction for future work.
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schranz, M.; Umlauft, M.; Sende, M.; Elmenreich, W. Swarm Robotic Behaviors and Current Applications. Front. Robot. AI 2020, 7, 36. [Google Scholar] [CrossRef]
- Tahir, A.; Böling, J.M.; Haghbayan, M.H.; Toivonen, H.T.; Plosila, J. Swarms of Unmanned Aerial Vehicles—A Survey. J. Ind. Inf. Integr. 2019, 16, 100106. [Google Scholar] [CrossRef]
- Domini, D.; Farabegoli, N.; Aguzzi, G.; Viroli, M. Towards Intelligent Pulverized Systems: A Modern Approach for Edge-Cloud Services. In Proceedings of the 25th Workshop “From Objects to Agents”, Bard, Italy, 8–10 July 2024; Volume 3735, pp. 233–251. [Google Scholar]
- Orr, J.; Dutta, A. Multi-Agent Deep Reinforcement Learning for Multi-Robot Applications: A Survey. Sensors 2023, 23, 3625. [Google Scholar] [CrossRef]
- Sosic, A.; KhudaBukhsh, W.R.; Zoubir, A.M.; Koeppl, H. Inverse Reinforcement Learning in Swarm Systems. In Proceedings of the 16th Conference on Autonomous Agents and MultiAgent Systems, AAMAS 2017, São Paulo, Brazil, 8–12 May 2017; Larson, K., Winikoff, M., Das, S., Durfee, E.H., Eds.; ACM: New York, NY, USA, 2017; pp. 1413–1421. [Google Scholar]
- Domini, D.; Aguzzi, G.; Pianini, D.; Viroli, M. A Reusable Simulation Pipeline for Many-Agent Reinforcement Learning. In Proceedings of the 28th IEEE/ACM International Symposium on Distributed Simulation and Real Time Applications, DS-RT 2024, Urbino, Italy, 5–9 October 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Malucelli, N.; Domini, D.; Aguzzi, G.; Viroli, M. Neighbor-Based Decentralized Training Strategies for Multi-Agent Reinforcement Learning. In Proceedings of the 40th ACM/SIGAPP Symposium on Applied Computing, SAC 2025, Catania, Italy, 31 March–4 April 2025; ACM: New York, NY, USA, 2024; pp. 3–10. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, R.; Li, M.; Zhou, M.; Zhang, W.; Wang, J. Mean Field Multi-Agent Reinforcement Learning. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 5567–5576. [Google Scholar]
- Domini, D.; Cavallari, F.; Aguzzi, G.; Viroli, M. ScaRLib: Towards a hybrid toolchain for aggregate computing and many-agent reinforcement learning. Sci. Comput. Program. 2024, 238, 103176. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Aguzzi, G.; Viroli, M.; Esterle, L. Field-informed Reinforcement Learning of Collective Tasks with Graph Neural Networks. In Proceedings of the IEEE International Conference on Autonomic Computing and Self-Organizing Systems, ACSOS 2023, Toronto, ON, Canada, 25–29 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 37–46. [Google Scholar] [CrossRef]
- Busoniu, L.; Babuska, R.; De Schutter, B. A Comprehensive Survey of Multiagent Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 156–172. [Google Scholar] [CrossRef]
- Tan, M. Multi-agent reinforcement learning: Independent versus cooperative agents. In Proceedings of the Tenth International Conference on International Conference on Machine Learning, ICML’93, San Francisco, CA, USA, 27–29 July 1993; pp. 330–337. [Google Scholar]
- Wang, X.; Ke, L.; Zhang, G.; Zhu, D. Adaptive mean field multi-agent reinforcement learning. Inf. Sci. 2024, 669, 120560. [Google Scholar] [CrossRef]
- Mondal, W.U.; Agarwal, M.; Aggarwal, V.; Ukkusuri, S.V. On the approximation of cooperative heterogeneous multi-agent reinforcement learning (MARL) using Mean Field Control (MFC). J. Mach. Learn. Res. 2022, 23, 1–46. [Google Scholar]
- Li, C.; Wang, T.; Wu, C.; Zhao, Q.; Yang, J.; Zhang, C. Celebrating Diversity in Shared Multi-Agent Reinforcement Learning. In Proceedings of the Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021, Virtual, 6–14 December 2021; pp. 3991–4002. [Google Scholar]
- Nayak, S.; Choi, K.; Ding, W.; Dolan, S.; Gopalakrishnan, K.; Balakrishnan, H. Scalable Multi-Agent Reinforcement Learning through Intelligent Information Aggregation. In Proceedings of the International Conference on Machine Learning, ICML 2023, Honolulu, HI, USA, 23–29 July 2023; Volume 202, pp. 25817–25833. [Google Scholar]
- Lin, Y.; Wan, Z.; Yang, Z. HGAP: Boosting permutation invariant and permutation equivariant multi-agent reinforcement learning with graph attention. In Proceedings of the 41st International Conference on Machine Learning (ICML 2024). PMLR, Vienna, Austria, 21–27 July 2024; pp. 30615–30648. [Google Scholar]
- Mahjoub, O.; Abramowitz, S.; de Kock, R.; Khlifi, W.; du Toit, S.; Daniel, J.; Nessir, L.B.; Beyers, L.; Formanek, C.; Clark, L.; et al. Performant, Memory Efficient and Scalable Multi-Agent Reinforcement Learning. arXiv 2024, arXiv:2410.01706. [Google Scholar] [CrossRef]
- Jiang, J.; Dun, C.; Huang, T.; Lu, Z. Graph Convolutional Reinforcement Learning. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Khan, A.; Ribeiro, A.; Kumar, V.; Jadbabaie, A. Graph policy gradients for large scale robot control. In Proceedings of the Conference on Robot Learning (CoRL 2019), PMLR, Osaka, Japan, 30 October 30–1 November 2019; pp. 823–834. [Google Scholar]
- Zhou, M.; Liu, Z.; Sui, P.; Li, Y.; Chung, Y.Y. Learning implicit credit assignment for cooperative multi-agent reinforcement learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS 2020), Virtual, 6–12 December 2020; Volume 33, pp. 11853–11864. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-decomposition networks for cooperative multi-agent learning. arXiv 2017, arXiv:1706.05296. [Google Scholar]
- Rashid, T.; Samvelyan, M.; de Witt, C.S.; Farquhar, G.; Foerster, J.N.; Whiteson, S. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 4292–4301. [Google Scholar]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.; Yi, Y. QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 5887–5896. [Google Scholar]
- Wang, J.; Ren, Z.; Liu, T.; Yu, Y.; Zhang, C. QPLEX: Duplex Dueling Multi-Agent Q-Learning. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, 3–7 May 2021. [Google Scholar]
- Baisero, A.; Bhati, R.; Liu, S.; Pillai, A.; Amato, C. Fixing Incomplete Value Function Decomposition for Multi-Agent Reinforcement Learning. arXiv 2025. [Google Scholar] [CrossRef]
- Foerster, J.N.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual Multi-Agent Policy Gradients. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th Innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018; McIlraith, S.A., Weinberger, K.Q., Eds.; AAAI Press: Menlo Park, CA, USA, 2018; pp. 2974–2982. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Basar, T. Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. arXiv 2019, arXiv:1911.10635. [Google Scholar]
- Li, Y.; Wang, L.; Yang, J.; Wang, E.; Wang, Z.; Zhao, T.; Zha, H. Permutation Invariant Policy Optimization for Mean-Field Multi-Agent Reinforcement Learning: A Principled Approach. arXiv 2021, arXiv:2105.08268. [Google Scholar]
- Hao, J.; Hao, X.; Mao, H.; Wang, W.; Yang, Y.; Li, D.; Zheng, Y.; Wang, Z. Boosting Multiagent Reinforcement Learning via Permutation Invariant and Permutation Equivariant Networks. In Proceedings of the The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Amato, C. An Introduction to Centralized Training for Decentralized Execution in Cooperative Multi-Agent Reinforcement Learning. arXiv 2024, arXiv:2409.03052. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, S.; Qing, Y.; Chen, K.; Zheng, T.; Huang, Y.; Song, J.; Song, M. Is Centralized Training with Decentralized Execution Framework Centralized Enough for MARL? arXiv 2023, arXiv:2305.17352. [Google Scholar] [CrossRef]
- Sukhbaatar, S.; Szlam, A.; Fergus, R. Learning Multiagent Communication with Backpropagation. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016; pp. 2244–2252. [Google Scholar]
- Das, A.; Gervet, T.; Romoff, J.; Batra, D.; Parikh, D.; Rabbat, M.; Pineau, J. TarMAC: Targeted Multi-Agent Communication. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 1538–1546. [Google Scholar]
- Singh, A.; Jain, T.; Sukhbaatar, S. Learning when to Communicate at Scale in Multiagent Cooperative and Competitive Tasks. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Hu, D.; Zhang, C.; Prasanna, V.K.; Krishnamachari, B. Learning Practical Communication Strategies in Cooperative Multi-Agent Reinforcement Learning. In Proceedings of the Asian Conference on Machine Learning, ACML 2022, Hyderabad, India, 12–14 December 2022; Volume 189, pp. 467–482. [Google Scholar]
- Shao, J.; Zhang, H.; Qu, Y.; Liu, C.; He, S.; Jiang, Y.; Ji, X. Complementary Attention for Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Machine Learning, ICML 2023, Honolulu, HI, USA, 23–29 July 2023; Volume 202, pp. 30776–30793. [Google Scholar]
- Guo, X.; Shi, D.; Fan, W. Scalable Communication for Multi-Agent Reinforcement Learning via Transformer-Based Email Mechanism. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI 2023, Macao, SAR, China, 19–25 August 2023; pp. 126–134. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J.; Shi, E.; Liu, Z.; Niyato, D.; Ai, B.; Shen, X. Graph Neural Network Meets Multi-Agent Reinforcement Learning: Fundamentals, Applications, and Future Directions. Wireless Commun. 2024, 31, 39–47. [Google Scholar] [CrossRef]
- Du, H.; Gou, F.; Cai, Y. Scalable Safe Multi-Agent Reinforcement Learning for Multi-Agent System. arXiv 2025, arXiv:2501.13727. [Google Scholar] [CrossRef]
- Baldazo, D.; Parras, J.; Zazo, S. Decentralized Multi-Agent Deep Reinforcement Learning in Swarms of Drones for Flood Monitoring. In Proceedings of the 27th European Signal Processing Conference, EUSIPCO 2019, A Coruña, Spain, 2–6 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv 2017, arXiv:1712.01815. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Debiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Baker, B.; Chociej, M.; Józefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 2020, 39, 3–20. [Google Scholar] [CrossRef]
- OpenAI; Akkaya, I.; Andrychowicz, M.; Chociej, M.; Litwin, M.; McGrew, B.; Petron, A.; Paino, A.; Plappert, M.; Powell, G.; et al. Solving Rubik’s Cube with a Robot Hand. arXiv 2019, arXiv:1910.07113. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.A.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Chen, G. A New Framework for Multi-Agent Reinforcement Learning—Centralized Training and Exploration with Decentralized Execution via Policy Distillation. In Proceedings of the 19th International Conference on Autonomous Agents and Multiagent Systems, AAMAS ’20, Auckland, New Zealand, 9–13 May 2020; Seghrouchni, A.E.F., Sukthankar, G., An, B., Yorke-Smith, N., Eds.; International Foundation for Autonomous Agents and Multiagent Systems: Istanbul, Turkey, 2020; pp. 1801–1803. [Google Scholar]
- Azzam, R.; Boiko, I.; Zweiri, Y. Swarm Cooperative Navigation Using Centralized Training and Decentralized Execution. Drones 2023, 7, 193. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: A review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Bayindir, L. A review of swarm robotics tasks. Neurocomputing 2016, 172, 292–321. [Google Scholar] [CrossRef]
- Domini, D.; Cavallari, F.; Aguzzi, G.; Viroli, M. ScaRLib: A Framework for Cooperative Many Agent Deep Reinforcement Learning in Scala. In Proceedings of the Coordination Models and Languages—25th IFIP WG 6.1 International Conference, COORDINATION 2023, Held as Part of the 18th International Federated Conference on Distributed Computing Techniques, DisCoTec 2023, Lisbon, Portugal, 18–23 June 2023; Proceedings. Jongmans, S., Lopes, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; Volume 13908, pp. 52–70. [Google Scholar] [CrossRef]
- Bettini, M.; Kortvelesy, R.; Blumenkamp, J.; Prorok, A. VMAS: A Vectorized Multi-agent Simulator for Collective Robot Learning. In Proceedings of the Distributed Autonomous Robotic Systems—16th International Symposium, DARS 2022, Montbéliard, France, 28–30 November 2022; Bourgeois, J., Paik, J., Piranda, B., Werfel, J., Hauert, S., Pierson, A., Hamann, H., Lam, T.L., Matsuno, F., Mehr, N., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 28, pp. 42–56. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1987, Anaheim, CA, USA, 27–31 July 1987; Stone, M.C., Ed.; ACM: New York, NY, USA, 1987; pp. 25–34. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hamilton, W.L.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 1024–1034. [Google Scholar]
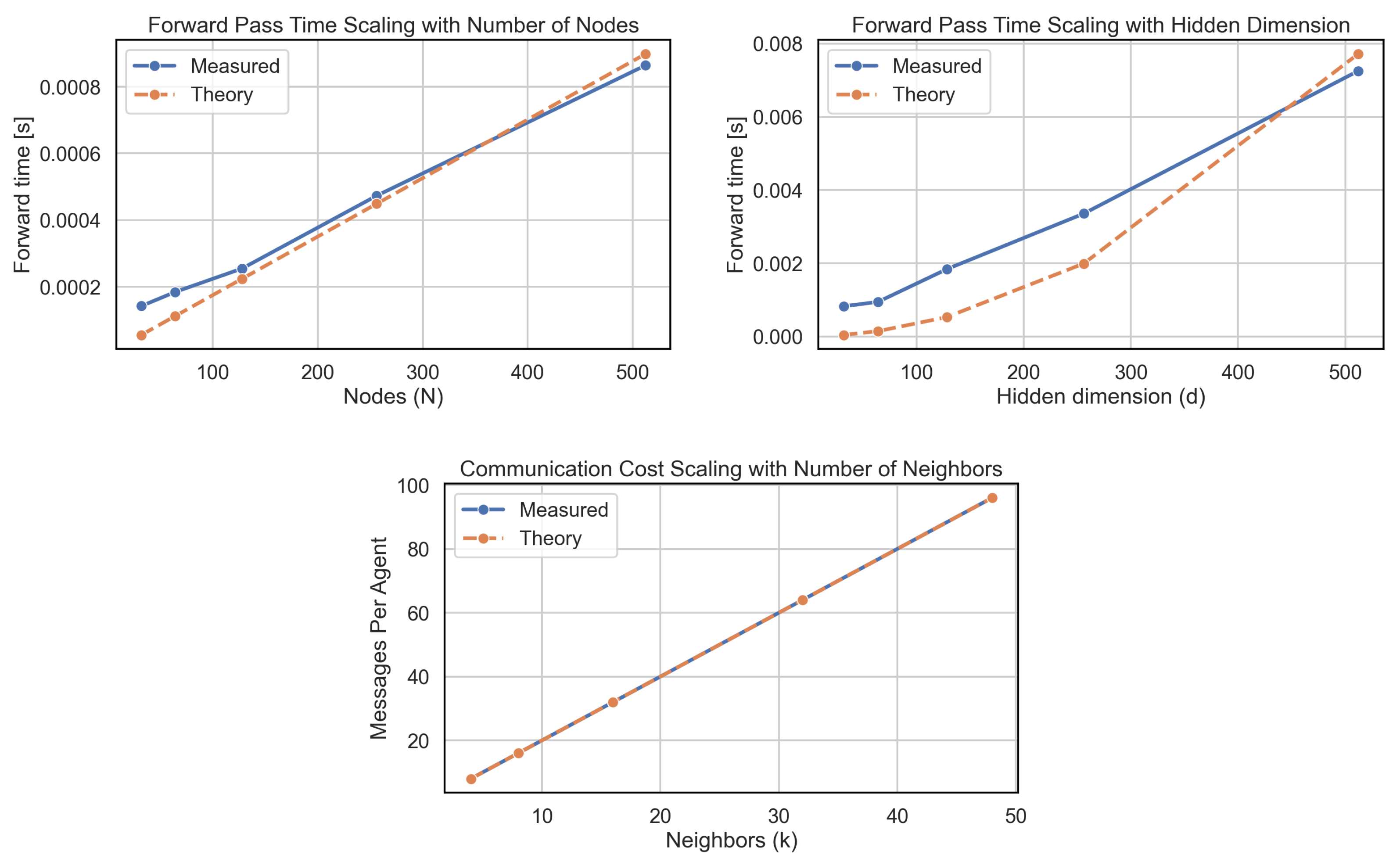
| Simulation Parameters | |
|---|---|
| Environment | |
| Environment size | m |
| Goal position (training) | |
| Initial agent region | near |
| Episode length (max) | 100 steps |
| Training episodes | 1000 |
| Agents (training) | 10 |
| Neighborhood | k-NN () |
| Position noise | |
| Obstacle center | |
| Obstacle radius | m |
| Action Space | 9 discrete translations |
| Model | |
| GNN layer (GAT) | 32 hidden units |
| Dropout | 0.1 |
| MLP head | 2 layers, 32 units |
| Training | |
| Optimizer | Adam () |
| Replay buffer | |
| Batch size | 32 |
| Discount | 0.99 |
| Target update | every 200 steps |
| Exploration | exp. decay |
| Decay rate | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguzzi, G.; Domini, D.; Venturini, F.; Viroli, M. Scaling Swarm Coordination with GNNs—How Far Can We Go? AI 2025, 6, 282. https://doi.org/10.3390/ai6110282
Aguzzi G, Domini D, Venturini F, Viroli M. Scaling Swarm Coordination with GNNs—How Far Can We Go? AI. 2025; 6(11):282. https://doi.org/10.3390/ai6110282
Chicago/Turabian StyleAguzzi, Gianluca, Davide Domini, Filippo Venturini, and Mirko Viroli. 2025. "Scaling Swarm Coordination with GNNs—How Far Can We Go?" AI 6, no. 11: 282. https://doi.org/10.3390/ai6110282
APA StyleAguzzi, G., Domini, D., Venturini, F., & Viroli, M. (2025). Scaling Swarm Coordination with GNNs—How Far Can We Go? AI, 6(11), 282. https://doi.org/10.3390/ai6110282












